Как решать примеры со скобками / Бери и делай
С порядком выполнения действий в математических примерах часто возникает путаница. Ситуация осложняется, когда появляются скобки, которые могут не просто разделять длинное выражение на отдельные части, но и менять порядок действий.
«Бери и Делай» собрал в одной статье все, о чем нужно помнить, когда вы решаете примеры со скобками.
Порядок выполнения действий в выражениях без скобок
Для решения простых примеров без скобок, вычисления корней и дробей достаточно запомнить правила:
- Все действия выполняются по порядку слева направо.
- Сначала выполняются действия умножения и деления, а затем — сложения и вычитания.
Как это применяется на практике?
Пример № 1. Вычислите: 15 − 3 + 7.
Сначала выполняем все действия по порядку слева направо:
1) 15 − 3 = 12
2) 12 + 7 = 19
Получаем ответ: 15 − 3 + 7 = 19.
Пример № 2. Вычислите: 10 ÷ 2 × 8.
Вычислите: 10 ÷ 2 × 8.
Здесь тоже выполняем все действия по порядку слева направо:
1) 10 ÷ 2 = 5
2) 5 × 8 = 40
Получаем ответ: 10 ÷ 2 × 8 = 40.
Пример № 3. Вычислите: 5 × 4 − 8 ÷ 2.
Здесь тоже двигаемся слева направо, но держим в уме правило о том, что умножение и деление необходимо выполнить в первую очередь. Поэтому действуем так:
1) 5 × 4 = 20. Это умножение, и оно стоит на первом месте, если двигаться слева направо.
2) 8 ÷ 2 = 4. Это деление, и у него есть приоритет перед действием вычитания, поэтому, несмотря на то, что оно находится правее, из-за приоритета мы выполняем его сразу после умножения.
3) 20 − 4 = 16. Здесь по порядку: выполнив умножение и деление, переходим к вычитанию.
Получаем ответ: 5 × 4 − 8 ÷ 2 = 16.
Если выражение состоит из нескольких действий или вы только учите их порядок, можно над знаками арифметических действий проставлять числа, подсказывающие порядок выполнения вычислений, как на картинке выше.
Важно: Скобки не нужно ставить, если действия сложения и вычитания выполняются в последовательности слева направо. К примеру, вместо (4 − 2) + 3 достаточно написать просто 4 − 2 + 3. Также нет необходимости добавлять скобки, чтобы выделить действия, которые и так имеют приоритет. К примеру, вместо 5 + (4 × 3) достаточно написать лишь 5 + 4 × 3, так как в этом случае действие умножения и без скобок имеет приоритет перед действием сложения.
Порядок выполнения действий в выражениях со скобками
Выражение может содержать скобки, задача которых — изменить привычный порядок выполнения математических действий. Чтобы не запутаться, запомните следующие правила:
- Сначала нужно выполнить действия в скобках.
- Затем все остальные по порядку, двигаясь слева направо.
- При этом сначала выполняются действия умножения и деления, а после — сложения и вычитания.
- Внутри скобок действует аналогичный порядок.
- Если в выражении есть дроби или степени, по возможности их следует вычислить до того, как вы перейдете к умножению и делению, а затем сложению и вычитанию.

Как это применяется на практике?
Пример № 1. Вычислите: 5 × (8 − 4) ÷ 2.
Следуя вышеуказанным правилам, сначала выполним действие в скобках, а затем по порядку все остальные. Тогда получается:
1) 8 − 4 = 4
Зная результат действия в скобках, в черновике для удобства мы можем записать выражение как 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Теперь по порядку выполним действия умножения и деления:
2) 5 × 4 = 20
3) 20 ÷ 2 = 10
Получаем, что 5 × (8 − 4) ÷ 2 = 10.
Ответ: 5 × (8 − 4) ÷ 2 = 10.
Пример № 2. Вычислите и сравните результаты: 7 − 3 + 2 и 7 − (3 + 2).
Вычислим результат первого выражения: 7 − 3 + 2 = 6. Теперь посчитаем результат второго выражения: 7 − (3 + 2) = 7 − 5 = 2. Наличие скобок во втором примере изменило порядок действий, поэтому результаты двух выражений различаются.
Пример № 3. Вычислите 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2).
На первый взгляд, это выражение кажется сложным. Чтобы упростить процесс вычисления, разложите его на отдельные действия по порядку:
Чтобы упростить процесс вычисления, разложите его на отдельные действия по порядку:
1) Сначала выполните действия в скобках. Чтобы получить результат выражения в первых скобках, нужно вспомнить о том, какие действия имеют приоритет. Таким образом, сначала вычисляем 4 × 3, затем результат вычитаем из числа 15. Получаем в ответе 3. Проделайте то же самое со вторыми скобками: вычислите 3 × 2 и к результату прибавьте 7. В ответе получаете 13.
2) Зная результаты вычислений в скобках, в черновике вы можете упростить выражение до вида: 8 − 2 × 3 + 13. Теперь нужно выполнить умножение, а затем по порядку вычитание и сложение: 8 − 6 + 13 = 2 +13 = 15. Получаем ответ: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15.
Важно: Можно встретить выражения, где в одних скобках содержатся другие скобки. В этом случае действия аналогичные: сначала надо вычислить результат выражения во внутренних скобках, затем работать с внешними и в конце перейти к тому, что находится вне скобок. Кроме того, вид скобок может различаться: чаще всего это ( ), но допускается также использование { } и [ ].
Кроме того, вид скобок может различаться: чаще всего это ( ), но допускается также использование { } и [ ].
Распространенные ошибки, из-за которых большинство неверно решают примеры со скобками
- Знак умножения опускается перед скобкой, из-за чего можно перепутать порядок действий
К примеру, нужно вычислить, чему равно выражение 8 + 4(3 − 1). Решая этот пример, можно по ошибке сначала посчитать результат вычитания в скобках, затем результат сложения, после чего перемножить полученные числа. Правильный порядок иной: сначала получаем результат вычитания в скобках, затем умножаем его на 4, после чего прибавляем полученное число к 8. Получается следующее: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16.
Чуть сложнее может выглядеть вот такое выражение: 8 ÷ 4(3 − 1). Здесь алгоритм действий аналогичный. Сначала выполняем действия в скобках, затем по порядку слева направо нужно выполнить деление и умножение: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.
- Неправильно раскрыты скобки, перед которыми стоял минус
Бывают ситуации, когда скобки надо раскрыть, чтобы упростить выражение. В таком случае, если перед скобкой стоит минус, то при раскрытии скобки вместе с минусом опускаются, а знаки всех слагаемых, которые были внутри скобок, заменяются на противоположные, как если бы вы каждое число умножили на −1. К примеру, выражение 6 + 5 − (4 + 3 − 2) при раскрытии скобок превращается в 6 + 5 − 4 − 3 + 2. Чаще всего ошибки допускаются в выражениях, где есть переменные и много действий, к примеру: 3 + 2(x + 1) − 2(x − 1). Не зная значение переменной, мы не можем посчитать результат выражения в скобках, поэтому необходимо избавиться от скобок и упростить выражение до вида 3 + 2х + 2 − 2х + 2 = 7. Если скобки раскрыть неправильно, то можно получить 3 + 2х + 2 − 2х — 2 = 3.
- Вычисления производятся на калькуляторе
Далеко не все калькуляторы способны выполнить действия в правильном порядке, хотя есть модели, которые запрограммированы отделять простые операции от сложных вычислений в рамках одного выражения. Как проверить свой калькулятор? Попробуйте найти результат выражения 1 + 5 × 7. Если в ответе получилось 36, значит, калькулятор может решать сложные примеры, выполняя действия в правильном порядке.
Как проверить свой калькулятор? Попробуйте найти результат выражения 1 + 5 × 7. Если в ответе получилось 36, значит, калькулятор может решать сложные примеры, выполняя действия в правильном порядке.
Как решать примеры со скобками
С порядком выполнения действий в математических примерах часто возникает путаница. Ситуация осложняется, когда появляются скобки, которые могут не просто разделять длинное выражение на отдельные части, но и менять порядок действий.
«Бери и Делай» собрал в одной статье все, о чем нужно помнить, когда вы решаете примеры со скобками.
Порядок выполнения действий в выражениях без скобок
Для решения простых примеров без скобок, вычисления корней и дробей достаточно запомнить правила:
- Все действия выполняются по порядку слева направо.
- Сначала выполняются действия умножения и деления, а затем — сложения и вычитания.
Как это применяется на практике? Пример № 1. Вычислите: 15 − 3 + 7. Сначала выполняем все действия по порядку слева направо: 1) 15 − 3 = 12 2) 12 + 7 = 19 Получаем ответ: 15 − 3 + 7 = 19. Пример № 2. Вычислите: 10 ÷ 2 × 8. Здесь тоже выполняем все действия по порядку слева направо: 1) 10 ÷ 2 = 5 2) 5 × 8 = 40 Получаем ответ: 10 ÷ 2 × 8 = 40. Пример № 3. Вычислите: 5 × 4 − 8 ÷ 2. Здесь тоже двигаемся слева направо, но держим в уме правило о том, что умножение и деление необходимо выполнить в первую очередь. Поэтому действуем так: 1) 5 × 4 = 20. Это умножение, и оно стоит на первом месте, если двигаться слева направо. 2) 8 ÷ 2 = 4. Это деление, и у него есть приоритет перед действием вычитания, поэтому, несмотря на то, что оно находится правее, из-за приоритета мы выполняем его сразу после умножения. 3) 20 − 4 = 16. Здесь по порядку: выполнив умножение и деление, переходим к вычитанию. Получаем ответ: 5 × 4 − 8 ÷ 2 = 16.
Пример № 2. Вычислите: 10 ÷ 2 × 8. Здесь тоже выполняем все действия по порядку слева направо: 1) 10 ÷ 2 = 5 2) 5 × 8 = 40 Получаем ответ: 10 ÷ 2 × 8 = 40. Пример № 3. Вычислите: 5 × 4 − 8 ÷ 2. Здесь тоже двигаемся слева направо, но держим в уме правило о том, что умножение и деление необходимо выполнить в первую очередь. Поэтому действуем так: 1) 5 × 4 = 20. Это умножение, и оно стоит на первом месте, если двигаться слева направо. 2) 8 ÷ 2 = 4. Это деление, и у него есть приоритет перед действием вычитания, поэтому, несмотря на то, что оно находится правее, из-за приоритета мы выполняем его сразу после умножения. 3) 20 − 4 = 16. Здесь по порядку: выполнив умножение и деление, переходим к вычитанию. Получаем ответ: 5 × 4 − 8 ÷ 2 = 16.
Если выражение состоит из нескольких действий или вы только учите их порядок, можно над знаками арифметических действий проставлять числа, подсказывающие порядок выполнения вычислений, как на картинке выше. Важно: Скобки не нужно ставить, если действия сложения и вычитания выполняются в последовательности слева направо. К примеру, вместо (4 − 2) + 3 достаточно написать просто 4 − 2 + 3. Также нет необходимости добавлять скобки, чтобы выделить действия, которые и так имеют приоритет. К примеру, вместо 5 + (4 × 3) достаточно написать лишь 5 + 4 × 3, так как в этом случае действие умножения и без скобок имеет приоритет перед действием сложения.
К примеру, вместо (4 − 2) + 3 достаточно написать просто 4 − 2 + 3. Также нет необходимости добавлять скобки, чтобы выделить действия, которые и так имеют приоритет. К примеру, вместо 5 + (4 × 3) достаточно написать лишь 5 + 4 × 3, так как в этом случае действие умножения и без скобок имеет приоритет перед действием сложения.
Порядок выполнения действий в выражениях со скобками
Выражение может содержать скобки, задача которых — изменить привычный порядок выполнения математических действий. Чтобы не запутаться, запомните следующие правила:
- Сначала нужно выполнить действия в скобках.
- Затем все остальные по порядку, двигаясь слева направо.
- При этом сначала выполняются действия умножения и деления, а после — сложения и вычитания.
- Внутри скобок действует аналогичный порядок.
- Если в выражении есть дроби или степени, по возможности их следует вычислить до того, как вы перейдете к умножению и делению, а затем сложению и вычитанию.
Как это применяется на практике? Пример № 1. Вычислите: 5 × (8 − 4) ÷ 2. Следуя вышеуказанным правилам, сначала выполним действие в скобках, а затем по порядку все остальные. Тогда получается: 1) 8 − 4 = 4 Зная результат действия в скобках, в черновике для удобства мы можем записать выражение как 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Теперь по порядку выполним действия умножения и деления: 2) 5 × 4 = 20 3) 20 ÷ 2 = 10 Получаем, что 5 × (8 − 4) ÷ 2 = 10. Ответ: 5 × (8 − 4) ÷ 2 = 10. Пример № 2. Вычислите и сравните результаты: 7 − 3 + 2 и 7 − (3 + 2). Вычислим результат первого выражения: 7 − 3 + 2 = 6. Теперь посчитаем результат второго выражения: 7 − (3 + 2) = 7 − 5 = 2. Наличие скобок во втором примере изменило порядок действий, поэтому результаты двух выражений различаются.
Вычислите: 5 × (8 − 4) ÷ 2. Следуя вышеуказанным правилам, сначала выполним действие в скобках, а затем по порядку все остальные. Тогда получается: 1) 8 − 4 = 4 Зная результат действия в скобках, в черновике для удобства мы можем записать выражение как 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Теперь по порядку выполним действия умножения и деления: 2) 5 × 4 = 20 3) 20 ÷ 2 = 10 Получаем, что 5 × (8 − 4) ÷ 2 = 10. Ответ: 5 × (8 − 4) ÷ 2 = 10. Пример № 2. Вычислите и сравните результаты: 7 − 3 + 2 и 7 − (3 + 2). Вычислим результат первого выражения: 7 − 3 + 2 = 6. Теперь посчитаем результат второго выражения: 7 − (3 + 2) = 7 − 5 = 2. Наличие скобок во втором примере изменило порядок действий, поэтому результаты двух выражений различаются.
Пример № 3. Вычислите 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2). На первый взгляд, это выражение кажется сложным. Чтобы упростить процесс вычисления, разложите его на отдельные действия по порядку: 1) Сначала выполните действия в скобках. Чтобы получить результат выражения в первых скобках, нужно вспомнить о том, какие действия имеют приоритет. Таким образом, сначала вычисляем 4 × 3, затем результат вычитаем из числа 15. Получаем в ответе 3. Проделайте то же самое со вторыми скобками: вычислите 3 × 2 и к результату прибавьте 7. В ответе получаете 13. 2) Зная результаты вычислений в скобках, в черновике вы можете упростить выражение до вида: 8 − 2 × 3 + 13. Теперь нужно выполнить умножение, а затем по порядку вычитание и сложение: 8 − 6 + 13 = 2 +13 = 15. Получаем ответ: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15. Важно: Можно встретить выражения, где в одних скобках содержатся другие скобки. В этом случае действия аналогичные: сначала надо вычислить результат выражения во внутренних скобках, затем работать с внешними и в конце перейти к тому, что находится вне скобок. Кроме того, вид скобок может различаться: чаще всего это ( ), но допускается также использование { } и [ ].
Таким образом, сначала вычисляем 4 × 3, затем результат вычитаем из числа 15. Получаем в ответе 3. Проделайте то же самое со вторыми скобками: вычислите 3 × 2 и к результату прибавьте 7. В ответе получаете 13. 2) Зная результаты вычислений в скобках, в черновике вы можете упростить выражение до вида: 8 − 2 × 3 + 13. Теперь нужно выполнить умножение, а затем по порядку вычитание и сложение: 8 − 6 + 13 = 2 +13 = 15. Получаем ответ: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15. Важно: Можно встретить выражения, где в одних скобках содержатся другие скобки. В этом случае действия аналогичные: сначала надо вычислить результат выражения во внутренних скобках, затем работать с внешними и в конце перейти к тому, что находится вне скобок. Кроме того, вид скобок может различаться: чаще всего это ( ), но допускается также использование { } и [ ].
Распространенные ошибки, из-за которых большинство неверно решают примеры со скобками
- Знак умножения опускается перед скобкой, из-за чего можно перепутать порядок действий
К примеру, нужно вычислить, чему равно выражение 8 + 4(3 − 1). Решая этот пример, можно по ошибке сначала посчитать результат вычитания в скобках, затем результат сложения, после чего перемножить полученные числа. Правильный порядок иной: сначала получаем результат вычитания в скобках, затем умножаем его на 4, после чего прибавляем полученное число к 8. Получается следующее: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16. Чуть сложнее может выглядеть вот такое выражение: 8 ÷ 4(3 − 1). Здесь алгоритм действий аналогичный. Сначала выполняем действия в скобках, затем по порядку слева направо нужно выполнить деление и умножение: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.
Решая этот пример, можно по ошибке сначала посчитать результат вычитания в скобках, затем результат сложения, после чего перемножить полученные числа. Правильный порядок иной: сначала получаем результат вычитания в скобках, затем умножаем его на 4, после чего прибавляем полученное число к 8. Получается следующее: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16. Чуть сложнее может выглядеть вот такое выражение: 8 ÷ 4(3 − 1). Здесь алгоритм действий аналогичный. Сначала выполняем действия в скобках, затем по порядку слева направо нужно выполнить деление и умножение: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.
- Неправильно раскрыты скобки, перед которыми стоял минус
Бывают ситуации, когда скобки надо раскрыть, чтобы упростить выражение. В таком случае, если перед скобкой стоит минус, то при раскрытии скобки вместе с минусом опускаются, а знаки всех слагаемых, которые были внутри скобок, заменяются на противоположные, как если бы вы каждое число умножили на −1. К примеру, выражение 6 + 5 − (4 + 3 − 2) при раскрытии скобок превращается в 6 + 5 − 4 − 3 + 2. Чаще всего ошибки допускаются в выражениях, где есть переменные и много действий, к примеру: 3 + 2(x + 1) − 2(x − 1). Не зная значение переменной, мы не можем посчитать результат выражения в скобках, поэтому необходимо избавиться от скобок и упростить выражение до вида 3 + 2х + 2 − 2х + 2 = 7. Если скобки раскрыть неправильно, то можно получить 3 + 2х + 2 − 2х — 2 = 3.
Чаще всего ошибки допускаются в выражениях, где есть переменные и много действий, к примеру: 3 + 2(x + 1) − 2(x − 1). Не зная значение переменной, мы не можем посчитать результат выражения в скобках, поэтому необходимо избавиться от скобок и упростить выражение до вида 3 + 2х + 2 − 2х + 2 = 7. Если скобки раскрыть неправильно, то можно получить 3 + 2х + 2 − 2х — 2 = 3.
- Вычисления производятся на калькуляторе
Далеко не все калькуляторы способны выполнить действия в правильном порядке, хотя есть модели, которые запрограммированы отделять простые операции от сложных вычислений в рамках одного выражения. Как проверить свой калькулятор? Попробуйте найти результат выражения 1 + 5 × 7. Если в ответе получилось 36, значит, калькулятор может решать сложные примеры, выполняя действия в правильном порядке.
Правила умножения сложения без скобок. Урок «порядок выполнения действий»
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2
. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6
. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3)
. Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5
. Подставив найденное значение, получаем 3+1+4·5
. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции.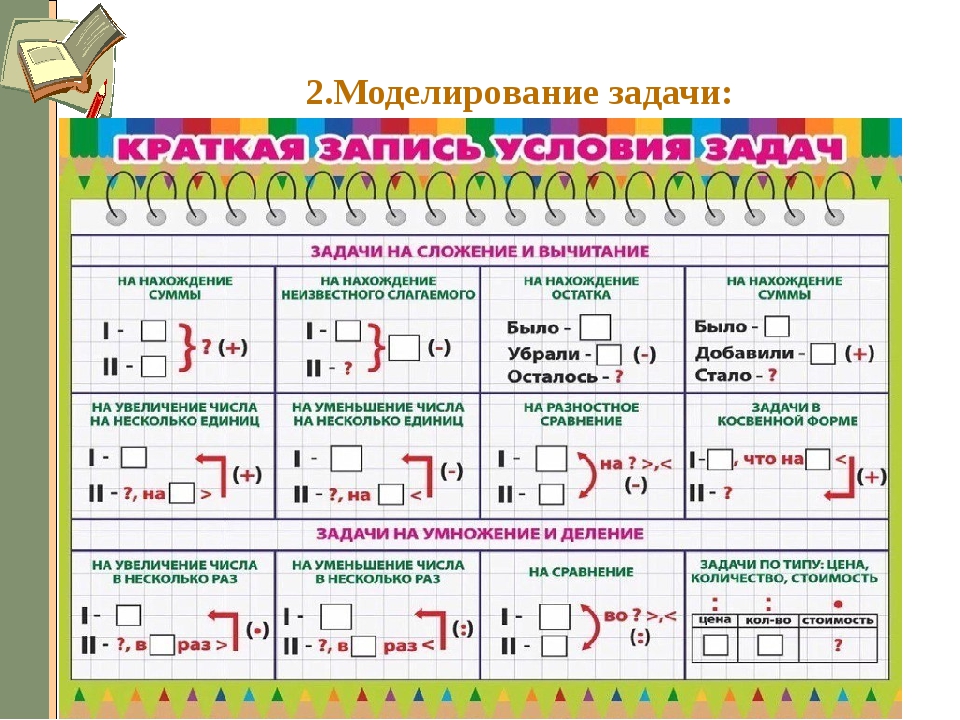
В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.
Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом.
Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.
Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок. В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.
В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.
Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.
Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.
Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.
В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.
Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.
Тема урока: « Порядок выполнения действий в выражениях без скобок и со скобками».
Цель урока : создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока.
Образовательные:
Закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
Развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,
коммуникативные навыки;
Воспитательные:
Воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
работать по предложенному плану, инструкции;
выдвигать свои гипотезы на основе учебного материала;
осуществлять самоконтроль.
Познавательные УУД:
знать правила порядка выполнения действий:
уметь разъяснить их содержание;
понимать правило порядка выполнения действий;
находить значения выражений согласно правилам порядка выполнения;
действий, используя для этого текстовые задачи;
записывать решение задачи выражением;
применять правила порядка выполнения действий;
уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
слушать и понимать речь других;
выражать свои мысли с достаточной полнотой и точностью;
допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
устанавливать связь между целью деятельности и её результатом;
определять общие для всех правила поведения;
выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
Знать правила порядка выполнения действий.
Уметь разъяснить их содержание.
Уметь решать задачи с помощью выражений.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД ).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД ).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД ).
Ход урока
1. Организационный момент.
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
И друг другу улыбнитесь.
Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
Устный счёт.
Игра «Найди правильный ответ».
(У каждого ученика лист с числами)
Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
Соедините полученные результаты.
Какую геометрическую фигуру вы получили? (Треугольник)
Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
Продолжаем работать по карточке.
Найдите разность чисел 100 и 22. (78)
Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
Сколько треугольников получилось? (5)
3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
4. Закрепление Выполнение тренировочных заданий на изученное правило
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
5. Подведение итогов.
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.
Составление выражения со скобками
1. Составь из следующих предложений выражения со скобками и реши их.
Из числа 16 вычти сумму чисел 8 и 6.
Из числа 34 вычти сумму чисел 5 и 8.
Сумму чисел 13 и 5 вычесть из числа 39.
Разность чисел 16 и 3 прибавь к числу 36
Разность чисел 48 и 28 прибавь к числу 16.
2. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
2.1. Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78?
2.2. Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?
3. Реши примеры правильно выполняя последовательность действий:
45: 5 + 12 * 2 -21:3
56 — 72: 9 + 48: 6 * 3
7 + 5 * 4 — 12: 4
18: 3 — 5 + 6 * 8
Решение выражений со скобками
1. Реши примеры правильно раскрывая скобки:
1 + (4 + 8) = | 8 — (2 + 4) = | 3 + (6 — 5) = | 59 + 25 = |
82 + 14 = | 29 + 52 = | 18 + 47 = | 39 + 53 = |
37 + 53 = | 25 + 63 = | 87 + 17 = | 19 + 52 = |
2. Реши примеры правильно выполняя последовательность действий:
Реши примеры правильно выполняя последовательность действий:
2.1. 36: 3 + 12 * (2 — 1) : 3
2.2. 39 — (81: 9 + 48: 6) * 2
2.3. (7 + 5) * 2 — 48: 4
2.4. 18: 3 + (5 * 6) : 2 — 4
3. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше. Сколько упаковок порошка стало на складе?
3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?
3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?
ФИ _________________________________
21: 3 * 6 — (18 + 14) : 8 = | 63: (81: 9) + (8 * 7 — 2) : 6 = | 64:2: 4+ 9*7-9*1= |
37 *2 + 180: 9 – 36: 12 = | 52 * 10 – 60: 15 * 1 = | 72: 4 +58:2= |
5 *0: 25 + (72: 1 – 0) : 9 = | 21: (3 * 7) – (7* 0 + 1)*1 = | 6:6+0:8-8:8= |
91: 7 + 80: 5 – 5: 5 = | 64:4 — 3*5 +80:2= | (19*5 – 5) : 30 = |
19 + 17 * 3 – 46 = | (39+29) : 4 + 8*0= | (60-5) : 5 +80: 5= |
54 – 26 + 38: 2 = | 63: (7*3) *3= | (160-70) : 18 *1= |
200 – 80: 5 + 3 * 4 = | (29+25): (72:8)= | 72:25 + 3* 17= |
80: 16 + 660: 6 = | 3 * 290 – 800= | 950:50*1-0= |
(48: 3) : 16 * 0 = | 90-6*6+29= | 5* (48-43) +15:5*7= |
54: 9 *8 — 14: 7 * 4 = | 63: 7*4+70:7 * 5= | 24: 6*7 — 7*0= |
21: 7 * 8 + 32: 8 * 4 = | 27: 3* 5 + 26-18 *4= | 54: 6*7 — 0:1= |
45: 9 * 6 + 7 * 5 – 26 = | 28: 7 *9 + 6 * (54 – 47)= | 6*(9: 3) — 40:5 = |
21 * 1 — 56: 7 – 8 = | 9 * (64: 8) — 18:18 | 3 *(14: 2) — 63:9= |
4 * 8 + 42: 6 *5 = | 0*4+0:5 +8* (48: 8)= | 56:7 +7*6 — 5*1= |
31 * 3 — 17 – 80: 16 * 1 = | 57:19 *32 — 11 *7= | 72-96:8 +60:15 *13= |
36 + 42: 3 + 23 + 27 *0 = | 56:14 *19 — 72:18= | (86-78:13)* 4= |
650 – 50 * 4 + 900: 100 = | 630: 9 + 120 * 5 + 40= | 980 – (160 + 20) : 30= |
940 — (1680 – 1600) * 9 = | 29* 2+26 – 37:2= | 72:3 +280: (14*5)= |
300: (5 *60) * (78: 13) = | 63+ 100: 4 – 8*0= | 84:7+70:14 – 6:6= |
45: 15 – 180: 90 + 84: 7 = | 32+51 + 48:6 * 5= | 54:6 ?2 – 70:14= |
38: 2 – 48: 3 + 0 * 9 = | 30:6 * 8 – 6+3*2= | (95:19) *(68:2)= |
(300 — 8 * 7) * 10 = | 1:1 — 0*0 + 1*0 — 1*1= | (80: 4 – 60:30) *5 = |
2 * (120: 6 – 80: 20) = | 56:4+96:3- 0*7= | 20+ 20: 4 — 1*5= |
(18 + 14) : 8 – (7 *0 + 1) *1 = | (8*7-2):6 +63: (7*3)= | (50-5) : 5+21: (3*7)= |
19 + 17 * 3 – 60: 15 * 1 = | 80: 5 +3*5 +80:2= | 54: 9 *8-64:4 +16*0= |
72 * 10 — 64: 2: 4 = | 84 – 36 + 38:2 | 91:13+80:5 – 5:5 |
300 – 80: 5 + 6 * 4 = | 950:190 *1+14: 7*4= | (39+29) : 17 + 8*0= |
(120 — 30) : 18 * 1- 72: 25 = | 210:30*60-0:1= | 90-6*7+3* 17= |
240: 60 *7 – 7 * 0 = | 60:60+0:80-80:80= | 720: 40 +580:20= |
9 *7 – 9 *1 + 5 * 0: 25 = | 21: 7 * 6 +32: 4 *5= | 80:16 +66:6 -63:(81:9)= |
(19 * 5 – 5) : 30 + 70: 7 = | 15:5*7 + 63: 7 * 5= | 54: 6 * 7 — (72:1-0):9= |
3 *290 – 600 – 5 * (48 – 43) = | (300-89*7)*10 — 3?2= | (80: 4) +30*2+ 180: 9= |
30: 6 * 8 – 6 + 48: 3 + 0 *9 = | (95:19) *(68:34) — 60:30*5= | 27: 3*5 — 48:3= |
3* 290 – 800 + 950: 50 = | 80:16 +660:6*1-0= | 90-6*6+ 15:5*7= |
5*(48 — 43) + (48: 3) :16*0= | 280: (14*5) +630: 9*0= | 300: (50*6)* (78: 6)= |
Если в примерах встретится вопросительный знак (?), следует его заменить на знак * — умножение.
1. РЕШИ ВЫРАЖЕНИЯ:
35: 5 + 36: 4 — 3
26 + 6 х 8 – 45: 5 24: 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27:3
2. РЕШИ ВЫРАЖЕНИЯ:
48: 8 + 32 – 54: 6 + 7 х 4
17 + 24: 3 х 4 – 27: 3 х 2 6 х 4: 3 + 54: 6: 3 х 6 + 2 х 9
100 – 6 х 2: 3 х 9 – 39 + 7 х 4
3. РЕШИ ВЫРАЖЕНИЯ:
100 – 27: 3 х 6 + 7 х 4
2 х 4 + 24: 3 + 18: 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35: 7 х 5 – 16: 2: 4 х 3
4. РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 6: 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 — 11 24: 6 + 18: 2 + 20 – 12 + 6 х 7
21: 3 – 35: 7 + 9 х 3 + 9 х 5
5. РЕШИ ВЫРАЖЕНИЯ:
42: 7 х 3 + 2 + 24: 3 – 7 + 9 х 3
6 х 6 + 30: 5: 2 х 7 — 19 90 — 7 х 5 – 24: 3 х 5
6 х 5 – 12: 2 х 3 + 49
6. РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 7 + 54: 6: 3 х 5
50 – 45: 5 х 3 + 16: 2 х 5 8 х 6 + 23 – 24: 4 х 3 + 17
48: 6 х 4 + 6 х 9 – 26 + 13
7. РЕШИ ВЫРАЖЕНИЯ:
42: 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18: 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:
РЕШИ ВЫРАЖЕНИЯ:
90 – (40 – 24: 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – (27 + 9) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + (26 + 16) : 6
(5 х 6 – 3 х 4 + 48: 6) +(82 – 78) х 7 – 13
54: 9 + (8 + 19) : 3 – 32: 4 – 21: 7 + (42 – 14) : 4 – (44 14) : 5
9. РЕШИ ВЫРАЖЕНИЯ:
9 х 6 – 6 х 4: (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48: 8 х 3 + 7 х 6 — 34
10. РЕШИ ВЫРАЖЕНИЯ:
(8 х 6 – 36: 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54: 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6:2
11. РЕШИ ВЫРАЖЕНИЯ:
(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28: 4 + 27: 3 – (17 + 31) : 6
12. РЕШИ ВЫРАЖЕНИЯ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56: 7) – (2 х 6 – 4) х 3 + 54: 9
13. РЕШИ ВЫРАЖЕНИЯ:
(8 х 5 + 28: 7) + 12: 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14: 7) + (7 х 4 + 12: 6) – 10: 5 + 63: 9
Тест «Порядок арифметических действий» (1 вариант)
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
110 – (60 +40) :10 х 8
а) 800 б) 8 в) 30
а) 3 4 6 5 2 1 4 5 6 3 2 1
3 4 6 5 1 2
5. В каком из выражений последнее действие умножение?
В каком из выражений последнее действие умножение?
а) 1001:13 х (318 +466) :22
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025:5 – (524 – 24:6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
Выбери верный ответ:
9. 90 – (50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 — 4х4) х2
а) 100 б) 200 в) 60
11. (10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150: (80 – 60:2) х 3
а) 9 б) 45 в) 1
Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4. Выбери верный вариант расстановки действий:
Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320: 8 х 7 + 9 х (240 – 60:15) в) 320:8 х 7+9х(240 – 60:15)
3 4 6 5 2 1
б) 320: 8 х 7 + 9 х (240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001:13 х (318 +466) :22
б) 391 х37:17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025:5 – (524 + 24 х6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и: , затем + и — в) + и -, затем х и:
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и:, затем + и — в) по порядку записи
Выбери верный ответ:
9. 120 – (50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 — 4х4) х2
а) 596 б) 1192 в) 60
11. (20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12. 160: (80 – 80:2) х 3
160: (80 – 80:2) х 3
а) 120 б) 0 в) 1
Октябрь 24th, 2017 admin
Лопатко Ирина Георгиевна
Цель: формирование знаний о порядке выполнения арифметических действий в числовых выражениях без скобок и со скобками, состоящих из 2-3 действий.
Задачи:
Образовательная: формировать у учащихся умение пользоваться правилами порядка выполнения действий при вычислении конкретных выражений, умение применять алгоритм действий.
Развивающая: развивать навыки работы в паре, мыслительную деятельность учащихся, умение рассуждать, сопоставлять и сравнивать, навыки вычисления и математическую речь.
Воспитательная: воспитывать интерес к предмету, толерантное отношение друг к другу, взаимное сотрудничество.
Типа: изучение нового материала
Оборудование: презентация, наглядности, раздаточный материал, карточки, учебник.
Методы: словесный, наглядно- образный.
ХОД УРОКА
- Организационный момент
Приветствие.
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
Маркушевич сказал великие слова: “Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели .” Добро пожаловать на урок математики!
- Актуализация знаний
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)
Предлагаю выполнить логические задания. Вы готовы?
Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)
Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)
Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)
На руках 10 пальцев. Сколько пальцев на 6 руках? (30)
У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)
Сколько всего детей в семье? (7)
Сколько хвостов у семи котов?
Сколько носов у двух псов?
Сколько ушей у 5 малышей?
Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.
Оценивание: словесное.
Устный счет
КОРОБКА ЗНАНИЙ
Произведение чисел 2 * 3, 4 * 2;
Частные чисел 15: 3, 10:2;
Сумма чисел 100 + 20, 130 + 6, 650 + 4;
Разность чисел 180 – 10, 90 – 5, 340 – 30.
Компоненты умножения, деления, сложения, вычитания.
Оценивание: ученики самостоятельно оценивают друг друга
- Сообщение темы и цели урока
“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)
Вы готовы поглощать знания с аппетитом?
Ребята, Маше и Мише была предложена такая цепочка
24 + 40: 8 – 4=
Маша её решила так:
24 + 40: 8 – 4= 25 правильно? Ответы детей.
А Миша решил вот так:
24 + 40: 8 – 4= 4 правильно? Ответы детей.
Что вас удивило? Вроде и Маша и Миша решили правильно. Тогда почему ответы у них разные?
Они считали в разном порядке, не договорились, в каком порядке будут считать.
От чего зависит результат вычисления? От порядка.
Что вы видите в этих выражениях? Числа, знаки.
Как в математике называют знаки? Действия.
О каком порядке не договорились ребята? О порядке действий.
Что мы будем изучать на уроке? Какая тема урока?
Мы будем изучать порядок арифметических действий в выражениях.
Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях
«Корзина знаний» . (Корзина висит на доске)
Ученики называют ассоциации связанные с темой.
- Изучение нового материала
Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?
180 – (9 + 2) =
Прочитайте выражения. Сравните их.
Сравните их.
Чем похожи? 2 действия, числа одинаковые
Чем отличаются? Скобки, разные действия
Правило 1.
Прочитайте правило на слайде. Дети читают вслух правило.
В выражениях без скобок, содержащих только сложение и вычитание или умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.
О каких действиях здесь говорится? +, — или : , ·
Из данных выражений найдите только те, которые соответствуют правилу 1. Запишите их в тетрадь.
Вычислите значения выражений.
Проверка.
180 – 9 + 2 = 173
Правило 2.
Прочитайте правило на слайде.
Дети читают вслух правило.
В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
:, · и +, — (вместе)
Есть скобки? Нет.
Какие действия будем выполнять сначала? ·, : слева направо
Какие действия будем выполнять потом? +, — слева, направо
Найдите их значения.
Проверка.
180 – 9 * 2 = 162
Правило 3
В выражениях со скобками, сначала вычисляют значение выражений в скобках, затем выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
А здесь какие арифметические действия указаны?
:, · и +, — (вместе)
Есть скобки? Да.
Какие действия будем выполнять сначала? В скобках
Какие действия будем выполнять потом? ·, : слева направо
А затем? +, — слева, направо
Выпишите выражения, которые относятся ко второму правилу.
Найдите их значения.
Проверка.
180: (9 * 2) = 10
180 – (9 + 2) = 169
Еще раз все вместе проговариваем правило.
ФИЗМИНУТКА
- Закрепление
“Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.” , говорил М.В. Остроградский. Вот и мы сейчас вспомним, что мы только что изучили и применим новые знания на практике.
Страница 52 №2
(52 – 48) * 4 =
Страница 52 №6 (1)
Учащиеся собрали в теплице 700 кг овощей: 340 кг огурцов, 150 кг помидоров, а остальные – перец. Сколько килограммов перца собрали учащиеся?
О чем говорится? Что известно? Что нужно найти?
Давайте попробуем решить эту задачу выражением!
700 – (340 + 150) = 210 (кг)
Ответ: 210 кг перца собрали учащиеся.
Работа в парах.
Даны карточки с заданием.
5 + 5 + 5 5 = 35
(5+5) : 5 5 = 10
Оценивание:
- быстрота – 1 б
- правильность — 2 б
- логичность – 2 б
- Домашнее задание
Страница 52 № 6 (2) решить задачу, записать решение в виде выражения.
- Итог, рефлексия
Кубик Блума
Назови тему нашего урока?
Объясни порядок выполнения действий в выражениях со скобками.
Почему важно изучать эту тему?
Продолжи первое правило.
Придумай алгоритм выполнения действий в выражениях со скобками.
“Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)
Спасибо за работу на уроке!!!
ПОДЕЛИТЬСЯ Вы можете
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. В таких случаях применяется следующее правило:
В таких случаях применяется следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить множимое 2. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 – положительное число, а (−5) отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях применяется следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4) = 3 : 1 = 3
Снова получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Порядок действий в скобках в математике
Содержание
- 0.
 1 Вывод:
1 Вывод: - 1 Сначала умножение и деление, затем сложение и вычитание
- 2 Действия первой и второй ступени
- 3 Порядок выполнения арифметических действий в выражениях со скобками
- 4 Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 — 9 = 1
Сначала выполняем действия в скобках:
16 — 2 · 7 + 4 = 16 — 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 — 2 · 6 + 6 · 7 =
= 9 + 4 — 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 — 6 = 2
10 — 2 · 3 = 10 — 6 = 4
действия в квадратных скобках дают:
14 — 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 — 20 = 10
35 — 10 = 25
100 — 25 = 75
75 · 2 = 150
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:Поделись с друзьями в социальных сетях:
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2 :3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
| Табличка на двери |
Правило BODMAS — Что такое правило BODMAS? Полная форма BODMAS
Правило BODMAS — это аббревиатура, которая используется для запоминания порядка операций, которым необходимо следовать при решении выражений в математике. Это означает B — скобки, O — порядок степеней или корней (в некоторых случаях «из»), D — деление, M — умножение, A — сложение и S — вычитание. Это означает, что выражения с несколькими операторами необходимо упрощать слева направо только в этом порядке. Сначала мы решаем скобки, затем степени или корни, затем деление или умножение (в зависимости от того, что окажется первым из левой части выражения) и, наконец, вычитание или сложение, в зависимости от того, что окажется в левой части выражения.
Это означает, что выражения с несколькими операторами необходимо упрощать слева направо только в этом порядке. Сначала мы решаем скобки, затем степени или корни, затем деление или умножение (в зависимости от того, что окажется первым из левой части выражения) и, наконец, вычитание или сложение, в зависимости от того, что окажется в левой части выражения.
В этом уроке мы узнаем о правиле БОДМАС, которое помогает решать арифметические выражения, содержащие множество операций, таких как сложение (+), вычитание (-), умножение (×), деление (÷) и скобки ( ).
| 1. | Что такое БОДМАС? |
| 2. | Полная форма БОДМАС |
| 3. | BODMAS против PEMDAS |
| 4. | Часто задаваемые вопросы о правиле BODMAS |
Что такое БОДМАС?
BODMAS, который называется порядком операций, представляет собой последовательность для выполнения операций в арифметическом выражении. Математика основана на логике и некоторых стандартных правилах, упрощающих наши расчеты. Итак, BODMAS — это одно из стандартных правил упрощения выражений с несколькими операторами.
Математика основана на логике и некоторых стандартных правилах, упрощающих наши расчеты. Итак, BODMAS — это одно из стандартных правил упрощения выражений с несколькими операторами.
В арифметике выражение или уравнение состоит из двух компонентов:
- Номера
- Операторы
Числа
Числа — это математические значения, используемые для подсчета и представления величин, а также для выполнения вычислений. В математике числа могут быть классифицированы как натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, комплексные числа и мнимые числа.
Операторы или операции
Оператор — это символ, который объединяет два числа и дает выражение или уравнение. В математике наиболее распространенными операторами являются сложение (+), вычитание (-), умножение (×), деление (÷). Для математических выражений или уравнений, в которых задействован только один оператор, найти ответ довольно просто. В случае нескольких операторов найти решение становится немного сложнее! Давайте разберемся в этом на примере. Дженни и Рон по отдельности решили математическое выражение 6 × 3 + 2. Ниже приведены два разных метода, с помощью которых Дженни и Рон решили выражение:
В случае нескольких операторов найти решение становится немного сложнее! Давайте разберемся в этом на примере. Дженни и Рон по отдельности решили математическое выражение 6 × 3 + 2. Ниже приведены два разных метода, с помощью которых Дженни и Рон решили выражение:
Метод Дженни: 6 × 3 + 2 = 6 × 5 = 30, Метод Рона: 6 × 3 + 2 = 18 + 2 = 20.
Как мы видим, Дженни и Рон получили разные ответы. В математике мы знаем, что может быть только один правильный ответ на это выражение. Как определить, кто прав? В таких случаях мы используем BODMAS , чтобы найти правильный ответ. Давайте посмотрим на приведенный ниже пример, чтобы получить представление о том, как работает BODMAS:
Полная форма БОДМАС
Правило BODMAS используется для оценки математических выражений и выполнения сложных вычислений гораздо более простым и стандартным способом.
BODMAS Значение
В соответствии с правилом BODMAS, чтобы решить любое арифметическое выражение, мы сначала решаем термины, записанные в скобках, а затем упрощаем экспоненциальные члены, или решаем операцию «из», что означает умножение и перемещение впереди операции деления и умножения, а затем, в конце, работа над сложением и вычитанием. Следование порядку операций в правиле BODMAS всегда приводит к правильному ответу. Упрощение терминов внутри скобок можно сделать напрямую. Это означает, что мы можем выполнять операции внутри скобки в порядке деления, умножения, сложения и вычитания. Если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно. Например, (14 + 19) ÷ (13 — 2) = 33 ÷ 11 = 3.
Следование порядку операций в правиле BODMAS всегда приводит к правильному ответу. Упрощение терминов внутри скобок можно сделать напрямую. Это означает, что мы можем выполнять операции внутри скобки в порядке деления, умножения, сложения и вычитания. Если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно. Например, (14 + 19) ÷ (13 — 2) = 33 ÷ 11 = 3.
Обратите внимание на приведенную ниже таблицу, чтобы понять термины и операции, обозначаемые аббревиатурой BODMAS, в правильном порядке.
| Б | [{()}] | Кронштейны |
|---|---|---|
| О | х² | Орден Сил или Корней (в некоторых случаях «из») |
| Д | ÷ | Подразделение |
| М | × | Умножение |
| А | + | Дополнение |
| С | — | Вычитание |
- Следует отметить, что, когда у нас есть все 3 типа скобок, мы начинаем решение с самых внутренних скобок/круглых скобок (), за которыми следуют фигурные скобки {}, а затем квадратные скобки [ ].

- Еще один момент, который следует помнить, это то, что для буквы «О» мы используем «Порядок степеней или корней», однако в некоторых случаях, когда дается «из», мы решаем «из», что означает умножение.
BODMAS против PEMDAS
BODMAS и PEMDAS — это две аббревиатуры, которые используются для запоминания порядка операций. Правило BODMAS почти аналогично правилу PEMDAS. Существует разница в аббревиатуре, потому что некоторые термины известны под разными названиями в разных странах. При использовании правила BODMAS или правила PEMDAS мы должны помнить, что когда мы подходим к шагу деления и умножения, мы решаем операцию, которая идет первой с левой стороны выражения. То же правило относится к сложению и вычитанию, то есть решаем то действие, которое стоит первым в левой части.
Когда использовать БОДМАС?
BODMAS используется, когда в математическом выражении имеется более одной операции. Существует ряд определенных правил, которые необходимо соблюдать при использовании метода БОДМАС. Это дает правильную структуру для получения уникального ответа для каждого математического выражения.
Это дает правильную структуру для получения уникального ответа для каждого математического выражения.
Условия для выполнения:
- Если есть какие-либо скобки, откройте скобки, затем добавьте или вычтите члены. а + (Ь + с) = а + Ь + с, а + (Ь — с) = а + Ь — с
- Если есть отрицательный знак, просто откройте скобку и умножьте отрицательный знак на каждое слагаемое внутри скобки. а — (б + в) ⇒ а — б — в
- Если есть какой-либо термин сразу за скобками, умножьте этот внешний термин на каждый термин внутри скобки. а(б + в) ⇒ аб + ас
Простые способы запомнить правило BODMAS
Ниже приведены простые правила для запоминания правила BODMAS:
- Сначала упростите скобки.
- Решите все экспоненциальные члены.
- Выполнить деление или умножение (слева направо)
- Выполнить сложение или вычитание (слева направо)
Распространенные ошибки при использовании правила BODMAS
Можно допустить некоторые распространенные ошибки при применении правила BODMAS для упрощения выражений, и эти ошибки приведены ниже: неправильный ответ. Таким образом, если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно.
Таким образом, если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно.

☛ Похожие темы
- Дополнение
- Вычитание
- Умножение
- Подразделение
- Порядок действий
- Порядок действий Рабочие листы 5-й класс
- Рабочие листы PEMDAS 5-й класс
Примеры правил BODMAS
Пример 1: Упростите выражение, используя правило BODMAS: [18 — 2(5 + 1)] ÷ 3 + 7
Решение:
Данное выражение равно [18 — 2(5 + 1)] ÷ 3 + 7
Начнем с решения самой внутренней скобки. Начиная с 5 + 1 = 6. Таким образом, [18 — 2(6)] ÷ 3 + 7
Далее работаем с порядком, тем самым умножая 2 (6) или 2 × 6 = 12. Таким образом, [18 — 6 = 12 12] ÷ 3 + 7
Осталась одна скобка, [18 — 12] = 6. Итак, 6 ÷ 3 + 7
После B и O идет D, следовательно, 6 ÷ 3 = 2. Итак, 2 + 7
И, наконец, сложение, 2 + 7 = 9
∴ Выражение упрощается, и ответ равен 9.
Пример 2: Вычислите порядок операций по правилу BODMAS: (1 + 20 — 16 ÷ 4²) ÷ {(5 — 3)² + 12 ÷ 2}
Решение:
Шаг 1: Во-первых, нам нужно упростить самую внутреннюю скобку, (1 + 20 — 16 ÷ 4²) ÷ {2² + 12 ÷ 2}
Шаг 2: Теперь мы должны оценить показатели степени, (1 + 20 — 16 ÷ 16) ÷ {4 + 12 ÷ 2}
Шаг 3: Теперь нам нужно разделить 16 на 16 и 12 на 2 в скобках, и мы получим (1 + 20 — 1) ÷ {4 + 6}
Шаг 4: Добавьте 1 к 20 и 4 к 6, (21 — 1) ÷ 10
Шаг 5: Отнимите 1 от 21, чтобы решить скобку, мы получим, 20 ÷ 10
Шаг 6: Делим 20 на 10, чтобы получить окончательный ответ, получаем 2.
∴(1 + 20 — 16 ÷ 4²) ÷ {(5 — 3)² + 12 ÷ 2} = 2Пример 3: Упростите выражение, используя правило BODMAS: (9 × 3 ÷ 9 + 1) × 3
Решение:
последует за этим). Здесь сначала нам нужно умножить 9на 3 в данном выражении, (9 × 3 ÷ 9 + 1) × 3, и мы получаем, (27 ÷ 9 + 1) × 3
Шаг 2: Теперь нам нужно разделить 27 на 9 внутри скобки, и мы получим (3 + 1) × 3
. Шаг 3: Удаляем скобки после добавления 3 и 1, получаем, 4 × 3
Шаг 4: Умножьте 4 на 3, чтобы получить окончательный ответ, который равен 12.∴ (9 × 3 ÷ 9 + 1) × 3 = 12
Пример 4: Решите данное выражение, применяя правило BODMAS: [50-{3×(9+7)}]
Решение:
Чтобы решить это выражение, [50-{3×(9+7)}], мы будем использовать следующие шаги:
Шаг 1: Решите самую внутреннюю скобку, добавив 9 на 7, то есть 16. Таким образом, упрощенное выражение будет [50-{3×16}]
Шаг 2: Умножьте 3 на 16, чтобы получить [50-48]
. Шаг 3: Вычтите 48 из 50, чтобы получить окончательный ответ, то есть 2.
Шаг 3: Вычтите 48 из 50, чтобы получить окончательный ответ, то есть 2.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы BODMAS
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о правиле BODMAS
Что такое правило Бодмаса в математике?
Правило BODMAS относится к правилу, которому следуют для решения математических выражений. BODMAS — это порядок операций для математических выражений, включающий более одной операции. Аббревиатура расшифровывается как B — скобки, O — порядок степеней, D — деление, M — умножение, A — сложение и S — вычитание.
Как работает правило БОДМАС?
В любом арифметическом выражении, если используется несколько операций, нам нужно решать члены в порядке правила BODMAS. Сначала решаем часть, написанную в скобках. После решения скобок выполняем операции умножения и деления, в зависимости от того, что стоит первым в выражении слева направо. Затем мы получаем упрощенное выражение только с операциями сложения и вычитания. Решаем сложение и вычитание слева направо и получаем окончательный ответ. Вот как работает БОДМАС.
Сначала решаем часть, написанную в скобках. После решения скобок выполняем операции умножения и деления, в зависимости от того, что стоит первым в выражении слева направо. Затем мы получаем упрощенное выражение только с операциями сложения и вычитания. Решаем сложение и вычитание слева направо и получаем окончательный ответ. Вот как работает БОДМАС.
Применяется ли BODMAS при отсутствии скобок?
Да, даже если нет скобок, все равно используется правило BODMAS. Нам нужно решить другие операции в том же порядке. Следующим шагом после скобок (B) является порядок степеней или корней, за которым следует деление, умножение, сложение и затем вычитание.
Что означает буква O в Bodmas?
O в Bodmas означает порядок, что означает упрощение показателей степени или корней в выражении, если таковые имеются, перед арифметическими операциями. В некоторых странах буква «О» используется для обозначения «из», что опять-таки означает умножение.
Как применить правило Бодмаса?
Правило BODMAS можно применять в случае выражений, содержащих более одного оператора. В этом случае мы упрощаем скобки сначала от самой внутренней скобки до самой внешней [{()}], затем мы вычисляем значения показателей или корней, затем упрощаем умножение и деление, а затем, наконец, выполняем операции сложения и вычитания. при движении слева направо.
В этом случае мы упрощаем скобки сначала от самой внутренней скобки до самой внешней [{()}], затем мы вычисляем значения показателей или корней, затем упрощаем умножение и деление, а затем, наконец, выполняем операции сложения и вычитания. при движении слева направо.
Почему порядок операций важен в реальной жизни?
Порядок операций — это сокращенное правило, позволяющее соблюдать правильный порядок при решении различных частей математического выражения. Универсальным правилом является выполнение всех математических операций для получения правильного ответа.
Когда правило Бодмаса неприменимо?
Правило BODMAS неприменимо к уравнениям. Он применим к математическим выражениям, имеющим более одного оператора.
Кто изобрел правило Бодмаса? Когда он был представлен?
Правило БОДМА было введено математиком Ахиллесом Реселфельтом в 1800-х годах.
Что такое Полная форма правила Бодмаса?
Полная форма BODMAS: скобки, порядок, деление, умножение, сложение, вычитание.
Используют ли калькуляторы BODMAS?
Калькуляторы также используют правило BODMAS. Научные калькуляторы автоматически применяют операции в правильном порядке.
Умножение и деление целых чисел
К умножению и делению целых чисел применяются несколько правил. В этом уроке мы рассмотрим каждый из них.
При умножении и делении целых чисел обращайте внимание на знаки чисел. Они определят, какое правило следует применить. Следует также изучить несколько законов умножения и деления. Изучение этих правил поможет избежать некоторых досадных ошибок в будущем.
Законы умножения
Мы рассмотрели некоторые законы математики на уроке Законы математики. Но мы не смотрели на все законы. Законов в математике много и имеет смысл изучать их последовательно по мере необходимости.
Для начала вспомним, из чего состоит умножение. Умножение состоит из двух параметров: — множимое , — множитель и — произведение . Например, в выражении 3 × 2 = 6 число 3 — множимое, число 2 — множитель, число 6 — произведение.
Например, в выражении 3 × 2 = 6 число 3 — множимое, число 2 — множитель, число 6 — произведение.
Множимое точно показывает, что мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает, во сколько раз нужно увеличить множимое. В нашем примере множитель равен 2. Этот множитель показывает, во сколько раз нужно увеличить множитель 3. То есть в операции умножения число 3 будет удвоено.
Произведение на самом деле является результатом операции умножения. В нашем примере произведением является число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать как сумму двух троек (3+3). Множитель 2 в этом случае покажет, сколько раз повторить цифру 3:
Таким образом, если дважды подряд повторить число 3, получится число 6.
Коммутативный закон умножения
фактора . Переместительный закон умножения выглядит следующим образом: Мы можем поменять местами множимое и множитель и получить тот же результат (результат).
Проверим, так ли это. Умножим, например, 3 на 5. Здесь 3 и 5 — множители.
3 × 5 = 15
Теперь поменяйте местами множители:
5 × 3 = 15
В обоих случаях мы получаем ответ 15, поэтому мы можем поставить знак равенства между выражениями 3 × 5 и 5 × 3, потому что они равны одному значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — коэффициенты
Ассоциативный закон умножения
При умножении не имеет значения, как мы меняем местами и группируем числа .
Например, выражение 3 × 2 × 4 состоит из нескольких множителей. Для его вычисления можно умножить 3 на 2, затем полученное произведение умножить на оставшееся число 4. Это будет выглядеть так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это была первая версия решения.
Второй вариант — умножить 2 и 4, затем умножить полученное произведение на оставшееся число 3. Это будет выглядеть так:
Это будет выглядеть так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях получаем ответ 24. Следовательно, между выражениями (3 × 2) × 4 можно поставить знак равенства и 3 × (2 × 4), потому что они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
и используя a,b,c,
ассоциативный закон умножения можно записать следующим образом:
a × b × c = (a × b) × c = a × (b × c)
где a, b, c могут быть любым числом.
Распределительный закон умножения
умножение числа на группу чисел, сложенных вместе , такое же, как и умножение каждого числа по отдельности.
Например, найдите значение выражения (2 + 3) × 5
Выражение в скобках представляет собой сумму. Эту сумму нужно умножить на число 5. Для этого нужно каждое слагаемое этой суммы, то есть числа 2 и 3, умножить на число 5, а затем сложить результаты:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Таким образом, значение выражения (2 + 3) × 5 равно 25.
Используя переменные, дистрибутив закон умножения записывается следующим образом:
(a + b) × c = a × c + b × c
, где a, b, c может быть любым числом.
Свойство нуля при умножении
Этот закон гласит, что если в любом умножении есть хотя бы один ноль, ответ будет равен нулю.
Произведение равно нулю, если хотя бы один из множителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает, во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Дословно это выражение читается так: «увеличить ноль в два раза». Но как можно удвоить ноль, если это ноль?
Другими словами, если «ничего» удвоить или даже миллион раз, вы все равно получите «ничего».
А если поменять местами множители в выражении 0 × 2, то снова получим ноль. Это мы знаем из предыдущего закона перестановки:
0 × 2 = 2 × 0
0 = 0
Использование закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах есть несколько факторов. Когда мы увидели в них ноль, то тут же поставили в ответ ноль, применив закон умножения на ноль.
Когда мы увидели в них ноль, то тут же поставили в ответ ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Теперь давайте посмотрим на само умножение целых чисел.
Умножение целых чисел
Пример 1. Найдите значение выражения -5 × 2
Это умножение чисел с разными знаками. -5 — отрицательное число, а 2 — положительное число. Для таких случаев следует применять следующее правило:
Когда вы умножаете на два целых числа с разными знаками , результат всегда отрицательный.
−5 × 2 = − (5 × 2) = − (10) = −10
Обычно пишут короче: −5 × 2 = −10
Любое умножение можно представить в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множитель в этом выражении — число 3. Этот множитель показывает, во сколько раз нужно увеличить двойку. Но выражение 2 × 3 можно понимать и как сумму трех двоек:
То же самое происходит с выражением -5 × 2. Это выражение можно представить как сумму
Это выражение можно представить как сумму
И выражение (-5) + (-5) равно -10. Мы знаем это из прошлого урока. Это сложение отрицательных чисел. Напомним, что результатом сложения отрицательных чисел является отрицательное число.
Пример 2. Найдите значение выражения 12 × (-5)
Это умножение чисел с разными знаками. 12 — положительное число, (-5) — отрицательное число.
Снова применяем предыдущее правило. Когда вы умножаете на два целых числа с разными знаками , результат всегда отрицательный:
12 × (−5) = − (12 × 5) = − (60) = −60
более короткая форма:
12 × (−5) = −60
Пример 3. Найдите значение выражения 10 × (-4) × 2
Это выражение состоит из нескольких множителей. Сначала умножаем 10 на (-4), затем умножаем это число на 2. При этом применим изученные ранее правила:
Первое действие:
10 × (−4) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(40 × 2) = -(80) = -80
Таким образом, значение выражения 10 × (-4) × 2 равно -80
Запишем решение короче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найдите значение выражения (-4) × (-2)
Найдите значение выражения (-4) × (-2)
Это умножение отрицательных чисел. В таких случаях следует применять следующее правило:
Когда вы умножаете два отрицательных числа (с одинаковыми знаками) , результат всегда положительный
(−4) × (−2) = 8 просто запишите ответ 8.
Давайте запишем более короткое решение (-4) × (-2) = 8
Возникает вопрос, почему умножение отрицательных чисел вдруг приводит к положительному числу. Попробуем доказать, что (-4) × (-2) равно 8 и ничему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Добавим к этому выражению наше выражение (-4) × (- 2). Его также заключаем в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Приравняем все это к нулю:
(4 × (−2)) + ( (−4) × (−2)) = 0
Теперь начинается самое интересное. Дело в том, что мы должны вычислить левую часть этого выражения, и результат равен 0,9. 0005
0005
Итак, первое произведение (4 × (-2)) равно -8. Запишем в нашем выражении число -8 вместо произведения (4 × (-2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно положим пунктирная линия
−8 + … = 0
Теперь внимательно посмотрите на выражение -8 + … = 0. Какое число должно стоять вместо многоточия, чтобы выполнялось равенство? Ответ очевиден. Вместо «…
» должно быть положительное число 8 и никакое другое число. Только так можно сохранить равенство. Потому что -8 + 8 равно 0,
Вернуться к выражению -8 + ((-4) × (-2)) = 0 и вместо произведения ((-4) × (-2)) записать число 8
−8 + 8 = 0
Пример 5. Найдите значение -2 × (6 + 4)
Примените распределительный закон умножения, т. е. умножьте -2 на каждое слагаемое (6 + 4)
−2 × ( 6 + 4) = −2 × 6 + (−2) × 4
Теперь давайте выполним умножение и сложим результаты. При этом применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
-2 × 6 = -12
Второе действие:
-2 × 4 = -8
Третье действие: — 20 Таким образом, значение выражения -2 × (6 + 4) равно -20 Запишем решение короче: −2 × (6 + 4) = (−12) + (−8) = −20 Пример 6: Найдите значение (-2) × (-3) × (-4) Выражение состоит из нескольких множителей. Первое действие: (−2) × (−3) = 6 Второе действие: 6 × (−4) = −(6 × 4) = −24 Тогда значение выражения (-2) × (-3) × (-4) равно -24 Запишем решение короче: (−2) × (−3) × (−4) = 6 × (− 4) = −24 Прежде чем вы сможете делить целые числа, вы должны изучить два закона деления. Прежде всего, вспомним, из чего состоит деление. Деление состоит из трех параметров: делимое , делитель и частное . Например, в выражении 8 : 2 = 4 8 — делимое, 2 — делитель, 4 — частное. Делимое точно показывает, что мы делим. В этом примере мы делим число 8. Делитель — это число, на которое нужно разделить другое число. Частное на самом деле является результатом операции деления. В нашем примере частное равно числу 4. Это частное есть результат деления 8 на 2. Далее рассмотрим законы деления. Любое число нельзя делить на ноль. Дело в том, что деление обратно умножению. Эту фразу можно понимать в буквальном смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2,9.0005 Вы видите, что второе выражение записано в обратном порядке. Если, например, у нас есть два яблока и мы хотим увеличить их число в пять раз, мы пишем 2 × 5 = 10. Получится десять яблок. Затем, если мы хотим записать десять яблок обратно в два яблока, мы пишем 10 : 5 = 2. Мы можем сделать то же самое с другими выражениями. Если, например, 2 × 6 = 12, мы можем вернуться к исходному числу 2. Для этого достаточно написать выражение 2 × 6 = 12 в обратном порядке, разделив 12 на 6 12 : 6 = 2 Теперь рассмотрим выражение 5 × 0. 5 × 0 = 0 Если мы запишем это выражение в обратном порядке, то получим: 0 : 0 = 5 Сразу бросается в глаза ответ 5, который является результатом деление нуля на ноль. Это невозможно. Другое подобное выражение можно записать в обратном порядке, например, 2 × 0 = 0 0 : 0 = 2 В первом случае, разделив ноль на ноль, мы получили 5, а во втором случае получили 2. То есть при каждом делении нуля на ноль мы можем получить разные значения , а это недопустимо. Второе объяснение состоит в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое. Например, выражение 8 : 2 означает найти такое число, которое при умножении на 2 дает 8 … × 2 = 8 Здесь вместо точек должно быть число, которое при умножении на 2 даст ответ 8. 8 : 2 = 4 Получили число 4. Запишем его вместо «…» : 4 × 2 = 8 Теперь представим, что нам нужно найти значение выражения 5 : 0. В этом случае, 5 — делимое, 0 — делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 дает 5 … × 0 = 5 Здесь вместо «…» должно быть число, которое при умножении на 0 дает ответ 5. Но нет числа, которое при умножении на ноль дает 5. Выражение … × 0 = 5 противоречит закону умножения на ноль, который гласит, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Так что нет смысла записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0. Поэтому и говорят, что на ноль делить нельзя. Используя переменные, этот закон записывается следующим образом: , at b ≠ 0 Это выражение можно прочитать так: Число a можно разделить на число b при условии, что b не равно нуль. Свойство частного Этот закон гласит, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3 12 : 4 = 3 Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, то в ответе снова должно получиться число 3 Получили ответ 3. Теперь попробуем не умножать, а разделить делитель и делитель на число 4 Получил ответ 3. Мы видим, что если делимое и делитель умножить или разделить на одно и то же число, частное не не изменить. Мы рассмотрели два закона деления. Далее, давайте посмотрим на деление целых чисел. Пример 1. Это деление чисел с разными знаками. 12 — положительное число, (-2) — отрицательное число. Чтобы решить этот пример, разделите модуль делимого на модуль делителя и перед ответом поставьте минус. 12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6 Обычно записывают короче: 12 : ( −2) = −6 Пример 2. Найдите значение выражения -24 : 6 Это деление чисел с разными знаками. -24 — отрицательное число, 6 — положительное число. Снова делим модуль делимого на модуль делителя и перед ответом 9 ставим минус0004 . −24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4 Запишем решение вкратце: −24 : 6 = − 4 Пример 3. Найдите значение выражения -45 : (-5) Это деление отрицательных чисел. Чтобы решить этот пример, разделите модуль делимого на модуль делителя и перед ответом поставьте плюсик. −45 : (−5) = |−45| : |−5| = 45 : 5 = 9 Коротко запишем решение: −45 : (−5) = 9 Пример 4. Найти значение выражения -36 : (-4) : (-3) Согласно порядку операций, если выражение содержит только умножение или деление, все действия нужно выполнять слева направо по порядку. Разделите -36 на (-4) и разделите полученное число на -3 Первое действие: −36 : (−4) = |−36| : |−4| = 36 : 4 = 9 Второе действие: 9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3 Запишем решение вкратце: −36 : (− 4) : (−3) = 9 : (−3) = −3 Авторов: Мандут Рамчандер Abstract: Вычисление выражений, включающих умножение и деление, может привести к ошибке, что скобки могут быть произвольно вставлены в выражения, включающие умножение и деление. Ключевые слова: Скобки,
умножение,
разделение,
операции,
заказ. ProcediaAPABibTeXChicagoEndNoteHarvardJSONMLARISXMLISO 690PDF
Скачано 268 Ссылки: [1] Г. Вивинетто, «Можете ли вы решить это математическое уравнение, которое ставит Интернет в тупик?» Сегодня, 2 августа 2019 г. Доступно: https://www.today.com/popculture/math-equation-stumping-folks-internet-t16008. Правила экспоненты объясняют, как решать различные уравнения, которые, как и следовало ожидать, содержат экспоненты. Но есть несколько различных типов экспоненциальных уравнений и экспоненциальных выражений, которые могут показаться сложными… поначалу. Овладение этими основными правилами экспоненты вместе с основными правилами логарифмирования (также известными как «логарифмические правила») сделает ваше изучение алгебры очень продуктивным и приятным. Имейте в виду, что во время этого процесса по-прежнему будет применяться порядок операций. Как и большинство математических приемов, существуют стратегии обучения, которые можно использовать для упрощения выполнения правил экспоненты. Чтобы помочь вам в обучении этим понятиям, у нас есть бесплатный рабочий лист правил экспоненты , который вы можете загрузить и использовать в своем классе! Показатель степени, также известный как степень, представляет собой величину, показывающую, сколько раз нужно умножить базовое число само на себя. Например, 43 говорит вам умножить четыре само на себя три раза. 43= 4 × 4 × 4 = 64 Число, возведенное в степень, известно как по основанию , а надстрочное число над ним — это показатель или степень . Кредит: To The Square Inch Вышеприведенное уравнение звучит как «четыре в степени три». Степень двойки также может быть выражена как « в квадрате », а степень числа три — как « в кубе ». Запись числа в экспоненциальной форме означает его упрощение до основания со степенью. Например, преобразование 5 × 5 × 5 в экспоненциальную форму выглядит как 53 . Экспоненты — это способ упростить уравнения, чтобы их было легче читать. Это становится особенно важным, когда вы имеете дело с такими переменными, как «𝒙» и «𝑦» — как 𝒙7× 𝑦5= ? легче читать, чем (𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝒙)(𝑦)(𝑦)(𝑦)(𝑦)(𝑦) = ? Понимание свойств экспоненты не только поможет вам решать различные алгебраические задачи, экспоненты также используются на практике в повседневной жизни при расчете квадратных футов, квадратных метров и даже кубических сантиметров. Экспоненциальные правила также упрощают вычисление очень больших или очень малых величин. Они также используются в мире компьютеров и технологий при описании мегабайтов, гигабайтов и терабайтов. Есть семь правил экспоненты, или законов экспоненты, которые необходимо изучить вашим ученикам. Каждое правило показывает, как решать различные типы математических уравнений и как складывать, вычитать, умножать и делить степени. Тщательно изучите каждое правило экспоненты в классе, так как каждое из них играет важную роль в решении уравнений на основе экспоненты. При умножении двух оснований одного и того же значения оставьте основания одинаковыми, а затем сложите их показатели, чтобы получить решение. 42× 45 = ? Поскольку оба базовых значения равны четырем, оставьте их одинаковыми, а затем сложите вместе показатели степени (2 + 5). 42 × 45= 47 Затем умножьте четыре на себя семь раз, чтобы получить ответ. 47 = 4 × 4 × 4 × 4 × 4 × 4 × 4 = 16 384 Давайте расширим приведенное выше уравнение, чтобы увидеть, как работает это правило: ответ. Попробуйте задать более сложный вопрос: (4𝒙2)(2𝒙3) = ? Перемножьте коэффициенты вместе (четыре и два), так как они не являются одним и тем же основанием. Затем оставьте «𝒙» таким же и добавьте показатели степени. (4𝒙2)(2𝒙3) = 8𝒙5 Умножение и деление противоположны друг другу — во многом то же самое, правило частного действует как противоположность правилу произведения. При делении двух оснований одного и того же значения оставьте основание одинаковым, а затем вычтите значения степени. 55 ÷ 53 = ? Оба основания в этом уравнении равны пяти, что означает, что они остаются прежними. Затем возьмите показатели и вычтите делитель из делимого. 55÷ 53 = 52 Наконец, упростим уравнение, если это необходимо: 52= 5 × 5 = 25 Еще раз, расширение уравнения показывает нам, что это сокращение дает правильный ответ: Взгляните на этот более сложный пример: 5𝒙4 / 10𝒙2 = ? Одинаковые переменные в знаменателе отменяют переменные в числителе. 5𝒙4 / 10𝒙2 = 5𝒙/10 Затем упростите, где это возможно, как с любой дробью. Пять можно превратить в десять, пять раз превратив дробь в ½ с оставшимися 𝒙 переменными. 5𝒙4/10𝒙2= 1𝒙2/2 = 𝒙2/2 Это правило показывает, как решать уравнения, в которых степень возводится в на другой степенью. (𝒙3)3 = ? В уравнениях, подобных приведенному выше, умножьте показатели степени и оставьте основание одинаковым. (𝒙3)3 = 𝒙9 Посмотрите на расширенное уравнение, чтобы увидеть, как это работает: показатель степени до каждая часть основания. (𝒙𝑦)3 = ? В этом уравнении степень троицы должна быть распределена как по 𝒙, так и по 𝑦 переменным. (𝒙𝑦)3 = 𝒙3𝑦3 Это правило применяется, если к основанию также присоединены экспоненты. (𝒙2𝑦2)3 = 𝒙6𝑦6 В расширенном виде уравнение будет выглядеть так: Обе переменные в этом уравнении равны в квадрате и представляют собой , возведенное в степень 3. Это означает, что три умножаются на показатели степени в обеих переменных, превращая их в переменные, которые возводятся в степень шесть. Частное просто означает, что вы делите две величины. В этом правиле тебе возведение частного в степень. Подобно силе правила произведения, показатель степени должен распространяться на все значения в скобках, к которым он присоединен. (𝒙/𝑦)4 = ? Здесь обе переменные в квадратных скобках увеличьте в четыре степени. Взгляните на это более сложное уравнение: (4𝒙3/5𝑦4)2 = ? Не забудьте распределить показатель степени, на который вы умножаете, на как на коэффициент, так и на переменную. Затем упростите, где это возможно. (4𝒙3/5𝑦4)2= 42𝒙6/52𝑦8 = 16𝒙6/25𝑦8 Любое основание, возведенное в нулевую степень, равно единице. Самый простой способ объяснить это правило — использовать правило отношения степеней. 43/43 = ? Следуя правилу отношения степеней, вычтите показатели степени друг из друга, что аннулирует их, оставив только основание. Любое число, деленное само на себя, равно единице. 43/43= 4/4 = 1 Независимо от длины уравнения, все, что возводится в нулевую степень, становится единицей. (82𝒙4𝑦6)0 = ? Как правило, внешний показатель степени должен быть умножен на каждое число и переменную в скобках. Однако, поскольку это уравнение возводится в нулевую степень, эти шаги можно пропустить, и ответ просто станет единицей. (82𝒙4𝑦6) 0 = 1 Полное расширенное уравнение будет выглядеть следующим образом: (82𝒙4𝑦6) 0 = 80𝒙0𝑦0 = (1) (1) (1) = 1 Когда есть число, возводимое в отрицательную степень, превратите его в обратную, чтобы превратить степень в положительную. Не используйте отрицательную степень для превращения основания в отрицательное. Авторы и права: Thinglink Мы уже говорили об обратных величинах в нашей статье « Как делить дроби за 3 простых шага ». По сути, обратные числа — это то, на что вы умножаете число, чтобы получить значение единицы. Например, чтобы превратить два в один, умножьте его на ½. Теперь посмотрите на этот пример с показателем степени: 𝒙-2 = ? Чтобы сделать число обратным: Цель уравнений с отрицательными показателями степени заключается в том, чтобы сделать их положительными. Теперь взгляните на более сложное уравнение: 4𝒙-3𝑦2/20𝒙𝑧-3 = ? В этом уравнении есть два показателя степени с отрицательными степенями. Упростите то, что можете, а затем преобразуйте отрицательные показатели в их обратную форму. В решении 𝒙-3 перемещается в знаменатель, а 𝑧-3 перемещается в числитель. Поскольку в знаменателе уже есть значение 𝒙, к этому значению добавляется 𝒙3. 4𝒙-3𝑦2/20𝒙z-3 = 𝑦2𝑧3/5𝒙4 Имея эти семь правил в задних карманах ваших учеников, они смогут ответить на большинство экспоненциальных вопросов, с которыми они столкнутся! Prodigy — это математическая игра, адаптированная к учебной программе, которую вы можете использовать для постановки вопросов, отслеживания прогресса и выявления проблем в обучении ваших учеников . И вы можете бесплатно создавать учетные записи учителей и учеников! С таким количеством различных правил экспоненты, которым нужно следовать, и нескольким ученикам, которых нужно отслеживать, может быть трудно понять, кому и в чем нужна помощь. Статистика отслеживается в режиме реального времени, когда ученики играют в игру, и обратная связь доступна мгновенно. В большинстве случаев ваши ученики даже не осознают, что они участвуют в уроках математики. Все это часть их персонализированного игрового опыта! На панели управления учителя вы можете создавать планы уроков, просматривать статистику в реальном времени, вводить пользовательские задания и готовить своих учеников к предстоящим тестам. Вот как вы можете использовать Prodigy для : Рабочие листы по математике — это удобные инструменты, которые могут показать, как учащиеся понимают ключевые понятия. С помощью нашей команды учителей мы составили рабочий лист правил экспоненты, чтобы помочь вам с уроками экспоненты. Щелкните здесь , чтобы загрузить нашу таблицу правил экспоненты с ключом ответа! Экспоненты используются, чтобы показать, сколько раз базовое значение умножается само на себя. Это упрощает уравнения до более удобного для чтения формата. (𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙)(𝑦𝑦𝑦𝑦𝑦𝑦)(𝑧𝑧𝑧𝑧𝑧) = 𝒙9𝑦6𝑧5 Напомним, что есть семь основных правил, которые включают в себя решение большинства математических уравнений. Правила экспоненты: Показатель степени имеет тенденцию появляться на протяжении всей нашей жизни, поэтому важно, чтобы учащиеся понимали, как они работают, двигаясь вперед. Правило или порядок, который мы используем для упрощения выражений в математике:
называется правилом BODMAS. Очень
просто способ запомнить правило BODMAS! B —-> Скобки O —-> Из (заказы
: Степени и радикалы) D —-> Деление M —-> Умножение A —-> Сложение S —-> Вычитание 2.
Деление не всегда предшествует умножению. Мы должны сделать один за другим
в порядке слева направо. 3.
В конкретном упрощении, если у вас есть и сложение, и вычитание, сделайте
операции одну за другой в порядке слева направо. Примеры
: 12
÷ 3 х 5 = 4 х 5 = 20 13
— 5 + 9 = 8 + 9 = 17 В
приведенное выше упрощение, мы имеем и деление, и умножение. Слева
справа у нас сначала деление, а потом умножение. Итак, мы делаем деление
сначала и умножение потом. Проблема
1 : Оценка
: 6 +
7 x 8 Решение
: Оценка = 6
+ 7
х 8 = 6 + 56 =
62 Операция Умножение Сложение Результат Задача 2 : Оценка : 10 2 — 16 ÷ 8 Решение : Оценка = 10 2 — 16 ÷ 8 = 100 — 16 ÷ 8 = 100 — 2 = 98 Операция Степень Деление Вычитание Результат Задача 3 : Оценка : (25 + 11) x 2 Решение : Оценка = (25 + 11) x 2 = 36 х 2 = 72 Операция Скобка Умножение Результат Задача 4 : Оценка : 3 + 6 x (5 + 4) ÷ 3 -7 Решение : Оценка = 3 + 6 x (5 + 4) ÷ 3 -7 = 3 + 6 x 9 ÷ 3 -7 = 3 + 54 ÷ 3 -7 = 21 — 7 = 14 Операция Скобка Умножение Деление Сложение Вычитание Результат Задача 5 : Оценка : 56 — 2(20 + 12 ÷ 4 x 3 — 2 x 2) + 10 Решение : Оценка = 56 — 2(20 + 12 ÷ 4 x 3 — 2 x 2) + 10 = 56 — 2 (20 + 12 ÷ 4 x 3 — 2 x 2) + 10 = 56 — 2 (20 + 3 x 3 — 2 x 2) + 10 = 56 — 2 (20 + 9 — 4) + 10 = 56 — 2 (29 — 4) + 10 = 56 — 2(25) + 10 = 56 — 50 + 10 = 6 + 10 = 16 Операция Скобка Деление Умножение Сложение Вычитание Умножение Сложение 0247 Результат Задача 6 : Оценка : 6 + [(16 — 4) ÷ (2 2 + 2)] — 2 Решение :5 9010 Оценка = 6 + [(16 — 4) ÷ (2 2 + 2)] — 2 = 6 + [12 ÷ (2 2 + 2)] — 2 = [12 ÷ (4 + 2)] — 2 = 6 + [12 ÷ 6] — 2 = 6 + 2 — 2 = 8 — 2 = 6 Операция Квадратная скобка Мощность Квадратная скобка Квадратная скобка Сложение Вычитание Результат Задача 7 : Оценка : (96 ÷ 12) + 14 x (12 + 8) ÷ 2 Решение : Оценка = (96 ÷ 12) + 14 х (12 + 8) ÷ 2 = 8 + 14 х 20 ÷ 2 = 8 + 280 ÷ 2 = 8 + 140 = 148 Операция Скобка Умножение Деление Сложение Результат Задача 8 : Оценка : (93 + 15) ÷ (3 x 4) — 24 + 8 Решение : Оценка = (93 + 15) ÷ (3 x 4) — 24 + 8 = 108 ÷ 12 — 24 + 8 = 9 — 24 + 8 = -15 + 8 = -7 Операция Скобка Деление Вычитание Вычитание Результат Задача 9 : Оценка : 55 ÷ 11 + (18 — 6) x 9 Решение : Оценка = 55 ÷ 11 + (18 — 6) x 9 = 55 ÷ 11 + 12 x 9 = 5 + 12 х 9 = 5 + 108 = 113 Операция Скобка Деление Умножение Сложение Результат Задача 10: Оценка: (7 + 18) x 3 ÷ (2 + 13) — 28 Решение: Оценка = (7 + 18) x 3 ÷ (2 + 13) — 28 = 25 х 3 ÷ 15 — 28 = 75 ÷ 15 — 28 = 5 — 28 = -23 Операция Скобка Умножение Деление Вычитание Результат Задача 11 : Оценка : [11 — 20 ÷ (5 2 — 13) ÷ 3 + 8] x 2 Решение : 72 — 1 — +
 Сначала умножьте -2 и -3, а полученное произведение умножьте на оставшееся число -4. Опустим запись по модулю, чтобы не загромождать выражение
Сначала умножьте -2 и -3, а полученное произведение умножьте на оставшееся число -4. Опустим запись по модулю, чтобы не загромождать выражение Законы деления
 В данном примере делителем является число 2. То есть при операции деления число 8 будет разделено на две части.
В данном примере делителем является число 2. То есть при операции деления число 8 будет разделено на две части. На ноль делить нельзя
 Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из множителей равен нулю. Таким образом, выражение 5 × 0 равно нулю
Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из множителей равен нулю. Таким образом, выражение 5 × 0 равно нулю Чтобы найти это число, просто напишите выражение в обратном порядке:
Чтобы найти это число, просто напишите выражение в обратном порядке:
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Деление целых чисел
 Найти значение выражения 12 : (-2)
Найти значение выражения 12 : (-2)
Видеоурок
Заблуждение, связанное со вставкой скобок для вычисления выражений, включающих умножение и деление
 Цель этой статьи заключалась в том, чтобы на основе математической теории доказать, что скобки нельзя произвольно вставлять в выражения, включающие умножение и деление, и, в частности, в выражения, в которых деление предшествует умножению. При этом он демонстрирует, что представление о том, что возможны два разных ответа при оценке выражений, включающих умножение и деление, на самом деле является ложным. Поиски, проведенные в ряде научных баз данных, выявили правила, которые должны применяться при удалении скобок из выражений, что показало, что необходимо учитывать изменения знака при удалении скобок. Затем правило, относящееся к выражениям, включающим умножение и деление, было расширено в его обратном формате, чтобы доказать, что скобки не могут быть произвольно вставлены в выражения, включающие умножение и деление. Применение правила показывает, что выражение, включающее умножение и деление, может иметь только один правильный ответ. Рекомендуется включить в учебную программу как правило, так и его обратную сторону, желательно на стыке, когда вводятся манипуляции со скобками.
Цель этой статьи заключалась в том, чтобы на основе математической теории доказать, что скобки нельзя произвольно вставлять в выражения, включающие умножение и деление, и, в частности, в выражения, в которых деление предшествует умножению. При этом он демонстрирует, что представление о том, что возможны два разных ответа при оценке выражений, включающих умножение и деление, на самом деле является ложным. Поиски, проведенные в ряде научных баз данных, выявили правила, которые должны применяться при удалении скобок из выражений, что показало, что необходимо учитывать изменения знака при удалении скобок. Затем правило, относящееся к выражениям, включающим умножение и деление, было расширено в его обратном формате, чтобы доказать, что скобки не могут быть произвольно вставлены в выражения, включающие умножение и деление. Применение правила показывает, что выражение, включающее умножение и деление, может иметь только один правильный ответ. Рекомендуется включить в учебную программу как правило, так и его обратную сторону, желательно на стыке, когда вводятся манипуляции со скобками.
[2] Г. Кристал, Алгебра: элементарный учебник для высших классов средних школ и колледжей, том 1, Эдинбург, 1904.
[3] С. Строгац, «Уравнение, которое пыталось поставить Интернет в тупик», The New York Times, 2 августа 2019 г. Доступно: https://www.nytimes.com/2019/08/02/science/math- уравнение-pedmas-bemdas-bedmas.html.
[4] С. ЛеКонте, С., «Все спорят об этом очень простом математическом уравнении — вот почему оно становится вирусным», BuzzFeed, 2 августа 2019 г. Доступно: https://www.buzzfeed.com/stephenlaconte/viral-math -уравнение-спорный-пемдас.
Доступно: https://www.buzzfeed.com/stephenlaconte/viral-math -уравнение-спорный-пемдас.
[5] С. Строгац, «Это надоедливое математическое уравнение? Вот дополнение», The New York Times, 5 августа 2019 г.. Доступно: https://www.nytimes.com/2019/08/05/science/math-equation-pemdas-bodmas.html.
[6] А. Дэниелс, «Эта простая математическая задача свела с ума весь наш персонал. Сможете ли вы ее решить?» Popular Mechanics, 31 июля 2019 г. Доступно: https://www.popularmechanics.com/science/math/a28569610/viral-math-problem-2019-solved/.
[7] Н. де Местре, «Открытие с Невиллом де Местре», Австралийский учитель математики, том. 65, нет. 3, стр. 20-21, 2009.
[8] К. Флориан, История математических обозначений, Чикаго: паб Open Court. Ко., 1928.
[9] Р. Гуннарссон и А. Карлссон, Скобки и смысл структуры, Школа образования и коммуникации, Йонкопингский университет, 2014.
[10] А. Карлссон и Р. Гуннарссон, «Восприятие скобок учащимися», In Lindmeier, A.M. и А. Хайнце. (ред.), Материалы 37-й конференции Международной группы психологии математического образования, т. 1, с. 40, нет. 2, стр. 173-176, 2013.
Хайнце. (ред.), Материалы 37-й конференции Международной группы психологии математического образования, т. 1, с. 40, нет. 2, стр. 173-176, 2013.
[11] К. Киран, К., «Оперативное мышление детей в контексте заключения в скобки и порядка операций», В материалах Д. Талла (ред.) 3-й конференции Международной группы по психологии математического образования, стр. 128-133, Уорик. Великобритания: PME, 19 лет79.
[12] Р. Гуннарссон, Б., Хернелл и В.В. Соннерхед, «Бесполезные скобки в арифметических выражениях со смешанными операциями», Материалы 36-й конференции Международной группы по психологии математического образования, 2012 г., стр. 275-282, 2012 г.
[13] К.М. Робинсон и Дж. ЛеФевр, «Обратная связь между умножением и делением: концепции, процедуры и когнитивная структура», Educational Studies in Mathematics, vol. 79, нет. 1, стр. 409-428, 2012.
[14] Робинсон, К.М., Дубе, А.К., и Дж. Битч, «Детские ярлыки умножения и деления: расширение использования ярлыков зависит от того, как оцениваются ярлыки», Learning and Individual Differences, vol. 49, нет. 1. С. 97-304, 2016.
49, нет. 1. С. 97-304, 2016.
[15] К.Н. Джозеф, «Неверное представление студентов колледжа о порядке операций», неопубликованная магистерская диссертация, Государственный университет Нью-Йорка, Фредония, Нью-Йорк, 2014.
[16] Д. Гордон, Г. Ачиман и Д. Мелман, «Правила математики», «Математика в школе», т. 10, №, 3, стр. 2–4, 19.81.: 7 законов экспоненты для решения сложных уравнений

 Эти термины часто используются при нахождении площади или объема различных фигур.
Эти термины часто используются при нахождении площади или объема различных фигур.

 Вы можете показать это своим ученикам, зачеркнув равное количество 𝒙 сверху и снизу дроби.
Вы можете показать это своим ученикам, зачеркнув равное количество 𝒙 сверху и снизу дроби.

 Правило отрицательного показателя
Правило отрицательного показателя 
 Prodigy позволяет легко отслеживать прогресс и создавать уникальные игровые возможности для каждого учащегося в зависимости от его потребностей.
Prodigy позволяет легко отслеживать прогресс и создавать уникальные игровые возможности для каждого учащегося в зависимости от его потребностей.
Бесплатный рабочий лист правил экспоненты  Вы можете увидеть, как учащиеся придумывают ответы, где они борются, и нужно ли более подробно осветить какие-либо концепции.
Вы можете увидеть, как учащиеся придумывают ответы, где они борются, и нужно ли более подробно осветить какие-либо концепции. Есть много правил, которые нужно запомнить, но как только ваши ученики поймут их, решать показатели степени, вероятно, станет легче!
Есть много правил, которые нужно запомнить, но как только ваши ученики поймут их, решать показатели степени, вероятно, станет легче! Правило BODMAS

Решенные проблемы
50 1 0 10 10
Оценка
= [11 — 20 + (5 2 — 13) ÷ 3 x 8] x 2
= [11 — 20 + (5 2 — 13) ÷ 3 x 8] x 2
5 =
5 [11 — 20 + (5
2 — 13) ÷ 3 x 8] x 2.
= [11 — 20 + (25 — 13) ÷ 3 x 8] x 2
= [11 — 20 + 12 ÷ 3 x 8] x 2
= [11 — 20 + 4 x 8] x 2
= [11 — 20 + 32] x 2
= [-9 + 32] x 2
= 23 x 2
= 46
Операция
Кронштейн 2
Кроншена 2
Экспонент 2
Кронтация
Дивизион
Умножение
.Задача 12 :
Оценка :
a 3 — (b 2 + c) ÷ a + (ab + c)
, если a = 4, b = -3.
Решение:
a 3 — (b 2 + c) ÷ a + (ab + c)
Подставить a = 4, b = -3 и c = 7.
4 3 — [(-3) 2 + 7 ] ÷ 4 + [4(-3) + 7]
Оценка = 4 3 — [(-3) 2 + 7] ÷ 4 + [4(-3) + 7] = 4 3 — [(-3) 2 9+ 7] ÷ 4 + [4(-3) + 7] = 4 3 — [9 + 7] ÷ 4 + [4(-3) + 7] = 4 3 — 16 ÷ 4 + [-12 + 7] = 4 3 — 16 ÷ 4 — 5 = 64 — 16 ÷ 4 — 5 = 64 — 4 — 5 = 60 — 5 = 55 | 7 Operation Brackets 2 Exponent 2 Brackets 2 2 Bracket 2 Exponent 2 Division Subtraction Subtraction Результат |
Problem 13 :
Evaluate :
Solution :
Problem 14 :
Evaluate :
Solution :
Problem 15 :
Evaluate :
Решение:
Задача 16:
Чему равно число
, если a = -2, b = 3 и c = 5.
Решение0005
Задача 17:
Каково значение
Если A = 4, B = -3 и C = 7.
Решение:
Проблема 18:
Что есть значение
, если a = 3, b = -1 и c = -2.
Решение:
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Что такое правило БОДМАСА и как оно применяется в математике
- Дом
- >
- Блог
- >
- Что такое правило БОДМАСА и как оно применяется в математике
Джессика Камински
5 минут чтения
20 мая 2022 г.
Что такое БОДМАС в математике? В математике правило BODMAS или Bodmas определяет порядок операций, которым необходимо следовать при выполнении вычислений. Ребенку необходимо знать, в каком порядке выполнять действия, чтобы получить правильный ответ. Это руководство поможет вам понять, как применять правило к математическим задачам.
Что такое БОДМАС?
Что означает БОДМАС? BODMAS означает скобки, порядки (степени и корни), деление, умножение, сложение и вычитание. Интерпретация правила такова: сначала нужно решать скобки, затем порядки (степени, квадратные корни), деление и умножение, и, наконец, сложение и вычитание.
Порядок операций BODMAS важен, поскольку все мы можем по-разному интерпретировать арифметические выражения. Один человек может первым складывать, а другой может первым умножать. Использование BODMAS гарантирует, что все производят вычисления в заданном математическом выражении по одному и тому же шаблону.
BODMAS помогает нам узнать правильный порядок операций для решения математических задач. Кроме того, правило говорит нам, что мы должны найти ответ на любую сумму в определенном порядке. Вот краткое изложение того, как мы можем прийти к правильному ответу при работе с BODMAS:
Кроме того, правило говорит нам, что мы должны найти ответ на любую сумму в определенном порядке. Вот краткое изложение того, как мы можем прийти к правильному ответу при работе с BODMAS:
Числа
Числа — это объекты, которые позволяют нам считать вещи, сравнивать суммы и производить вычисления. Мы не отдаем приоритет числам в BODMAS. Мы относимся к ним как к равным, независимо от того, маленькие они или большие.
1:1 Уроки математики
Хотите воспитать гения?
Начните изучать математику с Brighterly
Давайте начнем изучать математику!
Операторы
Операторы — это символы, которые выполняют математические операции со значением. Они применимы в выражениях, которые представляют собой группы символов, оценивающие одно значение. Кроме того, математические операторы — это символы, представляющие действия, такие как сложение или умножение. Операторы выполняют определенные действия при использовании в математических уравнениях. Это:
Это:
- Дополнение (+)
- Вычитание (-)
- Отдел (/)
- Умножение (*)
BODMAS Пример
Порядок операций всегда важен. Например, возьмем выражение
3 + 2 x 5 =
. Поскольку в нем нет скобок и порядков, перед сложением чисел необходимо выполнить умножение. Это потому, что умножение имеет более высокий приоритет, чем сложение.
BODMAS Значение
Полная форма BODMAS: Скобки, Порядок, Деление, Умножение, Сложение и Вычитание. Вам необходимо следовать этому порядку при выполнении вычислений, включающих более одной операции. Если вы не будете следовать ему, вы получите неправильный ответ.
Как использовать правило БОДМАС
Правило БОДМАС в математике:
- Если есть скобки, то сначала решить скобки.
- Если скобок нет, то сначала решить Приказы.
- Если порядок не очевиден, решите Умножение и Деление.
- Если нет ни умножения, ни деления, решите сложение и вычитание.

- Сложение и вычитание слева направо.
Порядок, в котором вы выполняете операции, важен, потому что он определяет, как вычислить окончательный ответ. Например, вам нужно вычислить ответ на это уравнение:
2 + 3 x 4
Вы получите ответ 20, если сначала выполните сложение, а затем умножение. Однако, если вы сначала выполнили умножение, а затем сложение, вы получите ответ 14. Другими словами, порядок, в котором вы выполняете операции, может изменить окончательный ответ.
BODMAS против PEMDAS
BODMAS и PEMDAS — это аббревиатуры, призванные помочь вам запомнить порядок операций в математике. Их также можно использовать при решении уравнений, поскольку оба обозначают порядок операций.
Разница между этими двумя правилами в том, что они работают по-разному. Мы используем BODMAS, когда в скобках или квадратных скобках есть несколько операций. Мы применяем PEMDAS в случае нескольких операций вне круглых или квадратных скобок.
PEMDAS означает Скобки, Экспоненты, Умножение, Деление, Сложение и Вычитание, тогда как BODMAS означает Скобки, Порядки (или экспоненты), Деление, Умножение, Сложение и Вычитание.
Эти два метода имеют одинаковые шаги для решения проблемы. Разница в том, как вы их применяете. В BODMAS операционные приказы следуют слева направо, а в PEMDAS — справа налево.
Как и когда преподается БОДМАС?
BODMAS следует преподавать после того, как дети изучили четыре действия с числами: сложение, вычитание, умножение и деление. Правило БОДМАСа обычно изучают в начальной школе учащиеся в возрасте 9-12 лет и используют для выполнения математических операций в правильном порядке.
Заключение
Если вы не уверены в последовательности операций, используйте BODMAS, чтобы определиться с выбором.
Как только учитель убедится, что дети понимают концепцию БОДМАС и могут применять ее для решения простых задач, он может продолжить использовать правило в более сложных задачах.
