правила, примеры, решения, как вычесть из десятичной дроби обыкновенную дробь
Изучаем другие действия, которые можно совершать с десятичными дробями. В этом материале мы узнаем, как правильно подсчитать разность десятичных дробей. Отдельно разберем правила для конечных и бесконечных дробей (как периодических, так и непериодических), а также посмотрим, как считать разность дробей столбиком. Во второй части мы объясним, как вычесть десятичную дробь из натурального числа, обыкновенной дроби, смешанного числа.
Отметим заранее, что в этой статье рассмотрены только случаи, когда меньшая дробь вычитается из большей, т.е. результат этого действия положителен; другие случаи относятся к нахождению разности рациональных и действительных чисел и должны быть объяснены отдельно.
Основные правила вычитания десятичных дробей
Процесс вычисления как конечных, так и бесконечных периодических десятичных дробей можно свести к нахождению разности дробей обыкновенных. Раньше мы говорили о том, что десятичные дроби можно записывать в виде обыкновенных дробей. Исходя из этого правила, разберем несколько примеров нахождения разности.
Исходя из этого правила, разберем несколько примеров нахождения разности.
Найдите разность 3,7-0,31.
Решение
Переписываем десятичные дроби в виде обыкновенных: 3,7=3710 и 0,31=31100.
Что делать потом, мы уже изучали. Мы получили ответ, который переводим обратно в десятичную дробь: 339100=3,39.
Подсчеты, связанные с десятичными дробями, удобно производить столбиком. Как же пользоваться этим методом? Покажем, решив задачу.
Пример 2Вычислите разность между периодической дробью 0, (4) и периодической десятичной дробью 0,41(6).
Решение
Переведем записи периодических дробей в обыкновенные и подсчитаем.
0,4(4)=0,4+0,004+…=0,41-0,1=0,40,9=49.0,41(6)=0,41+(0,006+0,0006+…)=41100+0,0060,9==41100+6900=41100+1150=123300+2300=125300=512
Итого: 0,(4)-0,41(6)=49-512=1636-1536=136
Если нужно, ответ мы можем представить в виде десятичной дроби:
Ответ: 0,(4) −0,41(6) =0,02(7).
Разберем далее, как найти разность, если у нас в условиях стоят бесконечные непериодические дроби. Такой случай также можно свести к нахождению разности конечных десятичных дробей, для чего понадобится округлить бесконечные дроби до определенного разряда (обычно самого меньшего из возможных).
Пример 3Найдите разность 2, 77369…-0,52.
Решение
Вторая дробь в условии – конечная, а первая – бесконечная непериодическая. Мы можем округлить ее до четырех знаков после запятой: 2,77369…≈2,7737. После этого можно выполнять вычитание: 2,77369…−0,52≈2,7737−0,52.
Ответ: 2,2537.
Как считать разность десятичных дробей столбиком
Вычитание столбиком – быстрый и наглядный способ узнать разность конечных десятичных дробей. Процесс подсчета очень схож с аналогичным для натуральных чисел.
Определение 1Чтобы подсчитать разность десятичных дробей столбиком, необходимо:
- если в указанных десятичных дробях отличается количество знаков после запятой, уравняем его.
 Для этого допишем к нужной дроби нули;
Для этого допишем к нужной дроби нули; - запишем вычитаемую дробь под уменьшаемой, разместив значения разрядов строго друг под другом, а запятую под запятой;
- выполним подсчет столбиком так же, как мы это делаем для натуральных чисел, запятую при этом игнорируем;
- в ответе отделим нужное количество чисел запятой так, чтобы она располагалась на том же месте.
Разберем конкретный пример использования этого метода на практике.
Пример 4Найдите разность 4 452,294-10,30501.
Решение
Для начала выполним первый шаг – уравняем количество десятичных знаков. Допишем два нуля в первую дробь и получим дробь вида 4 452,29400, значение которой идентично исходной.
Запишем получившиеся числа друг под другом в нужном порядке, чтобы получился столбик:
Считаем как обычно, игнорируя запятые:
В получившемся ответе поставим запятую в нужном месте:
Подсчеты окончены.
Наш результат : 4 452,294−10,30501=4 441,98899.
Как вычесть натуральное число из десятичной дроби и наоборот
Найти разность между конечной десятичной дробью и натуральным числом легче всего описанным выше способом – столбиком. Для этого число, из которого мы вычитаем, необходимо записать в виде десятичной дроби, в дробной части которой стоят нули.
Пример 5Вычислите 15-7,32.
Запишем уменьшаемое число 15 в виде дроби 15,00, поскольку дробь, которую нам нужно вычесть, имеет два знака после запятой. Далее выполняем подсчет столбиком, как обычно:
Таким образом, 15−7,32=7,68.
Если из натурального числа нам нужно вычесть бесконечную периодическую дробь, то мы опять же сводим эту задачу к аналогичному вычислению. Заменяем периодическую десятичную дробь на обыкновенную.
Пример 6Вычислите разность 1-0, (6).
Решение
Указанной в условии периодической десятичной дроби соответствует обычная 23.
Считаем: 1−0,(6)=1−23=13.
Полученный ответ можно перевести в периодическую дробь 0,(3).
Если данная в условии дробь непериодическая, поступаем так же, предварительно округлив ее до нужного разряда.
Пример 7Отнимите 4,274… от 5.
Решение
Указанную бесконечную дробь мы округлим до сотых и получим 4,274…≈4,27.
После этого вычисляем 5−4,274…≈5−4,27.
Преобразуем 5 в 5,00 и запишем столбик:
В итоге 5−4,274…≈0,73.
Если перед нами стоит обратная задача – вычесть натуральное число из десятичной дроби, то мы выполняем вычитание из целой части дроби, а дробную часть не трогаем совсем. Мы поступаем так и с конечными, и с бесконечными дробями.
Пример 8Найдите разность 37,505 – 17.
Решение
Отделяем от дроби целую часть 37 и вычитаем требуемое число из нее. Получаем 37,505−17=20,505.
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Эту задачу также необходимо свести к вычитанию обыкновенных дробей – как в случае со смешанными числами, так и с десятичными дробями.
Вычислите разность 0,25-45.
Решение
Представим 0,25 в виде обыкновенной дроби – 0,25=25100=14.
Теперь нам нужно найти разность между 14и 45.
Считаем: 45−0,25=45−14=1620−520=1120.
Запишем ответ в виде десятичной записи: 0,55.
Если в условии стоит смешанное число, из которого надо вычесть конечную или периодическую десятичную дробь, то поступаем аналогично.
Пример 10Условие: отнимите 0,(18) от 8411.
Решение
Перепишем периодическую дробь в виде обыкновенной. 0,(18)=0,18+0,0018+0,000018+…=0,181-0,01=0,180,99=1899=211
Получается, что 8411-0,(18)=8411-211=8211.
В виде десятичной дроби ответ можно записать как 8,(18).
Таким же образом мы действуем, когда вычитаем смешанное число или обыкновенную дробь из конечной или периодической дроби.
Пример 11Подсчитайте 940-0,03.
Решение
Заменяем дробь 0,03 на обыкновенную 3100.
У нас получается, что: 940−0,03=940−3100=90400−12400=78400=39200
Ответ можно оставить так или преобразовать в десятичную дробь 0,195.
Если нам требуется выполнять вычитание с участием бесконечных непериодических дробей, то нам нужно будет свести их к конечным. Со смешанными числами поступаем аналогично. Для этого запишем обыкновенную дробь или смешанное число в виде десятичной дроби и округлим вычитаемую дробь до определенного разряда. Проиллюстрируем нашу мысль примером:
Пример 12Отнимите 4,38475603…. из 1027.
Решение
Преобразуем смешанное число в неправильную дробь.
1027=10·7+27=727
Далее эту дробь запишем в десятичном виде и получим 10, (285714).
В итоге 1027-4,38475603…=10,(285714)-4,38475603….
Теперь округлим вычитаемые числа до седьмого знака: 10, (285714) =10,285714285714…≈10,2857143 и 4,38475603…≈4,3847560
Тогда 10, (285714) −4,38475603…≈10,2857143−4,3847560.
Единственное, что осталось сделать – вычесть одну конечную десятичную дробь из другой. Выполним подсчет столбиком:
Ответ: 1027-4,38475603…≈5,9009583
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Вычитание десятичных дробей — правила и алгоритмы решения » Kupuk.net
Для большинства повседневных дел, так или иначе связанных с вычислениями, хватает понимания операций над «простыми», целыми, числами. Но иногда нужно знать, как производится вычитание десятичных дробей. Например, именно с их помощью обычно указывают объём жидкости в бутылке, будь то вода или моющее средство.
Но иногда нужно знать, как производится вычитание десятичных дробей. Например, именно с их помощью обычно указывают объём жидкости в бутылке, будь то вода или моющее средство.
Определение дроби
До перехода к тому, как отнимают десятичные дроби, нужно определить, как их записывают и чем они являются в принципе. Так называют частный вариант обычного дробного выражения, у которого знаменатель — степень десяти. Фактически при записи такого числа его отбрасывают и пишут числитель через запятую (или точку, в некоторых странах) после целой части. Например, «¼» будет записана как 0,25.
В изначальной дроби целой части не было, поэтому перед запятой стоит 0.
Над десятичными дробями можно производить все те же действия, что и над обычными. То есть их можно:
- складывать;
- вычитать;
- делить;
- умножать.
С этой темой знакомятся в пятом классе школьного курса и начинают с первых двух действий, ввиду их простоты в сравнении с последними двумя.
Сложение и вычитание
При необходимости сложить или отнять от одного дробного числа другое, нужно пользоваться тем же алгоритмом действий, как и при вычитании/сложении двух чисел столбиком, с некоторой разницей касательно записи нулей. Понять, как вычитать десятичные дроби столбиком, несложно.
Например, если необходимо от «14,635» отнять «7,12», то нужно записать 7 под 4. Под 5 ничего нет, так как у второго числа только 2 знака после запятой. В таком случае дописывают 0, так как у дробного числа нули, дописанные после знака запятой, ничего не «весят» и не меняют число.
Следующий шаг — вычесть эти 2 числа друг из друга столбиком, как если бы это были обычные числа. В конкретном примере ответом будет «7,515». Сложение происходит по тому же принципу — записать числа друг под другом относительно запятой и добавить в конце нули, если необходимо. Если в задаче требуется сложить положительное и отрицательное число, это по сути вычитание и нужно руководствоваться соответствующими правилами.
Нужно также знать, как из натурального числа вычесть десятичную дробь. Найти такую разность несложно. Опять же, проще всего это сделать в столбик. Пример — вычесть из 6 1,24. У второго числа после запятой находиться 2 символа. Значит, нужно написать запятую и добавить 2 нуля первому — «6,00». Это не влияет на размер, но позволяет «минусовать» от натурального числа дробное. Ответом будет 4,76.
Сложение, в свою очередь, гораздо проще. Знаки после запятой просто переписываются, а целая часть складывается. Используя те же числа, что в предыдущем примере: 6 + 1,24 = 7,24.
Умножение и деление
Вычисление разности и суммы — дело нехитрое. Умножение, а в особенности деление, уже сложнее и принципиально отличается. Для начала имеет смысл рассмотреть умножение, так как оно будет в результате использоваться и в делении.
Правило умножения несложное. При перемножении двух десятичных дробей знак запятой учитывается постфактум. Например, необходимо перемножить 1,45 на 3,59. Запятые «отбрасываются» и теперь умножаются 145 и 359. Промежуточный ответ — 24505. Теперь необходимо учесть запятые. Следует вернуться к изначальному выражению и посчитать количество знаков после запятой в каждом числе и суммировать это значение.
Например, необходимо перемножить 1,45 на 3,59. Запятые «отбрасываются» и теперь умножаются 145 и 359. Промежуточный ответ — 24505. Теперь необходимо учесть запятые. Следует вернуться к изначальному выражению и посчитать количество знаков после запятой в каждом числе и суммировать это значение.
В конкретном примере у обеих десятичных дробей 2 знака, а значит общая сумма — 4. Столько же знаков после запятой должно быть и у полученного ранее произведения. С конца отсчитываются 4 цифры и ставится запятая. Окончательный ответ — 2,4505.
Важно помнить, что если в конце произведения оказались нули, они тоже учитываются. Но после выставления запятой их можно отбросить, так как, например, 4,600 = 4,6, а лишние символы будут лишь мешать.
Деление, в свою очередь, «в лоб» не считается. Нужно провести преобразования и фактически свести деление к умножению. Для этого необходимо следовать алгоритму:

Для переведения десятичной в обычную дробь нужно вернуться к её определению — значения после запятой — это числитель. Знаменатель — это степень десяти и его не записывают.
Следовательно, 0,625 можно представить, как 625/1000. Количество нулей в знаменателе будет каждый раз разным, но здесь всё просто — оно должно совпадать с количеством символов после запятой. В примере дано 0,625, цифр 3, следовательно, в знаменателе 1000. Если было бы 2 цифры, в знаменатель пошла 10 во второй степени — 100, и так далее.
Полученную дробь сокращать сразу не нужно, так как это затруднит последующий процесс вычисления. При делении обычных дробей выражение, на которое делят, «переворачивается», а знак заменяется на умножение.
Допустим, нужно поделить 0,25 на 0,5. 25/100 делится на 5/10. Или же 25/100 умноженное на 10/5. Очевидно, что их легко можно сократить и получится 5/10 или же 0,5.
Вычитание десятичных дробей — правила и алгоритмы решения
Для большинства повседневных дел, так или иначе связанных с вычислениями, хватает понимания операций над «простыми», целыми, числами. Но иногда нужно знать, как производится вычитание десятичных дробей. Например, именно с их помощью обычно указывают объём жидкости в бутылке, будь то вода или моющее средство.
Содержание
- Определение дроби
- Сложение и вычитание
- Умножение и деление
Определение дроби
До перехода к тому, как отнимают десятичные дроби, нужно определить, как их записывают и чем они являются в принципе. Так называют частный вариант обычного дробного выражения, у которого знаменатель — степень десяти. Фактически при записи такого числа его отбрасывают и пишут числитель через запятую (или точку, в некоторых странах) после целой части. Например, «¼» будет записана как 0,25.
В изначальной дроби целой части не было, поэтому перед запятой стоит 0.
Над десятичными дробями можно производить все те же действия, что и над обычными. То есть их можно:
- складывать;
- вычитать;
- делить;
- умножать.
С этой темой знакомятся в пятом классе школьного курса и начинают с первых двух действий, ввиду их простоты в сравнении с последними двумя.
Сложение и вычитание
При необходимости сложить или отнять от одного дробного числа другое, нужно пользоваться тем же алгоритмом действий, как и при вычитании/сложении двух чисел столбиком, с некоторой разницей касательно записи нулей. Понять, как вычитать десятичные дроби столбиком, несложно.
Например, если необходимо от «14,635» отнять «7,12», то нужно записать 7 под 4. Под 5 ничего нет, так как у второго числа только 2 знака после запятой. В таком случае дописывают 0, так как у дробного числа нули, дописанные после знака запятой, ничего не «весят» и не меняют число.
Следующий шаг — вычесть эти 2 числа друг из друга столбиком, как если бы это были обычные числа. В конкретном примере ответом будет «7,515». Сложение происходит по тому же принципу — записать числа друг под другом относительно запятой и добавить в конце нули, если необходимо. Если в задаче требуется сложить положительное и отрицательное число, это по сути вычитание и нужно руководствоваться соответствующими правилами.
Нужно также знать, как из натурального числа вычесть десятичную дробь. Найти такую разность несложно. Опять же, проще всего это сделать в столбик. Пример — вычесть из 6 1,24. У второго числа после запятой находиться 2 символа. Значит, нужно написать запятую и добавить 2 нуля первому — «6,00». Это не влияет на размер, но позволяет «минусовать» от натурального числа дробное. Ответом будет 4,76.
Сложение, в свою очередь, гораздо проще. Знаки после запятой просто переписываются, а целая часть складывается.
Используя те же числа, что в предыдущем примере: 6 + 1,24 = 7,24.
Умножение и деление
Вычисление разности и суммы — дело нехитрое. Умножение, а в особенности деление, уже сложнее и принципиально отличается. Для начала имеет смысл рассмотреть умножение, так как оно будет в результате использоваться и в делении.
Правило умножения несложное. При перемножении двух десятичных дробей знак запятой учитывается постфактум. Например, необходимо перемножить 1,45 на 3,59. Запятые «отбрасываются» и теперь умножаются 145 и 359. Промежуточный ответ — 24505. Теперь необходимо учесть запятые. Следует вернуться к изначальному выражению и посчитать количество знаков после запятой в каждом числе и суммировать это значение.
В конкретном примере у обеих десятичных дробей 2 знака, а значит общая сумма — 4. Столько же знаков после запятой должно быть и у полученного ранее произведения. С конца отсчитываются 4 цифры и ставится запятая.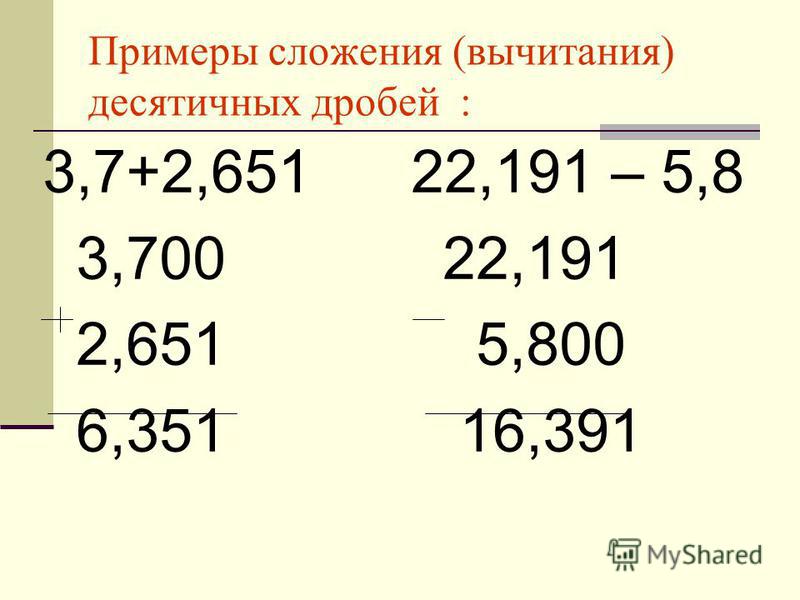 Окончательный ответ — 2,4505.
Окончательный ответ — 2,4505.
Важно помнить, что если в конце произведения оказались нули, они тоже учитываются. Но после выставления запятой их можно отбросить, так как, например, 4,600 = 4,6, а лишние символы будут лишь мешать.
Деление, в свою очередь, «в лоб» не считается. Нужно провести преобразования и фактически свести деление к умножению. Для этого необходимо следовать алгоритму:
Для переведения десятичной в обычную дробь нужно вернуться к её определению — значения после запятой — это числитель. Знаменатель — это степень десяти и его не записывают.
Следовательно, 0,625 можно представить, как 625/1000. Количество нулей в знаменателе будет каждый раз разным, но здесь всё просто — оно должно совпадать с количеством символов после запятой. В примере дано 0,625, цифр 3, следовательно, в знаменателе 1000. Если было бы 2 цифры, в знаменатель пошла 10 во второй степени — 100, и так далее.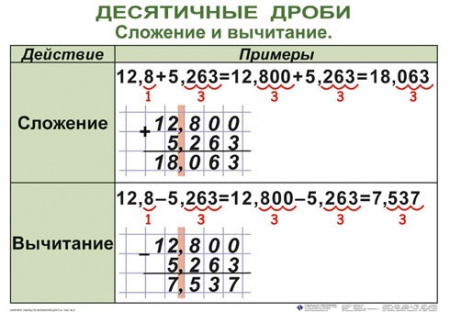
Полученную дробь сокращать сразу не нужно, так как это затруднит последующий процесс вычисления. При делении обычных дробей выражение, на которое делят, «переворачивается», а знак заменяется на умножение.
Допустим, нужно поделить 0,25 на 0,5. 25/100 делится на 5/10. Или же 25/100 умноженное на 10/5. Очевидно, что их легко можно сократить и получится 5/10 или же 0,5.
Предыдущая
МатематикаДеление с остатком — алгоритмы и примеры решения для 5 класса
Следующая
МатематикаПриведение дробей к общему знаменателю — алгоритмы и правила для 5 класса
Вычитание десятичных дробей — определение, правила, факты, примеры
Вычитание десятичных дробей означает нахождение разницы между десятичными числами и другими числами. Другое число может быть целым числом, десятичным числом или натуральным числом. Существуют определенные правила и шаги, которые необходимо учитывать при вычитании десятичных знаков. На этой странице мы узнаем больше о вычитании десятичных дробей, их правилах и примерах.
На этой странице мы узнаем больше о вычитании десятичных дробей, их правилах и примерах.
| 1. | Что такое вычитание десятичных дробей? |
| 2. | Правила вычитания десятичных дробей |
| 3. | Вычитание десятичных дробей с перегруппировкой |
| 4. | Вычитание десятичных дробей из целых чисел |
| 5. | Часто задаваемые вопросы о вычитании десятичных дробей |
Что такое вычитание десятичных дробей?
Вычитание десятичных дробей аналогично обычному вычитанию целых чисел. Нам просто нужно разместить десятичные числа, одно под другим, в соответствии с их разрядностью вместе с десятичной точкой. В некоторых случаях два заданных числа различны. При необходимости меняем данные десятичные дроби на , как десятичные дроби , чтобы упростить вычитание. Два десятичных знака называются , как и десятичные дроби , если они имеют одинаковое количество знаков после запятой. Например, 0,23 и 0,65 похожи на десятичные дроби, тогда как 7,5 и 7,58 не похожи на десятичные дроби. После того, как десятичные числа преобразуются в
Два десятичных знака называются , как и десятичные дроби , если они имеют одинаковое количество знаков после запятой. Например, 0,23 и 0,65 похожи на десятичные дроби, тогда как 7,5 и 7,58 не похожи на десятичные дроби. После того, как десятичные числа преобразуются в
Например, вычтем данные числа:
Пример: Вычесть: 0,56 — 0,42.
Решение:
Так как это как десятичные дроби , мы расположим их по порядку и выполним обычное вычитание.
0,56
-0,42
0,14
Правила вычитания десятичных дробей
Существуют определенные правила и шаги, которые следует помнить при вычитании десятичных знаков.
- Изменить данные десятичные дроби на как десятичные дроби .
- Запишите меньшее число под большим так, чтобы цифры располагались на соответствующих местах, а десятичные запятые располагались на одной вертикальной линии.

- Затем вычтите числа так же, как и в случае с целыми числами.
- После вычитания поместите десятичную точку на одной линии с другими десятичными точками.
Вычитание десятичных дробей с перегруппировкой
Вычитание десятичных дробей с перегруппировкой аналогично перегруппировке целых чисел. Следующие шаги объясняют способ вычитания десятичных дробей путем перегруппировки.
- Шаг 1: После изменения чисел на , как десятичных дробей , и размещения меньшего числа под большим числом, убедитесь, что десятичные точки выровнены, а цифры размещены в соответствующем столбце разряда.
- Шаг 2: Вычтите цифры в каждом столбце отдельно, начиная справа и двигаясь влево.
- Шаг 3: Если число в верхней строке меньше числа в нижней строке, мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот шаг известен как перегруппировка.
- Шаг 4: Поскольку 1 был заимствован, это число уменьшается на 1.
 Соответственно измените число и продолжайте вычитание.
Соответственно измените число и продолжайте вычитание.
Например, давайте вычтем данные числа.
Пример: Вычтите 0,84 из 0,93.
Решение:
В приведенных выше числах 0,93 и 0,84 цифра 3 меньше, чем 4 в столбце сотых, поэтому нам нужно заимствовать 1 из 9, чтобы выполнить вычитание. Нам нужно уменьшить 1 из 9, так как он дал 1 к числу слева от него. Итак, 9 станет 8, а 3 станет 13. Теперь вычитаем 13 — 4 = 9 и 8 — 8 = 0
Наконец, мы помещаем десятичную точку в ответ, чтобы получить 0,09
Вычитание десятичных знаков с одинаковым количеством знаков после запятой
Вычитание десятичных знаков с одинаковым количеством знаков после запятой очень просто. Нам просто нужно выполнить простой процесс вычитания, а затем расставить десятичные точки в соответствии с заданными числами.
Например, давайте вычтем 3,67 из 4,98
Мы видим, что числа имеют одинаковые десятичные разряды. Итак, мы будем вычитать их обычным способом.
4,98
-3,67
1,31
Вычитание десятичных знаков с разными десятичными разрядами В этом случае мы подсчитываем количество знаков после запятой в обоих числах и определяем в них большее. Затем мы добавляем необходимое количество нулей к меньшему десятичному числу, чтобы сделать его такой же длины, как и другое число. После этого мы вычитаем десятичные числа.
Например, давайте вычтем 7,483 из 237,8
Мы видим, что оба числа имеют разные десятичные разряды. Поскольку 7,483 имеет 3 цифры после запятой, мы добавим два нуля к 237,8, чтобы привести его к той же длине. Это составит 237.800, после чего мы вычтем числа.
237,800
— 7,483
230,317
Вычитание десятичных дробей из 1
Для вычитания десятичных дробей из 1 мы используем ту же процедуру, что и для других десятичных чисел. Десятичные числа в пределах 1 означают, что данные числа меньше 1.
Например, вычтем 0,56 из 0,98.
Мы видим, что числа находятся в пределах единицы. Итак, чтобы решить эту проблему, мы расставим числа по порядку и сделаем обычное вычитание.
0,98
-0,56
0,42
Вычитание десятичных дробей из целых чисел
Чтобы вычесть десятичные числа из целых чисел, мы помещаем десятичную точку в целое число в соответствии с количеством цифр (после запятой) в другом числе. Затем добавляем необходимое количество нулей, чтобы оба числа имели одинаковую длину.
Например, давайте вычтем 0,999 из 6.
Решение: Поскольку в числе 0,999 после запятой три цифры, мы поставим десятичную запятую после 6 и добавим после нее три нуля.
Статьи по теме
Ознакомьтесь со следующими темами, связанными с вычитанием десятичных дробей.
- Вычитание
- Двоичное вычитание
- Калькулятор вычитания десятичных дробей
Часто задаваемые вопросы о вычитании десятичных знаков
Как вычитать десятичные дроби, если верхнее число меньше?
При вычитании десятичных знаков, если число в верхней строке меньше числа в нижней строке, мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот процесс также называется перегруппировкой или заимствованием. После этого соответствующим образом меняем число и продолжаем вычитание. Поскольку 1 присваивается следующему числу, это число уменьшается на 1. Давайте поймем это, вычитая данные числа.
Этот процесс также называется перегруппировкой или заимствованием. После этого соответствующим образом меняем число и продолжаем вычитание. Поскольку 1 присваивается следующему числу, это число уменьшается на 1. Давайте поймем это, вычитая данные числа.
3,52
-0,45
3,07
В этом случае, если мы посмотрим на цифры в столбце сотых, мы увидим, что 2 меньше 5, поэтому мы заимствуем 1 из предыдущего столбца (столбца десятых) и перегруппируем это число, то есть 2 станет 12. Из 12 вычтем 5 и получим 7. Теперь, так как из десятого столбца дана 1, 5 сводится к 4, а 4 — 4 = 0. После этого вычитание продолжается в обычным способом, и ответ, который мы получаем после вычитания, равен 3,07.
Какие советы по вычитанию десятичных дробей?
Для вычитания десятичных дробей нам нужно помнить несколько полезных советов.
- Запишите числа в таком порядке, чтобы большее число располагалось над меньшим, а десятичные запятые совпадали.

- Добавьте нули к нужному числу, чтобы оба числа были одинаковой длины.
- Затем вычтите числа так же, как и в случае с целыми числами, и соответствующим образом поставьте десятичную точку.
Как брать взаймы при вычитании десятичных дробей?
При вычитании десятичных дробей могут быть случаи, когда число в первой строке меньше числа во второй строке. В этом случае мы заимствуем 1 из цифры слева и добавляем 10 к текущей цифре. Этот процесс также называется перегруппировкой или заимствованием. Например, если нам нужно вычесть 3,58 из 5,4, мы увидим, что в столбце сотых 0 меньше 8.
5,40
-3,58
1.82
Итак, заимствуем 1 из десятого столбца и перегруппируем число 0 как 10 + 0 = 10. Вычтем 8 из 10 и получим 2. Теперь, поскольку 1 была дана из десятого столбца, 4 сводится к 3 что снова приводит к заимствованию числа из столбца единиц. Итак, 3 становится 13, и мы вычитаем 5 из 13, чтобы получить 8. Переходя к следующему столбцу (столбец единиц), пересекая десятичные дроби, 5 уменьшается до 4 и 4 — 3 = 1. Это дает окончательный ответ как 1,82.
Это дает окончательный ответ как 1,82.
Как вычитать десятичные дроби из целых чисел?
Чтобы вычесть десятичные числа из целых чисел, мы помещаем десятичную точку в целое число в соответствии с количеством цифр (после запятой) в другом числе. Затем добавляем необходимое количество нулей, чтобы оба числа имели одинаковую длину. Например, чтобы решить эти числа, 4 — 0,67, мы можем записать это как 4,00 — 0,67. Теперь мы можем легко вычитать числа. (4,00 — 0,67 = 3,33)
Каково правило сложения и вычитания десятичных дробей?
Основные правила сложения и вычитания десятичных знаков следующие:
- Изменить данные десятичные дроби на как десятичные дроби .
- Выровняйте числа таким образом, чтобы цифры располагались на соответствующих местах в соответствии с их разрядными значениями, а десятичные запятые располагались на одной вертикальной линии.
- Затем вычтите числа так же, как и в случае с целыми числами, и соответствующим образом поставьте десятичную точку.

Чем сложение десятичных знаков похоже на вычитание десятичных?
Сложение десятичных знаков аналогично вычитанию десятичных знаков, поскольку в обоих случаях используются одни и те же правила. Нам нужно разместить десятичные числа одно под другим, в соответствии с их разрядностью вместе с десятичной точкой. Прежде всего, нам нужно изменить данные десятичные дроби на , как десятичные дроби , чтобы упростить сложение или вычитание. После того, как десятичные числа преобразуются в подобно десятичным дробям , путем добавления необходимого количества нулей два заданных числа складываются или вычитаются так же, как мы решаем обычные числа.
Приведите пример вычитания десятичных дробей.
Вычитание десятичных дробей аналогично вычитанию целых чисел. Единственное, что нужно иметь в виду, это то, что десятичные точки должны быть выровнены, а заданные числа должны быть одинаковой длины. Например, вычтем из 2 0,456. Для этого сначала нужно поставить десятичную точку после 2 и после этого поставить три нуля, чтобы числа были одинаковой длины. После этого выравниваем цифры и вычитаем числа обычным способом. (2,000 — 0,456 = 1,544)
После этого выравниваем цифры и вычитаем числа обычным способом. (2,000 — 0,456 = 1,544)
Что такое вычитание десятичных дробей? Определение, правила, примеры, факты
Бен покупает продукты на $\$$155,50. Он передает продавцу $\$$500 и, в свою очередь, получает обратно $\$$344,50.
Без знания десятичных дробей узнать точную сумму, которую он должен был заплатить за продукты, было бы невозможно.
Десятичные числа — это числа, в которых есть десятичная точка. Они состоят из двух частей: первая — целое число (слева от запятой), а вторая — дробная часть (справа от запятой).
Например, Сэм покупает апельсины за $\$$3,50. Здесь
- $\$$3,50 — десятичное число (цена апельсинов)
- 3 — целое число (слева от запятой)
- 50 — дробная часть (справа от запятой) )
Десятичные дроби повышают точность счета и часто используются в повседневной деятельности.
Десятичные числа можно складывать, вычитать, умножать или делить в зависимости от конкретного сценария. Сегодня мы обсудим вычитание десятичных дробей , их правила и несколько примеров.
Сегодня мы обсудим вычитание десятичных дробей , их правила и несколько примеров.
Как вычитать десятичные дроби
Вычитать десятичные дроби так же просто, как найти разницу между большим целым числом и меньшим целым числом. Возьмем первый пример, где цена на продукты составляла $\$$155,50. В этом сценарии 155 — это целое число, а 0,50 — его дробная часть.
В зависимости от разрядности десятичные числа должны располагаться одно под другим, не забывая при вычитании десятичной точки. Однако, если два десятичных числа различны, вычитание может быть немного сложным.
Следовательно, чтобы избежать такой путаницы, десятичные числа можно изменить на , как и десятичные числа , добавив необходимое количество нулей.
Количество знаков после запятой будет одинаковым в одинаковых десятичных дробях. Например, 5,23 и 7,89 похожи на десятичные дроби, тогда как 4,53 и 2,753 не похожи на десятичные дроби.
Вычитание десятичных дробей без перегруппировки
Допустим, нам нужно вычесть 14,2 из 25,83. Вот как это сделать.
Вот как это сделать.
Шаг 1 : 25,83 и 14,2 отличаются от десятичных дробей. Итак, сначала нам нужно преобразовать их в одинаковые десятичные дроби, добавив ноль в крайний правый угол числа 14,2, чтобы получилось 14,20.
Шаг 2 : Расположите меньшее число под большим так, чтобы десятичные запятые совпадали.
Шаг 3: Вычтите каждый столбец справа налево, как если бы вычитали целое число.
Шаг 4 : Разместите десятичную точку на одной линии с другими десятичными точками.
Вычитание десятичных дробей с перегруппировкой
Перегруппировка при вычитании десятичных чисел очень похожа на перегруппировку, выполняемую при вычитании целых чисел. Давайте разберемся с помощью примера.
Возьмем пример вычитания десятичного числа 2,37 из 5,10. Вот как это сделать.
Шаг 1 : Десятичные дроби похожи на десятичные дроби. Итак, давайте перейдем к шагу 2.
Шаг 2: Расположите меньшее число под большим числом. Убедитесь, что цифры размещены в соответствии с их разрядами, а десятичные запятые точно выровнены.
Шаг 3: Вычтите каждый столбец отдельно, начиная справа и постепенно сдвигаясь влево.
- Если число в верхней строке меньше, чем в нижней, то из левой цифры следует заимствовать 1, добавляя 10 к соответствующей цифре. Это называется перегруппировка.
- После заимствования 1 из левой цифры она уменьшается на 1. Следовательно, вычитание можно продолжить с уменьшенным числом.
Вычитание десятичных знаков из целых чисел
Допустим, мы вычитаем десятичное число 0,569 (десятичное число) из 3 (целое число). Вот как это сделать:
Шаг 1 : Первым шагом является преобразование целого числа в десятичное число. Для этого мы добавляем десятичную точку и необходимое количество нулей справа от целого числа.
Помните, что количество добавляемых нулей должно совпадать с длиной другого заданного десятичного числа.
Здесь мы добавим три нуля после 3, чтобы получить 0,569. Таким образом, 3 станет 3.000.
Шаг 2: Расположите меньшее число под большим так, чтобы десятичные запятые совпадали.
Шаг 3: Вычтите числа, следуя обычному методу вычитания десятичных чисел.
Использование вычитания десятичных дробей в реальной жизни
Вычитание десятичных дробей используется в различных повседневных делах, некоторые из которых следующие: заплатите $\$$10 продавцу магазина. Затем, чтобы вернуть оставшуюся сумму, продавец возвращает нам $\$$4,50.
- Научные расчеты. Ученые используют десятичные числа для получения точных показаний в своих экспериментах.
- Медицинские показания: при использовании термометра для измерения температуры тела он покажет вам показания в виде десятичных чисел, например 98,6° F.

- Строительные измерения: Строительные проекты требуют измерения длины, ширины и высоты различных объектов , которые представлены десятичными числами.
- Здоровье и фитнес: различное оборудование для фитнеса, используемое в тренажерных залах, такое как гантели, штанги и т. д., имеет определенный предел веса, например, 8 или 10 фунтов, чтобы вы могли заниматься фитнесом в соответствии со своими возможностями. Беговая дорожка покажет вам мили, которые вы прошли или пробежали, с помощью десятичных чисел. Весы также отображают вес в десятичных дробях.
- Одометры: Вы можете рассчитать расстояние, пройденное на автомобиле или велосипеде, с помощью одометра, который использует десятичные точки для отображения точных показаний.
Решенные примеры
Пример 1. Вычтите 0,30 из 0,70.
Решение:
Пример 2: Вычтите 0,25 из 5,22.
Решение:
Пример 3: Вычтите 86,9 из 635,78.
Solution:
Practice Problems
1.37
3.25
0.96
1.55
Correct answer is: 1.37
$9.57 − 8.20 = 1.37$
1.37
6.05
8
7.15
Correct ответ: 1.37
Чтобы найти ответ, вы можете добавить к результату другое десятичное число.
Следовательно, пропущенное десятичное число равно 8.
Верно
Ложно
Правильный ответ: Ложно
При вычитании десятичного числа 79,98 с 298,20 мы получаем 218,22, а не 216,30
16,2
24,861
21,6
18,22
Правильный ответ: 24,861
. Сначала нам нужно, чтобы изменить децимальные номера, а также по изменению децимальных номеров, чтобы изменить Decimal Decimal Numbmal, а также по изменению Decimal Numbrim, а также по изменению Decimal Decimal-Decimal Numbermal. нули. Итак, 36.1 будет переписано как 36.100
нули. Итак, 36.1 будет переписано как 36.100
Тогда:
Часто задаваемые вопросы
Может ли вычитание десятичных чисел дать целое число?
Да, вычитая десятичные числа, можно получить в результате целое число. Однако цифры после запятой должны быть одинаковыми для обоих десятичных чисел.
Например, если из 4,25 вычесть 1,25, получится 3, то есть целое число.
Как проверить правильность вычитания двух десятичных чисел?
Чтобы проверить правильность вашего ответа после вычитания десятичных чисел, вы можете добавить результат с меньшим десятичным числом. Если ответ правильный, в результате вы получите большее десятичное число.
Например, если из 9,01 вычесть 2,33, получится 6,68. Теперь, если вы хотите проверить свой ответ, прибавьте 6,68 к 2,33. В результате вы получите 90,01, что означает, что ответ правильный.
Можно ли вычесть целое число из десятичного числа?
Да, целое число можно преобразовать в десятичное число, добавив нули после запятой.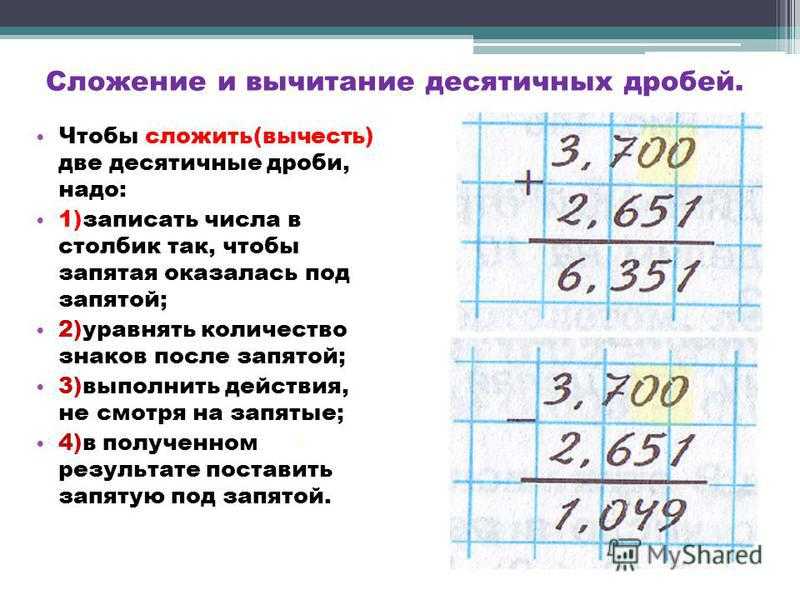 Затем процесс аналогичен вычитанию десятичных чисел.
Затем процесс аналогичен вычитанию десятичных чисел.
| Забавные факты – Китайцы были первыми, кто начал использовать дроби и десятичные числа. |
Изучите логарифмическую линейку
Изучите логарифмическую линейку — Раздел 02| Слайд правила ГЛАВНАЯ страница | ИНСТРУКЦИИ | СОДЕРЖАНИЕ |
РАЗДЕЛ ВТОРОЙ
Дроби — ДЕСЯТИЧНЫЕ
Дроби, сложение и вычитание — умножение и деление — Десятичные числа, Преобразование Десятичные дроби в обыкновенные дроби — Сложение и вычитание — Умножение и деление — Контрактные методы — Преобразование обычные дроби в десятичные дроби — повторяющиеся Десятичные дроби — Преобразование Повторяющиеся десятичные дроби в обычные дроби.
THE логарифмические шкалы логарифмических линеек, за некоторыми исключениями,
подразделяются на десятичные дроби, или, как мы чаще говорим, на десятичные дроби. это
невозможно использовать практические преимущества логарифмической линейки без практических знаний
десятичная система. Мы считаем, что краткое пояснение может помочь тем читателям, которые
думают, что логарифмическая линейка бесполезна для них, потому что они не могут легко работать с десятичными дробями.
Этот раздел не предназначен для читателей, знакомых с десятичной системой, и может
используйте его без труда.
это
невозможно использовать практические преимущества логарифмической линейки без практических знаний
десятичная система. Мы считаем, что краткое пояснение может помочь тем читателям, которые
думают, что логарифмическая линейка бесполезна для них, потому что они не могут легко работать с десятичными дробями.
Этот раздел не предназначен для читателей, знакомых с десятичной системой, и может
используйте его без труда.
Предлагаем начать с краткой справки об обыкновенных дробях.
Слово дробь означает «часть». Таким образом, когда мы говорим об дюйме, т.е.
иногда называемая обыкновенной дробью, в отличие от десятичной дроби — мы думаем о
длину 1″ разделить на две равные части, из которых мы возьмем одну часть. Когда мы
упоминая как дробь, мы думаем о чем-то, скажем, о ярде, или часе, или шиллинге,
делим на четыре равные части, из которых берем три. Верхняя фигура
обыкновенная дробь называется числителем, а меньшая цифра знаменателем. А
дробь, у которой числитель меньше знаменателя, всегда меньше 1, а
иногда называют правильной дробью. Дробь, например 7 / 5 ,
у которого числитель больше знаменателя, называется неправильным
дробная часть. Эти термины «собственный» и «неправильный» применительно к дробям не имеют практического значения.
важность.
Дробь, например 7 / 5 ,
у которого числитель больше знаменателя, называется неправильным
дробная часть. Эти термины «собственный» и «неправильный» применительно к дробям не имеют практического значения.
важность.
Значение дроби не меняется, если мы умножаем или делим числитель и знаменатель на любое число. Например,
| 3 | = | 3 х 4 | = | 12 | = | 12 х 2 | = | 24 | |
| 5 | 5 х 4 | 20 | 20 х 2 | 40 |
Дроби 3 /5, 12 /20 и 24 /40 точно равны друг другу, но мы можем
сказать, что 3 / 5 самая простая форма, и вообще это
как это написано. Вы увидите, что дробь можно сократить до 3 / 5 путем деления числителя и знаменателя на 8. Такое упрощение называется
отмена.
Вы увидите, что дробь можно сократить до 3 / 5 путем деления числителя и знаменателя на 8. Такое упрощение называется
отмена.
Сложение и вычитание
Чтобы сложить две или более дроби, мы выражаем их через общий знаменатель, а затем сложить числители.
Пример: сложите 2 / 3 и 4 / 5 .
| 2 | + | 4 | = | (2 х 5) | + | (4 х 3) | = | 10 | + | 12 | = | 22 | |
| 3 | 5 | (3 х 5) | (5 х 3) | 15 | 15 | 15 |
Результат: 22 / 16 или 1 7 / 15
Проблема 1 . Добавьте вместе 1 / 6 + 1 / 4 2 / 5
Добавьте вместе 1 / 6 + 1 / 4 2 / 5
Вычитание одной дроби из другой производится аналогичным образом.
Пример: Найдите результат взятия 1 / 6 из 3 / 8
Наименьшее число, кратное 6 и 8, равно
24.
| 3 | — | 1 | = | (3 х 3) | — | (1 х 4) | = | 9 | — | 4 | = | 5 | |
| 8 | 6 | (8 х 3) | (6 х 4) | 24 | 24 | 24 |
Умножение и деление
Чтобы перемножить две или более дроби, нужно только перемножить все
числители, чтобы сформировать числитель результата и умножить все знаменатели на
получить знаменатель результата.
| Пример: оценка | 2 | х | 4 | х | 2 | = | (2 х 4 х 2) | = | 16 |
| 3 | 5 | 7 | (3 х 5 х 7) | 105 |
Отмена чисел, общих как для числителя, так и для знаменателя, должна производиться по мере возможности, поскольку это ведет к упрощению.
Пример: оценка 1 / 3 x 3 / 5 х 1 1 / 4
Это может быть записано 1 / 3 x 3 / 5 x 5 / 4 = 1 / 4 отмена троек и пятерок
оставив только 1 в числителе и 4 в знаменателе.
Задача 2. Оценить 1 3 / 5 x 3 / 4 х 2 1 / 6
Деление можно рассматривать как частный случай умножения. Делить число на дробь можно поменять местами числитель и знаменатель делителя, а затем умножить на инвертированный коэффициент. Простой пример — деление на 2, которое точно так же, как умножение на .
Пример: разделить 3 / 4 на 2 / 5
Это должно быть написано 3 / 4 x 5 / 2 = 15 / 8 = 1 7 / 8
Задача 3. Разделить произведение 3 / 8 и 2 1 / 5 по 3 / 4 .
Десятичные числа
Слово «десятичный» происходит от латинского слова, означающего «десять». десятичная система основана на 10. Рассмотрим, например, число 8888, оно состоит из
8000 + 800 + 80 + 8. Очевидно, что не все восьмерки равноценны и
важность. Первые 8 выражают число тысяч, вторые число
сотни, третья — количество десятков, а последняя — количество единиц.
десятичная система основана на 10. Рассмотрим, например, число 8888, оно состоит из
8000 + 800 + 80 + 8. Очевидно, что не все восьмерки равноценны и
важность. Первые 8 выражают число тысяч, вторые число
сотни, третья — количество десятков, а последняя — количество единиц.
Мы использовали число, состоящее из той же цифры 8, что и четыре раз; это было сделано, потому что мы хотели подчеркнуть, что одна и та же фигура может иметь ему придаются разные ценности в зависимости от его положения в группе. Число мог включать любую или все цифры от 0 до 9расположены в бесконечном количестве способов.
Давайте рассмотрим более простое число, скажем, 15. Здесь 1 на самом деле означает
10 единиц, а 5 представляет 5 единиц. Теперь мы можем захотеть добавить дробь к 15.
сделать его, скажем, 15, и кажется возможным сделать это, выйдя за пределы числа единиц
эта система нумерации десятками. Чтобы указать конец целого числа, мы пишем точку,
называется десятичной точкой, а любые цифры справа от нее представляют собой часть или
доля единицы.
Мы видели, что любая цифра на четвертом месте слева, считая из числа единиц, представляет столько-то тысяч, следующий справа столько-то сотни, затем столько-то десятков и столько-то единиц. Если мы продолжим, мы будем здесь пройти десятичную точку, а следующая цифра справа должна представлять столько-то десятых единица. Все еще двигаясь вправо, следующая цифра будет представлять столько сотых, следующий столько-то тысячных, и так до бесконечности.
Сейчас 1 / 2 , 5 / 10 , и помня, что цифра сразу справа от десятичной точки представляет
столько десятых, мы можем выразить 15 1 / 2 через 155. Вместо
говоря пятнадцать с половиной, мы должны сказать пятнадцать десятичных пяти, или, как это обычно бывает,
пятнадцать целых пять десятых. Не будет ошибкой выразить 155 через 1550 или 155000;
последние нули в обоих этих случаях не нужны, но на самом деле не являются неправильными. В виде
обыкновенной дроби 50 означает 50 / 100 , который отменяется на 5 / 10 ,
и, наконец, 1 / 2 и аналогично 5000 в виде обыкновенной дроби
становится 5000 / 10000 , что также отменяется до 1 / 2.
В виде
обыкновенной дроби 50 означает 50 / 100 , который отменяется на 5 / 10 ,
и, наконец, 1 / 2 и аналогично 5000 в виде обыкновенной дроби
становится 5000 / 10000 , что также отменяется до 1 / 2.
Иногда мы видим один или несколько нулей перед целым числом, например. 018. Ничто не имеет значения и используется только тогда, когда по какой-то причине мы хотим иметь одинаковое количество цифр в ряду чисел. 018 означает 18, а 002 означает 2. Мы должны понимать, что один или несколько нулей в начале целого числа, и нули следующие за десятичной частью числа не изменяют значение числа.
Преобразование десятичных дробей в обыкновенные дроби
Десятичную дробь легко преобразовать в обыкновенную.
Возьмем в качестве примера число 46823, что означает 46 единиц и долю единицы.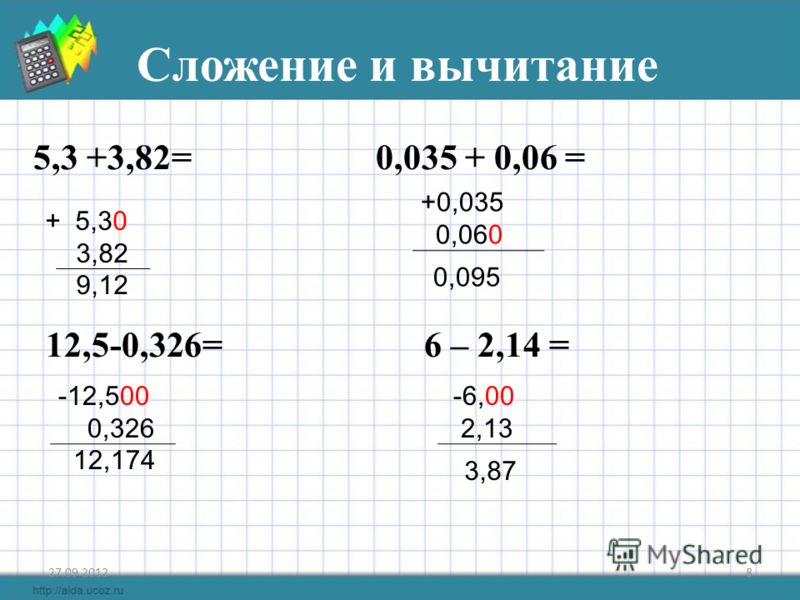 Ранее мы говорили, что первая цифра справа от запятой указывает на то, что
много десятых единицы, следующий справа столько-то сотых, а следующий столько-то
тысячные доли единицы. Таким образом, мы имеем
Ранее мы говорили, что первая цифра справа от запятой указывает на то, что
много десятых единицы, следующий справа столько-то сотых, а следующий столько-то
тысячные доли единицы. Таким образом, мы имеем
46 + 8 / 10 + 2 / 100 + 3 / 1000 что можно записать 46 + 800 / 1000 + 20 / 1000+ 3 / 1000 что сокращается до 46 823 / 1000 .
Отсюда выводим простое правило преобразования десятичной дроби в обыкновенную дробная часть. В качестве числителя дроби запишите все цифры после запятой точка, а в знаменателе напишите 1, а затем столько нулей, сколько цифр в числителе.
Пример: 15261 = 152 + 61 / 100 . 9903 = 9 903 / 1000
Задача 4. Преобразуйте следующие числа в числа и обыкновенные дроби, выраженные в
простейшие формы: 68, 1308, 19080, 20125, 410125, 86625.
Существует другое правило для повторяющихся десятичных знаков, которое будет дано позже.
Сложение и вычитание
Когда числа включают дроби, легко произвести сложение или вычитание в десятичной системе счисления. Нужно только записать цифры так что их десятичные точки находятся на вертикальной линии, а затем добавить или вычесть в обычном образом, и вставьте десятичную точку в ответ сразу после десятичной точки оригинальные фигуры.
Пример:
Сложите 1626, 8041 и 186902.
1626 |
| 211203 |
Вычесть 108694 из 42347.
423470 |
| 314776 |
Задача 5. Сложите 12801, 92, 5002 и 110. Вычтите 82607 из
962.
Умножение и деление
Число, выраженное в десятичной системе, очень легко умножается или делится на 10 или 100 и т. д. Чтобы умножить на 10, переместите запятую на один разряд вправо; к умножьте на 100, переместите запятую на два знака вправо и так далее. При делении переместите десятичную точку влево на один разряд для каждого деления на 10.
Примеры:
| 6124 | х | 10 | = | 612,4 |
| 6124 | х | 100 | = | 6124 |
| 6124 | х | 1000 | = | 61240 |
| 6124 | 10 | = | 6.124 | |
| 6124 | 100 | = | .6124 | |
| 6124 | 1000 | = | . 06124 06124 |
Умножение, когда ни один из множителей не равен 10 (или целочисленная степень из 10, т. е. 100, 1000 и т. д.) следует проводить обычным образом, а положение десятичная точка игнорируется до тех пор, пока не будет получено произведение. Количество десятичных цифр в ответ легко получить; он равен сумме чисел цифр после десятичные знаки коэффициентов.
Пример: Умножьте 62743 на 86.
| 62743 | Здесь есть 3 + 1 = 4 десятичных числа цифры в двух факторах. Начиная с последней цифры в продукте отсчитываем 4 десятичных знака и ставим запятую. |
| 86 | |
| 501944 | |
| 376458 | |
| 5395898 |
Проблема 6 . Умножить 9274 на 826.
При делении в десятичной системе счисления делитель целесообразно переводить в
целое число, перемещая десятичную точку. Если десятичная точка делимого передвинута
одинаковое количество мест и в том же направлении, на результат не повлияет
Эти изменения.
Если десятичная точка делимого передвинута
одинаковое количество мест и в том же направлении, на результат не повлияет
Эти изменения.
Следующий пример пояснит эту процедуру.
Пример: Разделить 89641 на 225.
| Здесь результат 398. Следующий цифра в ответе будет 4, так что если результат требуется только до одного десятичного знака место это 398. | 398 | |
| 225) | 8964. 1 | |
675 | ||
| 2214 | ||
| 2025 | ||
| 1891 | ||
| 1800 | ||
| 910 |
Если бы следующей цифрой было 5 или больше 5, результат был бы таким:
399, так как этот результат был бы ближе к точному ответу, чем 398. Когда
числовой результат, который не делится точно, должен быть выражен в указанное число
знаков после запятой, деление должно быть проведено с точностью до одного знака после запятой. Если
эта дополнительная цифра меньше 5 цифра, предшествующая ей, должна быть оставлена без изменений,
но если дополнительная цифра равна 5 или больше, предыдущая цифра должна быть увеличена на 1.
Когда
числовой результат, который не делится точно, должен быть выражен в указанное число
знаков после запятой, деление должно быть проведено с точностью до одного знака после запятой. Если
эта дополнительная цифра меньше 5 цифра, предшествующая ей, должна быть оставлена без изменений,
но если дополнительная цифра равна 5 или больше, предыдущая цифра должна быть увеличена на 1.
Контрактные методы
Когда множители, входящие в операции умножения или деления большие, следует использовать контрактные методы. Этот раздел не предназначен для иметь дело со всеми арифметическими правилами и процессами, но читатель найдет главу, посвященную с сокращенными методами в книгах по элементарной математике.
Преобразование обыкновенных дробей в десятичные дроби
Обыкновенная дробь может быть преобразована в десятичное выражение с помощью
деление числителя на знаменатель. Если мы хотим перейти к десятичным числам, мы делим
300 на 4. Обычно мы добавляем нули к 3, как показано. Это случай простого деления
над которым нам часто приходится работать мысленно, но для ясности выпишем его в
полный.
Если мы хотим перейти к десятичным числам, мы делим
300 на 4. Обычно мы добавляем нули к 3, как показано. Это случай простого деления
над которым нам часто приходится работать мысленно, но для ясности выпишем его в
полный.
4) 3,00
75
Теперь 4 не делится на 3, поэтому мы добавляем к 3 0, который следует за ним, и делим 4
в 30. Это дает 7 с 2 сверху, а 2 со следующим 0 дает 20, что делится на 4
и дает 5 без остатка. Мы вставляем десятичную точку сразу после десятичной запятой
точку в исходном числе и, таким образом, получить 75 как десятичный эквивалент 3 / 4 .
Примеры: Выразите десятичными дробями 5 / 8 и 13 / 16 .
8) 5.000
.625
.68
25)17.00
150
200
200
Задача 7. Выразите десятичными дробями 7 / 8 и 13 / 16
Выразите десятичными дробями 7 / 8 и 13 / 16
Читатель увидит, что мы можем преобразовать обыкновенную дробь в десятичной дроби путем преобразования дроби в форму, в которой знаменатель равен 10 или 100 или 1000, как говорят математики, в целой положительной степени числа 10.
Возврат к 17 / 25 немного задумался ранее мы могли преобразовать 25 в 100, умножив на 4, но чтобы сохранить значение дробь без изменений, мы также должны умножить 17 на 4. Таким образом, мы имеем
| 17 | = | (17 х 4) | = | 68 | = 0,68 | |
| 25 | (25 х 4) | 100 |
Этот метод преобразования иногда быстрее и проще, чем деление
знаменатель в числитель.
Повторяющиеся десятичные дроби
Если мы попытаемся преобразовать дробь 1 / 3 в десятичные числа с помощью деления, мы получаем результат, который бесконечен.
3) 10000
.3333 . . .
. | ||
| Этот результат называется повторяющимся десятичным числом и часто написано | 3. | Точка над цифрой 3 означает, что цифра 3 повторяется на неопределенный срок. |
. . | ||
| Номер, например | 248216 | означает 2482161616 — 16 повторяются бесконечно. |
Преобразование повторяющихся десятичных дробей в обыкновенные дроби
Правило, о котором мы упоминали ранее:
Вычесть не повторяющиеся цифры из всего десятичного выражения и
разделить на число состоящее из 9за каждую повторяющуюся фигуру и 0 за каждую не
повторяющаяся фигура.
 Для этого допишем к нужной дроби нули;
Для этого допишем к нужной дроби нули;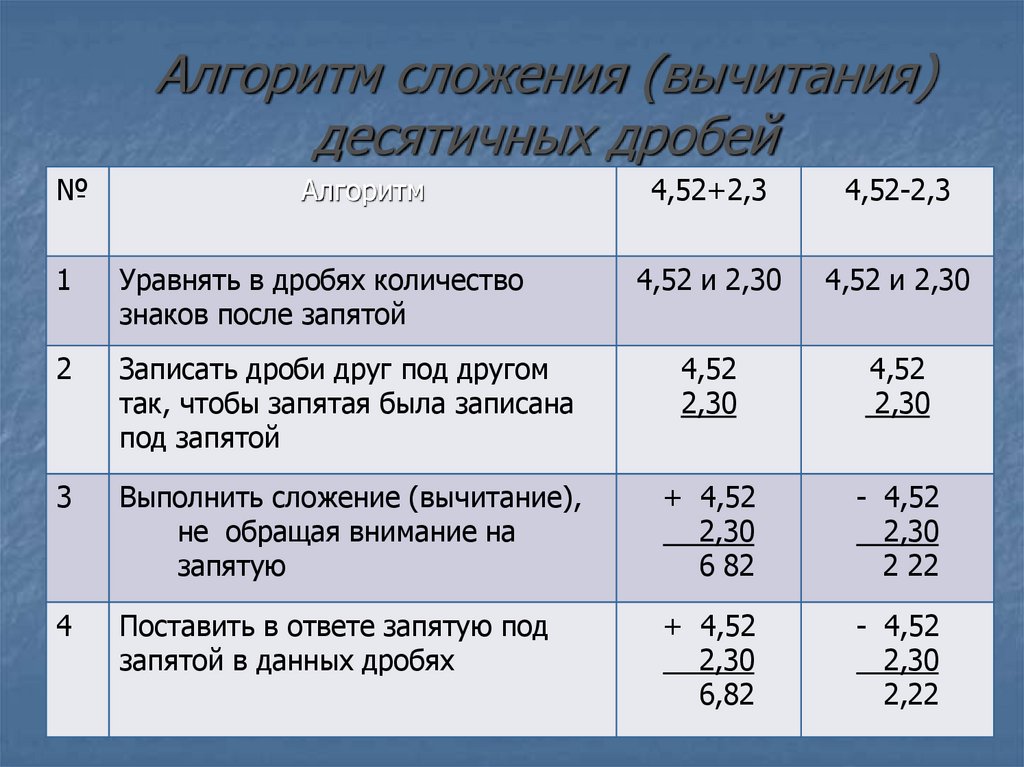
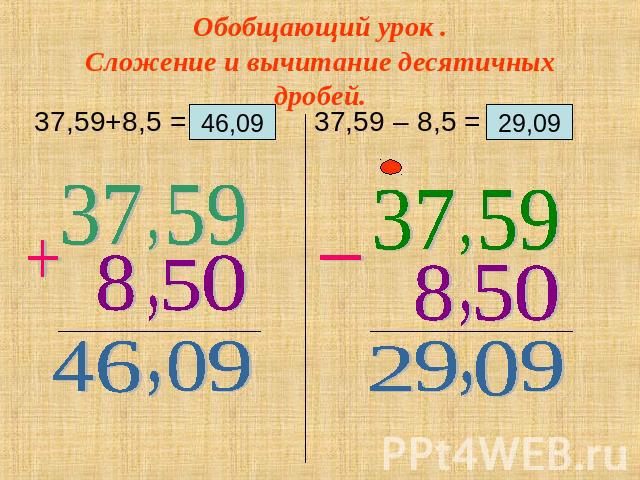 Используя те же числа, что в предыдущем примере: 6 + 1,24 = 7,24.
Используя те же числа, что в предыдущем примере: 6 + 1,24 = 7,24.
 Соответственно измените число и продолжайте вычитание.
Соответственно измените число и продолжайте вычитание.

