§ Сложение десятичных дробей
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Сложение десятичных дробей выполняется по правилам сложения в столбик.
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. При этом запятые должны стоять чётко друг под другом.
Неправильная запись
Правильная запись
Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Запомните!Если исходные десятичные дроби имеют разное
количество знаков (цифр) после запятой, то к дроби с меньшим количеством
десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять
в дробях количество знаков после запятой.
Разберёмся на примере. Найдём сумму десятичных дробей.
0,678 + 13,7 =
Уравняем количество знаков после запятой в десятичных дробях. Допишем два нуля справа к десятичной дроби 13,7 .
0,678 + 13,700 =
Запишем ответ.
0,678 + 13,7 = 14,378
Если сложение десятичных дробей вами усвоено уже хорошо, то недостающие нули можно приписывать мысленно.
Итак, ещё раз коротко основные правила сложения:
- уравниваем количество знаков после запятой;
- записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом;
- выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел;
- ставим в ответ запятую под запятыми.
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Ваши комментарии
Важно!Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
30 апреля 2020 в 9:31
Фархад Гафуров Профиль Благодарили: 0Сообщений: 1 +0.3= 0 СпасибоОтветить
3 мая 2020 в 20:33
Ответ для Фархад Гафуров
Сообщений: 3
+0.3= + = · + · =
| 22+9 |
| 30 |
5 сентября 2016 в 19:06
Милана Хвастунова Профиль Благодарили: 0Сообщений: 1 Вычислить
1,75 ?1
| 11 |
| 17 |
| 51 |
| 56 |
(4
?3 +2 ) :5 · 1 ? 3,72+8| 4,75+7 |
| 33:4 |
Пожалуйста помогите мне буду благодарна ???
0 СпасибоОтветить6 сентября 2016 в 13:22
Ответ для Милана Хвастунова
Сообщений: 11 1.
1.75-| 28 |
| 17 |
2.(4 -3 + 2 ): 5 =3 : 5 =3 : 5 =
| 33 |
| 10 |
3. · -3.72 + 8=1 ? 3.72 + 8=5.28
4.(4.75 +7.5) :(33 : ): 0.25=12.25: 7: 0.25=1.75: 0.25=7 0 СпасибоОтветить
3 сентября 2016 в 15:15
Альбина Королева Профиль Благодарили: 0Сообщений: 3 0.5+ как решить и объясние 0 СпасибоОтветить
3 сентября 2016 в 18:52
Ответ для Альбина Королева
Сообщений: 11
= 0,5(из обыкновенной дроби перевели в десятичную) теперь решим 0,5+0,5 =1
или 0,5= = (из десятичной перевели в обыкновенную и по ходу сократили) решаем + = =1
5 сентября 2016 в 13:44
Ответ для Альбина Королева
Сообщений: 3 спасибо 0 СпасибоОтветить
13 апреля 2016 в 8:34
Даша Ненахова Профиль Благодарили: 0Сообщений: 1 Попробуйте решить:
120,78 + 7 · 6 = ?
| 10 |
| 100 |
Зарание спасибо, .
0
СпасибоОтветить13 апреля 2016 в 9:14
Ответ для Даша Ненахова
Сообщений: 197
1) Первое действие умножение, второе сложение:
120,78+7 · 6=120,78 +42=162,78
2)
| 10 |
| 100 |
+ = = =0,2
Ответ: 1) 162,78
2)0,2 0 СпасибоОтветить
26 октября 2015 в 18:54
Екатерина Смирнова Профиль Благодарили: 0Сообщений: 1
5,7+3 -7
0 СпасибоОтветить15 сентября 2016 в 10:53
Ответ для Екатерина Смирнова
Сообщений: 197
=5,7 + 3,4 ? 7,5 = 1,6
0 СпасибоОтветить4 сентября 2015 в 19:16
Олеся Комарова Профиль Благодарили: 0Сообщений: 2
(1,3+0,7(6)+0,(36)) ·
| 110 |
| 401 |
24 сентября 2022 в 16:31
Сообщений: 1
2/3
0 СпасибоОтветить4 сентября 2015 в 19:15
Олеся Комарова Профиль Благодарили: 0Сообщений: 2
( + 2,708333.
..): 2,5=
28 апреля 2017 в 10:34
Ответ для Олеся Комарова
Сообщений: 1 самой бы знать
очень надо и никто не знает
ладно удачи 0 СпасибоОтветить
7 февраля 2023 в 0:30
Ответ для Олеся Комарова
Сообщений: 1 1) + 2, 708 (3) = + 2
| 7083 — 708 |
| 9000 |
| 6375 |
| 9000 |
| 5625 + 6375 |
| 9000 |
| 12000 |
| 9000 |
=3
= 32) 3
: 2 = :| 25 |
| 10 |
| 10 |
| 25 |
| 20 |
| 15 |
Сложение и вычитание десятичных дробей – правило (5 класс, математика)
4.
3
Средняя оценка: 4.3
Всего получено оценок: 118.
4.3
Средняя оценка: 4.3
Всего получено оценок: 118.
Сложение и вычитание десятичных дробей не самая сложная тема в курсе математики 5 класса. Но особую сложность представляет правильный перенос запятой. Чтобы ни у кого не возникало проблем с этой операцией, рассмотрим алгоритм сложения и вычитания дробей.
Десятичная дробь и ее знаменатель
Дробь в общем случае это незаконченная операция деления. Что это значит? Очень часто в вычислении не получится вычислить деление в точности до последнего знака. Поэтому для повышения точности в математике придумали заменять деление на дробь. Так получаются обычные дроби.
Но обычные дроби хорошо подходят для математических вычислений. В сложных вычислениях, которые применяются, к примеру, в бухгалтерском учете, использовать такие дроби слишком сложно. Почему?
Слишком громоздкими получаются расчеты. Сложно представить себе документ на 15-20 страниц, где вместо вычислений будут только большие дроби с огромными знаменателями.
Поэтому для рядовых вычислений придумали строчную запись дробей со знаменателем кратным 10.
Обратите внимание, знаменатель должен быть кратным 10. А это не только число 10, но и 100, 1000 и так далее. Количество нулей в десятичной дроби равняется количеству знаков после запятой.
Именно на количестве знаков после запятой и прячется основная доля ошибок. Дело в том, что для правильного сложения дробей нужно знак запятой перенести ,чтобы превратить дробь в обычное число. После выполнения операции запятая переносится обратно. При обратном перенесении запятой очень важно не ошибиться с количеством знаков после запятой, иначе получится ошибка. Но обо всем по порядку.
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей выполняется с помощью переноса запятой. Для того, чтобы правильно перенести запятую, нужно посмотреть на число с наибольшим количеством знаков после запятой. После этого нужно представить число с таким же количеством знаков после запятой, но одной значащей цифрой, равной 1.
В числе значащей цифрой называют все цифры, кроме нуля. Значащие цифры иногда подсчитывают по порядку слева направо.
В нашем случае это должна быть первая и единственная значащая цифра. Приведем пример использования правила сложения и вычитания десятичных дробей:
30,0598=300598*0,0001 – в этом примере искомым числом будет 0,0001. Как видно, количество знаков после запятой равняется количеству знаков после запятой в изначальном числе. Благодаря вынесению множителя мы смогли передвинуть запятую.
Теперь, нужно вспомнить распределительное свойство умножения и воспользоваться им. Распределительное свойство выглядит так:
а*(в+с)=а*в+а*с – только свойством мы воспользуемся наоборот.
Решим пример: 30,0598+0,783 – обратите внимание, что количество знаков после запятой у каждого числа разное, поэтому нужно выбирать число, у которого знаков после запятой больше. Это 30,0598. Множитель для него мы уже нашли: 0,0001
Вынесем множитель:
30,0598+0,783=0,0001*(300598+….
– здесь очень интересный момент. Дело в том, что знаков после запятой в числе 0,783 меньше. Значит, для того, чтобы понять, какое число получится после вынесения множителя, нужно решить небольшое уравнение:
0,783=0,0001*х
$$Х={0,783\over{0,0001}}=0,783*10000 = 7830$$ – обратите внимание, что мы просто перенесли запятую вправо на то же количество знаков, какое содержится в общем множителе. Поэтому в условиях урока не нужно решать уравнение, достаточно просто переносить запятую нужным образом.
В итоге мы получим следующий пример:
30,0598+0,783=0,0001*(300598+7830)=0,0001*308428=30,8428 – вот и весь пример.
После выработки навыка все дополнительные операции будут выполняться сами собой в уме. Нужно просто запастись терпением и решать как можно больше примеров.
Что мы узнали?
Мы узнали, что такое десятичные дроби и как с ними работать. Обучились базовым навыкам сложения и вычитания десятичных дробей. Разбили эти операции на отдельные шаги, чтобы никогда не допускать досадных ошибок по неправильному перенесению запятой.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Руслан Лунин
10/10
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 118.
А какая ваша оценка?
5.3: Сложение и вычитание десятичных знаков
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22489
- Дэвид Арнольд
- Колледж Редвудс
Сложение десятичных знаков
Сложение десятичных чисел очень похоже на сложение целых чисел. Например, предположим, что нас просят добавить 2,34 и 5,25.
Мы могли бы изменить эти десятичные числа на смешанных дроби и добавить.
\[ \begin{align} 2,34 + 5,25 & = 2 \frac{34}{100} + 5 \frac{25}{100} \\ & = 7 \frac{59}{100} \end{aligned }\nonumber \]
Однако мы также можем выровнять десятичные числа по их десятичным точкам и добавить по вертикали, как показано ниже.
\[ \begin{array}{r} 2.34 \\ + 5.25 \\ \hline 7.59 \end{array}\nonumber \]
Обратите внимание, что эта процедура выравнивания дает тот же результат: «семь и пятьдесят девять сотых. ” Это мотивирует следующую процедуру сложения десятичных чисел.
Добавление десятичных знаков
Чтобы добавить десятичные числа, выполните следующие действия:
- Поместите добавляемые числа в вертикальном формате, выровняв десятичные точки.
- Сложите числа, как если бы они были целыми числами.
- Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ним.
Пример 1
Добавьте 3,125 и 4,814.
Решение
Разместите числа в вертикальном формате, выровняв их по десятичным точкам. Добавьте, затем поместите десятичную точку в ответе в тот же столбец, что и десятичные точки, которые появляются над ответом.
\[ \begin{array}{r} 3,125 \\ +4,814 \\ \hline 7,939 \end{array}\nonumber \]
Таким образом, 3,125 + 4,814 = 7,939.
Упражнение
Добавить: 2,864 + 3,029
- Ответ
5,893
Пример 2
У Джейн в кошельке 4,35 доллара. У Джима в кошельке 5,62 доллара. Если они суммируют свои деньги, какова общая сумма?
Решение
Расположите числа в вертикальном формате, выровняв десятичные точки, затем сложите.
\[ \begin{array}{r} \$ 4,35 \\ + \$ 5,62 \\ \hline \$ 9.97 \end{array}\nonumber \]
Упражнение
У Алисы в кошельке 8,63 доллара, а у Джоанны 2,29 доллара. Если они объединят сумму своих денег, какова будет сумма?
- Ответить
10,91 $
Прежде чем рассматривать другой пример, давайте вспомним важное наблюдение.
Важное замечание
Добавление нулей в конец дробной части десятичного числа не меняет его значения. Точно так же удаление нулей в конце десятичного числа не меняет его значения.
Например, мы можем добавить два нуля в конце дробной части числа 7,25, чтобы получить 7,2500. Числа 7,25 и 7,2500 идентичны, как показывает следующий аргумент:
\[ \begin{aligned} 7,2500 & = 7 \frac{2500}{10000} \\ & = 7 \frac{25}{100} \\ & = 7.25 \end{aligned}\nonumber \]
Пример 3
Добавьте 7.5 и 12.23.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем завершающий ноль для улучшения выравнивания столбцов.
\[ \begin{array}{r} 7,50 \\ +12,23 \\ \hline 19,73 \end{array}\nonumber \]
Следовательно, 7,5 + 12,23 = 19,73.
Упражнение
Дополнение: 9,7 + 15,86
- Ответ
25,56
Пример 4
Найдите сумму: 12,2+8,352 + 22,44.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце, чтобы улучшить выравнивание столбцов.
\[ \begin{array}{r} 12,200 \\ 8,352 \\ + 22,440 \\ \hline 42,992 \end{array}\nonnumber \]
Следовательно, 12,2+8,352 + 22,44 = 42,992.
Упражнение
Дополнение: 12,9+4,286 + 33,97
- Ответ
51,156
Вычитание десятичных чисел
Вычитание десятичных чисел происходит почти так же, как сложение десятичных чисел.
Вычитание десятичных чисел
Чтобы вычесть десятичные числа, выполните следующие действия:
- Поместите числа, которые нужно вычесть, в вертикальном формате, совместив десятичные запятые.
- Вычитание чисел, как если бы они были целыми числами.
- Поместите десятичную точку в ответе в тот же столбец, что и десятичные точки над ним.
Пример 5
Вычтите 12,23 из 33,57.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце, затем вычтите. Обратите внимание, что мы вычитаем 12,23 из 33.57.
\[ \begin{array}{r} 33,57 \\ -12,23 \\ \hline 21,34 \end{array}\nonumber \]
Следовательно, 33,57 − 12,23 = 21,34.
Упражнение
Вычесть: 58,76 − 38,95
- Ответ
19,81
Как и при сложении, мы добавляем конечные нули к дробной части десятичных чисел, чтобы облегчить выравнивание по столбцам.
Пример 6
Найдите разницу: 13,3 − 8,572.
Решение
Расположите числа в вертикальном формате, выровняв их десятичные точки в столбце. Обратите внимание, что мы добавляем нули в конце дробной части числа 13.3, чтобы улучшить выравнивание по столбцам.
\[ \begin{array}{r} 13,300 \\ -8,572 \\ \hline 4,728 \end{array}\nonnumber \]
Следовательно, 13,3 − 8,572 = 4,728.
Упражнение
Вычесть: 15,2 − 8,756
- Ответ
6.444
Сложение и вычитание десятичных чисел со знаком
Мы используем те же правила для сложения десятичных чисел со знаком, что и для сложения целых чисел.
Сложение двух десятичных дробей с одинаковыми знаками
Чтобы сложить две десятичные дроби с одинаковыми знаками, выполните следующие действия:
- Сложите величины десятичных чисел.
- Префикс общего знака.
Пример 7
Упрощение: −3,2+(−18,95).
Решение
Чтобы добавить подобные знаки, сначала добавьте величины.
\[ \begin{array}{r} 3.20 \\ +18.95 \\ \hline 22.15 \end{array}\nonumber \]
Префикс общего знака. Следовательно, −3,2+(−18,95) = −22,15
Упражнение
Упростим: −5,7 + (−83,85)
- Ответ
−89,55
Мы используем то же правило, что и для целых чисел, при сложении десятичных дробей с разными знаками.
Сложение двух десятичных знаков с разными знаками
Чтобы сложить два десятичных знака с разными знаками, выполните следующие действия:
- Вычтите меньшую величину из большей величины.
- Ставить перед знаком десятичного числа большее значение.
Пример 8
Упрощение: −3 + 2,24.
Решение
Чтобы добавить разные знаки, сначала вычтите меньшую величину из большей величины.
\[ \begin{array}{r} 3,00 \\ -2,24 \\ \hline 0,76 \end{array}\nonnumber \]
Ставьте перед знаком десятичного числа большее значение. Следовательно, -3 + 2,24 = -0,76.
Упражнение
Упрощение: −8 + 5,74
- Ответ
−2,26
Вычитание по-прежнему означает прибавление противоположного .
Пример 9
Упрощение: −8,567 − (−12,3).
Решение
Вычитание нужно сначала заменить на сложение, добавив обратное.
\[−8,567 − (−12,3) = −8,567 + 12,3\номер \]
У нас разные знаки. Во-первых, вычесть меньшую величину из большей величины.
\[ \begin{array}{r} 12,300 \\ − 8,567 \\ \hline 3,733 \end{array}\nonumber \]
Приставьте знак десятичного числа к большему значению. Отсюда:
\[ \begin{align} −8,567 − (−12,3) & = −8,567 + 12,3 \\ & = 3,733 \end{aligned}\nonumber \]
Упражнение
Упрощение: −2,384 − (− 15.2)
- Ответить
12.816
Порядок операций требует, чтобы мы сначала упрощали выражения, содержащиеся в круглых скобках.
Пример 10
Упростить: −11,2 − (−8,45 + 2,7).
Решение
Сначала нам нужно добавить в скобках. Поскольку у нас разные знаки, вычтите меньшую величину из большей величины.
\[ \begin{array}{r} 8,45 \\ − 2,70 \\ \hline 5,75 \end{array}\nonumber \]
Префикс знака числа с большей величиной.
Следовательно,
\[−11,2 − (−8,45 + 2,7) = −11,2 − (−5,75)\nonnumber \]
Вычитание означает сложение противоположного.
\[−11,2 − (−5,75) = −11,2+5,75\номер \]
Опять же, у нас разные знаки. Вычесть меньшую величину из большей величины.
\[ \begin{array}{r} 11.20 \\ − 5.75 \\ \hline 5.45 \end{array}\nonumber \]
Префикс знака числа с большим значением.
\[ −11,2+5,75 = −5,45\не число \]
Упражнение
Упрощение: −12,8 − (−7,44 + 3,7)
- Ответ
−9,06
Письмо по математике
Решение предыдущего примера должно быть записано следующим образом:
\[ \begin{aligned} −11,2 − (−8,45 + 2,7) & = −11,2 − (−5,75) \\ & = − 11,2+5,75 \\ & = −5,45 \end{aligned}\nonumber \]
Любая черновая работа, такая как вычисления в вертикальном формате в предыдущем примере, должна выполняться на полях или в блокноте.
Пример 11
Упростить: −12,3 −|− 4,6 − (−2,84)|.
Решение
Сначала мы упрощаем выражение внутри полос абсолютного значения, берем абсолютное значение результата, а затем вычитаем.
\[ \begin{align} -12,3 — |-4,6 -(-2,84)| ~ \\ = -12,3 -|-4,6 + 2,84| ~ & \textcolor{red}{ \text{ Добавить противоположное.}} \\ = -12,3 -|-1,76| ~ & \textcolor{red}{ \text{ Добавить: } -4,6 + 2,84 = -1,76.} \\ = -12,3-1,76 ~ & \textcolor{red}{ |-1,76|=1,76.} \\ =- 12,3 + (-1,76) ~& \textcolor{red}{ \text{ Добавить противоположное.}} \\ = -14,06 ~ & \textcolor{red}{ \text{ Добавить: } -12,3 + (-1,76) = -14.06.} \end{выровнено}\nonumber \]
Упражнение
Упростить: −8,6 −|− 5,5 − (−8,32)|
- Ответить
−11,42
Упражнения
В упражнениях 1-12 добавьте десятичные дроби.
1. \(31,9 + 84,7\)
2. \(9,39 + 7,7\)
3. \(4 + 97,18\)
4. \(2,645 + 2,444\)
5. \( 4 + 87,502\)
6.
\(23,69 + 97,8\)
7. \(95,57 + 7,88\)
8. \(18,7+7\)
9. \(52,671 + 5,97\)
10. \(9,696 + 28,2\)
11. \(4,76 + 2,1\)
12. \(1,5 + 46,4\)
9003 3 В упражнениях 13-24 вычтите десятичные дроби.
13. \(9 − 2,261\)
14. \(98,14 − 7,27\)
15. \(80,9 − 6\)
16. \(9,126 − 6\)
9 0033 17. \( 55,672 − 3,3\)18. \(4,717 − 1,637\)
19. \(60,575 − 6\)
20. \(8,91 − 2,68\)
21. \ (39,8 − 4,5\)
22. \(8,210 − 3,7\)
23. \(8,1 − 2,12\)
24. \(7,675 − 1,1\)
В упражнениях 25–64 сложите или вычтите десятичные дроби, как указано.
25. \(−19,13 − 7\)
26. \(−8 − 79,8\)
27. \(6,08 − 76,8\)
28. \(5,76 − 36,8\) 9003 6
29. \(−34,7+(−56,214)\)
30. \(−7,5+(−7,11)\)
31. \(8,4+(−6,757)\)
32. \(−1,94 + 72,85 \)
33. \(−50,4+7,6\)
34. \(1,4+(−86,9)\)
35. \(−43,3+2,2\)
36.
\(0,08 + (−2,33)\)
37. \(0,19 − 0,7\)
38. \(9 − 18,01\)
39. \(−7 − 1,504\) 9003 6
40. \(−4,28 − 2,6\)
41. \(−4,47 + (−2)\)
42. \(−9+(−43,67)\)
43. \(71,72 − (− 6)\)
44. \(6 − (−8,4)\)
45. \(−9,829 − (−17,33)\)
46. \(−95,23 − (−71,7)\)
47. \(2,001 − 4,202\)
48. \(4 − 11,421\)
49. \(2,6 − 2,99\)
50. \(3,57 − 84,21\)
51. \(−4,560 − 2,335\)
52. \(−4,95 − 96,89\)
53. \(−54,3 − 3,97\)
54. \(−2 − 29,28 5\)
55. \(−6,32 + (−48,663)\)
56. \(−8,8+(−34,27)\)
57. \(−8 − (−3,686)\)
58. \(− 2.263 — (−72.3) \)
59. \ (9,365 + (−5) \)
60. \ ( — 0,12 + 6,973 \)
61. \ (2,762 — ( — 7) \)
61. 62. \(65,079 — (-52,6)\)
63. \(-96,1+(-9,65)\)
64. \(-1,067 + (-4,4)\)
В упражнениях 65-80 упростите данное выражение.
65. \(−12,05 − |17,83 − (−17,16)|\)
66.
\(15,88 −|− 5,22 − (−19,94)|\)
67. \(−6,4 + |9,38 − (−9,39)|\)
68. \(−16,74 + |16,64 − 2,6|\)
69. \(−19,1 − (1,51 − (−17,35))\)
70. \(17,98 − (10,07 − (−10,1))\)
71. \(11,55 + (6,3 − (−1,9))\)
72. \(−8,14 + (16,6 − (−15,41))\)
73 \(−1,7 − (1,9 − (−16,25))\)
74. \(−4,06 − (4,4 − (−10,04))\)
75. \(1,2 + |8,74 − 16,5|\)
76. \(18,4 + |16,5 − 7,6|\)
77. \(−12,4 − |3,81 − 16,4|\)
78. \(13,65 − |11,55 − (−4,44)|\)
79. \(−11,15 + (11,6 − (−16,68))\)
80. \(8,5 + (3,9 − 6,98)\)
81. Крупные банки . Рыночная капитализация четырех крупнейших банков страны (по состоянию на 23 апреля 2009 г.)
| JPMorgan Chase & Co | 124,8 миллиарда долларов |
| Уэллс Фарго и Ко | 85,3 миллиарда долларов |
| Goldman Sachs Group Inc. | 61,8 миллиарда долларов |
| Банк Америки | 56,4 миллиарда долларов |
Какова общая стоимость четырех крупнейших банков страны? Associated Press Times-Standard 22.
04.09
82. Зеркало телескопа. Недавно запущенный телескоп Herschel имеет зеркало диаметром 11,5 футов, в то время как зеркало Хаббла имеет диаметр 7,9 фута.футов в диаметре. Насколько больше зеркало Гершеля в диаметре, чем зеркало Хаббла?
83. Средняя температура . Средние температуры в Сакраменто, штат Калифорния, в июле составляют высокую дневную температуру 93,8 градусов по Фаренгейту и низкую ночную температуру 60,9 градусов по Фаренгейту. Как меняется температура днем и ночью? Подсказка: Формулу для сравнения температур см. в разделе 2.3.
84. Средняя температура . Средние температуры в июле в Реддинге, штат Калифорния, составляют высокую дневную температуру 9 градусов тепла.8,2 градуса по Фаренгейту и низкая ночная температура 64,9 градуса по Фаренгейту. Как меняется температура днем и ночью? Подсказка: Формулу для сравнения температур см. в разделе 2.3.
85. Чистая стоимость .
Чистая стоимость определяется как активы за вычетом обязательств. Активы — это все ценности, которые могут быть конвертированы в наличные деньги, а пассивы — это сумма долгов. General Growth Properties, владельцы торгового центра Bayshore Mall, имеют активы в размере 29,6 млрд долларов и обязательства в размере 27 млрд долларов и обанкротились. Какова была чистая стоимость General Growth Properties до банкротства? Times-Standard 17.04.2009
86. Виноградная дробилка . Предварительный отчет Калифорнийского департамента продовольствия и сельского хозяйства показывает, что в 2009 году штат произвел 3,69 миллиона тонн винного винограда. Это немного меньше рекордного 2005 года — 3,76 миллиона тонн. На сколько тонн не дотянула до рекорда давка 2009 года? Ассошиэйтед Пресс-Таймс-Стандарт Калифорнийский урожай винограда подскочил на 23% в 2009 году.
87. Оборот . В обзоре вакансий и текучести кадров Министерства труда говорится, что в январе 2010 года работодатели наняли около 4,08 миллиона человек, а 4,12 миллиона человек были уволены или иным образом покинули свои рабочие места.
На сколько больше людей потеряло работу, чем было принято на работу? Превратите свой ответ в целое число. Ассошиэйтед Пресс-Таймс-Стандарт 03/10/10 Количество вакансий в январе резко увеличилось до 2,7 млн человек.
Ответы
1. 116,6
3. 101,18
5. 91,502
7. 103,45
90 033 9. 58.64111. 6.86
13. 6.739
15. 74.9
17. 52.372
19. 54.575
21. 35.3
23. 5.98
25. −26.13
27. −70.72
29. −90,914
31. 1,643
33. −42.8
35. −41.1
37. −0.51
39. −8.504
41. −6.47
43. 77.72
45. 7,501
47. −2,201
49. − 0,39
51. -6,895
53. -58,27
55. -54,983
57. -4,314
59. 4,365
61. 10.062
63. −105.75
65. −47.04
67 12.37
69. −37.96
71. 19.75
73. −19.85
75. 8.96
77.
−24,99
79. 17,13
81. 328,3 миллиарда долларов
83. −32,9 градуса по Фаренгейту
85. 2,6 миллиарда долларов 9003 6
87. 40 000
Эта страница под заголовком 5.3: Добавление и вычитание десятичных знаков предоставляется в соответствии с лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором этой страницы является Дэвид Арнольд.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Арнольд
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
Как складывать, вычитать, умножать и делить десятичные дроби
| База десяти — кратные десяти |
Наша система счисления основана на десятичной системе счисления, что означает, что она основана на десяти цифрах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Одиннадцатое числительное — это двузначное число, начинающееся с единицы за один десяток плюс ничего, 10, а двадцать первое числительное — это двузначное число, начинающееся с двойки за два десятка, 20. Когда мы доходим до десяти десятков, у нас есть трехзначное число 100. Это должно звучать очень похоже на то, что обсуждалось ранее о разрядности.
Одна тысяча, 1000, это 10 х 10 х 10. Таким образом, мы можем быстро увидеть, что, умножая еще на десять, мы получаем 10 000 и так далее.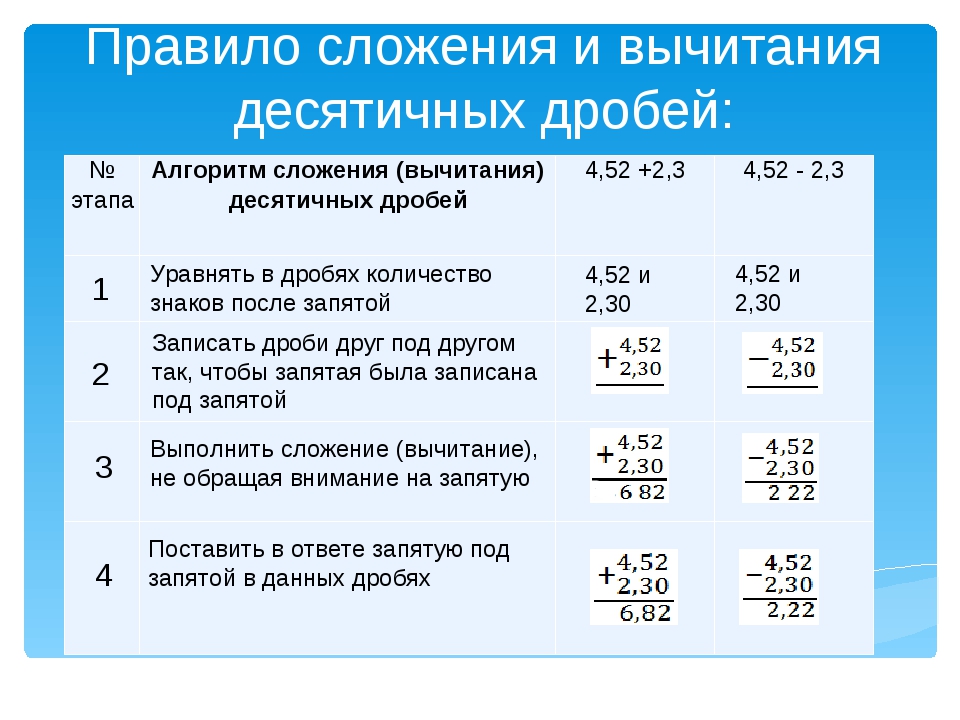
Обратите внимание, что число, которое меньше единицы и не содержит целых чисел, обычно имеет ноль на месте целого числа слева от десятичной точки.
| Перемещение десятичной точки для умножения или деления на число, кратное десяти |
Любое число, не являющееся смешанным, можно легко разделить или умножить на 10, просто переместив десятичную точку в числе.
Во всех числах есть десятичная точка, даже если вы ее не видите! Если это целое число или целое число, например 6, десятичная точка ставится после числа, например 6.
Если это ровно 6, его можно записать как 6,0. Если бы вам нужно было умножить его на 10, вы бы переместили десятичную точку на один разряд вправо, потому что в 10 стоит один ноль. Таким образом, 10 x 6,0 будет 60.
Если бы вам нужно было умножить это число на 10 000, вы бы переместили десятичную дробь на четыре знака вправо, потому что 10 000 имеет четыре нуля, обозначающих, что это 10 x 10 x 10 x 10, поэтому вы должны умножить 6 на 10 х 10 х 10 х 10, что составляет 60 000.
Чтобы разделить на десять или кратное десяти, вы перемещаете десятичную точку влево на такое же количество знаков, сколько нулей или десятичных знаков в числе, на которое вы делите.
Если у вас есть число 475 и вам нужно разделить его на десять, вы можете использовать длинное деление, и оно будет выглядеть так:
Однако вскоре после выполнения нескольких таких задач вы обнаружите, что при делении на десять вы просто переместили десятичную точку на один разряд влево.
Вы также заметите, что если вы разделите на 1000, вы переместите десятичную точку на три знака влево. Таким образом, 67 823 разделить на 1000 получится 67,823.
Хотите узнать больше? Пройдите онлайн-курс по базовой математике.
Если в числе уже есть десятичная точка, начните с этой десятичной точки и переместите ее вправо при умножении и влево при делении.
| Преобразование дробей в десятичные и десятичных дробей |
В данном случае запятая выходила даже на тысячных. Для этого курса дроби будут четными десятичными, или вам скажут, сколько знаков нужно выразить. Вам нужно будет выработать десятичную дробь на один разряд больше, чтобы правильно округлить.
В приведенном выше примере вам могли бы предложить округлить до сотых.
В этом случае вы бы доработали задачу до тысячных, где у вас 5. Поскольку это 5 или больше, вы округлили бы сотые до одного разряда и выразили ответ как 0,13. Если бы вас попросили выразить ответ с точностью до десятых, вы бы обработали его с точностью до сотых. Затем, поскольку сотые доли — это 2 (меньше 5), вы бы оставили это как 2 — даже если вы знаете, что следующим местом будет 5 или больше. Округлив до десятых: 0,1.
Ноль — это заполнитель справа от десятичной точки. Если бы мы не использовали ноль в качестве заполнителя, число было бы 0,625, что означало бы, что 16 входит в 10 шесть раз! Вместо этого он дошел до 100 шесть раз. Поэтому будьте осторожны, всегда используйте ноль в качестве заполнителя, если делитель не входит в делимое и вам нужно сбить еще одну цифру.
Сложение и вычитание десятичных дробей |
Сложение и вычитание десятичных дробей не слишком отличается от сложения и вычитания любых чисел.
Очень важно, чтобы вы записывали свои десятичные дроби так, чтобы десятичные точки совпадали, иначе вы обнаружите, что прибавляете десятые к единицам или вычитаете сотые из десятых.
Пока каждое из чисел, которые вы складываете или вычитаете, имеет одинаковое количество знаков после запятой, сложение или вычитание довольно легко.
В первой задаче вам нужно будет поставить десятичную точку после пяти, а затем поставить нулевые заполнители в десятых и сотых местах. Очевидно, что тогда вам нужно будет одолжить одно целое из пяти, чтобы получить 10 десятых, а затем одолжить одну из десятых, чтобы получить 10 сотых, прежде чем вы сможете вычесть 5 сотых или 2 десятых.
Умножение и деление десятичных дробей |
При умножении десятичных дробей не выравнивайте десятичные точки.