Страница не найдена — РОО «Ассоциация победителей олимпиад»

Ваши ФИО*

Ваш email*

Ваш номер телефона*

Какой предмет вы хотели бы преподавать?*

Расскажите кратко о своих олимпиадных достижениях*

Приложите резюме*
Объём файлов не должен превышать 20 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваша электронная почта*

Из какого вы региона?*

Расскажите, как мы могли бы сотрудничать*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО*

Ваша электронная почта*

Ваш номер телефона*

Образовательное учреждение*

Расскажите кратко, какая у вас сложилась ситуация с олимпиадным движением в школе и какого результата вы ожидаете от сотрудничества с АПО*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваш email

Каким предметом вы интересуетесь

Выберите наиболее подходящий статус Статус не выбранУченикРодительПредставитель школыПедагог

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Мотивационное письмо Объём файла не должен превышать 2 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Образовательное учреждение

Город образовательного учреждения

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Проект / отдел

Должность

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ребенка

Название образовательного учреждения

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Войти

---

Родитель

Буду покупать курсы для своего ребёнка Зарегистрироваться

---

Обучающийся

Сам буду проходить курсы Зарегистрироваться

---

Представитель школы

Буду заказывать услуги для своего образовательного учреждения и контролировать их исполнение Зарегистрироваться

«Порядок выполнения действий в выражениях со скобками» | План-конспект урока по математике (3 класс):

Тема урока : « Порядок выполнения действий в выражениях со скобками ».

Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях со скобками в различных ситуациях, умений решать числовые выражения со скобками.

Формируемые УУД:

Регулятивные УУД:

-работать по предложенному плану, инструкции;

-выдвигать свои гипотезы на основе учебного материала;

— осуществлять самоконтроль.

Познавательные УУД:

-знать правила порядка выполнения действий:

-уметь разъяснить их содержание;

-понимать правило порядка выполнения действий;

-находить значения выражений согласно правилам порядка выполнения

действий;

— применять правила порядка выполнения действий.

Коммуникативные УУД:

-слушать и понимать речь других;

— выражать свои мысли с достаточной полнотой и точностью;

— допускать возможность различных точек зрения, стремиться понимать позицию собеседника;

-работать в команде разного наполнения (паре, малой группе, классом), участвовать в обсуждениях, работая в паре;

Личностные УУД:

-устанавливать связь между  целью деятельности и её результатом;

-определять общие для всех правила поведения;

 — уметь осознанно и внимательно читать задания;

-выражать способность к самооценке на основе критерия успешности учебной деятельности.

Планируемый результат:

Предметные:

-Знать правила порядка выполнения действий.

-Уметь разъяснить их содержание.

Личностные:
-Уметь проводить самооценку на основе критерия успешности учебной деятельности.

Метапредметные: регулятивные УУД-

-Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке;  оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки;  планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

Коммуникативные УУД:

-Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им .

Познавательные УУД:

-Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке .

Тип урока : Комплексное применение знаний и способов действий.

Методы и формы обучения: методы- словесный, наглядный, практический. Формы- фронтальная, индивидуальная.

Оборудование: учебник В.Н. Рудницкая «Математика» часть 1, 3 класс, карточки

                                                          Ход урока

1. Организационный  момент.

— Чтоб урок наш стал светлее,

Мы поделимся добром.

Вы ладони протяните,

В них любовь свою вложите,

Ей с друзьями поделитесь

И друг другу улыбнитесь.

2. Проверка готовности к уроку. ( сигнальные карточки)
3. — Запишите в тетрадях  число, классная работа.

4. Устный счёт.

Два ученика за доской  на повторение. 42 : 7 ∙ 4 : 8 ∙ 0 ∙ 54 : 6 · 12  =

— Как смогли так быстро посчитать? (При умножении на 0, результат 0)

42 : 7 ∙ 4 : 8 · 9 =

42 — 7 + 29 + 16 – 50 = 

 Игра «Найди правильный ответ».  ( У каждого ученика лист с числами)

55	56	57	58	59	60	61
62	63	64	65	66	67	68
69	70	71	72	73	74	75
76	77	78	79	80	81	82
83	84	85	86	87	88	89
90	91	92	93	94	95	96
97	98	99	100	101	102	103

— Я читаю задания, а вы, выполнив в уме действия, должны полученный результат отметить точкой.

1. Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
2. Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
3. Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)

— Соедините полученные результаты.

— Какую геометрическую фигуру вы получили? ( Треугольник)

— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)

— Продолжаем работать по карточке.

4. Найдите разность чисел 100 и 22. (78)
5. Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
6. Возьмите число 25  4 раза. (100)

— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.

— Сколько треугольников получилось? (5)

5. Постановка проблемы

— В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

— А в математике обязательно ли выполнять арифметические действия в определенном порядке?

— Давайте проверим.

— На доске вы видите два примера. Что можете о них сказать.

2+ 5 х 3 = 17

2+ 5 х 3 = 21

— Вижу, вы удивлены. Почему?  (Примеры одинаковые, а результат разный)

— Какая возникла проблема? (Почему в одинаковых примерах бывают разные ответы?)

— Как нам изменить выражения, ведь, судя по результату, они не равны?  (Необходимо как-то обозначить в записи порядок действий)

6. Работа над темой урока. Поиск решения проблемы

— Давайте  рассуждать. 

Правые части одинаковые…

Чем отличаются левые части? Какие есть идеи? (Левые части отличаются порядком действий.)

— Какой порядок действий в первом примере? во втором примере?

В каком примере мы действовали по правилу? (В первом. )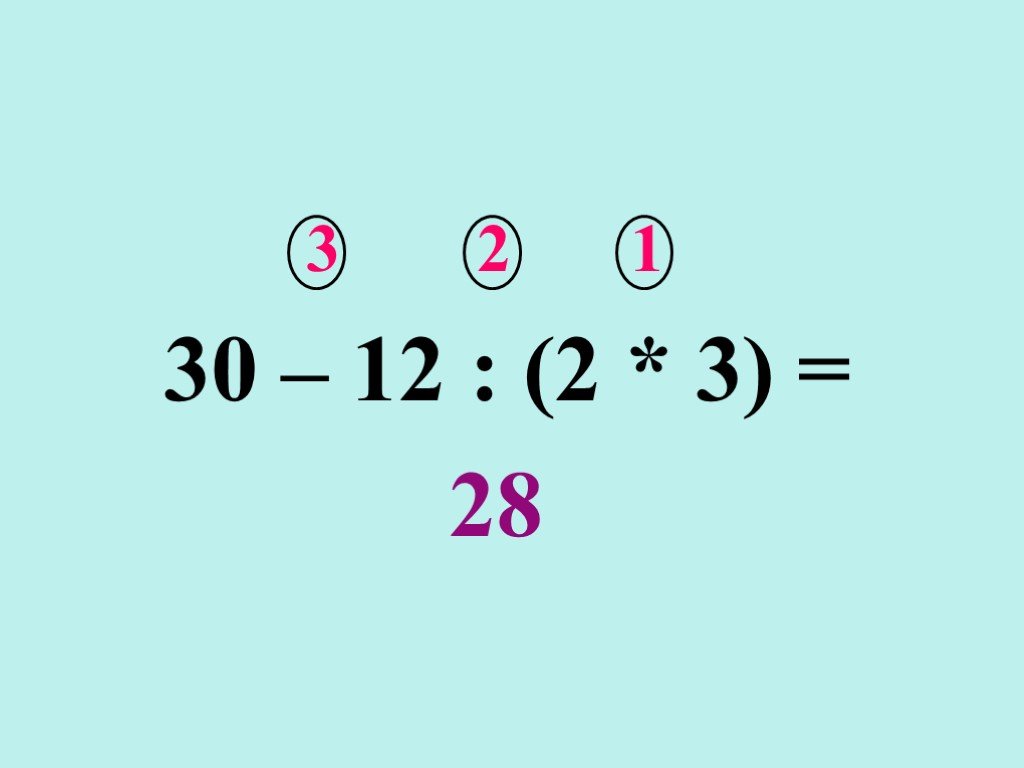

— А во втором примере мы нарушили правило! Как же нам догадаться, что здесь сложение выполняется первым? (Нужно поставить скобки.)

Сформулируйте тему урока. ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ СО СКОБКАМИ.

— Итак, цель нашего урока — научиться обозначать в записи порядок действий.

Чтобы указать, в каком порядке нужно выполнять действия применяют скобки.

Так что же обозначают скобки? (Действия, заключенные в скобки, выполняются раньше других.)

Прочитать памятку ( вывешивается на доску)

Порядок действий в выражениях особый. 
И в каждом случае, помни, он свой. 
В порядке все действия ты выполняй.

Сначала в скобках все посчитай.

Потом чередом, умножай или дели.

И, наконец, вычитай или сложи.

7. Закрепление нового материала.

— Откройте учебник на странице 116  №7. Внимательно посмотрите на выражения. Скажите, почему эти выражения можно записать без скобок? ( Эти действия итак выполняются по порядку).

Решаем по вариантам по столбику.  2 ученика (Козлова А. и Мягких У.) за доской.

— Давайте вместе составим алгоритм порядка выполнения действий.(карточки развешаны по классу группа красных собирают и составляют алгоритм)

1) (     )

2) «х»  или  «:»

3)  «+» или  «-»

ФИЗМИНУТКА

 Раз подняться, потянуться,

Два согнуться, разогнуться.

Три в ладоши три хлопка,

Головою три кивка.

На четыре руки шире,

Пять руками помахать,

Шесть на место тихо сесть.

7. Работа по учебнику

— Откройте учебник на странице 116 № 8.

Прочитайте задание. (Сигнал кому не понятно). Взаимопроверка.

8. Дифференцированная работа по карточкам.

— Сейчас посмотрим, как вы умеете определять порядок действий в выражениях. В карточках  вам надо расставить порядок выполнения действий на каждой схеме. (Синие – слабым ученикам,  зеленые – средним,  красные – сильным).

… + … : … + … х … — …

… : … + … х (… + …)

… + … (… х … + …) : … — … х

…х…х… — (… : … +…) +…

… * … * … — … (… * … — …) + … : …

… : (… — …) х… — … : … — ( … — …)

— Поменяйтесь карточками друг с другом и проверьте правильность выполнения.

10.  Работа в паре.

        Расставьте скобки. Задание записано на доске.

        38-10+6=34        24:3х2=16

        38-10+6=22        24:3х2=4

Для проверки сравним результаты

11.   Самостоятельная работа. Работа на карточках.

             Математический тест (4мин)

№	Вопросы	Ответы
1	Увеличь 8 в 2 раза и прибавь 6.	10	22	6
2	Найди частное чисел 42 и 6.	36	48	7
3	Каков результат выражения (24 : 4) + (24 : 6)	10	14	28
4	На сколько 3 меньше 20?	23	17	13
5	Во сколько раз 8 меньше 56?	7	48	64
6	Найди значение выражения  4 + 6 : 3 + 4 .	18	10	3
7	Чему равна сумма пяти одинаковых слагаемых, каждое из которых равно 3?	25	15	8
8	Чему равно выражение  5 + (13 – 7).	8	20	11
9	Сколько ушек  у 3 мышек?	6	9	3
10	Сколько ножек у двух сороконожек?	40	2	80

12.   Домашнее задание

На повторение № 17, стр 119. , а на закрепление задание по выбору

— придумать примеры со скобками;

— придумать математическую задачу, решая которую используем скобки.

13.  Подведение итогов урока. Рефлексия

— Ребята, вы прекрасно работали.  

— Кому всё понятно и хорошее настроение — покажите сигнальной карточкой. Если кому – то не все понятно и настроение грустное тоже сигнал.

— Давайте улыбнёмся друг другу и скажем спасибо.

Скобки: использование, типы, правило BODMAS, примеры

• Автор Мадхурима дас
• Последнее изменение 11-11-2022

Скобки подразумевают своего рода группировку, операторы в подвыражении имеют приоритет над операторами в окружающем выражении. Использование квадратных скобок обычно встречается в математических функциях. Мы видели такие выражения, как (3×2)–1. (3×2)–1. Мы можем рассмотреть две части выражения: часть в скобках и часть вне скобок.

Помните, если мы ошибемся в расчетах, мы можем получить неверный ответ. Как мы пойдем, если там больше одной скобки? Мы используем арифметические операции в соответствии с их приоритетом. Точно так же мы используем скобки в соответствии с их приоритетом. Давайте обсудим здесь различные типы скобок и их использование.

В математике скобки — это символы, которые часто используются для создания групп или для объяснения порядка выполнения операций в выражении. Некоторые скобки имеют несколько конкретных применений в математике.

Обычно мы используем квадратные скобки для группировки в математике. Мы обычно используем следующие типы кронштейнов:

1. \(\left({} \right)\) назвал скобку
2. \(\left\{{} \right\}\) назвал фигурные скобки
3. \(\left[{} \right ]\) называется квадратными скобками

Мы всегда используем пару скобок, которые имеют открывающую и закрывающую часть. Скобки используются для прозрачности порядка операций.

Например, предположим, что у вас есть выражение \(2 + 5 \times 7 — 2). Мы знаем, что порядок математических операций — деление, умножение, сложение и вычитание. Итак, мы будем двигаться вправо, начиная с умножения до выполнения сложений и вычитаний, и мы получим \(2 + 35 — 2 = 35.\)

Что мы будем делать, если мы хотим сначала выполнить сложение и вычитание и умножить результаты? Этого можно добиться, правильно используя скобки.

Если мы используем скобки, то проблема становится такой: \(\left({2 + 5} \right) \times \left({7 – 2} \right).\) Здесь круглые скобки или скобки говорят нам делать что-то отличное от порядка обычных операций. Иногда мы также используем их для визуальной ясности.

Изучите концепции BODMAS

Правило BODMAS

BODMAS — это краткая форма, используемая для скобок, порядка, деления, умножения, сложения и вычитания. Иногда люди используют PEMDAS (круглые скобки, экспоненты, умножение, деление, сложение и вычитание), похожие на BODMAS.

Описывает порядок выполнения математических операций при решении математического выражения. Согласно этому правилу, если в выражении присутствует несколько квадратных скобок, сначала начните упрощать самую внутреннюю круглую скобку или круглую скобку, затем квадратную скобку и фигурную скобку, а затем решите в соответствии с арифметическими операциями приоритета.

Другими словами, согласно правилу BODMAS, чтобы решить любое математическое выражение, сначала нужно решить члены, написанные в скобках, а затем упростить экспоненциальные члены. После этого решаем операции деления и умножения, затем, наконец, сложения и вычитания. Таким образом, правило BODMAS оценивает математические выражения и справляется со сложными вычислениями намного проще и правильнее.

Шаги для запоминания правила BODMAS

Упростите выражение внутри скобок. Помните о приоритете скобок. Начните решение внутри \(\left({} \right),\), затем \(\left\{{}\right\}\) и после этого следует \(\left[{} \right].\)
Затем выполните деление или умножение (слева направо).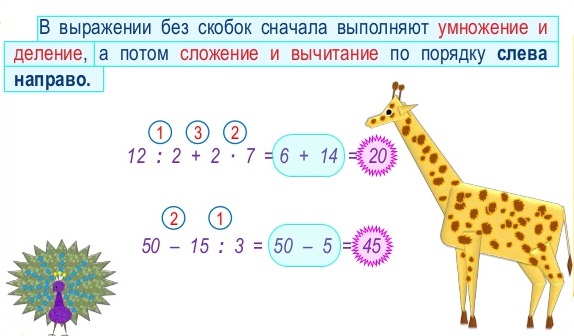
Затем выполните сложение или вычитание (слева направо).

Использование скобок

Согласно правилу BODMAS, чтобы решить любое математическое выражение, сначала решите члены, написанные в скобках, упростите экспоненциальные члены и перейдите к операциям деления и умножения, затем, наконец, к сложению и вычитанию.

Если в выражении есть какие-либо скобки, откройте скобки и добавьте или вычтите члены.
\(a + \left({b + c} \right) = a + b + c,\quad a + \left({b – c} \right) = a + b – c\)
Если есть знак минус, открываем скобку, умножаем знак минус на каждое слагаемое внутри скобки. \ (а — \ влево ({b + c} \ вправо) = а — б — с \) Если есть какой-либо член вне скобок, умножьте этот внешний член на каждый член в скобках. \(a\left({b + c} \right) = ab + ac\)
Пример, \(11 – \left({3 – 2} \right) = 11 – 3 + 2 = 11 – 1 = 10 \)
Пример, \(3\влево({5 – 2} \вправо) = 15 – 6 = 9\)

Реальный пример использования скобок

Давайте разберемся на примере. Во время вчерашней бури с дерева в нашем саду упало несколько гуав. Моя мама подобрала его в сумке. Я посчитал, что в пакете \(40\) гуавы. Оттуда я взял \(5\) гуавы, а моя сестра взяла \(6). Через некоторое время моя тетя нашла в саду еще \(10\) гуавы. Она разделила их всех поровну между \(13\) девочками и мальчиками по соседству. Сколько гуавы получил каждый? Давайте узнаем.

• Шаг 1 : Сколько гуавы было изначально? \(40\) гуавы.
• Шаг 2 : Сколько гуавы мы с сестрой взяли?
  \(\left({5 + 6} \right)\) Поместим это в первую скобку \(\left({} \right).\)
• Шаг 3 : После того, как мы взяли гуаву, как много осталось в мешке?
  \(\left\{{40 – \left({5 + 6} \right)} \right\}\) Помещаем во вторую скобку \(\left\{{} \right\}.\)
  Если тетя нашла \(10\) больше гуавы, общее количество гуавы будет \(\слева\{{40 – \слева({5 + 6} \справа)} \справа\} + 10\)
  У нас осталось больше задач. Итак, нам нужен еще один кронштейн. Мы будем называть эту скобку квадратной скобкой.
• Шаг 4 : Разделите поровну между \(13\) людьми. Каждый получит, \(\left[{\left\{{40 — \left({5 + 6} \right)} \right\} + 10} \right] \div 13\)
  \(\left[ {\left\{{40 — \left({5 + 6} \right)} \right\} + 10} \right] \div 13\)
  \( = \left[{\left\{{40 — 11} \right\} + 10} \right] \div 13\) (Упростить внутри круглых скобок)
  \( = \left[{29 + 10} \right] \div 13\) (Упростить внутри фигурных скобок)
  \( = 39 \div 13\) (Упростить в квадратных скобках)
  \( = 3\) (Разделить)
  Таким образом, каждый получит \(3\) гуавы.
  Вот как скобки помогают нам в решении экземпляра.
  Когда требуется больше вычислений и необходимо изменить порядок математических операций, мы прибегаем к помощи скобок.

10 математических приемов для быстрого счета

Решенные примеры в скобках

Q.1. Решите \(8 + 9 \дел 9 + 5 \умножить на 2 — 7\).
Ответ: Данное выражение равно \(8 + 9 \div 9 + 5 \times 2 – 7. \)
Поскольку здесь нет скобок, порядок математических операций будет деление, умножение, сложение и затем вычитание .
Сначала выполним операцию деления, т.е. \(9 \div 9 = 1\)
Таким образом, выражение станет \(8 + 1 + 5 \times 2 – 7\)
Затем мы выполним умножение, т.е. (5 \times 2 = 10\)
Теперь выражение принимает вид \(8 + 1 + 10 – 7\)
Затем выполните сложение, т.е. \(8 + 1 + 10 = 19\)
Наконец-то сделаем вычитание.
Теперь \(19 – 7 = 12\)
Следовательно, требуемый ответ равен \(12.\)

Q.2. Упростите \(\left\{ {25 – 3\left( {6 + 1} \right)} \right\} \div 4 + 9\).
Ответ: Данное выражение равно \(\left\{{25 – 3\left({6 + 1} \right)} \right\} \div 4 + 9.\)
Начнем решать внутри круглая скобка или круглая скобка, т. е. \(\left({6 + 1} \right) = 7\)
Затем умножьте \(3\left( 7 \right)\) или \(3 \times 7 = 21 \)
Теперь выражение принимает вид \(\left\{{25 – 21} \right\} \div 4 + 9\)
Оперируйте фигурными скобками, т. е. \(\left\{{25 – 21} \right\ } = 4\)
Таким образом, выражение принимает вид \(4 \div 4 +9\)
Следовательно, \(4 \div 4 = 1\)
Наконец, \(1 + 9 = 10\)
Следовательно, требуется ответ \(10\) после упрощения выражения.

Q.3. Решите \(\left( {1/4 + 1/8} \right)\) из 32.
Ответ: Здесь нам нужно решить выражение \(\left({\frac{1}{4} + \frac{1}{8}} \right)\) из \(32.\)
Во-первых, нам нужно обработать выражение внутри скобки, т. е. \(\left({\frac{1}{4} + \frac{1}{8}} \right) = \frac{{2 + 1 }}{8} = \frac{3}{8}\)
Теперь выражение принимает вид \(\frac{3}{8}\) of \(32\)
‘Of’ означает умножение. Итак, \(\frac{3}{8} \times 32 = 12\)
Следовательно, требуемый ответ равен \(12.\)

Q.4. Упростите \(150 \div 15\left\{ {\left( {12 – 6} \right) – \left( {14 – 12} \right)} \right\}\).
Ответ: Данное выражение равно \(150 \div 15\left\{{\left({12 – 6} \right) – \left({14 – 12} \right)} \right\}\ )
Во-первых, мы должны оперировать и упростить термины внутри \(\left({} \right)\), а затем \(\left\{{} \right\}. \)
Теперь, \(150 \div 15 \left\{{\left({12 – 6} \right) – \left({14 – 12} \right)} \right\}\)
\( = 150 \div 15\left\{{6 – 2} \right\}\) (Решение внутри круглой скобки)
\( = 150 \div 15\left\{ 4 \right\}\) (Решение внутри фигурной скобки)
\( = 10\left\{ 4 \right\}\) (Делить \(150\) на \(15\),т. е. \(12\))
\( = 10 \times 4\) (если перед скобкой нет оператора, считать как есть оператор умножения) \( = 40\) (Умножить \(10\) и \(4\))
Следовательно, требуется ответ \(40.\)

Q.5. Решите \(16\left[ {8 – \left\{ {5 – 2\left( {2 – 1 + 1} \right)} \right\}} \right]\), используя правило BODMAS.
Ответ: Данное выражение равно \(16\left[{8 – \left\{{5 – 2\left({2 – 1 + 1} \right)} \right\}} \right.] \)
Сначала разгадайте скобки.
Теперь \(16\влево[{8 – \влево\{{5 – 2\влево({1 + 1} \вправо)} \вправо\}} \вправо]\)
\( = 16\влево[ {8 – \left\{{5 – 2 \times 2} \right\}} \right]\)(решается внутри изогнутой скобки)
\( = 16\left[{8 – \left\{{5 – 4} \right\}} \right]\) (умноженное внутри фигурной скобки)
\( = 16\left[{8 – 1} \right]\)(Решается внутри фигурной скобки)
\( = 16 \times 7\) (Решается внутри квадратной скобки)
\( = 112\) (умножается)
Следовательно, требуется ответ \(112. \)

Часто задаваемые вопросы о кронштейнах

Q.1. Когда использовать скобки?
Ответ: В математике скобки — это символы, которые часто используются для создания групп или для объяснения порядка выполнения операций в выражении. Некоторые скобки имеют несколько конкретных применений в математике.

Q.2. Как использовать скобочную формулу в математике?
Ответ: Обычно мы используем скобки для группировки в математике. Эти символы скобок:
1. \(\left({} \right)\)
2. \(\left\{{} \right\}\)
3. \(\left[{} \right] \)
Мы всегда используем пару скобок, у которых есть открывающая и закрывающая. Скобки используются для прозрачности порядка операций. Порядок скобок следующий: \(\left({} \right),\left\{{} \right\}\) и \(\left[{} \right].\)

В.3. Что вы подразумеваете под БОДМАС?
Ответ: BODMAS — это краткая форма, используемая для скобок, порядка, деления, умножения, сложения и вычитания. Он описывает математические операции, которые необходимо выполнить при решении математического выражения. Согласно этому правилу, если в выражении присутствует несколько скобок, начните упрощение внутри круглой скобки, затем фигурной скобки, затем квадратной скобки, а затем решите вопрос о приоритете арифметических операций.

Q.4. Вы умножаете сначала, если нет скобок?
Ответ: Согласно правилу BODMAS, скобка должна быть решена первой. Если скобки нет, то следующим приоритетом будет деление или умножение (поскольку и деление, и умножение имеют одинаковый порядок предпочтения), и если умножение идет первым в математическом выражении слева направо. Таким образом, мы сначала умножаем, если нет скобок, так как умножение идет первым в выражении слева направо.

Q.5. Используете ли вы БОДМАС, когда нет брекетов?
Ответ: Да, мы используем правило BODMAS, чтобы получить правильный ответ, даже если нет скобок. Если скобок нет, начните решение с «порядка» или «из», затем следует деление или умножение (в зависимости от того, что наступит раньше слева направо), а затем сложение или вычитание (в зависимости от того, что наступит раньше).

2.1: Порядок действий (действовать упорядоченно)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

22069

• Жан-Поль Оливье
• Колледж прикладного искусства, науки и технологий Ред-Ривер

Вы только что выиграли в конкурсе 50 000 долларов. Поздравляем! Но прежде чем вы сможете претендовать на это, вы должны ответить на вопрос проверки математических навыков, и никакие калькуляторы не разрешены. После того, как вы передадите свой выигрышный билет агенту по выкупу, она вручит вам ограниченный по времени вопрос для проверки навыков: \(2 \times 5 + 30 ÷ 5\). Пока часы отсчитывают время, вы думаете о различных возможностях. Ответ 8, 14, 16 или вообще что-то другое? Не было бы ужасно потерять 50 000 долларов из-за того, что вы не можете решить вопрос! Если вы поняли, что решение равно 16, вы на правильном пути. Если вы думали, что это что-то другое, самое время пересмотреть порядок действий.

Символы

В то время как некоторые математические операции, такие как сложение, используют единственный символ (+), существуют другие операции, такие как умножение, для которых допустимо несколько представлений. С появлением компьютеров в математическую символику вкралось еще больше новых символов. В таблице ниже перечислены различные математические операции и соответствующие математические символы, которые вы можете использовать для них.

93.

Математическая операция
Умножение	\(\times\) или * или \(\cdot\) или 2(2) или (2)(2)	По порядку они называются временем, звездой или пулей. Последние два связаны с подразумеваемым умножением, когда два термина пишутся рядом друг с другом, соединенными только скобками.
Отдел	/ или \(\div\) или \(\dfrac{4}{2}\)	По порядку они известны как косая черта, делитель и делительная линия. Обратите внимание, что в последнем примере деление представлено горизонтальной линией.
Дополнение	+	Других символов нет.
Вычитание	—	Других символов нет.

Вы можете задаться вопросом, означают ли разные типы скобок разные вещи. Хотя математические области, такие как исчисление, используют специальные интерпретации для различных скобок, бизнес-математика использует все скобки, чтобы помочь читателю визуально соединить скобки. Рассмотрим следующие два примера:

\[\text { Пример } 1 : 3 \times(4 /(6-(2+2))+2)\номер \]

\[\text { Пример } 2 : 3 \times[4 / \{6-(2+2)\}+2]\номер \]

Обратите внимание, что во втором примере вы можете гораздо проще соединить скобки в пары, но изменение формы скобок не изменило математическое выражение. Это важно понимать при использовании калькулятора, который обычно имеет только круглые скобки. Поскольку форма скобки не имеет математического значения, решение примера 1 или примера 2 потребует повторного использования круглых скобок.

BEDMAS

В начале раздела ваш вопрос для проверки навыков был \(2 \times 5+30 \div 5\). Вы просто решаете это выражение слева направо, или вы должны начать с другого места? Чтобы избежать путаницы в отношении того, как выполнять эти математические операции, существует согласованная последовательность математических шагов, обычно называемая BEDMAS. BEDMAS является аббревиатурой от B ракеток, E экспонентов, D ivision, M умножения, Добавление и удаление S .

Как это работает

Шаг 1 : Сначала необходимо разрешить скобки. Поскольку скобки могут быть вложены друг в друга, вы должны сначала разрешить самый внутренний набор скобок, прежде чем переходить к следующему набору скобок. При разрешении набора скобок вы должны выполнить математические операции внутри скобок, выполнив оставшиеся шаги в этой модели (EDMAS). Если имеется более одного набора скобок, но они не вложены друг в друга, работайте слева направо и сверху вниз. 9{3}=2 \умножить на 2 \умножить на 2\). Более подробный обзор показателей можно найти в разделе 2.4.

Шаг 3 : Порядок умножения и деления не имеет значения. Однако вы должны разрешать эти операции в порядке слева направо и сверху вниз, как они появляются в выражении.

Шаг 4 : Последними операциями, которые необходимо выполнить, являются сложение и вычитание. Порядок появления не имеет значения; однако вы должны выполнять операции слева направо по выражению.

Важные примечания

Прежде чем продолжить работу с калькулятором Texas Instruments BAII Plus, необходимо изменить некоторые заводские настройки по умолчанию, как описано в таблице ниже. Чтобы изменить значения по умолчанию, откройте окно «Формат» на калькуляторе. Если по какой-либо причине ваш калькулятор сброшен (путем извлечения батареи или нажатия кнопки сброса), вы должны выполнить эту последовательность еще раз.

Кнопки нажаты	Дисплей калькулятора	Что это значит
Второй формат	ДЕК=2,00	Вы открыли окно Формат с его первой настройкой. DEC сообщает вашему калькулятору, как округлять вычисления. В бизнес-математике важно быть точным. Поэтому мы настроим калькулятор на то, что называется плавающим дисплеем, что означает, что ваш калькулятор будет отображать все десятичные знаки и отображать на экране как можно больше.
9 Введите	ДЕК=9	Параметр с плавающей запятой установлен. Давайте продолжим.
\(\стрелка вниз\)	ДЭГ	Этот параметр не имеет ничего общего с бизнес-математикой и просто оставлен в покое. Если он не читает DEG, нажмите 2nd Set, чтобы переключить его.
\(\стрелка вниз\)	США 31-12-1990	Даты можно вводить в калькулятор. Североамериканцы и европейцы используют немного разные форматы дат. Ваш дисплей показывает североамериканский формат и подходит для наших целей. Если он не читает США, нажмите 2nd Set, чтобы переключить его.
\(\стрелка вниз\)	1000 долларов США	В Северной Америке принято разделять числа на блоки по 3 с помощью запятой. Европейцы делают это немного иначе. Этот параметр приемлем для наших целей. Если на вашем дисплее не отображается US, нажмите 2nd Set, чтобы переключить его.
\(\стрелка вниз\)	Чн	Калькуляторы могут решать уравнения двумя способами. Это известно как цепной метод, что означает, что ваш калькулятор будет просто решать уравнения по мере того, как вы вводите его, не обращая внимания на правила BEDMAS. Это неприемлемо и должно быть изменено.
2-й комплект	АОС	AOS расшифровывается как алгебраическая операционная система. Это означает, что теперь калькулятор запрограммирован на использование BEDMAS при решении уравнений.
Второй выход	0	Вернуться к обычному использованию калькулятора.

Также обратите внимание, что в калькуляторе BAII Plus есть два способа ввести показатель степени:

9х 3\) =. Он вычисляет решение 8.

На что следует обратить внимание

Отрицательные признаки. Помните, что в математике используются как положительные числа (такие как \(+3\)) так и отрицательные числа (такие как \(−3\)). Перед положительными числами не нужно ставить знак +, так как это подразумевается. Таким образом, \(+3\) записывается как просто 3. Однако перед отрицательными числами должен стоять знак минус. Будьте осторожны, чтобы не перепутать терминологию отрицательного числа с вычитанием или знаком минус. Например, \(4 + (−3)\) читается как «четыре плюс минус три», а не как «четыре плюс минус три». Чтобы ввести отрицательное число на калькуляторе, сначала введите число, а затем нажмите кнопку ±, которая меняет знак числа.

Горизонтальная разделительная линия. Одна из областей, в которой люди делают больше всего ошибок, связана со «скрытыми скобками». Эта проблема почти всегда возникает, когда горизонтальная линия используется для обозначения деления. Рассмотрим следующее математическое выражение. [\dfrac{4+6}{2+3}\nonumber \]

Обратите внимание, что скобки исчезают из выражения, когда вы записываете его с горизонтальной разделительной линией, потому что они подразумеваются способом, которым появляется выражение. Лучший подход при работе с горизонтальной разделительной линией — повторно вставить скобки вокруг терминов как сверху, так и снизу. {2} \times 3\right\}}{\{(2+8) \div 2\} }\право]\номер \]

После повторной вставки символов вы готовы следовать модели BEDMAS.

Калькуляторы не запрограммированы на распознавание подразумеваемых символов. Если вы наберете «\(3(4 + 2)\)» на своем калькуляторе и не введете знак умножения между «3» и «\((4 + 2)\)», вы получите решение 6. Ваш калькулятор игнорирует цифру «3», так как не знает, какую математическую операцию с ней выполнять. Чтобы ваш калькулятор решил выражение правильно, вы должны ввести уравнение как «\(3 \times (4 + 2)\) =». Это дает правильный ответ 18.

Упрощение негативов. Если ваш вопрос включает в себя положительные и отрицательные числа, иногда бывает сложно понять, какой символ поставить при упрощении или решении. Запомните эти два правила:

Правило №1: Пара одинаковых символов всегда положительна. Таким образом, «\(4 + (+3)\)» и «\(4 − (−3)\)» становятся «\(4 + 3\)».

Правило №2: Пара противоположных символов всегда отрицательная. Таким образом, «\(4 + (−3)\)» и «\(4 − (+3)\)» становятся «\(4 – 3\)».

Простой способ запомнить эти правила — подсчитать общее количество задействованных палочек, где знак «+» соответствует двум палочкам, а знак «-» — одной палочке. Если у вас нечетное количество палочек, результатом является отрицательный знак. Если у вас четное количество палочек, результат является положительным знаком. Обратите внимание на следующие примеры: 9{2} \times 3\right\}}{\{(2+8) \div 2\}}\right]\)

Решение

Вам необходимо оценить каждое из выражений. Это означает, что вы должны решить каждое выражение.

Что вы уже знаете

Вам предоставляются математические выражения в формате формулы. Эти выражения готовы для решения.

Как вы туда доберетесь

Используйте знания BEDMAS, чтобы выполнить каждую операцию в правильном порядке.

Выполнить

\(2 \умножить на 5+30 \дел 5\)	Шаг 1 : Без скобок Шаг 2 : Без показателей Шаг 3 : Работая слева направо, сначала выполните умножение.
\(\mathbf{10}+30 \дел 5\)	Шаг 3 : Теперь разрешите деление. 92+18 \дел 2\)	Шаг 2 : Определите показатель степени.
\(\mathbf{81}+18 \дел 2\)	Шаг 3 : Выполните деление.
\(81+\mathbf{9}\)	Шаг 4 : Выполните добавление.
\(\mathbf{90}\)	Окончательное решение

9{2} \times 3\right\}}{\{\mathbf{10} \div 2\}}\right]\)

Внутренние скобки готовы, теперь их нужно отбросить.

Шаг 1 : У вас все еще есть два набора внутренних скобок {}. Начните с верхнего и выполните EDMAS

. \(4 \times\left[\dfrac{\{3+\mathbf{4} \times 3\}}{\{10 \div 2\}}\right]\) Экспонента разрешена. \(4 \times\left[\dfrac{\{3+\mathbf{12}\}}{\{10 \div 2\}}\right]\) Умножение выполнено. \(4 \times\left[\dfrac{\mathbf{15}}{\{10 \div 2\}}\right]\) Добавление выполнено. Вам больше не нужны скобки, поэтому вы их опускаете. Шаг 1: Теперь делаем нижние кронштейны, выполняя ЭДМАС. Вам нужно решить только одно деление. \(4 \times\left[\dfrac{15}{\mathbf{5}}\right]\)

Дивизия завершена. Вам больше не нужны скобки, поэтому вы их опускаете.

Шаг 1 : Остался последний набор кронштейнов! Остается только дивизия.

\(4 \times \mathbf{3}\)

Дивизия выполнена. Вам больше не нужны скобки, поэтому вы их опускаете.

Шаг 2 : Без показателей.

Шаг 3 9{\ клин} 2 * 3 \ справа) / ((2 + 8) / 2) \ справа) \)

Авторы и ссылки

• Шаблон:ContribBusiMathOlivier

---

Эта страница под названием 2.