Карточка № 2 Реши пример устно. 30 + 30 = | |
Карточка № 3 Реши пример устно. 80 — 20 = | Карточка № 4 Реши пример устно. 70 — 30 = | Карточка № 6 Реши пример. 70 – (30 + 10) = 40 + (50 – 20) = |
Карточка № 7 Реши пример. 80 – (20 + 20) = 10 + (50 – 30) = | Карточка № 8 Реши пример. 70 + (60 – 30) = 90 – (60 + 20) = |
Онлайн урок: Раскрытие скобок по предмету Математика 6 класс
Как вам уже известно, скобки в математических выражениях часто используют для разграничения рядом стоящих знаков или для объединения и перегруппировки чисел, с которыми будут выполнятся определенные математические действия.
Но иногда при решении математических выражений удобно раскрыть скобки, нежели высчитывать их значение.
Раскрыть скобки- это значит освободить выражение от скобок, избавить выражение от лишних знаков, тем самым упростить его для вычисления.
Значение выражение со скобками и значение выражения, полученное после раскрытия скобок, равны, их записывают в виде равенства.
При преобразовании громоздких выражений, в которых содержится большое количество скобок, возникает потребность записывать промежуточные результаты вычислений. В таких случаях решение записывается в виде цепочки равенств.
Рассмотрим правила раскрытия скобок.
Разберем случаи, когда перед скобками стоит знак плюс «+».
1. Выражение вида а + (-b) можно записать, опустив скобки.
Так как вычитание обратное действие сложению (т.е. прибавить число (-b) -это тоже самое, что вычесть положительное число b), получаем равенство
а + (-b) = а — b
2. Выражение вида а + (b+ c) можно записать без скобок.
Согласно сочетательному свойству сложения, если к числу прибавить сумму двух чисел, то нужно сначала к этому числу прибавить первое слагаемое, а затем второе слагаемое.
а + (b + c) = а + b + c
3. Рассмотрим еще одно выражение а + (b— c), и преобразуем это выражение в выражение без скобок.
Если первое слагаемое в скобках стоит без знака, то его знак определяется как знак плюс «+».
Известно, что вычитание можно заменить сложением, следовательно:
а + (b— c) = а + (b+ (-c))
Применив сочетательное свойство, упростим выражение а + (b+ (-c)), в результате получим:
а + (b — c) = а + b — c
Рассуждая подобным образом, попробуем преобразовать еще два выражения со скобками.
4. Преобразуем выражение вида а + (-b+ c) в выражение без скобок.
Зная, что вычитание можно заменить сложением и применив сочетательное свойство сложения, упростим выражение:
а + (-b+ c) = а + ((-b) + c) = а — b+ c, т.е. получаем равенство
а + (-b + c) = а — b + c
5. Преобразуем выражение вида а + (-b— c) в выражение без скобок.
Зная, что вычитание можно заменить сложением, и применив сочетательное свойство сложения, упростим выражение:
а + (-b— c) = а + ((-b) + (-c)) = а — b— c, т. е. получаем равенство
е. получаем равенство
а + (-b — c) = а — b — c
Заметим, что в левой части каждого из равенств перед скобкой стоит знак «+», а слагаемые, стоящие в скобке, после преобразования сохраняют свои знаки:
а + (-b) = а — b
Пример: 15 + (-5) = 15 — 5 = 10
а + (b + c) = а + b+ c
Пример: 15 + (5 + 2) = 15 + 5 + 2 = 22
а + (b — c) = а + b— c
Пример: 15 + (5 — 2) = 15 + 5 — 2 = 18
а + (-b + c) = а — b + c
Пример: 15 + (-5 + 2) = 15 — 5 + 2 = 12
а + (-b — c) = а — b— c
Пример: 15 + (-5 — 2) = 15 — 5 — 2 = 8
Сформулируем правило раскрытия скобок, перед которыми стоит знак плюс:
Если перед скобками стоит знак плюс или не стоит никакого знака, то этот знак «+» и скобки необходимо опустить, сохранив знаки слагаемых, которые стояли в скобках.
Пример:
Найдите значения выражения -4 + (3 — 1 + 4).
Решение:
Избавимся от скобок, используя правило раскрытия скобок, перед которыми стоит знак «+».
Затем найдем значение выражения, используя переместительное свойство сложения и правило сложения чисел с разными знаками.
-4 + (3 — 1 + 4) = -4 + 3 — 1 + 4 = 4 — 4 + 3 — 1= 0 + 3 — 1 = 3 — 1 = 2
Ответ: 2
Рассмотрим случаи, когда перед раскрываемыми скобками стоит знак минус «-».
Вспомним, какие числа называют противоположными: два числа называют противоположными, если они отличны друг от друга только знаками, модули их равны.
Число а противоположно числу (-а).
-(-а) противоположно числу (-а).
Тогда верно утверждение, что -(-а) = а
Найдем значение выражения: -(-8 + 4)
Определим значение данного выражения двумя способами:
1. Найдем значение суммы в скобках, затем полученную сумму запишем со знаком минус «-».
Найдем значение суммы в скобках, затем полученную сумму запишем со знаком минус «-».
-(-8 + 4) = -(-4) = 4
2. Раскроем скобки.
Чтобы найти сумму противоположную сумме нескольких слагаемых, действуем по аналогии с утверждением -(-а) = а — необходимо изменить знаки слагаемых на противоположные.
-(-8 + 4) = 8 — 4 = 4
В первом и во втором случае получили одинаковый результат, он равен четырем.
Сформулируем правило раскрытия скобок, перед которыми стоит знак минус.
Если перед скобками стоит знак минус, то этот знак «-» и скобки необходимо опустить, изменив знаки слагаемых, которые стояли в скобках на противоположные (знак минус меняется на плюс, знак плюс на минус).
Рассмотрим несколько равенств и раскроем скобки в них согласно данному правилу.
а — (-b) = а + b
Пример: 10 — (-5) = 10 + 5 = 15
а — (b + c) = а — b— c
Пример: 20 — (5 + 3) = 20 — 5 — 3 = 15 — 3 = 12
а — (b — c) = а — b + c
Пример: 20 — (5 — 3) = 20 — 5 + 3 = 15 + 3 = 18
а — (-b + c) = а + b— c
Пример: 20 — (-5 + 3) = 20 + 5 — 3 = 25 — 3 = 22
а — (-b — c) = а + b+ c
Пример: 20 — (-5 — 3) = 20 + 5 + 3 = 25 + 3 = 28
Пример:
Вычислите значение выражения 15 — (4 + 15 — 3).
Решение:
Избавимся от скобок, используя правило раскрытия скобок, перед которыми стоит знак «-».
Затем найдем значение выражения, используя переместительное свойство сложения и правило сложения чисел с разными знаками.
15 — (4 + 15 — 3) = 15 — 4 — 15 + 3 = 15 — 15 — 4 + 3 = 0 — 4 + 3 = -4 + 3 = -1
Ответ: -1
Разберем правило раскрытия скобок при умножении числа на сумму (суммы на число).
Правило раскрытия скобок для данного случая звучит так:
Для раскрытия скобок в выражениях, содержащих умножение суммы на число или числа на сумму, используется распределительное свойство умножения относительно сложения.
\(\mathbf{(a + b) \cdot c = a \cdot c + b \cdot c}\)
\(\mathbf{(a — b) \cdot c = a \cdot c + (-b) \cdot c = a \cdot c — b \cdot c}\)
Если число с положительное, то знаки слагаемых a и b не изменяются.
Если число с отрицательное, то знаки слагаемых a и b меняются на противоположные.
Пример:
Найдите значение выражения \(\mathbf{(7,2 — 5,3) \cdot 2}\)
Решение:
Воспользуемся правилом раскрытия скобок при умножении суммы на число.
\(\mathbf{(7,2 — 5,3) \cdot 2 = 7,2 \cdot 2 — 5,3 \cdot 2 = 14,4 — 10,6 = 3,8}\)
Ответ: 3,8
Пример:
Найдите значение выражения \(\mathbf{(7,2 — 5,3) \cdot (-2)}\)
Решение:
Воспользуемся правилом раскрытия скобок при умножении суммы на число.
\(\mathbf{(7,2 — 5,3) \cdot (-2) = 7,2 \cdot (-2) — 5,3 \cdot (-2) = -14,4 + 10,6 = -3,8}\)
Ответ: -3,8
| Табличка на двери |
| Табличка на двери |
Порядок действий в математике пример
В порядке оказания скорой математической помощи, решим тестовое задание для 5 класса. В этом тесте мы рассмотрим порядок действий в математике пример. У нас имеется набор математических действий с двумя парами скобок. Как решить такой пример? Сперва выполняем действия во внутренних скобках. После их выполнения внутренние скобки у нас исчезают и вместо них мы получаем число. Дальше выполняем математические действия в оставшихся скобках (в начале они были наружными скобками). В заключение операции «Порядок действий в математике» выполняем всё то, что осталось за скобками.При всех наших вычислениях в скобках строго соблюдаем незыблемое правило выполнения математических действий: сперва выполняем умножение и деление, только после этого выполняем сложение и вычитание. Если что-то из этого отсутствует — радуйтесь!
Теперь рассмотрим сам пример и порядок действий.
В самом начале рассматриваем внутренние круглые скобки. В них спрятаны вычитание и умножение. Первым действием выполняем умножение (деления нет — ура!), вторым — вычитание. С первой парой круглых скобок мы покончили. Но у нас остается ещё одни пара скобок, в которой есть деление, сложение, умножение. Прежде, чем выполнять сложение, необходимо выполнить деление и умножение. В какой последовательности выполнять эти два действия в данном примере — принципиального значения не имеет. Мы выполним по порядку — сперва деление, потом умножение. Полученные в результате числа складываем. В завершение всех мучений выполняем деление. Результат можно записать в виде числа с десятичной дробью (боюсь, что данное замечание не касается учеников пятых классов — сам-то я там не учусь), но обыкновенная дробь выглядит гораздо круче.
В нижней строчке решенный нами пример записан в несколько ином, более фотогеничном, виде. Различные формы записи математического выражения на порядок выполнения действий не влияют. Если, конечно, мы всё правильно записали.
Как порядочный лентяй, при решении этого примера я воспользовался математическим калькулятором, в который просто ввел выражение (41811/1267+506*(3000-2*877))/153 и нажал кнопочку «равно«. Подробного решения этот калькулятор онлайн не дает, но правильный ответ подсмотреть можно.
Ещё вам может очень пригодиться разложение числа на множители онлайн при сокращении дробей. Называется данная операция очень страшно: «Факторизация числа». Естественно, у меня возникает вопрос: чем разложение чисел на множители отличается от факторизации числа? Разложением чисел на множители занимаются дети в школе. Скорее всего, взрослым дядькам стыдно этим заниматься, поэтому они с умным видом занимаются факторизацией чисел (чем бы дитя не тешилось — лишь бы не плакало).
Порядок выполнения действий
Домашняя работа
- Упростить выражение
и найти значение :
18x + 23 x — x при х = 37
2. Решить уравнение:
5y + 12y = 3553
3.Вынести общий множитель за скобки :
(18+23-1)х=40х=40* 37=1480
17у=3553
8x – 16 y + 80
У=209
= 8(х-2у+10)
20a — 28b
= 4(5а-7в)
Тема урока
«Порядок выполнения действий. Степень числа. Квадрат и куб числа»
Какие действия относятся к действиям первой ступени — Какие действия относятся к действиям
второй ступени —
сложение и вычитание
умножение и деление.
В каком порядке выполняются действия в выражениях без скобок?
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
800-625+331+87-119=474
780÷39∙212÷106∙13=520
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
578-75÷25∙4+156÷12
Действия второй ступени 75÷25=3 3∙4=16 156÷12=13
Действия первой ступени 578-16=562 562+13=575
В каком порядке выполняются действия в выражениях со скобками?
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2)
36000÷(62+14∙2)-23∙5=
В каком случае в выражении, содержащем скобки, скобки можно не писать?
В выражениях скобки можно скобки не писать, если при этом порядок действий не меняется.
(53-12)+14
53-12+14
53-12=41 41 +14=55
Можно ли изменять порядок выполнения действий? В каких случаях?
Изменить порядок действий можно на основе свойств сложения и вычитания.
Определите порядок выполнения действий и вычислите значения выражений:
а) 78+22-28 = б) 54 2 50=
в) 318-(48+52):10 = г)318-48+50:5=
д) 34 8+66 8 = е)125:(43-38)-10=
ж) 132-(64:16+75:15)=
5400
72
280
308
15
800
123
Не производя вычислений определите, в каком из примеров указанный порядок действий приводит к неверному результату:
а) 87+54 14 +32
б) 1998-10 (8 9+28)
в) 50:2-3-1
г)111+(24-13) 4-7 3
Решите задачу, составив уравнение.
В двух больших и пяти маленьких бидонах 130 л молока. Сколько молока входит в маленький бидон, если его вместимость в четыре раза меньше вместимости большого?
4х
4х
х
х
х
х
х
130
8х + 5х = 130
Сумма, в которой слагаемые равны друг другу
+
+
+
+
+
+
3
3
3
3
3
3
3
1
5
4
3
6
7
2
?
3
7
=21
*
Произведение, в котором множители равны друг другу
3
3
3
3
3
3
3
*
*
*
*
*
*
2
1
3
5
4
6
7
?
7
3
= 2187
Запись 3 7 читают «три в седьмой степени»
Основные понятия
Показатель степени
7
3
Степень
Основание степени
Вторая степень числа называется квадратом числа
3 · 3 = 3 (три в квадрате)
2
Произведение n и n называют квадратом числа n и обозначают n
2
n · n = n
2
Таблица квадратов первых 10 натуральных чисел
п
п 2
1
1
2
3
4
4
9
16
5
6
25
7
36
8
49
64
9
10
81
100
Третья степень числа называется кубом числа
4 · 4 · 4 = 4 (четыре в кубе)
3
Произведение n · n · n называют кубом числа n
и обозначают n
3
n · n · n=n
3
Таблица кубов первых 10 натуральных чисел
п
1
п 3
1
2
3
8
4
27
5
64
6
125
7
216
8
343
9
512
10
729
1000
1
3 =
3
1
7 =
7
1
1 =
1
Первая степень любого числа равна самому числу
Немного истории
Понятие степени возникло свыше 400 лет назад. Индийские ученые называли степени с помощью комбинации слов: «ва» – 2-я степень , от слова «варга» — квадрат; «гха» – 3-я степень , от «гхана» — тело, куб.
Современную запись (например, 5 2 , 7 4 )
ввёл французский математик Рене Декарт в 1637 г.
Запись произведения равных множителей в виде степени помогает во множестве ситуаций, людям самых различных профессий.
Большую радость от изобретения степеней получили астрономы, которые работают с огромными числами. Например,
масса Земли
6.000.000.000.000.000.000.000.000 кг
24
= 6•10 кг
масса Солнца
1 983.000.000.000.000.000.000.000.000.000 кг
27
= 1 983•10 кг
Прочитайте степени
5
7
« Семь в пятой степени»
4
9
« Девять в четвертой степени »
2
3
« Три во второй степени»
или « Три в квадрате »
3
« Пять в третьей степени »
5
или « Пять в кубе »
Представьте произведение в виде степени, назовите показатель и основание степени, вычислите
3 · 3 · 3 · 3 =
3 4 = 81
5 · 5 · 5 =
5 3 = 125
2 · 2 · 2 · 2 · 2 · 2 =
2 6 = 64
Надо помнить,
если в числовое выражение входят степени чисел, то их значение вычисляют до выполнения остальных действий.
6
Вычислите
=
6
7
8
При
—
)
(
32
5
=
?
0
7
6
8
1
Вычислите устно
2
3
—
=
1
8
?
3
3
2
4
24
2
?
=
+
2
2
—
(2+3)
4
?
9
=
2
=
?
3
12
2
*
2
2
(50:5)
—
8
=
?
36
Тест
1. Куб числа – это:
А) произведение трех одинаковых чисел
Б) сумма трех одинаковых чисел
В) сумма двух чисел
2. Числовое значение выражения 6² равно:
А) 12, Б) 36, В) 8.
3. Числовое значение выражения 4³ равно:
А) 12, Б) 16, В) 64.
4. Выражение 5 + 5 + 5 означает
А) 5³, Б) 5 + 3, В) 5 · 3.
Подведем итоги
7
3
3
Что это?
Основание
Что это?
Показатель
7
3
3
=3*3*3*3*3*3*3
7
3
3
“ Три в седьмой степени ”
3
“ Три в кубе ”
3
3
2
3
“ Три в квадрате ”
3
Тест
1. Куб числа – это:
А) произведение трех одинаковых чисел
Б) сумма трех одинаковых чисел
В) сумма двух чисел
2. Числовое значение выражения 6² равно:
А) 12, Б) 36, В) 8.
3. Числовое значение выражения 4³ равно:
А) 12, Б) 16, В) 64.
4. Выражение 5 + 5 + 5 означает
А) 5³, Б) 5 + 3, В) 5 · 3.
Проверьте тест
Номер задания
Правильный ответ
1
2
А
3
Б
4
В
В
Урок математики во 2-м классе по теме «Порядок действий в выражениях со скобками»
Урок математики во 2-м классе по теме «Порядок действий в выражениях со скобками»
Учитель: Яковенко Анастасия Алексеевна
Тема.
Цель урока: Ознакомить учащихся с порядком действий в выражениях со скобками. Формировать вычислительную компетентность.
Задачи
I. Образовательная
Научить читать выражения со скобками, используя слова «сумма», «разность».
Ознакомить с порядком действий со скобками.
Продолжить работу над составлением обратных задач.
Продолжить формировать умения рассуждать, обобщать и делать выводы.
II. Коррекционная
Развивать вычислительные навыки учащихся.
Развивать логическое мышление.
Формировать творческую активность, внимание.
III. Воспитательная
Воспитывать чувство товарищества к одноклассникам.
Пропогандировать здоровый образ жизни.
Воспитывать волю, умение доводить начатое до конца. .
Развивать интерес к математике, как к учебному предмету, через игровую форму обучения.
Оборудование:Сказочные герои: Буратино и Мальвина, веера с цифрами, таблицы для устного счёта, карточки с примерами 90-1, 59+1, 5+2+1=(5+2)+1,схема- чертёж к задаче 35 стр.33, разноуровневые задания на карточках (для самостоятельной работы на уроке и для домашней работы).
Ход урока.
I. Организационный момент.
Психологическая разминка (по таблице) Верхний ряд — буквы алфавита их нужно быстро произносить. Нижний ряд П- правая рука, Л- левая рука, В- руки вверх одновременно. Дети одновременно произносят буквы и поднимают руки. Цель: Согласовать полушария головного мозга. Улучшить внимание, память, мышление.
II.Сообщение темы и постановка цели урока.
Создание игровой ситуации.
За отдельным столом сидит мальчик в костюме Буратино, носом тычет в открытую книгу. -Что такое, почему ничего я не пойму? Будь неладна эта математика. И помочь мне некому? Пойду лучше погуляю на улице. Учитель останавливает Буратино. Может мы, тебе можем помочь? Какие у тебя трудности? ( Буратино показывает учителю задание). Учитель пишет пример на доске 15- ( 6+3)= Ребята, что нового в примере вы заметили? (Появились скобки) Чтобы помочь Буратино решить такие примеры, мы должны изучить новую тему. Называется она « Порядок действий со скобками». А теперь попробуйте сформулировать цель урока. (Научиться решать выражения со скобками.) Буратино по желанию садится за любую парту.
III. Математическая разминка (устный счёт)
а) Решение логических задач.(Сказочный калейдоскоп)
1. В очереди на приём к доктору Айболиту сидят 8 больных. Сначала доктор вызвал в кабинет тех, у кого очень болели зубы. Третий и пятый больные пошли в кабинет. Сколько больных осталось ждать своей очереди? (4)
2. Змей – Горыныч приказал кузнецу сделать для его дворца 3 замка и к каждому замку 3 ключа – медный, серебряный и золотой. Сколько ключей должен сделать кузнец? (9)
3. Винни – Пух и Пятачок были в гостя у Кролика. У кролика в шкафу стояли 5 горшочков с мёдом и 2 банки с вареньем. Сначала они съели всё варенье, а потом 3 горшочка с мёдом. Остался ли у Кролика хотя бы один горшочек с мёдом? ( Остался) Буратино тянет руку и задаёт свою задачу.
4. Половину всех своих золотых монет я отдал за обед в харчевне, а остальные 6 монет я по совету лисы Алисы и кота Базилио закопал в землю. Сколько золотых монет было у меня? (12)
б) Работа по таблицам. Игра « Молчанка»(используются числовые веера)
в) Составьте задачу по краткой записи.
На тарелке лежало 5 яблок и 3 груши. На сколько больше яблок, чем груш? Во время устного счёта 4 учащихся работают по карточкам. Задания разноуровневые.
1 уровеньРеши выражения
3+7=
4+2=
10-5=
6+3=
2+5=
8-4=
0+9=
2 уровеньСравни именованные числа
4 дес. 1ед. * 1дес. 4ед.
32см * 2дм 3см
1м * 99см
1ч. * 60сек.
Творческая работа 1учащийся Дорисуй фигуры, составленные из трёх равных квадратов так, чтобы получились изображения каких – либо предметов, зверей, птиц и др.
IV. Подготовительная работа к изучению нового материала.
На карточках выражения, они вывешиваются на доску.
14- 9= 7+5=
Прочитайте эти выражения разными способами. А теперь прочитайте эти выражения, используя слова «сумма», «разность». (Сумма чисел 7 и 5 равна 12. Разность чисел 14 и 9 равна 5.)
К доске выходят 3 учащихся, под диктовку записывают выражения: сумма чисел 7 и 4, разность чисел 17 и 9, сумма чисел 5 и 6. На доске появляется запись:
7+4= ; 17-9=; 5+6=
Далее дети решают их самостоятельно. Взаимопроверка.
V. Формирование новых знаний. Изучение нового материала.
Стук в дверь. Входит Мальвина. В руках сумочка. – У нас ещё один гость. Кто же это? – Здравствуйте ребята, вы узнали меня. Дошёл до меня слух, что Буратино вместе с вами. Пришла я не с пустыми руками и хочу помочь вам и Буратино познакомиться с новой темой. Воспитательный момент. Учитель: — Мальвина очень добрая. Она всегда помогает слабым людям. Я хочу, чтобы вы ребята тоже помогали друг другу в учёбе. А что же она принесла с собой? Переворачивается карточка.
5+2+1=(5+2)+1
— Рассмотрите равенство. — Чем похожи левая и правая части? (Числами и арифметическими знаками) — Чем отличаются? (В правой части появились скобки). — Сколько получится в левой части? (8)- Как нужно посчитать правую часть, чтобы получилось тоже 8.(Сначала сложить в скобках 5и 2, а потом к 7 прибавить 1).
На доске учитель записывает выражение (6+4)-1. Прочитайте его. (Из суммы чисел 6 и 4 вычесть 1).- В каком порядке нужно выполнить действия (Сначала найти сумму чисел 6 и 4, а потом вычесть, получится 9.)
Далее меняю скобки 6+(4-1)=; Дети читают выражение (К 6 прибавить разность чисел 4 и 1) – Что изменилось в выражении? (Скобки стоят в другом месте)- В каком порядке нужно выполнить действия в этом выражении? (Найти сначала разность чисел 4 и 1, а затем прибавить 6. Получится 9)
– А теперь сформулируйте правило, как выполнять действия в выражениях со скобками. Выслушиваются несколько вариантов.
VI. Физкультминутка.
Один, два, три, четыре, пять!
Все умеем мы считать,
Отдыхать умеем тоже-
Руки за спину положим,
Голову поднимем выше
И легко – легко подышим…
Один – два! Выше голова.
Три – четыре! Руки шире.
Пять – шесть! Тихо сесть.
VII. Закрепление нового материала.
а) Из учебника (с. 32) зачитывается правило: все читают про себя; вслух 2 учащихся; хором.
Действия, записанные в скобках, выполняются первыми.
б) Решение выражений.
Стр. 32 №1(1,2) – коллективная работа. Дети по цепочке записывают примеры и объясняют их решение.
Самостоятельная работа в тетрадях- с. 32 №1 (3) Проверяют консультанты.
Самостоятельная работа на доске. Решают 2 учащихся
4-1+2=1 8-5+1=2 12-5+4=3 6-4+9=11
Контроль над усвоением новой темы. Работа по перфокартам, работает весь класс. Проверяет перфокарты Мальвина. (7+9)+2=
16- (9-4)=
(20-10)+8=
VIII. Работа над составлением обратных задач.
Стр. 33 №5 Учащиеся читают задачу. – О чём эта задача? (О бассейне)
Воспитательный момент. -Кто из вас посещает бассейн? — Какую пользу приносит людям посещение бассейна? ( Укрепляет здоровье человека.)
-Вы тоже должны укреплять своё здоровье, заниматься спортом.
— Покажи отрезок, который обозначает длину всей дорожки. Чему он равен? (100 м)
–Что обозначает отрезок, длиной 60 м? (Сколько проплыл Коля)
— Что требуется узнать в задаче? ( Сколько ему осталось проплыть)
Решите самостоятельно. (Проверка фронтальная)
Обратные задачи составляются коллективно, на доске составляет чертежи Буратино, а решают их дети самостоятельно.
IX. Домашнее задание.( Разноуровневое)
Всем выучить правило на стр. 32
1уровень — стр. 30 №5 решение выражений
2 уровень — стр. 33 №6 задача
Творческое задание выполняет один ученик. Как число 1 можно записать тремя различными цифрами, соединив их знаками действий.
Пример: 4+5-8=1, 6-3-2=1 и т. п.
X. Итог урока.
а) Рефлексия Сказочные герои благодарят ребят. Буратино теперь научился решать примеры со скобками.- Что нового узнали сегодня на уроке? – Всё ли было понятно?- Что вызвало трудности?- Как вы думаете почему?
б) Самооценка учащихся. Оцени свою работу на уроке. Оцени работу своего одноклассника. – Ребята, покажите, как вы усвоили тему. Используется нотный стан. Нота ставится на ту линию, насколько дети поняли тему.
в) Оценивание учащихся учителем. Одобрение и похвала успевающих детей, подбадривание отстающих.
XI. Организационный конец.
Числовые и буквенные выражения. Порядок действий. 🐲 СПАДИЛО.РУ
Что такое числовое выражение?Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.
Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.
- 256 : 2 + 315×5
- (181 – 19)×6 – 121:11
- 13,5 + 16 – 11
- 122 — 14×8,5
Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.
Важно!Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей ступени.
Порядок действий в выражении, не содержащем скобки
Порядок действий без скобок- При наличии действий одной ступени их выполняют по порядку слева направо.
- При наличии действий разных ступеней — выполнение начинается с высшей ступени (то есть с третьей).
Пример №2.
890 – 567 + 2340 – 124
в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:
- 890 – 567 = 323
- 323 + 2340=2663
- 2663 – 124=2539
1260:20×3,7:10
в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:
- 1260:20=63
- 63 3,7=233,1
- 233,1:10=23,31
560:2 + 162 – 3×76,2
здесь присутствуют действия всех ступеней. Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:
- 162=256
- 560:2=280
- 3 76,2=228,6
- 280+256=536
- 536 – 228,6=307,4
Порядок действий в выражении, содержащем скобки
Порядок действий со скобкамиЕсли числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.
Пример №5.
(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125
здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):
- 67,92:2=33,96
- 3245+33,96=3278,96
- 126×2=252
- 321:3=107
- 252-107=145
Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):
- 3278,96×3=9836,88
- 9836,88+145=9981,88
- 9981,88 – 125=9856,88
Буквенные выражения. Числовое значение буквенного выражения.
Какие выражения называют буквенными?Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.
Пример №6. Примеры буквенных выражений:
- 5х + 6у
- 18 + a + b
- 12с – 11
- m + n
- (x + n) – 11m
Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.
Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17. Таким образом, числовое значение буквенного выражения с + х равно 23,17.
Пример №8. Найдем значение выражения 11х +(с — d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.
Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.
Обзор кронштейна
Обзор кронштейнакронштейны помогают интегрировать стратегию управления рисками непосредственно в создание ордера на акции или опционы. Брекет-заказы условны приказы, которые вы можете прикрепить к своим акциям или опционные приказы, которые позволяют вам предварительно определить целевые значения прибыли и убытков, где, если эти цели будут достигнуты, программа автоматически отправит рыночный приказ на выход из позиции.
Заказы в скобках состоят из основного заказа и до трех условных заказов. ордера, которые в случае срабатывания закрывают позицию, открытую первичный заказ.Brackets может обеспечить автоматическое управление рисками для вашего открывать позиции независимо от того, вошли ли вы в программу.
Для установки скобок:
- Во время ввода заявки: На вкладке «Торговля» нажмите «Добавить». Кронштейн, или, если панель Кронштейна уже открыта, проверьте выход тип, который вы хотите добавить к создаваемому заказу.
- В открытом заказе: На вкладке «Статус заказа» щелкните заказ и нажмите Применить скобу или на диаграмме щелкните правой кнопкой мыши индикатор заказа и выберите Добавить / изменить скобу .
- В позиции: На вкладке «Позиции» щелкните позицию и нажмите Применить скобу .
СОВЕТ. См. Раздел «Управление брекет-ордерами» для получения дополнительной информации о добавлении скобок для открытых ордеров и позиций.
Некоторые аспекты заказов скобок предопределены:
- Количество скобок Заказ (а) всегда будет равен количеству, заполненному в первичном заказе.
- Кронштейны остаются активными с их первичным заказом или первичной позицией (когда выполняется первичный заказ) на неопределенный срок, если они не удаляются вручную или не запускаются и не заполняются.
- Кронштейн заказы можно настраивается для любого ордера на акции или опционы, который открывается или дополняет существующий положение, независимо от места проведения первичного заказа.
- Скобки на символах с широким спредом могут не сработать, если разброс слишком большой.
- Кронштейн заказывается только активен во время стандартной сессии (с 9:30 до 16:00 по восточноевропейскому времени)
- Брекет-ордера всегда отправлено как ордер SmartEx Market независимо от места направления первичного заказа.
- Кронштейн приказов триггера от цены спроса / предложения как для акций, так и для опционов.
- В то время как Est. Цена рассчитывается исходя из предельной или внутренней цены бид / аск (для рыночных ордеров), фактическая цена выхода будет основана на средней цена исполнения из первичного заказа. Посмотреть кронштейн Раздел «Примеры заказа», чтобы лучше понять скобки в действие.
- Примечание: Количество заказа в скобках не изменится из-за корпоративных действий, в том числе но ограничивается дроблением акций, дивидендами по акциям, выделением, слияниями и имя меняется.
- Выходы из кронштейнов не работают в положениях в штучной упаковке.
- Кронштейны на стапелях которые не имеют котировок спроса / предложения, включая ценные бумаги Pink Sheet, будут не активировать.
- При размещении кронштейна приказ продать и закрыть длинную позицию, если торгуемое количество вашей позиции меньше, чем количество, которое вы укажите в заказе, программа отправит заказ на меньшую суммы, а не отклонить заказ из-за недостаточного количества доступных акций торговать.
Только StreetSmart: Скобки, условные заказы и оповещения, созданные на платформах StreetSmart, можно просматривать и управлять только из семейства приложений StreetSmart и в настоящее время недоступны на Schwab.com или других приложениях Schwab.
Вы можете установить до трех типов выходов:
- Прибыль
Выход: указывает увеличение (или уменьшение для коротких заказов на продажу).
в значении от средней цены исполнения, необходимой для срабатывания выхода из прибыли.Значение может быть определенным количеством баллов (pts) или процентным изменением.
от цены исполнения или самой цены выхода.
Например, если вы купили акцию по 10 долларов и хотели выйти из позиции при цене 12 долларов вы можете ввести 2 балла, 20% или 12 долларов. Est. Ценник покажет вам вероятный результат, если Срабатывает выход с прибылью, но эта цена будет скорректирована, если средняя Цена заполнения вашего заказа отличается.
- Висячий
Stop Exit: указывает сумму, на которую вы готовы позволить акции.
или цена опциона противоречит любой прибыли, которую он может получить до закрытия
это по рыночной цене.Ценность может быть определенным количеством баллов или
процент от цены исполнения.
Если вы используете трейлинг-стоп для выхода в сочетании с прибылью и / или при выходе с убытком, между этими двумя выходами будет действовать скользящий стоп. Если соблюдены либо цена выхода прибыли, либо стоп-лосс, скобка будет запускается независимо от установленного вами трейлинг-стопа.
Например, если вы купили акцию по 10 долларов и хотели продать, следует рынок движется против вас 5% (или.5 баллов за акцию) от исполнения цена, скользящий стоп разместит приказ только на закрытие вашей позиции если цена акции упадет на 5% от максимальной прибыли. Самая низкая цена, которая вызовет рыночный ордер на продажу, будет стоить 9,50 долларов, потому что он так и не заработал по цене исполнения. Важно помнить, что процент на этом выходе основывается на исходной цене исполнения, а не на текущей рыночная цена.
Другой пример: цена может двигаться вверх, но никогда не падала.5 точки. Это затем набирает 14 долларов, отступает до $ 13,5, и ордер срабатывает. Если бы вы также настроили выход с прибылью 10% и выход с убытком 3% в сочетании с вашим трейлингом остановить выход, скобка сработает на 3% ниже выполнения цена или на 10% выше этой цены при соблюдении. Это произойдет независимо от вашего расчет трейлинг-стопа.
- Стоп
Loss Exit: указывает уменьшение значения (или, для краткости, увеличение).
ордеров) от средней цены исполнения, необходимой для срабатывания стоп-лосса
выход.Значение может быть определенным количеством баллов (pts) или процентным соотношением.
изменение цены исполнения или самой цены стоп-лосса.
Например, если вы купили акцию по 10 долларов и хотели закрыть позицию после того, как он потерял 10%, вы можете ввести 1 пункт, 10% или 9 долларов. В Стандартное восточное время. Ценник покажет вам вероятный результат если сработал Stop Loss Exit.
Подробнее об управлении заказами на кронштейны
Авторские права © Charles Schwab & Co., Inc. 2005- 2014. Все права защищены. Член SIPC. (1213-8129)
Порядок математических операций
Когда мы выполняем вычислительные действия в математике, мы должны помнить о том, что существует последовательность, которую необходимо соблюдать для правильного выполнения вычислений. Операции делятся на три степени, и мы начинаем вычисления с операций первой степени. Поскольку одно математическое выражение может (но не обязательно) состоять из операций с разными степенями, мы должны помнить о двух вещах:
- , если выражение состоит из операций с одинаковой степенью , мы разрешаем их слева направо.
- , если выражение состоит из операций с разными степенями , мы разрешаем его , следуя порядку градусов.
Итак, это порядок действий относительно порядка решения:
- Экспоненты и корни (операции третьей степени)
- Умножение и деление (операции второй степени)
- Сложение и вычитание (операции первой степени)
Например, давайте попробуем решить эту проблему, соблюдая порядок операций, а затем попробуем сделать это наоборот, чтобы увидеть разницу.
Пример 1.5 + 4 \ cdot 2 =
?По порядку операций:
$ 5 + 4 \ cdot 2 = 5 + 8 = 13 $
Слева направо:
$ 5 + 4 \ cdot 2 = 9 \ cdot 2 = 18 $
Как видите, порядок операций имеет большое значение. Но что, если мы хотим, чтобы сложение выполнялось перед умножением? Мы можем это сделать? Что ж, конечно, можем — если заключить соответствующую часть скобками.
КронштейныСкобки — это не сами операции, а символы, которые имеют жизненно важное значение для порядка выполнения операций.Это потому, что мы можем использовать квадратные скобки, чтобы изменить правильный порядок операций.
Скобки заключаются в те части математических выражений, которые мы хотим решить в первую очередь. Есть три различных типа скобок: круглые скобки или круглые скобки (), квадратные скобки или жесткие скобки или просто скобки [] и фигурные скобки или скобки {}.
Существуют и другие типы скобок, но только они используются в контексте порядка операций. В математике они всегда идут парами: открывающая скобка — это {, [или (, и закрывающая скобка),] или}.
Скобки можно ставить вокруг других скобок, создавая так называемые вложенные скобки . Из-за наличия вложенных скобок и из-за того, что доступны три типа, существует порядок как для решения, так и для вложения скобок.
Скобки вложены следующим образом:
- Круглые скобки или круглые скобки являются скобками первой степени, и они не заключают никаких других скобок.
- Квадратные скобки используются, когда мы хотим создать выражение, которое включает выражение, уже заключенное в круглые скобки.
- Фигурные скобки используются, когда мы хотим создать выражение, которое включает выражение, уже заключенное в квадратные скобки.
Итак, выражение, в котором используются все три типа скобок, может выглядеть так:
$ 4 + 18 \ cdot {24-8 \ cdot [(23-8) + 3 \ cdot (32 + 4)] — 8 \ cdot (23-4)}
$Видите? Теперь, когда мы знаем правильный порядок операций, скобки дают нам точные инструкции о том, как эту проблему следует решить, чтобы получить правильный результат.И в каком порядке решаются скобки? Что ж, мы начинаем изнутри, сначала решая проблемы в круглых скобках, а затем работаем над выходом. Как это:
Пример:
$ 49 + 3 \ cdot {24-2 \ cdot [(23-8) + 3 \ cdot (3 + 4)] — 8 \ cdot (2-4)}
$$ = 49 + 3 \ cdot {24-2 \ cdot [15 + 3 \ cdot 7] — 8 \ cdot (-2)}
$$ = 49 + 3 \ cdot {24-2 \ cdot [15 + 21] — 8 \ cdot (-2)}
$$ = 49 + 3 \ cdot {24-2 \ cdot 36-8 \ cdot (-2)}
$$ = 49 + 3 \ cdot {24 — 72 + 16}
$$ = 49 + 3 \ cdot (-32)
$$ = 49 — 96 $
$ = — 47 $
Ради удовольствия, попробуйте решить эту задачу любым старым способом и посмотрите, какие результаты вы получите.
Ну вот и все, что касается нашего урока по порядку действий. Поскольку это очень важно и может быть немного сложно освоить, не стесняйтесь попрактиковаться, используя приведенные ниже рабочие листы.
квадратных скобок, фигурных скобок, угловых скобок, о боже!
Научитесь эффективно использовать скобки в письмеПозвольте мне познакомить вас с жизнью на Scribendi.com. Когда мы не безумно редактируем до раннего утра (что, честно говоря, мы проводим большую часть времени), мы проводим остальную часть нашего времени, обсуждая и пишя статьи, предназначенные для того, чтобы помочь вам (нашим замечательным клиентам) стать лучшими писателями. .
Когда мне назначили статью о скобках, я был вне себя от радости (ну ладно, не совсем). По правде говоря, я не был уверен, как я собираюсь написать всю статью о скобках, но, как я обнаружил в своем исследовании, скобки на самом деле более сложны, чем думает большинство людей.
Квадратные скобки
Иногда квадратные скобки используются для большей ясности текста. Когда цитата, используемая в статье, содержит слово «оно», автор статьи часто использует скобки, чтобы прояснить антецедент.Это делается по ряду причин, но чаще всего потому, что, когда писатель использует цитату в статье, читатель сталкивается с цитатой вне ее исходного контекста, и поскольку читатели полагаются на контекст для определения антецедента, антецедент должен быть при условии. Например:
Бланш Дюбуа утверждает, что «хотя Бенджамину Франклину часто приписывают открытие этого [электричества], древние египтяне на самом деле заслуживают наибольшего признания».
Квадратные скобки также используются для заключения латинского слова sic, , что означает «так, таким образом».»В академической литературе [sic] используется для обозначения ошибки, которая изначально появляется в исходном материале и не связана с автором, использующим цитату. Например:
В письме в CK Daily Post генерал Росс написал, что «длительный срок службы не способствует поддержанию позитивной групповой морали [sic]».
Квадратные скобки также используются для обозначения того, что определенная часть цитаты была пропущена.
Например, Гор Видал сказал: «Энди Уорхол — единственный гений, которого я встречал […] с IQ 60.«
Фигурные скобки
Если вы не физик или высококвалифицированный математик, вы вряд ли встретите фигурные скобки в своих исследованиях или чтении. Если вы программист, то наверняка воспользуетесь этими ушедшими маленькими волнистыми пометками. Но так же, как рубашки Hypercolor или шорты из спандекса для чего-либо, кроме езды на велосипеде, фигурные скобки во многом вышли из моды. Но на тот случай, если вы встретите фигурные скобки за пределами вышеупомянутых полей, они, вероятно, указывают на серию равных вариантов.Например:
Выберите начинку для пиццы {перец, лук, колбаса, помидоры, фета, анчоусы, бекон, вяленые помидоры, курица, брокколи} и следуйте за мной.
Единственное другое место, где вы можете встретить фигурные скобки, — это форумы или обмен мгновенными сообщениями. В этом контексте они используются для обозначения объятий. То, как смотрит фигурная скобка, указывает направление объятия. Фигурная скобка, которая открывается вправо, — это объятие справа, а фигурная скобка, которая открывается слева, — это объятие слева.Например:
AlaskanWolfHunter: эй, я просто подумал, я дам тебе знать, что принесу домой цветы
({) WasillaMomof5: Ой…. Спасибо бу… (})
Угловой кронштейн
Также известные как шевроны, эти типы скобок часто используются в математике и квантовой физике. Но, в отличие от фигурных скобок, вы можете столкнуться с ними при чтении за пределами этих дисциплин, хотя и не с какой-либо частотой. В лингвистике могут встречаться угловые скобки. Например:
Английское слово / kæt / пишется как «кошка».
Иногда, хотя и не часто, угловые скобки используются для обозначения внутренней мысли. Например:
Тодд вручил мне цветок. «Понюхай.»
Я принюхался. «Мило.» <Какая отвратительная вонь!>
Угловые скобки часто используются в комиксах для обозначения человека, говорящего на другом языке. Вместо кавычек иногда используются двойные угловые скобки. Они также используются в компьютерной коммуникации для обозначения действия или статуса.Например:
<<волны>>
<<офлайн>>
Заключение
Важно не злоупотреблять скобами и не полагаться на них слишком сильно. Некоторые авторы используют скобки вместо запятых. Другие считают, что проблему скобок лучше оставить в покое. Но вечно проблем не избежать. В какой-то момент вам, возможно, придется использовать скобки, или вы можете встретить их в своем исследовании, и в этом случае мы надеемся, что эта статья помогла.
Если вы все еще не уверены, как и когда использовать скобки, вы всегда можете отправить свой текст экспертам Scribendi для тщательной профессиональной корректуры.
Понять заказы — Документация | Альпака
Используя Alpaca Trade API, пользователь может отслеживать, размещать и отменять свои заказы с альпакой. Каждый заказ имеет уникальный идентификатор, предоставленный клиентом. Этот уникальный идентификатор заказа на стороне клиента будет автоматически сгенерирован системе, если она не предоставлена клиентом, и будет возвращена как часть объект заказа вместе с остальными полями, описанными ниже. Один раз заказ размещен, его можно запросить по идентификатору заказа на стороне клиента или присвоенный системой уникальный идентификатор для проверки статуса.Обновления по открытым заказам в Alpaca также будет отправляться через потоковый интерфейс, который является рекомендуемый способ поддержания порядка.
Покупательная способность
Для того, чтобы принимать ваши заказы, которые открывают новые позиции или добавляют к уже существующим, ваша учетная запись должна иметь достаточную покупательную способность. Альпака применяет проверку «покупательной способности» как для покупки длинных, так и для продажи коротких позиций.
Расчетное значение открывающего ордера на покупку — это предельная цена ордера, умноженная на цену ордера. количество.В случае рыночных ордеров на покупку предельная цена на 2,5–4% выше текущей рыночной цены, как указано выше.
Расчетное значение открывающего короткого ордера на продажу составляет MAX (предельная цена ордера, на 3% выше текущей цены предложения) умножается на количество заказа. В случае рыночных коротких ордеров, значение просто на 3% выше текущей цены предложения * количество ордеров.
Затем рассчитанная стоимость заказа сравнивается с вашей доступной покупательной способностью, чтобы определить, может ли он быть принят.Обратите внимание, что ваша доступная покупательная способность уменьшается из-за ваших существующих открытых длинных и коротких ордеров на покупку, в то время как ваши ордера на длинную продажу и покупку для покрытия не восполняют вашу доступную покупательную способность до тех пор, пока они не будут выполнены.
Например, если ваша покупательная способность составляет 10 000 долларов, и вы отправляете лимитный ордер на покупку вместе с ордером стоимостью 3000 долларов, ваш заказ будет принят, и ваша оставшаяся доступная покупательная способность будет быть 7000 долларов. Даже если этот ордер не исполнен, пока он открыт и не был отменен, он будет засчитан ваша доступная покупательная способность.Если затем вы отправите другой заказ на сумму 8000 долларов США, он будет отклонен.
Ордера, поданные в нерабочие часы торгов
Заказы, не подлежащие продлению, отправлены с 16:00 до 19:00 по восточноевропейскому времени. будет отклонено .
Заказы, не подлежащие продлению, отправлены после 19:00 по восточноевропейскому времени. будут поставлены в очередь и будут иметь право на исполнение во время следующего открытия рынка.
Заказы, допущенные к продленному времени и поданные вне 9:00 — 18:00 по восточному времени, обрабатываются, как описано в разделе ниже.
Торговля в расширенное время
Используя API v2, вы можете отправлять и выполнять заказы во время до рынка и в нерабочее время. Торговля в расширенные часы специфические риски из-за меньшей ликвидности. Пожалуйста, прочтите наше раскрытие Больше подробностей.
В настоящее время мы поддерживаем следующие расширенные часы:
Pre-market: 9:00 — 9:30 am
After-time: 4:00 — 18:00 pm
Кроме того, обратите внимание на следующие ограничения.
- Если заявка отправлена между 18:00 и 20:00 по восточноевропейскому времени в рыночный день, запрос заявки возвращается с ошибкой.Альпака резервирует это временное окно для будущего расширения поддерживаемых часов.
- Если заявка отправлена после 20:00, но до 9:00 утра по восточному времени следующего торгового дня, запрос заявки ставится в очередь. и будет иметь право на исполнение с начала следующих доступных поддерживаемых предпродажных часов в 9:00.
Отправка приемлемого заказа на продление рабочего дня
Чтобы указать, что ордер подходит для торговли в продленное время, вам необходимо указать логическое значение
параметр с именем extended_hours в запросе вашего заказа.Если установить для этого параметра значение true, порядок будет
имеют право на исполнение до рынка или в нерабочее время.
Только лимит дней заказов будут приняты в качестве допустимых часов продления. Все остальные типы заказов и TIF будут отклонены.
с ошибкой. Вы должны придерживаться этих настроек, чтобы участвовать в расширенных часах: \
- Тип ордера должен быть установлен на лимит
- Срок действия должен составлять
дней. Любой другой срок действия будет отклонен с ошибкой.
Все символы, поддерживаемые в обычные рыночные часы, также поддерживаются в расширенные часы. Короткие продажи также относился к тому же.
Типы заказов
При отправке заказа вы можете выбрать один из поддерживаемых типов заказа. В настоящее время Альпака поддерживает четыре различных типа заказов.
Рыночный ордер
Рыночный ордер — это запрос на покупку или продажу ценной бумаги по доступным в настоящее время рыночная цена.Это наиболее вероятный способ выполнения заказа. Рыночные заказы заполнить почти мгновенно.
В качестве компромисса ваша цена исполнения может снизиться в зависимости от доступной ликвидности на каждый уровень цен, а также любые ценовые движения, которые могут произойти, пока ваш ордер направляется к месту его исполнения. Также существует риск рыночных ордеров. что они могут быть заполнены по неожиданным ценам из-за краткосрочных скачков цен.
Альпака использует следующую механику округления в отношении заявок на покупку: (1) округление до двух десятичных знаков, если цена последней сделки превышает 1 доллар.00; в противном случае округляется до четырех знаков после запятой.
Лимитный ордер
Лимитный ордер — это приказ на покупку или продажу по указанной цене или лучше. А лимитный ордер на покупку (лимитный ордер на покупку) исполняется на указанном лимите цена или ниже (т.е. лучше). И наоборот, лимитный ордер на продажу (лимитный ордер на продажу) исполняется по указанной лимитной цене или выше (лучше). в отличие рыночный ордер, вы должны указать параметр предельной цены при отправке твоя очередь.
Хотя лимитный ордер может предотвратить проскальзывание, он может долгое время не исполняться. времени, если вообще.Для лимитного ордера на покупку, если рыночная цена составляет в пределах , указанных вами предельная цена, вы можете рассчитывать на исполнение ордера. Если рыночная цена составляет , эквивалент к ваша предельная цена, ваш ордер может быть исполнен или не исполнен; если заказ не может сразу исполнить против остаточной ликвидности, тогда он считается нерыночным и будет только исполнен как только рыночный ордер взаимодействует с ним. Вы можете упустить торговую возможность, если цена отходит от предельной цены до того, как ваш ордер может быть исполнен.
Отклонение сверхрыночного лимитного ордера Лимитные ордера с лимитной ценой, значительно превышающей текущую рыночную цену, будут отклонены в рамках наши проверки рисков для предотвращения ошибок «толстого пальца». В настоящее время мы используем правила обмена для ошибочных сделок для определения пороговых значений, при которых заказы отклоняются:
| Цена акции | Порог |
|---|---|
| От 0,00 до 25 долларов включительно.00 | 10% |
| От 25 долларов США до 50 долларов США включительно | 5% |
| Более 50,00 долл. США | 3% |
Пороговые значения удваиваются во время предпродажной подготовки и в нерабочее время.
Стоп-приказ
Стоп-ордер (рыночный) — это приказ на покупку или продажу ценной бумаги, когда ее цена проходит мимо конкретный момент, обеспечивая более высокую вероятность достижения заранее определенного цена входа или выхода. Как только рыночная цена пересекает указанную стоп-цену, стоп-приказ становится рыночным.Альпака конвертирует стоп-ордера на покупку в стоп-лимит ордера с лимитной ценой, которая на 4% выше, чем стоп-цена <50 долларов (или на 2,5% выше, чем стоп-цена> = 50 долларов США). Стоп-ордера на продажу , а не конвертируются в стоп-лимитные ордера.
Стоп-ордер не гарантирует, что ордер будет исполнен по определенной цене. после преобразования в рыночный ордер.
Для выставления стоп-приказа необходимо указать стоп-цену. параметр в API.
Стоп-лимитный приказ
Стоп-лимитный ордер — это условная сделка в течение определенного периода времени, которая объединяет особенности стоп-ордера с характеристиками лимитного ордера и используются для снижения риска.Стоп-лимитный ордер будет исполнен по указанной лимитной цене или, лучше, после того, как заданная стоп-цена была достигнута. Как только стоп-цена будет достигнута, стоп-лимитный ордер становится лимитным ордером на покупку или продажу по лимитной цене или лучше.
Чтобы подать стоп-лимитный ордер, вам необходимо указать как параметры limit и stop цены в API.
Распоряжения на открытие и закрытие аукционов
Рыночные открытые и лимитные открытые ордера могут быть исполнены только на открытии аукциона.Ордера Market on close и limit on close могут быть исполнены только на аукционе закрытия. Пожалуйста, смотрите раздел «Время в силе» для более подробной информации.
Заказы на скобу
Брекет-заказ — это цепочка из трех заказов, которые можно использовать для управления вашим вход и выход из позиции. Это распространенный вариант использования OTOCO (One Triggers OCO {Один отменяет другой}).
Первый ордер используется для открытия новой длинной или короткой позиции, и как только он полностью заполнены, активируются два условных ордера на выход.Один из двух закрытие ордеров называется тейк-профит, который является лимитным ордером, а Другой называется стоп-приказом, который является либо стоп-приказом, либо стоп-лимитом. Важно отметить, что может быть исполнен только один из двух приказов на выход. Когда-то один из ордера на выход заполняются, остальные отменяются. Обратите внимание, однако, что в чрезвычайно нестабильные и быстрые рыночные условия, оба ордера могут быть исполнены до происходит отмена.
Без брекет-ордера вы не сможете подавать одновременно вход и выход. заказов одновременно, поскольку система Альпаки принимает только заказы на выход для существующие позиции.Кроме того, даже если бы у вас была открытая позиция, вы бы не сможет подать два условных приказа на закрытие, поскольку система Альпаки будет рассматривать один из двух заказов как превышающий доступное количество позиций. Брекет-заказы решают обе эти проблемы, как признает система Альпака. заказы на вход и выход как группу и соответствующим образом ставят их в очередь на выполнение.
Для оформления заказа на скобу необходимо указать дополнительные параметры. к API. Сначала добавьте параметр order_class как «скобку».Во-вторых, дайте два дополнительные поля take_profit и stop_loss, оба из которых вложены Объекты JSON. Объект take_profit требует limit_price в качестве значения поля, которое указывает лимитную цену тейк-профита, а объект stop_loss требуется обязательное поле stop_price и необязательное limit_price. Если limit_price указывается в stop_loss, стоп-лосс ставится в очередь как стоп-лимитный ордер, но в противном случае он ставится в очередь как стоп-ордер.
Пример параметра тела JSON для отправки порядка скобок выглядит следующим образом.
{
"сторона": "купить",
"symbol": "ШПИОН",
"тип": "рынок",
"кол-во": "100",
"time_in_force": "gtc",
"order_class": "скобка",
"take_profit": {
"limit_price": "301"
},
"остановить потери": {
"stop_price": "299",
"limit_price": "298,5"
}
}
Это создает три заказа.
- Рыночный ордер на покупку 100 SPY с GTC
- Лимитный ордер на продажу для тех же 100 SPY с лимитной ценой = 301
- Стоп-лимитный ордер на продажу со стоп-ценой = 299 и лимитной ценой = 298.5
Второй и третий заказы не будут активны, пока первый заказ не будет полностью заполненный. Дополнительные сведения о заказе кронштейна включают:
- Если любой из заказов отменяется, любой оставшийся открытый заказ в группе отменяется.
-
take_profit.limit_priceдолжен быть вышеstop_loss.stop_priceдля ордера на покупку и наоборот для продажи. - Должны присутствовать и take_profit.limit_price, и stop_loss.stop_price.
- Расширенные часы не поддерживаются.
extended_hoursдолжно быть «ложным» или опущено. -
time_in_forceдолжно быть «день» или «gtc». - Каждый заказ в группе всегда отправляется с DNR / DNC (Не уменьшать / Не отменять) инструкция. Следовательно, цена заказа не будет корректироваться, и заказ не будет отменен в случае выплаты дивидендов или другие корпоративные действия.
- Если ордер тейк-профит частично исполнен, ордер стоп-лосс будет довести до оставшегося количества. Замена
- ордеров (PATCH / v2 / orders) поддерживается для обновления
limit_priceиstop_price.
Каждый заказ группы сообщается как независимый заказ в конечной точке GET / v2 / orders. Но если вы укажете дополнительный параметр nested = true, ответ заказа будет вложенным результат для включения дочерних заказов в родительский порядок с ножками поля массива в сущность заказа.
OCO Заказы
OCO (One-Cancels-Other) — еще один тип расширенного ордера.Это набор два ордера с одинаковой стороной (покупка / покупка или продажа / продажа) и в настоящее время единственный ордер на выход поддерживается. Другими словами, это вторая часть скобочных заказов. где ордер на вход уже заполнен, и вы можете отправить тейк-профит и стоп-лосс в одной подаче заявки.
С ордерами OCO вы можете добавить тейк-профит и стоп-лосс после открытия положение, не думая об этих двух ногах впереди.
Чтобы отправить заказ OCO, укажите «oco» для параметра order_class .
{
"сторона": "продавать",
"symbol": "ШПИОН",
"тип": "предел",
"кол-во": "100",
"time_in_force": "gtc",
"order_class": "ОК",
"take_profit": {
"limit_price": "301"
},
"остановить потери": {
"stop_price": "299",
"limit_price": "298,5"
}
}
Параметр типа всегда должен быть «limit», указывая на тейк-профит.
Тип — лимитный ордер. Стоп-лосс является стоп-приказом, если только stop_price указан, и является стоп-лимитным ордером, если limit_price и stop_price являются
указано (т.е. stop_price должен присутствовать в любом случае). Эти два порядка работают
точно так же, как заказывают две ножки кронштейна.
Обратите внимание, что при получении списка заказов с вложенным параметром true,
ордер тейк-профит отображается как родительский ордер, а стоп-лосс появляется
как дочерний заказ.
Как и ордера с скобками, замена ордера поддерживается для обновления limit_price и stop_price .
OTO Заказы
OTO (One-Triggers-Other) — вариант брекет-порядка.Требуется один из ордер тейк-профит или стоп-лосс в дополнение к ордеру на вход. Например, если вы хотите установить только стоп-лосс, прикрепленный к позиции, без тейк-профит, вы можете рассмотреть заказы OTO.
Отправка заказа выполняется с параметром order_class , равным «oto».
{
"сторона": "купить",
"symbol": "ШПИОН",
"тип": "рынок",
"кол-во": "100",
"time_in_force": "gtc",
"order_class": "oto",
"остановить потери": {
"stop_price": "299",
«limit_price»: «298.5 "
}
}
Должен присутствовать либо take_profit , либо stop_loss (приведенный выше пример
для случая тейк-профита), а остальные требования такие же, как
скобки заказов.
Как и в случае с брекетами, замена заказа пока не поддерживается.
Порог по стоп-цене стоп-лосс ордеров
Имейте в виду, что для части стоп-лосса продвинутых ордеров запрос ордера может быть отклонен из-за ограничения значения параметра stop_price .Входная стоп-цена должна быть как минимум на 0,01 доллара ниже (для стоп-лосса на продажу, выше для покупки), чем «базовая цена».
Базовая цена определяется следующим образом.
- Это предельная цена тейк-профита для OCO-ордеров.
- Это предельная цена ордера на вход для ордеров в скобках или OTO, если тип входа — лимит.
- Это также текущая рыночная цена для любых OCO, OTO и брекетов.
Это ограничение предназначено для того, чтобы избежать потенциальных состояний гонки при обработке заказов, но по мере того, как мы улучшаем нашу систему возможность, это может быть ослаблено в будущем.
Приказы со скользящим стопом
Трейлинг-стоп-приказы позволяют вам постоянно и автоматически обновлять пороговое значение стоп-цены в зависимости от движения цены акций. Вы запрашиваете одиночный ордер со значением смещения в долларах или процентным значением в качестве следа, и фактическая стоп-цена для этого ордера изменяется по мере того, как цена акций движется в вашу пользу, или остается на последнем уровне в противном случае. Таким образом, вам не нужно отслеживать движение цены и постоянно отправлять запросы на замену, чтобы обновить стоп-цену ближе к последнему движению рынка.
Трейлинг-стоп-ордера отслеживают самые высокие (для продажи, самые низкие для покупки) цены (называется высшей точкой или hwm) с момента подачи заказа, и параметры трейла, задаваемые пользователем, определяют фактическую стоп-цену для срабатывания относительно высокий уровень воды. После срабатывания стоп-цены ордер превращается в рыночный, и он может заполниться выше или ниже триггерной цены стопа.
Чтобы отправить скользящий стоп-ордер, вы установите для параметра type значение «trailing_stop».Есть два параметра подачи ордеров, связанных со скользящим стопом, один из которых требуется, когда тип , — «trailing_stop».
-
trail_price: string
значение в долларах от наивысшей отметки воды. Если вы установите значение 2,00 для скользящего стопа на продажу, цена стопа всегда будет равнаhwm - 2,00. -
trail_percent: строка
значение в процентах от наивысшей отметки воды. Если вы установите это значение 1.0 для скользящего стопа на продажу, цена стопа всегда равнаhwm * 0,99.
Одно из этих значений должно быть установлено для скользящих стоп-приказов. Ниже приведен пример параметра JSON для отправки конечного ордера.
{
"сторона": "продавать",
"symbol": "ШПИОН",
"type": "trailing_stop",
"кол-во": "100",
"time_in_force": "день",
"trail_price": "6,15"
}
Сущность Order, возвращаемая методом GET, имеет несколько полей, связанных с ордерами скользящего стопа.
-
trail_price: string
Это то же значение, которое было указано при отправке заказа. Если это не указано, оно будет нулевым. -
trail_percent: string
Это то же значение, которое было указано при отправке заказа. Если это не указано, оно будет нулевым. -
hwm: string
Максимальное значение отметки. Это постоянно меняется по мере того, как рынок движется в вашу пользу. -
stop_price: string
Это то же самое, что и стоп-цена в обычных стоп / стоп-лимитных ордерах, но получается из параметра hwm и trail и постоянно обновляется по мере изменения hwm.
Если ордер скользящего стопа принят, статус ордера становится «новым». Пока ордер ожидает триггера стоп-цены, вы можете обновить параметр следа с помощью метода PATCH.
-
trail: string
Новое значениеtrail_priceилиtrail_percent.Такой запрос на замену эффективен только для типа ордера «trailing_stop» до того, как будет достигнута стоп-цена. Обратите внимание, вы не можете изменить трейлинг цены на процентный трейлинг или наоборот.
Вот некоторые подробности о скользящем стопе.
- Трейлинг-стоп не срабатывает вне обычных часов работы рынка.
- Допустимые значения времени действия для скользящего стопа: «день» и «gtc».
- Приказы скользящего стопа в настоящее время поддерживаются только для одиночных заявок.Тем не менее, мы планируем поддерживать трейлинг-стоп в качестве стоп-лосса для ордеров с фиксированной ценой / OCO в будущем.
Правильное использование скользящих стоп-ордеров требует понимания цели и того, как они работают. Главное, о чем следует помнить при работе с ордерами скользящего стопа, — убедиться, что разница между скользящим стопом и ценой достаточно велика, чтобы типичные колебания цены не вызывали преждевременное исполнение.
На быстро движущихся рынках цена исполнения может быть менее выгодной, чем цена стопа.Потенциал такой уязвимости увеличивается для заказов GTC во время торговых сессий или для акций, торгующихся с остановками. Стоп-цена запускает рыночный ордер, и поэтому стоп-цена не обязательно совпадает с ценой исполнения.
Что касается дробления акций, Альпака оставляет за собой право отменить или скорректировать цены и / или разделить количество скользящих стоп-приказов по своему усмотрению. Поскольку Альпака полагается на третьих лиц для получения рыночных данных, корпоративные действия или неверные данные о ценах могут привести к преждевременному срабатыванию скользящего стопа.
Срок действия
Alpaca поддерживает следующие обозначения Time-In-Force:
-
день
Дневной ордер может быть исполнен только в день его действия. По умолчанию заказ действителен только в обычные торговые часы (с 9:30 до 16:00 по восточному времени). Если оно не заполнено после аукциона закрытия, оно автоматически аннулируется. Если отправлено после закрытия, оно ставится в очередь и отправляется на следующий торговый день. Однако, если он отмечен как подходящий для продленных часов, заказ также может быть выполнен в течение поддерживаемых продленных часов. -
gtc
Заказ действителен до отмены. Лимитные ордера GTC, не обращающиеся на рынке, подлежат корректировке цен для компенсации корпоративных действия, влияющие на проблему. В настоящее время мы не поддерживаем заказы «Не снижать» (DNR), чтобы отказаться от такой корректировки цен. -
opg
Используйте этот TIF с типом рыночного / лимитного ордера для подачи ордеров «рыночный при открытии» (MOO) и «лимит при открытии» (LOO). Этот ордер может быть исполнен только на аукционе открытия рынка. Любые невыполненные заказы после открытия будут отменены.Заказы OPG, поданные после 9:28, но до 19:00 по восточному времени, будут отклонены. Заказы OPG, поданные после 19:00, будут помещены в очередь и направлены на аукцион открытия следующего дня. При открытии / закрытии ордера направляются на первичную биржу. Такие ордера не обязательно исполняются точно в 9:30 / 16:00 по восточноевропейскому времени, но исполняются в соответствии с правилами аукциона биржи. -
cls
Используйте этот TIF с типом рыночного / лимитного ордера для подачи ордеров «рынок при закрытии» (MOC) и «лимит при закрытии» (LOC). Этот ордер может быть исполнен только на аукционе закрытия рынка.Любые невыполненные заказы после закрытия будут отменены. Заказы CLS, поданные после 15:50, но до 19:00 по восточному времени, будут отклонены. Заказы CLS, отправленные после 19:00, будут поставлены в очередь. и направляется на аукцион закрытия следующего дня. Доступно только с API v2. -
ioc
Ордер немедленного действия или отмены (IOC) требует немедленного исполнения всего или части приказа. Любые незаполненные часть заказа отменяется. Доступно только с API v2. Большинство маркет-мейкеров, которые получают заказы IOC, будут пытаться выполнить заказ только на принципиальной основе и аннулируют любой незаполненный баланс.Иногда это может привести к отмене всего ордера, если у маркет-мейкера нет существующего инвентаря рассматриваемой ценной бумаги. -
fok
Ордер на исполнение или аннулирование (FOK) выполняется только в том случае, если может быть заполнен весь объем заказа, в противном случае заказ отменяется. Доступно только с API v2.
Жизненный цикл заказа
Статус заказа, выполненного через Альпаку, может несколько измениться. в течение его жизненного цикла. Наиболее распространенные статусы подробно описаны ниже:
-
новый
Ордер получен Альпакой и направлен на биржи для исполнения.Это обычное начальное состояние заказа. -
частично заполнено
Заказ выполнен частично. -
исполнен
Заказ выполнен, и дальнейших обновлений для него не произойдет. -
done_for_day
Заказ выполнен, исполняется в течение дня и больше не будет получен обновляется до следующего торгового дня. -
отменен
Заказ был отменен, и дальнейших обновлений для приказ.Это может быть вызвано либо запросом на отмену пользователем, либо заказ был отменен биржами в связи с истечением срока его действия. -
истек
Срок действия заказа истек, и дальнейшие обновления для него производиться не будут. -
заменено
Ордер был заменен другим приказом или был обновлен из-за рыночного события, такого как корпоративное действие. -
pending_cancel
Ордер ожидает отмены. -
pending_replace
Ордер ожидает замены другим ордером.В этом состоянии заказ отклонит запрос на отмену.
Менее распространенные состояния описаны ниже. Обратите внимание, что эти состояния возникают только в очень редких случаях, и большинство пользователей, скорее всего, никогда не увидят свои заказы достигают этих состояний:
-
принят
Заказ получен Альпакой, но еще не отправлен место казни. Это часто можно было увидеть в нерабочее время торговой сессии. -
pending_new
Ордер был получен Альпакой и отправлен на биржи, но пока не принят к исполнению.Это состояние возникает только в редких случаях. -
accept_for_bidding
Заказ был получен биржами и оценивается для определения цены. Это состояние возникает только в редких случаях. -
остановлен
Ордер был остановлен, и сделка по нему гарантирована, обычно по заявленной цене или лучше, но еще не произошло. Это состояние возникает только в редких случаях. -
отклонено
Заказ отклонен, дальнейшие обновления для приказ.Это состояние возникает в редких случаях и может возникать в зависимости от различных условий, выбранных биржами. -
приостановлено
Ордер приостановлен и не может быть продан. Этот состояние возникает только в редких случаях. -
рассчитано
Ордер исполнен за день (исполнен или исполнен за день), но расчеты по оставшимся расчетам еще не завершены. Только это состояние встречается в редких случаях.
Заказ может быть отменен через API до тех пор, пока не будет достигнут
состояние либо заполнено, , отменено, , либо истекло .
Нечетные лоты и блок-сделки
При торговле акциями круглый лот обычно определяется как 100 акций или большее число, которое может быть равномерно разделено на 100. Нечетный лот — это все, что не может быть равномерно разделено на 100 акций (например, 48, 160 и т. Д.). Блочная сделка обычно определяется как сделка, в которой участвует 10 000 акций или более.
В торговых целях нечетные лоты обычно рассматриваются как круглые. Однако нормативные правила торговли позволяют по-разному относиться к нечетным лотам.Точно так же блочные сделки обычно разбиваются на исполнение, и исполнение может занять больше времени из-за того, что рынок должен поглотить пакет акций с течением времени, а не за одно крупное исполнение. В сочетании с редко торгуемыми акциями вполне возможно, что нечетные лоты и блочные сделки могут не быть заполнены или исполнены вовремя, а иногда и вовсе не в зависимости от других факторов, таких как используемые типы ордеров.
Короткие продажи
Короткая продажа — это продажа акций, которыми не владеет продавец.Как правило, короткий продавец продает заемные акции в ожидании снижения цены. Короткий продавец позже закрывает позицию, покупая акции. По правилу короткие продажи не могут быть размещены при падении рыночной цены акций. Это правило также применяется, когда рынки закрываются. Когда акция закрывается на нисходящем тике, ордера на короткие продажи не исполняются.
© 2021 Выпущено по лицензии MIT — Документация, созданная с помощью Хьюго с помощью Материальная тема.переходов — MATLAB и Simulink
Переход — это линия со стрелкой, которая связывает один графический
возражать другому.В большинстве случаев переход представляет собой переход системы из одного
режим (состояние) в другой. Переход обычно соединяет исходный и целевой объект.
Исходный объект — это место, где начинается переход и пункт назначения объект — это место, где заканчивается переход. Следующая диаграмма
показывает переход из исходного состояния, B , в состояние назначения, А .
Переходы делят переход на переходные сегменты.В этом случае полный переход состоит из сегментов, взятых из состояния отправления в состояние назначения. Каждый сегмент оценивается в процессе определения действительности полного перехода.
В следующем примере есть два сегментированных перехода: один из состояния на в состояние Выкл. , а другой из состояния Вкл. в
Сам:
Переход по умолчанию — это особый тип перехода, не имеющий исходного объекта. См. Подробности в разделе «Переходы по умолчанию».
Иерархия переходов
Переходы не могут содержать другие объекты так, как это могут делать состояния. Однако переходы содержатся в состояниях. Иерархия перехода описывается в терминах его родительского элемента, исходное и конечное состояния. Родитель — это самый низкий уровень, который содержит источник и пункт назначения перехода. Рассмотрим родителей для переходов в следующих пример:
В следующей таблице показано происхождение каждого перехода в предыдущем примере.Символ / представляет диаграмму. Каждый уровень в иерархии
состояния разделяются символом точки (. ).
Метка перехода | Родительский переход | Источник перехода | Переходный пункт назначения |
|---|---|---|---|
| | ||
| | | |
| | | |
Метки перехода
Метка перехода может состоять из события или сообщения,
условие, действие условия и действие перехода. Каждая часть этикетки не обязательна. ? Символ — это метка перехода по умолчанию.Метки перехода имеют
этот общий формат:
event_or_message [ condition ] { condition_action } / transition_action
В этом примере показаны части метки перехода.
| Переход | Триггер события | Условие | Условие Действие | Действие перехода | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Состояние | Состояние > 50 | func1 () | None | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| State A to state B | event2 | None | None | data1 = 5 rigger | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Следующий переход ... | Действителен, когда ... |
|---|---|
B до A | Состояние B |
A1 до A2 | Состояние A1 активно и событие E2 имеет место. |
См. Переход между исключительными состояниями для получения дополнительной информации о семантике этой нотации.
Переходы к соединениям и от них
На следующей диаграмме показаны переходы к соединениям и от них.
В диаграмме используется временная логика, чтобы определить, когда вход и равен
1.
| Если вход равен 1 ... | Переход происходит от ... |
|---|---|
| До t = 2 | Начало на Быстро | Start to Good |
| After t = 5 | Start to Slow |
Для получения дополнительной информации о временной логике см. Control Chart Execution Использование темпоральной логики.Для получения дополнительной информации о семантику этой нотации см. в разделе «Переход от общего источника к нескольким адресатам».
Переходы в исключительное (OR) суперсостояние и из него
В этом примере показаны переходы в исключительное (OR) суперсостояние и из него, а также использование переход по умолчанию.
Диаграмма имеет два состояния на верхнем уровне иерархии, Power_off и Power_on . По умолчанию, Power_off активен.Событие Switch переключает
между состояниями Power_off и Power_on . Power_on имеет три подсостояния: Первое , Второй и третий . По умолчанию, когда Power_on становится активным, First также становится
активный. Когда Shift равен 1, система переходит из Первый до Второй , Второй до Третий , Третий до Первый , для каждого
наступление события Переключатель , а затем шаблон повторяется.
Для получения дополнительной информации о семантике этой нотации см. Выполнение контрольной диаграммы с использованием переходов по умолчанию.
Переходы к подсостояниям и из них
В следующем примере показаны переходы к подсостояниям и обратно (OR).
Для получения подробной информации о том, как работает эта диаграмма, см. «Отражение сигналов с обнаружением неисправностей». Для получения информации о семантике этой нотации см. Переход от подсостояния к подсостоянию с событиями.
| Действия по присвоению : | |
set - Это действие изменяет содержимое существующего поля.Если поле не существует, оно создается. Действительный формат: установить <поле> на <поле> | установить pnx. "Display". "Contents" на TEMP "1" установите TEMP "1" на pnx. "Display". "Contents" |
create - Это действие создает поле отображения PNX и устанавливает для его содержимого значение указанного поля.Если поле отображения уже существует, добавляется дополнительное поле. Формат: создать <поле PNX> с <поле> | создать pnx. "Display". "Contents" с MARC "505". "A" |
| Действия подполя : | |
за исключением подполей num без сортировки - это действие использует только нечисловые подполя и помещает их в том порядке, в котором они появляются в записи MARC.Действительный формат: без учета подполей num без сортировки | создать pnx. "Display". "Contents" с MARC "505" за исключением подполей num без сортировки |
исключение подполей без сортировки - Это действие исключает все указанные подполя и помещает оставшиеся подполя в том порядке, в котором они появляются в записи MARC. Действительный формат: без учета подполей без сортировки " <список подполей> " | создать pnx."display". "contents" с MARC "505", исключая подполя без сортировки "a-c" |
подполя - Это действие использует либо все подполя, либо только указанные подполя и сортирует их по букве / номеру подполя, а не по порядку, в котором они появляются в записи MARC. Формат: подполя [" <список подполей> "] Удаляет символы, соответствующие указанному регулярному выражению, а затем помещает указанный разделитель между всеми указанными подполями: подполя « <список подполей> », разделенных «< строка >» удалить подстроку с помощью регулярного выражения « < Java_regex >» | создать pnx."display". "contents" с подполями MARC "505" создать pnx. "Display". "Contents" с подполями "a-c" MARC "505" создать pnx. "Display". "Contents" с MARC "505" подполями "a-c", разделенными знаком "-" удалить подстроку с помощью регулярного выражения "\\. + $" |
sub без сортировки - это действие использует указанные подполя и помещает подполя в том порядке, в котором они появляются в записи MARC.Действительный формат: подполя без сортировки " <список подполей> " Размещает указанный разделитель между всеми указанными подполями: подполя без сортировки " <список подполей> " , разделенные на "< строка >" При использовании вместе с действием преобразования заменить разделители переноса , вы можете добавить префиксы и разделители к каждому подполю, указанному в списке: подполя без сортировки " <список подполей> " подполя переноса | устанавливает TEMP "1" на MARC.Подача «710» без сортировки «a, b, c, d, e» установите TEMP "1" в MARC. Подложка "710" без сортировки "a, b, c, d, e", разделенная знаком "" установить TEMP "1" в MARC. Подложка "200" без сортировки "a, b, c, d, e, f, g, h, i, v" переносит подполя |
| Действия преобразования : | |
удалить подстроку с помощью регулярного выражения - Это действие удаляет подстроку из содержимого временного поля с использованием указанного регулярного выражения.Действительный формат: удалить подстроку с помощью регулярного выражения (TEMP " | удалить подстроку с помощью регулярного выражения (TEMP "1", "(/ |: |; | = |,) + $") |
объединить с разделителем - Это действие объединяет содержимое двух временных полей и разделяет их разделителем.Результат помещается в первое временное поле. Формат: объединить с разделителем (TEMP " | объединить с разделителем (TEMP "1", TEMP "2", "") |
добавить префикс - Это действие добавляет указанное значение в начало временного поля.Действительный формат: добавить префикс (TEMP « <индекс> », « <значение> ») | добавить префикс (TEMP "2", "$$ Q") |
добавить суффикс - Это действие добавляет указанное значение в конец временного поля. Действительный формат: добавить суффикс (TEMP " <индекс> ", " <значение> ") | добавить суффикс (TEMP "2", "$$ Q") |
заменить строку строкой - это действие заменяет все вхождения регулярного выражения указанным значением.0-9] "," \\? ") | |
заменить разделители переноса - Это действие используется в сочетании с действием подполя переноса подполей и позволяет разместить указанный разделитель до и после указанного подполя. Действительный формат: заменить разделители переноса (TEMP " Дополнительные примеры см. В стандартных правилах нормализации UNIMARC для полей отображения «Заголовок» и «Издатель». | установить TEMP "1" в MARC. Подложка "200" без сортировки "a, b, c, d, e, f, g, h, i, v" подполя переноса заменить ограничители упаковки (TEMP "1", "a", ";", "") заменить ограничители переноса (TEMP "1", "b", "[", "]") |
список возврата с использованием регулярного выражения - Это действие выполняет поиск всех вхождений регулярного выражения во втором временном поле и копирует их в виде списка в первое временное поле.Действительный формат: список возврата с использованием регулярного выражения (TEMP " | список возврата с использованием регулярного выражения (TEMP "1", TEMP "2", "[a-z] {3}") |
удалить строку - Это действие удаляет указанную строку из временного поля. Действительный формат: удалить строку (TEMP " <индекс> ", " <значение> ") | удалить строку (TEMP "1", "<<") |
удалить начальные и конечные пробелы - Это действие удаляет начальные и конечные пробелы во временном поле.Действительный формат: удалить начальные и конечные пробелы (TEMP " | удалить начальные и конечные пробелы (TEMP "1") |
заменить пробелы - Это действие заменяет все пробелы во временном поле указанным символом или строкой. Действительный формат: заменить пробелы (TEMP " | заменить пробелы (TEMP "1", "") |
нижний регистр - Это действие изменяет все буквы во временном поле на нижний регистр.Действительный формат: нижний регистр (TEMP " <индекс> ") | нижний регистр (ТЕМП "1") |
многоязычный - При добавлении к правилам нормализации для полей отображения «Тема», «Создатель» или «Участник» система использует таблицу сопоставления «Многоязычная конфигурация» для отображения записей, относящихся к языку отображения, выбранному в Primo VE.Дополнительные сведения см. В разделе «Многоязычная конфигурация в Primo VE». Действительный формат: многоязычный по " MARC_field " " Display_Field " "display" По умолчанию в правилах нормализации включено многоязычное преобразование. Если он не указан, все записи для поля отображения отображаются в фасетах и деталях записи независимо от настройки языка отображения в Primo VE. | правило «Primo VE Display - Subject 650» |
Примеры и определение круглых скобок
Определение круглых скобок
Круглые скобки - это стилистический прием, который происходит от греческого слова, означающего « поставить», или «рядом с ».Скобки - это уточняющее или поясняющее предложение, пункт или слово, которые авторы вставляют в абзац или отрывок. Однако, если они не укажут его, даже тогда это не повлияет на текст грамматически, что без него является правильным.
Авторы отмечают эти пояснительные пункты круглыми или квадратными скобками, запятыми, тире или маленькими линиями. Что касается своей цели, эта словесная единица предоставляет дополнительную информацию, прерывает синтаксический поток слов и позволяет читателям обращать внимание на объяснение.Однако чрезмерное использование скобок может сделать предложения неоднозначными и плохо структурированными.
Примеры скобок в литературе
Пример № 1:
One Art (Элизабет Бишоп)«… Даже потеряв вас (шутливый голос, жест
, который я люблю), я не солгал. Очевидно,
- искусство проигрыша - не так уж сложно освоить
, хотя это может выглядеть (напишите!) Как катастрофа ».
Бишоп использует резкие, мучительные скобки в конце стихотворения.Для этого она использует скобки, чтобы выразить недосказанность и предложить, как справиться с потерями через искусство, используя фразу «напиши это».
Пример № 2:
Элементы стиля (Вильям Странк младший и Э. Б. Уайт)«Теперь необходимо предупредить вас, что ваша забота о читателе должна быть чистой: вы должны сочувствовать читателю. тяжелое положение (у большинства читателей проблемы бывают почти половину времени), но никогда не пытайтесь узнать, чего хочет читатель. Вся ваша обязанность как писателя - доставить удовольствие и удовлетворить себя… »
В руководстве по стилю несколько раз приводится информация в скобках.Здесь вы можете увидеть, как авторы объяснили тяжелое положение читателя, дав описательное предложение в скобках, показывающее, как читатели находятся в затруднительном положении.
Пример № 3:
Кизил: отрочество (Автор Джон Апдайк)«Небольшая гравийная аллея, слишком маленькая, чтобы ее можно было обозначить дорожным знаком, но известная в окрестностях как Аллея Шиллинга, опасно петляющая вокруг собственности и дальше, мимо неопрятных задних строений (курятники, амбары без отвеса, оружейный магазин, небольшая лесопилка, лачуга, где жил слепой, и очаровательный грот гаража, цементные полы которого были покрытый до блеска черным деревом каплями масла… серебряная вода, такая холодная, что заставляла дрожать передние зубы) на Ланкастер-авеню, главную улицу, по которой бежали троллейбусы.
Смотрите, автор использовал подробные описательные скобки в этом отрывке. Он подробно объясняет последовательность неопрятных задних домов и почему они так убого выглядят.
Пример № 4:
Лошадь и его мальчик (Автор К.С. Льюис)«[В теплоте людей] рассказывание историй (правдивы они или выдуманы) - это то, чему вас учат, просто как английских мальчиков и девочек учат писать сочинения. Разница в том, что люди хотят слушать рассказы, в то время как я никогда не слышал о ком-либо, кто хотел бы читать эссе.
Здесь Льюис использует круглые скобки для описания истории, указывая, правдивы они или выдуманы. Он имеет в виду сказать, что людям нравится слушать рассказы, которые не преподают, как эссе. Следовательно, сочинения кажутся скучными.
Пример № 5:
Гаснет свет на территории (Иэн Синклер)”« Черная собака »- это настроение бездонного, самоубийственного отчаяния, которое, как известно, пережил Уинстон Черчилль (сам своего рода бульдог в подгузниках) , логотип Empire; рычание и дриблинг, свистящий дым, опухшие вены, залитые бренди).
В этом эссе Синклер дает читателям уникальную, просвещенную, провокационную, тревожную и чрезвычайно смелую картину современной городской жизни в Лондоне и его жителей. В процессе он раскрывает темную изнанку Лондона, поскольку вы можете видеть его провокационное преуменьшение и информацию в скобках о Уинстоне Черчилле.
Функция круглых скобок
Круглые скобки делают утверждения более убедительными, поскольку они с самого начала помещают читателей в правильную форму, в которой они читают это как объяснение.Однако его основная функция состоит в том, чтобы дать больше объяснений и добавить акцента, в то время как его повторное использование может вызвать фокус и, таким образом, сделать вставки в скобках доминирующей чертой предложения.
Круглые скобки также предлагают читателям понять истинные чувства и мнения персонажей и рассказчиков, в то время как они могут иметь тенденцию уклоняться от информации в скобках как неважной. Таким образом, скобки могут оставить их невежественными в отношении истинной цели предложения.



 А как показать это другим? (отделить)
А как показать это другим? (отделить) Изучение правила.
Изучение правила.

 114;
114;



 А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо. Для предыдущего примера это выглядело бы так: .
Для предыдущего примера это выглядело бы так: .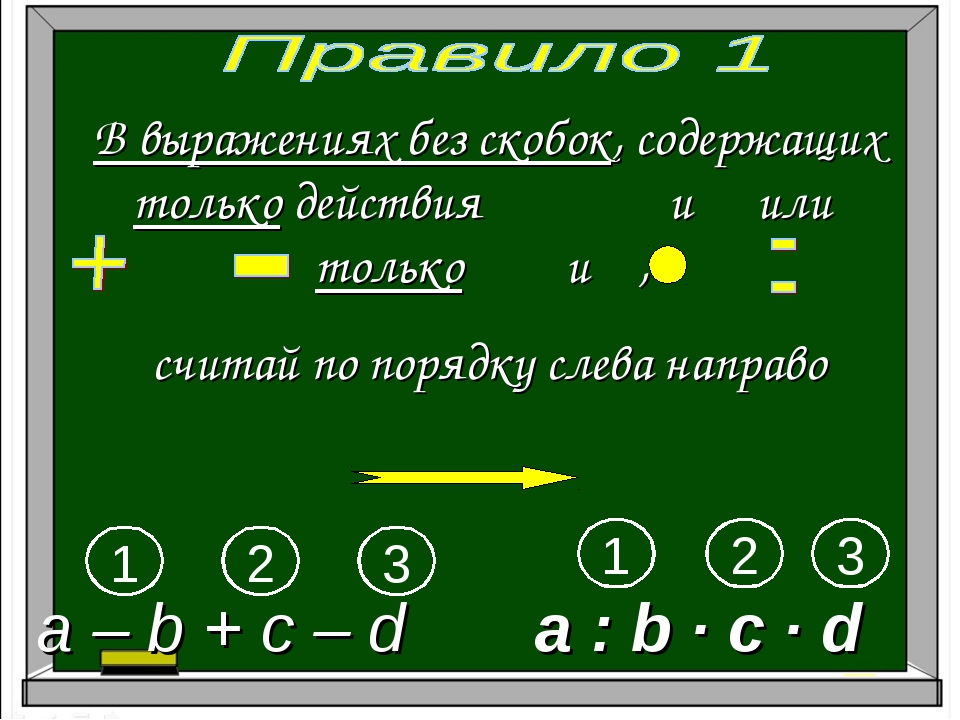 В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.



 действия, записанные в скобках;
действия, записанные в скобках; Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.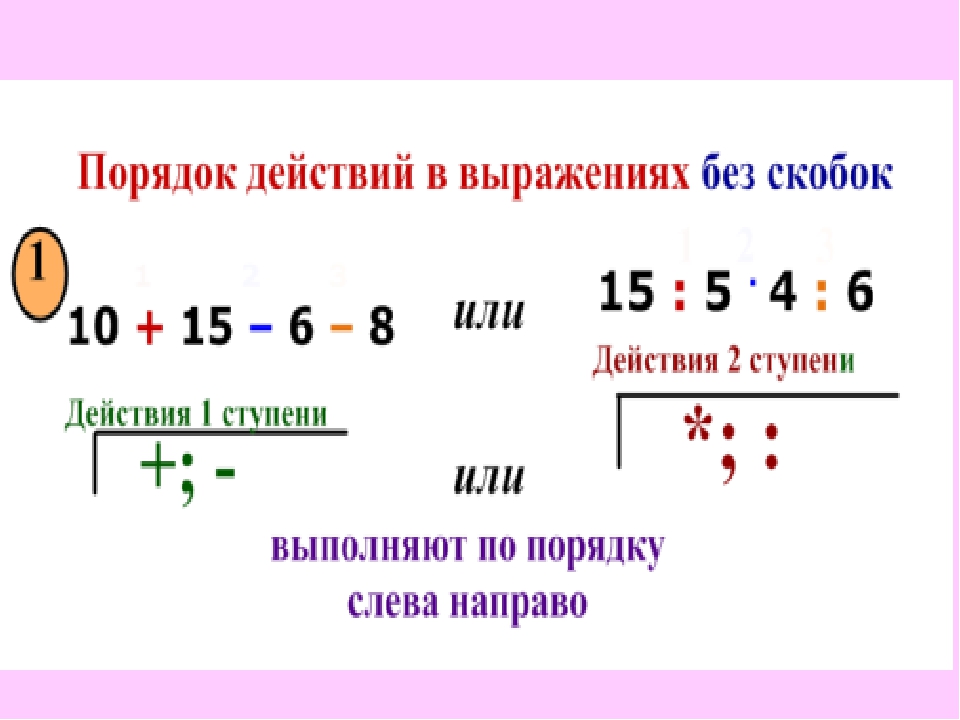 Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

 За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. На языке Зенона это выглядит так:
На языке Зенона это выглядит так: Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

 Это не математическое действие.
Это не математическое действие.
 Какой еще туалет?
Какой еще туалет? Вот как она звучит:
Вот как она звучит:




 ..
..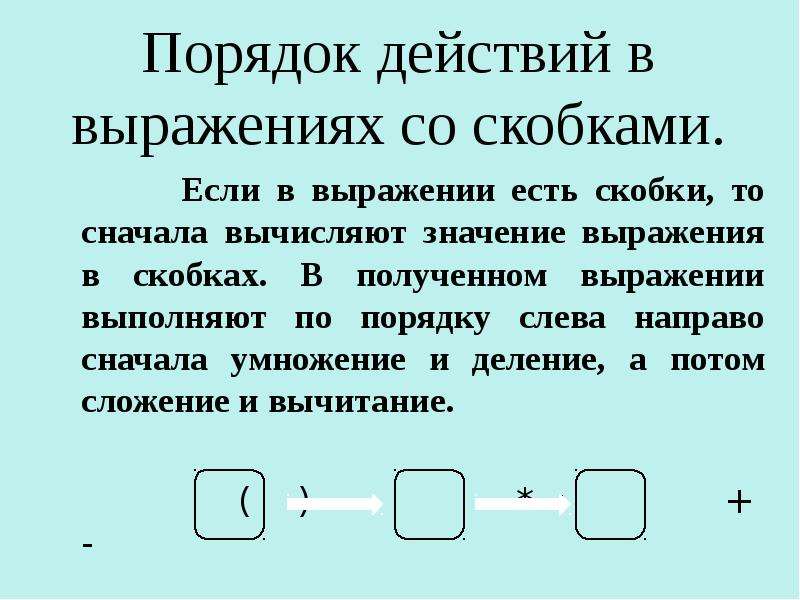

 Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
 И математики нас этому постоянно учат. Вот пример.
И математики нас этому постоянно учат. Вот пример.


 В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо. Для предыдущего примера это выглядело бы так: .
Для предыдущего примера это выглядело бы так: .
 Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера. Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
 Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки. Онлайн тренажер.
Онлайн тренажер. Затем выполняем сложение и вычитание по порядку:
Затем выполняем сложение и вычитание по порядку: