Переместительное и сочетательное свойство сложения и: Свойства сложения: переместительное и сочетательное

Содержание

Свойства сложения и умножения. Сочетательное и распределительное свойства умножения. Свойство сложения с нулем

Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.
Числа 3 и 4, которые мы сложили называется слагаемыми . А результат сложение число 7 называется суммой .

Сумма — это сложение чисел. Знак плюс “+”.
В буквенном виде этот пример будет выглядеть так:

a+ b= c

Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.

Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:

Называется такое свойство слагаемых переместительным законом сложения .

Переместительный закон сложения.

От перемены мест слагаемых сумма не меняется.

В буквенной записи переместительный закон выглядит так:

a+ b= b+ a

Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:

(1+2)+4=7

Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:

1+(2+4)=7

Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:

(1+2)+4=1+(2+4)

Это свойство сложения называется сочетательным законом сложения .

Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.

Сочетательный закон сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.

(a+ b)+ c= a+(b+ c)

Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30

Свойство сложения с нулем.

При сложении числа с нулем, в результате сумма будет тем же самым числом.

3+0=3
0+3=3
3+0=0+3

В буквенном выражение сложение с нулем будет выглядеть так:

a+0= a
0+ a= a

Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:

Второй вариант таблицы сложения.

Если посмотрим на таблицы сложения, видно как работает переместительный закон.

В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.

В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.

Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.

Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.

Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a

Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22

Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9

1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.

Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921

Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143 ). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.

Количество квадратов со стороной 1 см равно 5 * 3 . Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3 ) * 4 .

Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4 ).

Подсчет клеток на рисунке 143 двумя способами иллюстрирует

сочетательное свойство умножения для чисел 5, 3 и 4 . Имеем: (5 * 3 ) * 4 = 5 * (3 * 4 ).

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.

(ab)c = a(bc)

Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений .

Например, верны равенства:

abc = cba,

17 * 2 * 3 * 5 = (17 * 3 ) * (2 * 5 ).

На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.

Подсчитаем количество квадратов со стороной 1 см двумя способами.

С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2 . Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2 ).

Равенсто 3 * (3 + 2 ) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения .

Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.

В буквенном виде это свойство записывают так:

a(b + c) = ab + ac

Из распределительного свойства умножения относительно сложения следует, что

ab + ac = a(b + c).

Это равенство позволяет формулу P = 2 a + 2 b для нахождения периметра прямоугольника записать в таком виде:

P = 2 (a + b).

Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:

a(m + n + p + q) = am + an + ap + aq.

Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то

a(b − c) = ab − ac

Пример 1 . Вычислите удобным способом:

1 ) 25 * 867 * 4 ;

2 ) 329 * 75 + 329 * 246 .

1 ) Используем переместительное, а затме сочетательное свойства умножения:

25 * 867 * 4 = 867 * (25 * 4 ) = 867 * 100 = 86 700 .

2 ) Имеем:

329 * 754 + 329 * 246 = 329 * (754 + 246 ) = 329 * 1 000 = 329 000 .

Пример 2 . Упростите выражение:

1 ) 4 a * 3 b;

2 ) 18 m − 13 m.

1 ) Используя переместительное и сочетательное свойства умножения, получаем:

4 a * 3 b = (4 * 3 ) * ab = 12 ab.

2 ) Используя распределительное свойство умножения относительно вычитания, получаем:

18 m − 13 m = m(18 − 13 ) = m * 5 = 5 m.

Пример 3 . Запишите выражение 5 (2 m + 7 ) так, чтобы оно не содержало скобок.

Согласно распределительному свойству умножения относительно сложения имеем:

5 (2 m + 7 ) = 5 * 2 m + 5 * 7 = 10 m + 35 .

Такое преобразование называют раскрытием скобок .

Пример 4 . Вычислите удобным способом значение выражения 125 * 24 * 283 .

Решение. Имеем:

125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8 ) * (3 * 283 ) = 1 000 * 849 = 849 000 .

Пример 5 . Выполните умножение: 3 сут 18 ч * 6 .

Решение. Имеем:

3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.

При решении примера было использовано распределительное свойство умножения относительно сложения:

3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.

Мы определили сложение, умножение, вычитание и деление целых чисел. Эти действия (операции) обладают рядом характерных результатов, которые называются свойствами. В этой статье мы рассмотрим основные свойства сложения и умножения целых чисел, из которых следуют все остальные свойства этих действий, а также свойства вычитания и деления целых чисел.

Навигация по странице.

Для сложения целых чисел характерны еще несколько очень важных свойств.

Одно из них связано с существованием нуля. Это свойство сложения целых чисел утверждает, что прибавление к любому целому числу нуля не изменяет это число . Запишем данное свойство сложения с помощью букв: a+0=a и 0+a=a (это равенство справедливо в силу переместительного свойства сложения), a – любое целое число. Можно услышать, что целое число нуль называют нейтральным элементом по сложению. Приведем пару примеров. Сумма целого числа −78 и нуля равна −78 ; если к нулю прибавить целое положительное число 999 , то в результате получим число 999 .

Сейчас мы дадим формулировку еще одного свойства сложения целых чисел, которое связано с существованием противоположного числа для любого целого числа. Сумма любого целого числа с противоположным ему числом равна нулю . Приведем буквенную форму записи этого свойства: a+(−a)=0 , где a и −a – противоположные целые числа. Например, сумма 901+(−901) равна нулю; аналогично сумма противоположных целых чисел −97 и 97 равна нулю.

Основные свойства умножения целых чисел

Умножению целых чисел присущи все свойства умножения натуральных чисел . Перечислим основные из этих свойств.

Также как нуль является нейтральным целым числом относительно сложения, единица является нейтральным целым числом относительно умножения целых чисел. То есть, умножение любого целого числа на единицу не изменяет умножаемое число . Так 1·a=a , где a – любое целое число. Последнее равенство можно переписать в виде a·1=a , это нам позволяет сделать переместительное свойство умножения.

Приведем два примера. Произведение целого числа 556 на 1 равно 556 ; произведение единицы и целого отрицательного числа −78 равно −78 .

Следующее свойство умножения целых чисел связано с умножением на нуль. Результат умножения любого целого числа a на нуль равен нулю , то есть, a·0=0 . Также справедливо равенство 0·a=0 в силу переместительного свойства умножения целых чисел. В частном случае при a=0 произведение нуля на нуль равно нулю.

Для умножения целых чисел также справедливо свойство, обратное к предыдущему. Оно утверждает, что произведение двух целых чисел равно нулю, если хотя бы один из множителей равен нулю . В буквенном виде это свойство можно записать так: a·b=0 , если либо a=0 , либо b=0 , либо и a и b равны нулю одновременно.

Распределительное свойство умножения целых чисел относительно сложения

Совместно сложение и умножение целых чисел нам позволяет рассматривать распределительное свойство умножения относительно сложения, которое связывает два указанных действия. Использование сложения и умножения совместно открывает дополнительные возможности, которых мы были бы лишены, рассматривая сложение отдельно от умножения.

Итак, распределительное свойство умножения относительно сложения гласит, что произведение целого числа a на сумму двух целых чисел a и b равно сумме произведений a·b и a·c , то есть, a·(b+c)=a·b+a·c . Это же свойство можно записать в другом виде: (a+b)·c=a·c+b·c .

Распределительное свойство умножения целых чисел относительно сложения вместе с сочетательным свойством сложения позволяют определить умножение целого числа на сумму трех и большего количества целых чисел, а далее – и умножение суммы целых чисел на сумму.

Также заметим, что все остальные свойства сложения и умножения целых чисел могут быть получены из указанных нами свойств, то есть, они являются следствиями указанных выше свойств.

Свойства вычитания целых чисел

Из полученного равенства, а также из свойств сложения и умножения целых чисел вытекают следующие свойства вычитания целых чисел (a , b и c – произвольные целые числа):

Вычитание целых чисел в общем случае НЕ обладает переместительным свойством: a−b≠b−a .
Разность равных целых чисел равна нулю: a−a=0 .
Свойство вычитания суммы двух целых чисел из данного целого числа: a−(b+c)=(a−b)−c .
Свойство вычитания целого числа из суммы двух целых чисел: (a+b)−c=(a−c)+b=a+(b−c) .
Распределительное свойство умножения относительно вычитания: a·(b−c)=a·b−a·c и (a−b)·c=a·c−b·c .
И все другие свойства вычитания целых чисел.

Свойства деления целых чисел

Рассуждая о смысле деления целых чисел , мы выяснили, что деление целых чисел – это действие, обратное умножению. Мы дали такое определение: деление целых чисел – это нахождение неизвестного множителя по известному произведению и известному множителю. То есть, целое число c мы называем частным от деления целого числа a на целое число b , когда произведение c·b равно a .

Данное определение, а также все рассмотренные выше свойства операций над целыми числами позволяют установить справедливость следующих свойств деления целых чисел:

Никакое целое число нельзя делить на нуль.
Свойство деления нуля на произвольное целое число a , отличное от нуля: 0:a=0 .
Свойство деления равных целых чисел: a:a=1 , где a – любое целое число, отличное от нуля.
Свойство деления произвольного целого числа a на единицу: a:1=a .
В общем случае деление целых чисел НЕ обладает переместительным свойством: a:b≠b:a .
Свойства деления суммы и разности двух целых чисел на целое число: (a+b):c=a:c+b:c и (a−b):c=a:c−b:c , где a , b , и c такие целые числа, что и a и b делится на c , и c отлично от нуля.
Свойство деления произведения двух целых чисел a и b на целое число c , отличное от нуля: (a·b):c=(a:c)·b , если a делится на c ; (a·b):c=a·(b:c) , если b делится на c ; (a·b):c=(a:c)·b=a·(b:c) , если и a и b делятся на c .
Свойство деления целого числа a на произведение двух целых чисел b и c (числа a , b и c такие, что деление a на b·c возможно): a:(b·c)=(a:b)·c=(a:c)·b .
Любые другие свойства деления целых чисел.

Тема, которой посвящен этот урок, — «Свойства сложения».На нем вы познакомитесь с переместительным и сочетательным свойствами сложения, рассмотрев их на конкретных примерах. Узнаете, в каких случаях можно ими пользоваться, чтобы сделать процесс вычисления более простым. Проверочные примеры помогут определить, насколько хорошо вы усвоили изученный материал.

Урок: Свойства сложения

Внимательно посмотрите на выражение:

9 + 6 + 8 + 7 + 2 + 4 + 1 + 3

Нам нужно найти его значение. Давайте это сделаем.

9 + 6 = 15
15 + 8 = 23
23 + 7 = 30
30 + 2 = 32
32 + 4 = 36
36 + 1 = 37
37 + 3 = 40

Результат выражения 9 + 6 + 8 + 7 + 2 + 4 + 1 + 3 = 40.
Скажите, удобно ли было вычислять? Вычислять было не совсем удобно. Посмотрите еще раз на числа этого выражения. Нельзя ли их поменять местами так, чтобы вычисления были более удобными?

Если мы перегруппируем числа по-другому:

9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = …
9 + 1 = 10
10 + 8 = 18
18 + 2 = 20
20 + 7 = 27
27 + 3 = 30
30 + 6 = 36
36 + 4 = 40

Окончательный результат выражения 9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = 40.
Мы видим, что результаты выражений получились одинаковые.

Слагаемые можно менять местами, если это удобно для вычислений, и значение суммы от этого не изменится.

В математике существует закон: Переместительный закон сложения . Он гласит, что от перестановки слагаемых сумма не изменяется.

Дядя Федор и Шарик поспорили. Шарик находил значение выражения так, как оно записано, а дядя Федор сказал, что знает другой, более удобный способ вычисления. Видите ли вы более удобный способ вычисления?

Шарик решал выражение так, как оно записано. А дядя Федор, сказал, что знает закон, который разрешает менять слагаемые местами, и поменял местами числа 25 и 3.

37 + 25 + 3 = 65 37 + 25 = 62

37 + 3 + 25 = 65 37 + 3 = 40

Мы видим, что результат остался таким же, но считать стало гораздо проще.

Посмотрите на следующие выражения и прочитайте их.

6 + (24 + 51) = 81 (к 6 прибавить сумму 24 и 51)
Нет ли удобного способа для вычисления?
Мы видим, что если прибавить 6 и 24, то мы получим круглое число. К круглому числу всегда легче что-то прибавлять. Возьмем в скобки сумму чисел 6 и 24.
(6 + 24) + 51 = …
(к сумме чисел 6 и 24 прибавить 51)

Вычислим значение выражения и посмотрим, изменилось ли значение выражения?

6 + 24 = 30
30 + 51 = 81

Мы видим, что значение выражения осталось прежним.

Потренируемся еще на одном примере.

(27 + 19) + 1 = 47 (к сумме чисел 27 и 19 прибавить 1)
Какие числа удобно сгруппировать так, чтобы получился удобный способ?
Вы догадались, что это числа 19 и 1. Сумму чисел 19 и 1 возьмем в скобки.
27 + (19 + 1) = …
(к 27 прибавить сумму чисел 19 и 1)
Найдем значение этого выражения. Мы помним, что сначала выполняется действие в скобках.
19 + 1 = 20
27 + 20 = 47

Значение нашего выражения осталось таким же.

Сочетательный закон сложения : два соседних слагаемых можно заменить их суммой.

Теперь потренируемся пользоваться обоими законами. Нам нужно вычислить значение выражения:

38 + 14 + 2 + 6 = …

Сначала воспользуемся переместительным свойством сложения, которое разрешает менять слагаемые местами. Поменяем местами слагаемые 14 и 2.

38 + 14 + 2 + 6 = 38 + 2 + 14 + 6 = …

Теперь воспользуемся сочетательным свойством, которое разрешает нам два соседних слагаемых заменять их суммой.

38 + 14 + 2 + 6 = 38 + 2 + 14 + 6 = (38 + 2) + (14 + 6) =…

Сначала узнаем значение суммы 38 и 2.

Теперь сумму 14 и 6.

3. Фестиваль педагогических идей «Открытый урок» ().

Сделай дома

1. Вычислите сумму слагаемых по-разному:

а) 5 + 3 + 5 б) 7 + 8 + 13 в) 24 + 9 + 16

2. Вычислите результаты выражений:

а) 19 + 4 + 16 + 1 б) 8 + 15 + 12 + 5 в) 20 + 9 + 30 + 1

3. Вычислите сумму удобным способом:

а) 10 + 12 + 8 + 20 б) 17 + 4 + 3 + 16 в) 9 + 7 + 21 + 13

Можно отметить ряд результатов, присущих этому действию. Эти результаты называют свойствами сложения натуральных чисел . В этой статье мы подробно разберем свойства сложения натуральных чисел, запишем их при помощи букв и приведем поясняющие примеры.

Навигация по странице.

Сочетательное свойство сложения натуральных чисел.

Теперь приведем пример, иллюстрирующий сочетательное свойство сложения натуральных чисел.

Представим ситуацию: с первой яблони упало 1 яблоко, а со второй яблони — 2 яблока и еще 4 яблока. А теперь рассмотрим такую ситуацию: с первой яблони упало 1 яблоко и еще 2 яблока, а со второй яблони упало 4 яблока. Понятно, что на земле и в первом и во втором случае окажется одинаковое количество яблок (что можно проверить пересчетом). То есть, результат сложения числа 1 с суммой чисел 2 и 4 равен результату сложения суммы чисел 1 и 2 с числом 4 .

Рассмотренный пример позволяет нам сформулировать сочетательное свойство сложения натуральных чисел: чтобы прибавить к данному числу данную сумму двух чисел, можно к этому числу прибавить первое слагаемое данной суммы и к полученному результату прибавить второе слагаемое данной суммы . Это свойство с помощью букв можно записать так: a+(b+c)=(a+b)+c , где a , b и c – произвольные натуральные числа.

Обратите внимание, что в равенстве a+(b+c)=(a+b)+c присутствуют круглые скобки «(» и «)». Скобки используются в выражениях для указания порядка выполнения действий – сначала выполняются действия в скобках (подробнее об этом написано в разделе ). Иными словами, в скобки заключаются выражения, значения которых вычисляются в первую очередь.

В заключении этого пункта отметим, что сочетательное свойство сложения позволяет однозначно определить сложение трех, четырех и большего количества натуральных чисел .

Свойство сложения нуля и натурального числа, свойство сложения нуля с нулем.

Мы знаем, что нуль НЕ является натуральным числом. Так почему же мы решили рассмотреть свойство сложения нуля и натурального числа в этой статье? На это есть три причины. Первая: это свойство используется при сложении натуральных чисел столбиком . Вторая: это свойство используется при вычитании натуральных чисел . Третья: если считать, что нуль означает отсутствие чего-либо, то смысл сложения нуля и натурального числа совпадает со смыслом сложения двух натуральных чисел .

Проведем рассуждения, которые помогут нам сформулировать свойство сложения нуля и натурального числа. Представим, что в ящике нет ни одного предмета (иными словами, в ящике находится 0 предметов), и в него помещают a предметов, где a – любое натуральное число. То есть, сложили 0 и a предметов. Понятно, что после этого действия в ящике стало a предметов. Следовательно, справедливо равенство 0+a=a .

Аналогично, если в ящике находится a предметов и в него добавляют 0 предметов (то есть, не добавляют ни одного предмета), то после этого действия в ящике окажутся a предметов. Таким образом, a+0=a .

Теперь мы можем привести формулировку свойства сложения нуля и натурального числа: сумма двух чисел, одно из которых равно нулю, равна второму числу . Математически это свойство можно записать в виде следующего равенства: 0+a=a или a+0=a , где a – произвольное натуральное число.

Отдельно обратим внимание на то, что при сложении натурального числа и нуля остается верным переместительное свойство сложения, то есть, a+0=0+a .

Наконец, сформулируем свойство сложения нуля с нулем (оно достаточно очевидно и не нуждается в дополнительных комментариях): сумма двух чисел, каждое из которых равно нулю, равна нулю . То есть, 0+0=0 .

Теперь пришло время разобраться с тем, как выполняется сложение натуральных чисел .

Список литературы.

Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Урок 16. свойства сложения. применение переместительного и сочетательного свойств сложения — Математика — 2 класс — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Урок 16. свойства сложения. применение переместительного и сочетательного свойств сложения — Математика — 2 класс

Математика, 2 класс

Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения

Перечень вопросов, рассматриваемых в теме:

— Что такое сочетательное свойство сложения?

-В каких случаях можно использовать свойства сложения?

Глоссарий по теме:

Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.

Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47

2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19

3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29

Теоретический материал для самостоятельного изучения

Сравним выражения и их значения:

6+9 *9+6

45+5*5+45

Сумма чисел шесть и девять равна сумме чисел девять и шесть.

Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.

6+9 =9+6

45+5=5+45

Что заметили?

Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?

Правильно, оно называется переместительным свойством сложения.

Решим задачу.

В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?

Первый способ решения.

Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.

(3+5)+4=12 (м.)

Второй способ решения.

Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.

3+(5+4)=12 (м.)

В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)

Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.

Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.

Решим выражение: 1+7+9+3=?

Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.

1+7+9+3= (1+9)+(7+3)=10+10=20

В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.

Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.

Тренировочные задания.

1. Вычислите суммы удобным способом

30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________

Правильный ответ:

1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)

2. Совместите название математического свойства с его значением и выражением

Результат сложения не изменится, если соседние слагаемые заменить их суммой.

Слагаемые можно переставлять местами, при этом значение суммы не изменится.

9+5+1+5 = (9+1) + (5+5)

9+6 = 6 + 9

Правильный ответ:

Результат сложения не изменится, если соседние слагаемые заменить их суммой.

Слагаемые можно переставлять местами, при этом значение суммы не изменится.

9+5+1+5 = (9+1) + (5+5)

9+6 = 6 + 9

Свойства умножения: переместительное, сочетательное и распределительное

Переместительное свойство умножения

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство:

a · b = b · a,

выражающее переместительное свойство умножения.

Примеры:

6 · 7 = 7 · 6 = 42;

4 · 2 · 3 = 3 · 2 · 4 = 24.

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Сочетательное свойство умножения

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

a · b · c = (a · b) · c = a · (b · c),

выражающее сочетательное свойство умножения.

Пример:

3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30

или

3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Распределительное свойство умножения

Сначала рассмотрим распределительное свойство умножения относительно сложения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.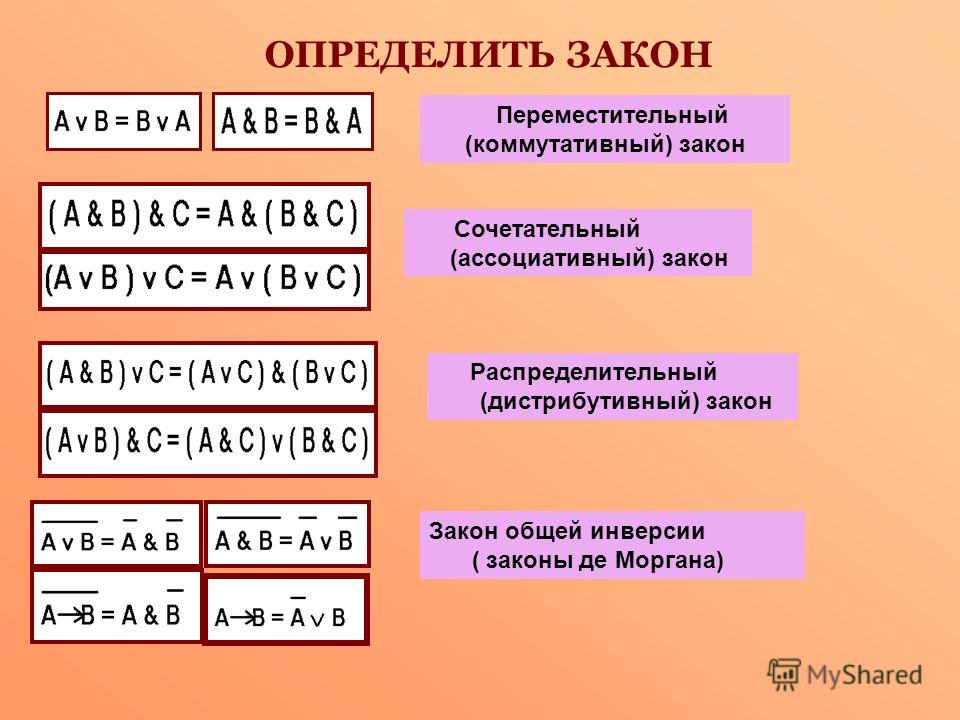

Следовательно, для любых чисел a, b и m верно равенство:

m · (a + b) = m · a + m · b,

выражающее распределительное свойство умножения.

Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

(a + b) · m = a · m + b · m.

Теперь рассмотрим распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

m · (a — b) = m · a — m · b.

Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

(a — b) · m = a · m — b · m.

Переход от умножения:

m · (a + b) и m · (a — b)

соответственно к сложению и вычитанию:

m · a + m · b и m · a — m · b

называется раскрытием скобок.

Переход от сложения и вычитания:

m · a + m · b и m · a — m · b

к умножению:

m · (a + b) и m · (a — b)

называется вынесением общего множителя за скобки.

Свойства сложения и вычитания. Переместительное и сочетательное

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

2 — это первое слагаемое,
5 — второе слагаемое,
7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства сложения

Переместительное свойство сложения
От перестановки мест слагаемых сумма не меняется.
a + b = b + a

Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c)

Свойство нуля при сложении
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a

На заметку!

При сложении нескольких чисел, их можно объединять в группы и переставлять в любом порядке. Например: a + b + с = (a + b) + c = a + (b + c).

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Рассмотрим пример 9 — 4 = 5, в котором:

9 — это уменьшаемое,

4 — вычитаемое,

5 — разность.

При этом саму запись (9 — 4) тоже можно назвать разностью.

Свойства вычитания

Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
a — 0 = a
Если из числа вычесть само число, то получится нуль.
a — a = 0

Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
a — (b + c) = a — b — c

Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) — c = (a — c) + b (если a > c или а = с)
(a + b) — c = (b — c) + a (если b > c или b = с)

На заметку!

Есть случаи, когда скобки не имеют значения при вычитании, и их можно опустить. Например: (a — b) — c = a — b — c.

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Скачать

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8

б) 9 + 11 + 2

в) 30 + 0 + 13

Как решаем:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2

б) 18 — 1 — 4

в) 55 — 55

Как решаем:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

в) 55 — 55 = 0

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9

б) 16 + (4 — 3) + 7

в) 0 + 2 + 4 — 0

Как решаем:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

в) 0 + 2 + 4 — 0 = 2 + 4 = 6

Сочетательное и распределительное свойства умножения

Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.

Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.

Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).

В буквенном виде это свойство записывают так:

(ab)c = a(bc)

Например, верны равенства:

abc = cba,

17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).

На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.

Подсчитаем количество квадратов со стороной 1 см двумя способами.

С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).

Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.

В буквенном виде это свойство записывают так:

a(b + c) = ab + ac

Из распределительного свойства умножения относительно сложения следует, что

ab + ac = a(b + c).

Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:

P = 2(a + b).

Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:

a(m + n + p + q) = am + an + ap + aq.

Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то

a(b − c) = ab − ac

Пример 1. Вычислите удобным способом:

1) 25 * 867 * 4;

2) 329 * 75 + 329 * 246.

Решение.

1) Используем переместительное, а затме сочетательное свойства умножения:

25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.

2) Имеем:

329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.

Пример 2. Упростите выражение:

1) 4a * 3b;

2) 18m − 13m.

Решение.

1) Используя переместительное и сочетательное свойства умножения, получаем:

4a * 3b = (4 * 3) * ab = 12ab.

2) Используя распределительное свойство умножения относительно вычитания, получаем:

18m − 13m = m(18 − 13) = m * 5 = 5m.

Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.

Решение.

Согласно распределительному свойству умножения относительно сложения имеем:

5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.

Такое преобразование называют раскрытием скобок.

Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.

Решение. Имеем:

125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.

Пример 5. Выполните умножение: 3 сут 18 ч * 6.

Решение. Имеем:

3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.

При решении примера было использовано распределительное свойство умножения относительно сложения:

3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.

Свойства действий с рациональными числами

Главная
Справочники
Справочник по математике 5-9 класс
Рациональные числа
Свойства действий с рациональными числами

Свойства сложения рациональных чисел

Из приведенных свойств сложения чисел следует, что в сумме нескольких рациональных чисел слагаемые можно менять местами и расставлять скобки, тем самым определяя наиболее удобный порядок выполнения действий.

Примеры:

1) 9 + 4 = (9 4) = 4 и 4 + (9) = (9 4) = 5;

2 + (6) = (2 + 6) = 8 и 6 + (2) = (6 + 2) = 8;

2) (5 + 2,5) + 1,5 = (5 2,5) + 1,5 = 2,5 + 1,5 = (2,5 1,5) = 1 и 5 + (2,5 + 1,5) = 5 + 4 = (5 4) = 1;

3) 3 + 0 = 3.

Свойства умножения рациональных чисел

Примеры:

1) (2)3 = (23) = 6 и 3(2) = 6;

(5)(2) = 10 и (2)(5) = 10;

2) (23)4 = 64 = 24 и 2(34) = 212 = 24;

3) 5(3 + 2) = 53 + (5)2 = 15 + (10) = 15 10;

4) 41 = 4;

5) ;

6) 70 = 0.

Из приведенных свойств умножения следует, что в произведении нескольких рациональных чисел множители можно менять местами, расставлять и раскрывать скобки, тем самым определяя наиболее удобный порядок выполнения действий.

Коэффициент

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом или просто коэффициентом.

Примеры:

1) В выражении коэффициентом является число 0,5.

2) В выражении коэффициентом является число .

3) В выражении коэффициентом является число 1, т.к. .

4) В выражении коэффициентом является число 1, т.к. .

5) В выражении ни одно из чисел 3 и 5 не является коэффициентом. Но данное выражение можно преобразовать, используя переместительное и сочетательное свойства умножения, получим новое выражение , в котором коэффициентом является число 15.

Обратите внимание, в выражении коэффициентом является число 3, но, как правило, коэффициент записывают перед буквенными множителями: .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Положительные и отрицательные числа. Координаты на прямой

Модуль числа

Рациональные числа

Сравнение рациональных чисел

Сложение рациональных чисел

Вычитание рациональных чисел

Умножение рациональных чисел

Деление рациональных чисел

Раскрытие скобок

Решение уравнений

Рациональные числа

Правило встречается в следующих упражнениях:

6 класс

Номер 984, Мерзляк, Полонский, Якир, Учебник

Номер 5, Мерзляк, Полонский, Якир, Учебник

Задание 1206, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1250, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1253, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1261, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1305, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1338, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1342, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1481, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Пользовательское соглашение

Переместительное и сочетательное свойства умножения рациональных чисел

Предмет: Математика		Класс: 6	2 четверть	Урок № 49
Тема	Переместительное и сочетательное свойства умножения рациональных чисел
	Учебник: Математика 6 класс часть 1 глава 2
	Дополнительные материалы (ссылки на видеоматериалы): Видеоуроки И.Жабровский. youtube.com›playlist?list=PL63ACBA1E85108554 Яндекс.Видео›видеоуроки 6 класс презентации в билим
	Иллюстративный материал: Презентации
Цель урока	Сегодня на уроке вы изучите: 1. Как применять переместительное и сочетательное свойство умножения; 2.Как упрощать выражения используя эти свойства;
Проверка учебного задания	Задание 1. Найдите значение выражения: (-0,54 – 1,56) = ( — 1 ) = = — Задание 2. Найдите корни уравнения: 6х -9 =0 6х = 9 х = 1,5 4х – 0,4 = 0 4х=0,4 х=0,1
Ответить на вопросы	1.Результат умножения двух чисел называется? 2. Как называются числа, которые умножаем? 3.Как умножать два числа с разными знаками? 4.Как умножать два отрицательных числа?
Краткий тезисный конспект урока	От перестановки множителей значение произведения не меняется Сочетательное свойство умножения рациональных чисел Чтобы произведение двух чисел умножить на третье число,можно первое число умножить на произведение второго и третьего числа. формулы переместительного и сочетательного свойств сложения и умножения — переместительное свойство относительно сложения;(повторим) — переместительное свойство относительно умножения; — сочетательное свойство относительно сложения;(повторим) — сочетательное свойство относительно умножения. Задание 1: Найдите значение выражения рациональным способом. Ответы:
	Более подробную информацию по данной теме, вы сможете получить, прочитав учебник математики 6 класс часть 1 глава 2 Просмотрев видеоуроки и презентации.
Учебные задания	Задание 1: Вставьте пропущенные слова. ü От перестановки мест слагаемых/множителей сумма/произведение ______________________________. ü Чтобы к сумме двух чисел прибавить ___________ число можно к первому числу прибавить сумму ____________и третьего числа. ü Чтобы ________________двух чисел умножить на третье число можно первое число ___________________на произведение второго и третьего чисел. ü При сложении нескольких чисел их можно как угодно объединять в группы и_____________________. ü При умножении нескольких чисел можно как угодно __________________в группы и переставлять. Задание 2: Найдите значение выражения рациональным способом. Задание 3: Учебник — учить правила.
Обратная связь с учителем	Уважаемый учащийся, все выполненные задания необходимо отправить на данную электронную почту либо в WhatsApp по номеру телефона

Переместительное и сочетательное свойства умножения рациональных чисел.

Коэффициент

Представим себе такую историю…

– Саша, чем ты занимаешься? – спросил у друга Паша.

– К следующему уроку математики нам задали решить пример. Он мне кажется сложным, – ответил Саша.

– Покажи мне, – попросил Паша. – Может, я смогу тебе помочь.

– Вот смотри: . Здесь надо перемножить три числа, и для этого придётся потрудиться, – грустно сказал Саша.

– Не расстраивайся. Может, можно как-то упростить эту задачу, – успокоил друга Паша. – А помнишь, на прошлом уроке мы говорили, что для рациональных чисел можно пользоваться переместительным свойством умножения? Тогда, чтобы быстро и легко решить этот пример, мы могли бы поменять местами 25 и , ведь произведение 25 и 4 даёт нам 100.

– А как же быть со скобками, в которые взяты первый и второй множители? – спросил Саша.

– Это хороший вопрос… Интересно, может, для рациональных чисел действует и сочетательное свойство умножения, – задумался Паша.

– Давай спросим у Мудряша, – предложил Саша.

– Давай, – ответил Паша.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

– А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, на прошлом уроке мы с вами сказали, что для рациональных чисел справедливо переместительное свойство умножения. Мы умножили на 4 и получили . И умножили 4 на и тоже получили . То есть произведение и 4 равно произведению 4 и .

У вас возник вопрос, справедливо ли сочетательное свойство умножения для рациональных чисел. Конечно, справедливо. Давайте вернёмся к вашему примеру: . Вы для удобства вычислений поменяли местами первый и второй множители: . Теперь заключим в скобки 25 и 4: . Произведение в скобках равняется 100. Умножим на 100. Для этого перенесём запятую в десятичной дроби на два знака вправо, так как умножаем на 100, и получим .

Запомните! Для любых рациональных чисел , и справедливы равенства:

– переместительное свойство умножения;

– сочетательное свойство умножения.

Теперь с помощью только что рассмотренных свойств умножения упростим вот такое выражение: . Напомним, что в буквенных выражениях знак умножения между буквенными множителями, а также между числовым и буквенным множителями, как правило, не ставится. Запишем вначале все числовые множители и возьмём их в скобки, а затем – буквенные: . Произведение и даёт нам . Знаем, что при умножении на получаем число, противоположное , то есть . Буквенную часть оставим без изменений. Тогда наше выражение принимает вид: . Здесь числовой множитель называют коэффициентом.

Ребята, посмотрите на следующие выражения: ; ; ; ; ; ; . Назовите их коэффициенты, – предложил Мудряш.

– В выражении коэффициент равен , – начали мальчики, – в выражении коэффициент равен , в выражении коэффициент равен . А в выражении чему равен коэффициент?

– В этом выражении коэффициент равен , – ответил Мудряш. – Просто он здесь записан после буквенных множителей, а, как правило, его записывают перед буквенными множителями.

– В выражении коэффициент равен или ? – снова задали вопрос Саша и Паша.

– В этом выражении ни одно из чисел не является коэффициентом. Чтобы найти здесь коэффициент, надо записать все числовые множители перед буквенными: . Затем перемножить эти числовые множители. Тогда число будет являться коэффициентом в полученном выражении, – объяснил Мудряш.

– А чему равны коэффициенты в выражениях и ? – спросили мальчишки.

– Выражение мы можем с вами записать так: . Поэтому коэффициент здесь равен единице. Выражение можно записать как , а значит, коэффициент в этом выражении равен .

– Паша, Саша, а сейчас давайте выполним несколько заданий, – сказал Мудряш.

Задание первое: Вычислите:

а) ; б) ; в) .

Решение: в примере для удобства вычисления воспользуемся сочетательным свойством умножения и заключим в скобки второй и третий множители: . Умножим на и получим произведение . Теперь перенесём запятую в десятичной дроби на три знака вправо, так как умножаем на , и в результате получим .

В примере воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Теперь заключим в скобки первый и второй множители: . Произведение двух отрицательных чисел в скобках равняется произведению модулей этих чисел и равняется 10. Осталось . Для этого перенесём запятую в десятичной дроби на один знак вправо и в результате получим .

Следующий пример . Давайте запишем первый множитель в виде неправильной дроби: . Обратите внимание, что нам будет удобно перемножить и , и . А значит, воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Теперь заключим в скобки первый и второй множители, третий и четвёртый множители: . Перемножим дроби в первых скобках: . Их произведение будет отрицательным, так как они имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 9, выполним вычисления и получим . Перемножим дроби во вторых скобках: . Их произведение также будет отрицательным, так как они имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 4, выполним вычисления и получим . Теперь запишем полученные значения в наше выражение: . Произведение двух отрицательных дробей будет положительным. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократить мы не можем, поэтому выполним вычисления и получим .

Второе задание: упростите выражение и укажите его коэффициент:

а) ; б) ; в) ; г) .

Решение: в первом выражении воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в скобки числовые множители: . Произведение числовых множителей будет положительным, так как они оба отрицательны. Перемножим их и в результате получим . Коэффициентом в полученном выражении является число .

Во втором выражении воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в первые скобки числовые множители, во вторые скобки – буквенные множители: . Произведение в первых скобках будет отрицательным, так как множители имеют разные знаки. Перемножим их и получим . Запишем буквенную часть без изменений и в результате получим . Коэффициентом в полученном выражении является число .

В следующем выражении также воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . В первые скобки заключим первый и второй множители, во вторые скобки – третий и четвёртый множители: . Выполним умножение в первых скобках: . Запишем второй множитель в виде неправильной дроби: . Произведение получится отрицательным, так как множители имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 3 и на 7. Выполним вычисления и получим . Запишем в наше выражение, буквенную часть оставим без изменений и в результате получим . Коэффициентом в этом выражении является число .

И последнее выражение . В первую очередь последний множитель запишем в виде произведения и : . Воспользуемся переместительным свойством умножения таким образом, чтобы все числовые множители оказались на первом месте, а за ними были буквенные множители: . Заключим в первые скобки все числовые множители, во вторые – все буквенные: . Теперь выполним умножение в первых скобках: . , . Буквенную часть оставим без изменений и в результате получим выражение . Коэффициент в этом выражении равен .

Определение реакции двойного вытеснения и примеры

Реакция двойного замещения — это тип реакции, в которой два реагента обмениваются ионами с образованием двух новых соединений. Реакции двойного вытеснения обычно приводят к образованию продукта в виде осадка.

Реакции двойного вытеснения имеют вид:
AB + CD → AD + CB.

Ключевые выводы: реакция двойного вытеснения

Реакция двойного вытеснения — это тип химической реакции, в которой ионы реагента обмениваются местами с образованием новых продуктов.
Обычно реакция двойного вытеснения приводит к образованию осадка.
Химические связи между реагентами могут быть ковалентными или ионными.
Реакция двойного замещения также называется реакцией двойного замещения, реакцией метатезиса солей или двойным разложением.

Реакция происходит чаще всего между ионными соединениями, хотя технически связи, образованные между химическими частицами, могут быть ионными или ковалентными по природе.Кислоты или основания также участвуют в реакциях двойного замещения. Связи, образованные в соединениях продукта, представляют собой тот же тип связей, что и в молекулах реагентов. Обычно растворителем для этого типа реакции является вода.

Альтернативные термины

Реакция двойного замещения также известна как реакция метатезиса солей, реакция двойного замещения, обмен или иногда реакция разложения двойной , хотя этот термин используется, когда один или несколько реагентов не растворяются в растворителе.

Примеры реакций двойного вытеснения

Реакция между нитратом серебра и хлоридом натрия представляет собой реакцию двойного вытеснения. Серебро обменивает свой нитрит-ион на хлорид-ион натрия, в результате чего натрий захватывает нитрат-анион.
AgNO ₃ + NaCl → AgCl + NaNO ₃

Вот еще один пример:

BaCl ₂ (водн.) + Na ₂ SO ₄ (водн.) → BaSO ₄ (с.) + 2 NaCl (водн.)

Как распознать реакцию двойного смещения

Самый простой способ идентифицировать реакцию двойного вытеснения — проверить, обмениваются ли катионы анионами друг с другом.Другой ключ, если указаны состояния вещества, — это поиск водных реагентов и образование одного твердого продукта (поскольку реакция обычно приводит к образованию осадка).

Типы реакций двойного вытеснения

Реакции двойного вытеснения можно разделить на несколько категорий, включая противоионный обмен, алкилирование, нейтрализацию, кислотно-карбонатные реакции, водный метатезис с осаждением (реакции осаждения) и водный метатезис с двойным разложением (реакции двойного разложения). Два типа, наиболее часто встречающиеся на уроках химии, — это реакции осаждения и реакции нейтрализации.

Реакция осаждения происходит между двумя водными ионными соединениями с образованием нового нерастворимого ионного соединения. Вот пример реакции между нитратом свинца (II) и иодидом калия с образованием (растворимого) нитрата калия и (нерастворимого) иодида свинца.

Pb (NO ₃) ₂ (водн.) + 2 KI (водн.) → 2 KNO ₃ (водн.) + PbI ₂ (с)

Иодид свинца образует так называемый осадок, в то время как растворитель (вода) и растворимые реагенты и продукты называются супернатантом или супернатантом.Образование осадка продвигает реакцию вперед по мере того, как продукт покидает раствор.

Реакции нейтрализации — это реакции двойного вытеснения между кислотами и основаниями. Когда растворителем является вода, реакция нейтрализации обычно дает ионное соединение — соль. Этот тип реакции протекает в прямом направлении, если по крайней мере один из реагентов представляет собой сильную кислоту или сильное основание. Реакция между уксусом и пищевой содой в классическом вулкане пищевой соды является примером реакции нейтрализации.Эта конкретная реакция затем продолжается с выделением газа (углекислого газа), который отвечает за возникающее шипение. Первоначальная реакция нейтрализации:

NaHCO ₃ + CH ₃ COOH (водн.) → H ₂ CO ₃ + NaCH ₃ COO

Вы заметите, что катионы обмениваются анионами, но из-за того, что составы написаны, немного сложнее заметить обмен анионов. Ключом к определению реакции как двойного вытеснения является рассмотрение атомов анионов и их сравнение с обеих сторон реакции.

Источники

Dilworth, J. R .; Hussain, W .; Hutson, A.J .; Jones, C.J .; Mcquillan, F. S. (1997). «Анионы тетрагалооксорхената». Неорганические синтезы , т. 31. С. 257–262. DOI: 10.1002 / 9780470132623.ch52
ИЮПАК. Сборник химической терминологии (2-е изд. ) («Золотая книга»). (1997).
Марш, Джерри (1985). Продвинутая органическая химия: реакции, механизмы и структура (3-е изд.). Нью-Йорк: Вили. ISBN 0-471-85472-7.
Майерс, Ричард (2009). Основы химии . Издательская группа «Гринвуд». ISBN 978-0-313-31664-7.

7.3 Классификация химических реакций | Вводная химия

Цели обучения

К концу этого раздела вы сможете:

Определите пять общих типов химических реакций (однократное замещение, двойное замещение, состав, разложение и горение).
Отнесите химические реакции к одному из этих трех типов, учитывая соответствующие описания или химические уравнения.

До сих пор мы представляли химические реакции как тему, но мы не обсуждали, как можно предсказать продукты химической реакции. Здесь мы начнем изучение определенных типов химических реакций, которые позволяют нам предсказать, какими будут продукты реакции.

Состав Реакция

Реакция состава (иногда также называемая реакцией комбинации или реакцией синтеза ) дает единое вещество из нескольких реагентов. Единичное вещество как продукт является ключевой характеристикой реакции композиции. Для вещества может быть коэффициент, отличный от единицы, но если в реакции используется только одно вещество в качестве продукта, ее можно назвать реакцией композиции. В реакции

[латекс] \ large {\ text {2 H}} _ {2} \ text {(} g \ text {)} + {\ text {O}} _ 2 \ text {(} g \ text {)} \ стрелка вправо {\ text {2 H}} _ {2} \ text {O (} l \ text {)} [/ latex]

вода производится из водорода и кислорода. Хотя образуются две молекулы воды, в качестве продукта используется только одно вещество — вода.Итак, это композиционная реакция.

Реакция разложения

Реакция разложения начинается с одного вещества и дает более одного вещества; то есть разлагается. Одно вещество в качестве реагента и более одного вещества в качестве продуктов являются ключевой характеристикой реакции разложения. Например, при разложении гидрокарбоната натрия (также известного как бикарбонат натрия)

[латекс] \ large {\ text {2 NaHCO}} _ {3} \ text {(} s \ text {)} \ rightarrow {\ text {Na}} _ {2} \ text {CO} _ {3 } \ text {(} s \ text {)} + {\ text {CO}} _ {2} \ text {(} g \ text {)} + {\ text {H}} _ {2} \ text { O (} l \ text {)} [/ латекс]

карбонат натрия, диоксид углерода и вода производятся из одного вещества гидрокарбоната натрия.

Состав и реакции разложения трудно предсказать; однако их должно быть легко распознать.

Пример 1:

Реакции состава и разложения

Обозначьте каждое уравнение как реакцию состава, реакцию разложения или ни то, ни другое.

[латекс] \ large {\ text {Fe}} _ {2} \ text {O} _ {3} \ text {(} s \ text {)} + \ text {3 SO} _ {3} \ текст {(} g \ text {)} \ rightarrow {\ text {Fe}} _ {2} {\ text {(} {\ text {SO}} _ {4} \ text {)}} _ {3} [/ латекс]
[латекс] \ large {\ text {NaCl}} \ text {(} aq \ text {)} + {\ text {AgNO}} _ {3} \ text {(} aq \ text {)} \ rightarrow { \ text {NaNO}} _ {3} \ text {(} aq \ text {)} + \ text {AgCl (} s \ text {)} [/ latex]
[латекс] \ large {\ text {(} {\ text {NH}} _ {4} \ text {)}} _ {2} {\ text {Cr}} _ {2} \ text {O} _ {7} \ text {(} s \ text {)} \ rightarrow \ text {Cr} _ {2} \ text {O} _ {3} \ text {(} s \ text {)} + {\ text { 4 H}} _ {2} {\ text {O}} \ text {(} l \ text {)} + {\ text {N}} _ {2} \ text {(} g \ text {)} [ / латекс]

Показать ответ

В этом уравнении два вещества объединяются в одно вещество. Это композиционная реакция.
Два разных вещества вступают в реакцию с образованием двух новых веществ. Это не соответствует определению ни реакции композиции, ни реакции разложения, поэтому не является ни тем, ни другим. Фактически, вы можете распознать это как реакцию двойной замены.
Одно вещество реагирует с образованием нескольких веществ. Это реакция разложения.

Проверьте свои знания

Определите уравнение как реакцию состава, реакцию разложения или ни то, ни другое.

[латекс] \ large {\ text {C}} _ {3} \ text {H} _ {8} \ text {(} g \ text {)} \ rightarrow {\ text {C}} _ {3} \ text {H} _ {4} \ text {(} g \ text {)} + \ text {H} _ {2} \ text {(} g \ text {)} [/ latex]

Покажи ответ

реакция разложения

Реакция с однократной заменой

Реакция однократного замещения (иногда называемая реакцией однократного замещения ) — это химическая реакция, в которой один элемент замещается другим элементом в соединении, образуя новый элемент и новое соединение как продукты. Например,

[латекс] \ large \ text {2 HCl} \ text {(} aq \ text {)} + {\ text {Zn}} \ text {(} s \ text {)} \ rightarrow {\ text {ZnCl} } _ {2} \ text {(} aq \ text {)} + {\ text {H}} _ {2} \ text {(} g \ text {)} [/ latex]

является примером реакции одиночного замещения. Атомы водорода в HCl заменяются атомами Zn, и при этом образуется новый элемент — водород. Другой пример реакции одиночного замещения —

[латекс] \ large \ text {2 NaCl} \ text {(} aq \ text {)} + {\ text {F}} _ {2} \ text {(} g \ text {)} \ rightarrow {\ текст {2 NaF}} \ text {(} aq \ text {)} + {\ text {Cl}} _ {2} \ text {(} g \ text {)} [/ latex]

Реакция двойной замены

Реакция двойного замещения (иногда называемая реакцией двойного замещения ) происходит, когда части двух ионных соединений обмениваются, образуя два новых соединения.Уравнение с двойной заменой характеризуется наличием двух соединений в качестве реагентов и двух различных соединений в качестве продуктов. Пример:

[латекс] \ large {\ text {CuCl}} _ {2} \ text {(} aq \ text {)} + {\ text {2 AgNO}} _ {3} \ text {(} aq \ text { )} \ rightarrow \ text {Cu} {\ text {(} {\ text {NO}} _ {3} \ text {)}} _ {2} \ text {(} aq \ text {)} + \ text {2 AgCl (} s \ text {)} [/ латекс]

Есть два эквивалентных способа рассмотрения уравнения двойной замены: либо катионы меняются местами, либо анионы меняются местами.(Вы не можете поменять местами оба; в конечном итоге вы получите те же вещества, с которых начали.) Любая перспектива должна позволить вам предсказывать правильные продукты, если вы соединяете катион с анионом, а не катион с катионом или анионом. с анионом.

Пример 2:

Реакции замещения

Предскажите произведения этого уравнения с двойной заменой:

[латекс] \ large {\ text {Na}} _ {2} \ text {SO} _ {4} \ text {(} aq \ text {)} + \ text {BaCl} _ {2} \ text { (} g \ text {)} \ rightarrow {\ text {?}} [/ latex]

Покажи ответ

Если рассматривать реакцию как переключение катионов или анионов, мы ожидаем, что продуктами будут BaSO ₄ и NaCl.

Проверьте свои знания

Предскажите произведения этого уравнения с двойной заменой:

[латекс] \ large {\ text {KBr}} \ text {(} aq \ text {)} + {\ text {AgNO}} _ {3} \ text {(} aq \ text {)} \ rightarrow { \ text {?}} [/ latex]

Покажи ответ

KNO ₃ и AgBr

Предсказать, произойдет ли реакция двойного замещения, несколько сложнее, чем предсказать реакцию одиночного замещения. Однако есть один тип реакции двойного замещения, который мы можем предсказать: реакция осаждения.Реакция осаждения происходит, когда два ионных соединения растворяются в воде и образуют новое ионное соединение, которое не растворяется; это новое соединение выпадает из раствора в виде твердого осадка . Образование твердого осадка является движущей силой, которая заставляет реакцию продолжаться.

Чтобы судить, будут ли происходить реакции двойного замещения, нам нужно знать, какие типы ионных соединений образуют осадки. Для этого мы используем правила растворимости , которые представляют собой общие утверждения, которые предсказывают, какие ионные соединения растворяются (растворимы), а какие нет (не растворимы или нерастворимы).В таблице 1 «Некоторые полезные правила растворимости» перечислены некоторые общие правила растворимости. Нам необходимо рассмотреть каждое ионное соединение (как реагенты, так и возможные продукты) в свете правил растворимости в таблице 1 «Некоторые полезные правила растворимости». Если соединение растворимо, мы используем метку (aq), указывающую, что оно растворяется. Если соединение нерастворимо, мы используем метку (и) с ним и предполагаем, что оно выпадет в осадок из раствора. Если все растворимо, то никакой реакции не ожидается.

Таблица 1 Некоторые полезные правила растворимости

Эти соединения обычно растворяются в воде (растворимы):	Исключения:
Все соединения Li ⁺, Na ⁺, K ⁺, Rb ⁺, Cs ⁺ и NH ₄⁺	Нет
Все соединения NO ₃^— и C ₂ H ₃ O ₂^—	Нет
Соединения Cl ^—, Br ^—, I ^—	Ag ⁺, Hg ₂²⁺, Pb ²⁺
Соединения SO ₄²	Hg ₂²⁺, Pb ²⁺, Sr ²⁺, Ba ²⁺
Эти соединения обычно не растворяются в воде (нерастворимы):	Исключения:
Соединения CO ₃^2- и PO ₄^3-	Соединения Li ⁺, Na ⁺, K ⁺, Rb ⁺, Cs ⁺ и NH ₄⁺
Соединения OH ^—	Соединения Li ⁺, Na ⁺, K ⁺, Rb ⁺, Cs ⁺, NH ₄⁺, Sr ²⁺ и Ba ²⁺

Яркий пример выпадения осадка наблюдается при смешивании растворов йодида калия и нитрата свинца, в результате чего образуется твердый йодид свинца:

[латекс] \ large2 \ text {KI (} aq \ text {)} + \ text {Pb} {\ text {(} {\ text {NO}} _ {3} \ text {)}} _ {2 } \ text {(} aq \ text {)} \ rightarrow {\ text {PbI}} _ {2} \ text {(} s \ text {)} + 2 {\ text {KNO}} _ {3} \ текст {(} aq \ text {)} [/ latex]

Это наблюдение согласуется с рекомендациями по растворимости: единственным нерастворимым соединением среди всех вовлеченных является йодид свинца, одно из исключений из общей растворимости йодидных солей.

Йодид свинца — это ярко-желтое твердое вещество, которое раньше использовалось в качестве художественного пигмента, известного как йодно-желтый (рис. 1). Свойства чистых кристаллов PbI ₂ делают их полезными для изготовления детекторов рентгеновского и гамма-излучения.

Рекомендации по растворимости, обсужденные выше, можно использовать для прогнозирования того, будет ли происходить реакция осаждения при смешивании растворов растворимых ионных соединений. Нужно просто идентифицировать все ионы, присутствующие в растворе, а затем подумать, может ли образование пары катион / анион привести к нерастворимому соединению.

Например, смешивание растворов нитрата серебра и фторида натрия даст раствор, содержащий ионы Ag ⁺, NO ^—, Na ⁺ и F ^—. Помимо двух ионных соединений, изначально присутствующих в растворах, AgNO ₃ и NaF, из этого набора ионов могут быть образованы два дополнительных ионных соединения: NaNO ₃ и AgF. Нормы растворимости указывают, что все соли нитратов растворимы, но AgF является одним из исключений из общей растворимости солей фторидов.Следовательно, прогнозируется реакция осаждения, описываемая следующим уравнением:

[латекс] \ large {\ text {NaF}} \ text {(} aq \ text {)} + {\ text {AgNO}} _ {3} \ text {(} aq \ text {)} \ rightarrow { \ text {AgF}} \ text {(} s \ text {)} + {\ text {NaNO}} _ {3} \ text {(} aq \ text {)} [/ latex]

Рис. 1. При смешивании растворов, содержащих Pb ²⁺ и I ^—, образуется осадок PbI ₂. (Источник: Der Kreole / Wikimedia Commons)

Пример 3:

Прогнозирование реакций осадка

Произойдет ли реакция двойного замещения? Если да, укажите продукты.

1. [латекс] \ large {\ text {KBr}} \ text {(} aq \ text {)} + \ text {Ca} {\ text {(} {\ text {NO}} _ {3} \ text {)}} _ {2} \ text {(} aq \ text {)} \ rightarrow {\ text {?}} [/ Latex]

[латекс] \ large {\ text {NaOH}} \ text {(} aq \ text {)} + \ text {Fe} \ text {Cl} _ {2} \ text {(} aq \ text { )} \ rightarrow {\ text {?}} [/ latex]

Показать ответ

Согласно правилам растворимости, оба Ca (NO ₃) ₂ и KBr являются растворимыми.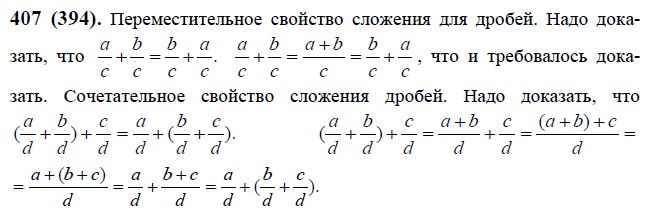 Теперь мы рассмотрим, какими будут продукты с двойным замещением при смене катионов (или анионов), а именно CaBr ₂ и KNO ₃.Однако правила растворимости предсказывают, что эти два вещества также будут растворимы, поэтому осадок не образуется. Таким образом, мы не прогнозируем никакой реакции в этом случае.

Согласно правилам растворимости, как NaOH, так и FeCl ₂ должны быть растворимыми. Если мы предполагаем, что может происходить реакция двойного замещения, нам необходимо рассмотреть возможные продукты, которыми могут быть NaCl и Fe (OH) ₂. NaCl растворим, но, согласно правилам растворимости, Fe (OH) ₂ — нет.Следовательно, произойдет реакция, и Fe (OH) ₂ (s) выпадет в осадок из раствора. Вычисленное химическое уравнение

[латекс] \ large {\ text {2 NaOH}} \ text {(} aq \ text {)} + \ text {Fe} \ text {Cl} _ {2} \ text {(} aq \ text {) } \ rightarrow \ text {2 NaCl} \ text {(} aq \ text {)} + \ text {Fe} {\ text {(} {\ text {OH}} \ text {)}} _ {2} \ текст {(} s \ text {)} [/ латекс]

Проверьте свои знания

Возникнет ли уравнение двойной замены? Если да, укажите продукты.

[латекс] \ large \ text {Sr} {\ text {(} {\ text {NO}} _ {3} \ text {)}} _ {2} \ text {(} aq \ text {)} + \ text {K} \ text {Cl} \ text {(} aq \ text {)} \ rightarrow \ text {?} [/ latex]

Покажи ответ

Нет реакции; все возможные продукты растворимы.

Реакция горения

A реакция горения происходит, когда реагент соединяется с кислородом, многократно из атмосферы, с образованием оксидов всех других элементов в качестве продуктов; любой азот в реагенте превращается в элементарный азот, N ₂. Многие реагенты, называемые топлива , содержат в основном атомы углерода и водорода, реагируя с кислородом с образованием CO ₂ и H ₂ O. Например, сбалансированное химическое уравнение для горения метана, CH ₄, имеет следующий вид: следующим образом:

[латекс] \ large {\ text {CH}} _ {4} \ text {(} g \ text {)} + {\ text {2 O}} _ 2 \ text {(} g \ text {)} \ стрелка вправо {\ text {CO}} _ {2} \ text {(} g \ text {)} + {\ text {2 H}} _ {2} \ text {O (} g \ text {)} [/ латекс]

Керосин можно аппроксимировать формулой C ₁₂ H ₂₆, а уравнение его горения —

[латекс] \ large \ text {2 C} _ {12} \ text {H} _ {26} \ text {(} l \ text {)} + {\ text {37 O}} _ 2 \ text {( } g \ text {)} \ rightarrow {\ text {24 CO}} _ {2} \ text {(} g \ text {)} + {\ text {26 H}} _ {2} \ text {O ( } г \ текст {)} [/ латекс]

Иногда топливо содержит атомы кислорода, которые необходимо учитывать при балансировании химического уравнения. Одним из распространенных видов топлива является этанол, C ₂ H ₅ OH, уравнение горения которого составляет

[латекс] \ large \ text {C} _ {2} \ text {H} _ {5} \ text {OH} \ text {(} l \ text {)} + {\ text {3 O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {2 CO}} _ {2} \ text {(} g \ text {)} + {\ text {3 H}} _ {2} \ текст {O (} g \ text {)} [/ latex]

Если в исходном топливе присутствует азот, он преобразуется в N ₂, а не в азотно-кислородное соединение. Таким образом, для сжигания топлива динитроэтилена, формула которого C ₂ H ₂ N ₂ O ₄, имеем

[латекс] \ large \ text {2 C} _ {2} \ text {H} _ {2} \ text {N} _ {2} \ text {O} _ {4} \ text {(} l \ text {)} + {\ text {O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {4 CO}} _ {2} \ text {(} g \ text {)} + {\ text {2 H}} _ {2} \ text {O (} g \ text {)} + \ text {N} _ {2} \ text {(} g \ text {)} [/ latex]

Пример 4:

Реакции горения

Заполните и сбалансируйте каждое уравнение горения.

Сгорание пропана, C ₃ H ₈
Сгорание NH ₃

Показать ответ

Продуктами реакции являются CO ₂ и H ₂ O, поэтому наше несбалансированное уравнение составляет
[латекс] \ large \ text {C} _ {3} \ text {H} _ {8} + {\ text {O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text { CO}} _ {2} \ text {(} g \ text {)} + {\ text {H}} _ {2} \ text {O (} g \ text {)} [/ latex]
Балансировка (и вам, возможно, придется пройти несколько раз, чтобы сбалансировать это), мы получаем
[латекс] \ large \ text {C} _ {3} \ text {H} _ {8} + {\ text {5 O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {3 CO}} _ {2} \ text {(} g \ text {)} + {\ text {4 H}} _ {2} \ text {O (} g \ text {)} [/ latex]
Атомы азота в аммиаке будут реагировать с образованием N ₂, а атомы водорода будут реагировать с O ₂ с образованием H ₂ O. [латекс] \ large \ text {N} \ text {H} _ {3} \ text {(} g \ text {)} + {\ text {O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {N}} _ {2} \ text {(} g \ text {)} + {\ text {H}} _ {2} \ text {O (} g \ text {)} [/ латекс]
Балансировка (и вам, возможно, придется пройти несколько раз, чтобы сбалансировать это), мы получаем
[латекс] \ large \ text {4 N} \ text {H} _ {3} \ text {(} g \ text {)} + {\ text {3 O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {2 N}} _ {2} \ text {(} g \ text {)} + {\ text {6 H}} _ {2} \ text {O (} g \ text {)} [/ латекс]

Проверьте свои знания

Заполните и сбалансируйте уравнение горения для циклопропанола, C ₃ H ₆ O.

Покажи ответ

[латекс] \ large \ text {C} _ {3} \ text {H} _ {6} \ text {O} \ text {(} l \ text {)} + {\ text {4 O}} _ 2 \ text {(} g \ text {)} \ rightarrow {\ text {3 CO}} _ {2} \ text {(} g \ text {)} + {\ text {3 H}} _ {2} \ текст {O (} g \ text {)} [/ latex]

Пропан — это топливо, используемое для обогрева некоторых домов. Пропан хранится в больших резервуарах, подобных показанному здесь. Источник: «Цветы и пропан» от vistavision под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 2.0 Generic

Основные выводы

В результате реакции композиции образуется одно вещество из нескольких реагентов.
В результате реакции разложения из одного реагента образуется несколько продуктов.
Реакции горения — это сочетание одного соединения с кислородом с образованием оксидов других элементов в виде продуктов (хотя атомы азота реагируют с образованием N ₂).
Реакция однократного замещения заменяет один элемент на другой в соединении.
В реакции двойного замещения происходит обмен катионов (или анионов) двух ионных соединений.
Реакция осаждения — это реакция двойного замещения, в которой один продукт представляет собой твердый осадок.
Правила растворимости используются, чтобы предсказать, произойдут ли какие-либо реакции двойного замещения.

Упражнения

1. Какая реакция является композиционной, а какая нет?

а. NaCl + AgNO ₃ → AgCl + NaNO ₃

г. CaO + CO ₂ → CaCO ₃

2. Какая реакция является композиционной, а какая нет?

а. H ₂ + Cl ₂ → 2 HCl

г. 2 HBr + Cl ₂ → 2 HCl + Br ₂

3.Что представляет собой композиционная реакция, а какая нет?

а. 2 SO ₂ + O ₂ → 2 SO ₃

г. 6 C + 3 H ₂ → C ₆ H ₆

4. Какая реакция является композиционной, а какая нет?

а. 4 Na + 2 C + 3 O ₂ → 2 Na ₂ CO ₃

г. Na ₂ CO ₃ → Na ₂ O + CO ₂

5. Что такое реакция разложения, а какая нет?

а.HCl + NaOH → NaCl + H ₂ O

г. CaCO ₃ → CaO + CO ₂

6. Что такое реакция разложения, а какая нет?

а. 3 О ₂ → 2 О ₃

г. 2 KClO ₃ → 2 KCl + 3 O ₂

7. Что такое реакция разложения, а какая нет?

а. Na ₂ O + CO ₂ → Na ₂ CO ₃

г. H ₂ SO ₃ → H ₂ O + SO ₂

8.Что такое реакция разложения, а какая нет?

а. 2 C ₇ H ₅ N ₃ O ₆ → 3 N ₂ + 5 H ₂ O + 7 CO + 7 C

г. C ₆ H ₁₂ O ₆ + 6 O ₂ → 6 CO ₂ + 6 H ₂ O

9. Что такое реакция горения, а какая нет?

а. C ₆ H ₁₂ O ₆ + 6 O ₂ → 6 CO ₂ + 6 H ₂ O

г.2 Fe ₂ S ₃ + 9 O ₂ → 2 Fe ₂ O ₃ + 6 SO ₂

10. Что такое реакция горения, а какая нет?

а. CH ₄ + 2 F ₂ → CF ₄ + 2 H ₂

г. 2 H ₂ + O ₂ → 2 H ₂ O

11. Что такое реакция горения, а какая нет?

а. П ₄ + 5 O ₂ → 2-пол. ₂ O ₅

г.2 Al ₂ S ₃ + 9 O ₂ → 2 Al ₂ O ₃ + 6 SO ₂

12. Что такое реакция горения, а какая нет?

а. C ₂ H ₄ + O ₂ → C ₂ H ₄ O ₂

г. C ₂ H ₄ + Класс ₂ → C ₂ H ₄ Класс ₂

13. Может ли реакция композиции быть также реакцией горения? Приведите пример, подтверждающий вашу позицию.

14. Может ли реакция разложения быть реакцией горения? Приведите пример, подтверждающий вашу позицию.

15. Заполните и сбалансируйте каждое уравнение горения.

а. C ₄ H ₉ OH + O ₂ →?

г. CH ₃ NO ₂ + O ₂ →?

16. Заполните и сбалансируйте каждое уравнение горения.

а. B ₂ H ₆ + O ₂ →? (Образовавшийся оксид бора — B ₂ O ₃.)

г. Al ₂ S ₃ + O ₂ →? (Образовавшийся оксид серы SO ₂.)

г. Al ₂ S ₃ + O ₂ →? (Образовавшийся оксид серы SO ₃.)

17. Предполагая, что происходит каждая реакция с одним замещением, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Zn + Fe (NO ₃) ₂ →?

г. F ₂ + FeI ₃ →?

18.Предполагая, что происходит каждая реакция с одним замещением, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Li + MgSO ₄ →?

г. NaBr + Cl ₂ →?

19. Предполагая, что происходит каждая реакция с однократным замещением, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Sn + H ₂ SO ₄ →?

г. Al + NiBr ₂ →?

20. Предполагая, что происходит каждая реакция с одним замещением, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Mg + HCl →?

г. HI + Br ₂ →?

21. Предполагая, что происходит каждая реакция двойного замещения, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Zn (NO ₃) ₂ + NaOH →?

г. HCl + Na ₂ S →

22. Предполагая, что происходит каждая реакция двойного замещения, предскажите продукты и запишите каждое сбалансированное химическое уравнение.

а. Ca (C ₂ H ₃ O ₂) ₂ + HNO ₃ →?

г. Na ₂ CO ₃ + Sr (NO ₂) ₂ →?

23. Предполагая, что происходит каждая реакция двойного замещения, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а. Pb (NO ₃) ₂ + KBr →?

г. K ₂ O + MgCO ₃ →?

24. Предполагая, что происходит каждая реакция двойного замещения, спрогнозируйте продукты и запишите каждое сбалансированное химическое уравнение.

а.Sn (OH) ₂ + FeBr ₃ →?

г. CsNO ₃ + KCl →?

25. Используйте правила растворимости, чтобы предсказать, будет ли происходить каждая реакция двойного замещения, и если да, напишите сбалансированное химическое уравнение.

а. Na ₂ CO ₃ + Sr (NO ₂) ₂ →?

г. (NH ₄) ₂ SO ₄ + Ba (NO ₃) ₂ →?

26. Используйте правила растворимости, чтобы предсказать, будет ли происходить каждая реакция двойного замещения, и если да, напишите сбалансированное химическое уравнение.

а. KC ₂ H ₃ O ₂ + Li ₂ CO ₃ →?

г. КОН + AgNO ₃ →?

27. Используйте правила растворимости, чтобы предсказать, будет ли происходить каждая реакция двойного замещения, и если да, запишите сбалансированное химическое уравнение.

а. K ₃ PO ₄ + SrCl ₂ →?

г. NaOH + MgCl ₂ →?

Показать ответы на избранные вопросы

1. а) не состав, б) состав

3. а) состав, б) состав

5. а) без разложения, б) с разложением

7. а) без разложения, б) с разложением

9. а) горение, б) горение

11. а) горение, б) горение

13. Да; 2 H ₂ + O ₂ → 2 H ₂ O (ответы могут быть разными)

15. a) C ₄ H ₉ OH + 6 O ₂ → 4 CO ₂ + 5 H ₂ O, b) 4 CH ₃ NO ₂ + 3 O ₂ → 4 CO ₂ + 6 H ₂ O + 2 N ₂

17. а) Zn + Fe (NO ₃) ₂ → Zn (NO ₃) ₂ + Fe, б) 3 F ₂ + 2 FeI ₃ → 3 I ₂ + 2 FeF ₃

19. а) Sn + H ₂ SO ₄ → SnSO ₄ + H _2, б) 2 Al + 3 NiBr ₂ → 2 AlBr ₃ + 3 Ni

21. а) Zn (NO ₃) ₂ + 2 NaOH → Zn (OH) ₂ + 2 NaNO _3, б) 2 HCl + Na ₂ S → 2 NaCl + H ₂ S

23. a) Pb (NO ₃) ₂ + 2 KBr → PbBr ₂ + 2 KNO ₃_, b) K ₂ O + MgCO ₃ → K ₂ CO ₃ + MgO

27. а) 2 K ₃ PO ₄ + 3 SrCl ₂ → Sr ₃ (PO ₄) ₂ (с) + 6 KCl, б) 2 NaOH + MgCl ₂ → 2 NaCl + Mg (OH) ₂ (т)

Комбинированная реакция также может быть реакцией замещения.

Укажите истину или ложь.

Математические комбинации: формулы и примеры задач

Комбинации — это расположение предметов, порядок которых не имеет значения.В этом уроке тренер баскетбольной команды Wildcats использует комбинации, чтобы помочь своей команде подготовиться к предстоящему сезону.

Перестановка: определение, формула и примеры

В этом уроке мы рассмотрим математический метод вычисления количества способов, которыми мы можем упорядочить группу отдельных объектов. Это предполагает использование математической концепции, известной как перестановка.

Круговая перестановка: формулы и примеры

Этот урок знакомит с концепцией круговых перестановок и их формулой.Узнайте, как определить количество способов расположить предметы по кругу, и когда вы закончите, пройдите тест, чтобы узнать, что вы узнали.

Перестановка и комбинация: проблемы и практика

В этом уроке мы попрактикуемся в решении различных задач перестановки и комбинирования с использованием формул перестановки и комбинирования. Мы можем продолжить нашу практику, пройдя тест в конце урока.

Введение в вероятность: формулы и примеры

Вы когда-нибудь рискнули? Прежде чем воспользоваться этим шансом, вы хотели знать, каковы ваши шансы на фактическую победу? Тогда вы имели дело с вероятностью, вероятностью того, что конкретное событие произойдет.

Как использовать фундаментальный принцип счета

Есть много ситуаций, в которых вам придется принимать несколько решений одновременно. Фундаментальный принцип подсчета поможет вам определить, сколько существует различных возможных результатов, когда вам нужно принять несколько одновременных решений.

Комбинаторика и принцип голубятни

В этом уроке мы исследуем раздел математики, называемый комбинаторикой.Мы также рассмотрим хорошо известный принцип комбинаторики, называемый принципом ящика, и рассмотрим несколько простых примеров, в которых этот принцип может быть применен.

По мере того, как математика становится все более и более сложной, и число летающих вокруг становится все больше и больше, становится действительно удобно поместить все эти числа в красивую организованную сетку. .. привет матрицы! Узнайте о том, что они из себя представляют и почему они используются.

Что такое вероятность в математике? — Определение и обзор

Помните, как бросали четверть и кричали орел или решку? Узнайте, какое отношение это имеет к вероятности.Также узнайте, как вы можете использовать полученные из этого урока навыки, чтобы решить, стоит ли вам вообще играть орлом или решкой!

Радианы и градусы: определение и примеры

Радианы и градусы — это два способа измерения углов. В этом уроке вы узнаете определение каждого метода, узнаете, как преобразовать один метод в другой, и решите некоторые практические задачи. Также в конце урока есть викторина.

децилей в наборе данных: определение, формула и примеры

При работе с большими объемами данных часто бывает полезно сгруппировать данные перед дальнейшим анализом.Учитывая, что мы работаем с десятичной системой счисления, логично, что мы могли бы захотеть использовать деления на 10 или децили в качестве основной формы числовой группировки.

Практические задачи для логарифмических свойств

По мере того, как вы углубляетесь в математику, логарифмы будут появляться все больше и больше. Цель этого урока — научить вас справляться с ними и научить вас понимать, что делать, когда вы видите целую строку, заполненную ими!

Факторные практические задачи

Хотя определение факториала несложно, их легко усложнить, сложив множество из них вместе и добавив некоторые дроби.Проверьте свои навыки здесь с помощью некоторых алгебраических примеров, которые заставят вас использовать факториалы без множества чисел.

Условная вероятность: определение и использование

Мы знаем, что монета может упасть либо орлом, либо решкой. Но что произойдет, если один подбрасывание монеты изменится на следующий? В этом уроке мы рассмотрим события, которые зависят друг от друга, и узнаем, как вычислить вероятность того, что два события происходят в сочетании.

Посмотрев этот видеоурок, вы сможете определять части круга. Вы узнаете названия четырех различных частей круга, а также то, что каждая часть делает для круга.

Реакция одиночного смещения: определение и примеры — стенограмма видео и урока

Как мы уже говорили ранее, мы обычно заменяем что-то, если замена лучше или лучше подходит для наших целей. Замена обычно аналогична оригинальному объекту. Таким же образом, для реакции одинарного смещения элемент может быть заменен только в том случае, если элемент, занимающий его место, является более реактивным. В реакциях однократного вытеснения металл заменяет металл, а неметалл — неметалл. В периодической таблице мы можем видеть, где расположены металлы и неметаллы. Металлы расположены с левой стороны лестницы, а неметаллы — с правой стороны.

Как узнать, какой элемент может заменить другой? Мы ссылаемся на серию мероприятий. Это говорит нам о реакционной способности металлов и неметаллов.Более химически активный металл заменяет менее химически активный металл. Более реактивный неметалл заменяет менее реактивный неметалл.

Если мы посмотрим на ряд активности металлов, мы увидим, что H включен, хотя H не является металлом. Это связано с тем, что для реакций однократного вытеснения H обычно ведет себя как металл в химических реакциях. В ряду активности металлов мы можем сказать, что Li может заменить K в реакции одинарного замещения, потому что Li более реактивен, чем K. То же самое можно сказать и о неметаллах: F может заменить Br в реакции одинарного вытеснения, потому что F более реактивен, чем Br. Br имеет относительно ту же реакционную способность, что и O.

Например, в этой реакции Cu заменяет Ag, потому что Cu более реактивна, чем Ag. Мы можем подтвердить это, посмотрев на ряды активности металлов.

Всегда важно правильно предсказать продукты химической реакции и убедиться, что окончательное химическое уравнение сбалансировано.В этой реакции она показывает, как мы уравновесили химическое уравнение. Мы ставим коэффициент 2 перед AgNO3 и Ag, чтобы сбалансировать количество атомов Ag и NO3 с обеих сторон.

Теперь, в этой химической реакции, более реактивный неметалл заменяет менее реактивный неметалл. В этом случае Cl заменяет Br, потому что Cl является более реакционноспособным неметаллом.

Следует отметить, что, когда Cl заменяет Br, Br имеет нижний индекс 2 на стороне продуктов. Это потому, что Cl и Br находятся в одной группе в периодической таблице, поэтому мы знаем, что они ведут себя одинаково.

Как завершить реакцию одиночного вытеснения

Чтобы завершить реакцию одиночного вытеснения, мы должны пройти несколько шагов, чтобы убедиться, что наши продукты и наша окончательная реакция верны.

Шаг первый: Определите, произойдет ли реакция.

Реакция будет продолжаться только в том случае, если элемент, который заменяет исходный элемент, более реактивен.В этой реакции возникает вопрос: может ли Zn заменить H? Нам нужно обратиться к серии занятий. Это говорит нам о том, что Zn может заменять H, поэтому эта реакция будет происходить.

Шаг второй: Определите продукты.

Когда H заменяется на Zn, H естественно встречается как h4, поэтому со стороны продуктов одним из продуктов является h4. Цинк, металл, будет соединяться с неметаллом Cl. Поскольку Zn находится во второй группе периодической таблицы, он будет иметь заряд +2. Поскольку Cl находится в группе галогенов в периодической таблице, мы знаем, что он имеет заряд -1.

Нам нужно объединить атомы Zn и Cl так, чтобы сумма их зарядов была равна нулю. В этом случае будет 1 атом цинка и 2 атома хлора. Тогда нашими продуктами будут ZnCl2 и h4.

Шаг третий: сбалансируйте химическую реакцию.

В этой реакции количество атомов H и Cl не сбалансировано, поэтому нам необходимо сбалансировать их, задав коэффициенты перед реагентами и продуктами, если необходимо.

В этом случае мы ставим коэффициент 2 перед HCl, чтобы уравновесить атомы H и Cl с обеих сторон.

Примеры реакций одинарного вытеснения

В нашем первом примере мы исследуем реакцию между Mg и CuSO4 . Эта реакция будет происходить, потому что Mg более реакционноспособен, чем Cu в ряду активности.

Cu, или медь, в природе встречается в твердом виде, поэтому одним из продуктов будет просто Cu.Mg находится в группе 2, поэтому у него будет заряд +2. SO4 можно рассматривать как отдельную группу атомов, а заряд SO4 равен -2.

В реакции будут продукты Cu и MgSO4. Как видим, реакция уже сбалансирована, так что это наш окончательный ответ.

Для нашего второго примера мы рассмотрим реакцию между Ca и h4O . Ca может заменять H в соответствии с рядом активности, поэтому эта реакция будет продолжаться.Когда мы сталкиваемся с подобными реакциями однократного вытеснения, мы перепишем уравнение как Ca + HOH.

H в природе встречается как h4, поэтому он станет одним из продуктов. Ca находится в группе 2, поэтому заряд Ca будет +2. Са соединяется с ОН, а общий заряд ОН равен -1. Эти два вместе станут Ca (OH) 2.

В реакции будут продукты h4 и Ca (OH) 2.Чтобы уравновесить реакцию, нам нужно поставить коэффициент 2 перед HOH. В финальной реакции мы пишем HOH как h4O.

Итоги урока

Давайте рассмотрим. Реакция одинарного вытеснения происходит, когда элемент заменяет другой элемент в соединении. Металл заменяет только металл, а неметалл заменяет только неметалл. Только более реактивный элемент может заменить другой элемент в соединении, с которым он реагирует.Нам необходимо обратиться к серии активности , чтобы определить реакционную способность металлов и неметаллов.

Чтобы правильно завершить реакцию одинарного смещения, нам сначала нужно определить, произойдет ли реакция, посмотрев на ряд активности. Затем нам нужно определить правильные продукты, определив правильную степень окисления. Наконец, нам нужно убедиться, что химическая реакция сбалансирована.

Результаты обучения

Когда вы закончите, вы сможете:

Вспомнить, что такое реакция одинарного смещения
Понять, что такое серия действий и ее цель
Обсудите шаги для завершения реакции одинарного смещения

хлор | Использование, свойства и факты

Хлор (Cl) , химический элемент, второй по легкости член галогенных элементов или Группа 17 (Группа VIIa) периодической таблицы. Хлор — это токсичный едкий газ зеленовато-желтого цвета, раздражающий глаза и дыхательную систему.

Британская викторина

118 Названия и символы из таблицы Менделеева

Периодическая таблица Менделеева состоит из 118 элементов. Насколько хорошо вы знаете их символы? В этой викторине вам будут показаны все 118 химических символов, и вам нужно будет выбрать название химического элемента, который представляет каждый из них.

Свойства элемента
атомный номер	17
атомный вес	от 35,446 до 35,457
точка плавления	−103 ° C (−153 ° F)	50	−34 ° C (−29 ° F)
плотность (1 атм, 0 ° C или 32 ° F)	3,214 г / литр (0,429 унции / галлон)
степени окисления	−1, +1, +3, +5, +7
электронная конфигурация	1 с ² 2 с ² 2 p ⁶ 3 с ² 3 p ⁵

История

Каменная соль (поваренная соль или хлорид натрия) известна уже несколько тысяч лет. Это основной компонент солей, растворенных в морской воде, из которых он был получен в Древнем Египте путем испарения. В римские времена солдатам частично платили солью ( salarium , корень современного слова salarium ). В 1648 году немецкий химик Иоганн Рудольф Глаубер получил сильную кислоту, которую он назвал спиртом соли, путем нагревания влажной соли в угольной печи и конденсации паров в приемнике. Позже он получил тот же продукт, который теперь известен как соляная кислота, путем нагревания соли с серной кислотой.

ионная связь: хлорид натрия или поваренная соль
Ионная связь в хлориде натрия. Атом натрия (Na) отдает один из своих электронов атому хлора (Cl) в химической реакции, и образующиеся положительный ион (Na ⁺) и отрицательный ион (Cl ^—) образуют стабильное ионное соединение. (хлорид натрия; поваренная соль) на основе этой ионной связи.
Encyclopædia Britannica, Inc.
В 1774 году шведский химик Карл Вильгельм Шееле обработал порошкообразный черный оксид марганца соляной кислотой и получил зеленовато-желтоватый газ, который он не смог распознать как элемент. Истинная природа газа как элемента была признана в 1810 году английским химиком Хамфри Дэви, который позже назвал его хлором (от греческого chloros , что означает «желтовато-зеленый») и объяснил его отбеливающее действие.
Возникновение и распространение
Помимо очень небольшого количества свободного хлора (Cl) в вулканических газах, хлор обычно находится только в форме химических соединений. Он составляет 0,017 процента земной коры. Природный хлор представляет собой смесь двух стабильных изотопов: хлора-35 (75.53 процента) и хлор-37 (24,47 процента). Наиболее распространенным соединением хлора является хлорид натрия, который в природе встречается в виде кристаллической каменной соли, часто обесцвеченной из-за примесей. Хлорид натрия также присутствует в морской воде, средняя концентрация которой составляет около 2 процентов от этой соли. Некоторые моря, не имеющие выхода к морю, такие как Каспийское море, Мертвое море и Большое соленое озеро в штате Юта, содержат до 33 процентов растворенной соли. В крови и молоке присутствует небольшое количество хлорида натрия.Другими хлорсодержащими минералами являются сильвит (хлорид калия [KCl]), бишофит (MgCl ₂ ∙ 6H ₂ O), карналлит (KCl ∙ MgCl ₂ ∙ 6H ₂ O) и каинит (KCl ∙ MgSO ₄ ∙ 3H ₂ O). Он содержится в минералах эвапорита, таких как хлорапатит и содалит. В желудке присутствует свободная соляная кислота.
Мертвый Море
Солевые месторождения на юго-западном берегу Мертвого моря недалеко от Масады, Израиль.
З. Радован, Иерусалим Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас
Современные солевые отложения, должно быть, образовались в результате испарения доисторических морей, сначала кристаллизовались соли с наименьшей растворимостью в воде, а затем соли с большей растворимостью. Поскольку хлорид калия более растворим в воде, чем хлорид натрия, некоторые отложения каменной соли, например, в Штассфурте, Германия, были покрыты слоем хлорида калия. Чтобы получить доступ к хлориду натрия, сначала удаляют калиевую соль, важную как удобрение.
Галогены в водном растворе и реакции их замещения | Эксперимент
Галогены в небольшой степени реагируют с водой, образуя кислые растворы с отбеливающими свойствами. Они также подвергаются окислительно-восстановительным реакциям с галогенидами металлов в растворе, вытесняя менее реактивные галогены из своих соединений. Эти реакции замещения используются для установления порядка реактивности вниз по 17-й группе периодической таблицы.
Эта серия простых экспериментов иллюстрирует некоторые химические свойства галогенов после введения в физические свойства элементов Группы 17.Это может быть демонстрация или классный эксперимент.
Исследование растворимости галогенов в неполярном растворителе может быть опущено или показано только в качестве демонстрации.
Если упражнение проводится в качестве демонстрации, оно должно занять около 15 минут. Если это будет классный эксперимент, вы должны выделить 30 минут.
Оборудование
Аппарат
Защита глаз
Штатив для пробирок на 10 пробирок
Пробирки x10
Пробковые или резиновые заглушки по размеру, 4 шт.
Пластиковые пипетки-капельницы x6
Плитка белая
Белая плитка
Стеклянный стержень
Бумажное полотенце или салфетка
Химическая промышленность
Около 10 см ³ каждого из следующих растворов галогенов в закрытых пробирках (см. Примечания 1 и 2):
Хлорная вода, 0.1% (мас. / Об.) (ВРЕДНО)
Бромная вода, 0,1% (мас. / Об.) (ВРЕДНО)
Раствор йода, 0,1 М
Половина пробирки с 0,1 М растворами каждого из следующих веществ:
Калий хлористый
Бромид калия
Иодид калия
Универсальная индикаторная бумага (полоски около 2 см), 3 шт.
Дополнительно
Циклогексан (легковоспламеняющийся, ВРЕДНЫЙ, ОПАСНЫЙ ДЛЯ ОКРУЖАЮЩЕЙ СРЕДЫ) или другой подходящий неполярный растворитель, около 10 см ³ (см. Примечание 1)
Примечания к химическим веществам
Каждой группе студентов должны быть предоставлены пробирки с пробками, содержащие около 10 см. ³ каждого из водных растворов галогенов и одного раствора циклогексана (по желанию).
Растворы галогенов можно дополнительно разбавить, чтобы минимизировать количество выделяемых паров хлора или брома, но не следует разбавлять их настолько, чтобы их отличительный цвет не был четко виден в пробирках (для хлорной воды может потребоваться белый фон).
По окончании экспериментов все смеси и растворы должны быть возвращены в подходящий контейнер для отходов в вытяжном шкафу для безопасной утилизации.
Примечания по технике безопасности и охране труда
Ознакомьтесь с нашим стандартным руководством по охране труда и технике безопасности.
Всегда используйте защитные очки.
Позаботьтесь о том, чтобы ограничить воздействие паров хлора и брома на учащихся. У некоторых учащихся с респираторными проблемами может проявляться аллергическая реакция на хлор, начало которой может быть отложено.
Хлорная вода, Cl ₂ (водн.) — см. CLEAPSS Hazcard HC022b и CLEAPSS Recipe Book RB025. Сам по себе раствор является НИЗКОЙ ОПАСНОСТЬЮ, но газообразный хлор (ТОКСИЧНЫЙ, ОПАСНЫЙ ДЛЯ ОКРУЖАЮЩЕЙ СРЕДЫ) улетучивается, поэтому маркировка ВРЕДНО будет разумной.
Бромная вода, Br ₂ (водный), (ВРЕДНО) — см. CLEAPSS Hazcard HC015b и книгу рецептов CLEAPSS RB017.
Раствор йода, I ₂ (водный) — см. CLEAPSS Hazcard HC054 и CLEAPSS Recipe Book RB050. Раствор йода — это на самом деле йод, растворенный в водном растворе йодида калия.
Растворы хлорида калия, KCl (водн.), Бромида калия, KBr (водн.) И йодида калия, KI (водн.) — НИЗКАЯ ОПАСНОСТЬ — см. CLEAPSS Hazcard HC047b и CLEAPSS Recipe Book RB068. Если соли калия недоступны, можно использовать натриевые соли. Концентрацию раствора йодида калия следует отрегулировать так, чтобы он давал светло-коричневый раствор при добавлении хлорной воды. Если реагенты слишком концентрированы, вместо коричневого раствора часто образуется черный осадок йода.
Циклогексан, C ₆ H ₁₂ (l), (ОЧЕНЬ ВОСПЛАМЕНЯЮЩИЙСЯ, ВРЕДНО, ОПАСНО ДЛЯ ОКРУЖАЮЩЕЙ СРЕДЫ) — см. CLEAPSS Hazcard HC045b.
Процедура
Галогены в воде и углеводородном растворителе (необязательно)
Налейте около 2 см ³ каждого из водных растворов галогенов в отдельные пробирки.Добавьте равные объемы углеводородного растворителя в каждую пробирку, закройте пробирку и, удерживая большой палец над пробкой, встряхните смесь, перевернув пробирку несколько раз.
Дайте двум слоям осесть. Наблюдайте и записывайте цвет каждого слоя. Может потребоваться снова встряхнуть пробирки для переноса большего количества галогена из воды в углеводородный слой.
Кислотные и отбеливающие свойства растворов галогенов
Положите кусок универсальной индикаторной бумаги на белую плитку. С помощью стеклянной палочки нанесите каплю хлорной воды на бумагу. Обратите внимание на цвет бумаги и запишите его.
Протрите стеклянный стержень и плитку бумажным полотенцем или салфеткой. Положите на плитку свежий кусок индикаторной бумаги и с помощью стеклянной палочки нанесите на нее каплю бромной воды. Обратите внимание на цвет бумаги.
Повторите шаг 2, используя раствор йода.
Реакции вытеснения
Используя пластиковую пипетку, нанесите две капли раствора хлора в каждую из трех ямок на плитке для пятен, как показано ниже.Таким же образом, используя чистую пластиковую пипетку для каждого раствора, добавьте бромную воду и раствор йода к плитке для пятен.
Показать полноэкранный режим
Добавьте две капли раствора хлорида калия в каждую из трех ямок в столбце 1 плитки. Наблюдайте и записывайте любые происходящие изменения цвета.
Добавьте две капли раствора бромида калия в каждую из трех ямок в столбце 2 плитки. Наблюдайте и записывайте любые происходящие изменения цвета.
Добавьте две капли раствора йодида калия в каждую из трех ямок в столбце 3 плитки. Наблюдайте и записывайте любые происходящие изменения цвета.
Дополнительно
Для реакций, в которых предполагается образование брома или йода, реакцию можно повторить с 2 см ³ каждого раствора в пробирке, а затем можно добавить гексан для подтверждения присутствия брома или йода.
Учебные заметки
Таблица результатов, подобная приведенной ниже, может использоваться для записи результатов.Он был завершен с ожидаемыми наблюдениями.
вода
Цвет после встряхивания с углеводородным растворителем Влияние на индикаторную бумагу Реакция с раствором хлорида калия Реакция с раствором бромида калия Реакция с раствором йодида калия
Хлор
Водный слой: от бледно-желто-зеленого до бесцветного
Углеводородный слой: от бесцветного до бледно-желто-зеленого
Становится красным, затем быстро обесцвечивается
Нет реакции
Появляется желто-оранжевый цвет брома
Появляется коричневый цвет йода
Бромная вода
Водный слой: от желто-оранжевого до бесцветного
Углеводородный слой: от бесцветного до бледно-желто-оранжевого
Становится красным, затем медленно обесцвечивается
Нет реакции
Нет реакции
Цвет темнеет от желто-оранжевого до коричневого
Раствор йода
Водный слой: от коричневого до бесцветного
Углеводородный слой: от бесцветного до фиолетового
Бумага морилка коричневая
Нет реакции
Нет реакции
Нет реакции
Галогены более растворимы в углеводородах и перемещаются в этот верхний слой при встряхивании с углеводородным растворителем. Для хлора и брома цвет не меняется. Вам может понадобиться белый фон, чтобы увидеть цвет раствора хлора. Однако для йода наблюдается изменение цвета от коричневого в воде до пурпурного в углеводородном слое.
Если между раствором галогена и раствором галогенида не происходит реакции замещения, может наблюдаться некоторое осветление цвета раствора, что можно объяснить эффектом разбавления.
Позаботьтесь о том, чтобы ограничить воздействие паров хлора и брома на учащихся.У некоторых учащихся с респираторными проблемами может проявляться аллергическая реакция на хлор, начало которой может быть отложено.
Йод наименее растворим в воде из галогенов. Он более растворим в растворе йодида калия, поэтому «раствор йода» здесь на самом деле йод в растворе йодида калия.
Обратите внимание студентов на сходство между цветом паров йода и его цветом в неполярном растворителе. Молекулы полярной воды взаимодействуют с молекулами йода, изменяя длину волны света, которую они поглощают.
Все три галогена реагируют с водой с образованием сильной кислоты (HX) и слабой кислоты (HOX), которая обладает отбеливающими свойствами и является окислителем.
X ₂ (водн.) + H ₂ O (л) → HX (водн.) + HOX (водн.)
Степень реакции снижается в группе 17. С йодом она настолько мала, что кислотные и отбеливающие свойства раствора не наблюдаются в этом эксперименте.
В реакциях замещения хлор вытесняет бром и йод из их соединений, а бром замещает йод.Например:
Cl ₂ (водн.) + 2KI (водн.) → I ₂ (водн.) + 2KCl (водн.)
Таким образом, реакционная способность будет следующей: хлор> бром> йод. Более продвинутая обработка идентифицирует галогены как окислители, принимающие электрон для образования галогенид-ионов:
Cl ₂ (водн.) + 2I ^— (водн.) → I ₂ (водн.) + 2Cl ^— (водн.)
Вопреки мнению многих студентов, реакция не имеет ничего общего с реакционной способностью калия «захватить» хлор. Калий здесь присутствует только в виде очень инертных ионов калия (ионов-наблюдателей) в растворе.
Живые науки для Науки 7 класса Глава 8
Стр. № 87:
Вопрос 1:
Что из этого является химическим изменением?
(a) Образуется субакне с разными химическими свойствами.
(b) Образуется вещество в другом состоянии, но с аналогичными химическими свойствами.
(c) Молекулы веществ не претерпевают никаких изменений.
(d) Образуется вещество другой формы и размера, но схожими химическими свойствами.
Ответ:
(a) Образуется вещество с различными химическими свойствами.
Химическое изменение происходит, когда два вещества вступают в химическую реакцию с образованием новых веществ с разными химическими свойствами.
Стр. № 87:
Вопрос 2:
Что из этого является необратимым физическим изменением?
(а) ржавление железа
(б) замерзание воды
(в) реакция двойного разложения
(г) разбитие стеклянного стакана
Ответ:
(d) разбитие стеклянного стакана
Разрушение стеклянного стакана является необратимым физическим изменением. Ржавчина железа — это химическое изменение. Замерзание воды — это обратимое физическое изменение. Реакция двойного разложения — это химическое изменение.
Стр. № 87:
Вопрос 3:
Стрелка, направленная вниз в химической реакции, показывает
(a) выделение газа
(b) образование осадков
(c) окисление
(d) вытеснение
Ответ:
(b) образование осадка
В химической реакции стрелка, направленная вниз, показывает образование осадка, а стрелка, направленная вверх, показывает выделение газа.
Стр. № 87:
Вопрос 4:
Химическая реакция, при которой выделяется тепло, называется
(a) экзотермическая реакция
(b) эндотермическая реакция
(c) реакция разложения
(d) реакция нейтрализации
Ответ:
(а) экзотермическая реакция
Экзотермические реакции сопровождаются выделением тепла. Эндотермические реакции сопровождаются поглощением тепла.
Стр. № 87:
Вопрос 5:
Сколько продуктов образуется в реакции сочетания?
(a) только два
(b) только один или два
(c) только один
(d) номер не может быть указан
Ответ:
(c) только один
В реакции сочетания из его элементов образуется соединение. Например, вода и кислород вместе образуют воду.
Стр. № 87:
Вопрос 6:
Что происходит при реакции вытеснения?
(a) Более реактивный элемент заменяет менее реактивный элемент.
(b) Менее реактивный элемент заменяет более реактивный элемент.
(c) Элемент заменяет элемент, обладающий равной реактивностью.
(d) Любой элемент может заменить любой другой элемент, не имеющий отношения к реактивности.
Ответ:
(a) Более реактивный элемент заменяет менее реактивный элемент.
В реакции замещения более реактивный элемент заменяет менее реактивный элемент из своего соединения.
Стр. № 87:
Вопрос 7:
Реакция нейтрализации — это реакция разложения
(а).
(б) реакция вытеснения.
(c) реакция комбинации.
(г) реакция двойного вытеснения.
Ответ:
(г) реакция двойного вытеснения.
Реакция нейтрализации — это реакция двойного замещения, в которой кислота реагирует с основанием и радикалы обмениваются с образованием соли и воды.
Стр. № 87:
Вопрос 8:
Реакция окисления включает добавление
(a) только кислорода
(b) только водорода
(c) кислорода или удаления водорода
(d) водорода или удаления кислорода
Ответ:
(c) кислород или удаление водорода
Реакция окисления включает добавление кислорода или удаление водорода из вещества.
Стр. № 87:
Вопрос 9:
Если в какой из следующих реакций присутствует только один реагент?
(а) реакция комбинации
(б) реакция разложения
(в) реакция одинарного вытеснения
(г) реакция двойного вытеснения
Ответ:
(b) реакция разложения
В реакции разложения соединение (реагент) распадается на два или более веществ (продуктов).
Стр. № 87:
Вопрос 10:
Если A более реактивен, чем B, что из следующего верно?
(a) A заменит B солью B.
(b) B заменит A солью A.
(c) Оба могут вытеснять друг друга из своих солей.
(d) Оба не могут вытеснить друг друга из своих солей.
Ответ:
(a) A заменит B из соли B.
Данная реакция является примером реакции замещения, в которой более реактивный элемент заменяет менее реактивный элемент из своего солевого раствора.
Стр. № 88:
Вопрос 1:
Почему водопроводные трубы оцинкованы?
Ответ:
Водопроводные трубы сделаны из железа. Ржавление железа происходит при взаимодействии железа с воздухом и водой.Поэтому, чтобы предотвратить ржавление железа, водопроводные трубы оцинковываются, то есть железные трубы покрываются металлами, такими как цинк или хром, чтобы предотвратить взаимодействие железа с воздухом.
Стр. № 88:
Вопрос 2:
Когда вода замерзает, она образует лед с разными свойствами. Почему же тогда мы говорим, что замораживание — это физическое изменение?
Ответ:
При физическом изменении изменяются только физические свойства вещества, а новые вещества не образуются.
Замерзание воды — это физическое изменение, потому что изменяется только физическое состояние воды; т. е. вода превращается в лед. Следовательно, замораживание — это физическое изменение.
Стр. № 88:
Вопрос 3:
Приведите по одному примеру каждой химической реакции, демонстрирующей следующие характеристики.
(a) выделение газа
(b) изменение цвета
(c) образование осадка
(d) изменение состояния с жидкости на газ
(e) изменение состояния с газа на жидкость
Ответ:
(а) Zn + H ₂ SO ₄ → ZnSO ₄ + H ₂ ↑
Цинк Серно-цинковый водород
сульфат кислоты
(б) CuCO ₃ → CuO + CO ₂ ↑
_{Медь Медь Углерод
Оксид карбоната _{Диоксид
(зеленый) (черный)}}
(c) CuSO ₄ + H ₂ S → CuS ↓ + H ₂ SO ₄
_{Медь Водород Медь Серная
сульфат сульфид сульфидная кислота}
(г) 2H ₂ O (л) → 2H ₂_{(г) + O ₂_{(г)
Водородный кислород}}
(д) 2H ₂ (г) + O ₂ (г) → 2H ₂ O (л)
Водород кислородная вода
Стр.
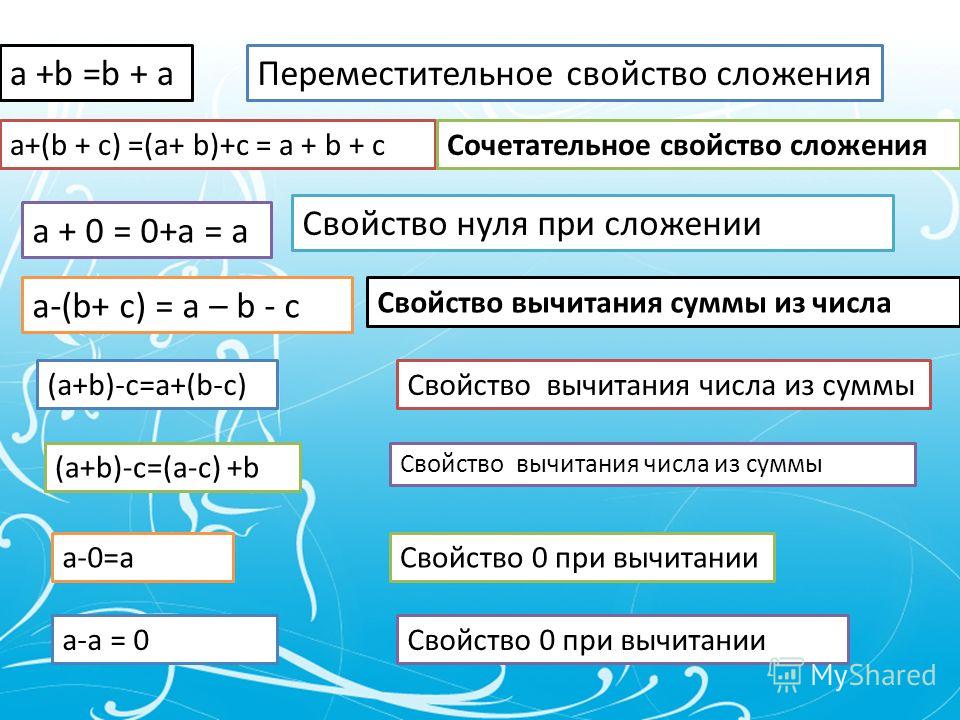
№ 88:
Вопрос 4:
Различают эндотермические и экзотермические реакции.
Ответ:
Эндотермическая реакция Экзотермическая реакция
Эти реакции сопровождаются поглощением тепла. Эти реакции сопровождаются выделением тепла.
Плавление твердых веществ, плавление, испарение и испарение являются примерами эндотермической реакции. Сжигание бензина и окисление аммиака являются примерами экзотермической реакции.
Стр. № 88:
Вопрос 5:
Что такое комбинированная реакция? Привести пример.
Ответ:
В реакции сочетания соединение образуется из его элементов или из более простых веществ. Например, магний реагирует с кислородом при нагревании с образованием оксида магния.
2Mg + O ₂ → 2MgO
Стр.
№ 88:
Вопрос 6:
Когда говорят, что вещество восстанавливается в результате химических реакций?
Ответ:
В химической реакции вещество восстанавливается, если к нему добавляют водород или удаляют кислород.
Стр. № 88:
Вопрос 7:
Что такое кристаллизация?
Ответ:
Кристаллизация — это процесс, при котором чистое твердое вещество отделяется от раствора в виде кристаллов.
Например, поваренная соль, полученная из морской воды, содержит растворимые примеси, такие как хлорид магния. Для очистки поваренной соли применяется процесс кристаллизации.
Стр. № 88:
Вопрос 8:
Что такое перенасыщенный раствор?
Ответ:
Раствор, в котором растворяется больше растворенного вещества при повышении температуры насыщенного раствора, называется перенасыщенным раствором. Когда перенасыщенный раствор охлаждается до комнатной температуры, он легко кристаллизуется.
Стр. № 88:
Вопрос 1:
Обсудите методы предотвращения коррозии железа.
Ответ:
Ржавчину железа можно предотвратить следующими методами:
(a) Покраска: слой краски, нанесенный на поверхность железного предмета, предотвращает взаимодействие кислорода и влаги, присутствующих в атмосфере, с железным предметом.
(b) Масло или смазка: Нанесение масла или смазки на поверхность металлических инструментов помогает предотвратить попадание кислорода и влаги из атмосферы.
(c) Гальванизация: Гальванизация — это процесс покрытия железных предметов тонким слоем металла, такого как цинк или хром.Тонкое покрытие из цинка или хрома защищает утюг от ржавчины.
Стр. № 88:
Вопрос 2:
Какой газ выделяется при добавлении разбавленной соляной кислоты к карбонату кальция?
Как вы будете проверять газ? Напишите химические уравнения для обеих реакций.
Ответ:
Двуокись углерода выделяется при добавлении разбавленной соляной кислоты к карбонату кальция.Используемое уравнение:
CaCO ₃ + HCl → CaCl ₂ + H ₂ O + CO ₂ ↑
Углекислый газ можно проверить, пропустив его через известковую воду. Известковая вода становится молочной. Используемое уравнение:
Ca (OH) ₂ + CO ₂ → CaCO ₃ + H ₂ O
Известь углерода, кальция вода
диоксид карбонат
Карбонат кальция, образующийся в реакции, имеет белый цвет. цвет и мало растворим в воде.Он придает молочный вид и используется в качестве теста на наличие углекислого газа.
Стр. № 88:
Вопрос 1:
При каких изменениях вещества подвергаются химическому превращению — физическому или химическому?
Ответ:
При химических изменениях вещества подвергаются химическому превращению с образованием новых веществ.
Стр. № 88:
Вопрос 2:
Rush — это смесь, не имеющая химической формулы.Правда или ложь?
Ответ:
Неверно.
Ржавчина — это соединение. Его химическая формула: Fe ₂ O ₃ .H ₂ O.
Стр. № 88:
Вопрос 3:
Процесс нанесения цинка на железо для предотвращения ржавчины называется __________
Ответ:
Процесс нанесения цинка на железо для предотвращения ржавчины называется гальваника .
Стр. № 88:
Вопрос 4:
Какой газ выделяется при нагревании карбоната кальция?
Ответ:
При нагревании карбоната кальция образуется оксид кальция и выделяется диоксид углерода.
CaCO ₃ → CaO + CO ₂
Стр. № 88:
Вопрос 5:
Когда два растворимых вещества в растворе реагируют с образованием нерастворимого вещества, образуется _________.
Ответ:
Когда два растворимых вещества в растворе реагируют с образованием нерастворимого вещества, образуется осадок .
Стр. № 88:
Вопрос 6:
Тепло поглощается _________ реакцией.
Ответ:
Тепло поглощается эндотермической реакцией.
Стр. № 88:
Вопрос 7:
Если в правой части уравнения написано «+ тепло», то какой это тип реакции?
Ответ:
Знак «+ тепло» означает, что реакция сопровождается выделением тепла. Реакция экзотермическая.
Стр. № 88:
Вопрос 8:
Определите, какой тип реакции каждый из следующих:
(a) X + Y → XY
(b) XY → X + Y
(c) AB + XY → AY + XB
(d) AB + X → AX + B
(e) AB + CD → AD + BC
(f) Кислота + основание → соль + вода
Ответ:
(a) Реакция сочетания
(b) Реакция разложения
(c) Реакция двойного вытеснения
(d) Реакция одиночного вытеснения
(e) Реакция двойного вытеснения
(f) Реакция нейтрализации
Стр.
№ 88:
Вопрос 9:
Окислитель обеспечивает ________ или удаляет _________ из вещества.
Ответ:
Окислитель обеспечивает кислородом или удаляет водород из вещества.
Стр. № 88:
Вопрос 10:
Какой метод вы будете использовать для получения чистой жидкости, если в ней есть растворенные примеси?
Ответ:
Мы будем использовать метод кристаллизации для получения чистой жидкости, если в ней есть растворенные примеси.
Стр. № 88:
Вопрос 11:
Соль получают из морской воды кристаллизацией. Правда или ложь?
Ответ:
Неверно.
Соль получают из морской воды испарением.
Стр. № 88:
Вопрос 12:
Перенасыщенный раствор твердого вещества в жидкости легко кристаллизуется.Правда или ложь?
Ответ:
Верно.
Перенасыщенный раствор содержит больше растворенного вещества, чем может оставаться растворенным в воде. Он очень нестабилен и легко кристаллизуется.
Стр. № 89:
Вопрос 3:
Объясните этапы получения основного гидроксида магния из металлического магния.
Ответ:
Для получения основного гидроксида магния из металлического магния используются следующие этапы:
(a) Возьмите небольшой кусок магниевой ленты.
(b) Очистите его кончик наждачной бумагой.
(c) Возьмите его щипцами и поднесите к пламени. Он горит ослепительным пламенем и образует порошкообразный пепел (оксид магния).
(e) Соберите золу в пробирку, смешайте ее с небольшим количеством воды и перемешайте.
Когда оксид магния растворяется в воде, он образует гидроксид магния. Уравнение:
2MgO + 2H ₂ O → 2Mg (OH) ₂
Магний Вода Магний
гидроксид оксида
Стр. № 89:
Вопрос 4:
Реакция разложения противоположна реакции сочетания.Объясните на примере.
Ответ:
Реакция, в которой соединение распадается с образованием двух или более простых веществ, называется реакцией разложения.
Например, при пропускании электрического тока через воду, в которую было добавлено небольшое количество серной кислоты, вода разлагается с образованием газов водорода и кислорода.
2H ₂ O → 2H ₂ + O ₂
Реакция, в которой два или более элемента объединяются с образованием единого соединения, называется реакцией сочетания.
Например, водород соединяется с кислородом с образованием воды.
2H ₂ + O ₂ → 2H ₂ O
Из приведенных выше примеров ясно, что реакция разложения противоположна реакции сочетания.
Стр. № 89:
Вопрос 5:
При каких двух условиях обычно протекают реакции разложения? Приведите по одному примеру каждого из них.
Ответ:
Двумя условиями, при которых обычно происходит реакция разложения, являются следующие:
(a) Нагревание: при нагревании гидроксида кальция образуются оксид кальция и водяной пар.
Ca (OH) ₂ → CaO + H ₂ O
Кальций Кальций Вода
гидроксид оксида
(b) Электролиз: когда электрический ток проходит через расплавленный оксид алюминия, он подвергается разложению с образованием алюминия и кислорода газ.
2Al ₂ O ₃ → 4Al + 3O ₂
Стр.
№ 89:
Вопрос 6:
Что такое реакция вытеснения? Какое правило регулирует смещение одного элемента в соединении другим элементом? Объясните на примере.
Ответ:
В реакции замещения один элемент заменяет другой элемент соединения. Как правило, более реактивный элемент заменяет менее реактивный элемент из своего соединения. Например, железо является более активным элементом, чем медь. Если в раствор медного купороса добавить железку, образуется сульфат железа. Металлическая медь оседает на железной детали.
CuSO ₄ + Fe → FeSO ₄_{+ Cu
Медь Железо Железо Медь
сульфат сульфат}
Стр. № 89:
Вопрос 7:
Что такое реакция двойного разложения? Сколько вам известно типов реакции двойного разложения? Приведите по одному примеру каждого из них.
Ответ:
Реакция, в которой два соединения реагируют с образованием двух других соединений путем взаимного обмена атомами или группой атомов, называется реакцией двойного замещения. Есть два типа реакции двойного вытеснения.
(a) Реакция осаждения: В этой реакции два соединения реагируют в их водном состоянии с образованием нерастворимого продукта, который появляется в виде осадка. Например, водный раствор хлорида натрия и нитрат серебра реагируют с образованием белого осадка хлорида серебра.
NaCl + AgNO ₃ → AgCl ↓ + NaNO ₃
Натрий Серебро Серебро Натрий
хлорид нитрат хлорид нитрат
(b) Реакция нейтрализации: при взаимодействии основания и кислоты они обмениваются ионами и образуют соединения называется солью, водой и иногда газом. Например, соляная кислота реагирует с гидроксидом калия с образованием хлорида калия (соли) и воды.
HCl + KOH → KCl + H ₂ O
Соляной калий Калийная вода
Гидроксид хлорид кислоты
Стр.
№ 89:
Вопрос 8:
Объясните термины «окислитель» и «окислитель».
Ответ:
Окисление — это химическая реакция, которая включает добавление кислорода или удаление водорода из вещества. Например, когда углерод реагирует с кислородом с образованием диоксида углерода, говорят, что он окисляется, получая кислород.
C + O ₂ → CO ₂
Углерод Кислород Углерод
диоксид
Аналогичным образом, когда сероводород реагирует с хлором, считается, что сероводород окисляется до серы за счет потери водорода.
H ₂ S + Cl ₂ → S + 2HCl
Водород Хлор Сера соляная
сульфидная кислота
Окислитель — это агент, который окисляет другие вещества, либо обеспечивая их кислородом, либо удаляя из них водород.
Стр. № 89:
Вопрос 1:
В каком городе, по вашему мнению, ржавчина будет более серьезной проблемой — в Дели или в Мумбаи? Почему?
Ответ:
Для образования ржавчины необходимы два условия: содержание кислорода и влаги в атмосфере. Климат Дели жаркий и сухой, тогда как климат Мумбаи влажный. Следовательно, ржавчина — большая проблема в Мумбаи, потому что в атмосфере больше влаги и кислорода.
Стр. № 89:
Вопрос 2:
Когда горит свеча, происходят как физические, так и химические изменения. Что это за изменения?
Ответ:
Плавление воска — это физическое изменение, а образование углекислого газа и водяного пара — это химическое изменение. Следовательно, при горении свечи происходят как физические, так и химические изменения.
Стр. № 89:
Вопрос 3:
LPG (сжиженный углеводородный газ) в газовом баллоне находится в виде жидкости.Какие физические и химические изменения происходят, когда он выходит из цилиндра и горит?
Ответ:
СНГ в баллоне существует в виде жидкости. Когда он выходит из цилиндра, он превращается в газ, что является физическим изменением. Сжигание сжиженного нефтяного газа — это химическое изменение.
Стр. № 89:
Вопрос 4:
При открытии бутылки с газированной водой выделяется газ.Происходит химическая реакция? Объяснять.
Ответ:
Нет, химической реакции не происходит. Когда бутылка из-под газировки открыта, выделяется углекислый газ. Углекислый газ уже растворен внутри бутылки с газировкой. После снятия крышки давление внутри сбрасывается, и углекислый газ выходит.
Стр. № 89:
Вопрос 5:
Почему нельзя класть ложки из нержавеющей стали в банки для маринадов?
Ответ:
Сталь реагирует с кислотами, присутствующими в травильном растворе, и образует ржавчину.
Презентация по математике на тему Переместительное и сочетательное свойство сложения и умножения(5 класс) доклад, проект
Слайд 1Текст слайда:
Урок математики
5 класс
Слайд 2Текст слайда:
Установка на урок
Я буду внимателен
Я буду старателен
Я буду трудолюбив
Я буду доброжелателен
Я буду активен
Я буду успешен
Слайд 3Текст слайда:
Устный счет
Решите устно
594
Запишите ответы в порядке возрастания
322
100
25
642
78
270
8
2500
У
К
А
Л
А
С
Р
Г
С
Слайд 4Текст слайда:
Вы узнаете
Работа с учебником
Слайд 5Текст слайда:
Вы узнаете
Работа с учебником
ИНТЕРЕСНО В истории математики известен такой случай.
Однажды в Германии в конце XVIIIв., для того чтобы заставить учеников поработать, учитель дал им задание – сложить все числа от 1 до 100.
Каково же было его удивление, когда уже через несколько минут один из учеников сказал ответ:
сумма равна 5050.
Этот ученик, Карл Фридрих Гаусс, впоследствии стал
великим математиком.
Слайд 6Текст слайда:
Сложение и умножение натуральных чисел
2 + 3 = 5
5 ∙ 7 = 35
Слайд 7Текст слайда:
Свойства сложения и умножения
Слайд 8Текст слайда:
Переместительное и сочетательное свойства
При перестановке слагаемых
сумма
не меняется
Переместительное свойство сложения
Слайд 9Текст слайда:
Переместительное и сочетательное свойства
11+25+75
11+ 25 + 75
(11+25)+75
11+(25+75 )
=
=
=
111
I
II
III
11+(25+75)
(11+25)+75
=
=
(a + b) + c
a + (b + c)
a + b + c
=
=
111
111
Слайд 10Текст слайда:
Переместительное и сочетательное свойства
В сумме трех чисел можно объединять в группу
как первые два слагаемые, так и последние два –
одним и тем же
Сочетательное свойство сложения
результат будет
Слайд 11Текст слайда:
Переместительное и сочетательное свойства
Действие умножения также обладает переместительным и сочетательным свойствами.
Переместительное свойство умножения
Сочетательное свойство умножения
Слайд 12Текст слайда:
Вычисление сумм
Назовите свойства,
на основании которых
выполнены преобразования,
и вычислите сумму:
УЧЕБНИК
№ 213
стр. 68
а) 19 + (11 + 6) = (19 + 11) + 6
сочетательное
ответ
б) 23 + (48 + 27) = 23 + (27 + 48) = (23 +27) + 48
переместительное
ответ
36
сочетательное
98
Слайд 13Текст слайда:
Переместительное и сочетательное свойства
При сложении и умножении нескольких чисел их можно как угодно переставлять и объединять в группы
!
Слайд 14Текст слайда:
Удобные вычисления
Слайд 15Текст слайда:
Удобные вычисления
Слайд 16Текст слайда:
Осваиваем алгоритмы
Запишите цепочку преобразований
и вычислите результат:
ТРЕНАЖЕР
а) 85 + 27 + 15 =
ответ
(85 + 15) + 27 = 127
б) 49 + 63 + 11 + 17 =
ответ
(49 + 11) + (63 +17) = 140
в) 54 + 92 + 68 + 46 =
ответ
(54 + 46) + (92 + 68) = 100 + 160 = 260
№ 96
стр. 42
Слайд 17Текст слайда:
Осваиваем алгоритмы
ответ
ответ
ответ
ТРЕНАЖЕР
№ 97
стр. 42
Запишите цепочку преобразований
и вычислите результат:
Слайд 18Текст слайда:
Найдите сумму чисел:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Как маленькому Гауссу удалось быстро найти сумму чисел от 1 до 100?
Слайд 19Текст слайда:
Метод Гаусса
Слайд 20Текст слайда:
Да
Выполнили вы установки?
Не все
Нет
Слайд 21Текст слайда:

1. У: стр. 66, 67 – читать,
рубрика «вопросы и задания»;
З: № 170(а, в), 171(б, г), 172;
2. Попробуйте найти сумму
1+2+3+4+…+98+99+100
Домашнее задание
Слайд 22Текст слайда:
Встретились два свойства – переместительное и сочетательное, и заспорили, кто из них главнее. Опиши их спор.
Чем он мог закончиться?
Творческое задание
Слайд 23
Скачать презентацию
Онлайн тест по Математике по теме Сочетательное свойство сложения
Для легкости и быстроты счета арифметика, вычислительная наука-искусство, имеет законы и свойства вычислительных операций. Сложение, одно из первых арифметических действий, изучаемых в начальных классах, имеет сочетательное и переместительное свойства. Освоение математических принципов и закономерностей зависит от нескольких факторов – знания состава чисел, доведенного до автоматизма; заучивание таблиц математических действий; использование особых приемов арифметики. В пятом классе рассматривается сочетательное свойство сложения в более широких рамках материала, одновременно включая повторение пройденной теории. В обобщении и систематизации знаний и умений по теме станет помощником тест.
Тестовые вопросы повторяют теоретический материал, выделяя понимание перемещения числа по числовой прямой. Правильность имеющихся представления об основах вычислительных действий последовательно проверяется заданиям теста, направленными на приобретение навыков сравнения, обобщения. Осмысленное использование сочетательного свойства позволяет правильно группировать числа. Практические тестовые примеры помогают ученику самостоятельно проверить свои способности справляться с заданием, применяя систематизированные и закрепленные теоретические правила.
Тестовые упражнения выявляют пробелы в знании, выделяют главные проблемы изучения, способствуют и формируют умение делать выводы из решенных практических задач. Самостоятельная работа с тест-примерами развивает внимание при группировке чисел по парам, необходимое для экономии время расчетов.
Работа с тестом – развитие логического мышления, памяти, воображения, формирование собственного мнения при высказывании предположений, поиск новой информации, стремление к быстрому решению заданий с нахождением суммы.
Пройти тест онлайн
1. Перемещение числа по числовой прямой вправо называется…
Сложение
Вычитание
Деление
Нет верного ответа
2. Действительно ли у сложения всего 2 свойства?
Да
Нет
Всего 3 свойства
Нет верного ответа
3. Какие есть свойства сложения?
Сочетательное и переместительное
Сочетательное и слагательное
Переместительное и слагательное
Нет верного ответа
4. Это свойство утверждает, что в примерах, где два и более множителя, сложение может производиться в любом порядке.Как оно называется
Слагательное
Переместительное
Смесительное
Сочетательное
5. Что главное, при использовании сочетательного свойства?
Правильно сгруппировать числа
Ничего
Правильно выбрать свойство
Нет верного ответа
6. Решить пример: 56+9+23+24+31+7=… используя сочетательное свойство.
(56+24)+(9+31)+(23+7)= 150
(23+24)+(9+31)+(56+7)= 150
(56+24)+(9+31)+(23+7)= 160
Нет верного ответа
7. Как удобнее сгруппировать данный пример: 45+67+33+5+89+11.
45+67+33+5+89+11
(45+5)+(67+33)+(89+11)
(45+11)+(67+33)+(5+89)
Нет верного ответа
8. Сочетательным свойством пользуются в том случае, когда в примере не менее… чисел.
1
2
3
4
9. Решить пример: 12*3+4+15-2-6-2.
35
40
45
55
10. Зачем пользоваться сочетательным свойством?
Чтобы экономить время для расчетов
Чтобы было по правилам
Чтобы пример был красивы
Нет верного ответа
Ещё никто не оставил комментария, вы будете первым.

Написать комментарий
Другие тесты
формулы и другие законы произведения, тождества и примеры для 5 класса
Математика
12.11.21
10 мин.
Арифметические операции произведения, сложения, вычитания и деления применяются в различных дисциплинах с физико-математическим уклоном. У каждой из них существуют определенные законы, позволяющие оптимизировать процессы вычисления. Для сложения и произведения следует применять распределительное, переместительное и сочетательное свойства умножения или сложения.

Оглавление:

Общие сведения

Базовые правила

Пример решения

Общие сведения
Для удобства описания арифметических операций следует ввести буквенные обозначения. Пусть первый коэффициент эквивалентен переменной «о», второй — «р», а результат — «r». К базовым арифметическим действиям относятся:
Сложение.
Вычитание.
Умножение.
Деление.
Сложение (+) — операция, увеличивающая исходное число на некоторое значение. Выражение состоит минимум из 3 коэффициентов, т. е. о+р=r. Первый и второй (о и р соответственно) называются слагаемыми, третий — суммой r.
Вычитанием (-) называется арифметическая операция, состоящая из уменьшаемого значения и вычитаемого, результатом которой является разность. Математическая запись имеет такой вид: о-р=r, где о — уменьшаемое, р — вычитаемое, а r — разность.
Третьей операцией является умножение (*), состоящая из коэффициентов, которых может быть более 2: первый и второй — множители, а третий — произведение. Операция записывается таким образом: о*р=r. Кроме того, существует краткая запись, при которой знак «*» не указывается, т. е. ор=r.
Деление (:) — арифметическая операция, позволяющая разделить одно число на другое. Математически она записывается следующим образом: о: р=r («о» — делимое, «р» — делитель и «r» — частное).

Следует отметить, что у каждой операции может быть и другое количество коэффициентов. Например, o*p*s*t=r, где o, p, s, t — множители, а r — результат. Однако при решении задач применяются некоторые законы, существенно оптимизирующие вычисления.
Базовые правила
При вычислении значения выражения математики рекомендуют применять определенные правила. Их можно комбинировать между собой. Эта методика позволяет сократить время на расчеты, а также тренирует мозг, при помощи которого появляется возможность выполнять сложные вычисления в устной форме. Кроме того, законы справедливы для любой арифметической операции.
Методы сложения
Для начала следует рассмотреть основные правила сложения. Они основываются на раскрытии скобок выражения, состоящего из нескольких слагаемых. К ним относятся сочетательный и переместительный. Первый закон можно сформулировать следующим образом: если 2 числа, находящиеся в скобках, связаны операцией сложения, при прибавлении к ним третьего значения можно сложить его с первым, а затем со вторым. Математическая форма записи приобретает такой вид: (о+р)+k=(о+k)+p. Возможна и такая запись: (о+р)+k=(р+k)+о.
Переместительный закон имеет такой вид: от перемены мест слагаемых величина алгебраической суммы не меняется. Математически запись выглядит так: о+р+k=р+k+о=р+о+к=к+о+р=к+р+о. Кроме того, существуют 2 следствия, на основании которых можно существенно сократить объем вычислений:
Если слагаемые эквивалентны между собой, тождество можно записать в виде произведения одного элемента на их количество, т. е. к+к+к+к+к=5к.
Нуль не учитывается при сложении.

Следующей операцией является вычитание. У него также существуют некоторые очень важные свойства.
Свойства вычитания
При выполнении арифметической операции вычитания специалисты рекомендуют придерживаться основных законов. К ним относятся следующие утверждения и формулы:
Если из произвольного «к» вычесть нулевое значение, результат будет эквивалентен этому числу. При вычитании из 0 числа «к» получается отрицательное число, равное величине с противоположным знаком, т. е. 0-к=-к.
Разность двух одинаковых чисел соответствует 0, т. е. к-к=0.
Если вычитаемое представлено суммой двух чисел, можно вычесть из уменьшаемого первое слагаемое, а затем второе, р-(о+к)=р-о-к.
Когда уменьшаемое записано в виде суммы, следует из первого слагаемого вычесть вычитаемое и к результату прибавить второй элемент суммы, т. е. (р+о)-к=р-к+о.
Этих правил будет достаточно для выполнения вычислений любого типа. Кроме операций сложения и вычитания, существуют более сложные арифметические действия.

Умножение и деление
Изучаются законы умножения в 5 классе. Они состоят из следующих формул и утверждений:
Результат умножения любой величины на нулевое значение равен 0.
Если умножить число на 1, получится оно же, т. е. к*1=к.
Переместительный закон произведения: при перемене мест множителей произведение неизменно, т. е. к*р*о=к*о*р=р*о*к=р*к*о=о*к*р=о*р*к.
Сочетательный закон умножения (ассоциативный): если количество множителей в выражении больше 2, можно перемножить 1 и 3, а затем их произведение использовать при расчетах, как второй множитель, т. е. (5*3)*2=(5*2)*3=10*3=30.
Распределительный: при умножении некоторого числа на сумму нужно умножить его на первое слагаемое и на второе, а затем сложить 2 величины, т. е. к (р+о)=кр+ко.
Наиболее сложной операцией является деление. У нее также есть некоторые важные свойства:
На 0 невозможно делить.
Если нуль разделить на произвольное значение, получится 0.
При делении на 1 получается первоначальное значение, т. е. к/1=к.
Переместительный закон: к/р/о=к/о/р.
Сочетательный: (к/р)/о=к/(р/о).
Следует отметить, что при использовании правил, нужно постоянно контролировать выполнение условия неравенства делителя 0. В противном случае тождество будет пустым множеством. Последняя тема изучается в высших учебных заведениях.

Пример решения
Для качественного усвоения материала нужно вычислить значение выражения, используя законы арифметических операций. Тождество имеет такой вид: [5*2*3*6*2+2*3*9*5+2 (о+р)-(р+2о)-(р+2)]/[(2*16*5−7*8)-2 (p-o). Для решения следует руководствоваться алгоритмом:
Расчет 5*2*3*6*2, используя ассоциативный закон: (5*2)*(3*2)*6=10*(6*6)=10*36=360.
Вычисление 2*3*9*5: (2*5)(3*9)=10*27=270.
Раскрытие скобок (распределительный): 2 (о+р)-(р+2о)-(р+2)=2о+2р-р-2о-р-2=-2.
Вычисление величины знаменателя, который не должен быть равен 0: 2*16*5−7*8−2 (р-о)=(2*5)*16−56−2р+2о=160−2р+2о.
Запись результата: [360+270−2]/[160−2р+2о]=628/[160−2р+2о].
Пример наглядно показывает оптимизацию вычислений, которые возможно произвести без помощи калькулятора.
Таким образом, формулы и утверждения для операций умножения, деления, сложения и вычитания используются для ускорения вычислений.
Не успеваете написать работу?

Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация
Контактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

«Сочетательное свойство умножения». 3-й класс
Цель: учить упрощать выражение, содержащее только действия умножения.
Задачи (Слайд 2):
Познакомить с сочетательным свойством умножения.

Формировать представление о возможности использования изученного свойства для рационализации вычислений.

Развивать представления в возможности решения «жизненных» задач средствами предмета «математика».

Развивать интеллектуальные и коммуникативные общеучебные умения.

Развивать организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять собственные ошибки.

Тип урока: изучение нового материала.
План урока:
1. Организационный момент.
2. Устный счёт. Математическая разминка.
Строка чистописания.
3. Сообщение темы и задач урока.
4. Подготовка к изучению нового маериала.
5. Изучение нового материала.
6. Физкультминутка
7. Работа по закреплению н. м. Решение задачи.
8. Повторение пройденного материала.
9. Итог урока.
10. Рефлексия
11. Домашнее задание.
Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.
ХОД УРОКА
I. Организационный момент

Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.

II. Устный счёт
– Посчитаем устно:
1) «Весёлые ромашки» (Слайды 3-7 таблица умножения)
2) Математическая разминка. Игра «Найди лишнее» (Слайд 8)
485      45       864        947     670 134   (классификация на группы ЛИШНЕЕ 45 – двузначное, 670 – в записи числа нет цифры 4).

9      45        72        90         54       81          27       22    18 (9 – однозначное, 22   не делится на 9)

Строка чистописания. Прописать в тетради числа, чередуя: 45     22   670     9
– Подчеркнуть самую аккуратную запись числа
III. Сообщение темы и задач урока. (Слайд 9)
– Запишите число, тему урока.
– Прочитайте задачи нашего урока
IV. Подготовка к изучению нового материала
а) Верно ли выражение
На доске запись:
(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7
– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное свойство?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок.

43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17

– Какие свойства сложения мы применяются в данном случае?
Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок. При этом вычисления можно выполнять в любом порядке.
– В таком случае как называется ещё одно свойство сложения? (Переместительное)

(2 * 6) * 3 = 12 * 3

– Вызывает ли это выражение затруднение? Почему?(Мы не умеем умножать двузначное число на однозначное)
V. Изучениенового материала
1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?

(2 * 6) * 3 = 2 * 3 * 6

2) Работа по учебнику с. 70, № 305 (Выскажи своё предположение о результатах, которые получат Волк и Заяц. Проверь себя, выполнив вычисления).
3) № 305. Проверь, равны ли значения выражений. Устно.
Запись на доске:

(5 • 2) • 3 и 5 • (2 • 3)
(4 • 7) • 5 и 4 • (7 • 5)

4) Сделай вывод. Правило.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на примерах
5) Коллективная работа
На доске: (8 • 3) • 2,     (6 • 3) • 3,     2 • (4 • 7)
VI. Физминутка
1) Игра «Зеркало». (Слайд 10)

Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.

2) Физминутка для глаз «Зоркие глазки».
– Закройте глаза на 7 секунд, посмотрите направо, затем налево, вверх, вниз, затем сделайте глазами 6 кругов по часовой стрелке, 6 кругов против часовой стрелки.
VII. Закрепление изученного
1) Работа по учебнику. решение задачи. (Слайд 11)
(с. 71, № 308) Прочитайте текст. Докажите, что это задача. (Есть условие, вопрос)
– Выделите условие, вопрос.
– Назовите числовые данные. (Три, 6, трёхлитровые)
– Что они обозначают? (Три ящика. 6 банок, в каждой банке по 3 литра сока)
– Какая это задача по структуре? (Составная задача, т. к. нельзя сразу ответить на вопрос задачи или для решения требуется составление выражения)
– Тип задачи? (Составная задача на последовательные действия))
– Решите задачу без краткой записи составлением выражения. Для этого используйте следующую карточку:
Карточка-помощница

  •  (  •  )

– В тетради решение задачи можно оформить следующим образом: (3 • 6) • 3
– Можем ли мы решить задачу в таком порядке?
Решение.
(3 • 6) • 3 = (3 • 3) • 6 = 9 • 6 = 54 (л).
3 • (3 • 6) = (3 • 3) • 6 = 9 • 6 = 54 (л )
Ответ: 54 литра сока во всех ящиках.
2) Работа в парах (по карточкам): (Слайд 12)
– Поставь знаки, не вычисляя:

(15 * 2) *4          15 * (2 * 4) (–Какое свойство?)
(8 * 9) * 6            7 * (9 * 6)
(428 * 2) * 0        1 * (2 * 3)
(3 * 4) * 2            3 + 4 + 2
(2 * 3) * 4          (4 * 2) * 3

Проверка: (Слайд 13)

(15 * 2) * 4      =   15 * (2 * 4)
(8 * 9) * 6       >     7 * (9 * 6)
(428 * 2) * 0   <     1 * (2 * 3)
(3 * 4) * 2       >      3 + 4 + 2
(2 * 3) * 4      =    (4 * 2) * 3

3) Самостоятельная работа (по учебнику)
(с. 71, № 307 – по вариантам)

1 в. (8 • 2) • 2 =           (6 • 2) • 3 =            (19 • 1) • 0 =
2 в. (7 • 3) • 3 =            (9 • 2) • 4 =            (12 • 9) • 0 =

Проверка:

1 в. (8 • 2) • 2 = 32         (6 • 2) •3 = 36            (19• 1) • 0 = 0.
2 в. (7 • 3) • 3 = 63         (9 • 2) • 4 = 72           (12 • 9) • 0 = 0

Свойства умножения: (Слайд 14).
Переместительное свойство

Сочетательное свойство

– Зачем нужно знать свойства умножения? (Слайд 15).
Чтобы быстро считать

Выбирать рациональный способ счета

Решать задачи

VIII. Повторение пройденного материала. «Ветряные мельницы». (Слайд 16, 17)
Числа 485, 583 и 681 увеличить на 38 и записать три числовых выражения (1 вариант)

Числа 583, 545 и 507 уменьшить на 38 и записать три числовых выражения (2 вариант)

485
+    38
523    583
+    38
621    681
+ 38
719
583
–    38
545 545
– 38
507 507
–   38
469
Учащиеся выполняют задания по вариантам (двое учащихся решают задания на дополнительных досках).
Взаимопроверка.
IХ. Итог урока
– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного свойства умножения?
Х. Рефлексия
– Кто считает, что понял смысл сочетательного свойства умножения? Кто доволен своей работой на уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы довольны своей работой, то поставьте руки на локти и покажите мне ладошки. А если вы были чем-то расстроены, то покажите мне обратную сторону ладошки.
XI. Информация о домашнем задании
– Какое домашнее задание вы бы хотели получить?
По выбору:
1. Выучить правило с. 70
2. Придумать и записать выражение на новую тему с решением
Оценки за урок.
Ассоциативное свойство сложения — примеры, определение, формула
LearnPracticeDownload
Ассоциативное свойство сложения — это свойство чисел, которое утверждает, что способ группировки трех или более чисел не меняет суммы этих чисел. Это означает, что сумма трех или более чисел остается неизменной независимо от того, как они сгруппированы. Давайте узнаем больше об ассоциативном свойстве сложения в этой статье.
1. Что такое ассоциативное свойство сложения?
2. Ассоциативное свойство формулы сложения
3. Ассоциативное свойство сложения и умножения
4. Часто задаваемые вопросы по ассоциативному свойству дополнения
Что такое ассоциативное свойство сложения?
Ассоциативное свойство сложения — это правило, которое гласит, что при сложении трех и более чисел мы можем сгруппировать их в любую комбинацию, и полученная сумма останется неизменной независимо от того, как они сгруппированы. В этом случае группировка относится к размещению скобок. Например, на приведенном ниже рисунке видно, что сумма чисел не меняется независимо от того, как сгруппированы слагаемые.
Ассоциативное свойство формулы сложения
Формула ассоциативности сложения показывает, что группировка чисел другим способом не влияет на сумму. Скобки, которые группируют числа, помогают упростить процесс сложения. Обратите внимание на следующую формулу для ассоциативного свойства сложения.
Давайте рассмотрим пример, чтобы понять и доказать формулу. Сгруппируем 13 + 7 + 3 тремя способами.
Шаг 1: Мы можем сгруппировать набор чисел как (13 + 7) + 3, 13 + (7 + 3) и (13 + 3) + 7.
Шаг 2: Сложите первый набор чисел, то есть (13 + 7) + 3. Далее это можно решить как 20 + 3 = 23.
Шаг 3: Добавьте второй набор, т. е. 13 + (7 + 3) = 13 + 10 = 23.
Шаг 4: Теперь решите третий набор, то есть (13 + 3) + 7 = 16 + 7 = 23.
Шаг 5: Сумма всех трех выражений равна 23. Это показывает, что как бы мы ни группировали числа с помощью скобок, сумма остается неизменной.
Ассоциативное свойство сложения и умножения
Ассоциативное свойство применимо к сложению и умножению, но не существует к вычитанию и делению. Мы знаем, что ассоциативное свойство сложения говорит о том, что группировка чисел не меняет суммы данного набора чисел. Это означает, что (7 + 4) + 2 = 7 + (4 + 2) = 13. Точно так же ассоциативное свойство умножения говорит о том, что группировка чисел не меняет произведения данного набора чисел. Эта формула выражается как (a × b) × c = a × (b × c). Например, (2 × 3) × 4 = 2 × (3 × 4) = 24,9.0003
Важные примечания:
Ассоциативность применима только к сложению и умножению.
Ассоциативные свойства соответствуют возможности связывать или группировать числа, что невозможно в случае вычитания и деления.
Ассоциативное свойство входит в список математических свойств, полезных при работе с математическими уравнениями и их решениями.
☛ Похожие темы
Свойства дополнения
Коммутативное свойство сложения
Нулевое свойство умножения
Свойство мультипликативной идентичности
Распределительная собственность
Коммутативное свойство
Аддитивная идентичность против мультипликативной идентичности
Распределительная собственность
Ассоциативное свойство дополнительных рабочих листов

Ассоциативное свойство примеров сложения
Пример 1: Следует ли данное уравнение ассоциативному свойству сложения?
(25 + 2) + 8 = 25 + (2 + 8)
Решение: Следующие шаги помогут выяснить, следует ли данное уравнение ассоциативному свойству сложения или нет:
Шаг 1: Складываем набор чисел, указанный в левой части, то есть (25 + 2) + 8 = 27 + 8 = 35,
Шаг 2: Теперь сложите набор чисел, указанный в правой части, то есть 25 + (2 + 8) = 25 + 10 = 35.
Мы видим, что сумма, полученная из левой части уравнения, равна сумме, полученной из правой части. Итак, уравнение следует ассоциативному свойству сложения.
Пример 2: Вставьте пропущенное число и напишите сумму:
7 + (10 + 6) = (7 + 10) + ___ = ___
Решение: Согласно ассоциативному свойству формулы сложения, a + (b + c) = (a + b) + c. Если мы подставим значения в эту формулу, мы получим 6 как пропущенное число, то есть 7 + (10 + 6) = (7 + 10) + 6 , а сумма равна 23.
Пример 3: Выберите правильный вариант для отсутствующего номера.
8 + (4 + 2) = (8 + ___) + 2
а) 4
б) 7
в) 6
Решение:
По ассоциативному свойству сложения: а + (b + c) = (a + b) + c. Подставляя значения в формулу: 8 + (4 + 2) = (8 + 4 ) + 2,
Следовательно, пропущенное число равно 4, потому что сумма обоих выражений равна 14,
Следовательно, правильный вариант (а).
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по ассоциативному свойству сложения

перейти к слайдуперейти к слайду
Часто задаваемые вопросы по ассоциативному свойству дополнения
Что такое ассоциативное свойство сложения?
Ассоциативное свойство сложения гласит, что независимо от того, как набор из трех или более чисел сгруппирован вместе, сумма остается неизменной. Группировка чисел осуществляется с помощью скобок. Формула для этого свойства выражается как, a + (b + c) = (a + b) + c = (a + c) + b. Например, если мы сгруппируем числа 3 + 4 + 5 как 3 + (4 + 5) или (3 + 4) + 5, сумма, которую мы получим из обоих наборов, равна 12.
Что является примером ассоциативного свойства сложения?
Ассоциативное свойство сложения гласит, что группировка чисел не меняет их суммы. Например, (75 + 81) + 34 = 156 + 34 = 190; и 75 + (81 + 34) = 75 + 115 = 190. Сумма обеих сторон равна 190.
В чем преимущество использования ассоциативного свойства сложения?
Преимущество ассоциативного свойства сложения заключается в том, что оно помогает формировать более мелкие компоненты, что упрощает вычисление сложения. Группировка чисел с помощью скобок облегчает процесс упрощения выражения.
Как проверить ассоциативность сложения?
Ассоциативность сложения легко проверить, сложив заданный набор чисел. Например, сгруппируем 6 + 7 + 8 двумя способами.
Шаг 1: Мы можем сгруппировать данный набор чисел как (6 + 7) + 8 и 6 + (7 + 8).
Шаг 2: Теперь давайте сложим первый набор чисел, то есть (6 + 7) + 8. В результате получится 13 + 8 = 21.
Шаг 3: Теперь добавим второй набор, т. е. 6 + (7 + 8) = 6 + 15 = 21,
Шаг 4: Сумма обоих выражений равна 21. Это доказывает ассоциативное свойство сложения, которое показывает, что независимо от того, как мы группируем числа с помощью скобок, сумма остается неизменной.
Всегда ли ассоциативное свойство сложения включает 3 или более чисел?
Да, ассоциативное свойство сложения всегда включает 3 или более чисел, потому что правило свойства гласит, что изменение группировки слагаемых не меняет суммы, а в случае только двух чисел мы не можем создавать группы.
Какова формула ассоциативного свойства сложения?
Формула ассоциативного свойства сложения утверждает, что сумма трех или более чисел остается неизменной независимо от того, как эти числа сгруппированы. Это выражается как, a + (b + c) = (a + b) + c = (a + c) + b.
В чем разница между коммутативным и ассоциативным свойством сложения?
Следующие пункты показывают разницу между коммутативным и ассоциативным свойством сложения:
Переместительное свойство сложения утверждает, что изменение порядка слагаемых не меняет сумму. Например, 4 + 6 = 6 + 4 = 10. Ассоциативное свойство сложения утверждает, что группировка чисел не меняет сумму. Например, 8 + (2 + 3) = (8 + 2) + 3 = 13.
Переместительное свойство сложения можно применять к двум числам, а ассоциативное свойство применимо к трем и более числам.
В коммутативном свойстве сложения порядок слагаемых не имеет значения, а в ассоциативном свойстве сложения не имеет значения группировка слагаемых.
Как ассоциативное свойство сложения используется в повседневной жизни?
Есть много мест, где мы можем применить ассоциативное свойство сложения. Например, если мы тратим 3 доллара на кекс, 6 долларов на мороженое и 2 доллара на конфеты, мы можем сложить стоимость предметов в любом порядке как 3 + (6 + 2) или (3 + 6). + 2. Оба выражения дают одну и ту же сумму, то есть 11. Это показывает ассоциативное свойство сложения, которое гласит, что независимо от того, как мы группируем 3 или более чисел, сумма остается неизменной.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Ассоциативное свойство сложения Рабочий лист
Рабочие листы по математике и
наглядный учебный план
Переместительное свойство — определение, примеры, формула
Переместительное свойство касается арифметических операций сложения и умножения. Это означает, что изменение порядка или положения двух чисел при их сложении или умножении не меняет конечный результат. Например, 4 + 5 дает 9, а 5 + 4 тоже дает 9.. Порядок сложения двух чисел не влияет на сумму. Та же концепция применима и к умножению. Свойство коммутативности не выполняется для вычитания и деления, так как конечные результаты совершенно другие после изменения порядка чисел.
1. Что такое коммутативная собственность?
2. Коммутативное свойство сложения
3. Коммутативное свойство умножения
4.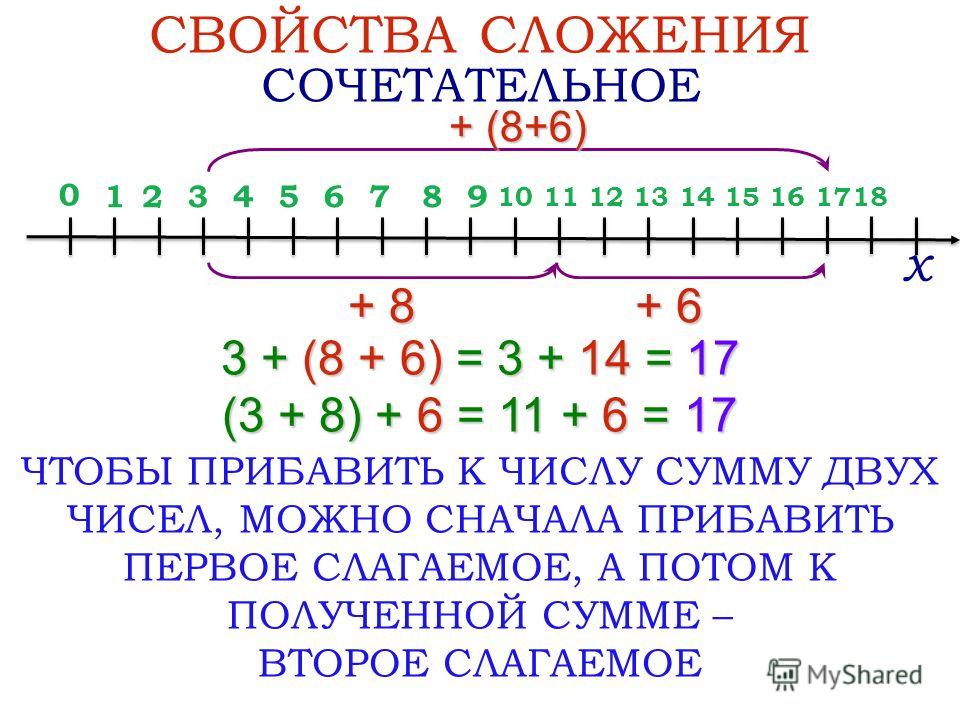 Коммутативное свойство против ассоциативного свойства
5. Часто задаваемые вопросы о коммутативном свойстве
Что такое коммутативное свойство?
Слово «коммутативный» происходит от слова «коммутировать», что означает передвигаться. Следовательно, свойство коммутативности связано с перемещением чисел. Таким образом, математически, если изменение порядка операндов не меняет результат арифметической операции, то эта конкретная арифметическая операция является коммутативной. Помимо этого, существуют и другие свойства чисел: ассоциативность, дистрибутивность и тождественность. Они отличаются от коммутативного свойства чисел. Кратко обсудим перестановочное свойство сложения и умножения.
Формула коммутативного свойства
Если даны два числа A и B, то формула коммутативного свойства чисел задается следующим образом:
A + B = B + A
А × В = В × А
А — В ≠ В — А
А ÷ В ≠ В ÷ А
Формула свойства коммутативности гласит, что изменение порядка двух чисел при их сложении и умножении не влияет на результат. Но при вычитании и делении любых двух действительных чисел порядок чисел важен и, следовательно, его нельзя изменить.
Коммутативное свойство сложения
Переместительное свойство сложения говорит о том, что изменение порядка слагаемых не меняет значения суммы. Если «A» и «B» — два числа, то свойство коммутативности сложения чисел может быть представлено, как показано на рисунке ниже.
Давайте возьмем пример коммутативного свойства сложения и поймем применение приведенной выше формулы. Если даны два числа 10 и 13, то 10 + 13 = 23 и 13 + 10 = 23. Следовательно, 10 + 13 = 13 + 10,
Коммутативное свойство умножения
Переместительное свойство умножения говорит о том, что порядок, в котором мы умножаем два числа, не меняет конечного произведения. Изображение, приведенное ниже, представляет коммутативное свойство умножения двух чисел.
Если 4 и 6 числа, то 4 × 6 = 24, а 6 × 4 также равно 24. Таким образом, 4 × 6 = 6 × 4. Следовательно, свойство коммутативности выполняется для умножения чисел.
Примечание: Свойство коммутативности не выполняется для операций вычитания и деления. Возьмем в качестве примера числа 6 и 2.
6 — 2 = 4, но 2 — 6 = -4. Таким образом, 6 — 2 ≠ 2 — 6.
6 ÷ 2 = 3, но 2 ÷ 6 = 1/3. Таким образом, 6 ÷ 2 ≠ 2 ÷ 6.
Коммутативное свойство против ассоциативного свойства
Есть четыре общих свойства чисел: замкнутость, коммутативность, ассоциативность и дистрибутивность. В этом разделе мы узнаем разницу между ассоциативным и коммутативным свойством. И ассоциативное, и коммутативное свойство утверждают, что порядок чисел не влияет на результат сложения и умножения. Итак, в чем разница между ними? Давай выясним.
Посмотрите на приведенную ниже таблицу, показывающую коммутативное и ассоциативное свойства.
Коммутативная собственность Ассоциативное свойство
Коммутативное свойство происходит от слова «коммутировать», что означает передвигаться, переключать или менять номера. Ассоциативное свойство происходит от слова «ассоциировать», которое имеет дело с группировкой чисел.
Порядок чисел может быть изменен в случае сложения и умножения двух чисел без изменения конечного результата. Группировка чисел может быть изменена в случае сложения и умножения трех чисел без изменения конечного результата.
Формула:
А + В = В + А
А × В = В × А
Формула:
А + (В + С) = (А + В) + С = (А + С) + В
А × (В × С) = (А × В) × С = (А × С) × В
Важные примечания:
Некоторые ключевые моменты, которые следует помнить о свойстве коммутативности, приведены ниже.
Коммутативное свойство утверждает, что «изменение порядка операндов не меняет результат».
Свойство коммутативности сложения: A + B = B + A.
Свойство коммутативности для умножения: A × B = B × A.
☛ Похожие темы
Ознакомьтесь с некоторыми интересными статьями, посвященными коммутативности в математике.
Свойства натуральных чисел
Свойства целых чисел
Свойства рациональных чисел
Свойства целых чисел

Примеры коммутативных свойств
Пример 1: Мать Джеки спросила его, является ли сложение двух натуральных чисел примером коммутативности. Можете ли вы помочь Джеки выяснить, является ли оно коммутативным или нет?
Решение:
Мы знаем, что свойство перестановочности сложения гласит, что изменение порядка слагаемых не меняет значения суммы. Если мы возьмем любые два натуральных числа, скажем, 2 и 5, то 2 + 5 = 7 = 5 + 2. Таким образом, сложение двух натуральных чисел является примером свойства коммутативности.
Пример 2: Найдите пропущенное значение: 132 × 121 = ___ × 132.
Решение:
Перестановочное свойство умножения утверждает, что если есть два числа x и y, то x × y = y × Икс. Если вы внимательно посмотрите на данное уравнение, то обнаружите, что здесь применимо свойство коммутативности. Если x = 132, а y = 121, то мы знаем, что 132 × 121 = 121 × 132.
∴ Недостающее число 121.
Пример 3: Укажите, является ли данное утверждение истинным или ложным.
«Деление 12 на 4 удовлетворяет свойству коммутативности.»
Решение:
Свойство коммутативности не выполняется для операции деления. Значит, данное утверждение неверно. Давайте проверим это.
12 ÷ 4 = 3
4 ÷ 12 = 1/3 = 0,33
⇒ 12 ÷ 4 ≠ 4 ÷ 12
∴ Данное утверждение неверно.
перейти к слайдуперейти к слайдуперейти к слайду
Разложите сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по коммутативной собственности

перейти к слайдуперейти к слайду
Часто задаваемые вопросы о коммутативном свойстве
Что такое коммутативное свойство в математике?
Свойство коммутативности гласит, что если порядок чисел поменять местами при выполнении сложения или умножения, сумма или произведение не изменится. Следует отметить, что свойство коммутативности справедливо только для сложения и умножения, но не для вычитания и деления. Например, 6 + 7 равно 13 и 7 + 6 также равно 13. Аналогично, 6 × 7 = 42 и 7 × 6 = 42.
Что такое коммутативное свойство сложения?
Согласно коммутативному свойству сложения, при сложении двух чисел в любом порядке сумма остается неизменной. Например, 3 + 9= 9 + 3 = 12.
Что такое коммутативное свойство умножения?
Согласно свойству перестановочности умножения порядок умножения чисел не меняет произведения. Например, 4 × 5 равно 20, а 5 × 4 также равно 20. Хотя порядок чисел изменился, произведение равно 20.
Можно ли использовать переместительное свойство для вычитания и деления?
Коммутативное свойство нельзя применять для вычитания и деления, поскольку изменение порядка чисел при выполнении вычитания и деления не дает того же результата. Например, 5 — 2 равно 3, тогда как 2 — 5 не равно 3. Точно так же 10, деленное на 2, дает 5, тогда как 2, деленное на 10, не дает 5. Следовательно, коммутативное свойство не верно для вычитания и деления.
В чем разница между коммутативной и ассоциативной собственностью?
Свойство коммутативности гласит, что изменение порядка двух чисел в операции сложения или умножения не меняет ни суммы, ни произведения. Коммутативное свойство сложения записывается как A + B = B + A. Коммутативное свойство умножения записывается как A × B = B × A. Ассоциативное свойство утверждает, что группировка или комбинация трех или более чисел, которые добавляются или умножение не меняет ни суммы, ни произведения. Ассоциативность сложения записывается как: (A + B) + C = A + (B + C) = (A + C) + B. Ассоциативность умножения записывается как (A × B) × C = A × (В × С) = (А × С) × В.
В чем разница между коммутативной собственностью и распределительной собственностью?
Свойство коммутативности гласит, что изменение порядка чисел в операции сложения или умножения не меняет результат. Перестановочное свойство сложения двух чисел «A» и «B» равно A + B = B + A. Распределительное свойство означает умножение числа на каждое число в скобках. Числа в скобках разделяются символом сложения или вычитания. Распределительное свойство сложения двух чисел «А», «В»: А(В + С) = АВ + АС.
Может ли коммутативное свойство иметь 3 числа?
Когда речь идет о группировке трех чисел, то это называется ассоциативным свойством, а не коммутативным свойством. Коммутативное свойство применимо к двум числам и гласит, что мы можем поменять местами эти два числа при их сложении или умножении без изменения результата.
Чем похожи коммутативные свойства сложения и умножения?
В обоих случаях, сложения и умножения, порядок чисел не влияет на сумму или произведение. Таким образом, свойство коммутативности верно для операций сложения и умножения.
Как научить коммутативному свойству сложения?
Лучший способ обучить перестановочному свойству сложения — это использовать предметы из реальной жизни, такие как камешки, игральные кости, семена и т. д. Дайте учащемуся 3 шарика, а затем еще 5 шариков ему/ей. Попросите ее/его посчитать общее количество шариков. Затем повторите тот же процесс сначала с 5 шариками, а затем с 3 шариками. Таким образом, учащиеся будут наблюдать это свойство самостоятельно. Используйте коммутативное свойство рабочих листов сложения, чтобы проверить их понимание.
Что такое коммутативные законы?
Коммутативное право — это еще одно слово, обозначающее коммутативное свойство, применимое к сложению и умножению. Коммутативный закон сложения гласит, что порядок сложения двух чисел не меняет суммы (A + B = B + A). Коммутативное свойство умножения гласит, что порядок умножения двух чисел не меняет произведения (A × B = B × A).
Переписывание выражений с использованием коммутативных и ассоциативных свойств
Результаты обучения
Определение ассоциативных и коммутативных свойств сложения и умножения
Использование ассоциативных и коммутативных свойств сложения и умножения для перезаписи алгебраических выражений
Подумайте о добавлении двух чисел, таких как [латекс]5[/латекс] и [латекс]3[/латекс].
[латекс]\begin{array}{cccc}\hfill 5+3\hfill & & & \hfill 3+5\hfill \\ \hfill 8\hfill & & & \hfill 8\hfill \end{array} [/латекс]
Результаты те же. [latex]5+3=3+5[/latex]
Обратите внимание, порядок добавления не имеет значения. То же самое верно и при умножении [латекс]5[/латекс] и [латекс]3[/латекс].
[латекс]\begin{array}{cccc}\hfill 5\cdot 3\hfill & & & \hfill 3\cdot 5\hfill \\ \hfill 15\hfill & & & \hfill 15\hfill \end{ array}[/latex]
Опять же, результаты те же! [латекс]5\cdot 3=3\cdot 5[/латекс]. Порядок, в котором мы умножаем, не имеет значения.
Эти примеры иллюстрируют коммутативные свойства сложения и умножения.
Коммутативные свойства
Коммутативное свойство сложения : если [латекс]а[/латекс] и [латекс]b[/латекс] — действительные числа, то
[латекс]а+b=b+а[/ латекс]
Коммутативное свойство умножения : если [латекс]а[/латекс] и [латекс]b[/латекс] — действительные числа, то
[латекс]а\cdot b=b\cdot a[/ латекс]
Коммутативные свойства связаны с порядком. Если изменить порядок чисел при сложении или умножении, результат будет тот же.
пример
Используйте коммутативные свойства, чтобы переписать следующие выражения:
1. [латекс]-1+3=[/латекс]
2. [латекс]4\cdot 9=[/латекс]
Решение:
1.
[латекс]-1+3=[/латекс]
Используйте свойство коммутативности сложения, чтобы изменить порядок. [латекс]-1+3=3+\влево(-1\вправо)[/латекс]
2.
[латекс]4\cdot 9=[/латекс]
Используйте свойство перестановочности умножения, чтобы изменить порядок. [латекс]4\cdot 9=9\cdot 4[/латекс]

попробуй
Как насчет вычитания? Имеет ли значение порядок, когда мы вычитаем числа? Дает ли [латекс]7 — 3[/латекс] тот же результат, что и [латекс]3 — 7?[/латекс]
[латекс]\begin{array}{ccc}\hfill 7 — 3\hfill & & \ hfill 3 — 7\hfill \\ \hfill 4\hfill & & \hfill -4\hfill \\ & \hfill 4\ne -4\hfill & \end{array}[/latex]
Результаты не совпадают. [latex]7 — 3\ne 3 — 7[/latex]
Поскольку изменение порядка вычитания не дало того же результата, можно сказать, что вычитание некоммутативно.
Давайте посмотрим, что произойдет, если мы разделим два числа. Является ли деление коммутативным?
[латекс]\begin{array}{ccc}\hfill 12\div 4\hfill & & \hfill 4\div 12\hfill \\ \hfill \frac{12}{4}\hfill & & \hfill \ frac{4}{12}\hfill \\ \hfill 3\hfill & & \hfill \frac{1}{3}\hfill \\ & \hfill 3\ne \frac{1}{3}\hfill & \ конец{массив}[/латекс]
Результаты разные. Итак, [latex]12\div 4\ne 4\div 12[/latex]
Поскольку изменение порядка деления не дало того же результата, деление не является коммутативным.
Сложение и умножение коммутативны. Вычитание и деление не коммутативны.
Предположим, вас попросили упростить это выражение.
[латекс]7+8+2[/латекс]
Как бы вы это сделали и каким был бы ваш ответ?
Некоторые люди могут подумать, что [латекс]7+8\текст{ равно }15[/латекс], а затем [латекс]15+2\текст{ равно }17[/латекс]. Другие могут начинаться с [латекс]8+2\текст{ дает }10[/латекс], а затем [латекс]7+10\текст{ дает }17[/латекс].
Оба способа дают одинаковый результат, как показано ниже. (Помните, что круглые скобки — это символы группировки, указывающие, какие операции следует выполнить в первую очередь.)

При добавлении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство сложения.
Тот же принцип справедлив и для умножения. Предположим, мы хотим найти значение следующего выражения:
[латекс]5\cdot \frac{1}{3}\cdot 3[/latex]
Изменение группировки чисел дает тот же результат.

При умножении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство умножения.
Если мы умножим три числа, изменение группировки не повлияет на произведение.
Вы, наверное, знаете это, но терминология может быть для вас новой. Эти примеры иллюстрируют ассоциативные свойства .
Ассоциативные свойства
Ассоциативное свойство сложения : если [латекс]а,б[/латекс] и [латекс]с[/латекс] — действительные числа, то
[латекс]\влево(а+б\вправо)+ c=a+\left(b+c\right)[/latex]
Ассоциативное свойство умножения : если [latex]a,b[/latex] и [latex]c[/latex] — действительные числа, затем
[latex]\left(a\cdot b\right)\cdot c=a\cdot \left(b\cdot c\right)[/latex]

пример
Используйте ассоциативные свойства для перезаписи следующее:
1. [латекс]\влево(3+0,6\вправо)+0,4=[/латекс]
2. [латекс]\влево(-4\cdot \frac{2}{5}\вправо)\cdot 15 =[/latex]
Показать решение

попробуйте
Помимо использования ассоциативных свойств для упрощения вычислений, мы часто будем использовать их для упрощения выражений с переменными.
пример
Используйте ассоциативное свойство умножения для упрощения: [латекс]6\влево(3х\вправо)[/латекс].
Показать раствор

попробуйте
В следующем видеоролике представлены дополнительные примеры упрощения выражений с использованием коммутативных и ассоциативных свойств умножения и сложения.

Что такое коммутативное свойство сложения? Определение, примеры
Сложение — это первый арифметический оператор, о котором учащиеся узнают при изучении элементарной математики. Сложение, как следует из названия, является простой темой, а также закладывает основу для умножения и некоторых многозначных арифметических операций. Одним из очень интересных свойств сложения является коммутативность.
Возьмем пример.
Предположим, у вас есть 3 яблока и 2 апельсина.
Как найти общее количество фруктов, которые у вас есть?
Сложите 3 и 2 и получите 5.
Но как вы думаете, получился бы другой ответ, если бы мы взяли сначала апельсины, а потом яблоки?
Нет, общее количество фруктов осталось прежним. Это 5.
И это интересное свойство коммутативности для сложения.
Что такое коммутативное свойство сложения?
«Коммутировать» означает путешествовать или передвигаться. Переместительное свойство сложения гласит, что изменение порядка слагаемых чисел не влияет на сумму. Мы можем определить коммутативное свойство сложения, так как сложение чисел в любом порядке даст один и тот же ответ.
Здесь a и b могут быть целыми, целыми, десятичными и даже дробными числами.
Коммутативное свойство сложения Примеры:
15 + 16 = 16 + 15 = 31
4 + (–6) = (–6) + 4 = (–2)
0,5 + 0,6 = 0,6 + 0,5 = 1,1
$\frac{1} {5}$ $+$ $\frac{2}{5}$ $=$ $\frac{2}{5}$ $+$ $\frac{1}{2}$ $=$ $\frac{ 3}{5}$
Другие операторы также соблюдают закон коммуникативности?
Не совсем так. Закон коммутативности можно применить только к понятиям сложения и умножения.
Допустим, мы хотим решить выражение 3 умножить на 4 или 3 ✕ 4.
Мы можем просто пропустить счет на 4 три раза, и мы получим 12.
Точно так же мы можем найти впадину 4 умножить на 3 или 4 ✕ 3, и мы снова получим 12.
Итак, изменение порядка умножения чисел на самом деле не изменило произведение.
Следовательно, умножение подчиняется закону коммутативности.
Однако, если мы говорим о вычитании, изменение порядка чисел в уравнении вычитания абсолютно изменит результат. Давайте разберемся с этим на примере.
Вычтем 3 из 4.
4 – 3 = 1
Теперь, если мы изменим порядок чисел,
3 – 4 = (-1)
Ну, числа не обязаны со всем соглашаться все время, да?
Деление, будучи самым капризным из всех наших операторов, которому нужно помнить так много, не следует закону коммутативности.
Решенные примеры
Пример 1. Проверьте, что «a + b = b + a», если a = 33 и b = 30.
Решение:
Подстановка значений в левой части уравнения,
a + b = 33 + 30 = 63
Подстановка значений в правой части уравнения,
b + a = 30 + 33 = 63
Таким образом, проверяется, что a + b = b + a.
Пример 2: Заполните заготовки:

20 + _ = _ + 20 = 55
: + 20 = 55
: + 55
: +0006
Поскольку результат тот же, уравнение должно обладать свойством коммутативности.
Итак, пропущенное число можно представить как «b».
Теперь у нас есть
20 + b = 55,
Следовательно, b = 55 – 20 = 35.
Пример 3. Докажите на примере, почему вычитание неприменимо для перестановочного закона?
Решение: Возьмем два числа: 3 и 5 .
Если из 5 вычесть 3, то получится 2 .
Но если мы обратим порядок и вычтем 5 из 3 , мы получим результат как – 2 .
Следовательно, свойство коммутативности не применяется к вычитанию, так как изменение порядка меняет ответ.
Пример 4: Какая из следующих дробей демонстрирует свойство коммутативности с $\frac{1}{3}$ $+$ $\frac{1}{2}$ ?
$\frac{1}{2}$ $\times $ $\frac{1}{3}$
$\frac{1}{3}$ $\div$ $\frac{1} {2}$
$\frac{1}{2}$ $+$ $\frac{1}{3}$
$\frac{1}{3}$ $-$ $\frac{1}{2}$
Решение: (c) $\frac{1}{2}$ $+$ $\frac{1}{3}$
По закону коммутативности сложения , $\frac{1}{ 2}$ $+$ $\frac{1}{3}$ даст тот же результат, что и $\frac{1}{3}$ $+$ $\frac{1}{2}$.
Практические задачи
42
67
39
81
Правильный ответ: 67
Используя свойство перестановочности сложения,
a + b = b + a,
Следовательно, 39 + 67 = 67 + 39,
Следовательно, пропущенное число равно 67.
c = a +b
a (b + c) = a ✕ b + b ✕ c
a + b = b + a
a + (b+c) = a+c
Правильный ответ: a + b = b + a
Закон кумулятивности утверждает, что в уравнении сложения изменение порядок чисел по-прежнему дает тот же результат.
Следовательно, a + b = b + a.
23
26
25
27
Правильный ответ: 25
Поскольку результат тот же, уравнение должно следовать свойству коммутативности.
Таким образом, мы можем представить пропущенное число как «b».
Теперь мы имеем
23 + B = 48,
Следовательно, B = 48 — 23 = 25.
5.009
5,990
3,789
1.22
Правильный ответ: 5,009
по закону о коммерческом. + 3,789 = 3,789 + 1,22 = 5,009
Часто задаваемые вопросы
Применяется ли свойство перестановочности сложения к дробям?
Да, согласно коммутативному свойству сложения, a + b = b + a для любых чисел a и b.
Существует ли коммутативное свойство для вычитания?
Нет, операции вычитания и деления не подчиняются законам коммутативности.
Каковы свойства операции сложения?
Три свойства сложения являются коммутативными: для любых двух чисел a и b, a + b = b + a.
Ассоциативное свойство: Для любых трех чисел a, b и c, a + (b + c) = (a + b) + c.
Свойство идентичности: для каждого числа a, a + 0 = a.
Сложение и умножение в математике. Коммутативное свойство и ассоциативное свойство преподаются в начальной или средней школе.
Свойство коммутативности и ассоциативности действительны для сложения и умножения. Коммутативность и ассоциативность не могут быть установлены вычитанием и делением. Однако вычитание можно преобразовать в сложение, а деление — в умножение. Это означает, что мы можем использовать эти правила во всех вычислениях.
В математике важно понимать эти правила. Понимание коммутативности и ассоциативности позволит нам выполнять все виды вычислений. Хотя мы больше не используем деление в математике в младших классах средней школы и выше, свойство коммутативности и свойство ассоциативности могут помочь нам понять, почему это так.
Мы объясним, как понимать и применять коммутативный закон и ассоциативный закон.
Содержание
1 Обзор коммутативного закона и ассоциативного закона
2 В коммутативном свойстве замена чисел дает тот же ответ
2.1 Разве коммутативное свойство не устанавливается вычитанием и делением?
2.2 Изменив знаки и сделав их отрицательными числами, установлено свойство коммутативности
3 Ассоциативное свойство, позволяющее менять местами скобки
3.1 Ассоциативный закон позволяет производить вычисления в любом месте
3. 2 Формулы вычитания и деления устанавливаются изменением знака
4 Использование умножения дробей вместо деления в математике
5 Упражнения: коммутативное и ассоциативное свойство положительных и отрицательных чисел
6 Изучите определение Закона и его использование в формулах
Обзор коммутативного права и ассоциативного права
Какие свойства перестановочности и ассоциативности мы изучаем в начальной или средней школе? Они следующие.
Коммутативное свойство: закон, который дает тот же ответ, даже если числа поменять местами.
Ассоциативное свойство: закон, который дает тот же ответ, даже если вы меняете место в скобках.
Что касается коммутативности и ассоциативности, которые используются во многих ситуациях, они необходимы при решении математических задач. Эти законы используются при сложении и умножении. Но на практике их также можно применять для вычитания и деления.
Другими словами, мы можем использовать коммутативность и ассоциативность во всех вычислениях. Это делает его удобным, и эти законы полезны для всех, в том числе для тех, кто занимается математическими расчетами в средней школе, колледже и даже в деловом мире.
В переместительном свойстве замена чисел дает тот же ответ
В переместительном свойстве, если вы поменяете числа местами, ответ будет таким же. Закон коммутативности выполняется сложением.
Например, у нас есть следующее.
Неважно, как вы переставите порядок; это называется коммутативным свойством сложения.
То же верно и для умножения. Свойство коммутативности выполняется не только при сложении, но и при умножении. Как показано ниже, ответ будет таким же при умножении, даже если числа поменять местами.
Неважно, как вы умножаете, и это называется коммутативным свойством умножения.
Разве коммутативное свойство не устанавливается вычитанием и делением?
Однако сказано, что коммутативный закон не действует для вычитания и деления. Давайте попробуем посчитать, поменяв числа местами.
Например, если мы поменяем местами числа при вычитании, мы получим следующее.
Таким образом, ответы разные. В одном уравнении ответ равен 2, а в другом уравнении ответ равен -2. Так как мы вычитаем разные числа, то и ответы, естественно, будут разными. Вот почему говорят, что коммутативность недействительна при вычитании.
То же самое верно и для деления. В случае деления дело обстоит следующим образом.
Если мы воспользуемся свойством коммутативности при делении, ответ изменится следующим образом. Следовательно, свойство коммутативности при делении не выполняется.
Изменение знаков и превращение их в отрицательные числа. Установлено свойство коммутативности
Если свойство коммутативности справедливо только для сложения и умножения, вы можете подумать, что оно бессмысленно, поскольку его применение ограничено. Однако коммутативный закон, который мы изучаем в математике начальной школы или средней школы, очень важен.
Почему свойство коммутативности так важно, хотя оно применимо только к сложению и умножению? Это потому, что при замене вычитания на сложение свойство коммутативности становится действительным. Для деления свойство коммутативности также устанавливается заменой его на умножение.
Сложение и вычитание одинаковы. Вычитание можно преобразовать в сложение. Например, ниже приведены все те же уравнения и тот же ответ.
$4-2=2$
$4+(-2)=2$
Как только вы выучите положительные и отрицательные числа, вы поймете, что сложение и вычитание — это одно и то же.
Как упоминалось выше, свойство коммутативности справедливо для сложения. Таким образом, заменяя вычитание сложением отрицательных чисел, устанавливается коммутативный закон.
Важен тот факт, что свойство коммутативности справедливо даже для отрицательных чисел. Ранее мы объяснили, что свойство коммутативности не устанавливается для вычитания. На самом деле, однако, мы можем использовать свойство коммутативности сложения даже для вычитания, потому что закон коммутативности устанавливается путем замены вычитания сложением.
— Использование дробей при делении и использование свойства перестановочности
То же самое верно и для деления. Преобразовав деление в умножение, мы можем использовать коммутативное свойство умножения.
Как превратить деление в умножение? Это делается с помощью дробей. Используя обратные числа, мы можем преобразовать деление в умножение дробей, как показано ниже.
Как упоминалось выше, свойство коммутативности справедливо при умножении. Как показано ниже, ответ будет таким же при умножении, даже если это дробь.
Если вы хотите изменить вычитание на сложение, вам просто нужно изменить знаки плюс и минус. Однако в случае деления вы должны изменить его на дроби. Это требует немного работы. В любом случае, вы можете использовать свойство коммутативности даже при делении.
Ассоциативное свойство, позволяющее менять место скобок
Когда мы изучаем коммутативное свойство, мы также изучаем ассоциативное свойство. Какой закон является ассоциативным законом?
Ассоциативность позволяет нам свободно менять место скобок. Как и коммутативное свойство, ассоциативное свойство действует только для сложения и умножения. Как показано ниже, ответ остается тем же, даже если мы дополнительно изменим положение скобок.
В математике принято сначала вычислять в скобках. Неважно, где дополнительно расставлены скобки.
Точно так же свойство ассоциативности действительно для умножения.
Почему действует ассоциативный закон? Это потому, что значение одинаково независимо от того, присутствуют скобки или отсутствуют. Ответ тот же, даже если убрать скобки следующим образом.
Ответ один и тот же, где бы вы ни поставили скобки, потому что не имеет значения, есть скобки или нет. Ассоциативность — это всего лишь закон очевидного.
Ассоциативный закон позволяет считать где угодно
Ассоциативность — это, по сути, закон, который можно вычислять где угодно. Например, при выполнении умножения вы должны были вычислить числа в другом порядке. Например, как бы вы сделали следующий расчет?
$2×6×13$
Слева направо расчеты следующие.
$\textcolor{red}{2×6}×13=\textcolor{red}{12}×13=156$
Вам нужно рассчитать $12×13$, что усложняет расчет. Итак, давайте воспользуемся ассоциативным свойством и изменим порядок чисел. Например, вместо $2×6×13$ мы меняем уравнение на $6×13×2$. В этом случае мы получаем следующее.
$\textcolor{red}{6×13}×2=\textcolor{red}{78}×2=156$
Таким образом, вычисление упрощается; меньше ошибок вычислений при умножении чисел с меньшим количеством цифр, чем при умножении чисел с двумя цифрами.
Формулы вычитания и деления устанавливаются изменением знака
Ассоциативность действительна для выражений сложения и умножения. Это то же самое, что коммутативное свойство, которое нельзя применить к вычитанию и делению. Например, при вычитании замена скобок изменит ответ следующим образом.
Если в уравнении есть скобки, мы должны сначала вычислить внутреннюю часть скобок. Поэтому при вычитании ответ изменяется с помощью ассоциативного свойства.
То же самое происходит и при делении. Ответ меняется при изменении положения скобок, как показано ниже.
Для вычитания и деления свойство ассоциативности недействительно.
— Вычисление путем сложения или умножения
Однако на практике не имеет значения, происходит ли вычитание или деление. Как и свойство коммутативности, вычитание можно преобразовать в сложение, а деление — в умножение. Результат следующий.
Его можно преобразовать в уравнение сложения или умножения, чтобы установить свойство ассоциативности. Ответ один и тот же, где бы вы ни поставили скобки. Другими словами, вы можете сначала выполнить расчет из любого места.
Обычно ассоциативное свойство недоступно для вычитания и деления. Однако, преобразовав его в уравнения сложения или умножения, ассоциативный закон становится справедливым. Поэтому свойство ассоциативности является правилом, которое можно использовать во всех расчетах.
Использование умножения дробей вместо деления в математике
Зачем нам нужно понимать свойства перестановочности и ассоциативности, в том числе в математике в начальной и средней школе? Это потому, что они необходимы для упрощения расчетов. Понимание свойств коммутативности и ассоциативности особенно важно для вычислений деления.
При преобразовании вычитания в сложение метод прост. Просто сделайте сложение, а затем сделайте его отрицательным числом. Это происходит следующим образом.
$2\textcolor{red}{-3}=2\textcolor{red}{+(-3)}$
С другой стороны, деление нельзя вычислить как есть. Чтобы заменить деление на умножение, нужно заменить его на умножение дробей. Используя обратные выражения, мы должны изменить форму.
$2\textcolor{red}{÷3}=2\textcolor{red}{×\displaystyle\frac{1}{3}}$
Сделав выражение только умножением, мы можем вычислять откуда угодно.
Мы не используем деление в математике в средней школе и выше, потому что свойства коммутативности и ассоциативности недействительны. Вместо этого мы вычисляем после преобразования деления в дроби.
Также в случае деления во многих случаях числа неделимы. С дробями, с другой стороны, вы можете получить ответ, даже если не можете делить. Важно понимать, что деление бесполезно и редко используется в математике.
Причина, по которой все мы преобразуем деление в умножение в средней школе и выше по математике, заключается в том, что мы можем использовать коммутативные и ассоциативные свойства. Это значительно упрощает расчеты и снижает вероятность ошибок в расчетах.
Упражнения: коммутативное и ассоциативное свойство положительных и отрицательных чисел
Q1: Выполните следующие вычисления.
$(6 ÷ 15) × 5$
$-4 ÷ 3 ÷ 6 × 15$
A1: Ответы.
Для сложения и вычитания вы можете без проблем решать задачи, используя коммутативный закон и ассоциативный закон. С другой стороны, если задействовано деление, вам нужно преобразовать его в умножение дробей. Поэтому используйте обратные числа и превратите их в дроби.
(a)
$(6\textcolor{red}{÷15})×5$
$＝(6\textcolor{red}{×\displaystyle\frac{1}{15}}) ×5$
$=6×\displaystyle\frac{1}{3}=2$
При делении мы всегда переводим его в умножение дробей. Затем в этом расчете мы сначала вычисляем $\displaystyle\frac{1}{15}×5=\displaystyle\frac{1}{3}$. Это проще вычислить, чем $6×\displaystyle\frac{1}{15}$.
(б)
$-4÷3÷6×15$
$=-4×\displaystyle\frac{1}{3}×\displaystyle\frac{1}{6}×15$
$=\textcolor{red}{-4×\displaystyle\frac{1}{6}}×\textcolor{blue}{\displaystyle\frac{1}{3}×15}$
$=\ textcolor{red}{-\displaystyle\frac{2}{3}}×\textcolor{blue}{5}$
$=-\displaystyle\frac{10}{3}$
Сначала мы преобразуем деление в умножение дробей. Затем, используя свойства коммутативности и ассоциативности, числа меняются местами, чтобы упростить вычисления.
Расчет с $-4×\displaystyle\frac{1}{3}$ и $\displaystyle\frac{1}{6}×15$ затруднен. Также трудно умножить две дроби.
С другой стороны, $-4 × \displaystyle\frac{1}{6}$ и $\displaystyle\frac{1}{3} × 15$ позволяют уменьшить число, упрощая вычисления. В уравнении, состоящем только из умножения, вы можете свободно менять местами числа. Таким образом, мы используем коммутативный закон и ассоциативный закон.
Изучите определение закона и используйте его в формулах
В математике есть несколько законов. Одним из таких законов является коммутативность и ассоциативность. Зачем нам нужно понимать эти правила? Причина в том, что законы облегчают вычисление выражений и уменьшают ошибки вычислений.
Одними из наиболее важных законов математики, которыми мы все пользуемся, являются свойство коммутативности и свойство коммутативности. Даже в начальной школе математики мы все используем свойство коммутативности и свойство коммутативности.
Однако, чтобы использовать законы в математических формулах, нам нужно понимать правила и определения. Коммутативность и коммутативность действительны только для уравнений со сложением или умножением. Поэтому, если есть вычитание или деление, преобразуйте их в сложение или умножение. Обратите внимание, что вычитание легко изменить, но с делением вы должны изменить его на дроби.
Кроме того, если вы изучите коммутативный закон и ассоциативный закон, вы поймете, почему никто не использует деление в математике в младших классах средней школы и выше. Разделение бесполезно. Обязательно используйте обратное число и преобразуйте его в умножение дробей, прежде чем выполнять вычисления.
Ранжирование
Потребности, желания и требования: три основных понятия в маркетинге (с примерами)
ЯМР-связь бензольных колец: орто-мета-пик и химические сдвиги
Квадрат и вычитание : Расчет фракций и квадратных корней
Тонкослойная хроматография (ТСХ): принципы, значения Rf и проявляющий растворитель
Межмолекулярные силы: сила Ван-дер-Ваальса, водородная связь, гидрофобный эффект
7.2: Коммутативные и ассоциативные свойства (Часть 1)
Последнее обновление
Сохранить как PDF
Идентификатор страницы
5034
OpenStax
OpenStax
Цели обучения
Использование коммутативных и ассоциативных свойств
Вычисление выражений с использованием коммутативных и ассоциативных свойств
Упрощение выражений с помощью коммутативных и ассоциативных свойств
будь готов!
Прежде чем приступить к работе, пройдите этот тест на готовность.
Упрощение: 7y + 2 + y + 13. Если вы пропустили эту задачу, просмотрите пример 2.3.10.
Умножить: $\dfrac{2}{3} \cdot 18$. Если вы пропустили эту проблему, просмотрите пример 4.3.10.
Найдите противоположное число 15. Если вы пропустили эту задачу, просмотрите пример 3.1.3.
В следующих нескольких разделах мы рассмотрим свойства действительных чисел. Многие из этих свойств будут описывать вещи, которые вы уже знаете, но это поможет дать имена свойствам и определить их формально. Таким образом, мы сможем ссылаться на них и использовать их при решении уравнений в следующей главе.
Использование коммутативных и ассоциативных свойств
Подумайте о сложении двух чисел, например 5 и 3.
\[\begin{split} 5 &+ 3 \qquad 3 + 5 \\ &\; 8 \qquad \qquad 8 \end{split}\]
Результаты те же. 5 + 3 = 3 + 5
Обратите внимание, порядок сложения не имеет значения. То же верно и при умножении 5 и 3.
\[\begin{split} 5 &\cdot 3 \qquad \; 3 \cdot 5 \\ & 15 \qquad \quad 15 \end{split}\]
Опять же, результаты те же! 5 • 3 = 3 • 5. Порядок умножения не имеет значения. Эти примеры иллюстрируют коммутативные свойства сложения и умножения.
Определение: коммуникативные свойства
Коммутативное свойство сложения: если a и b — действительные числа, то a + b = b + a
Коммутативное свойство умножения: если a и b — действительные числа, то a • b = b • a
Коммутативные свойства связаны с порядком. Если изменить порядок чисел при сложении или умножении, результат будет тот же.
Пример $\PageIndex{1}$:
Используйте коммутативные свойства, чтобы переписать следующие выражения: (a) −1 + 3 = _____ (b) 4 • 9= _____
Решение
(a) −1 + 3 = _____
Используйте свойство коммутативности сложения, чтобы изменить порядок. -1 + 3 = 3 + (-1)
(b) 4 • 9 = _____
Используйте свойство коммутативности умножения, чтобы изменить порядок. 4 • 9 = 9 • 4
Упражнение $\PageIndex{1}$:
Используйте коммутативные свойства, чтобы переписать следующие выражения: (a) −4 + 7 = _____ (b) 6 • 12 = _____
Ответить на
$-4+7=7+(-4)$
Ответ б
$6 \cdot 12=12 \cdot 6$
Упражнение $\PageIndex{2}$:
Воспользуйтесь коммутативными свойствами, чтобы переписать следующие выражения: (a) 14 + (-2) = _____ (b) 3(-5) = _____
Ответ
$14+(-2)=-2+14$
Ответ б
$3(-5)=(-5) 3$
Как насчет вычитания? Имеет ли значение порядок, когда мы вычитаем числа? Дает ли 7 — 3 тот же результат, что и 3 — 7?
\[\begin{split} 7 &- 3 \qquad 3 — 7 \\ &\; 4 \qquad \quad -4 \\ & \quad 4 \neq -4 \end{split}\]
Результаты не совпадают. 7 − 3 ≠ 3 − 7
Поскольку изменение порядка вычитания не дало того же результата, можно сказать, что вычитание не коммутативно. Давайте посмотрим, что происходит, когда мы делим два числа. Является ли деление коммутативным?
\[\begin{split} 12 &\div 4 \qquad 4 \div 12 \\ & \dfrac{12}{4} \qquad \quad \dfrac{4}{12} \\ &\; 3 \qquad \qquad \dfrac{1}{3} \\ &\quad \; 3 \neq \dfrac{1}{3} \end{split}\]
Результаты не совпадают. Итак, 12 ÷ 4 ≠ 4 ÷ 12
Поскольку изменение порядка деления не дало того же результата, деление не является коммутативным.
Сложение и умножение коммутативны. Вычитание и деление не коммутативны.
Предположим, вас попросили упростить это выражение.
\[7 + 8 + 2\]
Как бы вы это сделали и каким был бы ваш ответ?
Некоторые люди думают, что 7 + 8 равно 15, а затем 15 + 2 равно 17. Другие могут начать с 8 + 2, что дает 10, а затем 7 + 10 дает 17.
Оба способа дают одинаковый результат, как показано на рисунке \ (\PageIndex{1}\). (Помните, что круглые скобки — это символы группировки, указывающие, какие операции следует выполнить в первую очередь.)
Рисунок $\PageIndex{1}$
При добавлении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство сложения.
Тот же принцип применим и к умножению. Предположим, мы хотим найти значение следующего выражения:
\[5 \cdot \dfrac{1}{3} \cdot 3\]
Изменение группировки чисел дает тот же результат, как показано на рисунке \ (\PageIndex{2}\).
Рисунок $\PageIndex{2}$
При умножении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство умножения.
Если мы умножим три числа, изменение группировки не повлияет на произведение. Вы, вероятно, знаете это, но терминология может быть новой для вас. Эти примеры иллюстрируют ассоциативные свойства .
Определение: Ассоциативные свойства
Ассоциативное свойство сложения: если a, b и c — действительные числа, то (a + b) + c = a + (b + c)
Ассоциативное свойство умножения: если a, b и c — действительные числа, тогда (a • b) • c = a • (b • c)
Пример $\PageIndex{2}$:
Используйте ассоциативные свойства, чтобы переписать следующее: (a) (3 + 0,6) + 0,4 = __________ (b) $\left(−4 \cdot \dfrac {2}{5}\right) \cdot 15$ = __________
Решение
(a) (3 + 0,6) + 0,4 = __________
Изменить группировку. (3 + 0,6) + 0,4 = 3 + (0,6 + 0,4)
Обратите внимание, что 0,6 + 0,4 равно 1, поэтому сложение будет проще, если мы сгруппируем, как показано справа.
(b) $\left(−4 \cdot \dfrac{2}{5}\right) \cdot 15$ = __________
Измените группировку. (3 + 0,6) + 0,4 = 3 + (0,6 + 0,4)
Обратите внимание, что $\dfrac{2}{5} \cdot 15$ равно 6. Умножение будет проще, если мы сгруппируем, как показано справа.
Упражнение $\PageIndex{3}$:
Используйте ассоциативные свойства, чтобы переписать следующее: (a) (1 + 0,7) + 0,3 = __________ (b) (−9 • 8) • $\dfrac {3}{4}$ = __________
Ответить на
$(1+0,7)+0,3=1+(0,7+0,3)$
Ответ б
$(-9 \cdot 8) \cdot \frac{3}{4}=-9\left(8 \cdot \frac{3}{4}\right)$
Упражнение $\PageIndex{4}$:
Используйте ассоциативные свойства, чтобы переписать следующее: (a) (4 + 0,6) + 0,4 = __________ (b) (−2 • 12) • $\dfrac {5}{6}$ = __________
Ответ на
$(4+0,6)+0,4=4+(0,6+0,4)$
Ответ б
$(-2 \cdot 12) \cdot \frac{5}{6}=-2\left(12 \cdot \frac{5}{6}\right)$
Помимо использования ассоциативных свойств для облегчения вычислений, мы часто будем использовать их для упрощения выражений с переменными.
Пример $\PageIndex{3}$:
Используйте ассоциативное свойство умножения для упрощения: 6(3x).
Решение
Изменить группировку. (6 • 3)х
Умножить в скобках. 18x
Обратите внимание, что мы можем умножить 6 • 3, но мы не можем умножить 3 • x, не зная значения x.
Упражнение $\PageIndex{5}$:
Используйте ассоциативное свойство умножения, чтобы упростить данное выражение: 8(4x).
Ответить
$32x$
Упражнение $\PageIndex{6}$:
Используйте ассоциативное свойство умножения, чтобы упростить данное выражение: −9(7y).
Ответить
$-63г$
Вычисление выражений с использованием коммутативных и ассоциативных свойств
Коммутативные и ассоциативные свойства могут упростить вычисление некоторых алгебраических выражений. Поскольку при добавлении или умножении трех или более терминов порядок не имеет значения, мы можем изменить порядок и перегруппировать термины, чтобы упростить нашу работу, как показано в следующих нескольких примерах.
Пример $\PageIndex{4}$:
Вычислить каждое выражение, когда x = $\dfrac{7}{8}$. (a) x + 0,37 + (− x) (b) x + (− x) + 0,37
Раствор
(a) x + 0,37 + (− x)
Замена $\dfrac {7}{8}$ для х. $$\textcolor{red}{\dfrac{7}{8}} + 0,37 + \left(- \textcolor{red}{\dfrac{7}{8}}\right)$$
Преобразование дробей в десятичные. 0,875 + 0,37 + (-0,875)
Добавить слева направо. 1,245 — 0,875
Вычесть. 0,37
(b) x + (− x) + 0,37
Подставьте $\dfrac{7}{8}$ вместо x. $$\textcolor{red}{\dfrac{7}{8}} + \left(- \textcolor{red}{\dfrac{7}{8}}\right) + 0,37$$
Сначала добавьте противоположности. 0,37
В чем разница между частью (а) и частью (б)? Только порядок изменился. По коммутативному свойству сложения x + 0,37 + (− x) = x + (− x) + 0,37. Но разве часть (б) не была намного проще?
Упражнение $\PageIndex{7}$:
Оценить каждое выражение, когда y = $\dfrac{3}{8}$: (a) y + 0,84 + (− y) (b) y + (- у) + 0,84.
Ответить на
$0,84$
Ответ б
$0,84$
Упражнение $\PageIndex{8}$:
Оцените каждое выражение, когда f = $\dfrac{17}{20}$: (a) f + 0,975 + (− f) (b) f + (-f) + 0,975.
Ответить на
$0,975$
Ответ б
$0,975$
Давайте сделаем еще один, на этот раз с умножением.
Пример $\PageIndex{5}$:
Оценить каждое выражение при n = 17. (a) $\dfrac{4}{3} \left(\dfrac{3}{4} n\right )$ (b) $\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) n$
Решение
(a) $\dfrac{4}{3} \left(\dfrac{3}{4} n\right)$
Подставьте 17 вместо n. $$\dfrac{4}{3} \left(\dfrac{3}{4} \cdot \textcolor{red}{17} \right)$$
Сначала умножить в скобках. $$\dfrac{4}{3} \left(\dfrac{51}{4}\right)$$
Умножить еще раз. $$17$$
(b) $\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) n$
.
Замените n на 17. $$\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) \textcolor{red}{\cdot 17}$$
Умножить. Произведение обратных величин равно 1, $$(1) \cdot 17$$
Умножить еще раз.

admin
Навигация по записям
Ментальная математика что это такое ютуб: Урок 2 «Сложение в пятерке и десятке» | Ментальная арифметика — YouTube
Классный час мой зож: Классный час на тему «Мой выбор- здоровый образ жизни»
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Воспитывать
Дети
Подросток
Правильно
Разное
Рекомендации
Советы
2024 © Все права защищены.

Семейные советы
Как правильно ?
Дети
Воспитание

Эндотермическая реакция	Экзотермическая реакция
Эти реакции сопровождаются поглощением тепла.	Эти реакции сопровождаются выделением тепла.
Плавление твердых веществ, плавление, испарение и испарение являются примерами эндотермической реакции.	Сжигание бензина и окисление аммиака являются примерами экзотермической реакции.

485 + 38 523		583 + 38 621		681 + 38 719
583 – 38 545		545 – 38 507		507 – 38 469

1.	Что такое ассоциативное свойство сложения?
2.	Ассоциативное свойство формулы сложения
3.	Ассоциативное свойство сложения и умножения
4.	Часто задаваемые вопросы по ассоциативному свойству дополнения

1.	Что такое коммутативная собственность?
2.	Коммутативное свойство сложения
3.	Коммутативное свойство умножения
4.	Коммутативное свойство против ассоциативного свойства
5.	Часто задаваемые вопросы о коммутативном свойстве

1.
	[латекс]-1+3=[/латекс]
Используйте свойство коммутативности сложения, чтобы изменить порядок.	[латекс]-1+3=3+\влево(-1\вправо)[/латекс]

2.
	[латекс]4\cdot 9=[/латекс]
Используйте свойство перестановочности умножения, чтобы изменить порядок.	[латекс]4\cdot 9=9\cdot 4[/латекс]

Изменить группировку.	(6 • 3)х
Умножить в скобках.	18x

Замена \(\dfrac {7}{8}\) для х.	$$\textcolor{red}{\dfrac{7}{8}} + 0,37 + \left(- \textcolor{red}{\dfrac{7}{8}}\right)$$
Преобразование дробей в десятичные.	0,875 + 0,37 + (-0,875)
Добавить слева направо.	1,245 — 0,875
Вычесть.	0,37

Подставьте \(\dfrac{7}{8}\) вместо x.	$$\textcolor{red}{\dfrac{7}{8}} + \left(- \textcolor{red}{\dfrac{7}{8}}\right) + 0,37$$
Сначала добавьте противоположности.	0,37

Подставьте 17 вместо n.	$$\dfrac{4}{3} \left(\dfrac{3}{4} \cdot \textcolor{red}{17} \right)$$
Сначала умножить в скобках.	$$\dfrac{4}{3} \left(\dfrac{51}{4}\right)$$
Умножить еще раз.	$$17$$

Замените n на 17.	$$\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) \textcolor{red}{\cdot 17}$$
Умножить. Произведение обратных величин равно 1,	$$(1) \cdot 17$$
Умножить еще раз. admin Навигация по записям Ментальная математика что это такое ютуб: Урок 2 «Сложение в пятерке и десятке» \| Ментальная арифметика — YouTube Классный час мой зож: Классный час на тему «Мой выбор- здоровый образ жизни» Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Воспитывать Дети Подросток Правильно Разное Рекомендации Советы 2024 © Все права защищены. Семейные советы Как правильно ? Дети Воспитание