Урок математики на тему»Умножение и деление на 9. Девятая часть числа»(2 класс)

Конспект открытого урока математики во 2 классе на тему:

 «Умножение и деление на 9. Девятая часть числа».

Цели:

1.     Познакомить с новыми случаями умножения на 9; учить использовать знания таблицы умножения для нахождения результатов деления; закреплять табличные случаи умножения и деления на 6,7,8; находить девятую часть числа; закреплять и обобщать знания о решении задач.

2.     Развивать внимание и логическое мышление, речь учащихся, стимулировать активный учебный труд, интерес к предмету.

3.     Воспитывать культуру общения, культуру умственного труда – почувствовать радость, удовлетворение от проделанной работы.

ХОД УРОКА

1.     Орг. момент.

Настрой на работу. При использовании таблиц повторение правил поведения на уроке для успешного усвоения материала.

·         Не разговаривай на уроках, если это не связано с выполнением задания.

·         Не кричи с места, даже если знаешь правильный ответ.

·         Не выкрикивай на уроке. Если хочешь ответить – подними руку.

·         Не подсказывай.

·         Работаем дружно

2.     Разминка для ума.

·         Сколько будет 5 плюс 5 деленное на 5?    (2)

·         Как называют третий месяц года?                 (Март)

·         Что у зайца позади, а у цапли впереди?        (Ц)

·         Назови самое большое однозначное число.  (9)

·         Для карандаша это пенал. А для автомобиля? Для самолета? (ГАРАЖ, АНГАР)

·         Какая буква в алфавите третья с конца?  (Э) А пятая сначала? (Д)

·         Сколько будет, если к самому маленькому двузначному числу прибавить самое большое однозначное и все это умножить на 1? (19).

3.     Минутка красивого письма.

Число 19. Подчеркните самые красивые цифры. Покажите соседу по парте. Пусть он выберет самые красивые цифры.

 4. Проверка домашнего задания.  Т. «Дружим с математикой» с.75 №29.

— Какое чувство вы испытали, когда помогли котенку?

Проверим, испытаем ли мы такие же чувства от того, что выполним задание №26 и №27 на с.74.

5.Игра – эстафета.

Подготовка к игре. Дети хором отвечают на вопросы.

— Внимание наше растет?

— Голова мыслит ясно?

— Мы хотим учиться?

— Мы готовы к работе?

— Настроение у нас …. (отличное)

— Давайте мы теперь узнаем, на чем дальше отправимся в путь.

Соревнование по рядам и отгадывание слова.

1 ряд.                       2 ряд.                        3 ряд.

6×9                             18 : 3                        8×7

30 : 5                          32 : 8                        6×8

5×8                             24 : 4                        32 : 8

24 : 4                          6×9                           9×8

7×4                             5×8                           40 : 5

42 : 6                          64 : 8                         9×6

3×7                             48 : 8                         3×8

2×9                             6×2                            8×2      

54- Л, 40-Д,6-О        6-К, 8-Т, 4-А.              48-А, 24-Т,4-М, 54-Ё,          

21-А, 28-Ч,7-К.         40-Р, 54-Е, 8-О.          72-О, 56-С, 8-Л.      

ЛОДОЧКА                 КАТЕРОК                 САМОЛЁТ

— Какое слово здесь лишнее?

— Какой еще водный транспорт вы знаете ?

— Повторение таблицы умножения на 7 и на 8.

2 человека работают на компьютере, а весь класс на карточках (задания одинаковые) Можно работать индивидуально, а можно в паре.

Проверка.

— Что мы сейчас делали? ( Повторяли таблицу умножения)

Интересно? Устали? Отдохнем .

Физкультминутка.

Как настроение? Дальше пойдем?

6.     Определение темы и целей урока.

Чтобы определить тему урока, надо решить математический диктант.

Записываем только ответы.

1. У нашей кошки 9 мышат и все мышей ловить хотят. Каждый котенок поймал по 2 мышки. Сколько поймали мышат 9 маленьких котят? (18)

2. Паслись на лугу 9 телят, 9 овец, 9 коров, 9 ягнят.

 «Я мал»,- говорит пастушок,-

«Сосчитать не могу,

 Сколько животных паслось на лугу»?  (36)

3. Наталья Николаевна разложила пачку тетрадей для контрольных работ по вариантам. Получилось 3 стопки по 9 тетрадей. Сколько тетрадей в пачке?  (

27)

4. Уменьшить 60 на 6.  (54)

5. Уменьшите 100 на 28.  (72)

6. В одном автобусе ехало 9 человек. Сколько человек ехало в 5 таких автобусах?  (45)

7. Отгадайте число: 6×10 +3  (63)

8. Сколько будет трижды три?  (9)

На доске: 18, 36, 27, 54, 72, 45, 63,9.

-Расположить в порядке возрастания.

9,18, 27, 36, 45, 54, 63, 72.

-Что вы заметили? (Они все делятся на 9).

Делим на 9 и получаем ряд чисел:

1, 2, 3, 4, 5, 6, 7, 8.

 Составление таблицы умножения.

— Какого числа  не хватает? Как получить 9?

На доске слайд №2 с таблицей умножения на 9.

Значит, как можно определить тему урока?  На доске : Умножение и деление на 9.

Определим цели урока.

На доске:

1.     Запомнить таблицу умножения и деления на 9.

2.     Находить девятую часть числа.

3.     Учиться решать задачи.

4.     Поверить знания таблицы умножения и деления.

— Эту таблицу мы уже знаем, потому что знаем правило. Какое? ( От перестановки множителей произведение не меняется). Значит, нам надо выучить только один пример.

— Если у вас возникли сомнения, сложите цифры произведения – в результате всегда должно получиться 9. Например: 9×2 =18 (1+8=9)

                                                                   9×5 = 45 (4+5=9)

— Счет на пальцах.

Как вы думаете на пальцах можно считать?

На пальцах можно не только складывать, но и умножать.

Положите руки на стол ладонями вниз, растопырьте пальцы и пронумеруйте их слева направо. Левый мизинец – 1, а правый – 10. Если вам надо умножить 9 на 5, то отсчитайте слева 5 пальцев и посчитайте сколько пальцев у вас слева от пятого (4) и сколько справа (5).

Ответ 45.

Потренируемся: 2×9, 9×9 и т.д.

7.     Закрепление.

1.     Работа в тетрадях №2 с.23 №73,74,75

— Взаимопроверка.

2.     Деление на 9.  

— Повторение умножения и деления на 0 и на1.  Слайд №4.

3.     Девятая часть от числа.   Составьте примеры не деление. Слайд №5.

Т.№2 с. 23 №77, №78

Учебник с.46 № 23.

 

Физкультминутка.

 

8.     Работа в учебнике.

— Решение задачи №8 с.43. 

Составление краткой записи и решение в тетради.

— №2 с.42 и №13 с.44 по вариантам по одной строчке. Взаимопроверка.

9.     Самостоятельная работа.   

9 • 6 = 9 • 3 = 9 • 7 = 9 • 5 = 9 • 4 = 9 • 8 =

36 : 9 = 63 : 9 = 72 : 9 = 45 : 9 = 54 : 9 = 27 : 9 =

Проверка.

Резерв: учебник с. 43 задачи 1 вариант №6; 2 вариант №7.

2 ученика решают на доске. Проверка.

10.  Исследование.

— Давайте начертим отрезок длиной 9 см.

Какой прибор нам поможет? А знаете ли вы, что раньше не было таких точных, а главное одинаковых измерительных приборов?

В Древнем Египте мерили указательным пальцем. 4 пальца – ладонь.

В западной Европе – 1 фалангой большого пальца(дюйм)

В Древней Руси – 2 фаланги указательного пальца (вершок).

— Попробуем создать линейку Древнего мира. На столе лежат заготовки из картона.

1 вариант создает линейку Древнего Египта.

2 вариант – Западной Европы.

3 вариант – Древней Руси.

— А тетерь сравним одинаковые расстояния получились. Нет. Возникла необходимость появления единой таблицы измерения.

— в 1790 году во Франции собрались ученые и решили, расстояние от Северного полюса до экватора разделить на 10 миллионов и получилось расстояние равное 1 метру. С этого времени стала использоваться современная таблица единиц измерения длины.

— Итак, вернемся к нашему заданию. Выделите любым цветом девятую часть этого отрезка.  

— Как найти девятую часть числа?

РЕЗЕРВ. Повторение сложения и

вычитания чисел в пределах 100.

— Самостоятельная работа в парах.  

— Проверка.  

Составление слова молодцы.   Почему мы молодцы?  (смотрим на цели урока).

Выполнили?

11.  Подведение итогов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Конспект урока по математике в 3 классе на тему «Повторение. Таблица умножения и деления».

Автор: Т.В.Акульшина

Тема урока: Повторение. Таблица умножения и деления
Тип урока: урок повторения, систематизация и обобщение знаний
Цель урока : обобщить и закрепить знания обучающихся по теме
«Табличное умножение и деление» через решение задач и выражений
Задачи урока:
Образовательные:
• Контроль знания таблицы умножения и деления
• Закрепление умения решать задачи изученных видов
• Совершенствование вычислительных навыков, навыков устного счёта
Развивающие:
• развивать вычислительные навыки, логическое мышление, память, внимание
Воспитательные:
• воспитание ответственности и добросовестного отношения к учёбе, уважительных и доброжелательных отношений к товарищам
Планируемые результаты
Предметные результаты: обучающиеся научатся пользоваться таблицей умножения и деления; решать задачи изученных видов; осуществлять итоговый и пошаговый контроль своей деятельности; слушать других и принимать иную точку зрения.

Личностные универсальные учебные действия: ориентация на понимание причин успеха или неуспеха в учебной деятельности, в том числе на самоанализ , самоконтроль и самооценку результата.
Регулятивные универсальные учебные действия: планируют свои действия в соответствии с поставленной задачей; осуществляют итоговый и пошаговый контроль по результату; оценивают правильность выполнения заданий; вносят необходимые коррективы .
Познавательные универсальные учебные действия: осуществляют поиск необходимой информации для выполнения учебных заданий.
Коммуникативные универсальные учебные действия: контролируют действия партнёра; осуществляют взаимный контроль и оказывают в сотрудничестве необходимую взаимопомощь.
Ход урока
I.Организационный момент
Я держу в ладонях солнце,
Я дарю его друзьям.
Улыбнитесь – это ж просто!
Лучик солнца – это вам.
— Я рада, что у вас хорошее настроение. Надеюсь, что и урок пройдет хорошо.
— Итак, математика.
— Откройте тетради и оформите классную работу.
— Какое сегодня число?(12 декабря)
— Что вы можете сказать об этом числе?(двузначное, четное, в нем 1 десяток и 2 единицы, соседи 11 и 13, для записи этого числа потребовались две цифры – 1 и 2)
— Какие числа можно перемножить, чтобы получить число 12?
II. Определение темы и задач урока
— А сейчас я предлагаю вам самим попытаться сформулировать тему и задачи урока.
— А для того, чтобы сформулировать тему урока, я приготовила для вас задание. В результате его выполнения у нас сложится та задача, которую мы сегодня на уроке будем решать.
— Итак, задание: просчитать математические выражения. Каждое выражение имеет букву. Куда её нужно будет поставить, я думаю, вы догадаетесь.

2 3 4 5 3 8 7 5 6
п о в т о р я т ь

12:3+2 27:9 20:4-1 35:7 81:9-8:4 48:6 7*8-6*9
ь о в т я р п

О, Т
(Уч-ся выходят к доске, считают и подставляют буквы) Слайд 1
-Сегодня на уроке мы будем повторять. (Повторять пройденный материал по теме «Табличное умножение и деление». Подготавливаться к проверочной работе)
III. Актуализация знаний
— Ребята, а зачем мы проводим уроки повторения?(Повторение – мать учения; чтобы закрепить пройденный материал; чтобы наши знания стали твердыми, крепкими; надолго остались в памяти и т.д.)
— А это важно? (Да. )
— Особенно при изучении этой темы. Ведь таблица умножения полностью учится только в третьем классе, а применяется всю жизнь
IV. Работа по теме урока
1. –Начнем с арифметической разминки. Сегодня будет много разных заданий – и коллективных, и индивидуальных. Для индивидуальной работы у доски я приготовила три задания. Давайте проговорим, что нужно в этих заданиях сделать
1) Вставить нужный знак, чтобы равенства стали верными
8□4□2=34
8□4□2=10
8□4□2= 4
8□4□2=14
2) 7,3,21
-Составить два примера на умножение и два – на деление, используя эти числа
3) Сравнить
24:6 □ 72:8
9*2:6 □ 15:5*4
9*9-6 □ 7*9+12
1. Индивидуальная работа у доски(трое уч-ся)
2. В это время устный счет: учебник стр. 79 – задание на полях и №28
3. Проверка индивидуальной работы
4. Математический диктант
 Делимое 49, делитель 7, найти частное
 Умножьте 6 на 4
 Сколько раз по 6 содержится в числе 30?
 Во сколько раз 32 больше 4?
 Какое число меньше 18 в шесть раз?
 Увеличьте 5 в 4 раза
 Найдите произведение чисел 7 и 8
 Я задумала число, увеличила его в 3 раза и получила 24. Какое число я задумала?
Слайд 2
Проверка по эталону
V. Физкультминутка
VI. Продолжение работы по теме урока
1) №30 стр. 79 Записать решение этой задачи выражением
Слайд 3
Проверка по эталону
2) Слайд 4
Найти площадь и периметр прямоугольника со сторонами 6см и 3см(по вариантам)
Взаимопроверка
3) Работа в парах
81:(11-2)*8 54:(12-3)*7
(5*6-12):3 (7*8-16):5
72:8*4:6*2 24:4*6:9*5
63:7*4:6*5 81:9*4:6*8
VII. Рефлексия
— Поднимите руку те, кто может похвалить себя за работу на уроке
— А за что вы можете себя похвалить? (5-7 чел. )
— Какие задания вызвали затруднения?
— В целом я довольна вашей работой.
— Можем ли мы считать, что к проверочной работе мы подготовились хорошо?
VIII. Д/з(на листочках А4)
1)Обвести числа из таблицы умножения в кружок, а остальные зачеркнуть
2) Отгадать загадку(используя таблицу умножения)
В сенокос горька, а в мороз сладка. Что за ягодка?
7 3 6 5 4 2

□*8 32-Н 24-Я 40-И 16-А 48-Б 56-Р
Нарисовать отгадку
IX. Итог урока
Слайд №5
Умножения таблица
Всем нам в жизни пригодится.
И недаром названа
Умножением она.
— Молодцы! Спасибо за урок.

Рассуждения об умножении и делении: полный урок

Математика.Практика.MP7

Единые основные ГОСТы

• Математика: Математика
• Практика: Стандарты математической практики
• MP7:  Ищите и используйте структуру.

  Учащиеся со способностями к математике присмотритесь, чтобы различить узор или структуру. Например, молодые студенты могут обратите внимание, что три и еще семь равно количеству семи и трех, или они могут сортировать набор фигур по количеству сторон у фигур. Позже учащиеся увидят, что 7 х 8 равно хорошо запомнившимся 7 х 5 + 7 х 3, в процессе подготовки. для изучения распределительного свойства.

  В выражении х2 + 9x + 14, учащиеся старшего возраста могут видеть 14 как 2 x 7 и 9 как 2 + 7. Они узнают значение существующей линии в геометрической фигуре и может использовать стратегию рисования вспомогательной линии для решения задач. Они также могут отступить на обзор и изменение перспективы.

  Они могут видеть сложные вещи, например как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объекты. Например, они могут видеть 5 – 3(x – y)2 как 5 минус положительное число, умноженное на квадрат и использовать это, чтобы понять, что его значение не может быть больше 5 для любого реального числа х и у.

Загрузить общие основные государственные стандарты (PDF, 1,2 МБ)

|

Математика.3.OA.B.5

Единые основные ГОСТы

• Математика: Математика
• 3: Класс 3
• OA: Операции и алгебраическое мышление
• B:  Понимать свойства умножения и взаимосвязь между умножением и подразделение
• 5: 
  Применение свойств операций в качестве стратегий умножения и деления. (Ученики нет необходимости использовать формальные термины для этих свойств.) Примеры: Если известно 6 × 4 = 24, тогда также известно, что 4 × 6 = 24. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти как 3 × 5 = 15, тогда 15 × 2 = 30, или как 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения.) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)

Скачать Common Core State Standards (PDF, 1,2 МБ)

15 книг об умножении и делении

Умножение и деление — очень важные математические понятия, с которыми знакомятся во 2-м классе. Эти понятия могут быть немного сложными для понимания учащимися. Поэтому мне нравится давать учащимся способ относиться к концепции в реальном мире, что имеет смысл для них и их уровня развития, а также дает им визуальное представление концепции. Прочтите 15 книг об умножении и делении, которые эффективны для ознакомления и обучения этим понятиям!

Этот пост содержит партнерские ссылки. Вы можете увидеть мое раскрытие здесь .

Книги об умножении

1. А теперь мое следующее число! Songs for Multiplying Fun by Margaret Park

Если вы чем-то похожи на меня, вы, вероятно, сочиняете песни или стишки, чтобы помочь себе запомнить определенные фрагменты информации. Вот как я помню свой номер социального страхования, номер водительского удостоверения и буквально все!

Есть что-то в том, чтобы настраивать информацию, которая помогает нам запоминать вещи более эффективно, и то же самое касается наших учеников!

В этой книге об умножении представлены различные числа и их кратные в форме песен, рассказов и рифм, чтобы помочь учащимся запомнить их и выучить умножение.

Иллюстрации и сцены яркие и живые. Они показывают группы объектов таким образом, чтобы учащиеся могли понять концепцию еще глубже.

2. 2 x 2 = Бу! Сборник жутких историй об умножении от Лорин Лиди

 

Если вы ищете книги по умножению для начинающих, эта книга идеальна! В этой истории представлены основные понятия и факты умножения от 0 до 5 с забавными математическими историями.

От исчезновения вампиров до превращения одного мешка конфет в несколько пакетов или удвоения лосиной головы — с помощью этих глупых историй ученики узнают о силе умножения.

3. Два из всего Лили Той Хонг

Эта книга об умножении следует за старым мистером Хактаком, который выкапывает таинственный медный горшок из своего сада. Он не знает, для чего его можно использовать, но как только его кошелек для монет и шпилька миссис Хактак падают в горшок, они вскоре понимают магию горшка.

Они находят в горшке 2 шпильки и 2 кошелька для монет. С тех пор они используют волшебный горшок, чтобы умножить свои золотые монеты в надежде нажить состояние. Эта книга предлагает глупую историю и отличные визуальные эффекты для студентов, когда они изучают умножение.

4. The Best of Times: Math Strategies that Multiply by Greg Tang

Это одна из моих самых любимых книг об умножении. Мне нравится, как автор подходит к таблице умножения и помогает учащимся изучать инновационные и творческие способы умножения чисел и получения ответов без запоминания.

Эта книга побуждает учащихся критически мыслить и формировать глубокое понимание умножения и числовых понятий. Таким образом, они могут уверенно выучить факты умножения, не полагаясь на запоминание.

Он считает, что если дети могут умножать на 2, то они могут умножать и на 4, и на 8. То же самое верно и для умножения на 3, 6 и 9. 

5. The Grapes of Math, Грег Танг еще одна из книг Грега Танга об умножении. Эта книга полна математических загадок, которые побудят ваших учеников думать глубже и развивать мышление.

В этой истории ставится вопрос о том, сколько виноградин на лозе. Их подсчет занял бы слишком много времени, поэтому учащиеся учатся группировать ягоды и умножать их, получая ответ еще быстрее.

В этой книге об умножении используются рифмы, загадки и визуальные подсказки, чтобы помочь учащимся научиться группировать числа и быстро считать с помощью умножения.

6. Удивительный сон Аманды Бин Синди Нойшвандер

Эта книга не только образовательная, но и полностью развлекательная и веселая для учащихся благодаря забавным иллюстрациям и сюжетной линии. В нем также есть раздел с образовательными предложениями для учителей и родителей, что является отличным дополнением.

В этой истории главная героиня Аманда не понимает, почему умножение так важно, даже после того, как ей об этом говорит учитель. Однако после странного сна, полного математических задач, она вскоре понимает цель этого математического навыка.

Затем она учится умножать почти все! Она начинает считать все по 1, 2, 5 и 10.

Это отличная книга, которая поможет вашим неохотно изучающим математику понять цель умножения и то, как они будут использовать его в своей повседневной жизни. Добавьте это чтение вслух к своим урокам о счете пропусков для дополнительной практики!

7. Spunky Monkeys on a Parade by Stuart J. Murphy

Если вы читали какие-либо из моих предыдущих сообщений в блоге о книгах по математике, вы знаете, как сильно я люблю книги Stuart J. Murphy’s Math Start Series! Эта книга об умножении является вторым уровнем в этой серии, что делает ее идеальной для ознакомления с концепцией умножения во втором классе.

Эта книга отлично подходит для обучения учащихся счету 2, 3 и 4, используя разные группы обезьян в параде. Иллюстрации веселые и делают понимание концепции умножения еще более конкретным.

8. Угроза умножения: Месть Румпельштильцхена Пэм Калверт

Порадуйте своих учеников сказкой с участием Румпельштильцхена, когда они применят свои навыки умножения в этой умной математической версии классической истории.

По сюжету, Румпельштильцхен возвращается через 10 лет после поражения от королевы, и он возвращается, чтобы забрать свою плату! Его размножающаяся палка сеет хаос в королевстве, и он угрожает продолжить, если ему не отплатят.

Питер должен заполучить волшебную палочку-умножитель и научиться ею пользоваться, пока не стало слишком поздно. В этой книге рассказывается об умножении не только целых чисел, но и дробей, что делает ее идеальной для учащихся 2-4 классов.

Книги о разделении

9. The Multiplying Menace Divides Пэм Калверт

Эта книга о разделении является идеальным продолжением книги Multiplying Menace: The Revenge of Rumpelstiltskin о умножении. Теперь учащиеся проверят свои навыки деления в другом увлекательном математическом приключении.

Румпельштильцхен снова возвращается и начинает создавать проблемы после изгнания в Бездну Зеро. Его подруга Матильда и он замышляют отомстить Питеру, но на этот раз он использует свои силы, чтобы разделить королевство.

Питер должен найти Великий Множитель, чтобы найти способ отменить Великий Раздел, прежде чем Румпельштильцхен сможет объединить свои 2 волшебные математические палочки.

В этой книге рассказывается о делении целых чисел и дробей, а также о правилах деления на ноль. Опять же, это идеальная книга для учащихся 2-4 классов.

10. The Great Divide: A Mathematical Marathon by Dayle Ann Dodds

В этой книге о делении участвуют 80 гонщиков, гонка по пересеченной местности и множество опасностей на пути. Каждая опасность разделяет группу по-разному, заставляя наблюдателей гадать, останется ли кто-нибудь, чтобы пересечь финишную черту в конце.

Эта история заставит школьников задуматься о том, какая опасность их ждет впереди. Это также отличная книга для поощрения критического мышления и предвидения, поскольку они используют свои знания о разделении, чтобы определить, останется ли кто-нибудь!

11. The Doorbell Rang by Pat Hutchins

Что мне больше всего нравится в этой книге, так это то, что она знакомит с концепцией разделения, а также рассказывает о важных социальных навыках. В этой книге рассказывается о дружбе, совместном использовании и использовании файлов cookie, чтобы помочь учащимся понять концепцию равного деления.

По мере того, как все больше друзей будут делиться печеньками, они должны работать вместе, чтобы разделить их поровну, чтобы они могли поделиться ими со своими друзьями.

Это будет прекрасная возможность для учащихся нарисовать картинку или отработать сценарии с помощью манипуляторов или маленьких печенюшек во время перекуса, чтобы самим представить задачи на деление.

12. Bean Thirteen Мэтью МакЭллиготт

Это веселая история о неудачном 13-м бобе, который выбирает Флора, несмотря на то, что ее предостерегают от этого. Выбрав его, Флора и Ральф отправляются на поиски, чтобы он исчез как можно быстрее.

Они пытаются определить, как разделить бобы поровну, чтобы они все исчезли, но всегда остается тот злосчастный 13-й боб. Ваши ученики даже не поймут, что эта книга тайно посвящена математике!

13. Разделяй и путешествуй Стюарт Дж. Мерфи

Стюарт Дж. Мерфи снова вернулся с этой книгой о разделении. Это уровень 3 в его серии Math Start, что делает его отличным для продвинутых учеников 2-го и 3-го классов.

Эта история учит студентов, как разделить использование различных аттракционов на карнавале. 11 друзей должны придумать, как разделить их, чтобы поместиться на 2-местных американских горках и 4-местных аттракционах.

Это отличная возможность побудить ваших детей активно учиться, поднимая их, двигаясь и учась разделяться на равные группы.

14. Сто голодных муравьев Элинор Дж. Пинцес

Разделение 100 голодных муравьев может показаться сложной задачей.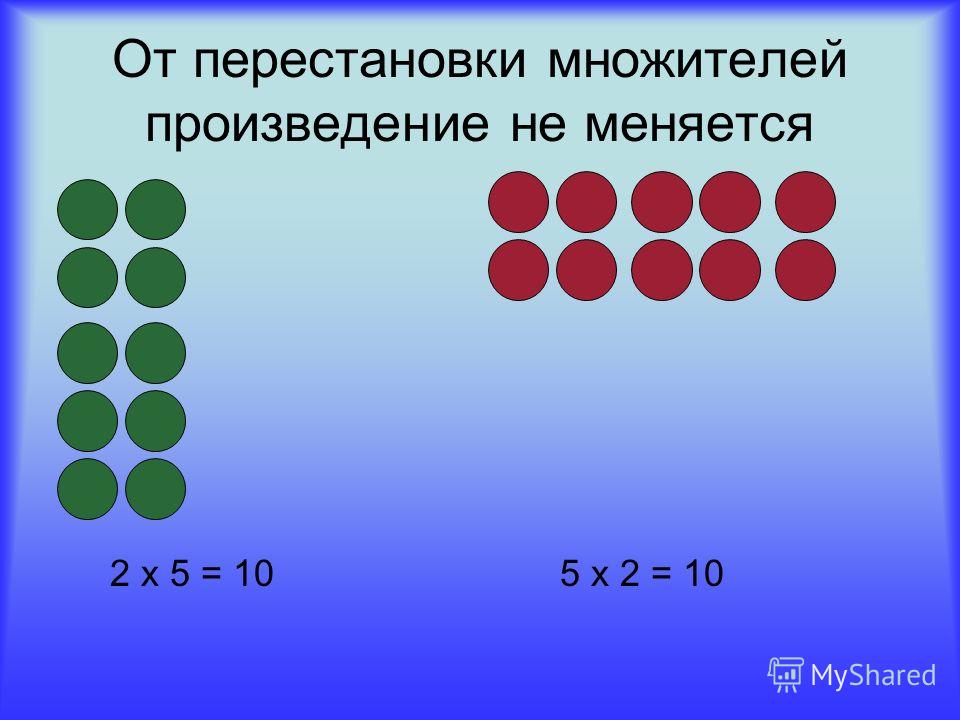 Однако по мере того, как муравьи маршируют в один ряд, чтобы отправиться на пикник, ученики вскоре поймут, что разделить 100 муравьев не так сложно, как кажется.

Они увидят, как разделение на ряды по 50 и 20 ускорит процесс! Это отличный способ для учащихся научиться делить большие числа.

15. Математика гепардов: узнаём о делении от маленьких гепардов Энн Уайтхед Нагда

Если ваши ученики любят животных и гепардов, им понравится эта книга о делении. Эта книга рассказывает о двух детёнышах гепарда, которые попадают в зоопарк Сан-Диего. Эти приятели-собаки становятся идеальными друзьями-животными, чтобы помочь гепардам найти свое место в зоопарке.

По мере того, как гепарды и собаки отправляются в свои приключения, ваши ученики узнают о разделении и дележе поровну.

Надеюсь, вам понравились эти книги об умножении и делении. Они обязательно сделают преподавание этих концепций более увлекательным и реальным для ваших учеников.

Узнайте больше об этих книгах в моем видео на YouTube ниже.