Деление на 0,5. Деление натурального числа на дробь.

• Альфашкола
• Статьи
• Как легко разделить на 0,5

Как быстрее разделить число на  \(0,5\)? Для этого тебе даже не понадобится калькулятор, ведь есть специальное правило. \(0,5-\) это десятичная дробь приведём её к виду обыкновенной дроби:

 

То есть деление на \(0,5\) можно заменить делению на \(\frac{1}{2}\), а при делении на \(\frac{1}{2}\) , дробь меняет местами числитель и знаменатель . Число обратное \(\frac{1}{2}-\) это \(2.\) То есть для того чтобы разделить на \(0,5\) надо умножить на \(2.\) Легко не так ли?

---

Пример 1.  Разделите \(9\) на \(0,5\).

Решение: \(9:0,5=9:\frac{1}{2}=9*2=18\)

Ответ: \(18\).

Пример 2.  Разделите \(25\) на \(0,5\).

Решение: \(25:0,5=25:\frac{1}{2}=25*2=50\)

Ответ: \(50\).

---

Пример 3.  Разделите \(125\) на \(0,5\).

Решение: \(125:0,5=125:\frac{1}{2}=125*2=250\)

Ответ: \(250\).

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Светлана Михайловна Радова

Репетитор по математике

Стаж (лет)

Образование:

Тираспольский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Танрыкули Азатович Сейткулиев

Репетитор по математике

Стаж (лет)

Образование:

Международный туркмено-турецкий университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Ольга Анатольевна Лизогуб

Репетитор по математике

Стаж (лет)

Образование:

Мозырский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Специализации

• Подготовка к ЕГЭ по математике (базовый уровень)
• Репетитор по алгебре
• Подготовка к ЕГЭ по математике (профильный уровень)
• Подготовка к ОГЭ по химии
• Репетитор для подготовки к ЕГЭ по физике
• Подготовка к ОГЭ по русскому языку
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Разговорный английский язык
• Репетитор для подготовки к ВПР по английскому языку
• Подготовка к ОГЭ по географии

Похожие статьи

• ЕГЭ по математике, профильный уровень.
  Иррациональное уравнение
• Разложение вектора по базису
• 17 задача профильного ЕГЭ на вклады с платежами равными взносами
• ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
• ОГЭ по математике, базовый уровень. Квадратные уравнения
• ОГЭ по математике, базовый уровень. Алгебраические дроби
• Пищевые отравления: как защитить ребенка в лагере, деревне и городе
• Детское переедание: что делать?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Плюс минус

Плюс минус

      Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками.

      Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно.

      При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число.

      В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. Плюс умноженный на минус дает минус. Плюс деленный на минус будет минус. Если положительную дробь умножить или разделить на отрицательную дробь получится отрицательное число. Это число может быть целым или дробным. Произведение положительного числа на отрицательное — число отрицательное, частное положительного числа на отрицательное число — отрицательное число. Если числитель дроби положительный, а знаменатель отрицательный — дробь (или целое число) будет отрицательной.

      При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число.

      Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс.

ВОПРОС — ОТВЕТ

«Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».

«Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. Теперь прилепливаем полученный плюс к ранее полученной двойке

(-6) : (-3) = +2

Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так:

(-6) : (-3) = 2

«Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше.

      13 ноября 2009 года — 22 сентября 2019 года.

© 2006 — 2021 Николай Хижняк. Все права защищены.

умножить и разделить в App Store

Математический слайд: умножение и деление — это многопользовательская игра, помогающая детям изучить основные факты умножения и деления чисел. Игроки играют и учатся, сдвигая плитки в центр, чтобы соответствовать изображению, ответу или уравнению. Чтобы прогрессировать и преуспевать в математике, дети должны быть в состоянии легко вспомнить основные факты о числах. Math Slide — это увлекательный способ научиться и попрактиковаться в этом ключевом навыке.

Характеристики
• Многопользовательская игра для одного, двух, трех или четырех игроков
• В игры можно играть в режиме соревнования или в режиме сотрудничества
• 10 игр, основанных на одной ключевой математической концепции
• Во все игры можно играть дважды бесплатно
• В игру 1 и игру 8 можно играть неограниченное количество раз
• Каждая игра немного сложнее, чем предыдущая игра
• Приложение фокусируется на критической математической концепции, жизненно важной для успеха

Чтобы выяснить, соответствует ли это приложение нужному уровню сложности, попробуйте Игру 1 и Игру 8. Если Игра 1 слишком сложна или Игра 8 слишком проста, это приложение не на нужном уровне.

Бесплатная версия этого приложения позволяет играть в каждую игру дважды. В игры 1 и 8 можно играть неограниченное количество раз бесплатно. Платная версия, которая содержит все эти игры и многое другое и может использоваться с программой Apple Volume Purchasing Program for Education VPP, называется Math Slide: Basic Facts.

Как играть
1. Выберите режим соревнования или режим сотрудничества
2. Выберите игру, в которую хотите играть
3. Игроки присоединятся к игре, нажав кнопку «Присоединиться»
4. Нажмите «Начать игру», дождитесь обратного отсчета , затем играйте
5. Переместите плитку в центр, чтобы она соответствовала изображению, ответу или уравнению.
6. Как только плитки используются, игра заканчивается. , ÷2, 5x, ÷5, 10x, ÷10 количество фактов
Игра 3 – 3x, 4x количество фактов
Игра 4 – 3x, ÷3, 4x, ÷4 количество фактов
Игра 5 – 2, 3, 4, 5 , 10, x ÷ количество фактов
Игра 6 – 6x, ÷6 количество фактов
Игра 7 – 7x, ÷7 количество фактов
Игра 8 – 8x, ÷8 количество фактов
Игра 9 – 9x, ÷9количество фактов
Игра 10 – 2, 3, 4, 5, 6, 7, 8, 9, 10, x ÷ число фактов

Maths Adventures Limited — новозеландская компания, помогающая детям изучать математику. Мы разрабатываем приложения, которые фокусируются на ключевых концепциях, которые необходимо полностью понять, чтобы прогрессировать и преуспевать в математике. Наши приложения варьируются от обучения счету до понимания и использования дробей и десятичных знаков, причем каждое приложение сосредоточено на одной ключевой концепции.

Мы верим:
• Каждый может выучить математику
• Игра в обучающие игры и приложения улучшает понимание
• Изучение математики должно быть веселым и захватывающим, полезным приключением

Math Slide — часть нашей серии игр «Играй и учись», представляющих собой игры с высокой образовательной ценностью, в которых дети учатся во время игры. Наши приложения основаны на исследованиях и тестируются в классе, чтобы убедиться, что они помогают детям учиться. Мы используем возможности iPad и технологий, чтобы расширить возможности учителей и помочь детям понять и усвоить основные математические понятия и разобраться в недоразумениях.

Умножение и деление рациональных выражений — Алгебра среднего уровня

Рациональные выражения и функции

Цели обучения

К концу этого раздела вы сможете:

• Определять значения, для которых рациональное выражение не определено
• Упростить рациональные выражения
• Умножение рациональных выражений
• Разделить рациональные выражения
• Умножение и деление рациональных функций

Прежде чем начать, пройдите этот тест на готовность.

1. Упрощение:

   Если вы пропустили эту проблему, просмотрите (рисунок).

2. Умножить:

   Если вы пропустили эту проблему, просмотрите (рисунок).

3. Разделить:

   Если вы пропустили эту проблему, просмотрите (рисунок).

Ранее мы рассмотрели свойства дробей и операции с ними. Мы ввели рациональные числа, которые представляют собой просто дроби, в которых числители и знаменатели являются целыми числами. В этой главе мы будем работать с дробями, числители и знаменатели которых являются полиномами. Мы называем такое выражение рациональным выражением.

Rational Expression

Рациональное выражение — это выражение в форме, где p и q — полиномы, а

Вот несколько примеров рациональных выражений:

Обратите внимание, что первое рациональное выражение из перечисленных выше, , является просто дробью. Поскольку константа является полиномом нулевой степени, отношение двух констант является рациональным выражением, если знаменатель не равен нулю.

Мы проделаем с рациональными выражениями те же операции, что и с дробями. Мы будем упрощать, складывать, вычитать, умножать, делить и использовать их в приложениях.

Определите значения, для которых рациональное выражение не определено

Если знаменатель равен нулю, рациональное выражение не определено. Числитель рационального выражения может быть равен 0, но не знаменатель.

Когда мы работаем с числовой дробью, легко избежать деления на ноль, потому что мы можем видеть число в знаменателе. Чтобы избежать деления на ноль в рациональном выражении, мы не должны допускать значений переменной, при которых знаменатель будет равен нулю.

Итак, прежде чем мы начнем какую-либо операцию с рациональным выражением, мы сначала исследуем его, чтобы найти значения, при которых знаменатель будет равен нулю. Таким образом, когда мы решаем, например, рациональное уравнение, мы будем знать, разрешены ли найденные нами алгебраические решения или нет.

Определите значения, для которых рациональное выражение не определено.

1. Установить знаменатель равным нулю.
2. Решите уравнение.

Определите значение, для которого каждое рациональное выражение не определено:

ⓐⓑⓒ

Выражение будет неопределенным, если знаменатель равен нулю.

ⓐ

ⓑ

ⓒ

Определите значение, для которого каждое рациональное выражение не определено.

ⓐⓑⓒ

Определите значение, для которого каждое рациональное выражение не определено.

ⓐⓑⓒ

Упрощение рациональных выражений

Дробь считается упрощенной, если в ее числителе и знаменателе нет общих множителей, кроме 1. Точно так же упрощенное рациональное выражение не имеет общих делителей, кроме 1, в числителе и знаменателе.

Упрощенное рациональное выражение

Рациональное выражение считается упрощенным, если в его числителе и знаменателе нет общих множителей.

Например,

Мы используем свойство эквивалентных дробей для упрощения числовых дробей. Мы повторяем его здесь, так как мы также будем использовать его для упрощения рациональных выражений.

Свойство эквивалентных дробей

Если a , b и c являются числами, где

Обратите внимание, что в свойстве эквивалентных дробей значения, при которых знаменатели равны нулю, специально запрещены. Мы видим ясно сказано.

Чтобы упростить рациональные выражения, мы сначала запишем числитель и знаменатель в факторизованной форме. Затем мы удаляем общие множители, используя свойство эквивалентных дробей.

Будьте очень осторожны при удалении общих факторов. Факторы умножаются, чтобы сделать продукт. Вы можете удалить фактор из продукта. Вы не можете удалить термин из суммы.

Удаление x равносильно удалению двойки в дроби

Как упростить рациональное выражение

Упрощение: .

Упростить:

Упростить:

Теперь мы суммируем шаги, которые вы должны выполнить, чтобы упростить рациональные выражения.

Упростить рациональное выражение.

1. Полностью разложите числитель и знаменатель на множители.
2. Упростите, выделив общие множители.

Обычно мы оставляем упрощенное рациональное выражение в факторизованной форме. Таким образом легко проверить, что мы удалили все общие факторы.

Мы будем использовать методы, которые мы изучили, для факторизации многочленов в числителях и знаменателях в следующих примерах.

Каждый раз, когда мы пишем рациональное выражение, мы должны делать заявление, запрещающее значения, которые делают знаменатель равным нулю. Однако, чтобы мы могли сосредоточиться на текущей работе, мы не будем писать ее в примерах.

Упрощение: .

Упрощение: .

Упрощение: .

Теперь мы увидим, как упростить рациональное выражение, числитель и знаменатель которого имеют противоположные множители. Ранее мы ввели противоположное обозначение: противоположное и

Числовая дробь, скажем, упрощается до . Мы также признаем, что числитель и знаменатель являются противоположностями.

Дробь , у которой числитель и знаменатель противоположны, также упрощается до .

Это говорит нам о том, что это противоположно

В общем, мы могли бы написать противоположное как Итак, рациональное выражение упрощается до

Противоположности в рациональном выражении

Противоположное

Выражение и его противоположное деление до

Мы будем использовать это свойство для упрощения рациональных выражений которые содержат противоположности в числителе и знаменателе. Будьте осторожны, чтобы не рассматривать и как противоположности. Напомним, что вдобавок порядок не имеет значения. Итак, если , то

Упростить:

The numerator factors into the quantity x minus 8 times the quantity x plus 4. The denominator factors into the quantity 8 minus x times the quantity 8 plus x. The factors x minus 8 and 8 minus x are opposites, so multiply the rational expression by negative 1. The result is the negative of the quantity x plus 4 divided by the quantity x plus 8.» data-label=»»>

Разложите числитель и знаменатель на множители.
Распознавайте противоположные факторы.
Упрощение.

Упрощение:

Упрощение:

Умножение рациональных выражений

Чтобы умножить рациональные выражения, мы делаем то же самое, что и с числовыми дробями. Умножаем числители и умножаем знаменатели. Затем, если есть какие-то общие факторы, мы удалим их, чтобы упростить результат.

Умножение рациональных выражений

Если p , q , r и s являются многочленами, где тогда

Чтобы умножить рациональные выражения, умножьте числители и умножьте числители.

Помните, что в этой главе мы будем предполагать, что все числовые значения, при которых знаменатель равен нулю, исключены. Мы не будем выписывать ограничения для каждого рационального выражения, но имейте в виду, что знаменатель никогда не может быть равен нулю. Итак, в следующем примере и

Как умножать рациональные выражения

Упрощение:

Упрощение:

Упрощение:

Умножение рациональных выражений.

1. Полностью разложить на множители каждый числитель и знаменатель.
2. Перемножить числители и знаменатели.
3. Упростите, выделив общие множители.

Умножить:

Упростить:

Упростить:

Деление рациональных выражений

Точно так же, как и для числовых дробей, для деления рациональных выражений мы умножаем первую дробь на обратную вторую.

Деление рациональных выражений

Если p , q , r , и s являются полиномами, где тогда

Чтобы разделить вторую дробь рационального выражения, умножьте первую дробь на обратную.

Как только мы перепишем деление как умножение первого выражения на обратное второму, мы затем все факторизуем и ищем общие множители.

Как разделить рациональные выражения

Разделить:

Упростить:

Упростить:

Разделить рациональные выражения.

1. Перепишите деление как произведение первого рационального выражения и обратного ко второму.
2. Полностью разложите числители и знаменатели на множители.
3. Перемножьте числители и знаменатели вместе.
4. Упростите, выделив общие множители.

Напомним из Use the Language of Algebra, что сложная дробь — это дробь, которая содержит дробь в числителе, знаменателе или в обоих. Кроме того, помните, что дробная черта означает деление. Сложная дробь — это еще один способ записи деления двух дробей.

Разделить:

Упростить:

Упростить:

Если у нас есть более двух рациональных выражений для работы, мы по-прежнему следуем той же процедуре. Первым шагом будет переписать любое деление как умножение на обратное. Затем факторизуем и умножаем.

Выполнить указанные операции:

To simplify the expression, rewrite the division as multiplication using the reciprocal of the quantity 2 x plus 12 divided by the quantity 8 x plus 16, which is the quantity 8 x plus 16 divided by the quantity 2 x plus 12. The result is the quantity 3 x minus 6 divided by the quantity 4 x minus 4 times the quantity x squared plus 2 x minus 3 divided by the quantity x squared minus 3 x minus 10 times the quantity 8 x plus 16 divided by the quantity 2 x plus 12. Factor the numerators and denominators. The numerator 3 x minus 6 factors into 3 times the quantity x minus 2. The numerator x squared plus 2 x minus 3 factors into the quantity x plus 3 times the quantity x minus 1. The numerator 8 x plus 16 factors into 8 times the quantity x plus 2. The denominator 4 x minus 4 factors into 4 times the quantity x minus 1. The denominator x squared minus 3 x minus 10 factors into the quantity x plus two times the quantity x minus 5. The denominator 2 x plus 12 factors into 2 times the quantity x plus 6. The result is the rational expression, 3 times the quantity x minus 2 divided by 4 times the quantity x minus 1 times the rational expression, the quantity x plus 3 times the quantity x minus 1 divided by the quantity x plus 2 times the quantity x minus 5 times the rational expression 8 times the quantity x plus 2 divided by 2 times the quantity x plus 6. Multiply the fractions, bringing the constants to the front of the expression to help remove common factors. The result is 3 times 8 times the quantity x minus 2 times the quantity x plus 3 times the quantity x minus 1 times the quantity x plus 2 all divided by 4 times 2 times the quantity x minus 1 times the quantity x plus 2 times the quantity x minus 5 times the quantity x plus 6. Simplify by removing the common factors. 8 is in the numerator and the product of 4 and 2 is 8 in the denominator. Remove the common factors, 8, x minus 1, and x plus 2 from the numerator and denominator. The result is 3 times the quantity x minus 2 times the quantity x plus 3 all divided by the quantity x minus 5 times the quantity x plus 6. » data-label=»»>

Перепишите деление как умножение по взаимному согласию.
Разложите числители и знаменатели на множители.
Умножьте дроби. Приведение констант к передний поможет при устранении общих факторов.
Упростите, выделив общие множители.
Упрощение.

Выполнить указанные операции:

Выполнить указанные операции:

Умножение и деление рациональных функций

Мы начали этот раздел с утверждения, что рациональное выражение — это выражение в форме, где p и q — многочлены и Аналогично, мы определяем рациональную функцию как функцию вида где и полиномиальные функции и не равно нулю.

Рациональная функция

Рациональная функция — это функция вида

, где и — полиномиальные функции, не равные нулю.

Областью определения рациональной функции являются все действительные числа, за исключением тех значений, которые вызывают деление на ноль. Мы должны исключить любые значения, которые составляют

Определить область определения рациональной функции.

1. Установить знаменатель равным нулю.
2. Решите уравнение.
3. Домен состоит из всех действительных чисел, за исключением значений, найденных на шаге 2.

Найдите домен

Домен будет состоять из всех действительных чисел, кроме тех значений, у которых знаменатель равен нулю. Мы установим знаменатель равным нулю, решим это уравнение, а затем исключим эти значения из области.

Найдите область определения

Область определения всех действительных чисел где и

Найдите область определения

Область определения всех действительных чисел где и

Для умножения рациональных функций умножим полученные рациональные выражения на правую часть уравнения, используя те же методы, которые мы использовали для умножения рациональных выражений.

Найти где и

Найти где и

Найти где и

выражения.

Найти где и

Найти где и

Найти где и

Ключевые понятия

• Определите значения, для которых рациональное выражение не определено.
  1. Установить знаменатель равным нулю.
  2. Решите уравнение.
• Эквивалентные дроби Свойство

  Если a , b и c это числа где тогда и

• Как упростить рациональное выражение.
  1. Полностью разложите числитель и знаменатель на множители.
  2. Упростите, выделив общие множители.
• Противоположности в рациональном выражении

       Противоположность

      

      Выражение и его противоположное деление на

• Умножение рациональных выражений

  Если p , q , r и s являются полиномами, где тогда

• Как умножать рациональные выражения.
  1. Полностью разложить на множители каждый числитель и знаменатель.
  2. Перемножить числители и знаменатели.
  3. Упростите, выделив общие множители.
• Отдел рациональных выражений

  Если p , q , r и s являются полиномами, где тогда

• Как делить рациональные выражения.
  1. Перепишите деление как произведение первого рационального выражения на обратное второму.
  2. Полностью разложите числители и знаменатели на множители.
  3. Перемножьте числители и знаменатели вместе.
  4. Упростите, выделив общие множители.
• Как определить область определения рациональной функции.
  1. Установить знаменатель равным нулю.
  2. Решите уравнение.
  3. Домен состоит из всех действительных чисел, за исключением значений, найденных на шаге 2.

Практика делает совершенным

Определите значения, для которых рациональное выражение не определено

В следующих упражнениях определите значения, для которых рациональное выражение не определено.

Упростите рациональные выражения

В следующих упражнениях упростите каждое рациональное выражение.

9

30003

Умножение рациональных выражений

В следующих упражнениях умножьте рациональные выражения.

Divide Rational Expressions

In the following exercises , разделить рациональные выражения.

Для указанных ниже операций, Умножение и деление рациональных функций

В следующих упражнениях найдите область определения каждой функции.

Для следующих упражнений найдите, где и приведены.

Для следующих упражнений найдите, где и приведены.

Письменные упражнения

Объясните, как найти значения x , для которых рациональное выражение не определено.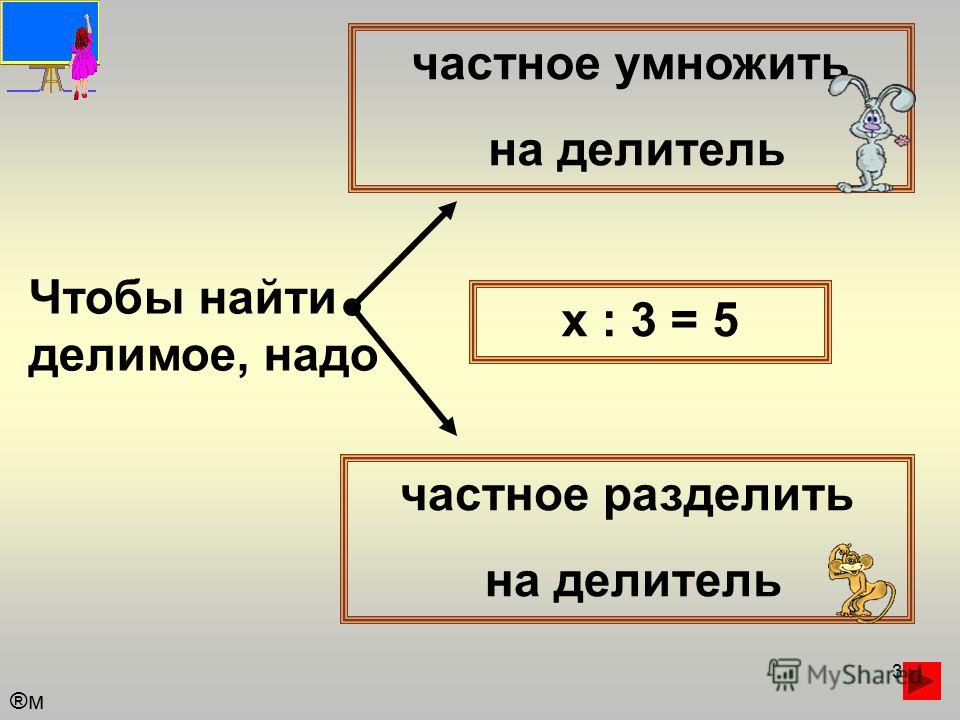

Ответы будут разными.

Объясните все шаги, которые вы предпринимаете, чтобы упростить рациональное выражение

ⓐ Умножьте и объясните все свои шаги.

ⓑ Умножьте и объясните все свои шаги.

ⓒ Оцените свой ответ на часть ⓑ когда . Вы получили тот же ответ, что и в части ⓐ? Почему или почему нет?

Ответы будут разными.

ⓐ Разделите и объясните все свои шаги.

ⓑ Разделите и объясните все свои шаги.

ⓒ Оцените свой ответ на часть ⓑ когда Вы получили тот же ответ, что и на часть ⓐ? Почему или почему нет?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.

ⓑ Если большинство ваших чеков:

…уверенно. Поздравляем! Вы достигли своих целей в этом разделе! Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать.