Ментальная арифметика: за и против

Современные родители стремятся всесторонне развивать детей всеми возможными способами. Одни нанимают нескольких репетиторов, другие отправляют чадо на внеклассные кружки.

В этой статье поговорим о ментальной арифметике — своеобразной системе совершенствования интеллекта при помощи обучения быстрому счету. Техника широко известна, но насколько умение быстро складывать, умножать или вычитать большие числа полезно для ребенка?

Источник: vsegda.by

Польза под вопросом

Отдавая своих детей на занятия ментальной арифметикой, родители надеются натренировать их память, воображение, логику и упорство. Им кажется, что умение легко справляться со сложными примерами по математике — хорошее подспорье в школе, особенно в старших классах. Но здесь не все так просто.

В отношении ментально арифметики учёные проведели много исследований. Их целью было доказать положительное влияние методики на развивающийся детский мозг. Результат оказался не так однозначен.

Когнитивные психологи и нейробиологи сошлись лишь в одном: быстрый счет без сомнения активизирует работу мозга, но минимально влияет на подвижный интеллект или рабочую памяти. Не стоит ожидать, что благодаря ментальной арифметике ребенок станет успешным во всех сферах жизни. Она не решает никаких специфических проблем.

Данная методика помогает успешнее справляться с арифметическими задачами, что производит большое впечатление на стороннего наблюдателя. Восторгаться ребенком-калькулятором точно будут, но такого ли эффекта вы хотели?

Каким детям все-таки стоит освоить быстрый счет?

Источник: img51994.kanal-o.ru

Обучение — это мыслительный процесс, который способствует наращиванию новых нейронных связей. Посещение групповых занятий быстрого счета будет полезно следующим категориям детей:

• со сниженной самооценкой;
• с плохой концентрацией внимания;
• с выраженной замкнутостью;
• с речевыми дефектами.

Коллективная работа объединяет, расширяет круг общения, помогает развитию коммуникабельности, а присутствие единомышленников мотивирует на достижение результата. Также занятия в коллективе заряжают энергией и положительными эмоциями, что благоприятно влияет на умственные способности человека.

Если у родители хотят просто научить ребенка быстро считать, можно заниматься и в индивидуальном порядке. Эмоциональная сфера развития в таком случае будет затронута меньше.

Несколько нюансов

Обучение ментальной арифметике — это тяжелый интеллектуальный труд для ребенка. Рекомендуем начинать занятия в возрасте 6-10 лет, когда ребенок разбирается в базовых математических действиях. Не нужно спешить и отдавать на занятия четырехлетку: в этом возрасте детская психика еще не готова к интенсивной учебной нагрузке.

В процессе учебы нужно тщательно следить за правильным режимом труда и отдыха. Растущему детскому организму нужно много времени на восстановление и усвоение новой информации. А эмоциональная перегрузка может привести к стрессу и потере интереса к учебе.

Все «за» и «против»

Источник: profilaktica.ru

Если родители готовы вкладывать деньги и время в дополнительное образование ребенка, уверены в надёжности образовательного центра и преподавателя, не ждут чего-то невозможного — почему бы и не попробовать? Вдруг ребенок всерьез заинтересуется устным счетом и сможет самостоятельно развить другие когнитивные способности. Для ознакомления с ментальной арифметикой можно посмотреть видеоуроки в интернете.

Минусы у посещения подобных занятий следующие:

1. Школьная программа по математике основывается на составе числа 10. В абакусе же, специальных счетах, сумма косточек на спице единиц равна 9. Это немного путает ребят, которые, например, совместили начало занятий арифметикой и обучение в 1-2 классе. У школьников постарше обычно никаких путаниц не возникает.
2. Решение примеров на скорость приводит к невнимательности и не очень аккуратному написанию цифр. Такие дети концентрируются лишь на самом процессе вычисления.
3. Большинству учеников, освоивших методику, становится скучно в школе. Кропотливый труд оформления задачи в тетради для них — ужасно рутинная и медленная работа. А возвращение к простым примерам и вовсе вызывает ступор.
4. Механический счет вырабатывает совершенно не правильные математические представления.

Важно определиться: быстрый счет нужен ребенку или все-таки родителям? Учеба в школе, дополнительные спортивные секции и одновременно ментальная арифметика — это огромный стресс для детского организма. Первоначально может не всё так гладко получаться, что ещё больше будет расстраивать ученика. Стоит ли уничтожать здоровье ребенка ради освоения новомодного метода развития математических способностей — решать только вам.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Как прокачать свои навыки счёта

Математику преподают, начиная с начальных классов школы: она занимает много времени и требует сил, концентрации и упорства, а также, конечно, способностей к ментальной арифметике.

Дальше становится только сложнее: разделение математики на алгебру и геометрию в средних классах, сложная программа со звёздочкой — в старших и, наконец, университет, где по сравнению с высшей математикой вся предыдущая программа покажется цветочками. Но и школьные темы могут оказаться не так просты: вычисление квадратного корня, тригонометрия, синусы и косинусы могут принести немало хлопот. Хорошо, что у нас есть советы, как справиться с математикой.

Лучшие преподаватели по математике доступны для занятий

Поехали!

Математика повсюду

Неважно, планируете ли вы связать свою профессиональную жизнь с математикой или нет, вам всё равно пригодятся эти навыки, ведь математика — повсюду. Даже если ваша работа — продавец на полставки в местном магазине, вы наверняка уже заметили на собственном опыте, как важна математика, особенно если аппаратура вышла из строя и что-то нужно посчитать в уме.

Не менее важно уметь быстро и правильно считать в уме в повседневной жизни: например, когда вам нужно быстро прикинуть примерную сумму покупок в продуктовом магазине, выполнить измерения для какого-нибудь проекта, сделать выкройки для нового платья и так далее.

Вам не избавиться от математики, как бы вы ни старались!

Математика нужна и для того, чтобы считать деньги, неправда ли? Источник: Unsplash

И даже несмотря на то, что сегодня у каждого из нас есть мобильный телефон, он не всегда может нас выручить, когда что-то надо быстро посчитать. Телефона может не оказаться под рукой, а с другой стороны — пока мы найдём калькулятор в огромном количестве установленных приложений, пройдёт уже немало времени. И потом: вбивать цифры, переключаться между приложениями в то время, как уведомления не перестают сыпаться — может помешать вычислениям…

Мы так привыкли к нашим электронным калькуляторам и так часто достаём их при малейшей задаче на сложение, что даже не задумываемся: а правильно ли они считают? В настоящее время мы стали настолько зависимыми от технологий, что в случае малейшей неполадки чувствуем себя беспомощными. При этом за «спиной» компьютера всегда стоял и стоит человек, который проверяет, что всё идёт именно так, как должно. Хотя человеческие ошибки могут случаться, мы надеемся, что им всё же, в целом, можно доверять.

Но, возвращаясь к основам ментальной арифметики, мы можем неплохо себе помочь — например, на экзаменах. Причём речь идёт не только о школе, но и о дополнительных уроках с частным репетитором.

Ну так как же это сделать? Как стать лучше в математике? Существуют ли упражнения, техники или специальные способы, чтобы прокачать свой математический уровень?

Преимущество быстрых вычислений

Неважно, учитесь вы или уже давно отучились, ментальная арифметика может существенно облегчить вашу повседневную жизнь.

Она поможет вам быстро справиться с цифрами, вне зависимости от ситуации, и, что особенно важно, — сделать это без помощи калькулятора.

Короче говоря, вы можете научиться считать быстро!

Каждому, кто хочет прокачать свой уровень математики, дорога — к ментальной арифметике. Она позволит вам лучше работать с цифрами и упростит некоторые вычислительные операции.

Вам может показаться, что это преувеличение, но, на самом деле, ментальная арифметика позволит вам выглядеть умнее (в то же время, прогресс в математике и правда сделает вас умнее). Когда в ресторане собравшиеся друзья пытаются поделить счёт, со стороны это выглядит неловко: всё происходит долго, несогласованно, суетливо. А тут ещё и официант наготове с мобильным терминалом, ждёт, когда же гости разберутся, кто на сколько наел. А потом ещё и посчитать, сколько полагается чаевых с каждого…

Представляете, если бы вы могли быстро справляться со сложными числами в уме? Вы бы быстро разрешили сложившуюся проблему! Умение быстро считать сегодня никому не кажется переоцененным. Более того, мужчины и женщины часто отмечают привлекательность математических навыков. Так что, всё больше и больше причин погрузиться в цифры!

Если считать в уме, не нужен калькулятор

Ментальная арифметика используется постоянно в самых разных ситуациях. Она позволяет понять, в какой последовательности лучше всего производить вычисления, а также пригождается при изучении десятичных дробей и пропорций.

Таблица умножения может пригодиться, даже когда вы просто пошли за покупками Источник: Unsplash

В конце концов, не стоит забывать тот факт, что ментальная арифметика может заострить ваш ум, изменить тип мышления, прокачать вашу память, а также аналитическое и рациональное мышление. Для старшего поколения, так же, как и для молодого, практика ментальной арифметики поможет держать мозг в лучшем состоянии, предотвращая риск ментальных заболеваний, таких как тревожность, панические атаки или, что хуже, альцгеймер или деменция.

Кстати, тем, кто страдает от панических атак, советуют в момент приступа вдыхать на четыре счёта и выдыхать на семь. Такая очередность помогает успокоиться, а также эта техника работает превентивно.

На первый взгляд может показаться, что это не так, но ментальная арифметика бывает весёлой! Если вы любите играть в «2048» или Судоку, то вы уже занимаетесь ментальной арифметикой! Значит, она уже помогает вашим нейронам работать на полную мощность в то время, как вы играете! Помните, что лучший способ учиться — это учиться с удовольствием.

А если найти хорошего репетитора на Superprof, то прогресс пойдёт ещё быстрее!

Зачем мне учиться считать быстрее?

Как ментальная арифметика может пригодиться

Существует несколько причин для изучения ментальной арифметики и развития ваших способностей считать в уме. Вот краткий список:

• Как только счёт в уме войдёт в привычку, вы сможете больше и лучше концентрироваться на рациональном мышлении. Вы сможете экономить время и, в некоторых случаях, деньги (если речь идёт об игроках в покер или банкирах)
• Путешествуйте налегке: вам больше не понадобится калькулятор с собой. Справедливости ради, стоит отметить, что калькулятор сегодня встроен в телефон, но с ментальной арифметикой вам не придётся доставать его каждый раз, когда надо умножить 8 на 7…
• Только представьте: благодаря вашим тренировках, вы сможете перемножать между собой числа вплоть до 11 и 12
• Вас больше никто и никогда не обсчитает на рынке
• Вы станете меньше пользоваться математическими шпаргалками и подсказками

Открывающиеся для вас перспективы

Если немного заострить внимание на одной из вышеупомянутых причин, то стоит отметить, что вам и правда стоит отточить свои математические навыки, если вы не хотите быть обманутыми — на рынке или где-то ещё, где важно умение правильно обращаться с цифрами.

Кроме того, мысль о том, чтобы впечатлить других людей своими математическими навыками, не так уже поверхностна и тщеславна. Речь идёт не только о межличностных отношениях, но и о финансовой грамотности, которая уж точно никому не повредит.

Как мы уже упоминали, хорошее знание математики поможет вам также выделиться в университете или на собеседовании при поиске работы.

Правда ли, что каждый рождается математиком?

Согласно статистике, молодым людям и правда не хватает математических навыков — во многом из-за системы преподавания математики в школе. Сегодня примерно 50% взрослых не способны решить базовые математические задачи. Если вы чувствуете, что относитесь к этой половине (или что скоро в ней окажетесь), самое время вложиться в математику и усовершенствовать свои знания в этой науке.

Некоторые учёные уверены в том, что каждый может стать экспертом в математике. Они считают, что у любого человека есть способности мыслить логически, но для этого нужно «разблокировать» определённую часть мозга. Вы когда-нибудь слышали о случаях, когда люди получив травму головы, внезапно заговорили на иностранном языке, который они никогда не учили? Представляете, если мы действительно обладаем спящими знаниями и способностями, которые только и ждут, когда же мы откроем дверь к ним, чтобы выйти на свободу?

Если это и правда так, тогда тренировка мозга с помощью ментальной арифметики может стать как раз-таки тем ключом, что откроет дверь к логической части вашего мозга. Как пример того, что всё в этом мире возможно, — статья о мужчине, который стал гением математики после травмы головы.

Это, конечно, не значит, что вам нужно как следует удариться головой. Но увеличение активности в левом полушарии мозга может действительно стать триггером для смены образа мышления.

Поэтому самое время найти опытного репетитора по математике на Superprof.

Существуют ли приёмы для быстрого счёта?

После того, как мы привели вам столько причин для изучения ментальной арифметики, непонятно, чего вы ещё ждёте?

Не волнуйтесь!

Правильно обращаться с цифрами — это всего лишь навык, которому можно обучиться. Математические способности — это не врождённое качество, а приобретённое.

Хотели бы добиться таких же успехов в математике, как героя Дастина Хоффмана в «Человеке дождя»? Источник: Unsplash

Если вам кажется, что некоторые люди просто обладают математическими способностями, это не значит, что они были с ними рождены. Это навык, которому они обучились. Или, возможно, они научились, как использовать свою логическую часть мозга.

Некоторым ученым удалось определить, что ментальная арифметика активирует области мозга, связанные с пространственным мышлением.

Когда мы считаем, неважно, складываем ли мы или отнимаем, мы как бы перемещаем цифры из одного угла в другой, чтобы получить результат.

Правда ли, что считать проще в молодости?

Развивать способность считать в уме полезно и детям, для этого можно применять самые разнообразные педагогические подходы. Игры с использованием чисел и счёта стимулируют соответствующую область мозга.

Так что имейте в виду: играть с детьми в математические ребусы и головоломки — очень полезно для их развития!

Всё ещё сомневаетесь?

Другие исследователи, сфокусировавшиеся на случае Рюдигера Гамма, немецкого «человека-калькулятора», попытались понять, как он справляется с такими сложными вычислениями в уме.

Выяснилось, что, в его случае, «калькулятор» активирует лобные доли мозга, которые обычно связаны с долговременной памятью. Получается, что в распоряжении Гамма находится большой объем памяти, который помогает ему бить рекорды в ментальной арифметике.

И, между прочим, Гамм довольно поздно увлёкся математикой — ему было 20 лет. И именно благодаря ежедневным тренировкам ему удалось развить свои навыки до такого уровня!

Вам стоит помнить о том, что память — ваш лучший союзник в работе с ментальной арифметикой.

Лучшие преподаватели по математике доступны для занятий

Поехали!

Научитесь быстро считать с помощью репетитора

В любом случае, практиковать ментальную арифметику нужно регулярно, примерно десять минут в день. Этого будет достаточно: вашему мозгу нужно довести вычисления до рефлекса, и повторение одних и тех же формул — то, что надо. Дойдите до уровня, когда вычисления станут для вас так же естественны, как езда на велосипеде.

Сначала займёмся математикой полегче! Источник: Unsplash

Ментальную арифметику нужно тренировать как устно, так и письменно, используя специальные тетради с упражнениями, программы и задачники, приложения и так далее.

Важно фиксировать собственные успехи, чтобы вы могли отслеживать прогресс.

Вот несколько базовых подсказок, чтобы прокачать ваши навыки ментальной арифметики:

• Выучите таблицы сложения и умножения
• Выучите состав числа 10
• Выучите квадратную степень чисел до 15 (15² = 225), а также последовательное возведение в степень числа 2 (до 10)
• Выучите умножение на 10 в отрицательной степени (перемещение десятичного знака влево) и положительной степени (перемещение десятичного знака вправо)
• Запомните, что деление на число аналогично умножению на его обратную дробь: например, деление на 0,25 — это то же, самое, что и умножение на 4
• Запомните несколько простых уравнений: (a+b) ² = a²+2ab+b², (a-b) ² = a²-2ab+b², (a+b) (a-b) = a²-b²,
• Изучите правила факторизации
• Запомните число Пи хотя бы до пяти цифр после запятой (3,14159) и золотое сечение (1,618).

Немного практики — и вы научитесь считать в уме без проблем! Источник: Unsplash

Хотите стать Эйнштейном? Вот несколько советов

Изложите проблему на бумаге

Прежде всего, не усложняйте себе жизнь. Никто не ожидает от вас великих открытий в математике. Делать сложнейшие вычисления в голове, одновременно складывать, вычитать, умножать и делить — по силам далеко не всем, а достичь хорошего уровня в ментальной арифметике можно, только если с удовольствием идти по этому пути.

Также помните, что при необходимости вы можете производить расчёты на бумаге. Некоторым легче справиться с вычислениями и другими задачами письменно — так им проще визуализировать. В то же время, другие люди могут удерживать много информации в голове и выполнять сложные вычисления без необходимости останавливаться и перепроверять работу.

Приблизительная точность — ваш друг

Не забывайте, что приблизительная точность может оказать вам существенную помощь при выполнении арифметических упражнений. Примерно определив, каким должен быть результат, вы можете с большей уверенностью продолжать работу. Допустим, вам нужно умножить 60 на 120. Начните с того, чтобы умножить первое число на 100, что гораздо проще и можно выполнить мгновенно. Теперь вы, как минимум, знаете, сколько цифр будет в финальном числе, а это уже кое-что!

Превращайте цифры в фигуры и объекты

Вот ещё один совет: постарайтесь не фокусироваться на цифрах. Попробуйте представлять отдельные числа как визуальные блоки или, для более сложных задач, представляйте части вычислений как строительные блоки. Просто превратив математическое уравнение в картинку, вы измените подход к ней, а это может неожиданно упростить задачу.

Пробуйте выйти за границы цифр. Подумайте о советах и приёмах, которые уже существуют и которые советуют другие люди. Попробуйте придумать собственные чит-коды, которые работают для вас лично.

Если этого недостаточно, продолжайте читать эту статью. Так вы узнаете ещё больше секретов о том, как начать прогрессировать в ментальной арифметике. Возможно, о некоторых из них вы никогда не слышали, и это может полностью изменить ваши представления о математике.

Смотрите на последнюю цифру

Вне зависимости от того, что за число перед вами, смотрите на его последнюю цифру.

Если она чётная (0, 2, 4, 6, 8) или 5, значит, число можно разделить на 2, 5, или 10.

Например, 22 кончается на чётную цифру, значит, его можно разделить на 2, а 45 кончается на 5 и делится на 5.

150 кончается на ноль, значит, делится на 10.

Можно ли разделить число на 3 или 9? Проверяем следующим образом:

Фактически, число делится на 3, если сумма его цифр равна или кратна трём (например, 18 = 1 + 8 = 9, а, значит, кратно трём).

Число делится на 9, если сумма его цифр равна или кратна 9 (пример: 936, 9 + 3 + 6 = 18, из которых 1 + 8 = 9, что кратно 9).

Также помните, что если сумма всех цифр числа делится на 3 и является чётной, то число также делится на 6.

Для сложения

Чтобы упростить задачу, разбейте числа на части.

Например, 72 + 29 — это (70 + 2) + (20 + 9) = (70 + 20) + (2 + 9) = 90 + 11 = 101.

Или, скажем: 13 + 48 — это 13 + (50 — 2) = 63 — 2 = 61.

Для вычитания

Учитесь упрощать числа.

Например: 1958 – 1907. Число 1900 включает в себя оба числа, так что достаточно вычесть: 58 — 7 = 51.

Японский метод умножения

Вы всё ещё не готовы к сложным умножениям в голове?

С этой наглядной японской техникой умножения вы начнёте видеть этапы вычислений яснее.  Всё, что вам нужно, это нарисовать линии, а результат появится по волшебству.

Просто, правда?

Как только вы выучите эту технику, вам станет намного проще производить те же операции в уме. Фактически, представляя эти линии в своей голове, вы можете визуализировать результат, не нуждаясь в ручке и бумаге.

Метод бабочки

Иногда работа с дробями может доставить немало хлопот.

Чтобы сложить или вычесть дроби, нужен единый знаменатель. Чтобы пропустить этот шаг, используйте метод бабочки. Немного практики, и вы сможете это делать в уме!

Например: 3/4 + 2/5

Сначала — перекрёстное умножение: 3 x 5 =15 и 4 x 2 = 8

Теперь сложите полученные числа, чтобы получить финальный числитель: 15 + 8 = 23

Чтобы найти знаменатель, перемножьте два изначальных знаменателя: 4 x 5 =20

Получается: 3/4 + 2/5 = 23/20

Вы также можете использовать эту технику для деления дробей.

И калькулятор больше не понадобится! Источник: Unsplash

Как умножать на 11?

Ничего проще не бывает.

Вот пример: чтобы умножить 32 на 11, вам нужно умножить 32 на 10 и затем добавить к результату 32. Таким образом: 320 + 32 = 352.

Знаете, какая вторая техника? Она и правда очень проста для вычислений в уме.

Для того же примера: 32 x 11, всё, что вам нужно, это сложить две цифры первого числа и поместить результат между ними.

То есть, 3 + 2 =5, ставим результат (5) между 3 и 2 и получаем: 352!

Или другой пример: 56 x 11. Решение будет простым: 5 + 6 = 11, ставим единицу между 5 и 6 и добавляем вторую единицу к пятёрке. Получаем: 616.

Ещё один совет как усовершенствовать ваши вычислительные навыки

• Перед тем, как что-то вычислять, упростите себе задачу. Например, 1,2 / 1,8 = 12 / 18 = 120 / 180
• Те числа, что в сумме дают 10, сгруппируйте вместе, чтобы упростить дальнейшие расчёты: 1 + 9, 2 + 8, 3 + 7 и так далее
• Сложение или вычитание с участием 9, 19, или 29. Просто замените их на 10, 20, или 30, а в конце отнимите или добавьте 1
• Деление на число — то же самое, что умножение на его перевёрнутую дробь
• Чтобы сложить две дроби, приведите их к единому знаменателю

Вот ещё несколько советов!

Онлайн ресурсы для прокачки ментальной арифметики

Чтобы стать лучше в математике и ментальной арифметике, существует множество ресурсов. Всё, что вы можете найти по этой теме в интернете, станет замечательным дополнением к вашим занятиям с репетитором.

Существует немало сайтов, где вы найдёте тесты, упражнения и квизы. Вот несколько из них:

• Khan Academy: здесь вы найдёте видеоуроки, а также практические задания
• internet урок: библиотека видеоуроков школьной программы, конспекты, тесты, тренажёры
• matematika.club: тренажёры по математике для любого класса

Когда вы получаете удовольствие от упражнений, вы даже не замечаете, как учитесь.

На наш взгляд, если вы хотите хорошо освоить математику и, в частности, ментальную арифметику, очень важно многое заучивать наизусть: вы должны выучить формулы и таблицы умножения. Повторяйте их время от времени.

Тренируйте ваш мозг, чтобы вычисления в уме стали для вас простыми и естественными.

Можете использовать разные стратегии для тренировки мозга, чтобы в конце концов всё стало получаться с лёгкостью.

Всё это требует, конечно, времени и личного вовлечения, но результат того стоит — полученные математические рефлексы останутся с вами на всю жизнь.

Используйте игры для тренировки быстрого счёта

Проблема с математикой — распространённое явление среди школьников. Недостаток практики ментальной арифметики может негативно сказаться на их будущем. Исследование, проведённое в 2014 году, показало, что 40% учеников начальной школы имеют проблемы с математикой.

Также исследование показало, что самыми проблемными задачами в начальной школе являются изучение таблицы умножения, деление, десятичные дроби и работа с большими числами.

С учётом этих данных были разработаны новые методики по преподаванию математики, и они включают в себя, как правило, ментальную арифметику. Она состоит из:

• Тренировки рефлексов,
• Развития логического мышления,
• Привыкания к работе с числами,
• Изучения свойств чисел.

Чтобы помочь детям прогрессировать в ментальной арифметике, вы должны убедиться в том, что эта практика доставляет им удовольствие. Надо учиться так, чтобы был интерес! Это отличный способ полюбить и научиться считать.

Продолжайте учиться с удовольствием

Обучение должно быть прогрессирующим. Игры — это хороший способ научиться считать, но для более серьёзных успехов вам понадобится репетитор по математике онлайн.

Сегодня у каждого школьника есть доступ к технологиям, а, значит, можно найти огромное количество приложений и игр для развития математических способностей.

Скачивать приложения стало таким привычным и обыденным процессом, так почему бы не использовать эту возможность для пользы? Просто вбейте «игры математика» в вашем AppStore или GooglePlay и увидите, что список подходящих программ по-настоящему огромен!

Конечно, как родитель, вы можете быть против того, чтобы ребёнок проводил весь день перед мобильным телефоном. Но почему бы не пойти от обратного: разрешить ему играть в телефон, только если это будут полезные игры? Или ограничьте время работы со смартфоном или планшетом до, скажем, 20 минут в день, а из разрешённых приложений оставьте только математические. Вам и не нужно говорить, что это для учёбы — пусть ребёнок воспринимает это, как игру!

Чемпионы мира по ментальной арифметике

Несмотря на то, что математические гении — это редкость, мы всё же должны вам рассказать о самых интересных случаях — чемпионах мира по вычислениям в уме.

Такого рода представления показывают, как далеко могут зайти люди в тренировке мозга и насколько у них получается улучшить свои способности и память. Вот список этих талантливых математиков.

Что у них общего? Высокий IQ, конечно, и, что особенно важно, невероятные способности к ментальной арифметике.

Рюдигер Гамм

Этот человек-калькулятор заинтересовался математикой лишь в 20 лет. Несмотря на то, что у него всегда была хорошая память на числа, он не очень хорошо разбирался в математике в школе. Но благодаря ментальной арифметике он научился специальным техникам для вычислений в уме. Теперь он может возводить двузначные числа в степень 15, делить и умножать сложные числа всего за несколько секунд.

Герт Миттринг

Ещё один невероятный пример! В 2016 Герт Миттринг вычислил корень из числа 89 247 числа за 6 минут 1,4 секунды. В результате получилось более миллиона цифр на 154 страницах. Впечатляет, правда? Теперь понятно, за какие заслуги этот немецкий психолог уже имеет 11 титулов чемпиона мира.

Алексис Лемэр

Алексис Лемэр в 2007 году вычислил корень 13-й степени из 200-значного числа, случайно выбранного компьютером, за 72 секунды. Чтобы получить этот результат, вам нужно умножить число само на себя 13 раз. Проделать такую операцию в уме по силам точно не каждому!

Мир ментальной арифметики действительно завораживает! Теперь вы знаете, что человеческий мозг способен на невероятные вещи. И у вас не осталось причин, чтобы не выучить хотя бы таблицу умножения!

Получайте удовольствие, тренируйтесь, используйте все доступные ресурсы, бросьте вызов самому себе и начните заниматься математикой регулярно. Так вы сможете овладеть ментальной арифметикой и научиться выполнять сложные расчёты в уме!

Сравнение абакуса и русских счет.

Создание видеоуроков по их использованию

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Волков А.В. 1

---

1МАОУ СОШ 15

Васильева И.В. 1

---

1МАОУ СОШ 15

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.

Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Однажды я посетил уроки ментальной арифметики и мне очень понравилось на уроках. Тогда я впервые узнал, что такое ментальная арифметика, попробовав посчитать на абакусе. Но так как уроки были дорогостоящие, тогда мной было принято решение искать информацию в интернете. Где и познакомился с русскими счётами. Тогда у меня возник вопрос: “На чём быстрее и удобнее вычислять?” В этот момент я решил сделать проект на тему вычислений на русских счётах и абакусе, сделав их сравнительный анализ. Поставил перед собой задачу тренироваться на данных вычислительных приборах каждый день, тем самым, нарабатывать вычислительный навык. Кроме этого, я решил сделать и записать видеоуроки, чтобы другие дети тоже смогли узнать о ментальной арифметике.

В ходе написания исследовательской деятельности передо мной была поставлена следующая цель: сравнить абакус и русские счёты, научиться быстро складывать и вычитать на данных приборах.

Для достижения поставленной цели, мной были сформулированы следующие задачи:

1. Собрать информацию об абакусе и русских счётах.

2. Произвести сравнительный анализ данных приборов.

3.Научиться быстро считать на абакусе и русских счётах.

4.Подготовить видеоуроки.

Предметом моего исследования является русские счеты и абакус, а объектом – ментальная математика.

Глава 1. Теоретическая часть

1.1. Ментальная арифметика

Ментальная арифметика – это программа развития умственных способностей и творческого потенциала с помощью арифметических вычислений на счетах, без использования калькулятора, компьютера и других вычислительных приборов… только перекидывая косточки счётов в уме. Обучаясь этой методике ребёнок может решить любые арифметические задачи за несколько секунд (сложение, вычитание, деление, умножение) в уме быстрее, чем с помощью калькулятора.

Ученые полагают, что человек научился считать более 100 тыс. лет назад. Вычислительные операции применялись во время обмена продуктами питания и орудиями труда с другими племенами и для определения времени посадки растений.

Естественными «счетными устройствами» были пальцы рук и ног, которых древним людям вполне хватало для нехитрых расчетов. Результаты счета фиксировались с помощью узелков на веревках или зарубок на ветках деревьев.[1]

Со временем стали появляться более сложные приборы для вычислений. Первым из них считается абак, придуманный в Вавилоне в III тыс. до н. э. Абак представлял собой дощечку с углублениями, по которым передвигали косточки или ракушки, имевшие определенное числовое значение. Такие счетные дощечки служили главным образом для выполнения действий сложения и вычитания. В V в. до н. э. египтяне усовершенствовали Вавилонскую счётную конструкцию, начав использовать вместо линий и углублений проволоку с нанизанными камешками.[2]

Абак завоевал популярность во всем мире, а в ходе продолжительной эволюции сформировались три основных вида абака — китайские, японские и русские счеты. Все они сохранили свое назначение и с успехом применяются до сих пор, к примеру, на занятиях по развитию устного счёта.

Суаньпань — деревянная рамка с рядами натянутых проволочек, на каждой из которых по 7 косточек, — появилась в Китае в XII в.

Китайцы разработали сложную технику работы на суаньпань, позволяющую складывать, вычитать, умножать, делить числа и даже вычислять квадратные и кубические корни.[2]

1.2. Сравнительный анализ “абакуса” и “русских счет”

Абакус — это счётная доска для вычислений, а попросту говоря, счёты,  которыми

впервые начали пользоваться в Месопотамии (примерно в третьем тысячелетии до нашей эры).Абакус кажется очень похожим на советские счеты, которые знакомые большинству ещё с детства. Однако числа обозначаются на абакусе положением на спице, а не количеством косточек. При счёте использованы сразу две руки, это считают полезным, потому что так задействована работа сразу обоих полушарий головного мозга.Абакус появился в 3 тысячелетии до нашей эры в Древнем Вавилоне. Им пользовались в Египте, Древней Индии. В Х веке с абакусом познакомился Герберт Аврилакский — ученый монах, который даже написал об этом книгу — «Правила счета на абаке».

Герберт был с 999 по 1003 годы римским папой под именем Сильвестра II. Он призывал к использованию абакуса и учил этому своих учеников. Благодаря этому — абак распространился по многим странам Европы.[3]

Русские счёты — простое механическое устройство (счётная доска с костями) для выполнения арифметических расчётов, согласно одной версии происходят от китайского счётного приспособления суаньпань, согласно другой имеют собственно русское происхождение.[4]

Представляют собой рамку, имеющую некоторое количество спиц; на них нанизаны костяшки, которых обычно по 10 штук. Счёты являются одним из ранних вычислительных устройств и вплоть до конца 20 века массово использовались в торговле, пока их не заменили калькуляторы.

Таблица 1

Сравнительная таблица абакуса и русских счет

№	Свойства	Абакус	Русские счеты
1	Количество косточек	5	10
2	Количество спиц	15	11
3	Популярность	До сих пор пользуется спросом	Забытые в 20 веке
4	Принцип вычисления	Перемещение косточек от краёв к планке (к центру)	Перемещение косточек справа налево и слева направо
5	Для чего применяются?	Применяются для устных вычислений где-либо, а также в торговле.

Сложение

Чтобы сложить на счетах два числа, нужно набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы понять, как правильно складывать числа на счетах, смотрите пример ниже (рис. 1).

Рис.1. Пример 987 + 134 = 1 121:

Вычитание

Вычитание на счетах производится точно таким же образом, как сложение, – сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже смотрите пример, как правильно считать разность на русских счетах (рис.2). [4]

Рис.2. Пример 121 – 98 = 23

Глава 2. Практическая часть

2.1. Сложение на русских счетах

Пример 1. 325 + 174 = 499 (рис.3).

Шаг 1. Перекидываем справа налево 3 косточки из разряда сотен;

Шаг 2. 2 косточки из разряда десятков;

Шаг 3. 5 косточек из разряда единиц. Начинаем складывать с последнего разряда:

Шаг 4. 1 косточку из разряде сотен;

Шаг 5. 7 косточек из разряда десятков;

Шаг 6. 4 косточки из разряда единиц.

Шаг 7. Считаем количество перекинутых косточек. Ответ: 499.

Рис. 3. Пример 325 + 174 = 499

Пример 2. 481+372=853 (рис.4).

Шаг 1. Перекидываем справа налево 4 косточки из разряда сотен;

Шаг 2. 8 косточек из разряда десятков;

Шаг 3. 1 косточку из разряда единиц. Начинаем складывать с последнего разряда:

Шаг 4. Добавляем 3 косточки из разряда сотен;

Шаг 5. 7 косточек из разряда десятков;

Шаг 6. 2 косточки из разряда единиц.

Шаг 7. Складываем: 4+3=7 (+1) =8

8+7=15 (5 остаётся так как единица, а 10 переходит в разряд сотен) =5

1+2=3 =3. Ответ: 853

Рис. 4. Пример 481+174=853

2.2.Вычитание на русских счетах

Пример 3. 302-136=166 (рис.5).

Шаг 1. Перекидываем справа налево 3 косточки из разряда сотен;

Шаг 2. 0 косточек из разряда десятков;

Шаг 3. 2 косточки из разряда единиц. Начинаем вычитать с первого разряда:

Шаг 4. 6 косточек из разряда единиц;

Шаг 5. 3 косточки из разряда десятков;

Шаг 6. 1 косточку из разряда сотен.

Шаг 7. Считаем количество перекинутых косточек. Ответ:166.

Рис. 5. Пример 302-136=166

Пример 4. 814-713=101 (рис.6).

Шаг 1. Перекидываем справа налево 8 косточек из разряда сотен;

Шаг 2. 1 косточку из разряда десятков;

Шаг 3. 4 косточки из разряда единиц. Начинаем вычитать с первого разряда:

Шаг 4. 3 косточек из разряда единиц;

Шаг 5. 1 косточки из разряда десятков;

Шаг 6. 7 косточку из разряда сотен.

Шаг 7. Считаем количество перекинутых косточек. Ответ:101.

Рис. 6. Пример 814-713=101

2.3. Сложение на абакусе

Пример 5. 325+174=499 (рис. 7)

Шаг 1. Перекидываем 1 косточку сверху вниз из разряда единиц;

Шаг 2. 2 косточки снизу верх из разряда десятков;

Шаг 3. 3 косточки снизу вверх из разряда сотен. Начинаем складывать с первого разряда:

Шаг 4. 4 косточки снизу вверх из разряда единиц;

Шаг 5. 2 косточки снизу вверх и 1 косточку сверху вниз из разряда десятков;

Шаг 6. 1 косточка снизу вверх из разряда сотен;

Шаг 7. Считаем количество косточек. Ответ: 499.

Рис. 7. Пример 325+174=499

Пример 6. 481+372=853 (рис.8).

Шаг 1. Перекидываем 1 косточку сверху вниз из разряда единиц;

Шаг 2. 2 косточки снизу верх из разряда десятков;

Шаг 3. 3 косточки снизу вверх из разряда сотен. Начинаем складывать с первого разряда:

Шаг 4. 4 косточки снизу вверх из разряда единиц;

Шаг 5. 2 косточки снизу вверх и 1 косточку сверху вниз из разряда десятков;

Шаг 6. 1 косточка снизу вверх из разряда сотен;

Шаг 7. Считаем количество косточек. Ответ: 499.

Рис. 8.Пример 481+372=853

2.4.Вычитание на абакусе

Пример 7. 302-136=166 (рис.9).

Шаг 1. Перекидываем 2 косточки снизу вверх из разряда единиц;

Шаг 2. 0 косточек из разряда десятков;

Шаг 3. 3 косточки снизу вверх из разряда сотен. Начинаем вычитать из последнего разряда:

Шаг 4. 1 косточку сверху вниз из разряда сотен;

Шаг 5. 3 косточки сверху вниз из разряда десятков;

Шаг 6. 1 косточка сверху вниз и 1 косточка снизу вверх из разряда единиц;

Шаг 7. Считаем количество косточек. Ответ: 166.

Рис. 9.Пример 302-136=166

Пример 8. 814-713=101 (рис.10).

Шаг 1. Перекидываем 4 косточки снизу вверх в разряде единиц;

Шаг 2. 1 косточка снизу вверх в разряде десятков;

Шаг 3. 3 косточки снизу вверх и 1 косточка сверху вниз в разряде сотен. Начинаем вычитать из последнего разряда:

Шаг 4. 1 косточка снизу вверх и 2 косточки снизу вверх в разряде сотен;

Шаг 5. 1 косточка сверху вниз в разряде десятков;

Шаг 6. 3 косточка сверху вниз в разряде единиц;

Шаг 7. Считаем количество косточек. Ответ: 101.

Рис. 10.Пример 814-713=101

Заключение

В ходе написания исследовательской деятельности была достигнута следующая цель: сравнил абакус и русские счёты, научился быстро складывать и вычитать на данных приборах.

Для достижения поставленной цели, мной были выполнены следующие задачи:

1. Собрал информацию об абакусе и русских счётах.

2. Произвел сравнительный анализ данных приборов.

3.Научился быстро считать на абакусе и русских счётах.

4.Подготовил видеоуроки.

У нас получилось научиться и разобрать, как происходят вычисления на русских счётах и абакусе. Сравнить, чем отличается абакус от русских счёт. Сделать видеоуроки. Поняли, что такое абакус, русские счёты и ментальная арифметика. Чтобы уметь быстро считать, считывать и обрабатывать информацию не обязательно нужно платить за дорогостоящие уроки. Достаточно захотеть научиться и узнать новое!

Список литературы:

1. https://nsportal.ru/ap/library/drugoe/2018/11/24/proektno-issledovatelskaya-rabota-abakus

2. https://abacus-plus.ru/mentalnaya-arifmetika/mentalnaya-arifmetika-kak-instrument-dlya-razvitiya-psixicheskix-processov-rebenka/

3. https://ru.wikipedia.org/wiki/Абакус

4. https://ru.wikipedia.org/wiki/Счёты

Просмотров работы: 790

Умственная арифметика, сложение и вычитание

Умственная арифметика. На предыдущем уроке я предложил ребятам попрактиковаться в умственной арифметике, сложении и вычитании. В этом видео я предложу пару приемов, которые облегчат вам вычисления в уме. Помните, даже если вы получаете калькулятор на GRE, выполнение как можно большего количества вычислений в уме — это огромная экономия времени.

Люди этого не осознают, если вы будете тянуться к калькулятору в каждой отдельной задаче, это займет гораздо больше времени в математическом разделе, и вы столкнетесь с проблемами со временем. В конце может быть цейтнот. Гораздо эффективнее как можно меньше пользоваться калькулятором и как можно больше полагаться на расчеты в уме.

В этом видео я надеюсь научить вас складывать и вычитать в уме любые двузначные числа. Практикуйтесь с этим, пока вы не будете уверены в этом, что значительно укрепит вашу общую уверенность в арифметике. И еще раз позвольте мне сказать, эти, эти трюки, которые я покажу, они могут быть незнакомы, потребуется время, чтобы попрактиковаться в них и привыкнуть к ним.

Но как только вы освоитесь с ними, вы действительно сможете овладеть этим материалом, и это принесет вам огромную пользу. Первый трюк состоит в том, чтобы просто помнить, конечно, что любое двузначное число может быть записано как сумма числа, кратного десяти, и однозначного числа. Так, например, эти числа можно записать так. Кратные десять плюс однозначные числа.

Это обычное разрядное значение, здесь нет ничего особенно сложного. Хорошо. Чем это полезно? Предположим, вам нужно сложить 47 плюс 36. Подумайте об этом таким образом, 47, конечно, это 40 плюс 7, 36 это 30 плюс 6. Мы можем разделить, мы можем сложить отдельно числа, кратные десяти, и однозначные числа.

40 плюс 30 не должно быть слишком плохо, чтобы сделать в уме, а 7 плюс 6 должно быть легко. Итак, мы добавляем их. Теперь нам просто нужно сложить эти две суммы, сложить все вместе, и, конечно же, 70 плюс 13 равно 83. Это сумма исходных двух чисел. А теперь попробуйте некоторые из них самостоятельно.

Возможно, вам будет полезно поставить видео на паузу, когда вы попробуете это. Вот такие результаты. Мы можем использовать этот же факт, по крайней мере, иногда и для вычитания. Если каждая цифра первого числа, цифра десятков и цифра единиц больше, чем соответствующая цифра во втором числе, то мы разделяем по цифрам, чтобы упростить вычитание.

Так, например, если у нас есть 59 минус 31, мы можем представить каждую из них как сумму 10 цифр плюс 1 цифра. Мы можем сгруппировать их, поэтому мы вычитаем числа, кратные 10, и отдельно вычитаем цифры 1. Итак, 50 минус 30, конечно же, 20, 9.минус 1 равно 8, если сложить их вместе, получится 28.

Вот еще несколько задач на вычитание этого жанра. Поставьте видео на паузу и потренируйтесь в голове. Вот такие результаты. А что, если меньшее из двух чисел, которое вы вычитаете, имеет большую цифру?

Например, 56 минус 19, 9 больше, чем 6. Что мы здесь делаем? Ну, для этого мы не можем просто обрабатывать цифры отдельно. Математика в начальной школе учит людей, заимствуя 1 из столбца десятков, но это боль для ментальной математики. Вместо «заимствования» подумайте об этом так.

Если мы вычитаем любые два числа, мы можем добавить новое число к каждому из них, и разница не изменится. Так, например, минус b, минус b будет равно a плюс k минус b плюс k. Другими словами, если мы добавим число k и к a, и к b, разница останется прежней. По сути, при этом мы добавляем как положительное k, так и отрицательное k.

Одно из k прибавляется и одно из k вычитается. И, конечно же, k плюс минус k равно 0, добавление 0 не меняет разницы. Мы воспользуемся этим фактом, прибавив к меньшему числу ровно столько, чтобы оно стало кратным десяти. Например, 56 минус 19.. Ну, 19 на единицу меньше 20, поэтому я добавлю к этому 1.

Ну, если я добавлю 1 к этому, то я должен добавить 1 к другому. Итак, 56 плюс 1 равно 57. 19 плюс 1 равно 20. Затем, когда я делаю вычитание, это просто вычитание десятков цифр. Итак, 50 минус 20 равно 30. Ответ равен 37.

Другой пример. 71 минус 26. 26 на четыре меньше, чем 30, поэтому я хочу добавить к этому 4. Если я добавлю 4 к первому, я должен добавить 4 и ко второму. Я должен добавить 4 к ним обоим. Таким образом, прибавляя 4, 71 перемещаем до 75, 26 перемещаем до 30.

Ну вот опять, нам просто нужно сделать вычитание в разряде десятков, и ответ будет 45. Вот еще несколько примеров для практики. Поставьте видео здесь на паузу и потренируйтесь делать это в уме. И вот результаты здесь.

В общем, занимайтесь арифметикой в ​​уме. Это было первое видео, в котором мы собираемся обсудить математические приемы в уме. Чем больше вы будете изучать эти ментальные математические трюки, применять их и практиковать, тем эффективнее вы будете в количественном разделе, а также тем больше у вас будет уверенности в математике в целом.

Вы можете упростить вычисления в уме для сложения двузначных чисел, рассматривая цифру отдельно. Вы также можете обрабатывать цифру отдельно при вычитании, если в вычитаемом числе обе цифры меньше. И мы также можем просто вычитать, добавляя одно и то же число к обоим терминам.

Уловки для ментальной арифметики Скоростная математика

Уроки ментальной арифметики в этом посте научат вас быстро и легко выполнять ментальную арифметику, которую вы раньше считали невозможной. Вы сможете делать сложные расчеты без помощи калькулятора полностью в вашей голове. Немного потренировавшись, вы быстро освоите эти математические трюки в уме, чтобы быстро считать. Вы окажетесь чрезвычайно уверенно с числами, как вы никогда не были раньше.

Сначала мы рассмотрим несколько простых, но впечатляющих вещей в качестве введения. Затем мы рассмотрим математические приемы в уме, чтобы выполнять сложение и вычитание. В следующем посте мы рассмотрим приемы умножения для ментальной математики. Эти техники требуют, чтобы вы не использовали ничего, кроме своего ума. Вы должны держаться подальше от ручки, бумаги или калькулятора, когда изучаете и применяете методы.

Каждая техника ментальной арифметики будет иметь два примера. Первый пример виден всем, но вам нужно будет зарегистрироваться/войти, чтобы увидеть работу второго примера каждой техники.

Прежде чем мы приступим к математическим приемам в уме, давайте быстро поймем, что такое множимое и множитель. Возьмем, к примеру, задачу на умножение 43 x 23. Здесь 43 — это множимое — число, на которое умножается, а 23 — множитель — число, на которое умножается первое число.

Попробуйте умножить 423 x 11. Это может занять некоторое время, если вы не знаете эту технику. Давайте посмотрим на ментальную арифметическую технику умножения на 11:

1. Первое число множимого (число умножения) записывается как левое число ответа.

1. Каждое последующее число множимого прибавляется к соседнему справа.

1. Последнее число множимого становится правым числом ответа.

Теперь попробуйте умножить 534 x 11. Процедура получения этого ответа та же, что и раньше, и вы можете найти ее ниже:

Попробуйте умножить 619 x 11. Если вы сказали 67109, значит, вы совершили ошибку новичка. о не переносе номера. Перенос чисел — обычное дело в скоростной математике. Шаги для умножения на 11 такие же, как и раньше, но с одним небольшим отличием.

1. Первое число множимого (число умноженное) записывается как левое число ответа, как и раньше.

1. Каждое последующее число множимого прибавляется к своему соседу слева, как и раньше. Если в результате сложения получается две цифры, перенесите 1 (Примечание: двухзначное число не будет больше 19), поэтому вы всегда будете переносить 1.

1. Последнее число множимого становится правым числом ответа, как и раньше.

Теперь попробуйте умножить 348 x 11. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже: мы входим в это, очень важно понять умственные математические приемы для сложения и вычитания, так как это служит основой для умножения. Мы рассмотрим приемы умножения для ментальной математики в следующем посте.

Решение математики справа налево затрудняет мысленную арифметику. Секрет ментальной арифметики заключается в том, чтобы решать слева направо, а не наоборот. В школе нас учат решать справа налево, потому что так легче решать математические задачи на бумаге. Но когда дело доходит до решения математических задач в уме, верно обратное. Когда вы будете решать слева направо, вы начнете называть ответ еще до того, как завершите полный расчет. Сначала это может показаться странным, но вы обнаружите, что это самый естественный способ производить вычисления в уме. Немного потренировавшись, вы научитесь очень быстро решать математические задачи слева направо.

Применение секрета математических приемов в уме к сложению

Применим секрет приемов в уме к сложению двух чисел 9881 + 1234.

Правило простое. Добавляйте слева направо. Одна цифра за раз.

Причина, по которой сложение слева направо происходит быстро, заключается в том, что вам приходится запоминать меньшие числа, когда вы пытаетесь складывать слева направо. Также вы сразу же начнете выкрикивать ответ с самого первого шага процесса.

Теперь попробуйте и сложите 5321 + 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже:

Сложение путем округления

Иногда сложение может привести к много номеров, которые нужно перенести. Самая сложная задача на сложение в уме, которую вы когда-либо могли решить, будет заключаться в том, что вам нужно переносить числа на всех этапах. В этом случае проще добавить его, сначала округлив число, а затем вычтя округленную сумму. Мы рассмотрим, как это сделать, когда будем добавлять 5492 + 8739.

1. Округлите число
в большую сторону.

1. Добавить слева направо

1. Вычтите округленную сумму

Теперь попробуйте сложить числа 9881 + 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти работу ниже: Вычитание

Вычитание в уме ничем не отличается от сложения. Вы просто вычитаете слева направо. Применим секрет математических приемов в уме, чтобы вычесть два числа 8431 – 5741.

1. Правило простое. Вычитание слева направо. Одна цифра за раз. Заимствуйте номера там, где это необходимо.

Теперь попробуйте и вычтите 5389 – 1234. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти ее ниже:

Вычитание путем округления вверх

Вычитание слева направо: легко и просто, когда нет заимствований. Иногда вычитание может привести к тому, что много чисел будет заимствовано у его соседа. В этом случае проще вычесть, округлив число и прибавив округленную сумму. Давайте посмотрим, как это сделать, вычитая 4530 – 389.8

1. Округлить число
в большую сторону

1. Вычесть слева направо

1. Добавьте округленную сумму.

Округляя, вы получаете задачу на сложение вместо задачи на вычитание. В ментальной арифметике немного проще складывать, чем вычитать.

У вас могут возникнуть проблемы с вычислением суммы, которую вы округлили. Есть простой способ узнать, сколько вы собрали. Но прежде чем мы углубимся в это, вы должны вычесть числа 7520 — 49.98 выстрел. Процедура получения этого ответа такая же, как и в предыдущем примере, и вы можете найти работу ниже:

Когда мы вычли 4530 — 3898, мы округлили 3898 до 4000. Вы округлили 102. Это может быть трудно вычислить. сколько вы округлили в этом случае 102. Вам понадобится это, чтобы добавить в конце (Шаг 3 нашего предыдущего примера).

Чтобы узнать, сколько вы округлили при округлении 3898 до 4000, вам нужно использовать дополнения. от 102 до 898 (последние три цифры 3 898 ).

Так как же найти дополнение числа? Это довольно просто. Возьмем, к примеру, 898. Дополнение этого числа также будет состоять из трех цифр. Число (898) должно складываться с дополнением (102), чтобы получить 1000. Первые две цифры дадут 9, а последняя цифра 10.

Если вы заметили:

1. Первая цифра номера (8) и первая цифра его дополнения (1), в сумме дают 9.
2. Аналогично вторая цифра номера (9) и вторая цифра его дополнения (0) в сумме дают 9.
3. Последняя цифра числа (8) и его дополнение (2) в сумме дают 10.

Таким образом, последняя цифра числа должна складываться с последней цифрой его дополнения, чтобы дать 10. Все остальные цифры должны складываться с соответствующей цифрой в дополнении, чтобы дать 9.

Хорошо, помня вышеизложенное, быстро найти дополнение:

47, 351, 4352

Дополнения: 53, 649, 5648.

Все числа будут складываться в дополнение, чтобы дать 9, за исключением последней цифры, которая в сумме дает 10. Используйте дополнения, чтобы узнать, сколько вы округлили при вычитании. Чтобы попрактиковаться в округлении с помощью дополнений, в практической рабочей тетради есть больше упражнений на вычитание.

Вы можете скачать несколько учебных пособий по методам, описанным в этом посте ниже.

Если вы хотите поднять свои математические навыки на новый уровень, вы действительно можете многому научиться на моем личном пути. Я не всегда был хорош в математике. Раньше я ненавидел это и был ужасен в этом. Я снял видео, чтобы поделиться своим личным путешествием и секретом, который я узнал, который навсегда изменил мое отношение к математике. Нажмите здесь, чтобы посмотреть видео сейчас.

Если у вас есть какие-либо вопросы или разъяснения по этому сообщению, опубликуйте их в разделах комментариев ниже. Возможно, вы поняли эту технику, но потребуется практика, прежде чем она станет вашей второй натурой. Поначалу вам обычно будет трудно запомнить все числа в голове, когда вы будете решать задачу. Но ваша память улучшится с практикой. Когда вы обнаружите, что в своей повседневной жизни вам приходится обращаться к калькулятору, сначала посчитайте слева направо, а затем дважды проверьте свой ответ с помощью калькулятора. С практикой ваша скорость и способность считать в уме улучшатся.

Этот пост служит основой для других продвинутых математических трюков в уме. После того, как вы попрактиковались и освоили приемы ментальной арифметики, описанные здесь, вы можете перейти к следующему посту, в котором рассматриваются приемы умножения для ментальной арифметики.

[нижняя часть поста]

Умственная математика с использованием счетов — LifeofMath

Общий: Этот курс предназначен для детей в возрасте от 4,5 до 13 лет. Это лучший возраст для развития навыков устного счета. Первый шаг к полноценному развитию мозга.  

Рекомендуемая возрастная группа: до 5 кг ^th Класс

Исключения: У нас было несколько учеников средней школы, которые выполняли эту курсовую работу, чтобы лучше понять системы счисления, улучшить скорость и улучшить умственные способности для выполнения вычислений.

Предварительное условие: 4,5 / 5 лет должны уметь распознавать и писать 0-9, прежде чем присоединиться к этому курсу

СТРУКТУРА ПРОГРАММЫ ВИДЕОКУРСА

Всего уровней: 7

Стоимость: $159,99 за уровень

В среднем на прохождение одного уровня программы LOM Abacus уходит от 4 до 6 месяцев.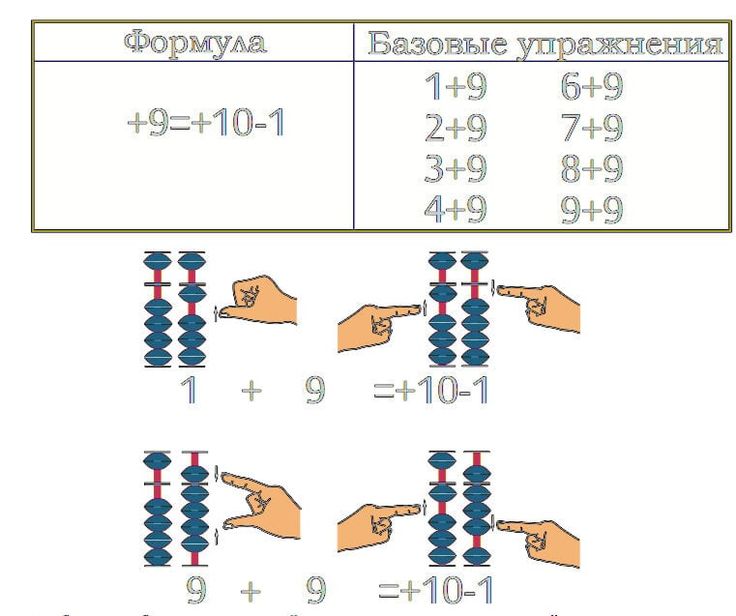 Это может стоить около 650 долларов США за наш физический класс или онлайн-интерактивные занятия с живым учителем в течение 6 месяцев. В варианте видеокурса ребенок может воспроизводить видеообъяснения столько раз, сколько необходимо для лучшего понимания, чтобы пройти уровень.  

ДИСЦИПЛИНА является ключом к успеху ребенка в короткие сроки при использовании видеокурсов.

Физические счеты Инструмент и материал: Эта опция доступна только для жителей США.

Если вам нужны физические счеты и вы хотите, чтобы мы доставили их вам, добавьте 30 долларов США к первому платежу вместе с платой за уровень. Это разовая покупка.

Кроме того, если вы хотите, чтобы мы доставили материалы, это будет стоить 40 долларов за уровень. Доставка 20 долларов. Вы можете отказаться от заданий в формате .pdf вместо физического материала.

Вы можете использовать цифровые счеты вместо физических. Существуют бесплатные, а также некоторые платные приложения, которые позволяют вам загружать инструмент Abacus. Ищите японский Соробан.

Перед покупкой уровня убедитесь, что у вас есть физические или цифровые счеты. Мы можем порекомендовать некоторые приложения, если хотите.

ЧТО ПРЕДОСТАВЛЯЕТ LOM: Каждый уровень будет сопровождаться видеоуроками и заданиями в формате .pdf, которые вы можете распечатать. Рекомендуется распечатать эти страницы с заданиями и попросить ребенка работать над заданиями карандашом. Однако вы можете просто вывести их на экран, а ребенок будет заниматься в блокноте.

Время доступа к видеоурокам: Доступ предоставляется на срок от 4 до 6 месяцев на уровень в зависимости от уровня. Если потребуется больше времени, будет взиматься дополнительная плата в размере 59,99 долларов США в месяц.

Что, если мой ребенок закончит уровень до 4 месяцев?: Учитывая, что ребенок может закончить уровень до 4 месяцев, по запросу на открытие следующего уровня до 4 месяцев доступ к первому уровню будет удален, а следующий уровень будет доступен один раз оплата получена.

  

Получу ли я возмещение или перенос оплаты, если мой ребенок закончит уровень до 4 месяцев?

НЕТ . Цель видеокурсов — дать полную гибкость, чтобы ребенок мог учиться в своем темпе. 159,99 долларов США за уровень — это фиксированная ставка за 4 месяца доступа к видео для каждого уровня.

Политика возврата: НЕ ВОЗВРАЩАЕТСЯ ни в коем случае. Все покупки окончательные. Независимо от того, используете ли вы видеоуроки или .pdf для заданий или нет, после оплаты деньги не возвращаются. Перед покупкой ознакомьтесь с обучающими видео и рабочими таблицами ниже.

Какое участие требуется от родителей? : Родители должны составить план игры, когда ребенок будет регулярно заниматься видеоуроками. Немногие дети требуют, чтобы родители сидели с ними, немногие из них являются независимыми работниками, и немногим требуется мало времени, чтобы понять, как работает процесс. Все зависит от конкретного ученика.