Что такое ментальная арифметика? | Обучение, курсы для детей в Москве

Содержание

История возникновения методики
Польза ментальной арифметики
Принцип работы менара
Когда начать?
Достижение целей и получение результата
Несколько слов о педагогах
Процесс обучения
Изучение ментальной арифметики в академии Itec
Результат занятий

Каждый ребенок стремится к развитию с рождения. Начиная с простых рефлексов и подражательных действий, малыш стремится освоить как можно больше физических навыков и научиться всем интеллектуальным премудростям мира, принятым в его окружении. Как правило, на этом этапе большую роль играет выбор педагога и самой системы развития, по которой ребенок будет ориентироваться в мире наук и творчества. Направление ментальная арифметика появилось на современном российском образовательном небосклоне не так давно и в настоящий момент представляет собой молодую и перспективную методику. Секрет ее успешности – в планомерном развитии логического, абстрактного и конкретного, образного мышления вследствие одновременного обращения к обоим полушариям головного мозга ребенка. Дети, которые учатся ментальной арифметике, считают в уме мгновенно и без ошибок: не только складывают, вычитают, умножают, делят, но и возводят в квадрат и извлекают квадратный корень. Они оперируют цифрами и числами легко и свободно.

История возникновения методики

Новаторскую систему расчёта подарил миру турок Шеном. В ее основе лежат древние счеты – абакус, которые были придуманы в Китае около пяти тысяч лет тому назад. С течением времени их несколько раз усовершенствовали японцы. Методика имела огромный успех и быстро распространялась среди близлежащих и отдаленных стран. Её использовали для обучения детей счету в Индии, Древней Греции и Риме. А одна из доработок абакуса – калькулятор дошла и до наших дней. В 1993 году в Азии впервые прозвучало название «ментальная арифметика» или «менар».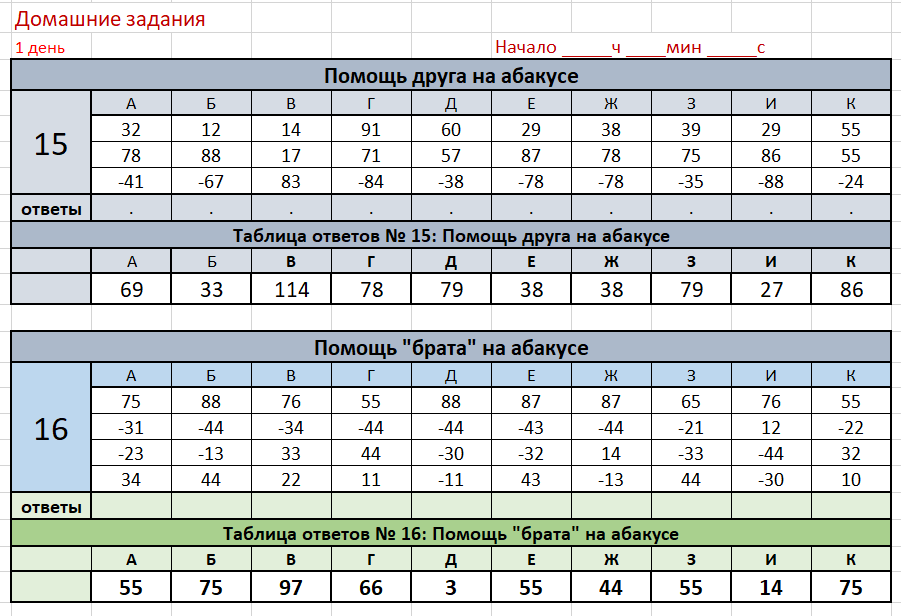

С тех пор программа стала набирать обороты, и на сегодняшний день существует около 5000 образовательных центров в 50 странах мира. Лидерами по применению данной методики в образовательном процессе детей являются такие страны, как Австрия, США, Таиланд, Канада, Австралия, Китай и страны Ближнего Востока. Сегодня школы, преподающие ментальную арифметику, можно также встретить в Киргизии и Казахстане, а в России данная программа переживает пик популярности.

Польза ментальной арифметики

Всем известно, что у человека есть два полушария мозга, и каждое отвечает за свою область: левое – за логику, а правое — за творческое и образное мышление. Развитие обоих полушарий позволяет получить ребенку огромный потенциал на будущее. И в этом ему помогает ментальная арифметика. Во время занятий дети задействуют все области мозга. Весь секрет в том, что для работы на счетах абакус используется сразу две руки: правая, которая активирует левое полушарие и левая – отвечающая за правую долю мозга.

Так, одним из «бонусов» ментальной арифметики, помимо всевозможных вычислений в уме, является развитие аналитических способностей.

Принцип работы менара

Обучение ментальной арифметике делится на два этапа. Первый – работа со счетами абакус и второй – переход на ментальный уровень, предполагающий вычисления в уме, без использования каких-либо приспособлений извне. Работа попеременно обеими руками, активизирующая оба полушария мозга, помогает быстро освоить материал начального уровня и перейти на следующий этап. За счёт работы образного мышления, которое особенно понятно детям, полученная информация легко усваивается и остаётся надолго. Как же происходит переход на ментальный уровень? Если наглядно проследить работу методики в действии, то получается, что левое полушарие мозга ребенка воспринимает цифры, заданные педагогом, а правое – картинку, которая размещена на косточках счетов абакус. Ученик мысленно проецирует в голове счеты и картинку, нарисованную на них, и в голове проводит необходимые операции.

Происходит работа с воображаемым абакусом, где числа воспринимаются ребенком, как картинки, а процесс вычисления ассоциируется с соответствующим движением косточек счетов.

Когда начать?

Начинать изучение ментальной арифметики можно в любом возрасте. Однако учёные выяснили, что наиболее активное развитие мозга у людей происходит с 4-х до 12-ти (реже до 16-ти) лет. И именно в этот период стоит закладывать базисные навыки, такие как изучение иностранных языков, развитие музыкальных и танцевальных способностей, обучение счету, письму и чтению. Полученные за это время знания становятся фундаментальными и позволяют впоследствии легче дополнять, развивать и даже восстанавливать утерянные навыки.

Достижение целей и получение результата

Основной задачей ментальной арифметики является обучение быстрому устному счету, при котором ребенок может складывать между собой десятизначные числа в течении очень короткого временного промежутка (меньше минуты). Однако это далеко не все возможности менара. С помощью данной методики у детей значительно повышается концентрация внимания, происходит развитие фотографической памяти, воображения, логики и слуха. Ребенок может выполнять несколько дел одновременно, с лёгкостью решая творческие и аналитические задачи. Все это придает ему уверенности в себе и позволяет отлично проявить себя в школьной, а затем и в студенческой жизни.

Несколько слов о педагогах

Рассказывая о современной ментальной арифметике, особое внимание стоит уделить педагогам. Как правило, преподавателем менары является человек, за плечами которого лежит не только педагогическое образование, но и диплом психолога. Существуют специальные центры, которые готовят специалистов в данной области. Обязательной ступенью обучения в таких образовательных учреждениях является практика и регулярное посещение курсов повышения квалификации, тренингов, семинаров и пр. Это позволяет не только выпускать специалистов высокого уровня, но и постоянно поддерживать их в «тонусе», не упуская новые тенденции методики.

Также по наличию диплома, количеству сертификатов с различных тренингов и благодарностей родители всегда могут оценить степень квалификации конкретного педагога.

Процесс обучения

В связи с тем, что дети начинают изучать ментальную арифметику в разном возрасте и движутся в процессе обучения с разной скоростью, как правило, в каждом центре есть несколько групп, сформированных согласно особенностям, описанным выше. Несмотря на то, что данный предмет требует большой усидчивости, методические материалы, которые состоят из теоретических пособий, брошюр с практическими заданиями и упражнений на онлайн-платформе, помогают усваивать менару без занудного зазубривания. В процессе игры и взаимодействия со сверстниками и педагогом дети легко и непринуждённо изучают правила счета и устройство абакуса, не думая, что находятся на важном уроке.

Изучение ментальной арифметики в академии Itec

Ментальная арифметика в Академии Itec — это эффективная система развития интеллектуальных способностей детей и подростков (а также взрослых). У нас нет отстающих. У нас каждый — лидер. Ведь занимаясь по такой методике, ребенок перестает бояться трудностей и достигает успеха.

Помимо занятий для школьников и подростков, мы также предлагаем детские курсы ментальной арифметики для детей дошкольного возраста, которые могут стать не просто хорошим досугом, но и прекрасной подготовкой к школе.

С преподавателем дети занимаются один раз в неделю по два академических часа с переменой. У малышей урок длится 35 минут; в средней, старшей и взрослой группах — 45 минут. Время занятий согласовывается с Академией Itec, мы идем навстречу ученикам, и, как правило, нам удается договориться об удобном для всех времени.

Позвольте своему ребенку полюбить математику до школы!

Это путь к новым возможностям и реализации его потенциала!

Полный курс ментальной арифметики — это 10 уровней по 2-3 месяца каждый. Полный процесс освоения ментальной математики занимает 2-2,5 года.

В нашем центре дети занимаются в мини-группах не более 8 человек, преподаватель отслеживает траекторию каждого ученика, чтобы ребенок надежно продвигался вперед.

Уже через три занятия дети, как правило, считают в уме быстрее, малыши легче запоминают цифры (например, номера телефонов родителей), младшие школьники легче заучивают наизусть стихи.

Результат занятий:

1. Умение быстро и точно считать в уме.

2. Хорошая успеваемость в школе по математике и другим предметам.

3. Умение концентрироваться на задаче и принимать решения.

4. Умение анализировать и систематизировать информацию.

5.Конструктивное отношение к ошибкам и позитивность.

6.Хорошая зрительная и слуховая память, хорошо развитые пространственные представления.

7.Высокий творческий потенциал и гибкость мышления.

Ментальная арифметика для детей

Ментальная арифметика для детей 3, 4, 5, 6, 7 лет. Детская академия ITEC

Записаться на пробный урок

5 августа/ 2019

Ментальная арифметика | Сеть школ развития интеллекта Нью-Ньютоны

+7 (991) 924-88-21

Личный кабинет

Раскрываем секрет популярности ментальной арифметики!

Разумеется, уже через 3-4 месяца неизбежны успехи в устном счёте и математике в школе. Этим никого не удивишь. Однако ментальный счёт даёт нечто большее. В процессе обучения и практики у учеников образуются новые нейронные связи между полушариями головного мозга, благодаря чему происходит апгрейд важнейших аспектов мышления: уровня интеллекта, памяти и внимания, наблюдательности и смекалки.

Онлайн-тренажер

Получить урок в подарок!

Ментальная арифметика для детей

Быстрый счет и скорость мыслительных процессов

Талант Цезаря — многозадачность

Фотографическая память и аналитическое мышление

Визуализация и мощное воображение

Слаженная работа обоих полушарий мозга

Обучение ментальной арифметике

Школа развития интеллекта Нью-Ньютоны является сертифицированным членом международной ассоциации ментальной арифметики.

Методика Нью-Ньютонов гарантирует освоение ментального счета каждым учеником вне зависимости от природных способностей к математике.

Секрет успеха – в опыте сертифицированных  педагогов ментальной арифметики, обучающих по строго расписанной методике. Но и без старания ребенка не обходится — пройденные темы должны каждый день закрепляться на онлайн-тренажере ментального счета, который получает наш каждый ученик.

Навыки ментального счета отрабатываются легко и естественно, поскольку каждое занятие наполнено практическими заданиями и играми. Кроме того, уроки дополнены «брейн-фитнесом» (гимнастикой ума) — всевозможными упражнениями на синхронизацию работы обоих полушарий мозга, внимание, концентрацию и логику.

Используются все каналы восприятия: аудиальный, визуальный, кинестетический. Учитываются как психологические, так и возрастные особенности детей.

В группах занимаются от 2 до 8 детей одного возраста.

Дети учатся с удовольствием еще и потому, что каждое занятие – это часть большой игры. В начале курса ученикам выдаются персональные карты достижений – настоящий квест в погоне за знаниями и призами!

Пройденные занятия отмечаются на картах наклейками, а каждая наклейка приближает ребенка к нескольким подаркам в течение года и главному призу в финале годового курса. Так прививается любовь к учёбе и нацеленность на результат.

С какого возраста можно заниматься

ментальной арифметикой?

Минимальный возраст для начала занятий ментальной арифметикой – полные 4 года. Именно в период с 4 до 16 лет у детей наиболее активно развивается головной мозг, в нем происходит рост новых клеток и интенсивное формирование между ними нейронных связей. Ментальная арифметика нужна не только для хороших отметок по математике. Эти занятия направлены на полноценное развитие интеллекта. Отмечено улучшение успеваемости по всем предметам, и даже иностранные языки покоряются намного легче. Ребёнок, владеющий ментальным счетом, ловит буквально на лету любую новую информацию, быстро воспринимая и запоминая её.

Как научиться считать на Абакусе?

Научиться быстро считать в уме можно только на практике, занимаясь с профессиональным тренером. Каждое занятие наполнено практическими заданиями и играми, все навыки отрабатываются легко и естественно. Мы дополнили программу быстрого устного счета «брейн-фитнесом» (гимнастикой ума) — упражнениями на развитие памяти, внимания и логики. Процесс обучения состоит из двух этапов.

Абакус против калькулятора: кто кого?

Переход к быстрому счету в уме

С помощью собственного воображения ребенок производит вычисления, мысленно перемещая бусинки на абакусе. Левым полушарием воспринимаются цифры, правым – образ бусинок абакуса. Навык, полученный в результате обучения, закрепляется на ментальном уровне и остается на всю жизнь.

Обучение счету на абакусе двумя руками.

Постановка техники счета на абакусе обеими руками. Ребенок, считая на косточках, учится быстро решать арифметические примеры. Достигается максимально быстрое выполнение и усвоение действий, поскольку так в работу включаются и правое, и левое полушарие.

 

Записаться на занятия

ментальной арифметикой

Ваше имя

E-mail

Отправка формы…

На сервере произошла ошибка.

Телефон

Спасибо за Ваш интерес!

Совсем скоро мы перезвоним для уточнения удобной даты и времени занятия.

Имя ребёнка

Возраст ребёнка

Город

Повсеместное распространение компьютеров, легко заменяющих людей для решения числовых задач, привело, в итоге, к деградации математического мышления целого поколения. Калькулятор спровоцировал леность ума — молодые люди даже сдачу в магазине проверяют на смартфоне. Неожиданно эту постиндустриальную проблему XXI века решила древняя методика быстрого счета — ментальная арифметика, использующая абакус — специальные счеты, которым уже более 2500 лет. Дети молниеносно решают сложные примеры в уме, не производя арифметических действий, они просто мысленно передвигают косточки на абакусе.

В Россию ментальная арифметика пришла сравнительно недавно, однако в десятках стран она уже введена в обязательную школьную программу. Абакус помог заново научиться современному ребенку не просто думать, но и, подобно Цезарю, делать несколько дел одновременно. Например, быстро решать в уме сложные примеры, выразительно читая по памяти стихи. Так аналитическое и образное мышление тренируются параллельно, обеспечивая невероятный прорыв в развитии интеллекта. Обученные дети тратят на решение каждой задачи меньше времени, чем требуется, чтобы набрать условие на калькуляторе. Поэтому можно сказать, что абакус в этой битве победил!

Ответы на вопросы родителей

• 1. Как проходят занятия? Не устают ли дети?

  Занятия организованы так, что дети в них вовлечены и активно, с удовольствием участвуют. Вперемешку с обучением дети играют в развивающие игры и выполняют упражнения, улучшающие память, внимание, воображение, а также укрепляющие осанку и зрение. После занятий дети прекрасно себя чувствуют, энергичны и в хорошем настроении.

• 2. Сколько человек в группе?

  Количество детей в группах не превышает 6-8 человек, для того чтобы брейн-тренер в ходе занятия уделил достаточно времени каждому.

• 3. В чем уникальность методики?

  Уникальность методики — в гармоничном развитии обоих полушарий мозга. Мы не просто учим детей считать, а занимаемся их всесторонним развитием. Достижение не только в том, что ребенок научается быстро считать большие числа. Это лишь следствие. Дети развивают способность концентрации внимания, наблюдательность, представление, воображение, слух и память.

  Несмотря на свое название, ментальная арифметика не ставит основной своей целью научить ребенка считать или решать математические задачи. Первоочередной задачей курса по ментальной арифметике является всестороннее развитие мозга, а развитый мозг успешнее справляется с задачами, что и ведет к повышению успеваемости в школе по всем предметам.

• 4. Есть ли возрастные ограничения?

  Эффективнее всего начинать обучение с 5–6 лет. Согласно данным ученых, до 14 лет происходит наиболее интенсивное развитие головного мозга. В этот период у детей наблюдается так называемая «пластичность» мозга, что способствует росту клеток мозга и образованию между ними нейронных связей.

• 5. Сколько длится курс обучения?

  Полный курс программы ментальной арифметики составляет 2 года. Первые результаты видны уже через 2 месяца занятий. Занятия проходят 1 раз в неделю (по 1,5 ч. для школьников, по 1 ч. для дошкольников). Плюс ежедневно по 10-15 минут работы на онлайн-тренажере для закрепления навыков ментального счета.

Хотите, чтобы ребенок раскрыл потенциал своего мозга на 100%?

Получить урок в подарок!

Реквизиты:

ООО «НЬЮ-НЬЮТОНЫ»

ОГРН 1165053051327

ИНН 5053043335

КПП 505301001

Оплата занятий

Скорочтение и развитие памяти

О нас

Скорочтение для взрослых

Контакты

Ментальная арифметика

Правила посещения занятий

ТРИЗ

Цены на занятия

Стратегическое мышление

Политика конфиденциальности

Бесплатный урок

Предпринимательское мышление

Визуальное мышление

Франшиза Нью-Ньютонов

Центральный офис: Московская область, г.

Электросталь, ул. Рабочая, д. 37

Телефон: +7 (991) 924-88-21

E-mail: [email protected]

Математика 2-го класса Умственная математика В пределах 20 2.OA.2

Бережливый в третьем классе Кэсси Смит

19,7 тыс. подписчиков

Включает Google Apps™ , слайды и др.).

Также входит в комплект

1. Интерактивные уроки математики для 2-го класса — цифровой пакет Google Classroom

   Вы ищете интерактивный способ привлечь учащихся к уроку математики? Эти цифровые уроки математики идеально подходят для ознакомления с темами или вовлечения учащихся в групповую математическую игру с использованием интерактивной доски! Вы также можете назначить эти цифровые уроки своим ученикам с помощью Go 9.0003

   12

   Продукция

   $ 28,75PRICE $ 28,75 $ 56,502 Цена $ 56,50. Оценка Кэсси Смит

   Вы ищете интерактивный способ вовлечь учащихся в уроки ментальной арифметики? Эти цифровые уроки математики идеально подходят для ознакомления с темами или вовлечения учащихся в групповую математическую игру с использованием интерактивной доски! Вы также можете поручить эти цифровые уроки своим ученикам, используя Google™ Classroom для самостоятельной практики. Они могут стать отличным цифровым математическим центром!

   Это цифровое руководство по математике для 2-го класса включает семь цифровых уроков по математике на тему мысленного сложения и вычитания в пределах 20. Это цифровые уроки в Google™ Slides для использования в Google™ Classroom.

   Эти уроки НЕ включены в разделы «Управляемая математика» в моем магазине. Это цифровые компаньоны, которые вы можете использовать вместе с устройствами.

   Каждый цифровой урок математики включает:

   • Несколько простых для понимания обучающих слайдов
   • Десять практических задач
   • Возможности взаимодействия со слайдами путем перемещения фрагментов, набора текста или и того, и другого

   ❤️ Любимые способы учителей использовать эти уроки:❤️

   • Групповые уроки для ознакомления и отработки тем
   • Интерактивные занятия для всей группы с вашим классом
   • Назначение в Google™ Classroom для самостоятельной практики
   • Использование в качестве цифрового математического центра во время управляемой математики

   Что включено:

   • Урок 1: Добавить десять, чтобы добавить
   • Урок 2: Создание десяти до вычтения
   • Урок 3: Факты
   9003
   • . Урок 5: Двойные числа +1
   • Урок 6: Сложение путем обратного счета
   • Урок 7: Вычитание путем обратного счета

   Этот модуль Digital Guided Math сочетается с этим модулем Digital Guided Math.

   ⭐ Узнайте, как работают цифровые компаньоны, посмотрев это видео. ⭐

   Часто задаваемые вопросы:

   Как получить доступ к цифровой/интерактивной версии?

   Внутри pdf есть ссылка, по которой вы щелкнете и получите копию интерактивной версии Google Slides ™ . Цифровой урок подготовлен и готов к назначению вашим ученикам. (Редактируемые поля готовы для ввода учащимися, а перемещаемые объекты загружены на слайды.) Ключ ответа находится в PDF-файле.

   ©Thrifty в третьем классе

   ВСЕ ПРАВА ЗАЩИЩЕНЫ

   CCSS2.OA.B.2

   Свободно складывать и вычитать в пределах 20, используя умственные стратегии. К концу 2 класса знать наизусть все суммы двух однозначных чисел.

   Вопросы и ответы

   Решения KSEEB для математики для класса 5, глава 3, ментальная арифметика

   Учащиеся могут загрузить главу 3, математика, ментальная арифметика. Доска Syllabus и получить больше баллов на экзаменах.

   Kseeb Class 5 Математическая психическая арифметическая ревизия упражнения

   I. Круглый каждую из следующих чисел до ближайших тысяч человек:

   1. 7 547

   7 547 лежат между 7000 и 8000
   заменить на ноль
   

   2. 3,469
   . 3469 лежат между 2000 и 3000
   Заменить на ноль
   

   3. 15,238
   15,038
   Заменить на ноль
   

   4. 32,658
   32,658
   заменить на Zero616169 61616161619. Округлите каждое из следующих чисел до ближайшего десятитысячного разряда:

   1. 26,674
   26,674
   Replace to zero
   

   2. 32,464
   32,464
   Replace to zero
   

   3. 46,379
   46,379
   Replace to zero
   

   4. 53,668
   53,668
   Replace to zero
   

   III. Оценочная сумма с округлением до тысячного разряда:

   1. 42 125 + 35 637
   42 125 округляется до ближайшей тысячи – 42 000
   35 637 округляется до ближайшей тысячи – 36 000
   
   Оценка Сумма составляет 78 000
   Проверка по фактическому добавлению — 42125
   

   2. 54 837 + 41 354
   54 837 Окружена до Стоящего тысячи — 55 000
   41,354 — округленная спиртная доть. фактическое прибавление
   

   3. 33 231 + 20 097
   33 321 округляется до тысячи – 33 000
   20 097 округляется до тысячи – 20 000
   
   Расчетная сумма 53 000
   Проверка по фактическому дополнению
   

   4. 47 463 + 41 541
   47 463 закруглен до ближайших тысяч — 47 000
   41 541. Оцените сумму следующих чисел путем округления до десятка тысяч:

   1. 56 256 + 24 872
   56 256 округляется до десятка тысяч – 55 000
   24 872 округляется до десятка тысяч – 25 000
   
   Оценка Сумма составляет 80 000
   Проверка по фактическому дополнению
   

   2. 47 671 + 28 745
   47 671 закруглен до ближайших десяти тысяч — 50 000
   28 745. Проверка фактическим сложением
   

   3. 32 184 + 45 138
   32 184 округляется до десяти тысяч – 30 000
   45 138 округляется до десяти тысяч – 50 000
   
   Оценка, сумма 80 000
   Проверка по фактическому добавлению
   

   4. 15 025 + 40,165
   15 025 закруглен до ближайших десяти тысяч — 20 000
   40,165, закругленные до ближайших десяти тысяч — 40 000
   . Сотые вручную ·

   V. Оцените разницу следующих чисел путем округления до ближайшего тысячного разряда:

   1. 65 487 – 46 502
   65 487 округляется до ближайших десяти тысяч – 64 000
   46,502 закруглена до ближайших десяти тысяч — 46 000
   
   Оценка. десять тысяч – 30 000
   
   Расчетная сумма 14 000
   Проверка фактической подстановкой
   

   3. 57 146 – 25 472
   57 146 округляется до десяти тысяч – 56 000
   20 290, округляется до десяти тысяч0161
   Оценка сумма составляет 32 000
   Проверка по фактической подложке
   

   4. 60,046 — 15 247
   60,046 закруглены до ближней десяти тысяч — 60161161 15 247 фактическое вычитание
   

   VI. Оцените разницу следующего округления до десяти тысяч:

   1. 51 689 – 34 685
   51 689 округляется до десяти тысяч – 50 000
   34,685 закруглена до ближайших десяти тысяч — 30 000
   
   Оценка сумма составляет 20 000
   Проверка по фактической подложке
   

   2. 86 853 — 47,829
   86 853 за круглым до десяти тысяч — 85 000 9016 47,8 29.829. — 45 000
   
   Оценка.0161
   Оценка Разница составляет 30 000
   Проверка с помощью фактического субстратиори
   

   4. 77,777 — 44 444
   77 777 закруглен до ближайшего десяти тысяч — 70 000
   444444. фактическое вычитание
   

   VII. Оцените произведение каждого из следующих hy при округлении до большего разряда:

   1. 428 × 54
   428 округляется до ближайшей сотни как 400
   54 округляется до ближайших десяти как 50
   
   Оценочное произведение равно 20 000
   

   2. 878 × 46
   876 округляется до ближайших сотен как 900
   46 округляется до ближайших десяти как 50
   
   

   Проверка фактическим умножением
   

   3. 5 476 × 11
   5 476 округляется до сотен как 5000
   11 округляется до ближайших десяти как 10
   
   Проверка фактическим умножением

   Проверка по фактическому умножению
   

   4. 2645 × 18
   2 645 закруглено до ближайших сотни 3000
   18 VIII. Оцените частное каждого из следующих hy, округлив его до наивысшего разряда.

   1. 398 ÷ 82
   398 округляется до сотен как S 400
   82 округляется до ближайших десятков как ÷ 80
   Оценочное частное \(\frac{800}{40}\) = 5

   2. 786 ÷ 22
   786 округляется до сотен как 800
   22 округляется до ближайших десяти как ÷ 20
   Оценочное частное \( \frac{800}{20}\) = 40

   3. 3,265 ÷ 58
   3,265 округляется до ближайшей сотни как 3000
   58 округляется до ближайшей десятки как ÷ 60
   Расчетное частное \(\frac{3000} {60}\) = 50

   4. 7 687 ÷ 43
   7 687 округляется до сотен как 8000
   43 округляется до ближайших десятков как ÷ 40
   Расчетное частное \(\frac{8000}{40}\) = 200

   IX. Решите следующие проблемы.

   Вопрос 1.
   Швейная компания сшила 16 783 рубашки и 12 438 брюк за месяц. Оцените общее количество сшитых платьев с точностью до десяти тысяч.
   Ответ:
   Швейная компания сшила рубашки – 16 783
   Швейная компания сшила брюки – 12 438.
   (с точностью до десяти тысяч) – 20 000
   (с точностью до десяти тысяч) – 10 000
   
   

   Вопрос 2.
   Агент газеты продает 36 721 газету в первый месяц и 24 172 газеты во второй месяц. Оцените снижение продаж газеты за второй месяц с точностью до десяти тысяч.
   Ответ:
   В первый месяц агенты газеты продают – 36 721
   Во второй месяц агенты газеты продают – 24 172
   (с точностью до десяти тысяч)
   Первый месяц – 40 000
   Второй месяц – 20 000 продажа газеты 20 000

   Вопрос 3.