Состав числа Математика Рабочая тетрадь дошкольника Маврина Л 0+
41
Артикул:
H00000686632
Есть в наличии
45
Скидки от 10% до 25%
Цена действует только при заказе через интернет магазин!
Кол-во товара
В корзину! Перейти в корзину
Избранное Удалить
В избранное!
Сравнить Удалить
Добавить к сравнению
| Система скидок при заказе с сайта | ||
| Сумма заказа | Скидка | Цена товара |
| до 5000 р. | 10% | 41 |
от 5000 р. | 15% | 38 |
| от 10000 р. | 20% | 36 |
| от 15000 р. | 25% | 34 |
- Переплет: мягкий
- Предмет: Математика
- Автор: Маврина
- Класс: 100
- Год выпуска: 2019/2023
- УМК/Линия Учебников: 0
- Тип литературы: Рабочая тетрадь
- Уровень образования: Дошкольное образование
- ISBN: 5-9951-2958-5
- Издательство: Стрекоза
- Относится к УМК: 2019
- Описание
- В наличии: в
1 магазинах
Рабочая тетрадь разработана, чтобы помочь родителям развить способности ребенка.
 Ребенок легко добьется успеха, освоив все необходимые для своего возраста знания. В тетради представлены задания на развитие математических способностей. Для совместных занятий детей и родителей.
Ребенок легко добьется успеха, освоив все необходимые для своего возраста знания. В тетради представлены задания на развитие математических способностей. Для совместных занятий детей и родителей.Название магазина и адрес Время работы магазинов Остаток Учебно-методический центр «Эдвис»
г. Уфа, ул.50 лет СССР, 12
8 (347) 282-52-01Много
| Название магазина и адрес | Время работы магазинов | Остаток | ||
|---|---|---|---|---|
| Учебно-методический центр «Эдвис» г. Уфа, ул.50 лет СССР, 12 8 (347) 282-52-01 | Пн-Сб: 09:00-20:00 Вс: 09:00-19:00 | Много |
«Число 10.
 Состав числа 10″
Состав числа 10″
Тема: Число 10. Состав числа 10.
Тип урока: Ознакомление с новым материалом.
Задачи:
- Познакомить с числом 10 и его составом.
- Учить операциям сложения и вычитания в пределах 10 с опорой на его состав.
- Закрепить знания составов чисел до 9, действий в пределах 9.
- Учить самостоятельности и умению слушать других.
- Развивать речь, память, внимание и логическое мышление.
Ход урока
I. Орг. момент.
— Прозвенел звонок, начинается урок.
II. Актуализация знаний.
— Ребята, посмотрите на доску. В домиках № 7 и № 9 некоторые жильцы получили странное послание. Хотите узнать какое?
— Тогда в тетрадях запишите этих жильцов –
пропущенные числа в парах состава чисел 7 и 9, а на
доске работают двое.
— Сейчас расположите числа в порядке убывания, и в соответствии с буквенным кодом прочитайте им послание. Что у вас получилось?
— Что такое клад?
— Хотите найти математический клад?
— Какими качествами должны обладать кладоискатели?
— А кто ещё всегда ищет клады?
— Откроем учебник на стр. 35 № 8. Посмотрите, пираты нас хотят опередить, они уже на острове. Давайте узнаем, найдут ли они клад, для этого вычислим примеры по стрелкам. Что у вас получилось?
— Что заметили? Верно, ответ предыдущего примера становится началом следующего. Такие примеры называются “круговыми”. Ответ последнего должен быть началом всей цепочки:
— Где можно было ещё замкнуть круг?
— Это нам позволит обогнать пиратов. Пусть они ходят по кругу, а мы пойдём вперёд к цели. Вот и нужное место. Надо копать.
III. Физкультминутка.
Копаем землю и её выбрасываем их ямы (имитация
движений под счёт до 9).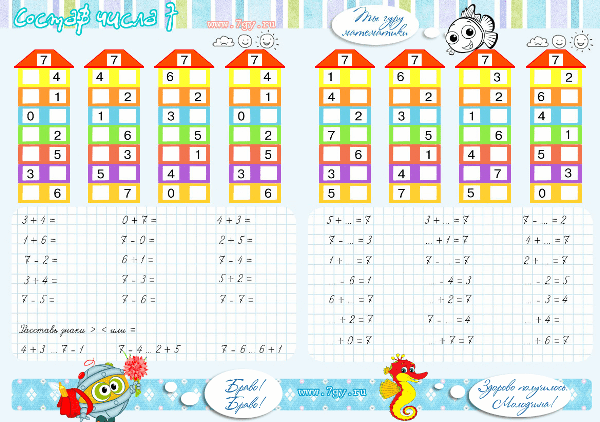
IV. Новый материал.
— Ну, вот и заветный сундук, но на нём замок. На замке числа. Какие, узнаем, выполнив математический диктант. Все пишут в тетради, а на двое доске. Внимание:
— запишите число, следующее за 7 (8)
— запишите число, предыдущее 5 (4)
— запишите число, стоящее между 6 и 8 (7)
— запишите соседей числа 2 (1 и 3)
— запишите число, стоящее справа от 8 (9)
— запишите число, стоящее слева от 6 (5)
— я задумала число, оно предшествует 3 (2)
— Елена Илларьевна задумала число, оно следует за 5 (6)
— Проверяем (взаимопроверка) работу на доске.
— У нас получился числовой ключ, чтобы им открыть замок, надо числа расположить в порядке возрастания. Пишите и диктуйте: (учитель на доске)
1, 2, 3, 4, 5, 6, 7, 8, 9.
— Какое число следует в ряду чисел за 9?
— Вот он и наш клад – число 10!
— Какая же тема нашего урока?
— Чему будем учиться?
— Что знаете про число 10?
— Число 10 – самое маленькое двузначное число, в
записи берутся 2 цифры. Что обозначает цифра 1? Что
у человека есть в количестве 1 десятка?
Что обозначает цифра 1? Что
у человека есть в количестве 1 десятка?
— В тетради запишем строчку числа 10. сколько получилось десятков? Кто знает, какое это число?
— Нам надо разложить 10 алмазов из нашего клада в 2 мешочка. Как можно это сделать? (В тетради – дети, учитель – на доске)
— Что у нас получилось? Какие случаи лишнее? Почему? (По переместительному свойству сложения)
— Что будем запоминать? (Хором, по одиночке, с закрытыми глазами)
— Кто сможет закончить состав 10 в разбивку? (Учитель – 10 это 8 — ученик – 2,
6 — 4 9 — 1 7 — 3 5 — 5)
— У дружных кладоискателей всё делится как? Какой случай из состава подойдёт?
V. Физкультминутка
Физкультминутка
“5 на 5” (5 – прыжков, 5 — хлопков)
VI. Закрепление изученного.
— А сейчас, давайте возьмём другие пары из состава 10. Запишите все взаимосвязанные равенства с: 8 + 2 = 10 (I ряд)
7 + 3 = 10 (II ряд)
6 + 4 = 10 (III ряд)
— Если затрудняетесь, консультируетесь в паре с соседом. Что у вас получилось?
8 + 2 = 10
2 + 8 = 10
10 – 8 = 2
10 – 2 = 8
— Что же за взаимосвязанные равенства должны быть? (Переместительное свойство сложения обратные случаи вычитания)
— Откроем учебник на стр. 39 № 5. Что нужно сделать? Сравним с объяснением:
1 столбик – с опорой на числовой отрезок.
(10 больше 8, т.к. на числовом отрезке стоит справа, 7 меньше 10, т.к. на числовом отрезке стоит слева)
2 столбик – не вычисляя
(10 + 0 = 10 – 0, т.к. нуль есть ничего,
10 – 2 > 10 – 5, т. к. при одинаковом уменьшаемом
чем меньше убираем, тем больше остаётся)
к. при одинаковом уменьшаемом
чем меньше убираем, тем больше остаётся)
3 столбик – не вычисляя
(3 + 7 = 2 + 8, т.к. первое слагаемое убыло на 1, а второе уменьшилось тоже на 1,
1 + 9 > 5 – 5, т.к. справа число самоуничтожается в 0)
— Решим уравнения № 6 (стр 39, по вариантам). Что получилось? Что такое Х?
— В тетрадь решим задачи № 7 (стр. 39). Читаем задачу (а). Какая схема на доске подойдёт к этой задаче? Что подпишем? Ведёт решение ученик на доске. (Аналогичная работа над двумя другими задачами.)
VII. Рефлексия.
— Что сегодня изучали?
— Игра “Часики”: за 1 минуту вы должны восстановить соседей числа 10 на песочных часиках (у каждого ученика – листок с заданием). Приготовились. Начали. Что получилось?
— Встаньте, у кого верные часики.
— Хлопните в ладоши, кому было легко выполнить это задание.
— Подпрыгните 10 раз, кому было интересно сегодня
на уроке.
VIII. Домашнее задание.
— В дневниках д/з – стр. 36.
Композиция функций
«Композиция функций» — это применение одной функции к результатам другой:
Результат f() передается через g()
Записывается: (g º f)(x)
Что означает: g(f(x))
Пример:
f(x) = 2x+3 и g(x) = x 2«x» просто заполнитель . Чтобы избежать путаницы, назовем это просто «ввод»:
f(ввод) = 2(ввод)+3
g(вход) = (вход) 2
Начнем:
(g º f)(x) = g(f(x))
Сначала применим f, затем применим g к результат:
(g º f)(x) = (2x+3) 2
Что, если мы поменяем порядок f и g на ?
(f º g)(x) = f(g(x))
Сначала мы применяем g, затем применяем f к этому результату:
(f º g)(x) = 2x 2 + 3
Получаем другой результат!
Когда мы меняем порядок, результат редко бывает таким же.
Будьте осторожны, какая функция стоит первой.
Символ
Символом композиции является маленький кружок:
(g º f)(x)
Это , а не закрашенная точка: (g · f)(x), так как это означает умножить .
Составлено с самим собой
Мы можем даже составить функцию с самим собой!
Пример:
f(x) = 2x+3
(f º f)(x) = f(f(x))
Сначала мы применяем f, затем применяем f к этому результату:
(f º f)(x) = 2(2x+3)+3 = 4x + 9
Мы должны сделать это без красивой диаграммы:
(f º f)(x)= f(f(x) )
= f(2x+3)
= 2(2x+3)+3
= 4x + 9
Доменов
До сих пор это было легко, но теперь мы должны рассмотреть Доменов функции.
Домен – это набор всех значений , которые входят в функцию.
Функция должна работать для всех значений, которые мы ей даем, поэтому зависит от нас, , чтобы убедиться, что мы правильно определили домен!
Пример: домен для √x (квадратный корень из x)
Мы не можем получить квадратный корень из отрицательного числа (если только мы не используем мнимые числа, но мы ими не являемся), поэтому мы должны исключить отрицательные числа:
Домен √x состоит из всех неотрицательных действительных чисел
В числовой строке это выглядит так:
Используя нотацию конструктора множеств, записывается:
{ x | x ≥ 0}
Или, используя интервальную запись, это:
[0,+∞)
Важно правильно указать Домен, иначе мы получим плохие результаты!
Домен составной функции
Мы должны получить оба домена правильно (композитная функция и первая используемая функция).
При выполнении, например, (g º f)(x) = g(f(x)):
- Убедитесь, что мы правильно получили домен для f(x) ,
- Затем также убедитесь, что g(x) получает правильный домен
Пример:
f(x) = √x и g(x) = x 2Домен f(x) = √x состоит из неотрицательных вещественных чисел
Домен
3 из
g(x) = x 2 все действительные числаСоставная функция:
(g º f)(x) = g(f(x))
= (√x) 2
= x
Теперь «x» обычно имеет домен всех действительных чисел …
… но поскольку это составная функция , мы также должны рассмотрим f(x) ,
Итак, все домены состоят из неотрицательных действительных чисел
Почему оба домена?
Ну представь функции машины… первая проплавляет пламенем дырку (только для металла), вторая просверливает дырку побольше (работает по дереву или металлу):
То, что мы видим в конце, это просверленное отверстие, и мы можем подумать, что «это должно подойти для дерева или металла ». Но если мы подложим дрова в g º f, то первая функция f разожжет огонь и все сожжет! |
Итак, важно то, что происходит «внутри машины».
Разложение функции
Мы можем пойти другим путем и разбить функцию в состав других функций.
Пример:
(x+1/x) 2Эту функцию можно составить из следующих двух функций:
f(x) = x + 1/x
g(x) = x 2
И получаем:
(g º f)(x) = g(f(x))
= g(x + 1/x)
= (x + 1/x) 2
Это может быть полезно, если исходная функция слишком сложна для работы.
Резюме
- «Композиция функций» — это применение одной функции к результатам другой.
- (g º f)(x) = g(f(x)) , сначала применить f(), затем применить g()
- Мы также должны учитывать домен первой функции
- Некоторые функции можно разложить на две (или более) более простые функции.

Математическое сочинение – Подведение итогов
Я близок к финишу в Gattegno Textbook 1. Уже почти два года я пишу этот учебник в блоге. Мы заканчиваем серию «Исследования чисел», написав цифру 9.0289 математическая композиция .
Что такое математическая композиция? Я обсуждал композиции раньше здесь. Короткий ответ: математическая композиция — это набор выражений, которые учащийся пишет для заданного числа или ситуации. В конце изучения числа я прошу П написать как можно больше выражений для этого числа.
По мере того, как наши ученики приобретают опыт, их сочинения должны становиться длиннее, сложнее и креативнее. Здесь вы узнаете, что знает ваш ученик.
Рекомендации по написанию математического сочинения
- Учащиеся должны написать математическое сочинение, не используя стержни. (Мы не следовали этому правилу примерно 6 месяцев назад.)
- Мама не делает предложений.

- Вы можете установить ограничения с самого начала, но не перебивайте учащегося разговором, пока он пытается думать.
- канцелярская кнопкаНеважно, насколько длинна композиция, уж точно не в начале. Важно то, что они берут свои идеи и превращают их в символы.
Зачем писать математические сочинения
Математика в основном происходит в уме. Это не то, что происходит с жезлами или символами на бумаге, это в основном умственная деятельность. Композиции — это тоже умственная деятельность. Люди писали мне по электронной почте и говорили: «Как бы я показал это с помощью стержней…?» Это будет что-то с умножением квадратных корней, или отрицательных многочленов, или что-то в этом роде.
И я часто отвечаю: «Нет». Вы не делаете, потому что нет причин для этого. Если вы показываете, что с стержнями вам нужно сделать резервную копию.
Мы не стремимся конкретизировать каждую ситуацию. Мы хотим, чтобы учащиеся полностью владели символами, чтобы они могли трансформировать любую ситуацию во что-то другое. Иногда для развлечения мы делаем выражения более сложными, но обычно мы превращаем их в нечто более простое.
Иногда для развлечения мы делаем выражения более сложными, но обычно мы превращаем их в нечто более простое.
Я ищу не количество отдельных фактов, которые П. может вспомнить или какие факты он может вспомнить, а скорее его способность применять общие принципы сложения, вычитания, умножения, деления и дробей к определенному числу, начинать где угодно и преобразовывать то, что он знает, в многочисленные выражения.
Есть подсказки, которые я ищу в его письмах. Выражения на изображении ниже были взяты из композиции P.
Математическая композиция — что я замечаю и удивляюсь
Когда P диктует свою композицию, я замечаю и удивляюсь. Что меня интересует, так это мышление П. Мы говорили о добавлении 10 к 11, чтобы увеличить число. Он легко преобразовал то, что знал о сложении, в вычитание. И затем, как вы заметите, он продолжает использовать эту информацию, чтобы генерировать новые математические вычисления.
П. довольно последователен в своих композициях. Он начинает с чего-то и работает систематически. Это улучшение по сравнению с нашей работой в главе 3, где он выбрасывал идеи и факты без видимого порядка.
Он начинает с чего-то и работает систематически. Это улучшение по сравнению с нашей работой в главе 3, где он выбрасывал идеи и факты без видимого порядка.
Здесь он начинает с 21 минус 10, затем прибавляет 10 к 21 и вычитает 20, затем прибавляет 10 и вычитает 30, затем прибавляет еще 10 и вычитает 40. Эти преобразования исходят из нашей работы с общей разницей и лестницами.
Он знает, что 40 равно 4 x 10, так что это было легкое преобразование. Он разделил десятки пополам, а затем удвоил 4 до 8. Я нахожу это интересным, поскольку мы мало работали с делением пополам и удвоением, но поскольку он уже делает это с десятками, я знаю, что он готов. Я вытащу эту композицию, и мы сможем поговорить о его размышлениях, а затем распространим идею на более сложные деления пополам и удвоения.
Мы только что говорили о том, что пятак в квадрате = четвертак. А два пятака в квадрате = пятьдесят центов. Я также заметил, что он взял свои знания об умножении и применил их к квадратным корням.
Он продолжает идти по этому пути, используя свои знания об операциях для создания дополнительных математических вычислений, пока не решит пойти в совершенно другом направлении с 3 x 3 + 2.
Затем он применил свой любимый математический трюк — выполнил операцию, а затем обратный. Он умножил на 2, а затем разделил на 2. Такие вещи вызывают у него смех.
Что я знаю из этого, так это то, что P очень удобно манипулирует десятками, и у него есть хорошее представление о том, как они работают со всеми операциями. У него довольно хорошее представление о квадратах, но не о кубах, хотя мы немного поиграли с ними. Возможно, он просто не додумался использовать их в этой композиции. Он начинает использовать дробные показатели и квадратные корни, но это новинка. Я подозреваю, что ему комфортно только с 5 и 10. Мы хотим больше поиграть с языком в ближайшее время.
Подведение итогов: почему мы не используем рабочие тетради
Хотя это и конец моих постов по изучению чисел для учебника 1, это, конечно, не конец нашей работы с 11. Мы также сделали числа, кратные 11. и заметил и удивился. Я не писал об этом в блоге, потому что Gattegno еще не представил мультипликаторы.
Мы также сделали числа, кратные 11. и заметил и удивился. Я не писал об этом в блоге, потому что Gattegno еще не представил мультипликаторы.
Я также не включил игру с заменой 11. Эта игра больше связана с преобразованиями, а не с конкретным числом. У нас постоянно идет игра замен. Это требует отдельного отдельного поста.
В ходе нашего исследования у нас накопилось много бумаги по 11 исследованиям. Каждая написанная вещь была создана П. Во вступительном и заключительном упражнениях П. был допущен к творчеству. Средние упражнения больше касались изучения и изучения числа как можно больше; отслеживание этих данных; и как только у нас за плечами будет больше исследований в поисках закономерностей.
Если следовать подходу Гаттеньо, рабочие тетради просто отпадут. Учебник, конечно, не даст вам той обратной связи, которую может дать сочинение. Рабочие тетради также не позволят учащемуся серьезно изучить какое-либо конкретное число или ситуацию.
Учащиеся должны писать по математике (или диктовать для детей младшего возраста), чтобы:
- обнаруживать отношения между операциями;
- чувствуют, что обладают властью или властью над предметом;
- убедитесь, что символы имеют личное значение;
- ручная кнопканаучитесь трансформироваться;
- ручная кнопка узнайте секреты построения уравнений.

 Ребенок легко добьется успеха, освоив все необходимые для своего возраста знания. В тетради представлены задания на развитие математических способностей. Для совместных занятий детей и родителей.
Ребенок легко добьется успеха, освоив все необходимые для своего возраста знания. В тетради представлены задания на развитие математических способностей. Для совместных занятий детей и родителей.