Конспект урока «Деление в столбик»

Дата Урок № 32 5 класс

Тема: Деление в столбик

ЦЕЛИ:

Образовательные:

Обобщение и систематизация приобретенных по теме знаний и умений: умение делить многозначные числа столбиком, делить нацело; знание правил нахождения неизвестных компонентов.

Развивающие:

Развивать вычислительные навыки, устную и письменную математическую речь, память

Воспитательные:

Содействовать воспитанию интереса к математике, активности.

Планируемые результаты:

Предметные: уметь выполнять деление в столбик и выполнять проверку умножением; уметь применять алгоритм деления в столбик с нулями

Личностные: формировать внимательность и аккуратность в вычислениях; требовательное отношение к себе и своей работе, настойчивость в достижении цели.
Метапредметные: способствовать развитию способности определять цели и отстаивать свое мнение; определять цель выполнения заданий на уроке.

Тип урока: изучение нового материала.

Оборудование:

Ход урока: 

1. Организационный момент:

2. Актуализация знаний.

Математический диктант

1) от перестановки множителей произведение чисел меняется;

2) если число разделить само на себя, то получится 0;

3) число, на которое умножают, называется множителем;

4) если число умножить на 1, то число изменится;

5) неизвестный множитель находят с помощью действия умножения;

6) 0 можно разделить на любое натуральное число;

7) число, которое делят, называется делителем;

8) в частном х : 20, делимым является х.

Правильные ответы:  0, 0, 1, 0, 0, 1, 0, 1.

1. Формирование темы и целей урока.

Для того чтобы узнать тему урока отгадайте ребус. Запишите тему урока: Деление в столбик. Какие цели поставим перед собой? (Учащиеся формируют цели урока)

1. Изучение нового материала

Для деления чисел из двух и более цифр (знаков) применяют деление в столбик.

По традиции, разбираться как делить столбиком будем на примере.

Вычислить:

Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра 8.

Начинаем делить 512 на 8 следующим образом:

1. Определяем неполное частное. Для этого слева направо сравниваем цифры делимого и делитель.Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого.

1. 51 больше 8. Значит это неполное частное. Ставим точку в частном (под уголком делителя).

Запомните

Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.

Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.

1. Приступаем к делению. Вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение.
   6 · 8 = 48
   Записываем цифру 6 в частное.

Записываем 48 под 51.

Запомните!

При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.

Между 51 и 48 слева поставим «−» (минус). Вычтем по правиламвычитания в столбик48 и под чертой запишем результат.

1. В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.

Запомните!

Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.

Спишем из делимого 512 цифру 2 к 3.

Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение.
8 · 4 = 32

В остатке получился ноль. Значит числа разделились нацело (без остатка).

1. Первичное закрепление знаний

Карточка №1

1 вариант

Билет в общий вагон

(370 + 122): (317 – 313) – 23

1) 429 2) 4 3) 123 4) 100

Билет в купе

91793 : 307 :23 + 138

1) 299 2) 13 3)151

Билет в вагон — люкс

(2356 + 809 – 2841)*106 : 159

1) 3165 2)324 3)34344 4)216

2 вариант

Билет в общий вагон

(458 + 22): (230 – 218) + 60

1) 480 2) 12 3) 40 4) 100

Билет в купе

1092 : 39 * 26 – 577

1)28 2)728 3) 151

Билет в вагон – люкс.

111 + (1485 – 1248)*175:395

1)237 2)41475 3)106 4) 216

Итак, сколько же стоит билет в общий вагон? в купе? вагон – люкс? Сколько у нас человек поедут в общем вагоне? в вагоне – купе? в вагоне – люксе?

1. Итоги урока

2. Домашнее задание

Изучить п. ___, решить №

1. Рефлексия

3

Деление столбиком как научиться

Главная » Разное » Деление столбиком как научиться

Как объяснить ребенку деление столбиком

В процессе обучения в школе очень часто возникает проблема, когда ребенок не смог понять на уроке операцию деления простых чисел. Взрослые думают, что это совсем не сложно. Но школьник сталкивается с этим впервые и не всегда самостоятельно может во всем разобраться.

В такой ситуации родители, набравшись терпения, должны предельно просто и ясно объяснить ему все непонятные моменты. Как правильно и доступно объяснить ребенку деление столбиком, читайте в материалах этой статьи.

Что нужно знать, что бы научиться делить

Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.

Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел.

Без этих основ вряд ли получится проводить арифметические операции с числами. Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен.

Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку». Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик.

Алгоритм деления в столбик

Для решения примеров делением в столбик рекомендуется пользоваться простым алгоритмом.

1. Определить в примере, где находится делимое, а где делитель.
2. Записать делимое и делитель под «уголок».
3. Определить, какая часть делимого может использоваться для первичного деления.
4. Определить сколько раз делитель умещается в выбранной части делимого.
5. Произвести умножение делителя на полученное число под уголком, результат вписать под выбранную часть делимого.
6. Найти разницу (остаток).
7. Повторить действия, пока в остатке не окажется 0.

Более подробно этот алгоритм разберем на конкретном примере.

Методика обучения делению в столбик

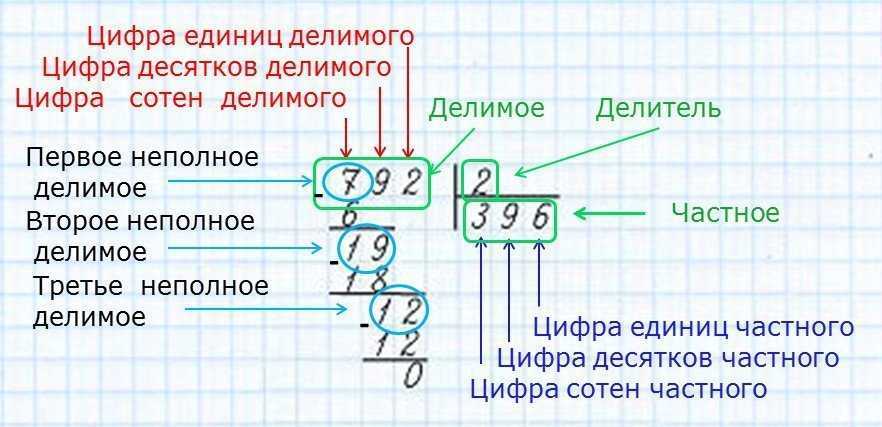
Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.

Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.

Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.

Деление в столбик на конкретном примере

Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.

Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное.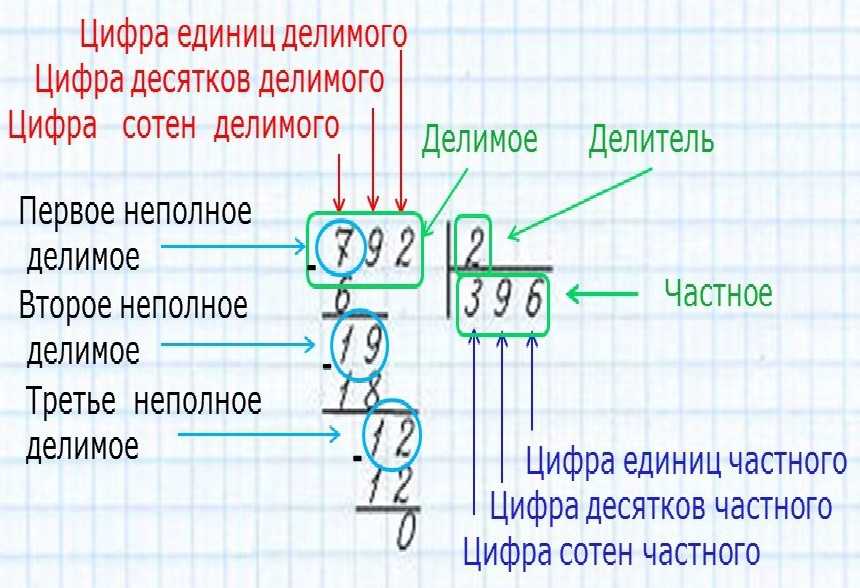 Собственно, это то, что и необходимо найти.

Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».

Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.

Вот и столбик скоро получится.

Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.

Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.

 

Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.

Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.

Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.

Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.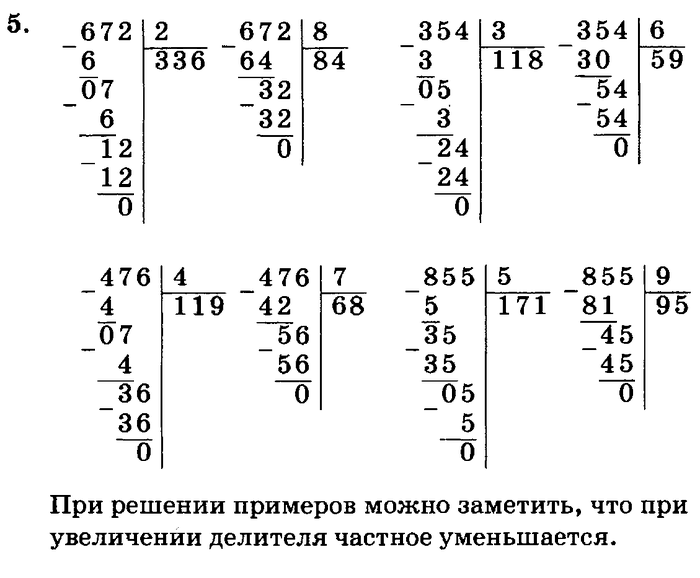

Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей. Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык.

Вместо заключения

Если у ребенка возникают проблемы с учебой, родители должны помочь ему преодолеть любые трудности.

Деление в столбик – программа 2-3 класса, конечно. Для родителей это давно забытые знания, но при необходимости и желании все можно восстановить в памяти и помочь своему школьнику.

Как научить делить в столбик: пошаговый метод

В этой статье я объясню, как обучить делению в столбик в несколько шагов. Вместо того, чтобы показывать студентам сразу весь алгоритм, мы искренне воспринимайте это «шаг за шагом».

До ребенок готов учить деление в столбик, он должен знать:

• таблицы умножения (по крайней мере неплохо)
• базовая концепция деления, основанная на таблицах умножения
  (например, 28 ÷ 7 или 56 ÷ 8)
  
• базовое деление с остатками (например 54 ÷ 7 или 23 ÷ 5)

Одна из причин, почему деление в столбик затруднено

Длинное деление — это алгоритм, который повторяет основные шаги
1) Делить; 2) Умножить; 3) Вычесть; 4) Отбросьте следующую цифру.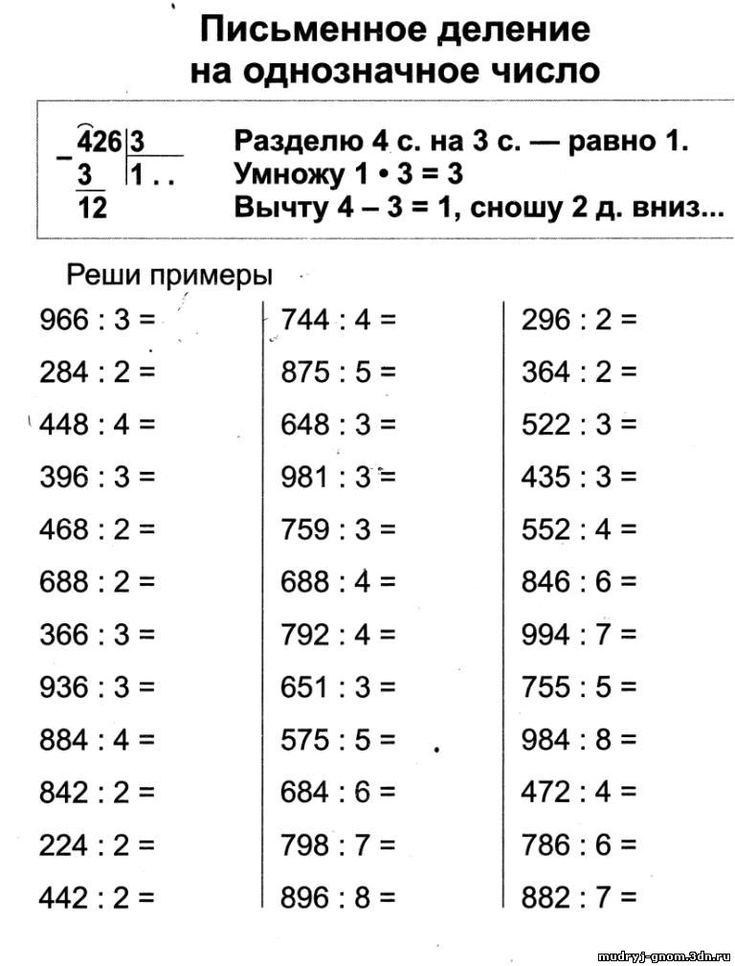

Из этих шагов №2 и №3 могут стать трудными и запутать учащихся, потому что они, по-видимому, не имеют отношения к разделению — они имеют отношение к нахождению остатка. На самом деле, чтобы указать на это, мне нравится объединять их в один «умножить и вычесть» шаг.

Чтобы избежать путаницы, я рекомендую обучать полному делению в таком мода на то, что дети сначала НЕ подвергаются всем этим шагам. Вместо этого вы можете научить этому в несколько «ступенек»:

• Шаг 1: Все цифры четные.Здесь студенты отрабатывают только разделительную часть.
• Шаг 2: Остаток в единицах. Сейчас, студенты практикуют часть «умножить и вычесть» и связать это с поиском остаток.
• Шаг 3: Остаток в десятках. Ученики теперь используйте весь алгоритм, в том числе «отбрасывание следующей цифры», с использованием 2-значного дивиденды.
• Шаг 4: Остаток в любом месте ценности. Студенты практикуют весь алгоритм, используя более длинные дивиденды.
  

Шаг 1.

Деление четное по всем цифрам

Мы делим числа, в которых каждая цифра сотен, десятков и единиц делится на делитель без остатка. ЦЕЛЬ на этом первом легком шаге чтобы студенты привыкли к двум вещам:

1. Чтобы привыкнуть к большому делению «угол», чтобы частное писалось сверху.
2. Чтобы привыкнуть спрашивать, сколько раз делитель переходит в различные цифры делимого.

Ниже приводятся примеры проблем для этого шага. Студенты должны проверить каждый деление на умножение.

На этом этапе ученики также учатся смотреть на первые две цифры делимого, если делитель не «входит» в первую цифру:

ч до 0 4 ) 2 4 8

.

Пошаговое руководство для длинного деления

Что такое длинное деление?

Деление в столбик — это способ решения задач деления с большими числами. По сути, это задачи разделения, которые вы не можете решить в уме.

Начало работы

Одна из проблем, с которой учащиеся сталкиваются с задачами с делением в столбик, — это запоминание всех шагов. Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, которая означает:

.

D = разделить
M = умножить
S = вычесть
B = сбить

Эту последовательность букв трудно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:

Папа, мама, сестра, брат.

Напишите D M S B в углу рабочего листа, чтобы запомнить последовательность, которую вы собираетесь использовать.

Как записать

Во-первых, вы должны записать проблему в формате длинного деления. Типичная задача деления выглядит так:

Дивиденд ÷ Делитель = Частное

Чтобы записать это в формате длинного деления, это выглядит так:

Давайте попробуем довольно простой пример:

65 ÷ 5 =?

Теперь давайте запишем эту проблему в формате длинного деления:

Мы готовы использовать аббревиатуру: D M S B

Шаг 1: D для разделения

Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.

Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ: 1. Итак, вы помещаете 1 в линию частного.

Шаг 2: M для умножения

Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.

Шаг 3: S для вычитания

Затем вы вычитаете.В этом случае это будет 6 — 5 = 1.

Шаг 4: B для обрушения

Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5. Вы пишете 5 рядом с 1, в результате получается число 15.

Теперь вы начинаете все сначала:

Шаг 1: D для разделения

Сколько раз можно разделить 5 на 15.Ответ — 3. Итак, вы ставите 3 на частную.

Шаг 2: M для умножения

Вы умножаете свой ответ, полученный на шаге 1, на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.

Шаг 3: S для вычитания

Теперь вычтем 15 из 15.15 — 15 = 0.

В шаге 4 нет необходимости. Мы решили проблему.

Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.

K5 Learning предлагает несколько бесплатных рабочих листов с полными делениями для 4-го, 5-го и 6-го классов. Проверьте их в нашем центре рабочих листов по математике.

,

Метод деления в столбик объяснил родителям | Как сделать длинное деление

Нужна помощь? Открыть

• Свяжитесь с нами
• Часто задаваемые вопросы
• Что говорят наши подписчики …
• Как посмотреть видео
Зачем присоединяться?

The School Run

Электронная почта или имя пользователя *

Пароль *

• Зарегистрируйтесь бесплатно
• Забыли пароль?

Войти Подписка Зарегистрироваться

Форма поиска

Поиск

Форма поиска

Поиск

Главное меню

• Домой
• Learning Journey
  • Английский
    • Reception English Learning Journey
    • Year 1 English Learning Journey
    • Year 2 English Learning Путешествие
    • Путешествие по изучению английского языка 3-го года
    • Путешествие по изучению английского языка 4-го класса
    • Путешествие по изучению английского языка 5-го года
    • Путешествие по изучению английского языка 6-го года
  • Математика
    • Прием Математика Учебное путешествие
    • Год 1-го года
    Обучение
  2-е учебное путешествие по математике
• 3-е учебное путешествие по математике
• 4-е учебное путешествие по математике
• 5-е учебное путешествие по математике
• 6-го года учебное путешествие по математике

Тема

• 11+ Обучение

Обучение дробям g Journey

Learning Journey

Key Stage 1 SATs Learning Journey

.

---

Смотрите также

• Как научиться осознавать свои чувства
• Как научиться быть с собой в гармонии
• Как научиться быстро грамотно разговаривать
• Как научиться писательскому мастерству
• Как научиться красиво плести
• Как научиться зарабатывать на партнерках
• Как быстро научиться отжиматься девушке от пола с нуля
• Как научиться владеть компьютером
• История как человек научился плавать
• Как научиться не додумывать
• Как научиться держать себя в руках с ребенком

Как делить на длинные числа в Mental Math – World Mental Calculation

Наиболее распространенный метод деления подходит только при делении на маленькие числа или при использовании ручки и бумаги. Умственный расчет более продвинутых делений требует другого метода.

Например, при использовании стандартного метода « деление на » для вычисления в уме 1829 ÷ 7,6543 нам потребуется вычислить кратные 7,6543, например 7,6543 × 3 = 22,9629, и вычесть каждое кратное из остатка, хранящегося в наша рабочая память.

Учитывая, что у всех людей ограниченная рабочая память, это становится неуправляемо трудным по мере увеличения объема вычислений.

К счастью, существует альтернативный метод , основанный на перекрестном умножении, который лишь умеренно нагружает нашу рабочую память и, следовательно, позволяет быстро делить числа произвольного размера с произвольной точностью. Вы можете использовать этот метод для вычисления 123 ÷ π с точностью до ста знаков после запятой, если хотите.

Я (пере)открыла для себя этот метод при подготовке в 2015 году к конкурсу Мемориада, и в этой статье я покажу вам, как это сделать самостоятельно.

Примечание: , когда достаточно оценки, а не многих цифр точности, тогда методы оценки более полезны.

 

Метод перекрестного деления

Чтобы решить 1829 ÷ 7,6543 методом перекрестного деления, мы сначала берем первые 1-2 цифры — в данном случае 76 — которые мы будем использовать для деления. Если ваш умственный расчет силен, вы должны использовать 2 цифры. Если для вас это очень сложно, при некоторых обстоятельствах вы можете использовать только 1 цифру ( 7 ).

Цифры после 76 — в данном случае 543

— будут использоваться для шага перекрестного деления.

Масштаб

765,43 < 1829  < 7654,3 , поэтому ответ будет между 100 и 1000, а первые цифры будут стоять на месте сотен.

Первая цифра

Для получения каждой новой цифры ответа выполняем те же действия — делим текущее число на 76 , вычислив остаток , а затем вычтя некоторые дополнительные условия для учета 543 .

• , потому что 76 × 2 < 182 < 76 × 3 , первая цифра- 2
• Остаток равен 182 – ( 76 × 2 ) = 30
• Умножьте на 10 и добавьте следующую цифру от 1829 , что равно 9 , чтобы дать 309
• Поперечное деление: вычесть 309 – 5 ×  2 = 299

[В следующем шаге я объясню, почему мы вычли 5 × 2 ]

Следующая цифра — с объяснением

Мы просто повторяем те же шаги для каждой новой цифры: 3 6 Потому что 76 × 3 < 299  < 76 × 4 , следующая цифра 3 [ответ 23 0-кое-что]

Остаток равен 299  – ( 76 × 3 ) = 71

Умножьте на 10 и добавьте следующую цифру от 1829 . 000…, что равно 0 , чтобы получить 710

Поперечное деление: вычесть 710 – 5 × 3 – 4 × 2  = 687

Вот как найти вычитание на этапе перекрестного деления:

• Начните со старшей цифры, на которую мы не делим — в данном случае это 5 из 543 , и умножьте это на самая новая цифра ответа — в данном случае это 3 из 23 0 с чем-то.
• Далее продолжайте по цифрам делителя, двигаясь к младшим значащим цифрам ( 4 , затем 3 ) в паре с цифрами ответа (пока только 2 ), продвигаясь к более старым цифрам. Итак, для этого примера у нас есть просто 4 × 2 , но позже у нас может быть больше вычитаний.
• Остановиться, когда либо в ответе больше нет цифр, либо все оставшиеся цифры в делителе равны 0. В этом случае в делителе есть еще одна ненулевая цифра ( 3 ), но нет более ранних цифр в ответ, так что мы уже остановимся.

Поначалу вам потребуется много практики, чтобы научиться разделению крестов, но оно довольно механическое.

Следующая цифра — пример с переполнением выпуска

Продолжение, как и раньше:

• , потому что 76 × < 687 , следующая цифра [Ответ 239 .SMATEL]
• Остаток равен 687  – ( 76 × 9 ) = 3
• Умножить на 10 и добавить следующую цифру от 1829 .000…, что равно 0 , чтобы получить 30
• Поперечное деление: вычесть 30
  – 5 × 9 – …

Здесь у нас проблема, потому что ответ отрицательный! Когда это происходит, это означает, что мы должны были взять меньшее кратное 76 и допустить « неправильный » остаток, больший, чем 76 . Это редко, но случается, когда остаток ( 3 ) очень мал, поэтому с некоторым опытом вы сможете быстро обнаружить такие ситуации! Давайте попробуем:

• Попробуйте использовать 8 для следующей цифры [ответ: 238 .something]
• Остаток равен 687  – ( 76 × 8 ) = 79
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 790
• Поперечное деление: вычесть 790 – 5 × 8  – 4 × 3 – 3 × 2 = 732

Следующая цифра

Продолжение, как и раньше:

• Потому что 76 × < 732 , следующая цифра — [Ответ 238,9 …]
.
• Остаток равен 732  – ( 76 × 9 ) = 48
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 480
• Cross Division: Вычитание 480 — 5
  × — 4 × 8 — 3 × 3 = 394

Следующая цифра

• Потому что 76 × 5 < 394 < 76 × 6 , следующая цифра 5 [Ответ 38.95 ]
.
• Остаток 394  – ( 76 × 5 ) = 14
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 140
• Cross Division: Вычитание 140 — 5 × 5 — 4 × — 3 × 8 = 55

Следующая цифра

• Потому что 55  < 76 × 1 , следующая цифра 0  [ответ 238,950 …]
• Остаток всего 55
• Умножьте на 10 и добавьте следующую цифру от 1829 . 000…, что равно 0 , чтобы получить 550
• Cross Division: Вычитание 550 — 5 × 0 — 4 × 5 — 3 × = 503

Следующая цифра

• Потому что 76 × 6 < 503 < 76 × 7 , следующая цифра — 6 [Ответ 238.9506 …]
• Остаток равен 503  – ( 76 × 6 ) = 47
• Умножьте на 10 и добавьте следующую цифру от 1829 .000…, что равно 0 , чтобы получить 470
• Поперечное деление: вычесть 470  – 5 × 6 – 4 × 0 – 3 × 5  =  425

И так далее, пока не будет достигнута требуемая точность.

 

Наглядный пример

Один из наших читателей представил наглядную иллюстрацию описанного выше метода с тем же примером. Спасибо Эльке Куге — коллеге-тренеру по умственным вычислениям в JMCWC и эксперту по Hectoc!

 

Советы и подсказки

Одноразрядные делители

Для новичков в ментальной арифметике лучше использовать однозначный делитель (например, 76,543 ), а не оставшийся шаг 06, чтобы упростить 3 90.0. Однако это означает, что проблема с переполнением возникает гораздо чаще!

В этом случае 76 является хорошим приближением к 76.543 , поэтому проблема переполнения возникает редко. Но 7 0 намного дальше от 76.543 , так что у вас будут проблемы очень часто.

Поэтому я рекомендую как можно больше использовать двузначные делители.

Подсчет остатков

На первый взгляд, решение, например, 503 — ( 76 × 6 ) = 47 кажется очень сложным, как 76 × 6 = 456 — это сложно, а затем выполнять 503 — 456 без тоже сложно.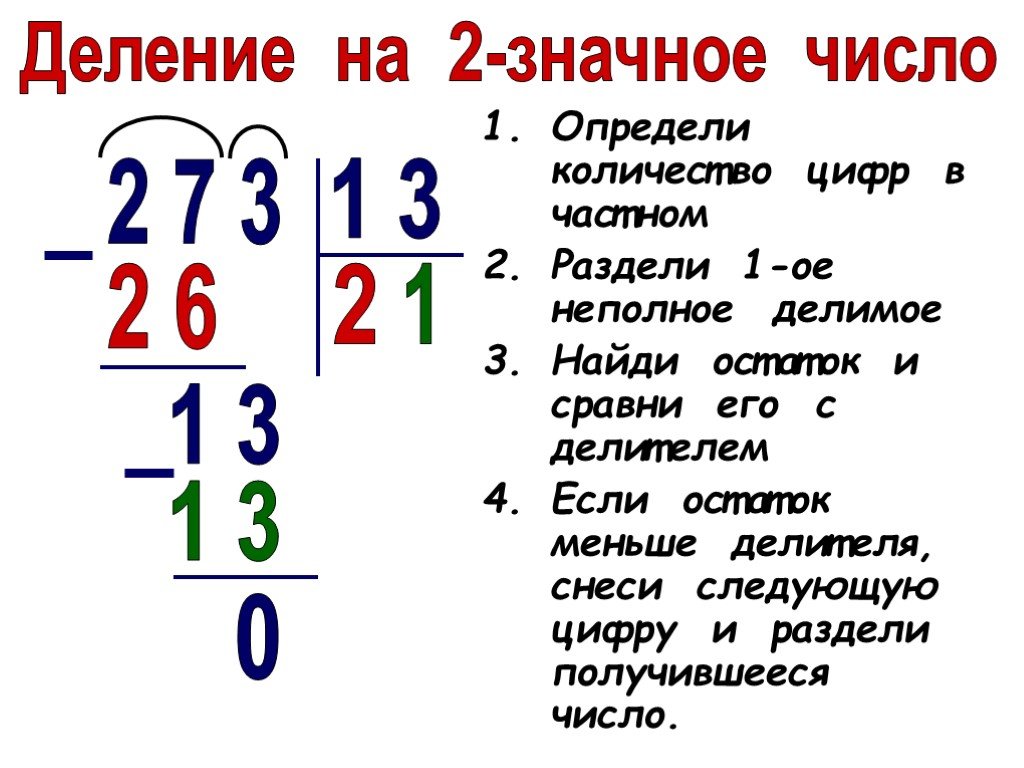

Тем не менее, более простой способ подумать об этом заключается в том, что 76 × 6 = 75 × 6 + еще 6 , так:

503 — ( 76 × 6 6. ) = ( 503 – 450 ) – 6 = 53 – 6 = 47

Разделение этих вычислений остатка в уме значительно облегчает такие вычисления.

Лучшие исполнители

Самые быстрые люди в мире могут вычислить с точностью до десяти цифр менее чем за одну минуту!

Обучение

Для начала предлагаю написать свои вопросы, разделив их на 4 или 5 цифр, но выбрав легкие первые две цифры. Например, 45,123 легко разделить, потому что 45 — это удобное число для умножения, а цифры 123 маленькие, поэтому вы, вероятно, автоматически избегаете проблем с переполнением.

Чтобы связаться со мной (Дэниелом Тиммсом) по поводу обучения умственным вычислениям, коучинга или чего-то еще на этом сайте, вы можете связаться со мной здесь.

Д-р Коттер о делении — RightStart™ Mathematics от Activity for Learning, Inc.

Полное деление раньше считалось конечной целью арифметики. Более ранний алгоритм деления был настолько сложным, что его не изучали до колледжа. Даже сегодня некоторые студенты изучают мнемонику, чтобы помнить, что делать дальше. Одним из примеров является DMSB (разделение, умножение, вычитание, уменьшение). Чтобы сделать его запоминающимся, некоторые учителя даже учат мнемонику для мнемоники: Папа, Мама, Сестра, Брат.

Сегодня учащимся не нужно учить деление на двузначные или трехзначные делители. Они редко будут использовать его в реальной жизни. И никакая продвинутая математика не зависит от изучения этого устаревшего навыка. Один автор предлагает преподавать длинное деление, потому что оно традиционно. Тогда почему бы нам до сих пор не обучать методу нахождения квадратных корней с помощью бумаги и карандаша?

Вместо этого учащиеся должны научиться выполнять короткое деление однозначных делителей, что означает, что частное или ответ записывается без записи каких-либо других промежуточных вычислений. К сожалению, сегодня многие взрослые так и не выучили короткое деление, несмотря на то, что оно появилось в учебниках по математике в 1800-х годах.

Короткое деление

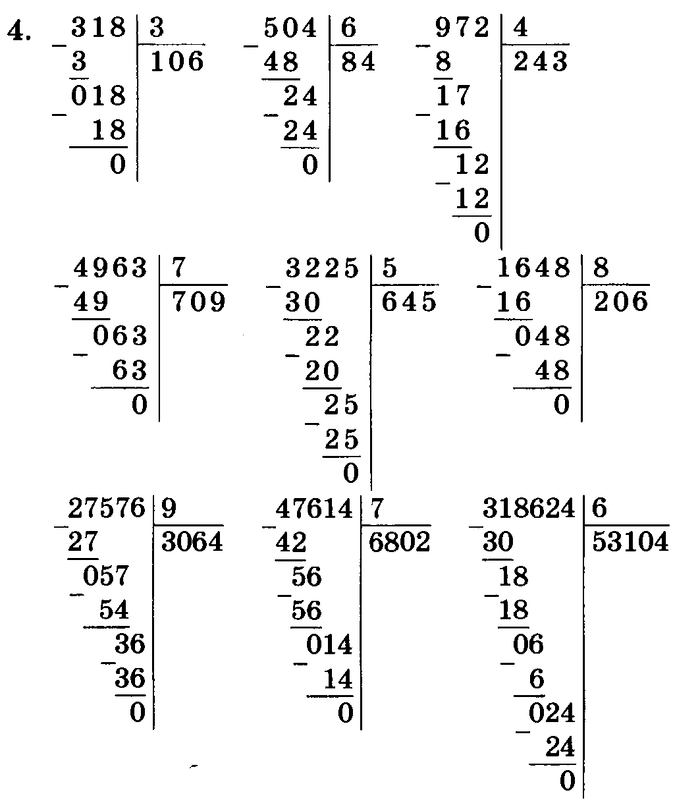
Давайте рассмотрим пример короткого деления: 471 ÷ 3.

Начните с деления сотен, 4 сотни разделить на 3 и получить 1 сотню с 1 сотней в остатке. Запишите 1 в разряде сотен для частного, ответ.

Далее разделите десятки. Поскольку 100 — это 10 десятков, у нас действительно 10 + 7, или 17 десятков. Это показано с маленькой единицей перед 7.

 

   

Разделив 17 десятков на 3, мы получим 5 десятков. Чтобы найти то, что осталось, не думайте, что 3 × 5 = 15, а 17 – 15 равно 2. Это слишком сложно. Лучше подумайте, начиная с 15, как далеко дойти до 17. Ответ — 2 десятка, то есть 20 единиц. Напишите немного 2, как показано ниже.

Наконец, 21 единица разделить на 3 равно 7 единицам. Частное равно 157.

Вот второй пример: 8053 ÷ 9.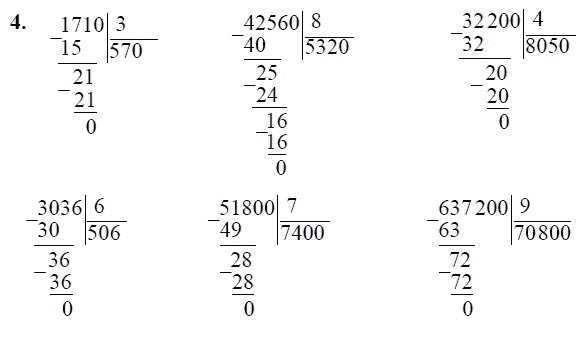

Начиная с разряда тысяч, 8 меньше 9, поэтому переходите к 80 сотням. Тогда 80 сотен разделить на 9 будет 8 сотен. Напишите 8 в разряде сотен в частном. Чтобы узнать, что осталось, умножьте 9 × 8 = 72. Затем увеличьте число от 72 до 80 сотен, что равно 8 сотням, также известным как 80 десятков. К 5 десяткам прибавить 80 десятков, получится 85 десятков; показать, что с небольшим 8 до 5.

Продолжайте, разделив десятки: 85 десятков разделить на 9 будет 9 десятков. Найдите остаток, пройдя от 81 до 85 десятков, что составляет 4 десятка.

Наконец, 43 единицы разделить на 9 будет 4 единицы с остатком 7. Частное равно 894 r7.

Выполнив несколько делений, подобных этому примеру, учащийся увидит закономерность, что остаток записывается перед следующей делимой цифрой.

Остатки

Знание того, что делать с остатком, имеет решающее значение для решения сюжетных задач, связанных с делением. Найдите ответы на следующие пять задач.

1. Тринадцать детей собираются на экскурсию. Если 4 ребенка могут ездить на машине, сколько машин потребуется?

2. Полине нужно посадить 13 петуний. Она хочет ровно 4 подряд. Сколько рядов она может посадить?

3. У четырех детей есть 13 долларов, которые нужно разделить поровну. Сколько получает каждый?

4. Четверо детей делят 13 шоколадных батончиков. Сколько получает каждый?

5. Джек упаковывает 13 печений по 4 штуки в пакет и доедает остатки. Сколько он ест?

Обратите внимание, что числа (13 и 4) и операция (деление) одинаковы для всех пяти задач. Но решения (4, 3, 3,25 доллара, 3 1/4 и 1) разные. Чтобы правильно ответить на такие задачи, нужно применить математику и немного подумать. Они также часто встречаются на тестах.

Длинное деление

Длинное деление можно изучать с точки зрения короткого деления. Вместо того, чтобы записывать оставшееся число перед следующей цифрой, следующая цифра перезаписывается рядом с остатком после вычитания, что приводит к эффекту снижения.