70+ вопросов викторины по математике для забавных упражнений в классе

Математика может быть увлекательной, особенно вопросы викторины по математике если правильно относиться. Кроме того, дети учатся более эффективно, когда занимаются практическими, приятными учебными занятиями и рабочими листами.

Детям всегда не нравится учиться, особенно такой сложный предмет, как математика. Поэтому мы составили список вопросов для детей, чтобы сделать урок математики интересным и информативным.

Эти веселые математические викторины побудят вашего ребенка решить их. Существует множество способов составления простых математических вопросов и ответов. Упражнения в математике с игральными костями, картами, головоломками и таблицами, а также участие в математических играх в классе гарантируют, что ваш ребенок будет эффективно заниматься математикой.

Вот несколько забавных и сложных типов вопросов викторины по математике.

• 17 простых вопросов по математике
• 19 вопросов по математике
• 17 сложных вопросов викторины по математике
• 17 вопросов с несколькими вариантами ответов в викторине по математике
• Takeaways

Поиск увлекательных, увлекательных и в то же время ценных вопросов для викторины по математике может занять у вас много времени. Вот почему мы все уладили для вас.

рядом вопросы викторины по математике, в качестве альтернативы, вы можете найти некоторые увлекательные математические игры для школьников K12 & как сделать зум викторину, или ознакомьтесь с двумя лучшими советами ниже

• Веселые игры, в которые можно играть в классе
• АгаСлайды Спиннер Колесо

Простые вопросы по математике

Начните свою игру с этих простых вопросов по математике, которые обучат и просвещат вас. Мы гарантируем вам, что вы прекрасно проведете время.

1. Число, у которого нет собственного числа?

              Ответ:                           0

2. Назовите единственное четное простое число?

             Ответ: Две

3. Как еще называют периметр круга?

             Ответ: Окружность

4. Каков фактический чистый номер после 7?

             Ответ: 11

5. 53 разделить на четыре сколько будет?

             Ответ: 13

6. Что такое Пи, рациональное или иррациональное число?

             Ответ: Пи — иррациональное число.

7. Какое самое популярное счастливое число от 1 до 9?

             Ответ:  Семь

8.      Сколько секунд в одном дне?

             Ответ: 86,400 секунд

9. Сколько миллиметров в одном литре?

             Ответ: Всего в одном литре 1000 миллиметров.

10. 9*N равно 108. Что такое N?

             Ответ: N = 12

11. Изображение, которое также можно увидеть в трех измерениях?

             Ответ: Голограмма

12. Что предшествует квадриллиону?

             Ответ:  Триллион предшествует квадриллиону

13. Какое число считается «магическим числом»?

           Ответ: Девять.

14. Какой день является числом Пи?

           Ответ: 14 марта.

15. Кто изобрел знак равенства ‘=’?

         Ответ:

Роберт Рекорд.

16. Первоначальное имя Зеро?

             Ответ:  Шифр.

17. Кто первым стал использовать отрицательные числа?

             Ответ: Китайский.

Вопросы по математике

Общие вопросы по математике

С незапамятных времен математика использовалась, о чем свидетельствуют древние сооружения, сохранившиеся до наших дней. Итак, давайте посмотрим на этот математический тест и ответим на вопросы о чудесах и истории математики, чтобы расширить наши знания.

1. Кто является отцом математики?

    Ответ: Архимед

2. Кто открыл Зеро (0)?

    Ответ: Арьябхатта, 458 г. н.э.

3. Среднее первых 50 натуральных чисел?

   Ответ: 25.5

4. Когда День Пи?

   Ответ: Март 14

5. Значение Пи?

   Ответ: 3.14159

6. Значение cos 360°?

   Ответ: 1

7. Назовите углы больше 180 градусов, но меньше 360 градусов.

    Ответ: Рефлекторные углы

8. Кто открыл законы рычага и шкива?

    Ответ: Архимед

9. Кто этот ученый, родившийся в день числа Пи?

    Ответ: Альберт Эйнштейн

10. Кто открыл теорему Пифагора?

     Ответ: Пифагор Самосский

11. Кто открыл Символ Бесконечности «∞»?

       Ответ: Джон Уоллис

12. Кто является отцом алгебры?

       Ответ: Мухаммад ибн Муса аль-Хорезми.

13. Какую часть оборота вы прошли, если встали лицом на запад и повернулись по часовой стрелке лицом на юг?

        Ответ: ¾

14. Кто открыл знак ∮ Контурный интеграл?

      Ответ: Арнольд Зоммерфельд

15. Кто открыл квантор существования ∃ (существует)?

     Ответ: Джузеппе Пеано

17. Откуда взялся «Волшебный квадрат»?

      Ответ: Древний Китай

18. Какой фильм вдохновлен Шринивасой Рамануджаном?

       Ответ: Человек, познавший бесконечность

19. Кто изобрел «∇» символ Набла?

     Ответ: Уильям Роуэн Гамильтон

Сложные вопросы викторины по математике

Теперь давайте проверим некоторые сложные математические вопросы, хорошо? Следующий тест предназначен для начинающих математиков. С наилучшими пожеланиями!

1. Какой последний месяц года с 31 днем?

    Ответ:    Декабрь

 2. Какое математическое слово означает относительный размер чего-либо?

    Ответ:  Шкала

3. Какому числу соответствует 334×7+335?

       Ответ: 2673

4. Как называлась система измерения до того, как мы перешли на метрическую?

     Ответ:   императорский

5. Какому числу соответствует 1203+806+409?

     Ответ: 2418

6. Какой математический термин означает максимально правильный и точный?

    Ответ:  точный

7. Какому числу соответствует 45×25+452?

    Ответ:  1577

8. Какому числу соответствует 807+542+277?

     Ответ: 1626

 9. Каков математический «рецепт» решения чего-либо?

      Ответ:   Формула

10. Как называются деньги, которые вы зарабатываете, оставляя наличные в банке?

     Ответ: Интерес

11.1263+846+429 равно какому числу?

       Ответ:   2538

12. Какие две буквы обозначают миллиметр?

       Ответ: Mm

13. Сколько акров составляет квадратную милю?

       Ответ:  640

 14. Какой единицей является сотая часть метра?

        Ответ: сантиметр

15. Сколько градусов в прямом угле?

      Ответ: 90 градусов

16. Пифагор разработал теорию о каких формах?

     Ответ: Треугольник

17. Сколько ребер у октаэдра?

       Ответ:  12

 

ВНО — Множественный выбор вопросов викторины по математике

Тестовые вопросы с несколькими вариантами ответов, также известные как элементы, являются одними из лучших доступных математических мелочей. Эти вопросы проверят ваши математические способности.

1. Количество часов в неделю?

(a) 60

(b) 3,600

(C) 24

(d) 168

Ответ : D

2. Какой угол образуют стороны 5 и 12 треугольника, стороны которого равны 5, 13 и 12?

а) 60°

(б) 45°

(с) 30°

(г) 90°

Ответ : D

3. Кто независимо от Ньютона изобрел исчисление бесконечно малых и создал двоичную систему?

а) Готфрид Лейбниц

(b) Герман Грассманн

(с) Иоганн Кеплер

(г) Генрих Вебер

Ответ:

4. Кто из перечисленных ниже был великим математиком и астрономом?

а) Арьябхатта

(б) Банабхатта

(с) Дханвантари

(г) Веталбатия

Ответ:

5. Какое определение треугольника в русской евклидовой геометрии?

а) четверть квадрата

(б) Многоугольник

(c) Двумерная плоскость, определяемая любыми тремя точками

г) Фигура, содержащая не менее трех углов

Ответ: c

6. Сколько футов в сажени?

(a) 500

(b) 100

(C) 6

(d) 12

Ответ: C

7. Какой греческий математик III века написал «Элементы геометрии»?

а) Архимед

(б) Эратосфен

(с) Евклид

(г) Пифагор

Ответ: c

8. Как называется основная форма Североамериканского материка на карте?

(площадь

(б) Треугольный

с) Циркуляр

(г) Шестиугольный

Ответ: б

9. Четыре простых числа расположены в порядке возрастания. Сумма первых трех равна 385, а последней — 1001. Самое значимое простое число —

(a) 11

(b) 13

(C) 17

(d) 9

Ответ: B

10 Сумма членов, равноудаленных от начала и конца АП, равна?

(а) Первый срок

(б) Второй срок

в) сумма первого и последнего членов

(г) последний срок

Ответ: c

11. Все натуральные числа и 0 называются _______ числами.

(целое

(б) премьер

(в) целое число

(г) рациональный

Ответ:

12. Какое самое значимое пятизначное число делится точно на 279?

(a) 99603

(b) 99882

(C) 99550

г) ничего из этого

Ответ: б

13. Если + означает ÷, ÷ означает –, – означает x и x означает +, то:

9 + 3 ÷ 5 – 3 х 7 = ?

(a) 5

(b) 15

(C) 25

г) ничего из этого

Ответ : D

14. Резервуар может быть заполнен двумя трубами за 10 и 30 минут соответственно, а третья труба может опорожниться за 20 минут. За сколько времени наполнится бак, если одновременно открыть три трубы?

(а) 10 мин

(б) 8 мин

(в) 7 мин.

г) ничего из этого

Ответ : D

15 . Какое из этих чисел не является квадратом?

(a) 169

(b) 186

(C) 144

(d) 225

Ответ: б

16. Как называется его, если натуральное число имеет ровно два различных делителя?

(а) Целое число

(б) Простое число

(c) Составной номер

(г) Совершенное число

Ответ: B

17. Какой формы имеют сотовые ячейки?

(а) Треугольники

(б) Пентагоны

(в) Квадраты

(г) Шестиугольники

Ответ : D

Вопросы по математике

Takeaways

Когда вы понимаете, что вы изучаете, математика может быть увлекательной, и с помощью этих забавных простых вопросов вы узнаете о самых забавных математических фактах, с которыми вы когда-либо сталкивались.

Ссылка: ischoolconnect

Школьный тест по алгебре: 20 вопросов для отличников и хорошистов — пройти тест онлайн — игра — вопросы с ответами

Выбрав правильный на ваш взгляд вариант ответа, жмите на кнопку «Проверить». Если хотите сразу увидеть правильные ответы, ищите под вопросами ссылку «Посмотреть правильные ответы»

1. 

Дроби бывают правильные и неправильные. Неправильная дробь …

больше 1

меньше 1

равна 1

больше или равна 1

2. 

Что в математике называют хордой? 

Радиус окружности

Прямую, соединяющую две точки кривой

Половину окружности

3. 

У какой фигуры только два катета? 

Прямоугольный треугольник

Квадрат

Прямоугольник

Ромб 

4. 

Если прямая имеет с окружностью две точки пересечения, то она назвается …

режущая

отсекающая

секущая

делящая 

5. 

Число π — это …

отношению длины окружности к её диаметру

отношение длины катета равнобедренного треугольника к его гипотенузе

отношению длины окружности к её радиусу

6.

 

Что такое ковариация в теории вероятностей?

Мера линейной зависимости двух случайных величин

Степень возможности наступления некоторого события

Многомерная функция распределения

7. 

Если в конце десятичной дроби добавить три нуля, измениться ли её значение?

Да, станет больше по своему значение

Да, станет меньше по своему значение

Нет

8. 

Слово «алгебра» произошло от арабского «аль-джабр». В переводе это …

«вычисление»

«понимание»

«восполнение»

9. 

Давайте вспомним графики! Каким он будет у линейной функции? 

Это прямая

Это парабола

Это синусоида

Это гипербола

10. 

Самые умные с предыдущим вопросом справились легко. Усложняем! График квадратичной функции — это …

гипербола

синусоида

парабола

11. 

Представьте себе треугольник, стороны которого равны 17, 10 и 15 см. Чему равна сумма его углов?

360°

180°

120°

12. 

По улице идут два отца и два сына. Сколько людей при этом может идти по улице?

Три или четыре

Два или четыре

Только четыре

13. 

Вспомните колесо европейской рулетки. Она разбита на 37 секторов с числами. Чему будет равно произведение всех этих чисел?

666

777

0

14. 

Что и с чем соединяет медиана? 

Две любые точки окружности

Противоположные углы квадрата или прямоугольника

Вершину треугольника с серединой противоположной стороны

15.

 

Косая сажень — это некогда распространённая на Руси единица измерения. Между чем и чем её расстояние?

Между кончиками пальцев разведённых в стороны рук: одна смещена вниз, другая вверх 

Между кончиков пальцев вытянутой вверх руки и пальцев противоположной ей ноги

Между кончиками пальцами двух ног растянутых в шпагат

16. 

Сажень бывает не только косой, но и прямой. К чему она приравнялась во времена Петра І, когда русские меры длины тех времён были уравнены с английскими?

7 английских футов

28 английских дюймов

7 футов и 28 английских дюймов

17. 

Аппроксимация — это …

умножение

деление

приближение

удаление 

18. 

Число, которое делится только на себя и на 1 называется в математике …

натуральным числом

сложным числом

ненатуральным числом

простым числом

19.

 

Какие буквы используются в шестнадцатеричной системе исчисления? Выберите ответ, в котором есть они все. 

A, B, C

A, B, C, D, E

A, B, C, D, E, F

20. 

Все математики любят делить и умножать. А что они получают, если делят синус угла на его косинус?

тангенс

котангенс

косинус 

Проверить посмотреть правильные ответы рестарт

Подпишитесь на нас в ВКонтакте, чтобы не пропускать наши новинки.

Mathematics Practice Questions 1

1. В магазине инструментов всем учащимся предоставляется скидка 10% от первоначальной стоимости инструмента. Во время распродажи «Снова в школу» скидка составляет 15% от цены со скидкой. Джули, ученица местной средней школы, покупает флейту за 306 долларов. Сколько он стоил изначально?

1. 325
2. 375
3. 400
4. 408
5. 425

2.

Если y (x-1) = z, то x =

1. Y-Z
2. z/y + 1
3. y(z-1)
4. z(y-1)
5. 1-zy

3. Какое из следующих значений НЕ равно 34(58+9)?

1. 34 * 67
2. 58 (34 + 9)
3. 34 * 58 + 34 * 9
4. 1 972 + 306
5. (9 + 58) 34

4. Два углы из меры треугольника. 85°. Чему равен третий угол?

1. 50°
2. 55°
3. 60°
4. 80°
5. 90°

5. Если 5 унций равны 140 граммам молотого мяса, то сколько граммов мяса составляет 2 фунта?

1. 863
2. 878
3. 896
4. 915
5. 932

6. В каком году больше всего детей занималось плаванием?

1. 1990
2. 1991
3. 1992
4. 1994
5. 1995

7. Между каким годом произошло наибольшее сокращение детей, занимающихся плаванием?

1. 1990-1991
2. 1991-1992
3. 1992-1993
4. 1993-1994
5. 1994-1995

8.

Сколько в среднем детей посещало уроки плавания с 1990 по 1995 год?

1. 250
2. 308
3. 385
4. 450
5. 1850

9. Какое из следующих чисел равно 5,93 * 10-2?

1. 0,0593
2. 0,00593
3. 593
4. 5930
5. 59300

10. На карте 201 миля. Расстояние между двумя городами равно 6 1/5 дюйма. Сколько миль на самом деле между двумя городами?

1. 65 миль
2. 84 мили
3. 124 мили
4. 138 миль
5. 145 миль

11. Какой из следующих графиков является правильным графиком x>1, x

<4?

1. Строка A
2. Строка B
3. Строка C
4. Строка D
5. Строка E

глубина на 12 дюймов в ширину и 9 дюймов в высоту, при этом крышка все еще может быть закрыта?

1. 18
2. 24
3. 32
4. 36
5. 43

13. Сара вдвое старше своего младшего брата. Если разница между их возрастами составляет 15 лет.

Сколько лет ее младшему брату?

1. 10
2. 15
3. 20
4. 25
5. 30

Какая из следующих дробей равна 6

/ 8 ?

1. ²⁰ / ₃₀
2. ¹⁵ / ₂₄
3. ²⁵ / ₃₀
4. ⁴⁰ / ₅₄
5. ² /
6. ² /
8. ² /
10. ² /
12. ² /
14. ² /
15. шириной на 20 футов в длину, если плитка стоит 8,91 доллара за квадратный ярд?
    1. 224,51
    2. 237,6
    3. 246,55
    4. 271,38
    5. 282,32

    Второй занявший второе место получает ¼ того, что выиграл победитель. Какова общая сумма призовых, если победитель получит 6000 долларов?

    1. 6000$
    2. 8500$
    3. 12000$
    4. 15000$
    5. 18500$

    17.

    Вы находитесь в футах от дерева 120 Вы смотрите на вершину дерева. Приблизительно на каком расстоянии от вершины дерева по прямой находится ваш слух?
    1. 50 футов
    2. 75 футов
    3. 120 футов
    4. 130 футов
    5. 150 футов

    Какова средняя скорость велосипедиста за поездку туда и обратно в милях в час?

    1. 8.1
    2. 8,3
    3. 8,6
    4. 8,9
    5. 9,0

    19. Если бывание стоила 2,32 долл. США за 12-дюймовый камень, и вы хотите двойной слой края вокруг вашей цветочной кровати, который составляет 6 ярдов 1 ярды. . Сколько будет стоить окантовка вашей клумбы?

    1. $32.48
    2. $64.96
    3. $97.44
    4. $129.92
    5. $194.88

    20. If 3x=6x-15 then x + 8=

    1. 5
    2. 10
    3. 11
    4. 12
    5. 13

    21. Количество миллилитрах в 1 литр составляет

    1. 10 000
    2. 1000
    3. 0,1
    4. 0,01
    5. 0,001

    22.

    и водитель с дополнительной стоимостью 50 центов за пассажира. Если плата за посадку на паром составляет 6,50 долларов, сколько человек было в машине?
    1. 1
    2. 2
    3. 3
    4. 4
    5. 5

    23. Что такое

    ¹ / ₉ из 9?
    1. ¹ / ₉
    2. 0
    3. 1
    4. 2
    5. 3

    24. В своем кармане мальчик имеет 3 красных шарика, 4 синих шарика и 4 зеленых храмовых. Сколько ему придется вынуть из кармана, чтобы убедиться, что он вынул хотя бы по одной фишке каждого цвета?

    1. 3
    2. 7
    3. 8
    4. 9
    5. 11

    25. Какая дробь равна 0,20%?

    1. ¹ / ₂₀
    2. _{¹ /40}
    3. ¹ / ₅₀
    4. ¹ / ₄₀₀
    5. ¹ / ₅₀₀

    26 Найдите пропущенный член в следующей последовательности: 4, 9, 19, __, 79

    1. 36
    2. 37
    3. 38
    4. 39
    5. 40

    апрель 2001?

    1. $ 617,80
    2. $ 620,92
    3. $ 622,50
    4. $ 626,38
    5. $ 633,20

    28.

    Какова средняя сумма денег, которую бюджет Джессики позволила для одежды первые шесть месяцев 2001 года?
    1. $ 249,90
    2. $ 250,40
    3. $ 251,32
    4. $ 253,33
    5. $ 255,75

    29. Если Джессика потратила только 20% вместо 25% запланированного на еду в мае 2001 года.

    1. 131,10 $
    2. 144,30 $
    3. $ 148,32
    4. $ 152,22
    5. $ 153,33

    Работая вместе, сколько времени им потребуется, чтобы напечатать один и тот же документ?

    1. 5 минут
    2. 10 минут
    3. 15 минут
    4. 18 минут
    5. 20 минут

    31. Из следующих дробей, которая меньше

    ² / ₃ ?
    1. ⁷ / ₈
    2. ⁵ / ₆  
    3. ³ / ₄
    4. ³ / ₅
    5. ⁵ / ₇

    32 Хоккейная команда выиграла 6 игр и проиграла 8.

    Каково отношение побед к количеству игр?
    1. ⁶ / ₈
    2. ⁸ / ₆
    3. ³ / ₇
    4. ⁸ / ₁₄
    5. ⁶ / ₇

    33. Получает еженедельную комиссию от всех продаж плюс 1 $

    . На этой неделе у Сью было 3000 долларов продаж. Сколько всего она заработала?

    1. $ 375
    2. $ 450
    3. $ 480
    4. $ 510
    5. $ 525

    34. Если периметр прямоугольного дома составляет 25

    ¹ / ₃ Yards, и длина. Какова ширина?
    1. 16 футов
    2. 35 футов
    3. 37 футов
    4. 40 футов
    5. 42 фута

    . Лодка продана за сколько?

    1. $ 17 2550,00
    2. $ 16 540,44
    3. $ 16 230,34
    4. $ 15 980,55
    5. $ 15 870,88

    36. Увеличение в последнее время на уровне 10 00015

    . Какая дробь равна 0,15%?

    1. ³ / ₂₀₀₀
    2. ² / ₇₅₀
    3. ⁷ / ₄₀₀₀
    4. ⁵ / ₃₄₆₂
    5. ¹ / ₅₀₀

    37 .

    6.334 * 10 ⁴ =
    1. 0,0006334
    2. 0,06334
    3. 6334
    4. 63340
    5. 633400

    38. Если 3x + 5x = -8, тогда x + 100065

16. .
17. 545.9000 9000. 9000.9000 9000. 9000.9000 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 9000. 1
18. 0
19. 1
20. 2

39. Два угла в треугольнике равны 120°. Чему равен третий угол?

1. 60°
2. 70°
3. 80°
4. 90°
5. 120°

40. Какая из следующих единиц будет подходящей единицей измерения сахара для рецепта печенья?

1. литров
2. чашек
3. кварт
4. килограммов
5. фунтов

 

---

1.  C:  Уравнение x -0,10 x -0,15( x -0,10 x )=306 можно использовать для решения задачи. Решение для x дает 0,90 x – 0,15 x + 0,015 x  = 306, где x  = 400. Таким образом, исходная цена составляла 400 долларов.

2. B:  Уравнение можно решить, сначала распределив y по выражению x – 1 в левой части уравнения. Это дает:  x y  –  y  =  Z . Добавление y к обеим частям уравнения дает: x y  = Z  + y . Наконец, деление обеих частей уравнения на y дает: x = ( Z + y )/ y или x = Z / 906,95.

3.  B:  Эта задача иллюстрирует распределительное свойство умножения над сложением. Распределяемый фактор может не измениться.

4.  D:  Величина третьего угла треугольника равна 180°-(15° + 85°) или 80°.

5.  C:  Поскольку в 2 фунтах содержится 32 унции (16 унций = 1 фунт), можно записать следующую пропорцию: 5/140=32/ x  . Решение для x дает x = 896. Таким образом, в 2 фунтах мяса содержится 896 граммов.

6.  E:  Наибольшее количество детей, занимающихся плаванием в течение одного года, составляло 500 человек в 1995 году.

7.  C:  Единственное уменьшение числа детей, посещающих уроки плавания, произошло с 1992 по 1993 год, на 200 детей.

8.  B:  Среднее значение может быть записано как (200+250+400+200+300+500)/6, что примерно равно 308.

9.  A:  Перемещение запятой на два знака слева дает 0,0593.

10.  C:  Для решения задачи можно использовать следующую пропорцию: 1/20=6,2/ x . Решение для x дает x = 124, поэтому на самом деле между двумя городами 124 мили.

11.  A:  Правильный график должен показывать отрезок между 1 и 4, включая точки 1 и 4.

12.  D:  Объем жестяной банки составляет 972 дюйма”. Объем каждого кусочка помадки составляет 27 дюймов». 972 ÷ 27 = 36.

13.  B:  Для решения задачи можно использовать следующую систему уравнений: ( s =2 b @ s – б =15). Подстановка 2 b вместо s во втором уравнении дает: 2 b  –  b  = 15, где b  = 15. Младшему брату 15 лет.

14.  C:  Умножение числителя и знаменателя данной дроби на 5 дает дробь 25/30, которая эквивалентна.

15.  B:  Преобразуя футы в ярды, размеры можно переписать как 4 ярда на 6 2/3 ярда. Таким образом, площадь пола равна 26 2/3 ярда». Умножение этой площади на стоимость квадратного ярда дает выражение 26 2/3×8,9.1, что равно 237,6. Таким образом, стоимость составляет $237,60.

16. C: Следующее уравнение может быть решено для x : 6000 = 1/2 x . Решение для x дает x = 12 000. Таким образом, сумма розыгрыша призовых составила 12 000 долларов.

17. D:  Расстояние можно определить, написав и решив следующее уравнение для c : 50 ² +120 ² = c ² . с  = 130, таким образом, расстояние равно 130 футам.

18.  D:  Средняя стоимость поездки туда и обратно равна общему пройденному расстоянию, деленному на общее время в пути. Пройденное расстояние = 2x. Время в пути = х/10+х/8=4х/40+5х/40=9х/40. Средняя скорость = 2xx9x/40=(2xx40)/9x=80/9 = приблизительно 8,9 миль в час.

19.  E:  Длина равна 216 дюймам. Ширина равна 36 дюймам. Таким образом, длину можно покрыть 18 камнями по 12 дюймов, а ширину — 3 камнями по 12 дюймов. Всего на один слой нужно 42 камня, а на два слоя нужно 84 камня. Умножение 84 на 2,32 доллара дает 19.4.88. Таким образом, общая стоимость составляет $194,88.

20.  E:  Уравнение можно решить для x , сначала вычитая 6 x  из обеих частей уравнения. Это дает -3 x  = -15, где x  = 5. Подстановка 5 вместо x во второе выражение дает 5 + 8, что равно 13.

21. B: 0 в 1 л.

22.  D:  Задачу можно смоделировать с помощью уравнения 6,50 = 5,00 + 0,50 x , где x  – количество пассажиров. Решение для x дает x  = 3. Таким образом, в машине было 3 пассажира плюс 1 водитель, всего 4 человека.

23. C: Эта задача может быть представлена ​​как 1/9 ^. 9, что равняется 1.

24.  D:  Извлечение по 3 каждого цвета гарантирует, что у него будет по 1 каждому цвету. Таким образом, всего ему нужно вынуть 9 шариков.

25.  E:  0,20% = 0,002, а 1/500 = 0,002.

26.  D:  Увеличение от семестра к семестру вдвое больше, чем за два предыдущих семестра. Таким образом, увеличение от 19 до недостающего члена будет 20, или удвоенное увеличение 10. Таким образом, недостающий член равен 19 + 20, или 39.

27.  C:  Решение может быть смоделировано с помощью выражение, 0,25(2490). Таким образом, в ее бюджете на апрель 2001 г. было выделено 622,50 доллара на жилье.0)+0,10(2622)+0,10(2555))/6, что упрощается как (257,80+243,20+266,80+249,00+262,20+255,50)/6 или 255,75. Средняя сумма бюджета на одежду за первые шесть месяцев 2001 года составила 255,75 долларов.

29.  A:  Сумма, которую она сэкономила, может быть представлена ​​выражением 0,25(2622) – 0,20(2622), что равно 131,10. Таким образом, она сэкономила 131,10 доллара.

30.  B:  Задачу можно смоделировать с помощью уравнения 1/40+1/30+1/24=1/ t . Решение для t дает t  = 10. Таким образом, работая вместе, они могут напечатать один и тот же документ за 10 минут.

31.  D:  Дробь 3/5 равна 0,6, что меньше 2/3.

32.  C:  Отношение может быть записано как 6/14, что сокращается до 3/7.

33. B: Сумма заработанных ею денег может быть представлена ​​выражением 90 + 0,12 x , где x представляет собой объем продаж. Если заменить x на 3000, получится 90 + 0,12(3000), что равно 450. Итак, на этой неделе она заработала 450 долларов.

34.  A:  Во-первых, измерение периметра может быть преобразовано в футы. Умножение 25 1/3 ярда на 3 дает эквивалентное измерение 76 футов. Таким образом, можно написать следующее уравнение: 76 = 2(22) + 2 w 90 695 , что упрощается до 76 = 44 + 2 90 694 w 90 695 , где 90 694 w 90 695  = 16. Ширина дома составляет 16 футов 90 689.

35. A:  Задачу можно смоделировать с помощью выражения 15 000 + 0,15 (15 000), что равно 17 250. Таким образом, он продал лодку за 17 250 долларов.

36. А: 3/2000=0,0015, что эквивалентно 0,15%.

37.  D:  Перемещение десятичной точки на 4 знака вправо дает 63 340.

38.  C:  Решение данного уравнения для x дает x  = -1. Подстановка -1 вместо x во втором уравнении дает -1 + 1 = 0,

39, A: Внутренний угол треугольника в сумме равен 180°. Таким образом, мера третьего угла равна разности 180° и 120°, или 60°.

40.  B:  Чашки – это подходящая мера вместимости сахара.

Математические вопросы и решения для 11 класса

The Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя различные вопросы, основанные на новых технологиях.

Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Сопоставление таблиц, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнения/числа, Расширенный построенный ответ, Короткий ответ и многое другое. .

Эта страница содержит несколько примеров вопросов и ссылки на практические тесты по математике для 11 класса, которые помогут вам составить представление о вопросах, которые ваши учащиеся, скорее всего, увидят на тесте. После каждого примерного вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, потребуется рассмотреть для навыков, процессов и информации, которые должны знать ваши студенты.

Домен: 11 класс >> Число и количество – Система реальных чисел

Пример вопроса: Умножить 36/49 и 21/63. Какой тип числа получается в результате

1. Числа нельзя умножать
2. 57/112, рациональный
3. 12/49, рациональный
4. 12/49,иррациональный

Ответ Пояснение: Напомним, что рациональное число — это любое число, которое может быть выражено как отношение или частное двух целых чисел (дробей). Иррациональные числа — это числа, которые нельзя представить в виде дроби. Оба числа дробные. Следовательно, они оба являются рациональными числами. Перемножьте их вместе и упростите ответ:
36/49,21/63=(4/7,9/7).3/9,7/7=12/49. Ответ — дробь. Таким образом, это рациональное число.

Стандарты: HSN.RN.B.3

Нажмите здесь, чтобы попрактиковаться: Число и количество – Реальная система счисления Пример вопроса: На приведенном ниже графике показаны колебания одной из струн скрипки при игре на ней. Что верно в отношении масштаба оси Y графика?

1. Каждая отметка на оси Y, вероятно, может быть равна одному футу.
2. Каждая отметка на оси Y, вероятно, может быть равна одному сантиметру.
3. Каждая метка на оси Y, вероятно, может быть равна одному миллиметру.
4. Каждая отметка на оси Y, вероятно, может быть равна одному дюйму.

Ответ Пояснение: На графике представлена ​​амплитуда колебания скрипичной струны. Когда струна скрипки следует этому графику, струна растягивается в одном направлении, а затем в другом. Каждый раз, когда струна пересекает ось x, она находится в исходном положении. Это движение настолько мало, что человеческий глаз почти не замечает его. Поэтому блок должен быть очень маленьким. Наименьший выбор — миллиметр.

. Стандарты: HSN.RN.A.1. Вопрос: Чему равно комплексное число 7+3i?

1. -7+3i
2. -7-3i
3. 3i
4. 7-3i

Объяснение ответа:

Стандарты: HSN.RN.A.1

Нажмите здесь, чтобы попрактиковаться: 11 класс. : Вычтите эти два вектора ⟨−12,−23⟩−⟨−8,−14⟩.

1. ⟨−4,−9⟩
2. (4,9)
3. ⟨−9,−4⟩
4. ⟨−20,−37⟩

Объяснение ответа:
В вопросе нам предлагается вычесть эти два вектора ⟨−12,−23⟩−⟨−8,−14⟩ . Если у нас есть два вектора, v→=(x ₁ ,y ₁ ) и w→=(x ₂ ,y ₂ ), то разность этих двух векторов равна v→−w→=⟨x ₁ −x ₂ , у ₁ −у ₂ ⟩ . В этом вопросе мы вычитаем ⟨−12,−23⟩−⟨−8,−14⟩ . Разница ⟨−12−(−8),−23−(−14)⟩=⟨−4,−9⟩

Стандарты: HSN. VM.B.4

Нажмите здесь, чтобы потренироваться: Число и количество – векторные и матричные количества Вопросы для 11 класса Математика

Предмет: 11 класс >> Алгебра – арифметика с многочленами и рациональными выражениями

. 3х-14

-3x ³ -4x ² -3x+14

3x ³ +4x ² +3x

3x ³ +4x ² +3x-14

Объяснение ответа: При комбинировании полиномов объединяйте одинаковые члены, комбинируя коэффициенты.
Вычесть (x ³ +2x ² -x+7) из (4x ³ +6x ² +2x-7)
(4x ³ }+6x ² +2x-901) – (5 3 +2x ² -x+7)
(4x ³ -x ³ ) +(6x ² -2x ² ) +(2x-(-x)) +(-7- 7)
3x ³ +4x ² +3x-14

Стандарты: HSA.APR.A.1

Нажмите здесь, чтобы попрактиковаться: Алгебра – арифметика с полиномами, вопросы по градации 1 и рациональные выражения

Предмет: 11 класс >> Алгебра – Видение структуры в выражениях

Пример вопроса: Чему равен коэффициент третьего члена выражения
5x ³ y ⁴ +7x 5 ^{8 89085 2 −6xy 2 −8xy?}

1. 6
2. 7
3. -8
4. -6

Объяснение ответа: Выражение 5x ³ y ⁴ +7x ² y ³ −6xy ² −8xy представляет собой полиномиальное выражение с четырьмя членами. Коэффициент члена – это число, стоящее перед членом. Если термин начинается с отрицательного, то коэффициент является отрицательным числом, независимо от того, есть ли у термина переменные. Третий член равен −6xy ^{2 , а число перед членом равно -6.}

Стандарты: HSA.SSE.A.1

Нажмите здесь, чтобы попрактиковаться: Алгебра – Наблюдение структуры в выражениях Вопросы для 11 класса Математика

Домен: 11 класс >> Алгебра. Создание уравнений

Пример вопроса: Мэдисон работает продавцом в компании, занимающейся перевозками. Каждый месяц она продает две машины на каждые 10 велосипедов и четыре мотоцикла на каждую машину. Если она продает 40 автомобилей в месяц, а переменная x представляет количество автомобилей, которые она продает, какое уравнение вы можете использовать, чтобы найти, сколько автомобилей она продает?

1. х+5х+4х=40
2. х+5х+4х=20
3. 2х+10х+8х=40
4. 2х+10х+8х=20

Объяснение ответа: Если мы используем переменную x для количества автомобилей, которые продает Мэдисон, и она продает две машины на каждые 10 велосипедов, то она продает в пять раз больше велосипедов, чем автомобилей. Таким образом, она продает 5x велосипедов. Тогда, если она продает четыре мотоцикла на каждую машину, количество проданных ею мотоциклов в 4 раза больше. В задаче говорится, что она совершает 40 продаж в месяц, поэтому сложите автомобили, велосипеды и мотоциклы и сделайте эту сумму равной 40. Уравнение x+5x+4x=40.

Стандарты: HSA.CED.A.1

Нажмите здесь, чтобы попрактиковаться: Алгебра – составление уравнений Вопросы для 11 класса по математике

Предмет: 11 класс >> Алгебра – рассуждения с помощью уравнений и неравенств Образец

0

2

2

0

2

0

2

2

2

0

2 Вопрос: Как решить 6x+5=101?

1. 19
2. 13
3. 17
4. 16

Объяснение ответа: Вопрос просит вас найти решение 6x+5=101. Начните с вычитания 5 из обеих частей уравнения. Это дает вам 6x=96. Затем разделите обе части на 6 и x=16.

Стандарты: HSA.CED.A.4

Нажмите здесь, чтобы попрактиковаться: Алгебра – рассуждения с помощью уравнений и неравенств. Вопрос: Функция f(x)=−1/8(x−7/2)2+3/2 — это траектория футбольного мяча в тренировочном матче. Его график показан ниже. Какая часть области этой функции фактически моделирует эту ситуацию?

1. [7,0]
2. [−1,7]
3. (-∞,∞)
4. [0,7]

Ответ Объяснение: Функция является полиномиальной функцией. Область определения всех полиномиальных функций в математическом контексте равна (−∞, ∞). Однако в контексте реального мира домен должен позволять функции подчиняться правилам реального мира. Мяч попадает в момент времени, равный 0 секундам, а мяч приземляется, согласно графику, в момент времени, равный 7 секундам. Следовательно, домен равен [0,7].

Стандарты: HSF.IF.B.5

Щелкните здесь, чтобы попрактиковаться: Функции – интерпретация функций. Чем график f(x) = x + 7 отличается от графика g(x) = x + 12?

1. Если f(x) сдвинуть вверх на 5 единиц, получится g(x)
2. g(x) получается сдвигом f(x) вниз на 5 единиц
3. Если g(x) сдвинуть вверх на 5 единиц, f(x) будет получено
4. f(x) получается сдвигом g(x) вверх на 5 единиц

Ответ Объяснение: Значение, добавляемое к функции, вызывает сдвиг графика по вертикали. Поскольку 12 на 5 единиц больше, чем 7, график g(x) получается путем сдвига f(x) на 5 единиц вверх.

Стандарты: HSF.BF.B.3

Нажмите здесь, чтобы попрактиковаться: Функции — построение функций Вопросы для 11 класса по математике

Область: 11 класс >> Функции — линейные, квадратичные и экспоненциальные модели

Пример вопроса: График какой функции изображен ниже?

1. f(x)=5(0,5) ^х
2. f(x)=5(0,4) ^х
3. f(x)=4(0,5) ^х
4. f(x)=5(1,5) ^х

Ответ Объяснение: График показывает, что функция является функцией экспоненциального роста. Формула экспоненциальной функции такова: f(x)=ab ^x , где a — точка пересечения с осью y, а b — коэффициент роста. Если экспоненциальная функция является функцией роста, то b>1. Если экспоненциальная функция является функцией затухания, то 0 х.

Стандарты: HSF.LE.A.2

Нажмите здесь, чтобы попрактиковаться: Функции — линейные, квадратичные и экспоненциальные модели.

Пример вопроса: Если cosσ=−1, каково значение sinσ ?

1. не определено
2. 1
3. 0
4. -1

Объяснение ответа: Правило :

В таблице ниже приведены точные значения триггерных функций для особых углов.

Угол, косинус которого равен -1, равен 180 градусам. Синус 180 градусов равен 0.

Стандарты: HSF.TF.C.8

Щелкните здесь для практики: Функции – тригонометрические функции PQRS переводится, как показано на рисунке ниже. Как переводится параллелограмм?

Ответ Объяснение: На рисунке показано, что перевод осуществляется вправо и вниз. Судя по рисунку, расстояние, на которое параллелограмм переместится вправо, равно длине стороны PQ. Кроме того, судя по рисунку, расстояние, на которое параллелограмм перемещается вниз, составляет примерно половину длины стороны QR.

Стандарты: HSG.CO.A.4

Нажмите здесь, чтобы попрактиковаться: Геометрия – вопросы на соответствие для 11 класса Математика

Область: 11 класс >> Геометрия – подобие, прямоугольные треугольники и тригонометрия

Пример вопроса: Выполнение расширение в точке C с центром в начале координат с масштабным коэффициентом, равным 1/2. Какова координата полученной точки изображения C’?

1. (2 , -3/2)
2. (-3/2, 2)
3. (8 , -6)
4. (-6, 8)

Ответ Объяснение: Когда расширение выполняется относительно начала координат, координаты точки изображения являются произведением коэффициента масштабирования и координат исходной точки. ½*4 = 2. ½* -3 = -3/2.

Стандарты: HSG.SRT.A.1

Нажмите здесь, чтобы попрактиковаться: Геометрия – подобие, прямоугольные треугольники и тригонометрия0688 Пример вопроса: Касательная проведена к окружности из точки вне окружности. Радиус проводится от центра окружности до точки касания прямой. Какой угол образует радиус с касательной?

1. 0 ^или
2. 90 ^или
3. 180 ^или
4. 270 ^или

Ответ Пояснение: Радиус окружности, проведенной к точке касания касательной, перпендикулярен касательной.

. Стандарты: HSG.C.A.2. Написав уравнение y=x ² +6x+7, Анжелика использовала следующие шаги. Если она сделала какие-либо ошибки, объясните их и напишите правильное уравнение.
у=х ² +6х+7
у-7=х ² +6х
y−7−9=x ² +6x+9
y−16=(x+3) ²
y=(x+3) ² +16

Ответ Пояснение: Поставить уравнение в стандартной форме, мы должны завершить квадрат, чтобы получить квадрат бинома, который необходим для стандартной формы. Чтобы завершить квадрат, мы берем половину коэффициента линейного члена, который будет равен 3, затем возводим его в квадрат и прибавляем к обеим сторонам. Затем разложите совершенный квадратный трехчлен, чтобы получить квадратный бином. Затем решить для y.

Стандарты: HSG.GPE.A.2

Нажмите здесь, чтобы попрактиковаться: Геометрия – Выражение геометрических свойств с помощью уравнений Вопрос: Какова плотность кирпича, занимающего 310 см ³ при массе 853 г?

1. 0,36 см ³ /г
2. 2,75 г/см ³
3. 2,64 г/см ³
4. 0,36 г/см ³

Объяснение ответа: V = Bh = lwh Объем прямоугольной призмы

Формула плотности: d = m/V. Объем равен 310 см ³ , а масса 853 г. Подставьте эти значения в формулу, чтобы найти плотность.

Стандарты: HSG.MG.A.2

Нажмите здесь, чтобы попрактиковаться: Геометрия – Моделирование с помощью геометрии1010

Пример вопроса: Полусфера радиусом 3 см находится на вершине конуса одинакового диаметра и высоты 10 см, как показано на диаграмме ниже.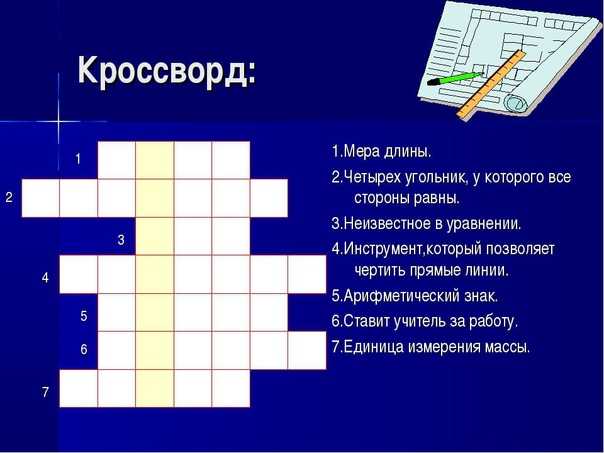 Найдите объединенный объем составного объекта.

1. 24πсм ³
2. 36πсм ³
3. 48πсм ³
4. 60πсм ³

Ответ Пояснение: Полный объем объекта равен сумме объемов полушария и конуса.
В = ½ (4/3) πr ³ +(1/3)πr ² h
В = ½ (4/3) π(3m) ³ +(1/3)π(3m) ² (10 см)V=48πcm ³

Стандарты: HSG.GMD.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия – вопросы по геометрическим измерениям и размерам для 11 класса Математика 906 11 >> Статистика и вероятность – интерпретация категорийных и количественных данных

Пример вопроса: Какое влияние оказывает группа очень больших значений на среднее и медиану набора данных?

1. Среднее значение и медиана увеличиваются
2. Среднее значение не изменилось, а медиана увеличилась
3. Среднее значение и медиана не изменяются
4. Среднее значение увеличивается, но медиана уменьшается

Объяснение ответа: На рисунке ниже показано влияние на среднее значение и медиану в результате добавления некоторых очень больших элементов в набор данных. Поскольку новые элементы очень большие, они оказывают существенное влияние на среднее значение, поскольку их очень большие значения усредняются с другими значениями в наборе. Медиана также затрагивается и движется в том же направлении, что и среднее.

Стандарты: HSS.ID.A.3

Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность – интерпретация категориальных и количественных данных. Вопросы для 11 класса по математике

Область: Статистика и вероятность Выводы и обоснование выводов

Пример вопроса: Есть десять игральных карт, четыре из них красные и шесть черных. Джулиан выбирает карту наугад. Какова вероятность того, что он выберет красную карточку?

Ответ Пояснение: Вероятность рассчитывается как отношение количества успехов к количеству возможных вариантов.

Вопрос касается вероятности выбора красной карточки. Из десяти карточек четыре красные.

Таким образом, вероятность выбора красной карточки составляет четыре из десяти, что сводится к двум из пяти. Это соотношение равно 2/5

.

Стандарты: HSS.IC.A.1

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – выводы и обоснование выводов Правила вероятности

Пример вопроса: На приведенной ниже диаграмме Венна показаны результаты опроса о том, какие виды спорта люди любят смотреть по телевизору. Участники опроса могли выбрать один вид спорта, два вида спорта или все три вида спорта. В каком регионе (регионах) есть ответы, в которых участник опроса указал, что ему нравится смотреть только один вид спорта?

1. Б, В, Г
2. Э, Ж, Г
3. Б, А, Д
4. А, Б, С

Объяснение ответа: Каждый кружок содержит ответы, которым нравится определенный цвет. Таким образом, регионы A, B, C, E содержат ответы, которые любят смотреть бейсбол. Области D, A, D, G содержат ответы, которые любят смотреть баскетбол. Регионы A, B, D, F содержат ответы, которые любят смотреть футбол. Если письмо находится в двух кругах, в регионе есть ответы, которые любили смотреть виды спорта, представленные в обоих кругах. Если регион указан во всех трех кругах, этот регион содержит ответы, в которых нравится смотреть все три вида спорта. Если регион находится только в одном круге, этот регион содержит ответы, в которых говорится, что им нравится смотреть только тот вид спорта, который представлен в этом круге. Области, которые находятся только в одном круге, это E, F, G.

Стандарты: HSS.CP.A.1

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Условная вероятность и правила теории вероятности Использование вероятности для принятия решений

Пример вопроса: Бюро переписи населения предоставило отчет, в котором говорится, что средний уровень дохода жителей Флориды составляет 47 463 человека. Основываясь на этой информации, если вы опросили 100 случайных рабочих во Флориде, какова вероятность того, что доход респондентов превышает 47 463?

1. 65%
2. 35%
3. 80%
4. 50%

Ответ Пояснение: Медиана — это среднее число, когда все числа в наборе расположены от наименьшего значения к наибольшему.