Правила нахождения компонентов | Материал по математике (4 класс) на тему:

Опубликовано 27.05.2016 — 13:17 — Ханходжаева Гузаля Асгатовна

Правила нахождения компонентов

Скачать:

Предварительный просмотр:

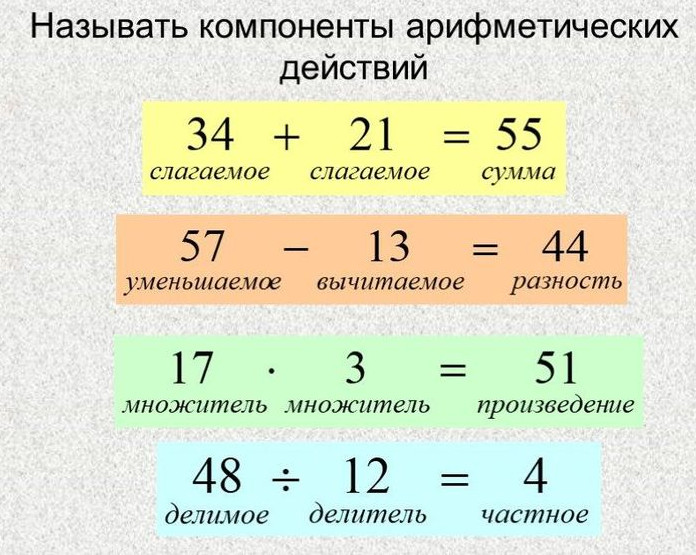
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:

1. Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
2. Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
3. Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
4. Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.

Выучи названия компонентов действий и правила нахождения неизвестных компонентов:

1. Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
2. Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
3. Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
4. Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.

По теме: методические разработки, презентации и конспекты

Памятка «Название и правила нахождения компонентов при сложении, вычитании, умножении и делении»

Памятка по математике…

Памятка «Название и правила нахождения компонентов при сложении, вычитании, умножении и делении»

Памятка по математике…

Памятка по математике. Название и правила нахождения компонентов при сложении, вычитании, умножении, делении.

Справочный материал для школников представлен в виде таблиц, которые удобно использовать на уроках и при выполнении домашнего задания….

Памятка Нахождение компонентов при математических действиях.

Памятка. Нахождение компонентов при математических действиях.Наибольшую сложность при решении примеров и задач представляет нахождение компонентов математических действий..Памятка разработана для помо…

Правила «Компоненты сложения и вычитания. Св-ва сложения. Нахождение компонентов. Действия при решении задач», 2 класс

Правила «Компоненты сложения и вычитания. Св-ва сложения. Нахождение компонентов. Действия при решении задач», 2 класс. Информация взята из интернет-источников….

ПОВТОРЕНИЕ О НАХОЖДЕНИИ КОМПОНЕНТОВ ПРИ РЕШЕНИИ УРАВНЕНИЙ

Здесь подобраны карточки для повторения по теме «НАХОЖДЕНЕИ КОМПОНЕНТОВ ПРИ РЕШЕНИИ УРАВНЕНИЙ». Карточки предназначены для школьников…

Правила на компоненты действий+ проверочная

Математика.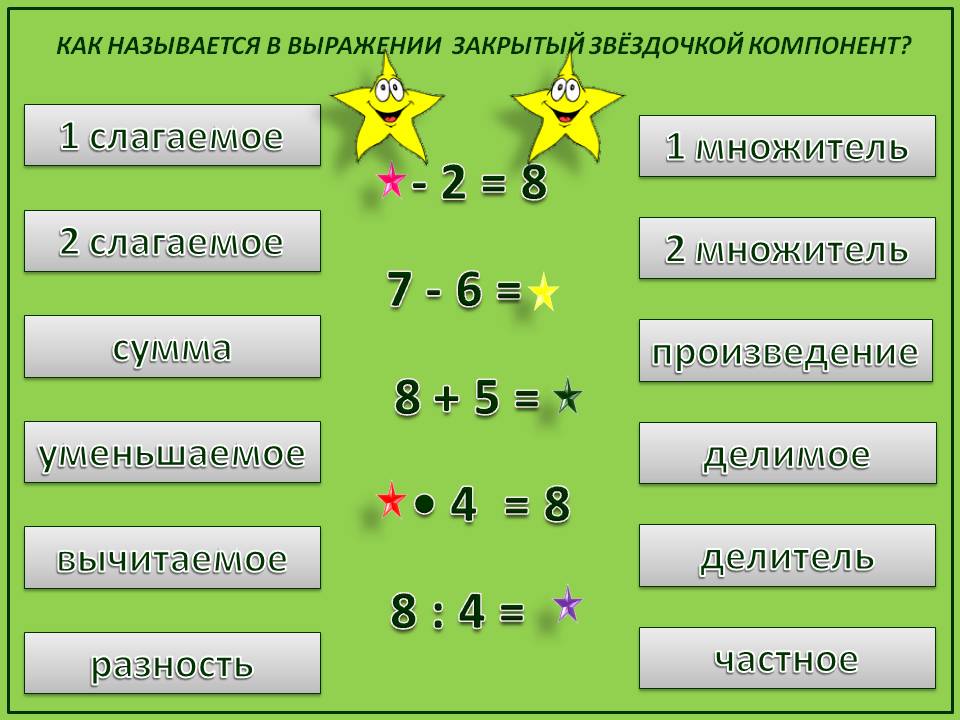 Компоненты действий…

Поделиться:

 

Компоненты сложения и вычитания.

Выражение вида 3 + 5 называют суммой. Числа 3 и 5 в этой записи называют слагаемыми. Поскольку число 8 в данном случае получено в результате суммирования, его также часто называют суммой.

Выражение вида 8 – 3 называют разностью. Число 8 называют уменьшаемым, а число 3 – вычитаемым. Значение выражения – число 5 также могут называть разностью.

Поскольку названия компонентов действий сложения и вычитания вводятся по соглашению (детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания, требующие распознавания компонентов действий и употребления их названий в речи.

Примеры заданий:

1. Среди данных выражений найдите такие, в которых первое слагаемое равно 3 (уменьшаемое, вычитаемое):

3 + 2 7 – 3 6 + 3 8 + 1 3 + 5 3 – 2 7 – 3 3 + 4 3 – 1

2. Составьте выражение, в котором второе слагаемое (уменьшаемое, вычитаемое) равно 5. Найдите его значение.

3. Уменьшаемое 18, вычитаемое 9. Найдите разность.

В дальнейшем дети знакомятся с правилами взаимосвязи компонентов сложения и вычитания, которые являются обобщением представлений ребенка о способах проверки сложения и вычитания:

Если из суммы вычесть одно слагаемое, то получится другое слагаемое.

Если сложить разность и вычитаемое, то получится уменьшаемое.

Если из уменьшаемого вычесть разность, то получится вычитаемое.

Эти правила являются основой для подготовки к решению уравнений, которые в начальной школе решаются с опорой на правило нахождения соответствующего неизвестного компонента равенства.

Задание: Решите уравнение 24 – х = 19.

Решение: В уравнении неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность: х = 24 – 19, х = 5.

В основе усвоения взаимосвязи между компонентами и результатами сложения и вычитания лежит осознание учащимися предметного смысла этих действий. При этом следует учитывать, что особую трудность для некоторых детей представляет вычленение и удаление части множества, т.е. осознание тех предметных действий, которые связаны со смыслом вычитания.

В исследовании Г.Г. Микулиной было выявлено, что значительная часть учащихся при выполнении предметных действий, связанных с вычитанием, фиксирует скорее пространственное отделение, разъединение двух множеств, чем вычленение и удаление части из целого.

Рассмотрим некоторые методические приёмы, в которых учитываются описанные выше психологические особенности младших школьников:

1. Работая у доски с рисунками и дидактическими пособиями, полезно сначала предложить ученику показать предметные совокупности, с которыми он действует, а затем уже назвать число предметов в них.

2. Выполняя задания с рисунками, к которым дана запись вида –=, рекомендуется заполнять «окошки» не только в прямом порядке, но и начиная с любого.

3. Можно использовать задания такого же рода, но со срытыми количествами. При их выполнении внимание учащихся сосредотачивается на соотнесении элементов схемы и предметных совокупностей.

4. Можно предложить трём ученикам взять со стола карточки (например, всего 5), соответствующие выражению (например, 5–2=3). После этого ученики убеждаются, что сразу всем карточки не взять.

5. Можно предлагать комплексные задания с карточками и со схемами.

Разрешение таких «противоречий» в игровой форме помогает детям усвоить взаимосвязь между компонентами и результатами действий сложения и вычитания. Однако, осознавая «предметную» взаимосвязь компонентов и результатов действий, не все дети могут описать её, пользуясь математической терминологией: слагаемые, значение суммы, уменьшаемое, вычитаемое, значение разности.

В этом случае целесообразно использовать понятия целого и части и соотношение между ними (часть всегда меньше целого; если убрать одну часть, то останется другая).

Понятие целого и части позволяет как бы «материализовать» такие термины, как слагаемые, уменьшаемое, вычитаемое (например, устанавливая соответствие между рисунком и математической записью).

Основные компоненты математики | Наука

••• математика изображение от jaddingt с сайта Fotolia.com

Обновлено 25 апреля 2017 г.

Автор: Jennifer VanBaren

Математика — это совокупный предмет, который преподается детям с самого раннего возраста. Поскольку математика является кумулятивной, каждый компонент основывается на других. Студенты должны освоить каждый компонент, прежде чем они смогут полностью освоить следующий. Основными компонентами или элементами математики являются: сложение, вычитание, умножение и деление.

Сложение

Сложение — это первый компонент, которому обучают детей в очень раннем возрасте.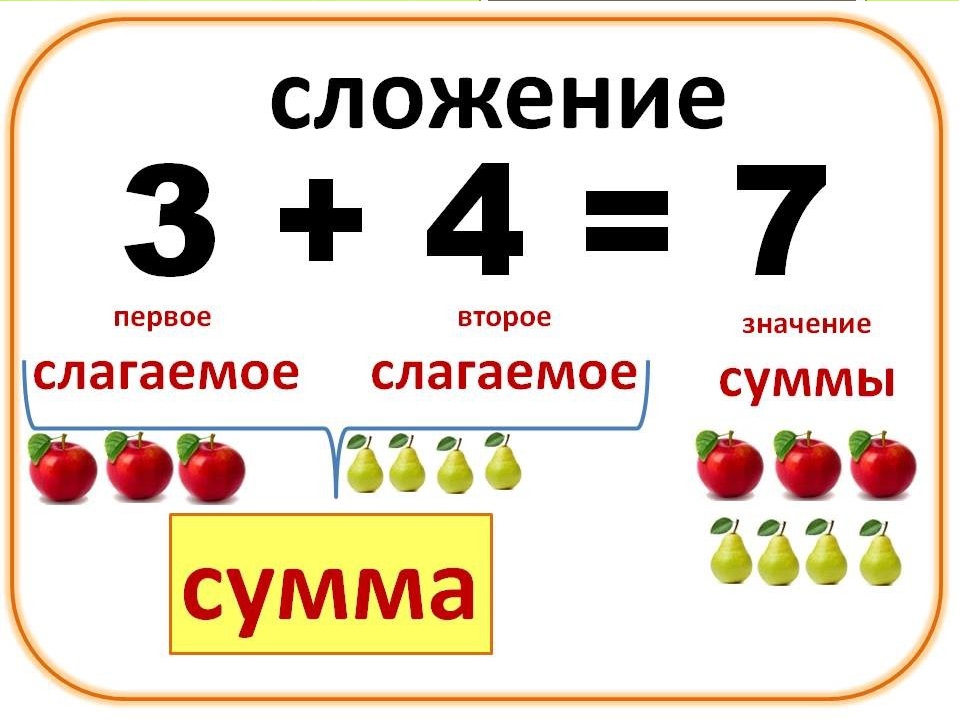 Родители начинают учить своих детей считать игрушки, печенье, пальцы на ногах и многое другое. Умение считать является обязательным условием для обучения сложению. Сложение — это простое сложение двух чисел. Дети начинают с очень простых задач, таких как 1 + 1 = 2, а затем постепенно переходят к более крупным числам, включающим принцип «переноса» чисел. Этот принцип иллюстрируется такой задачей, как 109+ 215 = 324. Ответ на задачу на сложение называется суммой. Чтобы перейти к следующему компоненту математики, необходимо хорошее понимание сложения.

Вычитание

Вычитание — это второй компонент, изучаемый в математике после изучения и понимания сложения. Вычитание часто считается противоположностью сложения. Вычитанием находят разность двух чисел. Вычитанию сначала обучают с помощью простых задач, таких как 4 – 1 = 3. Ответ на задачу на вычитание называется разностью. Постепенно она усложняется до задач, содержащих гораздо большие числа.

Умножение

Третий компонент математики — умножение. Два числа перемножаются, и произведение находится. Дети, изучающие умножение, часто называют это «раз». Компонент умножения в математике берет одно число, «умноженное» на другое число. Учителя часто читают таблицы умножения вслух с учащимися в классе, чтобы помочь учащимся запомнить эти математические факты. Студенты начинают изучать таблицу умножения на «1» и продолжают двигаться до 12 в целом.

Деление

Деление — это последний основной компонент, вокруг которого строится математика. Остальные три компонента должны быть полностью освоены до обучения делению. Деление часто рассматривается как противоположность умножения. Когда учащиеся хорошо знают факты умножения, деление обычно усваивается легче. Деление берет одно число и делит его на другое. Найденный ответ называется частным. Студенты начинают обучение с маленьких чисел в таких задачах, как 4/2 = 2. Затем деление переходит к большим числам, для которых вступают в игру остатки.

Статьи по теме

Ссылки

• Помощь по математике и чтению: базовый раздел
• Инструктор по деньгам: базовая математика: введение в дроби
• FCPS Teach: основные математические факты: последовательность обучения
  2 900 О
Дженнифер ВанБарен начала свою профессиональную карьеру онлайн-писателя в 2010 году. В течение пяти лет она преподавала бухгалтерский учет, математику и бизнес на уровне колледжа. Ее основные моменты письма включают публикацию статей о музыке, бизнесе, садоводстве и домашней организации. Она имеет степень бакалавра наук в области бухгалтерского учета и финансов, полученную в Колледже Святого Иосифа в Ренсселере, штат Индиана 9.0003

Фотокредиты

математическое изображение от jaddingt с сайта Fotolia.com

Сложение, вычитание и умножение комплексных чисел

Результаты обучения

• Сложение и вычитание комплексных чисел
• Умножение комплексных чисел


Так же, как и с действительными числами, мы можем выполнять арифметические операции над комплексными числами. Чтобы сложить или вычесть комплексные числа, мы объединяем действительные части и объединяем мнимые части.

Общее примечание: сложение и вычитание комплексных чисел

Сложение комплексных чисел:

[латекс]\влево(а+би\вправо)+\влево(с+ди\вправо)=\влево(а+с\вправо)+\влево(b+d\вправо) i[/latex]

Вычитание комплексных чисел:

[латекс]\left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right) )i[/latex]

Как: Даны два комплексных числа, найти их сумму или разность.


1. Определите действительную и мнимую части каждого числа.
2. Добавьте или вычтите действительные части.
3. Сложите или вычтите мнимые части.

Пример: добавление комплексных чисел

Добавьте [латекс]3 — 4i[/латекс] и [латекс]2+5i[/латекс].

Показать решение

Попробуйте

Вычтите [латекс]2+5i[/латекс] из [латекс]3 — 4i[/латекс].

Показать решение

Умножение комплексных чисел

Умножение комплексных чисел очень похоже на умножение двучленов. Основное отличие состоит в том, что мы работаем с реальной и мнимой частями отдельно.

Умножение комплексного числа на действительное число

Начнем с умножения комплексного числа на действительное число. Мы распределяем действительное число так же, как и биномиальное. Так, например,

[латекс]\begin{align}3(6+2i)&=(3\cdot6)+(3\cdot2i)&&\text{Distribute.}\\&=18+6i&&\text {Упрощение.}\end{align}[/latex]

Как: Даны комплексное и действительное числа, умножьте их, чтобы найти произведение.

1. Использовать свойство дистрибутива.
2. Упростить.

Пример: умножение комплексного числа на действительное число

Найдите продукт [латекс]4\влево(2+5i\вправо)[/латекс].

Показать решение

Попробуйте

Найдите продукт [латекс]-4\влево(2+6i\вправо)[/латекс].

Показать решение

Умножение комплексных чисел

Теперь давайте перемножим два комплексных числа. Мы можем использовать либо распределительное свойство, либо метод FOIL. Напомним, что FOIL — это аббревиатура для умножения первого, внешнего, внутреннего и последнего членов вместе. Используя либо распределительное свойство, либо метод FOIL, мы получаем 9{2}=-1[/латекс], у нас есть

[латекс]\левый(а+би\правый)\левый(с+ди\правый)=ас+ади+bci-bd[/латекс]

Для упрощения мы объединяем действительные части и объединяем мнимые части.