Математика «Состав числа 6»
| Предмет: | Математика |
|---|---|
| Категория материала: | Конспекты |
| Автор: | Абдраимова Екатерина Владимировна это Вы? |
Урок математики в 1-м классе на тему:
« Состав числа 6»
Учитель начальных классов:
Абдраимова Екатерина Владимировна
13.11.2014 г.
Урок математике в 1-м классе
Абдраимова Екатерина Владимировна, учитель начальных классов
Тема урока: « Состав числа 6»
Тип урока: урок изучения нового материала.
Продолжительность урока: 45 минут.
Цель урока: познакомить учащихся с числом и цифрой 6; с получением и составом числа 6; научить писать цифру 6.
Задачи:
Образовательные:
Научить правильно, соотносить полученные цифры с числом предметов.
Формировать умение образования чисел, научить учащихся писать цифру 6.
Продолжить работу по формированию пространственных представлений.
Развивающие:
Развивать психические процессы: внимание, мышление, память, творческую активность.
Создавать условия психологической комфортности для каждого ребёнка.
Воспитательные:
Оборудование: тетрадь, ручка и цветные карандаши, числовые карточки, цифровые «веера», счётный материал, состав числа (домики), таблица «Число и цифра 6», наборное полотно.
Ход урока
1. Организационный момент. Эмоциональный настрой.
Давайте, ребята, учиться считать,
Ему по плечу любая работа,
Но прежде разучим правила счёта.
Звонок прозвенел. Он позвал на урок.
Пора! Тишина! К нам наука идёт…
2. Актуализация знаний.
Какое число идёт первым при счёте?
Первым при счёте идёт число ОДИН
Какое число следует при счёте за ним?
За ним следует число два.
Какие числа идут перед числом четыре?
Перед числом четыре идут 1, 2, 3.
Какое число идёт за числом 4?
За числом 4 идёт 5.
Назови число (счёт хором)
от 1 до 5, от 3 до 7, от 6 до 10.
от 5 до 1, от10 до1…
3. Открытие нового знания.
-Послушайте и отгадайте.
Ежедневно в шесть утра,
Я трещу:
— Вставать пора!
Будильник (картинка вывешивается на доску)
Чёрен, да не ворон,
Два рога, а не бык,
Шесть ног – без копыт.
Отгадайте-ка, ребятки,
Что за цифра-акробатка?
Если на голову встанет,
Ровно на три больше станет.
Шесть. (картинка вывешивается на доску)
Как вы думаете, какая тема нашего урока?
Сегодня на уроке мы познакомимся с числом и цифрой 6
Что у вас в жизни связано с числом 6?
Где мы видим и слышим о числе и цифре 6?
Как можно показать число 6?
Число можно показать шестью пальчиками, шестью карандашами, шестью палочками…….
4. Работа в тетрадях. Написание цифры 6.
Числа обозначают знаками – цифрами.
-Рассмотрите цифру 6.
-Из каких элементов состоит цифра?
Написание цифры 6.
1.Показ образца написания учителем.
2. Письмо в воздухе.
3. Обведение образца цифры три раза.
4. Письмо в тетрадях.
5. Физкультминутка.
Раз — подняться, потянуться,
Два — нагнуть, разогнуться,
Три — в ладоши, три хлопка,
Головою три кивка.
На четыре — руки шире,
Пять — руками помахать,
Шесть — на место тихо сесть…
6. Состав числа 6
Что еще можете рассказать о числе 6?
обозначается цифрой 6;
однозначное;
между 5 и 7;(показываю на числовом ряду)
если 5+1=6 и 7-1=6 то 6>5 или 6<7;соседи 5 и 7.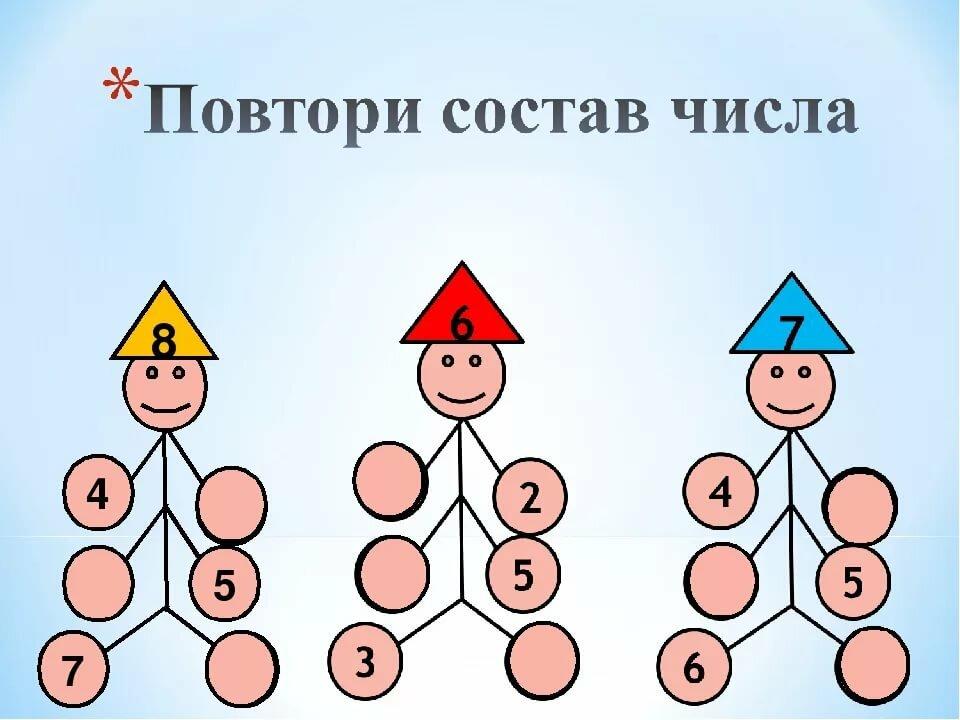
7. Закрепление.
Дети в течение 15 секунд запоминают геометрические фигуры, воспроизводят их по памяти в тетради и разбивают на части по разным признакам.
Дидактическая игра «Живой уголок» (Картинки животных на доске)
Учитель говорит: «В нашем живом уголке живут кролики: 3 серых и 2 белых, кролики грызут морковь. Сколько кроликов грызут морковь? ( ответ фиксируется показом цифры 5). Назовите какие кролики грызут морковь? К ним прибежал еще один серый кролик. Что изменилось? (кроликов стало больше). Сколько роликов теперь едят морковь? (Ответ фиксируется показом цифры 6). Перечисли их. Каких кроликов больше белых или серых? (Серых). Почему их больше? ( их 4, а четыре это 3+1). Почему 4больше 2?
8. Итог урока.
Какому числу был посвящён наш урок?
Заполни домики, чтобы получилось число 6
1
5
4
3
4
2
Общая информация
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
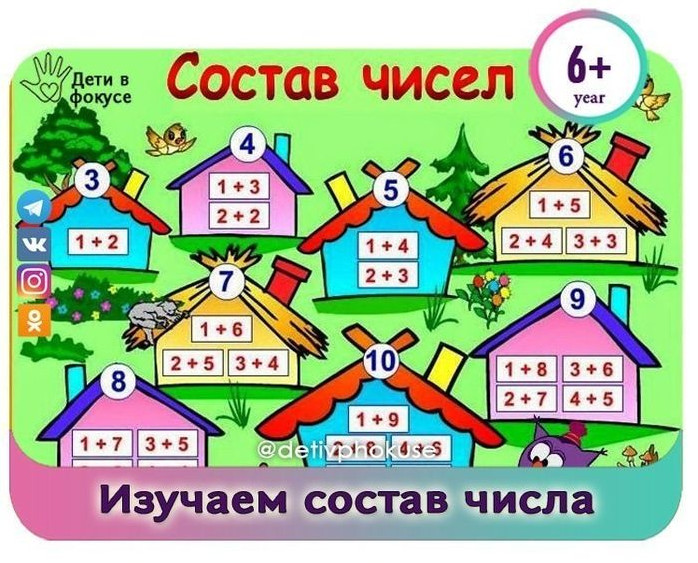
ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10
Здравствуйте-здравствуйте!
Дорогие мои читательницы, поздравляю вас с чудесным весенним праздником — 8 Марта!
Чтобы там не говорили, а хорошо, что этот праздник есть, правда ведь? ))))
Я желаю вам солнечного настроения и побольше улыбающихся людей вокруг!
Ну а у меня вот уже 8 месяцев праздник каждый день с #мой_сын_Сема ))) поэтому я с удовольствием работаю ночью даже 8 Марта )))
Спешу показать вам еще одно пособие, чтобы тот, кто очень захочет, смог приобрести его с праздничной скидкой.
Покажу пособие «ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10″, но я не только его покажу, а и подарю 10 страниц для скачивания — пусть это будет маленький восьмомартовский подарок от меня.
Над пособием «ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10″ я работала два года — крутила эти пирамидки и так и сяк на своих занятиях с дошкольниками, пока не получила вариант, который мне самой понравился)))
Все мои пособия в первую очередь я делаю для своих занятий.
Я по ним реально работаю. Как я с ними работаю — это отдельная история, но скажу, что я делаю всегда гораздо больше, чем мне надо на момент создания, чтобы был выбор в будущем. Это не хомячество — это экономия времени ПОТОМ.
Каждый год у меня новые группы и каждый год я адаптирую свою программу под конкретную группу, поэтому в моих пособиях часто задания представлены несколькими уровнями. Пришли слабенькие — им задание попроще, пришли сильные — им потруднее. Это я к чему? Если вы приобретаете у меня пособия — оценивайте возможности и уровень подготовки ваших детей, давайте им задания по силам.
Ну и о пособии)))
Числовые пирамиды, которые я покажу ниже — задания на изучение-закрепление состава числа в пределах 10. Также эти задания развивают умение логически мыслить и делать выбор.
От этих пирамид в восторге я и, самое главное, мои ребята их восприняли на ура.
Для начала я покажу, что собой представляют числовые пирамиды — смотрите картинки ниже.
Опытным путем я пришла к тому, что эти пирамидки должны быть на отдельных карточках — одна числовая пирамида — это одна карточка! Когда ребенок видит целую страницу заданий, он впадает в уныние))) «огооо сколько…», а когда он видит маленькую карточку, то таких мыслей не возникает — для него мало, значит просто… А вот сколько он сможет решить таких карточек за один присест, он даже и не догадывается! Решаются пирамидки легко, конечно, при условии, что вы отобрали для знакомства сначала простые пирамидки и уделили время для объяснения и совместного решения! Важно не только ЧТО вы даёте детям, а и то, КАК вы это подаёте.
Мои карточки я заламинировала, дороговато на первый взгляд получается, но карточки ведь многоразовые — сделал один раз и пользуйся до бесконечности)))
Чем еще мне нравятся ламинированные карточки? Ошибся — стёр!
Эти карточки я использую для самостоятельной работы.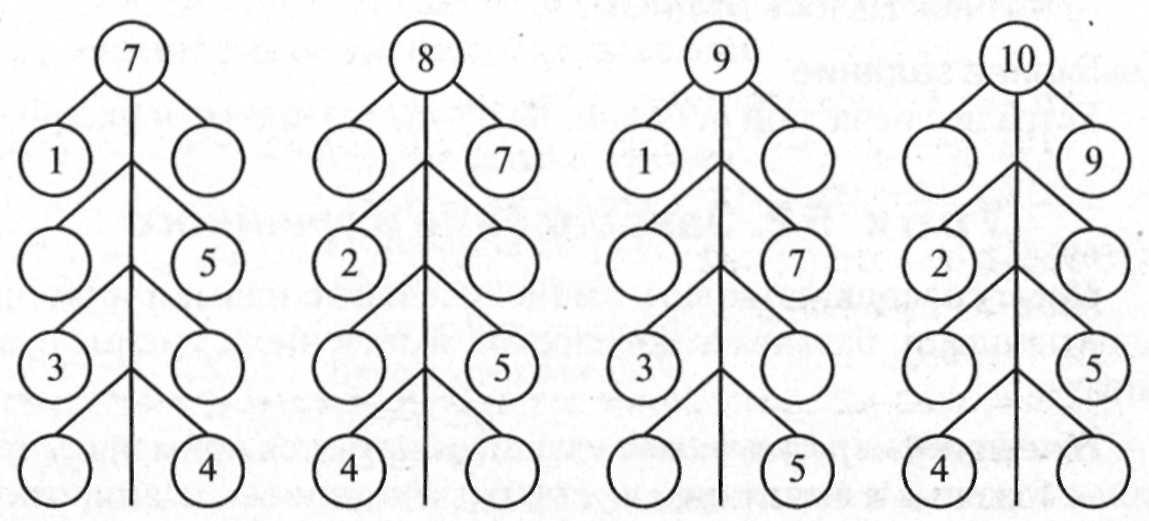
Работаем 5-10 минут.
Беру на урок 50 карточек, каждый берет столько, сколько хочет! Решает — берет еще и так до тех пор, пока группа не решит все 50 карточек.
Т.е. один может решить 10 карточек, другой 3 — каждый работает в своем темпе.
Никто не ждёт, что будет на доске или у соседа подсказка — ведь у каждого своя уникальная карточка! Сидят пыхтят — только посматривают, кто сколько решил, стараются догнать и перегнать — «а ты сколько решил?»
Работа кипит! Что остаётся мне? Я проверяю карточки по первому «я решил!», если вижу ошибку — возвращаю карточку, ребенок ищет ошибку, переделывает. Что скажу — я с трудом за ними успеваю))) так, что хоть работа и самостоятельная, я тоже с ними работаю)))
А это на фото ниже ученица, которая вдохновила меня на создание пособия «ПИШИ ЦИФРЫ ПРАВИЛЬНО!» ))) Она получает домой дополнительные задания с роботами, а остальные завистливо на неё смотрят и выпрашивают у меня дополнительные задания и себе.
Получила «заказ» от детей «еще роботов!»))))
Вот так мы щелкаем простые числовые пирамиды)) Ведь есть пирамиды сложнее! Моим ученикам с ними еще предстоит познакомиться, а вам я их покажу)))
Ниже 10 страниц с числовыми пирамидами на состав числа 1, 2, 3, 4, 5, 6, 7, 8, 9,10. На каждое число одна страница. На одной странице 9 пирамидок. Итого вы получаете в подарок 90 числовых пирамидок!
Обратите внимание: есть пирамидки простые — в них много данных, и есть сложные пирамидки, в них заложены разные варианты решений, т.е. одну и ту же пирамидку можно решить разными способами.
В полной версии пособия 130 страниц!
130 х 9= 1170 разных пирамидок!
Не следует давать детям СРАЗУ все пирамидки)))
Например, учим состав числа 5 — отобрали простые пирамидки на состав числа 5, закрепляем состав числа 5 — добавили сложные пирамидки на состав числа 5.
Работаем поэтапно, идём от простого к сложному!
Ребенок освоил состав чисел 1, 2, 3, 4 — смешали карточки сначала простые, потом добавили сложные.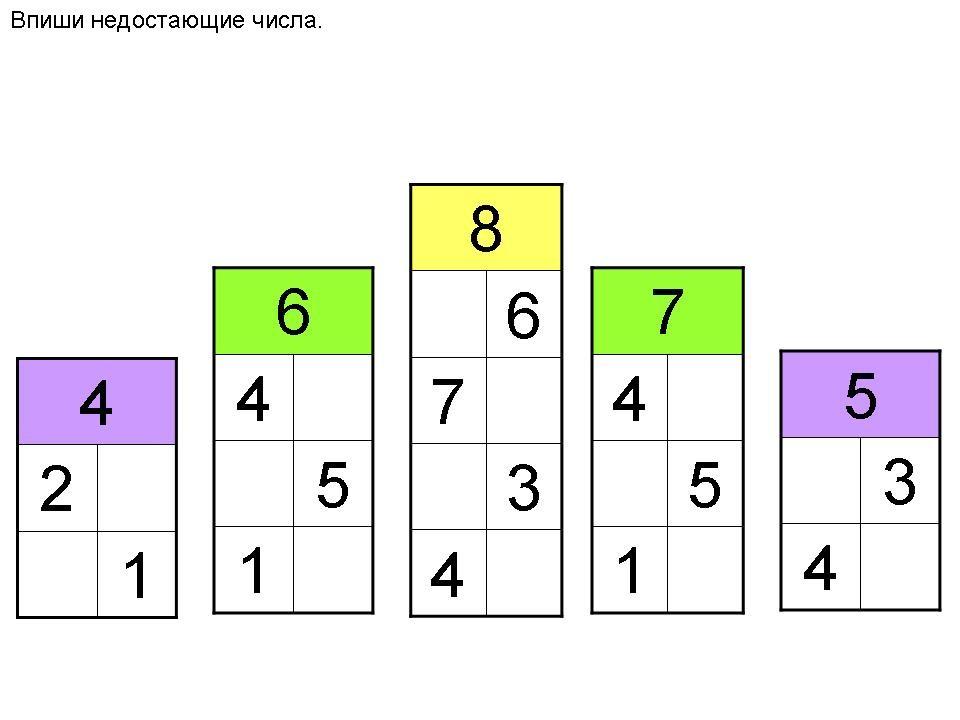
Таким образом этим пособием можно пользоваться целый год!
На какой возраст эти задания?
Младшим школьникам — эти задания в самый раз будут!
Я даю эти задания своим шестилеткам, моим пятилеткам пока, например, будет сложно.
Стоит ли раньше шести лет давать эти пирамидки?
В группе я бы не советовала, а в индивидуальной работе, можно попробовать.
Можно ли купить эту тысячу пирамидок?
Да, пособие «ЧИСЛОВЫЕ ПИРАМИДЫ: СОСТАВ ЧИСЛА В ПРЕДЕЛАХ 10″ уже можно купить, в списке пособий оно под №24.
Если вы скачали и апробировали подарочный вариант числовых пирамидок (см 10 страниц для скачивания выше), поделитесь вашими впечатлениями.
Еще раз с ПРАЗДНИИИИКОМ!!!!!!!
Статья авторская
и предназначена только для частного ознакомления.
Копирование и публикация в других источниках
без моего письменного согласия
ЗАПРЕЩЕНЫ.
Автор: Наталья Чистоклетова
Новости моего блога
можно получать на вашу любимую почту,
а подписаться можно
ЗДЕСЬ
ИГРАЙТЕ С РАДОСТЬЮ
НАТАЛЬЯ ЧИСТОКЛЕТОВА
Фотокомпозиции по номерам | Креативный фотограф
Примечание редактора: только в этом месяце — запишитесь на мой новый курс «В поисках своего творческого голоса» всего за 19 долларов! Кликните сюда, чтобы узнать больше.
Спасибо за прочтение, Андрей. Дискуссии о фотокомпозиции часто основываются на идее размещения — то есть, где вы должны поместить в кадре главный объект или фокус фотографии. Но бывают случаи, когда у вас может быть два, три или даже больше фокусных точек, особенно в более сложных композициях. Это дает вам возможность создавать интересные и динамичные фотографии. Давайте посмотрим, как это работает.
Группы из трех и фотографическая композиция
Включение в фотографию трех фокусных точек позволяет использовать два обычных композиционных приема — создание треугольников и создание узора.
Треугольники в композиции
Треугольники придают композиции динамичность. Взгляд зрителя перемещается между точками, следуя сторонам треугольника, охватывая разные части кадра.
На фото ниже хороший пример. Я наткнулся на эту сцену в приморском городке на юге Чили. Мне понравились яркие цвета и то, как рыбак раскрашивал лодку.
Вы видели треугольник? Должен признаться, что я не видел этого, когда делал фото, но когда смотрю сейчас, это становится ясно.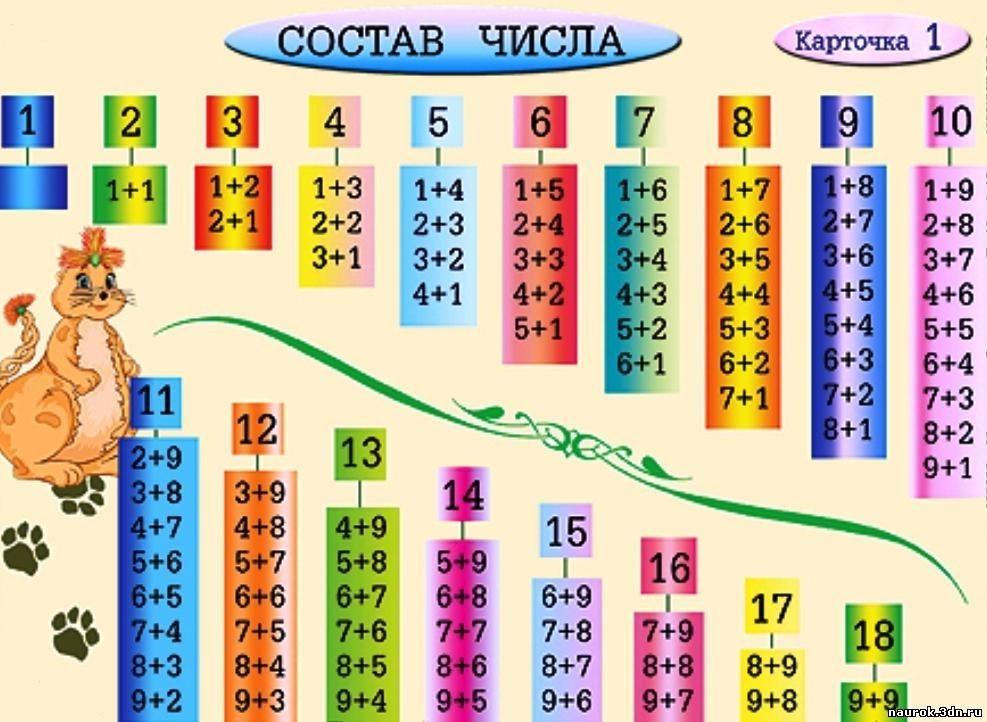
В следующем примере группа из трех состоит из статуи в центре рамы и цветочных горшков по бокам. Они создают симметричный треугольник, который переводит взгляд с одной стороны кадра на другую.
Фото ниже я сделал во время прогулки по городу на северо-западе Аргентины. На улице играли три девушки. Я спросил, могу ли я сделать фото, и они сказали, что да. Три грани образуют динамичный треугольник, который побуждает взгляд перемещаться по кадру от лица к лицу.
Группы из трех и узор
Иногда группы из трех могут располагаться в ряд, а не в треугольник. Это фото хороший пример. Группа из трех становится образцом повторяющихся форм и форм.
Когда глаз перемещается между объектами в группе, он создает своего рода ритм. Стрелки ниже показывают, как глаз перемещается по группе из трех.
На этом фото три красных цветка образуют еще один узор. Ему вторит меньший зеленый цветок в левой части кадра, который имеет ту же форму.
Пары и фотографическая композиция
Группы из двух фокусов или объектов также интересны по композиции.
Пары и симметрия
Три фотографии ниже показывают, как пары могут создавать интересные симметричные композиции. На каждой фотографии есть два одинаковых или похожих предмета.
Симметрия интересна, когда она нарушена. Когда я сделал фотографию двух шаров Баодин, я поместил их в рамку, чтобы расположить шары под углом, создав диагональную линию, которая проходит через кадр из левого нижнего угла в правый верхний. Это добавляет динамичный элемент в композицию.
На фото две головы будды, одна синяя, а другая красная. Это также нарушает симметрию и делает композицию более интересной. Это побуждает зрителя переводить взгляд с одного на другое, сравнивать их и замечать различия.
Пары и контрапункты
Пара образует контрапункт, когда она дает вам два различных фокуса, на которые можно смотреть.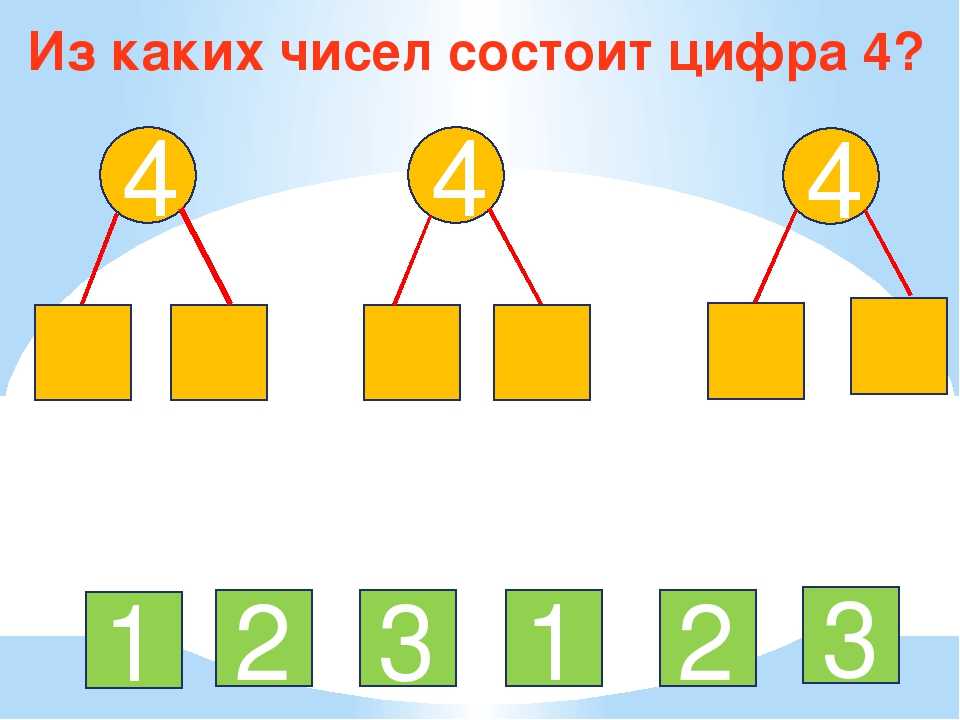
В любом фото с парой есть элемент контрапункта, потому что для глаза естественно перемещаться между ними. Но вы можете использовать его намеренно, чтобы помочь глазу перемещаться по кадру.
На этом пейзажном снимке два маяка образуют контрапункт. Взгляд переходит от одного к другому. Это помогает создать ощущение глубины, потому что по разнице в размерах зритель может увидеть, что второй маяк находится дальше.
Это уличное фото, сделанное в Пекине, демонстрирует еще один контрапункт. Две женщины не знали друг друга и действовали независимо друг от друга. Но их объединяет сходство в действиях и позициях.
Большие группы и фотокомпозиции
Возможно, вы сталкивались с таким понятием в композиции, как правило шансов — идея о том, что включение группы с нечетным числом субъектов лучше, чем с четным числом. Я знаю, что некоторым фотографам нравятся правила, поскольку они дают простые рекомендации, которым нужно следовать, но как концепция эта не имеет большого значения.
Давайте рассмотрим пример. Сколько инструментов вы видите на этом фото?
Если вы пересчитаете их точно, то увидите, что их 16. Какая разница, если их будет 15 или 17? Я так не думаю. Все, что имеет значение, это то, что есть группа инструментов, расположенных в ряд, который создает интересный узор.
Не имеет большого значения, четное или нечетное число в группе. Но это помогает создать более сильную композицию, если вы можете использовать форму, рисунок и ритм.
Фото ниже я сделал на уличном рынке в Уругвае. На базарном прилавке пять половинок тыквы.
Трое в центре составляют группу из трех, с треугольной композицией. Если бы на фото не было других половинок тыквы, получилась бы сильная композиция.
В целом пять половинок тыквы образуют спираль, которая переносит взгляд через рамку.
На последней фотографии, еще одной уличной фотографии, которую я сделал в Пекине, запечатлена группа из четырех человек.
Они позировали другому фотографу, но самое забавное, что пока они втроем смотрят на фотографа, девочка просто хотела поиграть со своей игрушкой. Четыре человека сгруппированы вместе, и в их промежутках есть ритм. Но это также показывает динамическое взаимодействие, которое происходит, когда вы собираете группы людей вместе. Контраст между действиями девушки и другими людьми делает фото более интересным.
Заключение
Группы объектов или людей открывают всевозможные интересные возможности, когда дело доходит до фотографической композиции. Это дает вам возможность исследовать закономерности, формы, симметрию и отношения между предметами. Это также поможет вам создать более интересную композицию, расположив фотографию таким образом, чтобы глаза двигались по кадру.
Дополнительная литература
- Композиция и заполнение кадра
- Обрамление, размещение и композиция
- Разоблачение правила третей
Об Эндрю С.
Гибсоне
Эндрю С. Гибсон — писатель, издатель, путешественник, руководитель семинаров и фотограф из Великобритании. Он начал писать о фотографии во время путешествия по Боливии и публиковался во многих престижных фотожурналах, включая журнал EOS, где он работал писателем и техническим редактором в течение двух лет. Его вдохновляют встречи с новыми людьми, посещение новых мест и получение новых впечатлений. Ознакомьтесь с его электронными книгами по фотографии здесь.
Просмотреть все сообщения Эндрю С. Гибсона
Состав чисел: 0–5 | NCETM
Состав чисел: 0–5 | НЦЭТМ- Мастерство PD Материалы
Состав чисел: 0–5
Корешок 1: Число, сложение и вычитание – Тема 1.3
Введение
Примените структуру разделения к числам до пяти и познакомьте детей с новыми понятиями, такими как субитизация, порядковый номер и линейчатая модель.
Точки обучения
- Точка обучения 1: Числа могут обозначать количество объектов в наборе; для небольших наборов мы можем распознавать количество объектов (субитизировать) вместо их подсчета.
- Учебный момент 2: Порядковые номера указывают на один элемент или событие, а не на количество.
- Учебный пункт 3: Каждое из чисел от одного до пяти можно разделить по-разному.
- Учебный пункт 4: Каждое из чисел от одного до пяти может быть систематически разбито на части.
- Учебный пункт 5: Каждое из чисел от одного до пяти можно разделить на две части; если мы знаем одну часть, мы можем найти другую часть.
