Сперва вычисляется находится скобках. Порядок выполнения действий

Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:

1. Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
2. Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
3. Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.

В качестве примера рассмотрим следующее выражение:

Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):

3 · 16 — 8: 2 + 20

Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):

И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):

48 — 4 + 20 = 44 + 20 = 64

Действия первой и второй ступени

Арифметические действия делятся на действия первой и второй ступени. Сложение и вычитание называются действиями первой ступени , умножение и деление — действиями второй ступени .

Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.

Пример 1.

15 + 17 — 20 + 8 — 12

Решение. Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.

Ответ: 42.

Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.

Пример. Вычислить значение выражения:

24: 3 + 5 · 2 — 17

Решение. Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.

Теперь приступим к вычислению.

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу.

В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание.

Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

1. Festival.1september.ru ().
2. Sosnovoborsk-soobchestva.ru ().
3. Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

Yandex.RTB R-A-339285-1

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .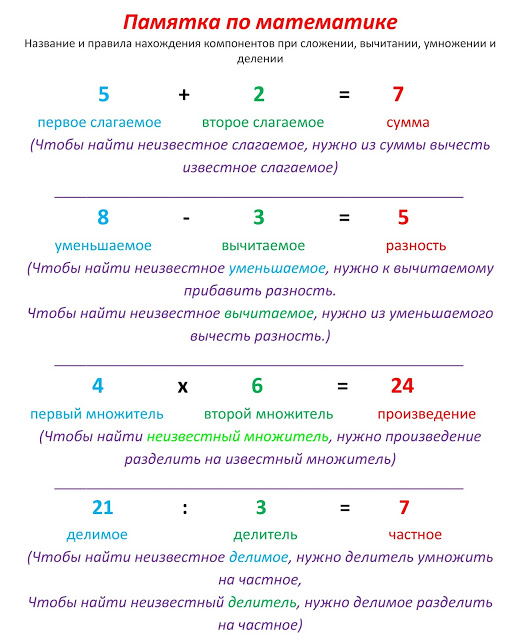

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Правила порядка выполнения действий в сложных выражениях изучаются во 2 классе, но практически некоторые из них дети используют еще в 1 классе.

Сначала рассматривается правило о порядке выполнения действий в выражениях без скобок, когда над числами производят либо только сложение и вычитание, либо только умножение и деление. Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно:

Аналогично: 6 — 1 — 1, 6 — 2 — 1, 6 — 2 — 2.

Так как для нахождения значений этих выражений школьники обращаются к предметным действиям, которые выполняются в определенном порядке, то они легко усваивают тот факт, что арифметические действия (сложение и вычитание), которые имеют место в выражениях, выполняются последовательно слева направо.

С числовыми выражениями, содержащими действия сложения и вычитания, а также скобки, учащиеся впервые встречаются в теме «Сложение и вычитание в пределах 10». Когда дети встречаются с такими выражениями в 1 классе, например: 7 — 2 + 4, 9 — 3 — 1 , 4 +3 — 2; во 2 классе, например: 70 — 36 +10, 80 — 10 — 15, 32+18 — 17; 4*10:5, 60:10*3, 36:9*3, учитель показывает, как читают и записывают такие выражения и как находят их значение (например, 4*10:5 читают: 4 умножить на 10 и полученный результат разделить на 5). К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.е. слева направо).

Несмотря на то, что в выражениях вида а+в+с, а+(в+с) и (а+в)+с наличие скобок не влияет на порядок выполнения действий в силу сочетательного закона сложения, на этом этапе учащихся целесообразнее сориентировать на то, что сначала выполняется действие в скобках. Это связано с тем, что для выражений вида а — (в+с) и а — (в — с) такое обобщение неприемлемо и учащимся на начальном этапе довольно трудно будет сориентироваться в назначении скобок для различных числовых выражений. Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.

Учитель обращает внимание детей на то, как важно соблюдать это правило при вычислениях, иначе можно получить неверное равенство. Например, учащиеся объясняют, каким образом, получены значения выражений: 70 — 36 +10=24, 60:10 — 3 =2, почему они неверны, какие значения в действительности имеют эти выражения. Аналогично изучают порядок действий в выражениях со скобками вида: 65 — (26 — 14), 50:(30 — 20), 90:(2 * 5). С такими выражениями учащиеся также знакомы и умеют их читать, записывать и вычислять их значение. Объяснив порядок выполнения действий в нескольких таких выражениях, дети формулируют вывод: в выражениях со скобками первым выполняется действие над числами, записанными в скобках. Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.

Следующим вводится правило порядка выполнения действий в выражениях без скобок, когда в них содержатся действия первой и второй ступени. Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику. Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий:

После объяснения ошибок можно дать задание: используя скобки, изменить порядок действий так, чтобы выражение имело заданное значение. Например, чтобы первое из приведенных выражений имело значение, равное 10, надо записать его так: (20+30):5=10.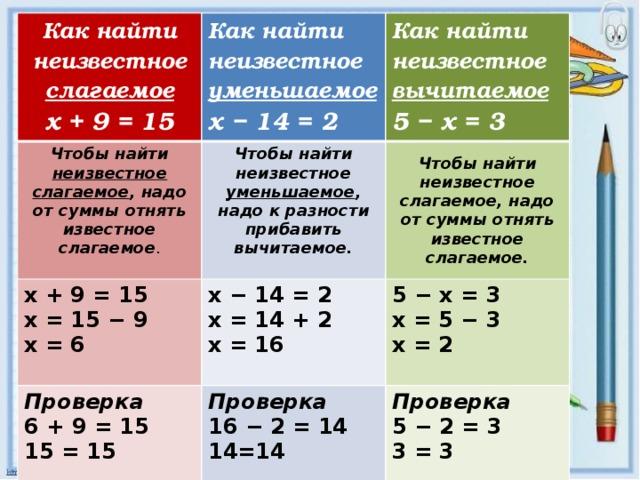

Особенно полезны упражнения на вычисление значения выражения, когда ученику приходится применять все изученные правила. Например, на доске или в тетрадях записывается выражение 36:6+3*2. Учащиеся вычисляют его значение. Затем по заданию учителя дети изменяют с помощью скобок порядок действий в выражении:

• 36:6+3-2
• 36:(6+3-2)
• 36:(6+3)-2
• (36:6+3)-2

Интересным, но более трудным является обратное упражнение: расставить скобки так, чтобы выражение имело заданное значение:

• 72-24:6+2=66
• 72-24:6+2=6
• 72-24:6+2=10
• 72-24:6+2=69

Также интересными являются упражнения следующего вида:

• 1. Расставьте скобки так, чтобы равенства были верными:
• 25-17:4=2 3*6-4=6
• 24:8-2=4
• 2. Поставьте вместо звездочек знаки «+» или «-» так, чтобы получились верные равенства:
• 38*3*7=34
• 38*3*7=28
• 38*3*7=42
• 38*3*7=48
• 3. Поставьте вместо звездочек знаки арифметических действий так, чтобы равенства были верными:
• 12*6*2=4
• 12*6*2=70
• 12*6*2=24
• 12*6*2=9
• 12*6*2=0

Выполняя такие упражнения, учащиеся убеждаются в том, что значение выражения может измениться, если изменяется порядок действий.

Для усвоения правил порядка действий необходимо в 3 и 4 классах включать все более усложняющиеся выражения, при вычислении значений которых ученик применял бы каждый раз не одно, а два или три правила порядка выполнения действий, например:

• 90*8- (240+170)+190,
• 469148-148*9+(30 100 — 26909).

При этом числа следует подбирать так, чтобы они допускали выполнение действий в любом порядке, что создает условия для сознательного применения изученных правил.

Сначала умножение и деление, затем сложение и вычитание

⇐ ПредыдущаяСтр 11 из 11 В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: · действия выполняются по порядку слева направо, · причем сначала выполняется умножение и деление, а затем – сложение и вычитание. Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия. Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий. Пример. Выполните действия 7−3+6. Решение. Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3, получаем 4, после чего к полученной разности 4 прибавляем 6, получаем 10. Кратко решение можно записать так: 7−3+6=4+6=10. Ответ: 7−3+6=10. Пример. Укажите порядок выполнения действий в выражении 6:2·8:3. Решение. Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо. Ответ: сначала 6 делим на 2, это частное умножаем на 8, наконец, полученный результат делим на 3. Пример. Вычислите значение выражения 17−5·6:3−2+4:2. Решение. Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3найденное значение 10, а вместо 4:2 — значение 2, имеем17−5·6:3−2+4:2=17−10−2+2. В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия:17−10−2+2=7−2+2=5+2=7. Ответ: 17−5·6:3−2+4:2=7. На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: . Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями. Выполните действия в выражении 4+(3+1+4·(2+3)). Решение. Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий:4+24=28. Билет № 28 КВАДРАТ. Из множества прямоугольников учащиеся вычленяют прямоугольники с равными сторонами – квадрат. Для знакомства с квадратом учащимся можно предложить выполнить такую практическую работу:1 из набора четырехугольников выбрать квадрат 2 найти прямоугольники у которых все стороны равны (перегибанием) 3 сообщить «Прямоугольник у которого все стороны равны – квадрат» 4 отыскиваем квадрат среди других фигур 5 выкладываем из палочек 6 черчение квадрата по клеточкам. КРУГ. Чертится окружность, учитель по окруж. Вырезает круг, а учащиеся заштриховывают лист внутри окруж. Сообщается что эта часть- круг. Обозначаем центр окружности точкойи соединяется с центром – радиус окруж.проводим несколько радиусов и делаем вывод что они равны. Круг – это часть плоскости ограниченная окружностью, сама окруж. Тоже входит в круг. СКОБКИ Билет № 29 КУБ. куб рассматривается в 3 классе при изучении объема. При рассмотрении объема куба дети знакомятся с гранями, ребрами, вершинами. «Рисунок куба» — это куб он имеет три измерения: длина – 1см, ширина – 1 см, высота 1 см, объем – 1 см в кубе, После измерения объема куба учащиеся через урок знакомятся со строением куба. Происходит это так : Это куб, он имеет 8 вершин. Отрезок, соединяющий две его вершины, называется ребром . Сколько ребер у куба? Посчитаем. Длина всех ребер одинаковая . Куб имеет 6 граней (передняя, задняя, нижняя, верхняя, левая и правая). Длину меряют отрезками, площадь – квадратами, а объем и вместимость – кубами). Куб – это прямоугольный паралепипед, у которого три измерения одинаковы: длина равна ширине и равна высоте. ПРЯМОУГОЛЬНИК. Обьяснить так: 1положить набор фигур, выбрать четырехугольник , доказать что это четырехугольник. 2 взять модель прямого угла, показать фигуры у которых есть прямые углы, проверить углы четырехугольника.выбрать четырехуг. С прямыми углами. 3 сообщить «Четырехугольник у которого все углы прямые называется прямоугольником» 4отыскиваем прямоугодльники среди других фигур и в очертании других предметов . ПАРАЛЛЕЛИППИПЕД . С прямоугольным параллелипипедом учащиеся знакомятся в 4 классе. Учащимся предлагается сравнить несколько фигур: Что ты заметил?Яв-ся ли эти тела кубами? Почему?чему равны измерения? (длина ширина высота) Затем учитель сообщает что это прямоуг. Параллелипипед. Он встречается в жизни с предметами различной формы. Чемодан и футбольный мяч. Могут иметь один и тот же цвет , они могут быть обтянуты одним и тем же материалом. Но не смотря на это чемодан или мяч совершенно не похожи друг на друга- они имеют разную форму. Обращенная сторона прямоугольника имеет форму прямоугольника. Это передняя грань. Точно такой же прямоугольник равный передней грани имеется сзади. Это задняя грань. Мы ее не видим. Сверху и низу имеется еще две грани. Верхняя грань нам видна, а нижняя не видна. Всего 6 граней. Каждая имеет форму прямоугольника. Та грань на которой прямоуг парал. Стоит – основание, а противоположная сторона – верхнее основание. Остальные грани – боковые. 2) В окружающей нас жизни возникает множество таких жизненных ситуаций, которые связаны с числами и требуют выполнения арифметических действий над ними, это — задачи. Чтобы решить задачу нужно лишь перевести ее с обыкновенного я зыка на язык символический — в алгебраический. Этот перевод означает составление уравнений, корни которого дают ответ на поставленный вопрос задачи. Рассм простую задачу : Саша помогает папе, утром принес несколько кирпичей , после обеда 9 кирпичей. А всего он принес 17 . Сколько кирпичей принес Саша утром? Переведем эту задачу на символический язык и получим: Утром Саша принес- х кирпичей, после обеда – х+9 кирпичей. По условию известно что Саша принес 17 кирпичей , по этому х+9=17 .Равенство х+9=17 – уравнение. Оно выражает условие и вопрос задачи в математической символике. Чтобы получить ответ нужно найти значение х. Билет № 30 1)Методика обучения информатике»Методика» — слово греческого происхождения («метод» — путь). Исходя из данного термина можно заключить, что «методика математики» – это научно-обоснованный путь к изучению математики. Методика начального обучения математике является той сферой конкретно-педагогической деятельности, где вырабатываются и теоретически систематизируются объективные знания о процессе обучения математике. Для учителя этот предмет является как бы инструментом рационального обучения математике. Методика математики в основном ориентируется на самого человека, на развитие его интеллекта, творческих способностей, культуры мышления, на создание духовных предпосылок его развития. Общепризнан тот факт, что методика математики призвана дать ответы на три основных вопроса, связанных с обучением: Зачем обучать математике? Что изучать из математики? Как обучать математике? Исходя из этих трёх задач можно сказать, что «предметом методики начального обучения математике является обоснование целей начального обучения математике (зачем обучать математике), научная разработка содержания обучения математике, получающего воплощение в программе (что изучать), методов обучения (как обучать), средств обучения — учебников, наглядных пособий и технических средств (при помощи чего обучать). Важной задачей является организация обучения и исследование процесса и результатов усвоения математических знаний учащимися. Процесс обучения методике математики будущих учителей представляет собой взаимодействие преподавателя и студентов, в ходе которого решается задача подготовки новых кадров. В этом процессе идет целенаправленная передача систематизированной информации с одной стороны (преподаватель) и должное усвоение этой информации с другой стороны (студент). Поэтому методика математики в данной ситуации становится учебным предметом. Данный предмет полностью отвечает за методическую подготовку учителя для организации процесса обучения математике учащихся. Методика обучения математике, как учебный предмет в педагогическом учебном заведении, состоит из двух разделов: 1) Общая методика обучения математике (например, изучение методов обучения, организация процесса обучения математике и т.п.). 2) Частная методика обучения математике (например, методика изучения нумерации, сложения в пределах десяти и т. п.). Основное содержание учебного предмета «Методика начального обучения математике» есть ответ на вопрос: «Как обучать математике?», который излагается в соответствующих учебниках математики. Ответ же на других два вопроса: «Зачем обучать математике?» и «Что изучать из математики?» в основном отражён в учебных программах и учебниках начальной школы, с учетом которых составляются учебники методики. Билет № 22 1) числовое равенствоЗнакомство с числовыми равенствами начинается на самом начальном этапе изучения математики в школе. Обычно это происходит в 1 классе сразу после того, как становятся известными первые числа от 1 до 9 и после того, как обретает смысл фраза «столько же». Тогда то и появляются первые числовые равенства, например,1=1, 3=3 и т.п., которые на этом этапе обычно называют просто равенствами без уточняющего определения «числовые». Равенствам указанного вида на этом этапе придается количественный или порядковый смысл, который вкладывается в натуральные числа. К примеру, числовое равенство 3=3 отвечало картинке, на которой изображены две ветки дерева, на каждой из которых сидят по 3 птицы. Или когда в двух очередях третьими по порядку стоят наши товарищи Петя и Коля. После изучения арифметических действий, появляются более разнообразные записи числовых равенств, например, 3+1=4, 7−2=5, 3·2=6, 8:4=2 и т.п. Дальше начинают встречаться числовые равенства еще более интересного вида, содержащие в своих частях различные числовые выражения, к примеру, (2+1)+3=2+(1+3),4·(4−(1+2))+12:4−1=4·1+3−1 и тому подобные. Дальше происходит знакомство с другими видами чисел, и числовые равенства приобретают все более и более разнообразный вид.Числовое равенство– это равенство, в обеих частях которого находятся числа и/или числовые выражения. основные свойства числовых равенств это: свойство рефлексивности: a=a; свойство симметричности: если a=b, то b=a; и свойство транзитивности: если a=b и b=c, то a=c, где a, b и c – произвольные числа. ⇐ Предыдущая234567891011 Читайте также:

Описание основных узлов: Арифметический узел

1. Представление чисел

Арифметический узел предназначен для выполнения четырех арифметических действий: сложения, вычитания, умножения и деления.

Числа, над которыми производятся действия, представляются в двоичной системе. Каждая цифра двоичного числа выражается одним из состояний соответствующей триггерной схемы.

Объем числа составляет 24 двоичных разряда, т.е. число представлено в виде цепочки из 24-х триггеров, которую в дальнейшем мы будем называть регистром. Принята система представления чисел в виде модуля и знака. Т.е. в регистре хранится модуль числа, и, кроме того, в него введен 25-й триггер, одно из положений которого соответствует знаку +, другое – знаку

Для удобства вычислений принято, что наивысший разряд числа соответствует 2^-1, т. е. вычисления производятся над дробными числами.

Такое допущение не сужает диапазон решаемых задач, так как при использовании чисел, превышающих по модулю единицу, они могут быть приведены к дроби нужной величины путем соответствующего изменения масштабов исходных данных и результатов

Иногда может возникнуть необходимость изменение масштаба в процессе решения задачи. Такая возможность также имеется, так как при получении в процессе вычислений чисел, превышающих по модулю единицу, АЦВМ автоматически останавливается на том этапе, где получено это число.

Выбор дробной системы удобен тем, что при умножении двух чисел произведение может только уменьшаться. Поэтому при умножении не может получиться число, превышающее по модулю единицу.

Число, модуль которого больше единицы, может получиться в некоторых случаях деления, но деление встречается в вычислениях гораздо реже, чем умножение. Кроме деления такое число может, очевидно, при сложении и вычитании.

2. Выполнение действий

При использовании цифровых методов вычислений, оказывается, что для выполнения всех четырех арифметических действий необходимо и достаточно, чтобы в АУ могла осуществляться только одна основная операция – сложение, и некоторые вспомогательные действия.

В двоичной системе эти действия, так же как и сложение , выполняются наиболее просто и представляют:

1. Сдвиг модуля числа в сторону высших или низших разрядов («влево» или «вправо»).
2. Взятие дополнения от модуля числа, состоящее в замене всех цифр числа на обратные им («0» на «1» или «1» на «0»).

Легко видно, что сдвиг числа влево или вправо соответствует соответствие умножению или делению его на 2.

Дополнение R числа А есть число, связанное с исходным числом А соотношением

R =1 – 2^-24 — А

Вычитание производится как сложение уменьшаемого с дополнением вычитаемого.

Умножение , очевидно, выполняется в виде последовательных сложений и сдвигов, т.е. точно также как при обычном умножении «столбиком».

Применение двоичной системы упрощает таблицу умножения, которая имеет вид:

0 х 0 = 0
0 х 1 = 0
1 х 1 = 1

Деление производится последовательным вычитанием и сдвигом.

3. Блок-схема АУ

Основной частью АУ, в которой совершаются действия, являются три триггерных регистра: регистр А, регистр В, регистр С. Кроме того в АУ имеется дополнительный регистр, называемый в дальнейшем программно-цифровой магистралью (ПЦМ). Через ПЦМ в АУ поступают из памяти и выдаются из АУ в память числа, над которыми совершаются действия, и результаты. Через ПЦМ кроме того в ГПД поступают инструкции, выбранные из памяти.

Местный программный датчик (МПД) получает из ГПД один из четырех возможных импульсов, указывающих какое действие необходимо совершить над числами, принятыми в регистры А, В, и С. После окончания действия МПД выдает результат в ПЦМ, посылая одновременно в ГПД ответный импульс, извещающий об окончании операции.

В АУ производится сложение чисел, набранных в регистрах А и В. Сумма чисел образуется в регистре В путем установки в каждом разряде регистра В состояния, соответствующего сумме цифр слагаемых, набранных первоначально в А и В в этом разряде, и переходной единицы из предыдущего разряда, если она есть.

Переходная единица образуется как в сложении «столбиком», если сумма цифр в предыдущем разряде равна или больше 2-х. Наличие или отсутствие переходной единицы из предыдущего разряда определяется состоянием триггера переходной единицы, устанавливаемого в соответствии с указанным выше правилом.

Для установки всех триггеров переходных единиц в правильное положение после приема в регистры А и В слагаемых требуется некоторое время, называемое «временем пробега переходной единицы», которое и определяет время занимаемое сложением. Только по прошествии времени пробега из МПД в регистр В поступает импульс выдачи суммы, образующий в регистре В результаты сложения.

Время пробега в нашем случае составляет 1 мксек/разряд.

При вычитании в регистр В принимается уменьшаемое, в регистр А вычитаемое. МПД после получения из ГПД импульса «вычитание» посылает в регистр А импульс дополнения, изменяющий состояние триггеров на обратные. После посылки импульса дополнения через время, соответствующее пробегу единицы, МПД посылает в регистр В импульс выдачи суммы. При этом в В, как и указывалось ранее, образуется искомая разность.

Если результат сложения (вычитания) по модулю превышает 1, то АЦВМ автоматически останавливается.

При умножении сомножители принимаются в регистры А и С, а в регистре В устанавливается 0. МПД посылает в регистр С 24 последовательных импульса сдвига вправо, т. е. в сторону младших разрядов. Таким образом, через 1-й триггер регистра С последовательно проходят все цифры числа, набранного в С, начиная с младшего разряда.

Перед каждым сдвигом, в зависимости от того, «0» или «1» находится в первом триггере регистра С, не производится или производится сложение чисел, находящихся в регистрах А и В. Результат сложения, Образованный в регистре В, затем сдвигается одновременно со сдвигом в С. Таким образом, в регистре В накапливается частное произведение, которое по истечении 24-х сдвигов и будет искомым результатом.

При делении, являющимся действием, обратным умножению, в регистр В, в котором ранее образовывалось произведение, принимается делимое, а в регистр А – делитель. Частное образуется в регистре С.

МПД посылает в регистр В 24 последовательных импульса сдвига влево. Деление при выбранной дробной системе представления чисел возможно, если делимое меньше делителя. В противном случае АЦВМ автоматически останавливается. Сдвиг влево означает умножение делителя на 2. После каждого сдвига происходит проверка, стало ли больше число в регистре В чем в А или нет. Если нет, то в младшем разряде С устанавливается «0», если больше, то после сдвига производится вычитание и в младшем разряде С устанавливается «1». Результат вычитания , образованный в В, продолжает сдвигаться влево. В регистре С после каждого сдвига в В также происходит сдвиг влево, так что устанавливаемые за каждый сдвиг в В цифры из младшего разряда С сдвигаются в сторону старших разрядов, образуя по истечении 24 сдвигов в С частное.

После окончания любого из действий МПД одновременно с ответным сигналом выдает в ПЦМ результат действия. Числа, поступающие из ПЦМ в регистры А, В и С, могут приниматься либо из устройства магнитной памяти, либо из электростатической памяти. Число из МП выдается одновременно во все разряды ПЦМ (параллельно).

Число, выбираемое из ЭП, выдается в ПЦМ последовательно, начиная со старших разрядов, для чего в ПЦМ предусмотрена возможность сдвига числа влево.

Регистры А, В. и С, а также программно-цифровая магистраль ПЦМ выполнены в виде 24 идентичных блоков (см. лист Р-АУ), каждый из которых содержит по одному разряду всех регистров АУ.

Все горизонтальные соединения на блок-схеме выполнены внутри каждого блока.

Вертикальные соединения выполнены в виде шин, проходящих вдоль стойки, на которой размещаются блоки.

Блок-схема АУ M-1

4. Местный программный датчик (МПД)

МПД состоит из трех блоков:

1. Блок для выполнения умножения-деления (лист УД-АУ).
   Для получения серий из 24 импульсов используется триггерный счетчик, отсчитывающий по приходе команды из ГПД заданные 24 импульса. Для формирования нужных импульсов использованы два кипп-реле с промежуточными усилителями и клапанными схемами.
2. Блок для выполнения сложения-вычитания (лист СВ-АУ). В этом блоке формируется импульс сложения, задержанный при помощи кипп-реле на время, необходимое для пробега переходной единицы. Кроме того, здесь же находятся триггеры разрядов знака числа регистров А, В, С и ПЦМ. Знаки чисел передаются из памяти в триггер ПЦМ, а оттуда в триггеры регистров А, В и С точно так же как в блоках (Р – АУ). Здесь же образуется знак результата.
3. Блок формирования и усиления импульсов, поступающих в регистры (РИ – АУ).
   В этом блоке осуществляется окончательное формирование импульсов и усиление их по мощности линейкой катодных повторителей.

Описание основных узлов: Магнитное запоминающее устройство.

Отчет помещен в музей 27.04.2009

Порядок операций (PEMDAS) – значение, правила, аббревиатура и примеры

Мы выполняем различные математические операции для решения задач, связанных с нашей повседневной жизнью. Некоторые общие операции, которые мы регулярно выполняем в арифметике, — это сложение, вычитание, умножение, деление и возведение в квадрат.

Порядок операций описывает шаги, в которых мы выполняем операции в выражении. Рассмотрим данное выражение целыми числами:

6 × (3 + 6 ² – 5) ÷ 5

Какую часть нужно вычислить первой?

Нам необходимо следовать порядку операций или правилу приоритета операторов, известному как PEMDAS, когда мы идем слева направо в выражении.

Что такое порядки операций

Математические порядки операций — это правила, описывающие последовательность, в которой выполняются операции в выражении.

Он был изобретен в 1913 году Вебстером Уэллсом и Уолтером У. Хартом.

Как я это помню

Способ запомнить порядок операций — это PEMDAS. Шаги:

Шаг 1: P для круглых скобок

Первый — решить все операции в круглых скобках ( ), { }, [ ]. Все выражения в скобках считаются группой.

Шаг 2: E для степени

Следующим шагом является решение выражений с показателем степени (степень и показатель степени).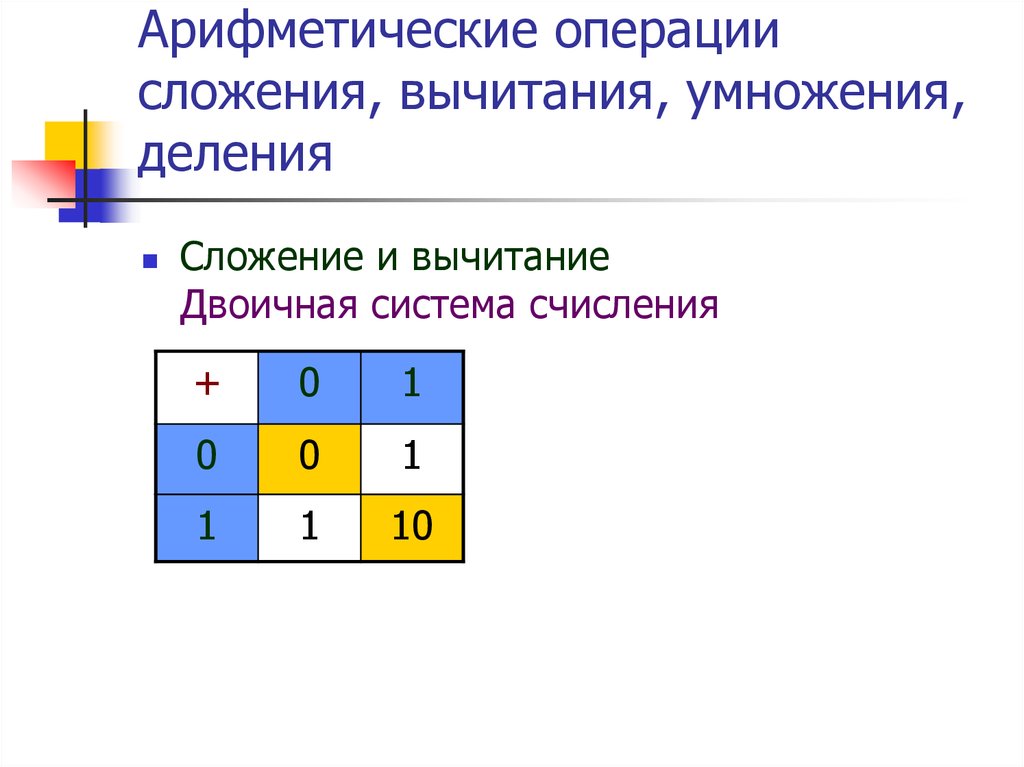

Шаг 3: MD для умножения и деления

Эти две операции (×) и (÷) имеют одинаковый ранг и должны выполняться на третьем шаге. Выполните операцию, которая придет первой.

Шаг 4: AS для сложения и вычитания

Наконец, подобно умножению и делению, сложение (+) и вычитание (-) также имеют одинаковый ранг и должны выполняться рядом с ними.

Order of Operations PEMDAS

Some other mnemonics are:

• P lease E at M om’s D elicious A pple S trudels
• P opcorn E very M onday D onuts A LWAY S UNDAY
• P EOPE E НЕЧИ M ADE D ECISOSS A BOUT S UMS

в BOUT S UMS

в BOUT S UMS

.

B для квадратных скобок, O для порядка, D для деления, M для умножения, A для сложения и S для вычитания

В Канаде они следуют BEDMAS.

B для квадратных скобок, E для степени, D для деления, M для умножения, A для сложения и S для вычитания

Теперь давайте решим выражение, данное нам в начале этой статьи: 6 × (3 + 6 ² – 5) ÷ 5 с помощью PEMDAS.

Здесь в выражении 6 × (3 + 6 ² – 5) ÷ 5

(3 + 6 ² – 5) заключено в скобки и должно выполняться первым. Однако есть две отдельные операции + и – . По правилу PEMDAS первым должен выполняться показатель степени 6 ² . Таким образом, выражение принимает вид

= 6 × (3 + 36 – 5) ÷ 5

Затем следует выполнить операцию сложения в скобках, а затем вычитание.

= 6 × (40 – 5) ÷ 5

= 6 × 35 ÷ 5

Теперь мы выполним деление с последующим умножением или умножение с последующим делением, поскольку они оба имеют одинаковый ранг.

= 6 × 7

= 42

Давайте решим еще несколько задач, которые немного сложно решить, используя порядок операций PEMDAS.

Решенные примеры

Решите данное выражение с целыми числами, используя PEMDAS
а) 5 × 4 – 2
б) 16 ÷ 4 + 6
C) (4 × 5 ² ) + 6

Решение:

Оценка (4 × 2 ÷ 1) — 2

Решение:

922290

. x (5 + 7) ÷ 3 – 7 с использованием PEMDAS.

Решение:

Упростить экспрессию алгебраии (8x — 2x) ÷ 3x с использованием PEMDAS

Решение:

19021. Обращение по заказу.

Решить данное выражение (5/2 × 7/2) + (7/3 × 5/3)

Решение:

9002 Решить в порядке 21 ВЫРАЖЕНИЕ с АБСОЛЮТНЫМ ЗНАЧЕНИЕМ

Решите данное выражение (-9 – (-3) x 7) ÷ |-3 ²  + 5|

Решение:

Почему порядок операций важен

Он важен, потому что предлагает универсальное правило, которому мы все можем следовать, чтобы выполнить выражение и получить одинаковый результат.

Мы используем PEMDAS всякий раз, когда нам нужно решить повседневную проблему. Давайте рассмотрим простую текстовую задачу.

Предположим, мы купили 6 пицц по 15 долларов каждая. Если мы распределим 6 кусочков поровну между 6 вашими друзьями, каждый получит по одному кусочку. Если мы намерены найти стоимость каждой части, мы применяем PEMDAS для решения выражения.

Общее количество людей = 6

Количество кусочков пиццы = 6

Стоимость каждого кусочка = 15 долларов США

Выражение принимает вид (15 + 15 + 15 + 15 + 15 +15) ÷ 6 или (6 × 15) ÷ 6

According to PEMDAS,

(6 × 15) ÷ 6

Expression	Evaluation	Operations
(6 × 15) ÷ 6	Step 1 : (6 × 15) = 90 Шаг 2 : 90 ÷ 6  = 15	Скобка   Деление

Точно так же мы используем PEMDAS для решения многих подобных задач в нашей повседневной жизни.

Крис купил 6 бананов по 10 центов каждый и 1 яблоко по 60 центов. Напишите числовое выражение, представляющее эту ситуацию, а затем найдите общую стоимость в долларах.

Решение:

Согласно задаче выражение равно
6 × 10 + 2 × 60
Решение выражения с помощью PEMDAS
 = 60 + 120 (Умножение)
= 180 (Сложение)

3

(DMAS)

Введение

При упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.

Давайте разберемся с этим на примере.

Предположим, мы хотим найти значение 2 + 3 x 5

Есть два способа найти значение приведенного выше выражения.

В первом методе будем двигаться слева направо, решая выражение в указанном порядке. Это означает, что сначала мы найдем сумму 2 и 3. Мы получим, 2 + 3 = 5.

Теперь у нас есть 2 + 3 x 5 = 5 x 5

Теперь мы найдем произведение 5 на 5 чтобы получить ответ как 25. Следовательно, мы имеем

2 + 3 x 5 = 25 ……………………………….. ( 1 )

Теперь найдем значение этого выражения другим способом.

Сначала мы найдем значение 3 x 5 и добавим это произведение к 2. Таким образом, мы получим

3 x 5 = 15 и 15 + 2 = 17

Следовательно, теперь у нас есть

2 + 3 x 5 = 17 ………………………… ( 2 )

Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.

Каков основной порядок операций?

Порядок операций можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. Без последовательного порядка операций можно допустить большие ошибки во время вычислений. Существует ряд правил, определяющих порядок операций в зависимости от задействования операторов, скобок, показателей степени и других математических символов для операций. Это правило известно как DMAS, где

D означает деление (÷)

M означает умножение (x)

A означает сложение (+)

S означает вычитание (–)

Давайте разберемся с правилом более подробно.

Что такое DMAS?

MDAS, как определено выше, является основным порядком операций. Другими словами, он определяет порядок, в котором должны выполняться операции над числами, когда возникают ситуации, когда в выражении имеется на две операции больше, чем две. Итак, у нас порядок операций такой – 

Рассмотрим пример. Предположим, мы хотим найти значение 3 + 5 x 2.

Здесь у нас есть два оператора, а именно ( x ) и ( + ). Мы знаем, что в математике мы можем выполнять операции между двумя числами только за один раз. Если у нас есть более 2 чисел, результат первой операции используется для выполнения следующей операции. Итак, в приведенном выше примере необходимо выполнить две операции: (3 + 5) и (5 x 2). Нам нужно решить, с какой из них начать. Здесь вступает в действие правило MDAS.

Из этого правила видно, что умножение предшествует сложению. Поэтому сначала выполним операцию умножения. Полученный таким образом результат будет добавлен к 3. Шаги, связанные с этим процессом, будут – 

3 + 5 x 2

 = 3 + 10

 = 13

Следовательно, 3 + 5 x 2 = 13

Рассмотрим другой пример.

Пример

Упростите следующее выражение, используя порядок операций –

6 + 5 – 4 x 2

Решение

Нам дано выражение 6 + 5 – 4 x 2

Важно отметить, что здесь задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо.

Следовательно, мы имеем

6 + 5 – 4 x 2

 = 6 + 5 – 8 (Здесь мы решили 4 x 2, что дало нам результат 8)

= Затем мы сложим 6 и 3, чтобы получить 9. Итак, у нас есть

6 + 5 – 8 = 11 – 8  = 3

Следовательно, 6 + 5 – 4 x 2 = 3

Использование скобок в порядке операций

Мы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.

Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении. Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –

24 ÷ 3 x 4

= 8 x 4 = 32

Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как

24 ÷ ( 3 x 4 )

Теперь в соответствии с порядком действий сначала разгадаем скобки, чтобы получить,

 24 ÷ ( 3 x 4 )

= 24 ÷ 12

 = 2

В сложных выражениях иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, потому что чаще всего используются разные типы скобок)

Скобки Имя

( ) Круглые скобки

{ } Скобки или фигурные скобки

[ ] Скобки или квадратные скобки

Здесь важно отметить, что левая часть каждого символа скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.

Удаление скобок

Чтобы упростить выражения, включающие более одной скобки, мы будем использовать шаги, описанные ниже –

1. Посмотреть, содержит ли данное выражение винкулум или нет. Если винкулум присутствует, выполните операции с красным цветом, в противном случае перейдите к следующему шагу. Винкулум — это горизонтальная линия, расположенная над выражением, чтобы показать, что все, что ниже линии, является одной группой, например, $\overline{2\: x\: 3}$.
2. Теперь найдите самую внутреннюю скобку и выполните в ней операции.
3. Удалите самую внутреннюю скобку, выполнив следующие действия: 
   1. Если скобке предшествует знак плюс, удалите ее, записав ее термины как есть.
   2. Если скобке предшествует знак минус, измените положительный знак внутри нее на отрицательный и наоборот.
   3. Если между числом и символом группировки нет знака, то это означает умножение.
   4. Если перед некоторыми скобками стоит число, то мы умножаем число внутри скобок на число вне скобок.
4. Найдите ближайшую внутреннюю скобку и выполните в ней операции. Удалите второй в направлении, используя правила, указанные в предыдущих шагах. Продолжайте этот процесс, пока не будут удалены все скобки.

Давайте разберем приведенные выше шаги на примере.

Пример

Упрощение: 37 – [ 5 + { 28 – ( 19 – 7 ) } ]

Решение

Нам дано выражение, 37 – [ 1 9 – 28 – ( 1 ) } ]

Мы будем использовать порядок операций для решения данного выражения.

Сначала мы удалим самую внутреннюю скобку, чтобы получить

37 – [ 5 + { 28 – 12 } ] …………………… [ Удаление самой внутренней скобки ( ) ]

Далее мы удалим фигурные скобки, чтобы получить

37 — [ 5 + 16 ] …………………………. [ Удаление фигурных скобок ]

Теперь мы удалим квадратные скобки, чтобы получить,

37 – 21 …………………………… [удаление квадратных скобок ]

Наконец, мы найдем разницу между 37 и 21, чтобы получить 16.

Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] приведет к 16.

Как решать выражения, используя порядок операций?

Теперь, когда мы поняли, что мы подразумеваем под порядком операций, давайте узнаем о шагах, связанных с решением математических выражений с использованием порядка операций. Необходимые шаги: 

1. Всегда начинайте с вычисления всех выражений в круглых скобках

Прежде всего, мы должны искать удаление любых символов группировки в алгебраическом выражении. Это означает, что в верхней части списка всегда   упрощайте все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.

2. Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни

После удаления скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении. Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.

3. Выполните умножение и деление, начиная слева направо

Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.

4. Наконец, аналогично выполните сложение и вычитание, начиная слева направо.

Разберемся на примере.

Пример Найдите значение выражения 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )

Решение Нам дано выражение 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 ). Нам нужно решить ее с помощью MDAS.

Так как данное выражение содержит скобки; мы сначала решим скобки. Мы получим 

4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )

Теперь в скобках сначала решим раздел деления

4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 )

Далее в самой скобке решим умножение, чтобы получить

4 ( 10 + 3 × 4 – 2 × 2 )

Теперь внутри скобки решим сложение, чтобы получить

4 ( 10 + 12 – 4 ) 

Далее в скобках мы сложим числа 10 и 12, а затем вычтем из результата 4, чтобы получить

4 ( 22 – 4 )

После того, как скобка решена, возьмите число из снаружи и решить часть «Из» умножением:

= 4 × 18

= 72

Therefore,  4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )= 72

The steps used can be tabulated as

Brackets Of	4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Division	4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 )
Multiplication	4 ( 10 + 3 × 4 – 2 × 2 )
Addition	4 ( 10 + 12 – 4 )
Subtraction	4 ( 22 – 4 )
Answer	= 4 x 18
	72

Применение порядка операций в реальной жизни

Мы узнали, что в математике порядок операций помогает найти правильное значение выражения. Однако это не ограничивается задачами по математике. Порядок операций имеет значение и в повседневной жизни. Например, вы используете фиксированный порядок действий для приготовления блюда. Точно так же в химических реакциях необходимо соблюдать определенный порядок, чтобы получить желаемые результаты. Возвращаясь к математике, есть много повседневных дел, в которых используется порядок операций MDAS.

Давайте разберемся на примере.

Пример

Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Сколько всего он платит?

Решение

Нам известно, что Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Нам нужно узнать, сколько Джон платит за рубашки и джинсы. Чтобы найти это, мы должны сначала разместить все значения в виде выражения. Мы получим,

Цена 2 рубашек + Цена пары джинсов – Скидка = Общая стоимость, уплаченная Джоном

Следовательно, 

Общая стоимость, уплаченная Джоном = 2 x 8 + 20- – 3

Здесь мы видим, что есть задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо. Следовательно, мы получаем,

Общая стоимость, уплаченная Джоном = 16 + 20 – 3 = 36 – 3 = 33 £

Следовательно, общая стоимость, уплаченная Джоном за 2 рубашки и пару джинсов, = 33 фунта стерлингов

Теперь мы научились решать выражения, включающие более одного математического оператора. Но что, если в выражении используются скобки. Поступим ли мы так же или внесем некоторые дополнения в правило? Давайте узнаем.

Ключевые факты и сводка

1. Порядок работы можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.
2. MDAS — это базовый порядок операций, где MDAS, где M означает умножение (x), D означает деление (÷), A означает сложение (+), S означает вычитание (–).
3. Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении.
4. Правила порядка операций: – 
   • Всегда начинайте с вычисления всех выражений в скобках
   • Упростите все показатели степени, такие как квадратные корни, квадраты, куб и кубические корни.
   • Выполните умножение и деление, начиная слева направо.
   • Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
5. Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении.
6. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

PEMDAS: порядок операций

PEMDAS — это способ запоминания порядка операций, которые используются для упрощения числовых выражений и даже представлены в нашем подходе к решению уравнений. В этом уроке мы рассмотрим, что такое PEMDAS, и рассмотрим несколько примеров того, как он работает.

Содержание

1. Зачем нам PEMDAS?
2. Что означает PEMDAS?
3. Примеры использования PEMDAS и порядок операций

реклама

Зачем нам PEMDAS?

Рассмотрим вычисление \(1+3\умножить на 5\). Что из этого правильно?

\(1+3 \умножить на 5 = 4 \умножить на 5 = 20\)

или

\(1 + 3\умножить на 5 = 1 + 15 = 16\)

Если подумать, оба варианта кажутся разумными способами расчета. Проблема в том, что два подхода дают разные ответы! Чтобы избежать путаницы, существует стандартный согласованный порядок выполнения операций (где операция представляет собой что-то вроде сложения или умножения), известный как 9.0730 порядок операций .

Кстати, правильный расчет: \(1 + 3\умножить на 5 = 1 + 15 = 16\)

Что такое PEMDAS?

Легче всего запомнить порядок операций с помощью сокращения «PEMDAS». Вы даже можете добавить, чтобы запомнить это сокращение: «Пожалуйста, извините, моя дорогая тетя Салли». Это означает:

P скобки: Выполнить все операции, указанные в скобках. Если операций много, вы также должны соблюдать порядок операций внутри круглых скобок.

E экспоненты: Вычислить любые экспоненты, которые вы видите.

M умножение и D ivision: Выполните любое умножение или деление, которое вы видите, как правило, слева направо.

Сложение и вычитание Выполняйте любое сложение и вычитание слева направо.

Примеры применения PEMDAS / порядок операций

Давайте рассмотрим пару примеров, чтобы увидеть, как применять эти правила. 92 = 1 + 3 \умножить на 16\)

Далее нам предстоит выполнить любое умножение или деление (MD). Вы можете проверить на своем калькуляторе, что \( 3 \times 16 = 48\). Теперь у нас есть:

\(1 + 3 \умножить на 16 = 1 + 48\)

Наконец, мы прибавим/вычтем (AS), чтобы получить окончательный ответ:

\(1 + 48 = \в коробке{49}\)

Как видите, нам просто нужно пройтись по каждой части PEMDAS и тщательно выполнить все расчеты. Давайте попробуем другой пример, применяя те же правила, но просто взглянем на саму математику. 92 = 9\). Увидеть разницу? Если есть круглые скобки, это означает, что вы возводите в квадрат весь член, иначе отрицание «едет» как часть умножения.

реклама

Заключение

Порядок операций применим не только к числовым примерам, но также и к любой математической задаче, включая те, которые встречаются позже в алгебре и исчислении.