Математика Порядок выполнения действий

Этап усвоения новых знаний

 

Рассмотрим пример

48 – (10 + 9) + 2 · 9 — 18 : 3

Какие действия используются в данном числовом выражении?             
В числовом выражении есть такие действия, как вычитание, сложение, умножение, деление.

Как называются компоненты при сложении?             
слагаемое + слагаемое = сумма

Как называются компоненты при вычитании?             
уменьшаемое – вычитаемое = разность

Как называются компоненты при умножении?             
множитель · множитель = произведение

Как называются компоненты при делении?             
делимое : делитель =  частное

Чтобы правильно вычислить такое числовое выражение, нужно знать порядок действий.
Прежде, чем приступить к вычислениям, надо выяснить, какие действия в нем имеются, есть ли в нем скобки.

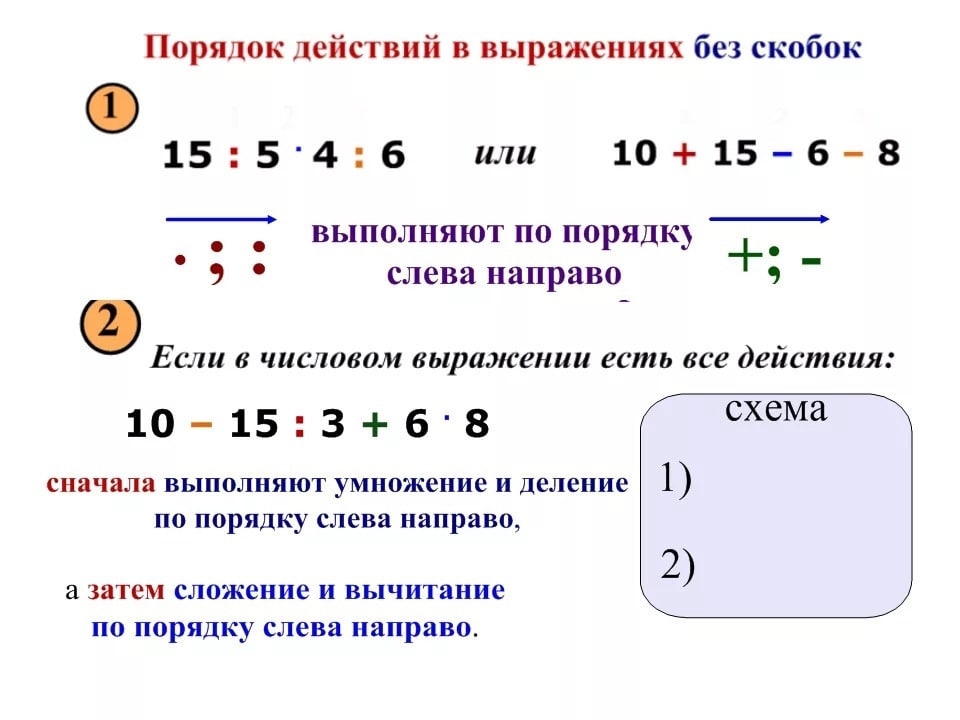
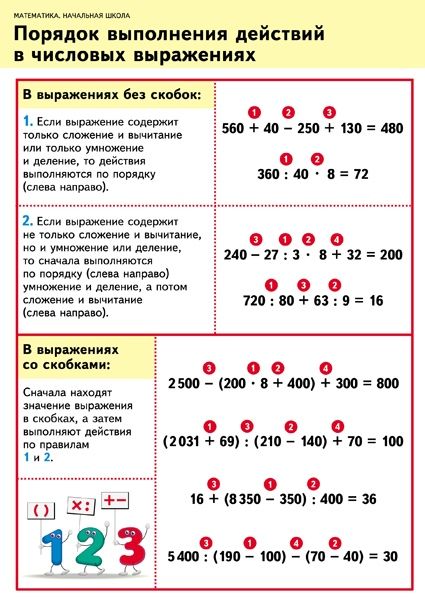
Если в выражении нет скобок, и в него входят только сложение и вычитание, то действия выполняются в том порядке, в котором они записаны.

     66     51

32 + 34 – 15 + 25 = 76

К 32 прибавим 34, получим 66, из 66 вычтем 15, будет 51, к 51 прибавим 25, будет 76.

Если в выражении нет скобок, и в него входят только умножение и деление, то действия выполняются в том порядке, в котором они записаны.

     9       3

27 :  3  :  3 · 2 =6

27 разделим на 3, будет 9; 9 разделим на 3, будет 3; 3 умножим на 2, получим 6.

Если в выражении нет скобок, и в него входят не только сложение и вычитание, но и  умножение или  деление, то сначала по порядку  выполняют умножение и деление, затем сложение и вычитание.

          5              18
        
48 – 10 : 2 + 8 + 9 · 2 = 69

Сначала 10 : 2 будет 5, 9 умножим на 2, получим 18.

Затем выполняем сложение и вычитание по порядку: из 48 вычтем 5, будет  43; к 43 прибавим 8, получим 51; к 51 прибавим 18, будет  69.

Если в числовом выражении есть скобки, то сначала выполняются действия в скобках, затем  по порядку умножение и деление, после по порядку сложение и вычитание.

Сначала выполняем действия в скобках: сложим 10 и 9, будет 19. Затем выполняем умножение и деление по порядку: 2 умножим на 9, будет 18, 18 разделим на 3, получим 6.

После выполним сложение и вычитание по порядку: из 48 вычесть 19, будет 29; к 29 прибавим 18, получим 47; из 47 вычтем 6, получим 41.

 

Запомните! Действия в числовых выражениях выполняются в следующем порядке:

Первыми выполняются действия, записанные в скобках. Затем выполняются по порядку умножение и деление. Потом выполняются сложение и вычитание.

Этап закрепления новых знаний

 

Чтобы пополнить запасы на корабле, выполните задания.

Установите порядок выполнения действий и выполните вычисления.

В данном числовом выражении нет скобок, действия – сложение и вычитание, значит, действия выполняем по порядку: к 25 прибавим 62, будет 87; из 87 вычтем 9, получим 78;  к 78 прибавим 14, будет 92.

В данном числовом выражении есть скобки, действия – сложение и вычитание. Первыми выполняем действия, записанные в скобках: к 15 прибавим 24, будет 39. Далее выполняем действия по порядку: из 45 вычтем 39, будет 6, к 6 прибавим 33, получим 39; из 39 вычтем 10, равно 29.

В числовом выражении нет скобок,  действия — умножение и деление. Их делаем по порядку:  30 разделим на 10, будет 3; 3 умножим на 9, равно 27.

В данном числовом выражении есть скобки, действия – умножение и деление. Первыми выполняем действия, записанные в скобках: 10 разделим на 2, получим 5, далее 3 умножим на 5, равно 15.

В данном числовом выражении есть скобки, действия – умножение,  сложение и вычитание. Первыми выполняем действия, записанные в скобках: из 36 вычесть 30, будет 6; далее выполняем умножение: 6 умножим на 2, будет 12, последним выполняем вычитание: из 92 вычесть 12, получим 80.

В числовом выражении нет скобок,  действия – сложение, умножение и деление. По порядку делаем умножение и деление: 2 умножим на 4. будет 8; 27 разделим на 3, равно 9. Далее выполняем сложение: к 8 прибавим 9, будет 17.

Помогите жителям острова собрать урожай.
Решите задачу в одно действие.

В первый день собрали  4 кг апельсинов, во второй день собрали 5 кг апельсинов, а кокосов в 2 раза больше, чем апельсинов в первый и во  второй день вместе, в третий день собрали ананасов  в 3 раза больше, чем апельсинов во второй день. Сколько всего килограмм фруктов собрали за три дня?

Проверьте себя и оцените свои успехи.

4 кг — собрали апельсинов в первый день.
5 кг – собрали апельсинов во второй день.
(4 + 5) · 2 – столько кг кокосов собрали во второй день.

5 · 3 – столько кг ананасов собрали в третий  день.

Сложим весь собранный урожай.

Решение

4 + 5 + (4 + 5) · 2 + 5 · 3 = 42 килограмма.

Ответ: собрали 42 кг фруктов за три дня.

В данном числовом выражении есть скобки, действия – умножение и  сложение. Первыми выполняем действия, записанные в скобках: 4 плюс 5 будет 9. Затем выполняем умножение: 9 умножим на 2, получим 18; 5 умножим на 3, равно 15.

Выполняем сложение по порядку:  сложим 4 + 5 + 18 + 15, выполним вычисления удобным способом: к 5 прибавим 15, будет 20, сложим 4 и 18, получим 22, 20 + 22, равно 42.

Ответ: жители острова собрали 42 кг фруктов.

Жители острова решили подарить капитану корабля бусы, но они рассыпались по палубе. Помогите собрать бусы.

В тех кружках, где цифр нет, расставьте минусы и плюсы, чтоб правильный получить ответ.

Проверьте себя.

38

—

22

+

13

—

20

=

9

Команде корабля пора отправляться в обратный путь, помогите поднять паруса, выполнив задания.

Решите логическое задание

Сколько четырёхугольников изображено на рисунке?               

На рисунке изображено 6 четырехугольников.
Один… два.. три…четыре…пять…шесть.
 

Задание

В соревнованиях по плаванию Маша, Саша и Таня заняли призовые места. Какое место заняла каждая девочка, если Таня заняла не третье место, Саша заняла не второе, а Маша не первое и не второе?

Так Маша заняла не первое и не второе, значит – третье.
Так как Саша заняла не второе, значит первое или третье, так как третье место заняла Маша, то Саша заняла первое место.
 А Таня второе.

 

Этап подведения итогов

 

Наше путешествие подходит к концу.

Давайте вспомним, в каком порядке выполняются  действия в числовых выражениях?

В числовых выражениях действия выполняются в следующем порядке:

1. Действия, записанные в скобках.
2. Умножение и деление.
3. Сложение и вычитание.

 

Рефлексия

 

Продолжите фразу:

сегодня я узнал
было интересно 
было трудно

Порядок выполнения действий — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1.

Порядок выполнения действий

2. Найдите значение этого выражения

37- 7 (18 — 6 2):7+9

3. Найдите значение этого выражения

37- 7 (18 — 6 2):7+9=40
Что нужно знать, чтобы выполнить это
задание без ошибок?

4. Цели урока

• повторить основные арифметические
действия
• вспомнить порядок выполнения
действий
• совершенствовать свои
вычислительные навыки

5. Арифметические действия

Действия 1 ступени:
Сложение и вычитание
Действия 2 ступени:
Умножение и деление
Порядок выполнения действий определяется
следующими правилами:
1. Если в выражении нет скобок, и оно
содержит только действия одной ступени, то
они выполняются по порядку слева направо
Пример 1 (действия выполняем в столбик)
800-625+331+87-119=474
1) 800-625=175
3)506+87=593
2) 175+331=506
4) 593-119=474
Пример2: (действия выполняем в столбик)
780÷39∙212÷106∙13=520
1) 780:39=20 2)20 ∙212=4240 3)4240:106=40 4) 40 ∙13=520
2. Если выражение содержит действия 1 и 2 ступени и в нем
нет скобок, то сначала выполняются действия второй
ступени, а потом действия первой ступени по порядку
слева направо.
Пример3:
5781-28 ∙75:25+156:12=5710
Порядок действий записываем сверху над примером,
действия выполняем в столбик ( в презентации это делать не
удобно)
1)28 ∙75=2100 2)2100:25=84 3)156:12=13
4)5781-84=5697 5)5697+13=5710
3.Если в выражении есть скобки, то сначала
выполняются действия в скобках, учитывая при этом
правила 1 и 2.
Пример 4:
36000 : ( 62+14 ∙ 2)- 23 ∙ 5=285
Установим порядок действий (записываем сверху
над примером),
действия выполняем в столбик
1)14 ∙2=28 2) 62+28=90 3)36000:90=400
4)23 ∙5=115
5)400-115=285

9. Самостоятельная работа

I задание
Решив пример, вы
узнаете, в каком году
Петр I завез в Россию
картофель.
631-224:16+18 60
2 задание
Решив пример, вы получите массу
черепахи-гиганта, живущей на
островах Тихого океана. Она такой
величины, что дети могут кататься,
сидя на ее панцире.
39 15+180:12
1697год
дермохелис
ее масса 600кг
1. В выражении 200 — (20+10:2) 8 последним выполняется:
1)Вычитание п
2)Сложение я
3)Умножение р
4)Деление
с
2. В выражении (120+50):17 15 — 65 первым выполняется
1)Вычитание п
3) Сложение я
2)Умножение р
4)Деление
с
3. Указать в каком из примеров указанный порядок действий приведет к
неправильному результату:
2
3 1
1) 87+54 — (14+32)
п
1
3
2
2) (435+18) (302 – 15) р
1
3 2
3) (372+28) 44 – 14
т
1 3 2
4) (24+37) – 12 15
с
4. Вычислить: (35+25):15+45
1 э
49 ь
48 ю
0 я
Ответ:

12. Решить

• № 627 д,ж,з

English     Русский Правила

Объединение одинаковых терминов и порядка действий

Результаты обучения

• Распознавание и объединение одинаковых терминов в выражении
• Используйте порядок операций для упрощения выражений

Прежде чем мы начнем, несколько важных терминов:

• операции/операторы:  В математике мы называем такие операции, как умножение, деление, сложение и вычитание. Это глаголы математического мира, выполняющие работу с числами и переменными. Символы, используемые для обозначения операций, называются операторами, например [латекс]+{, }-{, }\times{, }\div[/latex]. Чем больше вы будете изучать математику, тем больше вы узнаете операторов. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.

  Это показано в следующих примерах:

  Пример

  Объедините похожие термины:  [латекс]5x-2y-8x+7y[/латекс] 92+3x-1[/latex]

  Показать решение

  В следующем видео вам будет показан еще один пример сочетания похожих терминов. Обратите внимание, почему у вас не получается объединить в примере все три термина.

  Порядок операций

  Вы можете или не можете вспомнить порядок операций для применения нескольких математических операций к одному выражению. Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.

  Порядок действий

  • Сначала выполнить все операции внутри группирующих символов. К символам группировки относятся круглые скобки ( ), квадратные скобки [ ], фигурные скобки { } и дроби.
  • Вычисление показателей степени или квадратных корней.
  • Умножение или деление слева направо.
  • Сложение или вычитание слева направо.

  Этот порядок операций верен для всех действительных чисел.

  В следующем примере показано, как упростить выражение, содержащее как умножение, так и вычитание, используя порядок операций.

  Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также нужно будет вспомнить, как выполнять эти вычисления.

  В следующем видеоролике показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание с элементами, содержащими дроби.

  Экспоненты и квадратные корни

  В этом разделе мы расширяем наши навыки, применяя правила порядка операций к выражениям с экспонентами и квадратными корнями. Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] – основание, а [latex]2[/latex] – показатель степени; показатель степени определяет, сколько раз основание умножается само на себя.)

  Показатель степени представляет собой способ представления многократного умножения; порядок операций помещает его перед , выполняется любое другое умножение, деление, вычитание и сложение.

  В следующем видеоролике выражение с показателями в его терминах упрощается с использованием порядка операций.

  Если внутри группирующих символов есть символы группировки, вычисляйте их изнутри наружу. То есть сначала начните упрощение внутри самых внутренних группирующих символов.

  Помните, что круглые скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.

  В следующем видеоролике показано, как использовать порядок операций для упрощения выражения с помощью группировки символов, показателей степени, умножения и сложения. 9{3}}\cdot \,32[/latex]

  Используйте поле ниже, чтобы записать несколько мыслей о том, как упростить это выражение с помощью дробей и символов группировки.

  Показать раствор

  Некоторые люди используют поговорку, чтобы запомнить порядок действий. Эта поговорка называется PEMDAS или P лизинг E извините M y D ухо A unt S союзник. Первая буква каждого слова начинается с той же буквы арифметической операции.

  P аренда [латекс] \displaystyle \Rightarrow [/латекс] P арены (и другие символы группировки)
  E xcuse [латекс] \displaystyle \Rightarrow [/латекс] E экспоненты 9 0158 М y D ухо [латекс] \displaystyle \Rightarrow [/латекс] M умножение и D ivision (слева направо)
  A unt S союзник [латекс] \displaystyle \Стрелка вправо[/ латекс] A дополнение и S вычитание (слева направо)

  Примечание: Несмотря на то, что в пословице умножение предшествует делению, деление может быть выполнено первым. Что выполняется первым, между умножением и делением, определяется тем, что идет первым при чтении слева направо. То же самое верно для сложения и вычитания. Не позволяйте поговорке сбить вас с толку!

  Порядок операций дает нам согласованную последовательность для использования в вычислениях. Без порядка операций вы могли бы найти разные ответы на одну и ту же вычислительную задачу. (Некоторые из первых калькуляторов и некоторые недорогие НЕ используют порядок операций. Чтобы использовать эти калькуляторы, пользователь должен вводить числа в правильном порядке.)

  3.3 Порядок действий — Современная математика

  Рисунок 3.19 Калькуляторы могут автоматически применять порядок операций к вычислениям. (кредит: «Точность», Леонид Мамченков/Flickr, CC BY 2.0)

  После завершения этого модуля вы сможете:

  1. Упростите выражения, используя порядок операций.
  2. Упростите выражения, используя порядок операций, включающих группировку символов.

  Вычисляет, иначе убедитесь, что кто-то будет правилами ожидать явного, что мы должны сделать, мы для того, чтобы они вычислили, чтобы вычислить сначала.

  Вероятно, вы прочитали это предложение и не смогли его разобрать. Кажется, это может быть связано с расчетами, но, может быть, это касается потребностей? Возможно, вы даже пытаетесь расшифровать предложение по мере его чтения, расставляя слова в том порядке, в котором вы ожидаете их появления. Причина, по которой предложение не имеет смысла, заключается в том, что слова не следуют порядку, в котором вы ожидаете их следовать. . В расшифрованном виде это предложение должно было звучать так: «Чтобы быть уверенным, что кто-то другой вычислит, когда мы ожидаем, что он вычислит, нам нужны правила, которые четко определяют, что нужно вычислить в первую очередь».

  Аналогично, при работе с математическими выражениями и уравнениями, если мы не следуем правилам порядка операций, арифметические выражения теряют смысл. Простое выражение было бы проблематичным, если бы у нас не было некоторых правил, говорящих нам, что вычислять в первую очередь. Например, 4×22+3+524×22+3+52 можно вычислить разными способами. Вы можете получить 5184. Или вы можете получить 80. Или 96. Проблема в том, что без соблюдения набора правил расчета одно и то же выражение будет давать разные результаты. Если вам интересно, используя соответствующий порядок операций, мы находим 4×22+3+52=444×22+3+52=44.

  Упрощение выражений с использованием порядка операций

  Порядок, в котором выполняются математические операции, является соглашением, облегчающим правильное вычисление. Они следуют аббревиатуре EMDAS:

  .

  Е	Экспоненты
  М/Д	Умножение и деление
  А/С	Сложение и вычитание

  Итак, что нам говорит EMDAS? В уравнении, двигаясь слева направо, мы начинаем с вычисления всех показателей степени. Как только показатели степени были вычислены, мы снова двигаемся слева направо, вычисляя умножения и деления по одному. Умножение и деление занимают одно и то же место в упорядочении, поэтому, когда вы столкнетесь с одним или другим на этом шаге, сделайте это. Как только умножение и деление были вычислены, мы снова двигаемся слева направо, вычисляя сложения и вычитания, по одному. Сложения и вычитания занимают одно и то же место в порядке, поэтому, когда вы сталкиваетесь с одним или другим на этом шаге, сделайте это. (Возможно, вы уже изучили порядок операций в PEMDAS, сначала со скобками; мы добавим этот аспект позже.) Мы изучим это, работая на примере.

  Пример 3,43

  Используя два порядка операций

  Вычислить 21−4×1321−4×13.

  Решение

  В этом выражении нет показателей степени, поэтому следующие операции для проверки — умножение и деление.

  Шаг 1: Двигаясь слева направо, первое умножение, которое встретится, равно 4, умноженному на 13. Сначала мы выполняем эту операцию.

  21−4×13=21−5221−4×13=21−52

  Шаг 2: Осталась единственная операция — вычитание.

  21-52=-3121-52=-31.

  Итак, 21−4×13=−3121−4×13=−31.

  Твой ход 3,43

  1.

  Вычислить 43+18\умножить на 15.

  Пример 3,44

  Используя два порядка операций

  Вычислить 4×834×83.

  Решение

  Шаг 1: Двигаясь слева направо, мы видим, что есть показатель степени. Сначала вычисляем показатель степени.

  4×83=4×(8×8×8)=4×5124×83=4×(8×8×8)=4×512 92}/50.

  Пример 3,45

  Используя три порядка операций

  Вычислить 2+32×42+32×4.

  Решение

  Шаг 1: Чтобы вычислить это, двигайтесь слева направо и сначала вычислите все показатели степени. Единственная экспонента, которую мы видим, — это возведение в квадрат числа 3, поэтому оно вычисляется первым.

  2+32×4=2+(3×3)×4=2+9×42+32×4=2+(3×3)×4=2+9×4

  Шаг 2: Поскольку все показатели степени вычислены, теперь вычислите все умножения и деления слева направо. Единственное присутствующее умножение или деление — 93}-18.

  Даже если вычисляемое выражение усложняется, выполняем операции в следующем порядке: EMDAS.

  Пример 3,46

  Используя восьмой порядок операций

  Правильно примените порядок операций для вычисления следующего:

  4−25×6/10×32+7×234−25×6/10×32+7×23.

  Решение

  Шаг 1: Для этого сначала вычислите показатели степени, двигаясь слева направо. В выражении есть два вхождения показателей степени: 3 в квадрате и 2 в кубе.

  4−25×6/10×32+7×23=4−25×6/10×9+7×84−25×6/10×32+7×23=4−25×6/10×9+ 7×8

  Шаг 2: Теперь, когда показатели степени вычислены, выполните умножение и деление, двигаясь слева направо. Первый — произведение 25 и 6.

  4−25×6/10×9+7×8=4−150/10×9+7×84−25×6/10×9+7×8=4−150/10×9+7×8

  Шаг 3: Далее 150 делится на 10.

  4−150/10×9+7×8=4−15×9+7×84−150/10×9+7×8=4−15×9+7×8

  Шаг 4: Далее 15 умножить на 9.

  4−15×9+7×8=4−135+7×84−15×9+7×8=4−135+7×8

  Шаг 5: Наконец, умножьте 7 на 8.

  4−135+7×8=4−135+564−135+7×8=4−135+56

  После вычисления всех умножений и делений выполняются сложения и вычитания слева направо.

  4−135+56=−131+56=−131+56=−754−135+56=−131+56=−131+56=−75

  Вычисленное значение равно −75.

  Твой ход 3,46

  1.
  92}-3\х4.

  Пример 3,47

  Использование шести порядков операций

  Правильно примените правила порядка операций, чтобы точно вычислить следующее:

  10−3×53/15+56/410−3×53/15+56/4.

  Решение

  Шаг 1: Сначала вычислить показатели степени, двигаясь слева направо:

  10−3×53/15+56/4=10−3×125/15+56/410−3×53/15+56/4=10−3×125/15+56/4

  Шаг 2 : Умножение и деление слева направо: 93}-24\х25/10.

  Пример 3,48

  Использование порядка операций

  Правильно применяйте правила порядка операций для точного вычисления следующего: (-8)/2×3-9×24/12+9×(-4)2/23(-8)/2×3-9×24/12+9×(-4)2/23.

  Решение

  Шаг 1: Сначала вычислите показатели степени, двигаясь слева направо:

  (−8)/2×3−9×24/12+9×(−4)2/23=(−8)/2×3−9×16/12+9×122/23=(−8) /2×3−9×16/12+9×144/23=(−8)/2×3−9×16/12+9×144/8(−8)/2×3−9×24/12+9×(−4)2/23=(−8)/2×3−9×16/12+9×122/23=(−8)/2×3−9×16/12 +9×144/23=(−8)/2×3−9×16/12+9×144/8

  Шаг 2: Умножить и разделить, двигаясь слева направо:

  =(−8)/2×3−9×16/12+9×144/8=(−4)×3−9×16/12+9×144/8=(−12)−9×16/ 12+9×144/8=(−12)−144/12+9×144/8=(−12)−12+9×144/8=(−12)−12+1296/8=(−12 )−12+162=(−8)/2×3−9×16/12+9×144/8=(−4)×3−9×16/12+9×144/8=(−12) −9×16/12+9×144/8=(−12)−144/12+9×144/8=(−12)−12+9×144/8=(−12)−12+1296/ 8=(−12)−12+162

  Шаг 3: Складываем и вычитаем, двигаясь слева направо: 92}-9/3\х8.

  Использование порядка операций, связанных с группировкой символов

  Мы рассмотрели, как использовать порядок операций, обозначенный EMDAS, для правильного вычисления выражений. Однако могут быть выражения, в которых умножение должно происходить перед показателем степени или вычитание перед делением. Чтобы указать, что операция должна выполняться не по порядку, операция помещается в круглые скобки. При наличии круглых скобок в первую очередь выполняются операции внутри круглых скобок. Добавив скобки к нашему списку, мы получили PEMDAS, как показано ниже.

  П	Скобки
  Е	Экспоненты
  М/Д	Умножение и деление	(деление это просто умножение на обратное)
  А/С	Сложение и вычитание	(вычитание — это просто сложение минуса)

  Как было сказано ранее, круглые скобки указывают на то, что некоторая операция или операции будут выполняться вне стандартного порядка правил операций. Например, возможно, вы хотите умножить 4 и 7 перед возведением в квадрат. Чтобы указать, что умножение происходит перед показателем степени, умножение помещается в круглые скобки: (4×7)2(4×7)2.

  Это означает, что операции внутри круглых скобок имеют приоритет или выполняются раньше других операций. Теперь первым шагом в вычислении арифметических выражений с использованием порядка операций является выполнение сначала операций внутри круглых скобок. Внутри скобок вы соблюдаете порядок работы правил EMDAS.

  Пример 3,49

  Приоритизация скобок в порядке операций

  Правильно примените правила порядка операций, чтобы точно вычислить следующее:

  (10−3)×53(10−3)×53.

  Решение

  Шаг 1: Выполните все вычисления в скобках перед всеми другими операциями.

  (10−3)×53=7×53(10−3)×53=7×53

  Шаг 2: Поскольку все скобки сняты, двигайтесь слева направо и затем вычисляйте все показатели степени. 92})/7.

  Имейте в виду, что может быть несколько наборов скобок и скобок внутри скобок. Когда один набор скобок находится внутри другого набора, сначала сделайте самый внутренний набор, а затем работайте снаружи.

  Пример 3,50

  Работа с самыми внутренними скобками в порядке операций

  Правильно применять правила порядка операций для точного вычисления следующего:

  4+2×(32−(2+5)2×4)/(3+8) 4+2×(32−(2+5)2×4)/(3+8).

  Решение

  Шаг 1: Выполните все вычисления в скобках перед другими операциями. Сначала оцените самые внутренние скобки. Мы можем работать с отдельными выражениями в скобках одновременно. Самый внутренний набор скобок содержит 2 + 5 внутри. 3 + 8 находится в отдельном наборе круглых скобок, так что сложение может происходить одновременно с 2 + 5.

  4+2×(32−(2+5)2×4)/(3+8)=4+2×(32−(7)2×4)/(11)4+2×(32−(2) +5)2×4)/(3+8)=4+2×(32−(7)2×4)/(11)

  Шаг 2: Теперь, когда эти скобки обработаны, перейдите к следующему набору скобок.