Пример по математике заставил Сеть поспорить / news2.ru
В Сети разгорелся очередной спор. На этот раз в Twitter выясняют, кто из пользователей лучше знает математику. Началось все с просьбы о помощи в решении простого примера.
К подписчикам обратилась девушка, которая сомневалась в правильности совершаемых ею действий при решении математической задачи.
oomfies solve this pic.twitter.com/0RO5zTJjKk
— em ♥︎ (@pjmdolI) 28 июля 2019 г.
В комментариях единого мнения тоже не было. Ответов на приведенный пример оказалось два, причем каждый из них пользователи считали правильным. Некоторые утверждали, что в ответе «8 ÷ 2 (2+2) =?» будет непременно единица.
oomfies solve this pic.twitter.com/0RO5zTJjKk
— em ♥︎ (@pjmdolI) 28 июля 2019 г.
«Удивительно, что люди вообще это обсуждают. Это программа для третьего класса», — возмущались пользователи. Впрочем, согласны с ними были отнюдь не все. Кто-то получил в результате решения 16.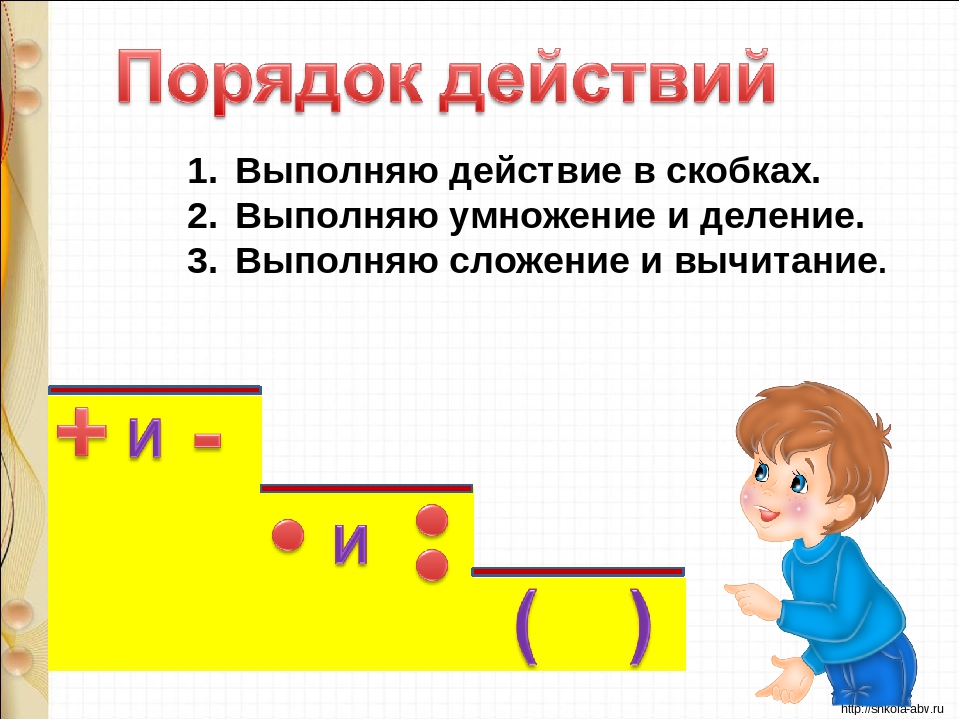
oomfies solve this pic.twitter.com/0RO5zTJjKk
— em ♥︎ (@pjmdolI) 28 июля 2019 г.
По мнению автора поста, пример стоит решать в следующей последовательности: сначала выполняется действие в скобках, потом — умножение, а последним — деление. Именно так и получается единица. Ее умозаключения нашли поддержку.
oomfies solve this pic.twitter.com/0RO5zTJjKk
— em ♥︎ (@pjmdolI) 28 июля 2019 г.
Точку в споре попытался поставить один из комментаторов, предположив, что верными можно счесть оба ответа.
oomfies solve this pic.twitter.com/0RO5zTJjKk
— em ♥︎ (@pjmdolI) 28 июля 2019 г.
«Это либо 1, либо 16. Зависит от того, по какой системе вы учились», — написал он, напомнив о двух наиболее распространенных системах, которыми определяется порядок операций в математических примерах. В одной из них приоритет остается за умножением, а во второй предпочтение отдается делению.
Однако пользователи продолжили дискуссию, причем в ход пошел юмор, намекающий на абсурдность самого обсуждения.
На данный момент пост получил свыше 12 тысяч лайков. Его репостнули более трех тысяч раз. Под публикацией набралось около 16 тысяч комментариев.
App Inventor — описание математического блока Math
Новый материал по детскому программированию расскажет про работу с встроенными блоками в app inventor. Описание математической логики программы откроет новый цикл лекций. Вскоре появятся обучающие статьи по следующим направлениям: управление, логика, текст, массивы, цвета, переменные и процедуры. Ну а пока вернемся к математике и рассмотрим, что означают программные элементы блока!
Описание элементов блока: Математика
Вначале немного занудной информации с описание функционала каждого элемента блока Математика. Кому эта информация не интересна переходите к следующему разделу, в котором будет разбираться последовательность математических действий при конструировании визуальных блоков программирования.
- проверяет данные на числовое и текстовое значений. Если информация числовая, то возвращает параметр ИСТИНА
- Выдает случайное целое число
- Элемент позволяет округлить число до ближайшего целого
- Округление числа до ближайшего целого значения в меньшую сторону
- Округление числа до ближайшего целого значения в большую сторону
- Выбор минимального или максимального значения числа (меняется в настройках — шестеренка)
*** — описание сделано еще не для всех блоков, в ближайшее время я расширю и более подробно расскажу о каждом элементе математических действий в App Inventor
Логика последовательности выполнения математический действий в Апп Ивентор
Последовательность действий в Апп Инвекторе очень простая и чем-то напоминает работу со скобками в математике. Все вычисления идут из внутреннего блока к наружному последовательно.
Немного поясню! Допустим у меня есть формула расчета идеального веса человека исходя из его роста и выглядит она следующим образом:
А вот как будет выглядеть эта формула при составлении ее из визуальных блоков программирования app inventor:
Порядок, в котором будет работать этот код имеет следующий вид:
Как мы помним из математики? первыми выполняются действия в скобках и именно по такому принципу работает Апп Инвентор. Каждый его математически блок это и есть условные скобки и последовательность выполнения идет от самого глубокого блока к самому крайнему!
ПРИМЕЧАНИЕ:
Не забывайте, что app inventor имеет ограничение по количеству окон в программе — 10 штук! Старайтесь не использовать лишние окна и активно пользуйтесь параметром — Видимый. Такой подход не только позволит уменьшить код, но и сократить количество окон, увеличить скорость работы приложения!
Вместо этого я добавил кнопку расчета и написал код таким образом, что при ее нажатии старые элементы скрываются, а новые появляются. Это позволило не заводить переменные, уменьшит код и избавиться от ненужного окна расчета!Перед тем, как перейти к объяснению блока Text отмечу одну особенность программирования в App Inventor. Это даже не столько особенность, сколько схожесть с реальными языками программирования, например с python. В Апп Инвенторе есть два вида значений в переменных: текстовые и числовые и задаются они следующими блоками:
Причем, если мы в красное текстовое поле занесем число, скажем — 12, то оно будет воспринято программой не как число, а как текст! Не забывайте об этом занимаясь программированием в app inventor.
Так же обратите внимание на наличие шестеренки у некоторых блоков. С помощью нее можно добавить еще несколько элементов для выполнения математической операции. Настройки делаются следующим образом:
Вопросы и комментарии:
Основы логики.
Логические операции и таблицы истинностиСодержание:
На данной странице будут рассмотренны 5 логических операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность, которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам воспользоваться нашими программами для решения задач по математике, геометрии и теории вероятности. Помоми большого количества программ для решения задач на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать
истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат
отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда
и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Слишком сложно?
Основы логики. Логические операции и таблицы истинности не по зубам? Тебе ответит эксперт через 10 минут!
Читать онлайн «Репетитор по математике. Арифметика» бесплатно
Введение или как работать с этой книгой
1. Почему репетитор? Название возникло сразу.
Не потому, что подобных названий почти нет. Судите сами, это ведь не учебник, где весь учебный материал подаётся от более простого к сложному. В учебнике существует тенденция перескакивания с одной темы на другую, а потом возвращение к уже более сложными заданиям. В репетиторе такого нет. Если вы начали изучать какую-то тему, то изучаете её от начала и до конца. Кроме этого, в репетиторе теоретический материал подан в самом необходимом минимальном объёме без каких-либо доказательств и выведения формул. Это также и не справочник, где существует множество формул, определений, таблиц, где много теоретического материала, но почти нет практического применения теоретических знаний. Цель же репетитора — обучение практическим навыкам решения разнообразных математических задач. Наиболее похож репетитор на практикум, там тоже большое внимание уделяется практическим занятиям, но в отличие от практикума, где почти нет теоретического материала, в репетиторе он присутствует. Кроме этого, в данном учебном пособии есть тестовые задания, которые, как правило, отсутствуют в учебниках, справочниках, практикумах.
2. Кому прежде всего будет полезна эта книга? Репетитор ориентирован на основные задания, которые могут встретиться на экзаменах по математике. Поэтому данное пособие прежде всего станет незаменимым помощником именно для учащихся средней школы. Она также может быть применима и учителями, и выпускниками средних школ, и даже абитуриентами, а так же тем, кто хочет повысить свою математическую грамотность и научиться решать типовые математические задачи. Автор отдаёт себе отчёт в том, что никакое учебное пособие не заменит реального живого репетитора, который сможет подкорректировать и направить свои усилия на те разделы математики, в которых ученик разбирается не совсем хорошо. Увы, книга лишена такой возможности. Она может служить только дополнением к занятиям с реальным репетитором. Однако репетитор стоит немалых денег и не у всех есть возможность его нанять. Поэтому данное учебное пособие является хоть и неполной, но альтернативой. Ещё будучи учителем в школе, автор обратил внимание, что овладеть основными математическими навыками может практически любой человек.
Есть только небольшой процент людей, которые не могут этого сделать по разным объективным причинам. Остальные не знают математику и не умеют решать математические задачи потому что, или не хотят, или не хватает времени, или просто в жизни это может не пригодится, или лень заниматься каждый день. Таким людям я не рекомендую открывать репетитор. Вы не добьётесь желаемого результата и будете винить во всем автора. А для тех, кто решил серьёзно заняться изучением математики — добро пожаловать на страницы этого пособия. Если хотя бы половине этих людей репетитор поможет, автор будет считать, что его труд не был напрасным.
3. Чем же репетитор отличается от других учебных пособий? Прежде всего простотой подачи материала. Автор общается с обучаемым и указывает на характерные ошибки, которые могут встретиться при решении задач. В репетиторе показано решение типовых задач, а также задач повышенной трудности. Каждая задача или пример решается досконально с пояснениями, что позволяет усвоить базовые навыки даже людям, которые считали, что математика не для них.
4. О структуре данной книги. Вся книга поделена на темы. В каждой теме есть необходимый минимум теоретического материала, примеры решения задач. В конце каждого раздела даются два тестовых задания и задачи для самостоятельного решения.
Поговорим отдельно о каждой из этих составляющих.
Теоретический материал. Как было уже сказано ранее, это тот необходимый минимум, без которого невозможно обойтись при решении заданий. Если формула выведена крупным шрифтом — её необходимо запомнить. Тоже самое касается формулировок и прочих элементов теории. Таких обязательных элементов для запоминания в книге немного. Обучение построено по американской системе, где от учащегося не требуется зазубривание теоретического материала, а предпочтение отдаётся только навыкам его применения на практике. Поэтому, при самостоятельном решении задач автор разрешает пользоваться формулами. Запоминание формул произойдёт автоматически при практическом их применении. В конце книги собран и изложен в кратком виде весь теоретический материал.
Им вы можете пользоваться при решении задач. Это не значит, что теоретический материал можно совсем не изучать или изучить бегло. Как я уже сказал, в конце каждой темы есть тестовые задания и без базовых знаний теоретического материала, вы вряд ли сможете их пройти.
Примеры решения задач. В репетиторе рассмотрены решения как базовых типовых задач, так и задач повышенной сложности. Все задания взяты из разных источников: учебных пособий, экзаменационных работ и т. д. Автор уважает авторские права других, поэтому в конце книги дан список использованной литературы. Как было сказано выше, все примеры решения задач приведены с подробными пояснениями.
Тестовые задания. К каждой теме предложено два тестовых задания. Каждое тестовое задание включает 32 вопроса с четырьмя вариантами ответов, один из которых является правильным. Оценивание тестовых заданий производится по 12-ти бальной системе. Чтобы не путаться, привожу перевод 12-ти бальной системы в пятибальную.
12 баллов — оценка 5+
11 баллов — 5
10 баллов — 5-
9 баллов — 4+
8 баллов — 4
7 баллов — 4-
6 баллов — 3+
5 баллов — 3
4 балла — 3-
3 балла — 2+
2 балла — 2
1 балл — 2 —
Я надеюсь, что последние шесть строчек вам не понадобятся при оценивании тестовых заданий.
Только все должно быть по честному. Помните, если вы будете не объективны, то в первую очередь обманите сами себя.
Теперь, как оценивать тестовые задания. За каждое правильное тестовое задание начисляется 1 балл.
Если вы набрали 31—32 балла, то это 12 баллов по 12-ти бальной системе оценивания.
29 —30 — 11 баллов
27 — 28 — 10 баллов
25 — 26 — 9 баллов
23 — 24 — 8 баллов
21 — 22 — 7 баллов
19 — 20 — 6 баллов
17 — 18 — 5 баллов
15 — 16 — 4 балла
Если вы набрали меньше 15 баллов, то вам следует вернуться к изучению теоретического материала, а потом пройти тест заново.
Продолжительность тестирования — 45 минут. Выделите для тестирования отдельный день. Берите чистый лист бумаги и вперёд. Тесты это не только интересно, но и познавательно. Желательно пройти все предложенные тесты (но не в один день), в конце книги имеются ответы на тестовые задания для проверки. Не стоит в них заглядывать раньше времени.
Задачи для самостоятельного решения.
Автор сознательно не выделял какими-то знаками задания повышенной сложности и считает, что такое приём способствует более спокойному решению задач без излишнего волнения и стресса. В процессе решения вы сами сможете понять, сложна для вас данная задача или нет. Притом сложность задачи — это субъективная оценка. Некоторые с лёгкостью могут решать подобные задачи, а вот более простые в нашем понимании могут вызвать затруднение. Если вы поняли, что можете приступать к решению задач, то не медлите. Каких-то ограничений по количеству решаемых задач в день нет. Когда поняли, что устали, то занятие можно прекратить, но хотя бы 30 — 40 минут в день вы должны уделять решению задач. Это не обязательно делать изо дня в день. Через какое-то время можно сделать себе 1- 2-х дневный перерыв. Но с отдыхом не затягивайте. Почувствовав, что немного отдохнули и есть свободное время, приступайте снова к решению задач. Автор рекомендует решить все задачи, которые есть в разделе для самостоятельного решения.
Решив какую-то задачу, загляните в раздел ответы и, убедившись, что вы все решили правильно, продолжайте дальше. Если ваш ответ не совпадает с ответом в конце книги, рекомендуется ещё раз пройтись по своему решению и выявить ошибки. Если вы их не обнаружили, то загляните в раздел « Указания к решению задач». Он находится после раздела ответов. Прочитав указания к решению задач (они есть ко всем задачам), снова приступайте к решению сложной для вас задачи. К задачам для самостоятельного решения есть полные и подробные решения, которые находятся в соответствующем разделе. Но это последний раздел, в который вам следует заглянуть. Это в том случае, когда задача не решается без посторонней помощи. Не злоупотребляйте этим разделом, иначе вы так никогда и не научитесь решать математические задачи. Постарайтесь ограничиться только разделом «Указания к решению задач». Этого бывает достаточно, чтобы понять свою проблему и попытаться её искоренить.
В конце книги, как я уже сказал, находится справочный раздел, ответы к тестовым заданиям, ответы к задачам для самостоятельного решения, указания к решению задач, решение задач.
Кроме этого, там же находится список использованной литературы. Структура книги максимально удобна для использования.
Кроме этого, в конце книги будет предложена итоговая контрольная работа из 8 заданий (2 варианта). Выбирайте любой вариант и приступайте к решению. Время решения контрольной работы полтора часа. Только когда решены все задания контрольной работы, можно заглянуть в ответы и оценить свои знания. Если из 8 заданий вы решили полностью правильно 5-6, то можете себя поздравить. Вы не зря потратили время, работая с этой книгой. Пользоваться справочными материалами при решении контрольной работы не рекомендуется, как и другими учебниками и учебными пособиями. Разрешается использовать только калькулятор.
Автор будет благодарен за любые замечания и обнаруженные неточности и ошибки при написании этого пособия. А также будет рад любому мнению и практическим советам от учителей и преподавателей математики по улучшению данной книги.
Примечание: некоторые понятия, изложенные в этом пособии (например,
бесконечная периодическая дробь, среднее геометрическое и др.
) не относятся к разделу «Арифметика», но они введены здесь для целостности восприятия.
Арифметика
Арифметика — базовая дисциплина для овладения более сложной составляющей математики — алгебры. Без навыков решения арифметических задач невозможно выучить алгебру и геометрию. Это нижний фундамент и основа грандиозного сооружения под названием математика. Очень часто на экзаменах по математике учащиеся делают именно арифметические ошибки, которые в итоге снижают им общий балл. Обидно? Конечно. А всё из-за того, что некоторые игнорируют учебный материал, изучаемый в пятом-щестом классе средней школы и считают его чем-то несерьёзным и ненужным. Это заблуждение.
Понятно, что для многих содержимое этой книги известно, но для целостности восприятия я всё-таки рекомендую вам ознакомиться с предложенными темами, решить типовые задачи и ответить на тестовые задания. Это совсем несложно и поэтому на него вы потратите минимум времени, но зато, поверьте мне, в дальнейшем вам будет намного проще осваивать более сложный материал.
Итак, вперёд, друзья мои! Время не ждёт.
Тема 1
Числа, цифры, арифметические действия, порядок действий, скобки
Само название «арифметика» происходит от греческого слова означающего «число». Само число — это простейшие понятие, его можно пояснить лишь предметным образом. По мере развития человечества возникла необходимость счета людей, животных, предметов домашнего обихода и прочих вещей. Так возникла количественная оценка предметов. Многие задают вопрос, чем же число отличается от цифры? Цифра — это письменный знак, изображающий число. Сейчас, в основном, мы пользуемся арабской системой записи чисел. И совсем не задумываемся, написав цифру 2, мы отлично понимаем, что это цифра больше, чем цифра 1 и меньше, чем цифра 3. Арабская система исчисления — десятичная. Это означает, что названия всех чисел образованы из названий чисел первого десятка и чисел 10, 100, 1000.
Например, 17 (семнадцать — семь на (сверху) десять), 50 (пятьдесят — пять десятков), 400 (четыреста — четыре сотни).
Особняком стоит 90 (девяносто),образованное по другому принципу (девять до ста) и число 40 (сорок) — единственное исключение.
У разных народов были разные системы нумерации. До наших дней дошла ещё римская нумерация чисел. Но она очень неудобна при операциях сложения, умножения и так далее, поэтому в математике не используется. Для желающих познакомиться более детально с римской нумерацией чисел, добро пожаловать в дополнительный раздел. Но мы не будем сейчас на этом останавливаться. Следует заметить, не все числа, которыми мы сейчас пользуемся, возникли одновременно. Первыми числами, которыми пользовался человек, были натуральные числа, обозначаемые буквой N. Именно, они возникли первыми при счёте предметов. Натуральные числа начинаются с единицы и продолжаются до бесконечности. Примеры таких чисел довольно просты: на улице 18 домов, в коробке 12 карандашей, в библиотеке 5432 экземпляра книг, в городе проживает 252 196 жителей. Далее возникла необходимость ввести число 0, ведь при вычитании одинаковых натуральных чисел получалось «нечто», не имеющее материального обоснования.
Перед тем как появилась необходимость введения отрицательных чисел для обозначения этого «ничего» ввели число 0. По мере дальнейшего совершенствования человеческих отношений, развития науки и техники возникла необходимость в отрицательных числах. Натуральные числа, противоположные к ним и 0 составили множество целых чисел Z. Потом возникли дробные числа. О дробных числах мы поговорим подробнее в соответствующей теме. Целые и дробные числа составляют множество рациональных чисел Q. Если к множеству рациональных чисел добавить иррациональные числа, мы получим множество действительных чисел R. Для наглядности составлена такая таблица. (табл.1)
Для удобства чтения и запоминания больших чисел их разбивают на классы. Справа отделяют три цифры (первый класс), потом ещё три цифры (второй класс) и т. д. Между собой классы отделяются небольшим пробелом. Первый класс даёт число единиц, второй — число тысяч, третий — миллионов. Каждая из цифр класса наз. его разрядом, счёт разрядов также идёт справа.
Числа в первом классе справа налево: единицы, десятки, сотни, во втором классе соответственно: тысячи, десятки тысяч, сотни тысяч. В третьем классе: миллионы, десятки миллионов, сотни миллионов. Единица четвёртого класса называется миллиардом, пятого триллионом. Существует единица и для 6, 7, 8 и т. д. классов, но мы их рассматривать не будем. А теперь поупражняемся.
Таблица 1
35 461 298 читается так: 35 миллионов 461 тысяча 298.
Не следует бояться больших чисел, число 12 021 306 200 025 имеет 5 классов, поэтому читается таким образом: 12 триллионов 21 миллиард 306 миллионов 200 тысяч 25.
Теперь перейдём непосредственно к арифметическим действиям. Мы не будем давать здесь определений арифметических действий, они известны всем. Итак, арифметические действия — это сложение, вычитание, умножение и деление, а также возведение в степень и извлечение корня. Степени и корни изучаются в курсе алгебры и мы их рассматривать не будем. Здесь приведём примеры основных арифметических действий:
Сложение.
8 +5 = 13. Здесь 8 и 5 — слагаемые, 13 — сумма.
Вычитание.
15 — 8 = 7. Здесь 15 — уменьшаемое, 8 — вычитаемое, 7 — разность.
Умножение.
6 × 5 = 30. Здесь 6 — множимое, 5 — множитель, 30 — произведение.
Деление.
30 ÷ 6 = 5. Здесь 30 — делимое, 6 — делитель, 5 — частное.
Эти термины нам понадобятся в дальнейшем.
Важнейшим понятием арифметики есть порядок действий. При вычислениях им нельзя игнорировать. Поэтому 4—2+1 будет равно трём если проводить действия в порядке их записи. Если же сначала сложить 2+1 и вычесть полученную сумму из 4, то получим совсем другой ответ, которой равен единице. Чтобы указать в каком порядке нужно выполнять действия пользуются скобками. Действие, заключённое в скобки, выполняется раньше других. Таким образом, порядок действий при вычислениях:
1. Сначала выполняются действия, заключённые в скобки. Умножение и деление делается в порядке их следования, но раньше, чем сложение и вычитание.
2.
Затем выполняются оставшиеся действия, причём опять умножение и деление делается в порядке их следования, но раньше сложения и вычитания.
Рассмотрим пару примеров: (2+4) ×5.
Сначала вычисляем действие в скобках 2+4 = 6, далее следует умножение на 5:
6×5 = 30.
Это простой пример. Рассмотрим более сложный:
9+16:4—2 × (16—2×7+4) +6 × (2+5)
Сначала выполняем действия в скобках, не забывая о том, что умножение и деление идёт впереди сложения и вычитания.
Первая скобка: 2 × 7 = 14, 16 — 14 = 2, 2 +4 = 6.
Вторая скобка: 2 +5 = 7.
Наш пример примет вид: 9 +16: 4 — 2 × 6 +6 × 7. Теперь выполняем операции умножения и деления в порядке их следования:
16: 4 = 4, 2 × 6 = 12, 6 × 7 = 42.
И окончательно, выполняем операции сложения и вычитания в порядке их следования. Имеем 9 +4 — 12 +42 = 43.
Иногда приходится заключать скобки в скобки, поэтому пользуются ещё и квадратными скобками.
Порядок действий: сначала выполняются в круглых скобках, потом в квадратных, а потом все остальные действия.
Например,
5+2× [14—3× (8—6)] +32: (10—2×3)
Выполняем действия в круглых скобках, имеем:
8 — 6 = 2, 10 — 2 × 3 = 10 — 6 = 4
Действия в квадратных скобках дают: 14 — 3 × 2 = 8
Выполняя оставшиеся действия, имеем:
5 +2 × 8 +32: 4 = 5 +16 +8 = 29.
А теперь немного отвлечёмся. Сейчас в соц. сетях некоторые пользователи придумывает такое развлечение, они выкладывают простой арифметический пример и просят других пользователей дать правильный ответ. Вот, например,
10:2 (4—2).
Наиболее часто встречающиеся ответы 10 и 2.5. Вы уже немного продвинулись в арифметике и поэтому для вас не составит труда дать правильный ответ. Это число 10. 70％ пользователей дают правильный ответ на эту арифметическую задачу. И это, я считаю, неплохо. А теперь на этом примере рассмотрим характерные ошибки, которые делают остальные 30％.
Наиболее существенная ошибка. Простой арифметический пример пытаются решить алгебраическими методами, в частности раскрывая скобки (об этом методе поговорим в дальнейшем), тем самым нарушая порядок действий. Сразу замечу, алгебра и арифметика — это две разные дисциплины. В арифметике, в отличие от алгебры, основная функция скобки — обозначение приоритета очерёдности действий. Каких только определений не придумывается для этого ошибочного решения: коэффициент скобки, действия на скобку и т. д. Если вы таким образом решите данный пример, то получите 2.5. Внимание: неправильное решение.
10: (2×4 — 2×2) =10: (8—4) = 10:4 = 2.5
Другие пользователи помнят, что сначала выполняется действие в скобках, но потом делает характерную ошибку: они умножают двойку на то, что получилось в скобках, а потом уже выполняют деление. Запомните, никакого приоритета умножение перед делением не имеет, поэтому все оставшиеся действия делаются слева направо в порядке их написания. Если вы сделаете ошибку такого рода получите снова 2.5. Внимание: неправильное решение.
10:2×2 = 10:4 = 2.5.
Я не представляю, какие дебаты могли возникнуть, если был бы выложен более сложный арифметический пример. Часть тех, что делают ошибку утверждают, что их так учили и 30—50 лет назад этот пример решался именно так. Замечу, что арифметика — древняя наука и те правила, которые сложились ещё много веков назад действуют и по сей день. Интересно, что те, кто правильно решает данный пример не настолько агрессивны, как те, что решают его неправильно. В чём природа такого явления нужно спросить у психологов. Ещё одно ошибочное утверждение, некоторые доказывают, что правильных ответов может быть два и более. Это заблуждение, арифметика — точная наука и у любого задания есть единственно верный ответ (в отличие, кстати, от алгебры).
О единственно верном ответе есть отличный видеоролик, снятый американскими кинематографистами. Впрочем, смысл этого ролика немного в другом, я попытаюсь пересказать его содержание, но рекомендую вам самим посмотреть его. Достаточно в поисковой строке набрать 2+2=22 или название ролика «Альтернативная математика». В начале учительница пытается объяснить мальчику, что два плюс два равняется четырём, а не 22, как тот написал в тесте. Беседа с ребёнком ничего не даёт и тогда учительница приглашает родителей мальчика. Родители в недоумении и заявляют, что учитель не имеет права навязывать школьнику своё мнение, если ребёнок считает что два плюс два равняется 22, значит нужно согласится с его мнением. Дальше история становится ещё абсурдней. Директор школы настаивает на том, чтобы учительница извинилась перед родителями, т.к своим поведением она мешает школьникам мыслить самостоятельно и навязывает свои догмы. Дальше — больше, перед образовательным учреждением ученики выходят с плакатами на площадь, а учительницу вызывают на комиссию с требованием признать, что существует несколько правильных ответов. Учительница возражает: «Есть только один правильный ответ». В конце-концов учительница отстаивает свою точку зрения. Директор вызывает учительницу и перед журналистами и телевизионщиками говорит: « Нам придётся вас уволить, вы получите 4000. 2.000 за прошлый месяц и 2.000 за текущий. И тут учительница иронично замечает: « Не верно, это 22000». На этом ролик заканчивается. На самом деле он не о том что, математика — точная наука, здесь больше критика в сторону толерантного образования США. На самом деле создатели ролика немного ошиблись, т.к 2000 +2000 = 2 000 2 000,т.е 20 миллионов 2 тысячи, если считать по правилам альтернативной математики.
Мы пользуемся десятичной системой исчисления, это связано, скорее всего, с тем, что у нас на руках 10 пальцев. В компьютерных системах применяется двоичная система исчисления, а также восьмеричная и шестнадцатеричная. Кроме этого может существовать пятеричная, двенадцатеричная и какие угодно другие системы исчисления. Запись одного и того же числа в разных системах исчисления будет иной, чем в привычной нам десятичной системе. Кому это интересно, добро пожаловать в дополнительный раздел.
Тестовые задания к теме 1
Тест 1
1. Натуральные числа — это числа вида:
А) 0, 1, 2, 3,… Б) 1/1, 2/2,3/3,… В) 0, ±1, ±2, ±3,… Г) 1, 2, 3,…
2. — Выделить натуральное число:
А) 4/2 Б) 0 В) -3 Г) 1998
3. Какие действия выполняются всегда на множестве
натуральных чисел:
А) извлечение корня Б) сложение В) вычитание
Г) все вышеперечисленные
4. Целые числа — это числа вида:
А) 0, ±1, ±2, ±3,… Б) ± 1/1, ± 2/2, ± 3/3,… В) -2, -1, 1, 2,…
Г) 0, 1, 2, 3,…
5. Какие подмножества включают в себя множество целых чисел:
А) только целые положительные числа
Б) только натуральные и нуль
В) целые отрицательные, натуральные и нуль
Г) только натуральные
6. Указать целые числа:
А) 1/2 Б) -34 В) -0.2 Г) нет таковых
7. Рациональные числа — это числа вида:
А) a/b, где a — целое, b — натуральное
Б) a/b, где a, b — целые неотрицательные числа
В) a/b, где a — натуральное, b — целое
Г) a/b, где a, b — целые числа
8. Укажите целые числа меньше 0, но больше -5:
А) -5, -4, -3, -2, -1 Б) -4, -3, -2, -1 В) -5, -4, -3, -2, -1, 0
Г) -4, -3, -2, -1, 0
9. Укажите целые числа меньше -2, но больше -7:
А) -7, -6, -5, -4, -3 Б) -7, -6, -5, -4, -3, -2 В) -6, -5, -4, -3
Г) -6, -5, -4, -3, -2
10. Укажите целые числа больше -1,но меньше 1:
А) -1, 0, 1 Б) 0 В) -1, 0 Г) 0, 1
11. Укажите целые числа не больше 0, не меньше -1:
А) нет таких Б) 0 В) -1, 0 Г) -1
12. Найдите произведение чисел 11 и 125:
А) 12 625 Б) 11 125 В) 1 375 Г) 1 225
13. Вычислите 984: 8:
А) 150 Б) 125 В) 120 Г) 123
14. Какое действие выполняется последним при
нахождении значения выражения
1500 +800 × 300 — 500: 5
А) сложение Б) умножение В) вычитание Г) деление
15. Найдите частное чисел 84 и 7:
А) 12 Б) 11 В) 13 Г) 14
16. Вычислите 103 × 9:
А) 827 Б) 927 В) 1 027 Г) 977
17. Какое действие выполняется первым при
нахождении значения выражения
850 — 350 + (620 ×3 +50):2
А) вычитание Б) умножение В) сложение Г) деление
18. Сколько тысяч в числе 1 628 255:
А) 628 Б) 162 В) 1 628 Г) 28
19. Сколько сотен тысяч в числе, полученном при сложении
чисел 999 999 и 111 111:
А) 111 Б) 1 В) 11 Г) 1 111
20. Как правильно записать цифрами число:
два миллиарда пятьсот тринадцать миллионов
триста пятьдесят шесть тысяч восемьсот?
А) 25 133 568 Б) 250 013 300 568 В) 2 513 356 800
Г) 20 513 035 608
21. Запишите три раза подряд число 87 и три раза подряд
число 13. Сложите полученные числа. В результате будет:
А) один миллион десять тысяч сто
Б) сто одна тысяча сто
В) десять миллионов сто одна тысяча
Г) сто одиннадцать тысяч сто
22. Какое из чисел больше: 20 000 +9 000 +900 +90 +9
или 30 000 +1 000 +100 +10 +1
А) второе Б) первое В) числа равны Г) не знаю
23. Какое из нижеперечисленных чисел самое большое:
А) 1234567890 Б) 9876543210 В) 102030405060 Г) 980780680
24. Какое из нижеперечисленных чисел самое маленькое:
А) 576675765 Б) 574475754 В) 578875785 Г) 557755575
25.На сколько отличается число 30 000 +8 000 +600 +40 +5
от числа 20 000 +7 000 +500 +30 +4?
А) на 11 111 Б) на 1 В) на 11 Г) на 1 111
26. Выполните действие и отметьте правильный результат
124 × 20 +65:
А) 2 550 Б) 2 545 В) 2 445 Г) 2540
27. Выпишите все двузначные числа, которые можно
записать помощью цифр 1, 0, 3, используя каждую цифру
только один раз. Найдите сумму этих чисел.
А) 40 Б) 53 В) 84 Г) 74
28. Скорость автомобиля 80 км/ч, а скорость пешехода
5 км/ч. Во сколько раз скорость автомобиля больше
скорости пешехода?
А) в 12 раз Б) в 24 раза В) в 16 раз Г) в 20 раз
29. Из цифр 2, 4, 6 составляются всевозможные
трёхзначные числа. Найдите разность самого большого
и самого маленького из них.
(каждая цифра используется только один раз):
А) 216 Б) 396 В) 378 Г) 180
30. Из четырёх цифр 1, 2, 3, 4 составьте два
различных двузначных числа (каждая цифра используется
один раз), произведение которых будет наибольшим.
Найдите это произведение.
А) 1300 Б) 1312 В) 903 Г) 1462
31. Из четырёх цифр 1, 2, 4, 5 составьте два
различных двузначных числа (каждая цифра используется
один раз), произведение которых будет наименьшим.
Найдите это произведение.
А) 252 Б) 168 В) 288 Г) 350
32.Укажите такой порядок расположения чисел, чтобы
каждое последующее число было меньше предыдущего
(порядок убывания).
1) 5525 2) 5670 3) 5340 4) 5420
А) 1, 2, 3, 4 Б) 3, 4, 1, 2 В) 2, 1, 3, 4 Г) 2, 1, 4, 3
Тест 2
1.Укажите такой порядок расположения чисел,
чтобы каждое последующее число было больше
предыдущего (порядок возрастания).
1) 2151 2) 2178 3) 2193 4) 2132
А) 1, 2, 3, 4 Б) 4, 1, 2, 3 В) 4, 3, 2, 1 Г) 1, 4, 2, 3
2. Дано 5 чисел: 814, 129, 1235, 756, 307. Наибольшее
значение суммы двух из этих чисел равно:
А) 2049 Б) 1991 В) 2149 Г) 2089
3. Укажите цифры, которые можно поставить вместо звёздочек
так, чтобы были верны неравенства: *428> 4*39> 43*1> *502.
А) (4, 4, 3, 2) Б) (3, 5, 1, 3) В) (5, 9, 2, 6) Г) (5, 5, 9, 3)
4. В четырёх коробках лежат красные, синие и
зелёные карандаши.
В какой из коробок больше всего карандашей?
А) 1 Б) 2 В) 3 Г) 4
5. Исходя из предыдущего условия задачи. В какой из
коробок больше синих и зелёных карандашей?
А) 1 Б) 2 В) 3 Г) 4
6. Исходя из предыдущего условия задачи. В какой из
коробок меньше всего красных и синих карандашей?
А) 1 Б) 2 В) 3 Г) 4
7. Сколько целых чисел удовлетворяют неравенству — 4 <x <8?
А) 12 Б) 10 В) 9 Г) 11
8. Укажите наименьшее число:
А) — 150 Б) -149 В) -151 Г) 0
9. Сколько существует целых чисел, которые
больше -10 и меньше 3?
А) 11 Б) 12 В) 10 Г) 9
10. Укажите наибольшее число:
А) 0 Б) -25 В) 12 Г) -45
11. Выполните действие: -30 +65:
А) 35 Б) -35 В) -95 Г) 95
12. Выполните действие: -30 — 65:
А) 35 Б) -35 В) -95 Г) 95
13.Какое число получается при сумме:
600 000 000 000 +40 000 000 +500 000 +10 000 +6?
А) 6 004 005 106 Б) 6 405 106 В) 6 040 510 006
Г) 600 040 510 006
14.В каком неравенстве знак поставлен неверно?
А) 72 035 122 <72 035 289 Б) 89 012 365 <89 013 365
В) 33 333 142> 33 333 049 Г) 54 235 189> 54 236 189
15. Какое число следует за числом 621 679 899?
А) 621 679 900 Б) 621 680 900 В) 621 679 000 Г) 621 680 899
16. Что отсутствует в числе 231 000 869 192?
А) разряд сотен тысяч Б) класс тысяч В) класс миллионов
Г) разряд сотен
17. Что показывает цифра 3 в числе 21 388 102?
А) единицы миллионов Б) сотни тысяч В) тысячи Г) десятки тысяч
18. В каком числе отсутствует разряд сотен?
А) 12 135 802 Б) 456 650 987 В) 23 156 089 Г) 326 205 122
19. Значение какого выражения самое большое?
А) 250:5 — (2 +10) Б) (250:5 — 2) +10 В) 250:5 — 2 +10
Г) 250: (5 — 2) +10
20. В каком выражении первым действием будет сложение?
А) 32:2 +3 × 7 Б) 32: (2 +3) × 7 В) (32:2 +3) × 7 Г) 32: (2 +3 × 7)
21. В каком числе 55 десятков?
А) 550 Б) 505 В) 515 Г) 55
22. В каком числе отсутствует разряд десятков?
А) 10 Б) 101 В) 110 Г) 11
23. Укажите число, в котором 5 единиц первого
разряда и 7 единиц третьего:
А) 507 Б) 705 В) 570 Г) 750
24. Запишите число пятнадцать тысяч сто шестьдесят два:
А) 150 162 Б) 15 000 162 В) 15 162 000 Г) 15 162
25. Найдите разность чисел 45 132 и 232:
А) 44 999 Б) 44 900 В) 44 990 Г) 44 890
26. Найдите произведение чисел 105 и 215:
А) 225 750 Б) 225 755 В) 275 550 Г) 22 575
27. Дано выражение 232 + (668 — 15 × 5):8.
Какое действие выполняется третьим?
А) умножение Б) деление В) сложение Г) вычитание
28. Найдите частное чисел 3857 и 19:
А) 3838 Б) 3876 В) 73 283 Г) 203
29. На сколько произведение чисел 203 и 69 больше
частного чисел 45 034 и 89?
А) на 234 Б) на 18 011 В) на 1000 Г) на 13 501
30. Запишите выражение: « частное суммы чисел
a и b и произведения чисел 7 и c»:
А) a + b:7×c Б) (a + b): (7×c) В) (a + b):7×c Г) a + (b:7) ×c
31. Укажите пару противоположных чисел:
А) -3 и 3 Б) 0 и -3 В) 0 и 3 Г) -5 и 3
32. Какой из данных примеров решён верно?
А) -2 +7 = -9 Б) -2 +7 = 5 В) -2 +7 =9 Г) -2 +7 = -5
Задачи для самостоятельного решения
1. Запишите цифрами числа:
А) два миллиона пять.
Б) триста двадцать шесть миллионов сто пять тысяч двенадцать.
В) сто два миллиона тридцать две тысячи сто два.
Г) четырнадцать миллионов одна тысяча два.
Д) семнадцать миллионов шестьдесят тысяч сорок три.
Е) один миллиард двадцать шесть миллионов пятнадцать тысяч десять.
2. Найдите значение выражения:
А) 5040: (28×4) — (888+219):27
Б) 29×104:16+ (5059—988):23
В) (8640:8+5250:5—130) ×3
Г) (9810:9—7560:7+290) -4
3. В городской библиотеке имеется 1 256 684 экземпляров книг, что на 39 684 экземпляра больше, чем в университетской библиотеке, но на 159 200 меньше, чем в областной библиотеке. Сколько экземпляров книг имеется в трёх библиотеках?
4. В гостинице 209 двуместных номера, 162 трёхместных и 89 четырёхместных. Сколько нужно заказать автобусов для экскурсии, чтобы вывезти всех постояльцев отеля, если в каждом автобусе 45 мест.
5. Груша и апельсин вместе весят 285 гр., апельсин и лимон 250 гр. Определите массу груши, лимона и апельсина, если лимон и груша вместе весят 215гр. (решите задачу арифметическим методом)
6. Из двух сёл одновременно навстречу друг другу выехали два велосипедиста. Их скорости 9 км/ч и 12 км/ч. Через два часа они встретились. Чему равно расстояние между сёлами?
7. От одной пристани до другой можно добраться на теплоходе со скоростью 12 км/ч или моторной лодке со скоростью 13км/ч. Моторная лодка проходит этот путь по течению реки за 4ч., а теплоход против течения реки за 6ч. Определите скорость течения? (решите задачу арифметическим методом).
8. Сравните числа:
А) 3617009 и 3616356
Б) 18532129 и 18532130
В) 198567333 и 198675333
Г) 13325325325 и 1325325325
9. Запишите пятизначное число, которое:
А) меньше 10016 и оканчивается цифрой 7.
Б) больше 9987 и оканчивается цифрой 6.
Тема 2
Арифметические законы, простые и составные числа, признаки делимости, разложение на простые множители, наименьшее общее кратное, наибольший общий делитель
Существует 5 математических законов, справедливых для любых чисел.
1. Переместительный закон сложения a + b = b + a, например 5 +4 = 4 +5 = 9
Выражаясь простым языком, можно сказать: от перемены мест слагаемых сумма не меняется.
2. Переместительный закон умножения a × b = b × a, например 6 × 2 = 2 × 6 = 12
Проще говоря, от перемены мест множителей произведение не меняется.
3. Сочетательный закон сложения (a + b) + c = a + (b + c), например (7 +5) +3 = 7 + (5 +3) = 15. Или, значение суммы не зависит от того как сгруппированы слагаемые.
4. Сочетательный закон умножения (а × b) × c = a × (b × c), например (3×2) ×5=3× (2×5) =30. Или, значение произведения не зависит от того как сгруппированы множители.
5. Распределительный закон умножения относительно сложения
(a + b) × c = a × c + b × c, например (5 +4) × 2 = 5 × 2 +4 × 2 = 18. То есть, чтобы сумму умножить на число, можно умножить на это число каждое из слагаемых, а затем сложить полученные произведения.
— Позвольте, — тут же заметит вдумчивый читатель. — Вы в прошлой теме утверждали, что в арифметике скобки раскрывать нельзя, а тут распределительный закон говорит о противоположном.
И тут же приведёте мне пример: 10:2 (4—2). А я рядом с вашим примером напишу такой: 10: [2 (4—2)]. Скажите, между этими примерами есть разница? Оказывается разница есть в порядке действий и соответственно в получаемом результате. Если в первом примере применить распределительный закон, то мы нарушим порядок действий. А вот во втором примере порядок действий не нарушается и мы можем применить распределительный закон. Действительно, результат не изменится, если сделать сначала действие в круглых скобках и результат умножить на 2, или умножить 2 на каждое из слагаемых в скобке, а потом вычесть из первого произведения второе. Как видите, никакого противоречия нет. Добавив квадратные скобки, мы меняем порядок действий и соответственно получаемый результат.
Нетрудно заметить, что арифметические законы позволяют упростить вычисления.
Например:
4 × 93 × 25 = 93 × (25 × 4) = 93 × 100 = 9300. Применён сочетательный закон умножения.
932 +869 +68 = 869 + (932 +68) = 869 +1000 = 1869. Применён сочетательный закон сложения.
158 × 6 +242 × 6 = (158 +242) × 6 = 400 × 6 = 2400. Применён распределительный закон умножения относительно сложения.
Натуральные числа больше единицы называются простыми, если они делятся только на единицу и на самого себя.
Натуральные числа больше единицы называются составными, если они делятся и на другие числа. Число 1 не относится ни к простым, ни к составным.
Например, числа 5, 7, 19, 31, 61, 89 простые. Они не делятся нацело на другие числа.
А вот число 21 и 81 составные. 21 делится не только на единицу и самого себя, но и на цифры 3 и 7. 81 делится на цифры 3, 9, 27.
Числа 1, 3, 7, 21 делители числа 21, числа 1, 3, 9, 27, 81 делители числа 81. Число 21 кратное для чисел 1, 3, 7, 21, т.к. делиться на эти числа без остатка.
Интересная задача.
Нумерация домов на улице от 1 до 11. Каких чисел больше, простых или составных в нумерации домов?
Так просто. Однако многие забывают, что единица не относится ни к простым, ни к составным числам, поэтому дают неправильный ответ. Отбрасываем единицу и начинаем считать: 2, 3, 5, 7, 11 — простые, 4, 6, 8, 9, 10 — составные. Простых и составных чисел оказалось поровну, хотя количество домов на нечётной стороне больше. Можете это проверить.
Часто задают вопрос, каких чисел в математике больше: простых или составных. Вы сами можете ответить на этот вопрос. Все чётные числа — составные, т.к они делятся на 2. А из нечётных чисел не все простые. Даже в первой десятке есть число 9, которое не является простым. В приведённых выше примерах нечётные числа 21 и 81 не являются простыми. Поэтому, простых чисел не так много. В первой тысяче их 168.
Переходим к формулировке основной теоремы арифметики.
Любое составное натуральное число можно представить единственным образом в виде произведения простых чисел. Такое представление называется разложением числа на простые множители.
Рассмотрим пример разложения числа на простые множители
Таким образом, 1421 = 7×7×29 = 7² ×29.
Как научиться правильно делать разложение чисел на простые множители? Обычно такое разложение записывают столбиком в две колонки. В левую колонку записывается исходное число.
1 шаг. Берём самое маленькое простое число 2 и проверяем делится ли исходное число на 2.
2 шаг. Если делится, то в правую колонку выписываем 2, далее делим исходное число на 2 и записываем результат в левую колонку под исходным числом
3 шаг. Если же число не делится на 2, то берём следующее простое число 3. И так далее.
Повторяем эти шаги при работе с последним числом в левой колонке и с текущим простым числом. Разложение заканчивается, когда в левой колонке будет записано простое число.
Чтобы лучше понять этот алгоритм разберём несколько примеров.
Пример 1: Разложить число 298 на простые множители.
Берём число 2 и проверяем делится ли 298 на 2. Делится. В остатке получаем 149. Записываем число 2 в правую колонку, а число 149 в левую. Число 149 простое. Поэтому, 298 = 2×149. Разложение закончено.
Пример 2: Разложить число 1962 на простые множители.
Аналогично, число 1962 делится на 2.
Остаток 981 не делится на 2, но делится на 3. Следующее полученное число 327 тоже делится на 3. Разделив 327 на 3 получим простое число 109.
Таким образом, 1962 = 2×3²×109.
Пример 3: Разложить число 2940 на простые множители.
Первый простой множитель 2. 2940: 2 = 1470. Второй простой множитель тоже 2. 1470: 2 = 735. Третий простой множитель 3. 735: 3 = 245. Четвёртый простой множитель 5. 245: 5 = 49. Пятый простой множитель 7. 49: 7 = 7. Число 7 простое. Разложение закончено.
Таким образом, 2940 = 2²×3×5×7²
Как видите разложение чисел на простые множители не представляет трудности, т.к. происходит по заранее заданному алгоритму. Кстати, множество задач, уравнений и неравенств по математике решается с помощью алгоритмов. Достаточно знать этот алгоритм решения и можно научиться решать практически любые задачи. Об алгоритмах в решении задач мы будем постоянно говорить в дальнейшем. А сейчас продолжим разговор об арифметике.
Чтобы упростить процесс разложения числа на простые множители необходимо знать признаки делимости.
Признаки делимости несложные и их легко запомнить. Гораздо важнее правило делимости суммы. Рассмотрим это правило на примерах.
Например, числа 8 и 24 делятся на 4. Их сумма 8+24 = 32 тоже делится на 4. Аналогично, числа 49 и 42 делятся на 7, их сумма 49+42 = 91 тоже делится на 7. 91: 7 = 13.
Последний вопрос, который мы рассмотрим в данной теме — это наибольший общий делитель и наименьшее общее кратное. Многие путают эти понятия из-за того, что аббревиатуры их схожи (НОД и НОК), а сами понятия делителя и кратного весьма расплывчаты, да ещё к этому добавляется полная идентичность нахождения наибольшего общего делителя и наименьшего общего кратного. Вспомните, в этой теме мы уже упоминали о кратном и делителе. Говорили, что числа 1, 3, 7, 21 являются делителями числа 21, а само число 21 является кратным для чисел 1, 3, 7, 21 так как делится на эти числа без остатка. А теперь представьте мы имеем несколько чисел и должны выбрать наибольшее число из тех, на которое данные числа делятся без остатка. Это это и есть наибольший общий делитель нескольких чисел.
НОД нескольких чисел называется наибольшее число, на которое делятся данные числа без остатка. Это уже математическая формулировка. Отыскание наибольшего общего делителя процесс несложный и происходит по определённому алгоритму.
1. Разлагаем числа на простые множители.
2. Выписываем общие простые множители с наименьшим показателем степени.
3. НОД равен произведению полученных чисел.
Рассмотрим один единственный пример и поймём, что это не так сложно.
Пример: Найти НОД чисел 120, 180 и 240.
Согласно первому пункту разлагаем все числа на простые множители.
120 = 2³×3×5, 180 = 2²×3²×5, 240 = 2⁴×3×5Выбираем все общие простые множители. Это 2², 3 и 5.Таким образом,
НОД (120,180,240) = 2²×3×5 = 60.
Следует запомнить, что числовое значение НОД нескольких чисел меньше, чем сами числа или, в крайнем случае, равно меньшему из них. Например, НОД (127,254,381) = 127. Можете легко это проверить. Возможен вариант, когда простых множителей, общих для всех данных чисел, не будет вообще. Тогда НОД будет равен 1. Два числа НОД которых равен единице, называются взаимно простыми. Например, 25 и 88 взаимно простые числа. Проверьте это.
Наименьшим общим кратным нескольких чисел (НОК) называется наименьшее число, которое делится без остатка на данные числа. Например НОК чисел 15, 6, 10 есть число 30. Это наименьшее число из всех, которое делится на 15, 6 и 10 без остатка. Алгоритм нахождения НОК нескольких чисел похож нахождение НОД, но имеет одно существенное различие. Обратите на это внимание.
1. Разлагаем числа на простые множители.
2. Выписываем все простые множители с наибольшим показателем степени (главное отличие от нахождения НОД).
3. НОК равен произведению полученных чисел.
Рассмотрим пример. Найти НОК чисел 240, 360, 1080.
Разлагаем числа на простые множители.
240 = 2⁴×3×5, 360 =2 ³×3²×5 1080 = 2³×3³×5
Выбираем числа с наибольшим показателем степени. Это 2⁴, 3³ и 5.
Таким образом, НОК (240, 360, 1080) = 2⁴×3³×5 = 16×27×5 = 2160.
Числовое значение НОК нескольких чисел больше, чем сами числа или, в лучшем случае, равно большему из них. Например, НОК (36,180,900) = 900. Проверьте это.
В отличие от НОД, НОК всегда определён. Даже, если все числа простые, то для нахождения НОК их достаточно перемножить.
Тестовые задания к теме 2
Тест 1
1. Определить математический закон,
выполняющийся на множестве натуральных чисел:
А) a/b = b/a Б) a×b = b×a В) (a:b):c =a: (b:c) Г) a× (b+c) = (a×b) +c
2. Определить математический закон,
выполняющийся на множестве натуральных чисел:
А) a-b = b-a Б) (a+b) ×c = (a+c) ×b В) (a+b) ×c = a×c+b×c
Г) (a+b) -c = a+ (b-c)
3. Найти частный случай математического закона
a+b = b+a, определённого на множестве натуральных чисел:
А) 10+ (-7) = 7—10 Б) 10+5 = 5+10 В) -7+5 = 5+ (-7) Г) 2+2 = 2×2
4. Найти частный случай математического закона
(a+b) +c = a+ (b+c), определённого на множестве
натуральных чисел:
А) (2+3) +15 = 2+ (3+15) Б) (4+7) + (-1) = 4+ (7—1)
В) (-7+5) +2 = -7+ (5+2) Г) (3+0) +2 = 3+ (0+2)
5. Найти частный случай математического закона
a×b = b×a, определённого на множестве натуральных чисел:
А) 5×1/2 = 1/2×5 Б) -5× (-2) = -2× (-5) В) 0×3 = 3×0 Г) 4×6 = 6×4
6. Найти частный случай математического закона
(a×b) ×c = a× (b×c), определённого на множестве
натуральных чисел:
А) (-2× (-3)) ×5 = -2× (-3×5) Б) (2×3) ×4 = 2× (3×4)
В) (5×2) ×4 = 5×4+2×4 Г) (1/2×0) ×3 = 1/2× (0×3)
7. Найти частный случай математического закона
(a+b) ×c = a×c+b×c, определённого на множестве
натуральных чисел:
А) (3+4):1/2 = 3×2+4×2 Б) (5+2) ×3 = 5×2+2×3
В) (2+3) ×5 = 2×5+3×5 Г) (-7+3) ×2 = -7×2+3×2
8. Для каких троек чисел выполняется признак делимости
суммы на множестве натуральных чисел?
А) 81,27,3 Б) 7,10,17 В) 42,43,5 Г) 3,6,8
9. Для того, чтобы число делилось на 12, необходимо,
чтобы число делилось одновременно:
А) на 3 и 8 Б) на 8 и 4 в) на 6 и 8 Г) на 3 и 4
10. Число делится на 2, если:
А) оно оканчивается на 0 Б) сумма всех цифр делится на 2
В) оканчивается чётной цифрой
Г) две последние цифры образуют число, делящееся на 4
11. Число делится на 3, если:
А) сумма цифр в записи числа делится на 3
Б) оканчивается нечётной цифрой
В) две последние цифры образуют число, делящееся на 3
Г) оканчивается на 3
12. Число делится на 4, если:
А) оканчивается чётной цифрой
Б) две последние цифры образуют число, делящееся на 4
В) сумма цифр в записи числа делится на 4
Г) оканчиваются на 0
13.Число делится на 5, если:
А) оканчивается нечётной цифрой
Б) сумма цифр в записи числа делится на 5
В) две последние цифры образую число, делящееся на 5
Г) оканчивается на 5 или 0
14. Число делится на 6, если:
А) оканчивается чётной цифрой Б) оканчивается на 6
В) делится одновременно на 2 и на 3
Г) сумма цифр в записи числа делится на 6
15. Число делится на 8, если:
А) две последние цифры образуют число, делящееся на 8
Б) три последние цифры образуют число, делящееся на 8
В) оканчивается чётной цифрой
Г) сумма цифр в записи числа делится на 8
16. Число делится на 9, если:
А) сумма цифр в записи числа делится на 3
Б) три последние цифры образуют число, делящееся на 9
В) оканчивается нечётной цифрой
Г) сумма цифр в записи числа делится на 9
17. Число делится на 10, если:
А) оканчивается на 0 Б) оканчивается чётной цифрой
В) три последние цифры образуют число, делящееся на 10
Г) делится одновременно на 2 и на 5
18. Число делится на 11, если:
А) оканчивается нечётной цифрой
Б) три последние цифры образуют число, делящееся на 11
В) сумма цифр на нечётных местах равна сумме цифр
на чётных или их разность делится на 11
Г) сумма цифр в записи числа делится на 11
19. Число делится на 25, если:
А) одновременно делится на 5 и на 10
Б) оканчивается на 00, 25, 50, 75
В) оканчивается на 0 и 5 Г) нет правильного ответа
20. Число делится на 100, если:
А) оканчивается на 00 Б) одновременно делится на 5 и на 10
В) оканчивается на 0,00,000 Г) нет правильного ответа
21. Признак делимости суммы:
А) если число к делится на сумму чисел a и b, то к делится
как на a, так и на b
Б) если каждое из слагаемых x и y делится на
некоторое число c, то и сумма x+y делится на это число c
В) если сумма чисел a и b делится на число k,
то и каждое из чисел делится на k
Г) если каждое из слагаемых x и y делится
на некоторое число c, то число с делится на сумму x+y
22. Основная теорема арифметики:
А) любое простое число можно представить в виде суммы
двух простых чисел
Б) любое составное натуральное число можно
представить единственным образом в виде произведения
простых чисел
В) любое составное число представимо единственным
образом в виде суммы простых чисел
Г) любое простое число единственно представимо
в виде произведения двух простых чисел
23. Разложите на простые множители число 126:
А) 2×33×7 Б) 2×32×7 В) 22×3×11 Г) 2×3×7×11
24. Разложите на простые множители число 270:
А) 2×33×5 Б) 33×52×2 В) 27×10 Г) 22×33×5
25. Разложите на простые множители число 2310:
А) 23×2×5 Б) 2×3×5×7×11 В) 10×11×21 Г) 23×3×13
26. Разложите на простые множители число 300:
А) 5×6×100 Б) 22×32×5 В) 22×3×52 Г) 3×2×5
27. Разложите на простые множители число 315:
А) 32×5×7 Б) 9×35 В) 32×52×7 Г) 3×1×5
28 Указать наименьшее из следующих натуральных
простых чисел:
А) 2 Б) 0 В) 1 Г) 3
29. Указать наименьшее из следующих натуральных
составных чисел:
А) 4 Б) 2 В) 6 Г) 3
30. Указать наименьшее из следующих натуральных
однозначных чисел:
А) 0 Б) 2 В) 1 Г) 3
31. Указать наименьшее из следующих натуральных
двузначных чисел:
А) 1 Б) 11 В) 10 Г) 0
32. Указать наименьшее из следующих натуральных
чётных чисел:
А) 2 Б) 6 В) 0 Г) 4
Тест 2
1. Указать наименьшее из следующих натуральных
нечётных чисел:
А) 1 Б) 2 В) 0 Г) 3
2. Указать наибольшее из следующих натуральных
простых чисел:
А) 997 Б) 97 В) 91 Г) 991
3. Указать наибольшее из следующих натуральных
составных чисел:
А) 100 Б) 99 В) 35 Г) 131
4. Указать наибольшее из следующих натуральных
однозначных чисел:
А) 7 Б) 8 В) 9 Г) 10
5. Указать наибольшее из следующих натуральных
двузначных чисел:
А) 99 Б) 97 В) 100 Г) 98
6. Какое из данных утверждений не верно?
А) 3 делитель 26 Б) 37 делитель 814 В) 23 делитель 943
Г) 67 делитель 3350
7. Какое из данных утверждений верно?
А) 33 кратно 11 Б) 565 кратно 15 В) 17 кратно 0 Г) 45 кратно 2
8. Какое из данных выражений принимает только
нечётные значения, если a и b-нечётные натуральные
числа и a> b?
А) a+b Б) a-b В) a×b Г) 2a-2b
9. Какое из данных выражений принимает только
чётные значения, если a и b-нечётные натуральные числа и a> b?
А) a×b Б) b+2 В) a+2b Г) a-b
10. Какое из данных выражений принимает только
нечётные значения, если a-чётное и b-нечётное
натуральные числа и a> 2b?
А) a+b Б) 3a-2b В) a×b Г) 2a-2b
11. Какое из данных выражений принимает только
нечётные значения, если a и b-чётные натуральные числа и a> b?
А) 3a×b Б) 2a+b+1 В) a+3b Г) 3a-b
12. Какая из данных сумм кратна 5?
А) 4523+7415 Б) 678+991+31 В) 230+179 Г) 128+123+56
13. Какая из данных сумм не кратна 5?
А) 7314+454 Б) 45232+74158 В) 378+981+31 Г) 361+125+744
14. Какая из данных сумм кратна 10?
А) 7231+231 Б) 451+458 В) 2568+459+111 Г) 221+346+123
15. Какая из данных сумм не кратна 10?
А) 1526+344 Б) 527+343+81 В) 380+120 Г) 623+124+353
16. Какое из данных чисел не кратно 3:
А) 1706 Б) 131421 В) 18279 Г) 12363
17. Какое из данных чисел не кратно 9:
А) 4347 Б) 123030 В) 3591954 Г) 3453
18. Найдите остаток от деления числа 78567 на 5:
А) 1 Б) 2 В) 3 Г) 4
19. Найдите остаток от деления числа 87656 на 9:
А) 3 Б) 5 В) 1 Г) 2
20. У какой из предложенных пар чисел НОД равен 4:
А) 24 и 20 Б) 24 и 30 В) 24 и 32 Г) 18 и 32
21. У какой из предложенных пар чисел НОК равен 60:
А) 30 и 2 Б) 18 и 15 В) 4 и 15 Г) 10 и 6
22. Сколько существует двузначных чисел
кратных 12, но не кратных 24?
А) 5 Б) 3 В) 4 Г) 6
23. Из данных чисел выберите число, которое делится на 2 и на 5:
А) 8016 Б) 195 В) 4050 Г) 1113
24. Из данных чисел выберите число, которое делится на 3 и 5:
А) 1113 Б) 914 В) 3040 Г) 7035
25. Из данных чисел выберите число, которое делится на 2 и на 3:
А) 2894 Б) 405 В) 2802 Г) 785
26. Какую цифру нужно поставить вместо * в числе 5*62,
чтобы полученное число делилось на 9?
А) 0 Б) 2 В) 9 Г) 5
27. Назовите число, кратное 25,которое
удовлетворяет неравенству 530 <x <560:
А) 545 Б) 555 В) 550 Г) 540
28. Укажите произведение, которое является разложением
числа на простые множители:
А) 2×8×11 Б) 16×3×11 В) 2×2×2×3×11 Г) 2×3×4×9
29. Укажите наибольший простой делитель числа 5460:
А) 21 Б) 17 В) 13 Г) 15
30. Найдите НОД чисел 585 и 525:
А) 5 Б) 3 В) 15 Г) 25
31. Найдите НОК чисел 50, 60 и 90:
А) 1800 Б) 900 В) 180 Г) 9000
32. Найдите НОД чисел 280, 140 и 350:
А) 35 Б) 70 В) 10 Г) 140
Задачи для самостоятельного решения
1. Пользуясь признаками делимости определить
на какие числа делятся числа:
А) 4004 Б) 15835 В) 10203 Г) 225225 Д) 174022
Е) 88776 Ж) 245322 З) 36463 И) 178000
2. Разложить вышеперечисленные числа на простые множители.
3. Найти НОД и НОК следующих чисел:
А) 252,441,1080 Б) 234,1080,8100 В) 1421,490,1237600
Г) 256128,820,5760
Тема 3
Простые дроби. Сокращение дробей. Сравнение дробей. Приведение к общему знаменателю. Сложение, вычитание, умножение и деление дробей. Действия с нулем. Целое и часть
Теперь мы переходим к более важным понятиям в арифметике. Дробными числами мы будем пользоваться в дальнейшем. Поэтому, для осмысления этой темы вам понадобится немного больше времени, сил и концентрации. Но результат не заставит себя долго ждать.
Простой дробью называется часть единицы или несколько равных частей единицы. Наглядно это можно пояснить с помощью круга. Вы ждёте в гости друзей и приготовили круглый пирог. Гостей будет 8 и вы заранее разделили своё чудо кулинарной мысли на 8 равных частей (чтобы никого не обидеть). Но вот незадача. Двое ваших друзей не пришли, а ещё трое, оказывается, не едят сладкого. Поэтому было съедено всего три кусочка. Напрашивается вопрос, какая часть пирога была съедена? Число восемь называется знаменателем дроби. Это именно то количество частей на которые разделена наша единица (пирог). На рисунке заштрихованы три части. Число 3-числитель дроби. Это количество взятых частей (долей). Таким образом мы получили дробное число, где 3- числитель дроби записан сверху, а 8-знаменатель дроби снизу.
Именно такой записью дробных чисел мы будем пользоваться в дальнейшем, она удобна для преобразований и вычислений. Если мы разделим единицу на 12 частей и возьмём 5 из них, то получим дробь.
Аналогично, — единица поделена на 355 частей, из которых взяты всего 3 (говорят, три триста пятьдесят пятых).
Мы привели примеры правильных дробей, у которых числитель меньше знаменателя.
Правильные дробиЕсть дроби неправильные, у них числитель больше знаменателя или равен ему:
Неправильные дробиА также смешанные дроби, которые имеют целую и дробные части
Смешанные дробиЛюбую неправильную дробь можно превратить в смешанную и наоборот. Делается это очень просто.
Например, превратим неправильную дробь
в смешанную. Для этого в столбик разделим 17:6. Получилось, что 2-целая часть, а остаток от деления 5-числитель новой дроби. Знаменатель остаётся без изменений. Таким образом,Теперь обратное действие. Превращение смешанной дроби в неправильную.
Например, превратим смешанную дробь
в неправильную. Умножаем целую часть на знаменатель и прибавляем к полученному результату числитель. 3×9+5 = 32. Полученное число является числителем новой дроби. Знаменатель остаётся без изменений. Таким образом,
Чтобы научиться преобразовывать действия с дробями нам нужно знать правила сокращения и расширения дроби, а также научиться их приводить к общему знаменателю. Величина дроби не изменится, если числитель и знаменатель дроби умножить или разделить на одно и тоже число. В первом случае говорим о расширении дроби, во втором случае о сокращении.
Примеры.
расширение дроби сокращение дробиСравнение дробей.
1.У дробей одинаковые числители. Больше дробь та, у которой знаменатель меньше.
Действительно, кусок пирога, разделённый на три части больше, чем кусок того же пирога, но разделённый на четыре части.
2. У дробей одинаковые знаменатели. Больше дробь та, у которой числитель больше.
Здесь ещё понятнее, три одинаковых куска пирога больше, чем один или два.
3.Если числитель и знаменатель двух дробей различны, то необходимо преобразовать дроби так, чтобы их знаменатели стали одинаковыми. Такая операция называется приведением дробей к общему знаменателю. Она может осуществляться двумя способами. Каждый может выбрать способ, который считает более удобным. Рассмотрим пример.
Пример. Сравним дроби
1 способ. Расширяем первую дробь на 12, а вторую на 8, имеем
Следовательно,
2 способ. Находим НОК чисел 8 и 12. НОК (8,12) = 24
Расширяем каждую дробь на частное, получаемое от деления НОК на знаменатель взятой дроби. Для первой дроби
Для второй дроби
Так же, как и при первом способе
Несмотря, на кажущуюся простоту первого способа, второй способ, можно так сказать, более профессиональный. При первом способе часто расчёты становятся трудоёмкими, если знаменатели дробей большие числа. Однако, часто для нахождения НОК двух чисел, их необходимо перемножить. Тогда первый способ является единственно применимым.
Теперь плавно переходим к основным арифметическим действиям над дробями. Рекомендуется освоить этот пункт полностью, чтобы, как говорят, от зубов отскакивало.
Сложение и вычитание дробей.
Рассмотрим сначала частные случаи.
А. Дроби с одинаковыми знаменателями.
Здесь все просто. Знаменатель остаётся без изменений, а числители прибавляются. Обратите внимание: в конце расчёта мы неправильную дробь перевели в смешанную (рекомендуется так делать).
Аналогично с вычитанием
Б. Знаменатели дробей взаимно простые числа.
Общий знаменатель получается умножением исходных знаменателей. Затем находятся дополнительные множители. Для первой дроби 2, для второй 3. Новый числитель — это сумма произведений числителей на соответствующие дополнительные множители.
Аналогично, для вычитания
В. Один знаменатель кратен другому.
За общий знаменатель принимается больший, который кратен всем остальным. Числитель получается суммой произведения первого числителя на дополнительный множитель и второго числителя. Обратите внимание, в конце вычисления мы сократили искомую дробь (делать обязательно).
Автор рекомендует и другой способ.
Разделим один знаменатель на другой. 6:2=3. Расширим первую дробь на 3 и получим две дроби с одинаковым знаменателем.
Аналогично, для вычитания
Для остальных случаев сложения и вычитания дробей их нужно привести к общему знаменателю. Рассмотрим несколько примеров.
И напоследок рассмотрим сложение и вычитание смешанных дробей.
Чтобы сложить или вычесть две смешанные дроби нужно сложить или вычесть отдельно целые и отдельно дробные части.
Посмотрите, чтобы избежать в конце написания неправильной дроби мы сразу же перевели её в смешанную.
Особое внимание обратите на вычитание смешанных дробей.
Независимо от того, делается ли сложение или вычитание смешанных дробей, полученные результаты для целой и дробной части складываются.
При вычитании смешанных дробей может возникнуть случай, когда дробная часть вычитаемого может оказаться больше дробной части уменьшаемого. Тогда из целой части занимаем единицу, а дробную часть превращаем в неправильную дробь. Как это действует рассмотрим на примере.
Здесь мы сразу перевели первую дробь в неправильную.
Ещё один пример вычитания.
Здесь целое число 13 заменено дробным, чтобы сделать одинаковыми знаменатели.
Существует ещё один способ сложения и вычитания смешанных дробей, но он не упоминается в учебниках математики ввиду того, что при этом способе приходится оперировать большими числами. Но этот способ удобен тем, что он легко запоминается. Суть его в том, что все смешанные дроби переводятся в неправильные. А потом уже по стандартной схеме находится общий знаменатель, дополнительные множители и так далее. Давайте рассмотрим один пример.
Способ не очень удобный, так как в конце нужно перевести неправильную дробь в смешанную. Но как альтернатива, такой способ тоже имеет право на жизнь.
Умножение и деление дробей.
Здесь всё намного проще. При умножении дроби на дробь их числители и знаменатели перемножаются, например:
Обратите внимание, ещё до перемножения можно сокращать любой множитель числителя с любым множителем знаменателя на их общий делитель. В данном случае, 3 и 9 имеют общий делитель 3, на который мы и сократили.
Если среди сомножителей есть смешанные дроби, то их предварительно переводят в неправильную дробь.
Пример.
МОУ «Гимназия с. Ивантеевка» Урок математики в 1 классе. Тема: «Сложение с переходом через десяток, вида +8» УМК «Начальная школа XXI века»
«Числовые и буквенные выражения».
Муниципальное казѐнное общеобразовательное учреждение «Дуровская средняя общеобразовательная школа» Сафоновского района Смоленской области «Числовые и буквенные выражения». Учитель математики I категории
ПодробнееУчитель начальных классов: Левыкина А. В
Конспект открытого урока по математике на тему «Сложение и вычитание трехзначных чисел на основе знания их разрядного состава». 2 «А» класс Учитель начальных классов: Левыкина А. В. 15.03.12. Цели: формирование
ПодробнееКОНСПЕКТ УРОКА МАТЕМАТИКИ В 3 КЛАССЕ
211 Беляева М. Ю. Учитель начальных классов КОНСПЕКТ УРОКА МАТЕМАТИКИ В 3 КЛАССЕ Тема: Нумерация многозначных чисел. Закрепление. Цели: Образовательные: закреплять умения читать, записывать, сравнивать,
ПодробнееМЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ
МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ Развёрнутый план урока по теме «Замена двузначного числа суммой разрядных слагаемых» ТЕМА: «Замена двузначного числа суммой разрядных слагаемых» (ч. 1: с. 15) ЦЕЛЕВЫЕ УСТАНОВКИ:
ПодробнееУрок по математике в 6-м классе
Урок по математике в 6-м классе ТЕМА: «Упрощение выражений » Кузнецова Надежда Владимировна, учитель математики Подготовка к уроку: Оборудование: Проектор, компьютеры или ноутбуки, экран, презентация Microsoft
ПодробнееТема: «Название чисел при умножении.»
Муниципальное общеобразовательное учреждение Падовская средняя общеобразовательная школа Урок математики во 2 классе Тема: «Название чисел при умножении.» Учитель: Носкова О.Н 2010 год Тема: «Название
ПодробнееУрок математики в 1 классе
Урок математики в 1 классе Злобина Ольга Федоровна, учитель начальных классов Тема: Уравнение Цель урока: создание условий для формирования универсальных учебных действий у учащихся начальной школы. Задачи
ПодробнееОТКРЫТЫЙ УРОК МАТЕМАТИКИ ВО 2 КЛАССЕ
115 Учитель начальных классов Беляева М. Ю. ОТКРЫТЫЙ УРОК МАТЕМАТИКИ ВО 2 КЛАССЕ Тема: Сложение и вычитание трёхзначных чисел. Цели урока: Учить приемам сложения и вычитания трёхзначных чисел вида: 261+124;
ПодробнееОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ Тема: Совместные выполнения действий над натуральными числами и нулем. Основные цели урока: -сформировать навык порядка выполнения действий -закрепить ранее приобретенные умения
ПодробнееТехнологическая карта урока
Технологическая карта урока Приложение 2. Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
ПодробнееУрок математики во 2 классе
Урок математики во 2 классе Автор: Матвеева С.А., учитель начальных классов Тема: Приемы вычислений для случаев вида 36-2, 36-20 Цели урока: 1. Познакомить детей с приемами устных вычислений вида 36-2,
ПодробнееОткрытый урок по математике в 1 классе.
Автор: Матющенко М.А., учитель начальных классов Предмет: Математика Класс: 1 класс Тип урока: урок изучения новой темы Открытый урок по математике в 1 классе. Оборудование: учебник «Математика» (Дорофеев
ПодробнееДата: Класс: 1-А
Дата: 26.02.2014 Класс: 1-А Тема. Упражнения на усвоение названий компонентов при сложении и вычитании. Сравнение выражений и чисел. Подготовительные упражнения к решению задач в два действия. Измерение
ПодробнееМатематика. Правило 1. Математика. Правило 1. Математика. Правило 2. Математика. Правило 2. В этой системе пользуются: единицами, в 10 раз.
Математика. Правило 1. Математика. Правило 1. Числа единицы счѐта (5, 16, 129,2087,10000,…) Числа единицы счѐта (5, 16, 129,2087,10000,…) Цифры знаки, которые используются для записи Цифры знаки, которые
ПодробнееЭтапы, время 1 Орг. момент
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ Тема: «Деление» Цели: — познакомить с понятием деление; — рассмотреть простые задачи на деление (на части и по содержанию) и сравнить их решения; — установить связь между действиями
ПодробнееТехнологическая карта урока
Мухтарова Лютфия Тухтамурадовна учитель начальных классов Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа 69 с углубленным изучением отдельных предметов Республика
ПодробнееВершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100. Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна
Подробнее7* : :2 31 4*
Открытый урок математики в 3в классе Тема: «Умножение числа на произведение» урок закрепления материала Цели урока: Образовательные: Обобщить материал по темам «Умножение многозначных чисел на однозначное»,
ПодробнееТехнологическая карта урока
Технологическая карта урока Вводная часть Ф.И.О. Заславская Татьяна Николаевна, учитель МОУ Зебляковская средняя общеобразовательная школа. Предмет: математика Класс: 1 Наименование учебно-методического
ПодробнееКонспект урока по математике.
Конспект урока по математике. Учитель: Виссарионова И.Е. Класс: 2 «А» Дата: 24.12.2018 г Предмет: математика УМК «Школа России» Тема: «Что узнали. Чему научились.» Раздел: «Устные вычисления» Урок 54 Тип:
ПодробнееТехнологическая карта урока математики
Технологическая карта урока математики Изучаемая тема: Устные и письменные приемы вычисления вида 32-5, 51-27 Место урока в изучаемой теме: 5 Дата проведения: 14.04.2017 г. Класс: 2 Программа: УМК «Перспектива»
ПодробнееОткрытый урок по математике во 2 классе
МКС(К) ОУ для обучающихся воспитанников с ограниченными возможностями здоровья Старогородковской специальной (коррекционной) общеобразовательной школы-интерната VIII вида им. Заслуженного учителя РФ Фурагиной
ПодробнееШАХМАТНЫЙ УЧЕБНИК ДЛЯ ДЕТЕЙ
Серия «Шахматы» Наталья Петрушина ШАХМАТНЫЙ УЧЕБНИК ДЛЯ ДЕТЕЙ Издание четырнадцатое Ростов-на-Дону «Феникс» 2014 УДК 087.5:794 ББК 75.581 КТК 762 П 30 П 30 Петрушина Н.М. Шахматный учебник для детей /
ПодробнееУДК *01/04 ББК я71 Б 39
УДК 7.67.*0/04 ББК я7 Б 9 Б 9 Безкоровайная, Елена Викторовна. Подготовка к итоговой аттестации : 4 классы / Е.В. Безкоровайная, И.С. Марченко. Москва : Эксмо, 206. 224 с. (В помощь младшему школьнику).
ПодробнееУрок 29 ( 3.19) Число пять. Цифра 5
Урок 29 ( 3.19) Число пять. Цифра 5 Помочь детям усвоить: получение числа 5 прибавлением 1 к числу 4 и обозначение его цифрой 5; построение натурального ряда чисел; написание цифры 5; состав числа 5, все
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Класс Предмет: Авторы учебника: Тарасова Екатерина Антоновна 1Г Математика В.Н. Рудницкая, Т.В.Юдачёва (Начальная школа XXI века) Тема урока. Прибавление числа 5. Тип
ПодробнееКак работать с пособием
Как работать с пособием Уважаемые взрослые! Предлагаемое пособие рассчитано на совместную работу воспитателей, педагогов и родителей с дошкольниками, готовящимися к школьному обучению. Первоначальной задачей
Подробнее
|
Порядок операций — что делать в первую очередь в математических задачах
См. Точечный прогон. Беги, посмотри Спот. Запустите Spot, смотрите.
Если мы используем одни и те же 3 слова в разном порядке, они звучат странно и не имеют смысла, даже если мы понимаем каждое слово само по себе.
Как и в нашем языке, когда мы пишем уравнение, нам необходимо понимать правила, чтобы кто-то, читающий (или решающий) уравнение, мог понять предполагаемое значение и правильно найти ответ. Этот порядок является частью математического языка.Мы естественно следуем правилам, когда говорим, читаем и пишем, но наш разговорный язык становится нашей второй натурой, и нам не нужно так много думать о правилах, которые мы используем, когда говорим. Мы можем добраться до этого с помощью математики с практикой. Дайте себе время выучить и применить правила, и математика станет более понятной и увлекательной.
Чтобы упростить запись и решение уравнений, у нас есть порядок операций . Это набор правил, которые помогают каждому решить математическую задачу одинаково — он помогает нам понять, что делать в первую очередь.Зачем это нужно? Что ж, это важно — очень много! Взгляните:
3-2 + 1 =? Если мы решим эту задачу слева направо, как при чтении, это будет 3-2 = 1, а затем 1 + 1 = 2
3-2 + 1 =? Если мы выберем это, начиная со сложения, 2 + 1 = 3, и поэтому 3-3 = 0
Два разных подхода дают нам два разных ответа. Нам нужны правила, которые помогут нам определить, какое из них подходит, чтобы каждый мог получить одинаковый результат, столкнувшись с одной и той же проблемой.
Мы используем PEMDAS как порядок действий для решения проблем. Что означает PEMDAS?
PEMDAS — это аренцев P , E xponents, M ultiplication, D ivision, A ddition, S ubtraction.
P означает круглые скобки (). Скобки — это первое, что нужно искать в уравнении. Они используются, чтобы сгруппировать части уравнения вместе и указать, что нужно сделать в первую очередь.Меньшие части уравнения могут быть «вложены» в большие части с помощью круглых скобок и должны обрабатываться изнутри.
E обозначает экспоненты. Как только круглые скобки помогли вам найти, с чего начать, переходите к показателям степени. Основное число с присоединенной экспонентой нельзя умножать, делить, складывать или вычитать без предварительного выполнения операции экспоненты.
M — для умножения, D — для деления.Есть места, где их можно поменять местами, но легче выучить порядок и придерживаться его.
A предназначен для сложения, а S — для вычитания. В первом примере выше вы видели, как их переключение может действительно испортить ситуацию, даже в простых уравнениях.
Примеры порядка операций — использование PEMDAS
Вот несколько примеров, включающих комбинации операций, чтобы мы могли увидеть, как это работает:
Пример 1
Должны ли мы после первой операции иметь 12 x 7 или 14 — 14? При использовании PEMDAS умножение предшествует вычитанию, поэтому это уравнение следует решить, выполнив сначала 2 x 7, а затем вычитание.Итак, 14 — (2 x 7), где круглые скобки вставлены, чтобы показать «группировку» и указать первую операцию, которая должна быть выполнена, становится 14 — 14 = 0
ПРИМЕЧАНИЕ: Если вы хотите описать уравнение, заставляющее сначала выполнить 14-2, используйте круглые скобки, как в (14-2) x 7, что тогда 12 x 7 = 84
Пример 2
Скобки действительно помогают разбить это на группы. Сначала 8 + 8 = 16, держитесь за это и переходите к следующей группе — начните здесь с экспоненты, 2 в квадрате равно 4, так что теперь у вас есть 5 + 4 = 9.Это дает нам (16) — (9), что равно 7!
Пример 3
Это определенно сложнее. Я бы не знал, с чего начать без правил порядка операций. Здесь у нас есть пара группировок, поэтому мы должны начать с самых внутренних круглых скобок. 12 — 2 = 10, достаточно просто, следующая группа имеет экспоненту, поэтому сделайте это первая — 9 x 9 равно 81, что приводит к 19 + 81 = 100. Теперь у нас есть внутренние группировки, и мы можем взглянуть на следующую выравнивать.(4 x (10) x (100)), поскольку все они находятся на одном уровне и все умножение, 4 x 10 x 100 = 4000. Теперь у нас осталось (4000) + 12/3, следуя PEMDAS, мы делаем Дивизия перед сложением дает 4000 + 4, что составляет… 4004!
Для развлечения, напишет несколько уравнений с несколькими операциями и посмотрите, сможете ли вы их решить. Затем передайте уравнения кому-нибудь еще и посмотрите, смогут ли они выполнить тот же порядок действий, чтобы получить тот же ответ, что и вы.
СвязанныеЧто такое BEDMAS?
Существуют акронимы, которые помогают людям запомнить, как выполнять набор процедур в математике.BEDMAS (также известный как PEMDAS) является одним из них. BEDMAS — это аббревиатура, помогающая запомнить порядок операций в основах алгебры. Когда у вас есть математические задачи, требующие использования различных операций (умножение, деление, экспоненты, скобки, вычитание, сложение), порядок необходим, и математики согласовали порядок BEDMAS / PEMDAS. Каждая буква BEDMAS относится к одной части операции, которая будет использоваться. В математике существует согласованный набор процедур для порядка, в котором выполняются ваши операции.Скорее всего, вы получите неправильный ответ, если будете производить расчеты не по порядку. Если вы соблюдаете правильный порядок, ответ будет правильным. Не забывайте работать слева направо, когда вы используете порядок операций BEDMAS. Каждая буква означает:
- B — Кронштейны
- E — Показатели
- D — Подразделение
- M — умножение
- A — Дополнение
- S — вычитание
Вы, наверное, тоже слышали аббревиатуру PEMDAS.При использовании PEMDAS порядок операций такой же, однако P просто означает круглые скобки. В этих ссылках круглые и квадратные скобки означают одно и то же.
При применении порядка операций PEMDAS / BEDMAS следует помнить о нескольких вещах. Скобки / круглые скобки всегда идут первыми, а показатели — вторыми. Когда вы работаете с умножением и делением, вы делаете то, что наступит раньше, слева направо. Если умножение идет первым, сделайте это до деления. То же самое верно и для сложения и вычитания: когда вычитание идет первым, вычитайте, прежде чем добавлять.Возможно, стоит взглянуть на БЕДМЫ так:
- Скобки (или круглые скобки)
- Экспоненты
- Деление или умножение
- Сложение или вычитание
Когда вы работаете со скобками и имеется более одного набора скобок, вы будете работать с внутренним набором скобок и переходите к внешним скобкам.
Уловки для запоминания PEMDAS
Чтобы запомнить PEMDAS или BEDMAS, были использованы следующие предложения:
Please Excuse My Dear Aunt Sally.
Большие слоны уничтожают мышей и улиток.
Розовые слоны уничтожают мышей и улиток
Вы можете составить собственное предложение, которое поможет вам запомнить аббревиатуру, и, безусловно, есть и другие предложения, которые помогут вам запомнить порядок действий. Если вы креативны, придумайте то, что запомните.
Если вы используете базовый калькулятор для выполнения расчетов, не забудьте ввести вычисления в соответствии с требованиями BEDMAS или PEMDAS. Чем больше вы практикуетесь в использовании BEDMAS, тем легче это становится.
Когда вы освоитесь с пониманием порядка операций, попробуйте использовать электронную таблицу для расчета порядка операций. Таблицы предлагают множество формул и вычислительных возможностей, когда ваш калькулятор неудобен.
В конце концов, важно понимать математику, стоящую за аббревиатурой. Даже если аббревиатура полезна, важнее понять, как, почему и когда она работает.
- Произношение: Бедмасс или Пемдасс
- Также известен как: Порядок операций в алгебре.
- Альтернативное написание: BEDMAS или PEMDAS (скобки против скобок)
- Распространенные орфографические ошибки: Скобки и круглые скобки имеют значение в аббревиатуре BEDMAS и PEMDAS
Примеры использования BEDMAS для порядка операций
Пример 1
20 — [3 x (2 + 4)] Сначала сделайте внутреннюю скобку (круглые скобки).
= 20 — [3 x 6] Сделайте оставшуюся скобку.
= 20 — 18 Выполните вычитание.
= 2
Пример 2
(6–3) 2 — 2 x 4 Сделайте скобу (скобки)
= (3) 2 — 2 x 4 Вычислить показатель степени.
= 9 — 2 x 4 Теперь умножим
= 9-8 Теперь вычтите = 1
Пример 3
= 2 2 — 3 × (10 — 6) Вычислить внутри скобок (скобки).
= 2 2 — 3 × 4 Вычислить показатель степени.
= 4 — 3 x 4 Произведите умножение.
= 4 — 12 Выполните вычитание.
= -8
Как изучать математику: алгебра
Урок алгебры — одно из немногих мест, где люди могут купить 64 арбуза, и никто не задается вопросом, почему.
Это также предмет, с которым сталкиваются многие студенты.
Одна из главных причин этой борьбы — они пытаются запомнить. Но когда проблема меняется, меняются и шаги, и ученики остаются в замешательстве. Ключ к успеху в алгебре — понимать, зачем вы делаете каждый шаг. Другими словами, речь идет не только о x , но и о , почему именно .
Мы знаем, о чем вы думаете: если бы только было легко понять алгебру. Что ж, с правильным объяснением, несколькими полезными советами и небольшой работой вы сможете!
Ниже приведены 14 советов по изучению и распространенных ошибок, которых следует избегать, чтобы добиться успеха в алгебре.
1. Знайте свою арифметикуЧтобы выучить алгебру, вы должны, ДОЛЖНЫ, ДОЛЖНЫ знать свои основы арифметики. Да, это включает в себя сложение, вычитание, умножение и деление. Мы знаем, что это математика в начальной школе. Но важно овладеть этими понятиями.
Мы не имеем в виду, что вам нужно запоминать таблицу умножения. Что является важным, так это то, что вы понимаете основную концепцию каждой операции. Например, умножение 3 и 4 на самом деле добавляет 3 вместе 4 раза:
Или что сложение 2 и 5 похоже на то, как если взять стопку из 2 яблок и положить туда еще 5, чтобы получить в сумме 7.
Это может показаться простым, но знание смысла базовой арифметики будет чрезвычайно полезным при изучении алгебры.
Так что не забудьте продумать эти четыре операции, даже если вам придется думать в терминах яблок!
2. Помните PEMDASОй, порядок операций. Вы узнаете это. Пройди тест. Затем удалите его из памяти, думая, что он больше не появится.
Вы и не подозревали, что будете сидеть на уроке алгебры и смотреть на сложное уравнение, думая: «Как вообще я собираюсь решить для x ?»
Вот где вам пригодится PEMDAS.Некоторые запоминают это с помощью мнемоники «Пожалуйста, извините, дорогая тетя Салли», или, другими словами:
P арентов, E компонентов, M ultiplication, D ivision, A ddition, S ubtraction
Это ваш план решения более простой проблемы. Не знаете с чего начать? Начнем со скобок. Опять заблудиться? Попробуйте разобраться с экспонентами! Далее займитесь умножением и делением. И, наконец, вы складываете и вычитаете.Вуаля, проблема, похожая на ту, которую вы знаете!
Вот одна вещь, на которую следует обратить внимание при использовании PEMDAS, которую многие люди упускают:
После того, как вы позаботитесь о скобках и показателях степени, вы выполните умножение и деление в порядке слева направо. Затем, когда вы переходите к сложению и вычитанию, вы также выполняете их в порядке слева направо.
Вот пример проблемы, которая сначала может показаться сложной, но становится полностью решаемой с помощью PEMDAS:
5 + (6 ÷ 2 x 5) 2 -2 + 3
Используя PEMDAS, мы начинаем с выражения в круглых скобках.Внутри скобок нет показателей, поэтому мы переходим к умножению и делению, работая слева направо. Это означает, что вы сначала сделаете деление:
5 + (3 x 5) 2 -2 + 3
Теперь умножаем в скобках:
5 + (15) 2 -2 + 3
После того, как вы закончите со скобками, следующим шагом будет обработка экспоненты в (15) 2 :
5 + 225 — 2 +3
На данный момент нет никакого умножения или деления слева, поэтому мы можем пропустить шаги справа, чтобы добавить и вычесть шаги слева направо:
230 — 2 + 3
228 + 3 = 231
Теперь рассуждая в терминах алгебры, вот пример с использованием переменных:
3.Позитивно комфортно с отрицательными числамиОтрицательные числа похожи на числа, которые вы знаете и любите, но, в общем, отрицательные. Не позволяйте этому крошечному знаку минус перед вами сбить с толку.
Обязательно освоите основные операции с отрицательными числами. То есть сложение, вычитание, умножение и деление двух отрицательных чисел И положительного и отрицательного числа. Это будет очень полезно в будущем! (Ха… ха… понял… числовая строка…? Да, плохой каламбур. Знай свои негативы.)
Вот несколько примеров и правил, которые следует запомнить:
а. Если числа имеют одинаковый знак, сложите их и сохраните исходный знак.
-3-5 = -3 + (-5) = -8
г. Если числа имеют разные знаки, сложите их и сохраните знак «большего» числа или числа с наибольшим расстоянием от нуля.
-10 + 7 = -3
г. Отрицательный, разделенный на отрицательный, считается положительным.
-4 ÷ -2 = 2
г. Отрицательный результат, умноженный на положительный, является отрицательным.
-15 x 3 = -45
4. Покажите свою работуМногие студенты пытаются быстро решить задачи по алгебре. Но если вы потратите время на то, чтобы показать все свои шаги, это не только поможет вам оставаться организованным и избежать мелких ошибок, но вы даже можете получить частичную оценку за неправильный ответ, если ваш инструктор увидит, что вы были на правильном пути.
Мы знаем: чтобы записать все свои шаги, потребуется немного больше времени. Но одна маленькая ошибка в задаче по алгебре может в итоге привести к большой головной боли.
Вот пример того, что мы подразумеваем, показывая все ваши шаги:
5. Не позволяйте буквам пугать васНа протяжении большей части своей ранней математической карьеры вы знали, что математика — это все о числах. Но затем алгебра бросила вам x , y , а иногда даже z . Будьте уверены, они не так плохи, как выглядят! Эти буквы называются переменными , и на самом деле они тоже числа.
Да, сначала это может сбивать с толку, но становится лучше! Математики используют буквы в качестве переменных, обозначающих то, что они хотят найти.
Подумайте о простой задаче: «Сколько будет дважды три?» Часть «что» — это переменная. В этом нет необходимости, но мы могли бы написать такую же задачу, как:
х = 2 х 3
где то «что» мы хотим решить.
Если проблема имеет более одной переменной, это означает, что есть еще кое-что, что нужно найти! В таких случаях не спешите. Найдите по одной переменной за раз.
6. Формулы — твои друзьяДумайте о формулах как о команде полезных помощников, особенно когда дело касается текстовых задач.В зависимости от вашего класса вам нужно будет запомнить и уметь использовать ряд формул.
Важно знать, что простое запоминание формулы не обязательно означает, что вы будете знать, что с ней делать! Обязательно знайте, что обозначает каждая переменная в формуле, чтобы вы могли расшифровать, какой номер какой переменной присвоен.
Вот некоторые из распространенных формул, которые вы увидите:
7. Обязательно ответьте на правильный вопросНе обводите свой ответ и не называйте его днем, пока вы дважды не проверите, что у вас есть то, о чем проблема.Вам может быть интересно, почему это вообще подсказка. Но это же обычная ошибка в алгебре!
Например, при выполнении некоторых задач может потребоваться определить размеры коробки, а вы нашли только длину. Тот факт, что у вас есть нижняя часть листа, не означает, что у вас есть ответ.
Перечитайте формулировку проблемы, просмотрите, что означают ваши переменные, и убедитесь, что вы получили то, о чем просили!
8. Проблемы производственной практикиПоследний совет для учебы: решайте столько задач, что у вас устает рука.Это относится ко всем математическим предметам, но особенно относится к алгебре. Способ усовершенствовать свою способность решать проблемы — это практиковаться, практиковаться, практиковаться!
Вы слышали это раньше миллион раз, но мы повторим еще раз: практика ведет к совершенству! Так что внимательно выполняйте домашнюю работу и переделывайте примеры из своих заметок. Запишите все свои шаги, и если вы допустите небольшую ошибку, поймите, что пошло не так, чтобы вы могли знать об этом в следующий раз!
9. Учитесь на своих ошибкахНе бойтесь ошибаться! Они являются частью учебного процесса.Их делают даже опытные математики. Когда вы совершаете ошибку, главное — научиться распознавать проблему, определять свою ошибку и затем исправлять ее. Вот где происходит настоящее обучение.
И, говоря об ошибках, в следующих нескольких советах мы рассмотрим некоторые понятия алгебры, которые обычно сбивают с толку студентов, чтобы вы сами смогли избежать этих ошибок.
10. Не делить на нольВы не можете этого сделать. Вы никогда не сможете этого сделать.Так что не делай этого. Это одно из первых правил Священной книги математики: «Не дели себя на ноль».
Когда вы действительно думаете о том, что значит делить, это правило имеет смысл.
Совершите короткую поездку с нами в начальную школу, где мы узнали, что деление — это вычисление того, сколько раз одно число содержится в другом. То есть, допустим, у нас есть 4 блока. Затем «4 разделить на 2» задается вопрос: «На сколько групп по 2 вы можете разделить 4 блока?» Таким же образом «4 разделить на 0» спрашивает: «На сколько групп по 0 вы можете разделить 4 блока?»
Но 0 — это ничего.Группы из 0 означает, что в группе нет блоков. Так как же разделить 4 блока на группы, в которые не может быть блоков? Мы этого не делаем. Мораль истории: не делить на 0.
11. Помните о скобкахСкобки важны, хотя могут показаться, что это не так. Очень важно .
Они много говорят вам о проблеме, например, что делать в первую очередь или что объединить.
Например, рассмотрим (-3) 2 и -3 2
(-3) 2 говорит: возьмите все число в скобках, -3, и умножьте его на себя:
(-3) 2 = -3x — 3 = 9
Но -3 2 без круглых скобок говорит, что возьмите число 3, умножьте его на само себя и поставьте знак минус впереди:
-3 2 = — (3 x 3) = -9
Как видите, мы получаем два разных ответа.Так что не забывайте следить за скобками! Не воспринимайте их важность как должное.
12. Следите за своим распределениемВот одна из самых распространенных ошибок в алгебре:
Проблема:
Развернуть (x + y) 2
Общее студенческое решение:
x 2 + y 2 => НЕПРАВИЛЬНО!
Если за пределами круглых скобок стоит показатель степени, а внутри скобок — вычитание или , ВЫ НЕ МОЖЕТЕ РАСПРЕДЕЛИТЬ ЭКСПОНЕНТ.
Действительно. Не делай этого.
Попробуйте подставить несколько цифр, чтобы убедиться в этом. Например:
(3 + 2) 2
Используя PEMDAS сверху, мы бы сначала добавили в скобках, чтобы получить:
5 2
Затем обработайте экспоненту, чтобы получить 5 × 5 = 25.
Но использование ошибочного метода даст нам 3 2 + 2 2 = 9 + 4 = 13, неправильный ответ.
Математически (x + y) 2 говорит: возьмите выражение (x + y) и умножьте его на себя, что требует использования метода FOIL.Когда вы это сделаете, вы получите x 2 + 2xy + y 2 , что не соответствует приведенному выше ответу.
13. Только коэффициенты отменыОтмена может быть трудной для понимания концепцией, но запомнить это поможет:
Можно только отменить множитель числителя множителем знаменателя, если они точно такие же.
Очень важной частью этого предложения является слово , фактор . Чтобы отменить условия, они должны быть коэффициентами .Член является множителем , если умножается на все в выражении.
Вот небольшой пример.
В этом примере множители числителя, которые также являются множителями знаменателя, равны 3x и (x — 1). Отмена их оставляет нам все, что осталось:
Прежде чем двигаться дальше, обратите внимание еще на одну вещь. В приведенном выше рациональном выражении мы видим, что и в числителе, и в знаменателе стоит x. Однако перед тем, как отменить их, запомните правило: отменить можно только факторы!
Здесь в числителе прибавляется к 3 (, а не умножается), а в знаменателе — до 2 (, а не умноженное).Таким образом, x не является фактором и поэтому не может быть отменен.
14. Не забывайте раздаватьЕще одна скорая вещь перед отъездом! Если перед скобками стоит x, внутри которых есть сложение или вычитание, то x необходимо умножить на КАЖДЫЙ член внутри скобок. Если впереди стоит отрицательный знак, его нужно распределить таким же образом!
Например:
Обладая всей этой информацией, вы готовы заняться алгеброй! Мы считаем, что если вы будете придерживаться этих советов, вы добьетесь больших успехов в этом классе.Главное, запомните: понимайте, а не запоминайте! А если вам нужна дополнительная помощь, наши репетиторы по алгебре Chegg всегда доступны 24/7!
Math Play: Как маленькие дети подходят к математике
Четырехлетняя Нита играет с четырьмя куклами из набора из шести. Проходя мимо, ее учитель спрашивает: «А где остальные?» Ее учитель слышит, как Нита говорит: «Эммм … [указывая на каждую куклу] Я называю тебя« одна ». Вы «два», «три» и «четыре». Где твои сестры, пять и шесть? » Еще минуту она играет с куклами.«О! Тебе шесть? А тебе пять? Ну, пойдем поищем сестер три и четыре». Я тоже должен их найти «.
Нита включила в игру счет, чтобы следить за своими куклами. Мы знаем, что игра важна для развития маленьких детей, поэтому неудивительно, что детская игра является источником их первого «предматематического» опыта.
Изучение математики в игре
Дети интенсивно увлекаются игрой. Преследуя свои собственные цели, они склонны решать проблемы, которые достаточно сложны, чтобы быть увлекательными, но все же не выходят за рамки их возможностей.Сохранение проблемы — разгадывание ее и различные подходы к ней — может привести к эффективному обучению; кроме того, когда несколько детей пытаются решить одну и ту же проблему, они часто придумывают разные подходы, обсуждают различные стратегии и учатся друг у друга . Эти аспекты игры могут способствовать мышлению и обучению как по математике, так и в других областях.
Маленькие дети исследуют узоры и формы, сравнивают размеры и считают. Но как часто они это делают? А что это значит для развития детей? Когда дети изучали детей во время свободной игры, возникло шесть категорий содержания математики.
1. Классификация. Одна девушка, Анна, вынула из контейнера все пластиковые жучки и отсортировала их по типу жуков, а затем по цвету.
2. Изучение звездной величины (описание и сравнение размеров объектов). Когда Брианна принесла газету к столу для художников, чтобы накрыть ее, Эми заметила: «Она недостаточно велика, чтобы накрыть стол».
3. Перечисление (произнесение числовых слов, подсчет, мгновенное распознавание ряда объектов или чтение или запись чисел).Три девочки нарисовали свои семьи и обсудили, сколько у них братьев и сестер и сколько лет их братьям и сестрам.
4. Исследование динамики (складывание, разборка или изучение движений, таких как переворачивание). Несколько девушек превратили глиняный шар в диск, разрезали его и сделали «пиццу».
5. Изучение узора и формы (определение или создание узоров или форм или изучение геометрических свойств). Дженни сделала бусы, создав узор желто-красного цвета.
6. Исследование пространственных отношений (описание или рисование местоположения или направления). Когда Тереза поставила диван в кукольном домике у окна, Кэти переместила его в центр гостиной, сказав: «Диван должен быть перед телевизором».
Диапазон математических исследований, изучаемых во время свободной игры, впечатляет. Мы видим, что бесплатная игра предлагает богатую основу для построения интересной математики. Эти повседневные опыты составляют основу более поздней математики.Позже дети развивают эти идеи. Мы называем этот процесс «математизацией». И мы понимаем, что детям нужны как базовые знания, так и конкретные математические задания.
Play не гарантирует математического развития, но предлагает богатые возможности. Значительные преимущества более вероятны, когда учителя продолжат обучение, вовлекая детей в размышление и представление математических идей, возникших в их игре. Учителя улучшают обучение детей математике, когда они задают вопросы, которые вызывают уточнения, расширения и развитие нового понимания.
Математические блоки: башни обучения
Преимущества блочного строительства глубоки и широки. Строя из кубиков, дети улучшают свои математические, естественные и общие способности к рассуждению. Рассмотрим, как развивается блочное строительство.
Младенцы не проявляют особого интереса к штабелированию. Укладка начинается в 1 год, когда младенцы показывают свое понимание пространственных отношений «на». Отношения «ближайшего окружения» развиваются примерно через полтора года. В 2 года дети ставят каждый следующий кубик на предыдущий или рядом с ним.Похоже, они понимают, что блоки не падают при таком размещении. Дети начинают размышлять и предвкушать. В возрасте от 3 до 4 лет дети регулярно строят вертикальные и горизонтальные элементы здания. Когда их просят построить высокую башню, они используют длинные блоки вертикально, потому что, помимо стремления сделать стабильную башню, их цель — сделать стабильную высокую башню, сначала используя только один блок таким образом, а затем несколько. Через 4 года они могут использовать множественные пространственные отношения, расширяя свои здания в разных направлениях и с множеством точек соприкосновения между блоками, демонстрируя гибкость в том, как они строят и интегрируют части конструкции.
Дошкольники используют, по крайней мере на интуитивном уровне, более сложные геометрические концепции, чем большинство детей испытывают в начальной школе, играя в блоки. Например, один дошкольник, Хосе, кладет двойной блок на ковер, два блока — на блок из двух блоков и треугольник — в середину, создавая симметричную структуру.
Представьте дошкольника, который строит нижний этаж блочного дома. Он кладет вниз два длинных блока, идущих в одном направлении.Затем он пытается соединить два конца коротким блоком. Он не достигает, поэтому он перемещает конец одного из длинных блоков, чтобы он достиг. Однако, прежде чем он снова попробует короткий блок, он осторожно регулирует другой конец длинного блока. Он пробует короткий блок. Он тянется. Он быстро ставит много коротких блоков, образуя пол своего дома.
Мы многому научились из этого и других подобных эпизодов. Как и этот маленький мальчик, многие дети интуитивно используют понятия параллельности и перпендикулярности.Мальчик даже, кажется, понимает в своих действиях, что параллельные линии всегда находятся на одинаковом расстоянии друг от друга!
Мы наблюдали, как другие дети регулируют два цилиндра так, чтобы расстояние между ними было равно длине длинного блока. Они оценивают, сколько еще блоков им нужно, чтобы отделать поверхность. По их оценкам, потребовалось восемь блоков, если каждый квадрат четырех размеров был покрыт двумя блоками. Мы знаем многих учителей математики, которые были бы в восторге, если бы их ученики продемонстрировали такое же понимание геометрии, измерений и чисел!
Ритм и паттерны
Дошкольники также занимаются ритмическими и музыкальными паттернами.Они могут добавлять в свой репертуар более сложные, продуманные паттерны, такие как «хлопок, хлопок, пощечина; хлопок, хлопок, пощечина». Они могут говорить об этих узорах, изображая узор словами. Воспитанникам детского сада нравится придумывать новые движения, соответствующие той же схеме, поэтому хлопки, хлопки в ладоши превращаются в прыжки, прыжки, падения; прыгать, прыгать, падать и вскоре символизируется шаблоном AABAAB. Воспитанники детского сада также могут описывать такие узоры цифрами («два чего-то, потом один чего-то другого»). На самом деле это первые четкие связи между шаблонами, числами и алгеброй.
Дети, которые испытали эти ритмические переживания, намеренно воссоздают и обсуждают шаблоны в своих произведениях искусства. Один четырехлетний ребенок любил знать цвета радуги (ROY G BFV, красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый) и рисовал радуги, цветы и рисунки, повторяющие эту последовательность несколько раз.
Математика течет сквозь воду Играть
Измерение часто лежит в основе игры в воде или на песчаном столе. Исследователь рассказывает о посещении двух классных комнат в один день и наблюдении за игрой в воде в обоих.Дети наливали воду в каждую комнату, но в одной они также взволнованно наполняли одну и ту же чашку в разные емкости, считая, сколько чашек они могли «уместить» в каждую емкость. Единственная разница между этими двумя классами заключалась в том, что в последнем учитель прошел мимо и небрежно спросил: «Интересно, в каком из них больше всего чашек воды?»
Развертывание математических концепций!
Такие материалы, как песок и пластилин, открывают множество возможностей для математического мышления и рассуждений.Учителя могут предоставить полезные материалы (формочки для печенья), параллельно играть с детьми и задавать вопросы или комментарии относительно форм и количества предметов. Например, они могут сделать несколько копий одной и той же формы в пластилине с помощью форм для лепки или превратить песок или пластилин в разные объекты. Одна учительница сказала двум мальчикам, что собирается «спрятать» шар пластилина, накрыв его плоским предметом и надавив. Мальчики сказали, что мяч все еще был на месте, но когда она подняла его, мяч «исчез».«Это их обрадовало, они скопировали ее действия и обсудили, что мяч находится« в »плоской части.
Математика и манипуляции
Детские игры с манипуляторами, в том числе комбинирование «плоских» блоков для создания картинок и рисунков, а также для решения головоломок, показывают прогресс в развитии, как и построение блоков. Дети сначала не умеют сочетать формы. Они постепенно учатся видеть как отдельные части, так и «целое», и узнают, что части могут составлять целое и при этом оставаться частями.Примерно к 4 годам большинство может решать головоломки методом проб и ошибок и создавать картинки с фигурами, расположенными рядом друг с другом. С опытом они постепенно учатся комбинировать формы, чтобы создавать более крупные формы. Они становятся все более преднамеренными, выстраивая мысленные образы форм и их атрибутов, таких как длина сторон и углы.
Создание концепций с помощью компьютеров
Создание рисунков с фигурами можно выполнять как с помощью строительных блоков, так и с помощью компьютерных фигур. Компьютерные версии имеют то преимущество, что они дают немедленную обратную связь.Например, фигуры могут быть прозрачными, чтобы дети могли видеть загадку под ними. Кроме того, дети часто больше говорят и больше объясняют то, что они делают на компьютере, чем при использовании других материалов. На более высоких уровнях компьютеры позволяют детям разбивать и складывать фигуры способами, которые невозможны с физическими блоками.
Компьютеры также могут облегчить игру. Добавление компьютерного центра не нарушает текущую игру, но облегчает позитивное социальное взаимодействие и сотрудничество.Исследования показывают, что компьютерная деятельность более эффективна в стимулировании вокализации, чем игра с игрушками, а также стимулирует более высокий уровень социальной игры. Кроме того, совместная игра за компьютером аналогична совместной игре в центре блока. Сотрудничество в компьютерном центре может обеспечить контекст для инициирования и поддержания взаимодействия, которое может быть передано и для игры в других областях, особенно для мальчиков.
Драматическая математика
Драматическая игра может быть естественно математической при правильной настройке.В одном исследовании учителя и дети организовали магазин в зоне драматических игр, где продавец заполняет заказы и просит у покупателя деньги (1 доллар за каждую игрушку динозавра).
В одном классе Габи работала продавцом. Тамика вручила ей пять карточек (5 точек и цифра «5») в качестве ее приказа. Габи отсчитала пять игрушечных динозавров.
Учитель (только входящий в зону): Сколько вы купили?
Тамика: Пять.
Учитель: Откуда ты знаешь?
Тамика: Потому что Габи считала.(Тамика все еще работала над своими навыками счета и доверяла счету Габи больше, чем ее собственному знанию пяти. Игра позволила ей развить свои знания.)
Жанель: Я получаю большой номер. (Она протянула Габи карты 2 и 5.)
Габи: У меня не так много.
Учитель: Вы можете дать Жанель 2 одного вида и 5 другого.
Пока Габи отсчитывала две отдельные стопки и складывала их в корзину, Джанель отсчитывала доллары.Она неправильно посчитала и дала ей 6 долларов.
Габи: Вам нужно 7 долларов.
Эта постановка драматической игры с помощью учителя «работала» для детей с разным уровнем математического мышления.
Играйте перед решением проблем
Мы видели, как различные виды игр улучшают математическое мышление детей. Исследования также показывают, что если дети играют с объектами до того, как их попросят решить с ними проблемы, они добиваются большего успеха и творчески.Например, в одном исследовании с тремя группами детей от 3 до 5 лет их попросили достать предмет с помощью коротких палок и соединителей. Одной группе разрешили поиграть с палками и соединительными устройствами, одну группу научили, как соединять палки, а одной группе было предложено выполнить задание без предварительной игры или обучения. Первые две группы показали одинаковые результаты и достигли лучших результатов, чем третья группа. Часто группа, которая просто играла с клюшками и соединителями, сначала решала проблему быстрее, чем группа, которую учили их использовать.
Математическая игра
Это подводит нас к последнему увлекательному и обычно упускаемому из виду типу игры: математической игре. Здесь мы не имеем в виду игру, включающую математику — мы говорили об этом на протяжении всей статьи. Мы имеем в виду игру с самой математикой.
Подумайте еще раз о Ните и ее куклах. Когда она назвала их, чтобы идентифицировать «сестер», с которыми она не играла, она использовала математику в своей игре. Но когда она решила переименовать куклы, которые были с ней, с «пять» и «шесть» на «три» и «четыре», она играла с представлением о том, что присвоение номеров коллекции объектов произвольно.Она также считала не только куклы, но и сами счетные слова. Она сосчитала слова «три, четыре» и увидела, что две сестры пропали без вести. Она играла с идеей, что подсчет слов можно считать.
Динамические аспекты компьютеров часто вовлекают детей в математические игры больше, чем физические манипуляции или бумажные материалы. Например, два дошкольника играли с заданиями под названием «Время вечеринки» из проекта «Строительные блоки», в котором они могли выставить любое количество предметов, а компьютер их подсчитывал и маркировал.»У меня есть идея!» — сказала одна девушка, убирая все предметы и перетаскивая салфетки на каждый стул. «Вы должны поставить чашки для всех. Но сначала вы должны сказать мне, сколько чашек это будет». Прежде чем ее подруга начала считать, она прервала его: «И всем нужна одна чашка молока и одна чашка сока!» Девочки сначала усердно работали вместе, пытаясь найти чашки в центре драматургии, но, наконец, сосчитали по два раза на каждой подставке для столовых приборов на экране. Их ответ — изначально 19 — не был точным, но они не расстроились, что их исправили, когда они на самом деле поставили чашки и обнаружили, что им нужно 20.Эти дети играли с математикой в ситуации, с решениями, играя вместе друг с другом.
Математика может быть интересна детям по своей сути, если они строят идеи во время математической игры.
Развитие математики в повседневной игре
Учителя поддерживают математику в игре, создавая благоприятную среду и надлежащим образом вмешиваясь. Вот что вы можете сделать:
Понаблюдайте за детской игрой. Если вы не видели много новых блочных конструкций, поделитесь книгами, иллюстрирующими различное расположение блоков, или разместите изображения в центре блока.Когда вы видите, как дети сравнивают размеры, предлагайте разные предметы, которые дети могут использовать для измерения своих структур, от кубиков до ниток и линейок.
Вступайте чутко. Полезная стратегия — спросить, развиваются ли социальное взаимодействие и математическое мышление или застопорились. Если они развиваются, просто понаблюдайте и оставьте детей в покое. Позже обсудите этот опыт со всем классом.
Обсудить и уточнить идеи. Каждый из детей может утверждать, что их блочное здание больше.Вы можете видеть, что один ребенок говорит о высоте, а другой — о ширине. Вы можете по-разному прокомментировать, как вы видите здания такими большими, как в примере «У вас очень высокое здание, а здание Криса кажется очень широким».
Запланируйте длинные отрезки времени для игры. Обеспечьте улучшенную среду и материалы, в том числе структурированные материалы, такие как блоки и лего, которые побуждают к математическому мышлению.
Маленькие дети активно используют математическое мышление и рассуждения в своей игре, особенно если они обладают достаточными знаниями об используемых материалах, если задача понятна и мотивирует, а контекст знаком и удобен.Математику можно легко интегрировать в текущие игры и действия детей, но для этого требуется знающий учитель, который создает благоприятную среду и предлагает соответствующие задачи, предложения, задания и язык. В классах, где учителя внимательны ко всем этим возможностям, детские игры обогащают математические исследования.
Ресурсы для учителей: веб-сайты
Самая важная роль учителей в отношении математики должна заключаться в нахождении частых возможностей помочь детям осмыслить и расширить математику, возникающую в их повседневной деятельности, беседах и играх, а также создать среду, поддерживающую такую деятельность.
1. Из NAEYC, статья, показывающая, как можно разрабатывать математические игры на основе детской литературы. NAEYC также предлагает «Математика для детей младшего возраста: содействие хорошему началу», совместное заявление Национальной ассоциации по образованию детей младшего возраста (NAEYC) и Национального совета учителей математики (NCTM).
2. Из Building Blocks (Национальный научный фонд), идеи по поиску математики и развитию математики с помощью детских занятий.
3. Национальный совет учителей математики (NCTM) предлагает математические стандарты, Принципы и стандарты школьной математики, а также множество мероприятий, программные среды на базе Интернета и видеоролики. «Teachers Corner» NCTM предоставляет информацию о возможностях профессионального развития, ресурсах и многом другом.
4. Центр развития учителей «Математические перспективы» предоставляет преподавателям математики от PreK до 6-го класса инструменты, стратегии и оценки, которые гарантируют, что все учащиеся добьются успеха в изучении математики и смогут использовать математику для решения задач, а также математического мышления .
12 практик для улучшения умственной математики + загружаемый список
Психическая математика не входит в явную часть большинства учебных программ, но учеников, которые не могут быстро или автоматически решать относительно простые уравнения в своей голове, скорее всего, будут бороться с более сложным содержанием. Но прежде чем ответить на вопрос: «Как я могу улучшить свою умственную математику?», Полезно знать определение (определения) умственной математики. Что такое ментальная математика? Ассоциация учителей математики Манитобы определяет ментальную математику как:Комбинация когнитивных стратегий, которая улучшает гибкое мышление и чувство чисел.Он производит мысленные вычисления без использования внешних запоминающих устройств. Он улучшает скорость вычислений за счет повышения эффективности, точности и гибкости.Или, с точки зрения учащихся, это:
- Математика, сделанная в вашей голове
- Математика, которая выполняется в уме, быстро и эффективно
- Разогревает голову математикой
- Чтобы делать математику мгновенно, без вложенных усилий операций и процессов
- Математика, которую вы понимаете настолько хорошо, что вам не нужно ничего записывать, чтобы делать вычисления / находить ответ
[Существует] значительная положительная корреляция между мысленными вычислениями и математическими рассуждениями. Примечательно, что вместо того, чтобы подвергать учащихся знакомым классическим задачам, учащиеся должны иметь возможность решать исключительные / нестандартные проблемы, и особенно маленьких детей следует поощрять к умственному вычислению для развития обоих навыков.Исследователи Duke опубликовали в журнале Clinical Psychological Science исследование о ментальной математике — с точки зрения здоровья.После сканирования мозга 186 студентов, результаты показали, что вовлечение префронтальной коры головного мозга во время мысленных математических упражнений связано с улучшением эмоционального здоровья. К счастью, вы уже помогаете студентам развить основные умственные математические навыки, когда учите округлять, оценивать и беглость фактов — развивая чувство числа, а также то, как они запоминают и воспроизводят шаги и решения.
Пора практиковаться в ментальной математике!
Чтобы улучшить то, как ваши ученики развивают и практикуют эти умственные математические навыки, попробуйте следующие 12 стратегий. Используйте те, которые лучше всего подходят для вас, и держите загружаемый список у себя на столе для быстрой справки. 1. Представьте мнемонические устройства Учащиеся, которые борются с беглостью базовых фактов, могут улучшить свои навыки, используя мнемонические приемы — такие подсказки, как рифмы и сокращения, чтобы помочь вспомнить информацию. В ее магистерской диссертации Обучение с помощью мнемоники в элементарных Школьные классы , Арианна Уэйт-Макгоф обнаружила, что учителя понимают положительное влияние, которое это устройство может оказать на учащихся в классной комнате и «за ее пределами».Текущее исследование показывает, что пение, движение и общее удовольствие от предмета улучшают процесс обучения и долгосрочное запоминание материала. Все эти требования присутствуют при использовании мнемоники в классе. Мои исследования подтвердили аналогичные результаты. Все учителя, которых я опрашивал, отметили более высокий уровень обучения, вовлеченности и веселья во время пения песен на основе основного материала.Возьмите этот мнемонический прием для умножения в качестве примера: Мне должно быть 16 лет, чтобы водить пикап с колесной формулой 4×4. Поскольку их должно быть легко запоминать, полезно, если в них задействованы:
- Рифмы
- Материальные объекты или сценарии
- Быстрые истории, извлекающие большие объемы информации
- У каждого апельсина было 8 ломтиков — В этой книге основное внимание уделяется счету и сложению, излагая задачи в простых для обработки предложениях. Он устанавливает новую сцену, полную вопросов, с каждым поворотом страницы.
- Виноград математики — Эта книга, содержащая основные задачи умножения, представляет собой серию иллюстрированных загадок.Каждая загадка предлагает подсказки и секреты решения определенного уравнения, помогая учащимся улучшить понимание прочитанного наряду с математическими навыками.
- Sir Cumference — Эта серия книг, созданная во времена средневековья, посвящена измерениям и геометрии. С помощью своего сына и жены, Радиуса и леди Ди из Аматера, рыцарь сэр Кумферент должен решать математические задачи, которые представляют угрозу для его семьи и королевства.
- Секреты ментальной математики — В отличие от детской книги, это руководство обещает «заставить вас думать как математический гений в кратчайшие сроки» с помощью «математика» Артура Бенджамина.Поскольку в нем более 200 страниц, вы можете добиться большего успеха в выборе ключевых отрывков и чтении — и применении — уловок в уме с учащимися. Есть также предисловие Билла Ная, ученого парня!
Само преподавание абстрактной теории демотивирует. Актуальность может быть установлена посредством: демонстрации того, как теория может быть применена на практике, установления релевантности к местным случаям, соотнесения материала с повседневными приложениями или поиска приложений в актуальных проблемах, заслуживающих освещения в печати.Другими словами, если учащиеся не сочтут ваш урок математикой релевантным, их мотивация к обучению значительно снизится. Простой, но эффективный способ оживить содержание — это придумывать математические задачи со словами. Это потому, что вы можете адаптировать вопросы к ученикам. Например, вы можете:
- Задайте актуальные вопросы — Задачи со словами, основанные на текущих событиях или проблемах, могут заинтересовать учащихся, предоставляя четкие, осязаемые способы применения знаний. Студенты не только найдут ваши уроки более интересными, но и сочтут, что об этом стоит знать.
- Включите имена учащихся — Назовите символы вопроса в честь учащихся — это простой способ сделать его более понятным, мотивируя класс к решению проблемы.
S найдите слово «проблема» T преобразовать слова в уравнение A Ответить на проблему R Ознакомьтесь с решением
4.Играйте в оценочные игры в классе Оценочные игры — это увлекательные математические упражнения, которые побуждают учащихся развивать навыки и методы, которые они могут использовать для упрощения уравнений в уме. В популярной во многих классах оценочной игре, которую легко запустить, но сложно играть, нужно всего два кубика и лист бумаги, разделенный на две колонки. В одном столбце перечислены значения на каждой грани игральных костей, а в другом — числа по вашему выбору. Например:| Сторона игральной кости | Число |
| 1 | 189 |
| 2 | 345 |
| 5 | 878 |
| 6 | 777 |
- Math Facts Bingo — Создавайте карточки бинго, которые содержат ответы на различные уравнения. Затем раздайте их студентам. Вместо того, чтобы набирать числа, укажите уравнения типа 8 x 7.Определив, что продукт — 56, они могут отметить число, указанное на их карточках.
- Вставай, садись — Выберите число и поделитесь им со студентами. Затем прочитайте уравнения вслух. Сидя в круге, ученики должны встать, если ответ совпадает с выбранным вами числом. Если они неправильно встают или остаются на своих местах, устраняйте их, пока не останется один ученик.
- 101 и аут — Как следует из названия, цель состоит в том, чтобы набрать как можно ближе к 101 очку, не превышая его.Начните с разделения класса на группы, дайте каждой кубик, бумагу и карандаш. Группы по очереди бросают кубик, решая, лучше ли посчитать число по номиналу или умножить его на 10. После каждого броска число добавляется к общей сумме группы. Игра заканчивается, когда группа набирает 101 очко или выходит из игры — в зависимости от того, что наступит раньше.
- Prodigy Game — Бесплатная и согласованная с учебными планами англоязычного мира, Prodigy автоматически дифференцирует контент и дает адаптивную обратную связь для каждого ученика.Учителя также могут выполнять внутриигровые задания по доставке нестандартного контента, что делает его любимым более чем миллиона преподавателей.
- NRICH — На этом веб-сайте, осуществляемом в рамках текущего проекта Кембриджского университета, представлены математические игры, статьи и задачи. Ресурсы делятся по ключевым этапам в Соединенном Королевстве и уровням обучения в США, что позволяет учащимся легко получить доступ к нужному контенту.
- Математика — это развлечение — Этот веб-сайт содержит контент, подходящий для младших школьников, с использованием кратких предложений и персонажей мультфильмов.Помимо упражнений, охватывающих основные математические навыки, есть игры и головоломки.
- 33 x 48
- 66 x 24
- 132 x 12
- 264 x 6
- 528 x 3
- 1,584
- Создание информационного бюллетеня по математике — Разделите лист на два столбца и запишите в левый столбец около 10 математических фактов, относящихся к одному и тому же навыку. Включите числовые предложения и ответы. В правом столбце напишите «Ответы.Раздайте студентам копии листов.
- Выполнение упражнения — Цель для учащихся — изучить математические факты в левом столбце, правильно воспроизведя их в столбце «Ответы». Для этого дайте им время изучить факты. Затем они складывают бумагу, чтобы закрыть левую колонку, записывая — по памяти — первый факт в колонке «Ответы». Если все правильно, студент может перейти к следующему факту. В случае ошибки ученик пытается снова, пока не воспроизведет математический факт должным образом.
- Запись освоенных навыков — После того, как учащийся заполнил определенное количество листов, относящихся к общему навыку, вы можете наградить его или ее значком, обозначающим овладение навыками. Эта стратегия геймификации может сделать упражнение более увлекательным.
Студенты с более высокими показателями PSAT по математике задействовали части мозга, левую надмаргинальную извилину и двустороннюю переднюю поясную извилину, которые были связаны с арифметическим извлечением фактов.Напротив, студенты с более низкими показателями PSAT по математике задействовали правую интрапариетальную борозду, область, связанную с обработкой числовых величин. Таким образом, при выполнении теста в сканере учеников с более высокими баллами PSAT по математике больше полагались на свою память об арифметических фактах .12. Number talk Рут Паркер, генеральный директор организации Mathematics Education Collaborative, и Кэти Ричардсон, одна из ведущих национальных преподавателей элементарной математики, разработали эту ментальную математическую практику.Для начала поставьте абстрактную математическую задачу. Возьмите пример задачи 18 x 5 и попросите своих учеников попытаться решить ее в уме. Естественно, в классе из 20+ учеников вы, вероятно, обнаружите, что они ответили правильно, но по-другому.
| Пять способов решения 18 x 5 | ||||
| 20 x 5 = 1002 x 5 = 10100 — 10 = 90 | 10 x 5 = 508 x 5 = 4050 + 40 = 90 | 18 x 5 = 9 x 109 x 10 = 90 | 18 x 2 = 362 x 36 = 7218 + 72 = 90 | 9 x 5 = 4545 x 2 = 90 |
Исследования говорят нам, что лучшие классы математики — это те, в которых студенты изучают числовые факты и чувство чисел посредством увлекательных занятий, которые сосредоточены на математическом понимании, а не на механическом запоминании.Итак, мы надеемся, что эти упражнения помогут вашим ученикам практиковать мысленную математику в этом учебном году и в дальнейшем. Загружаемый список практик мысленной математики Щелкните здесь , чтобы загрузить и распечатать упрощенный список из 12 практик мысленной математики, который будет всегда у вас на столе. Готовы поделиться этими математическими секретами в уме? Ладно, это не совсем секреты. Но использование этих методов мысленной математики должно помочь вашим ученикам развить навыки округления, оценки и владения фактами, что позволит им легко и автоматически решать многие уравнения, подготовив их к работе с более сложным содержанием.Вооружившись повышенной уверенностью, вы можете заметить рост вовлеченности и мотивации студентов. Эти преимущества сами по себе являются убедительным аргументом в пользу практики мысленной математики.
>> Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной платформе, которая помогает учащимся развивать умственные математические навыки, практикуясь в увлекательной игровой среде обучения. Он соответствует учебным планам англоязычных стран, его любят более миллиона учителей и 50 миллионов студентов.
Чем можно заниматься со степенью математика?
Что такое математика?
В системах образования по всему миру, от начальных до высших учебных заведений, существует один постоянный предмет, язык, на котором говорят во всем мире: математика.
Основное определение математики (или математики, или математики, в зависимости от того, в какой части мира вы находитесь) состоит в том, что это образование в области числовых наук с использованием ряда различных подходов, включая алгебру, исчисление и базовую арифметику.В то время как математика является ключевым элементом различных предметов, от экономики до физики, математика как университетский предмет часто фокусируется на понимании и проверке теорий в математическом и научном дискурсе или так называемой «чистой математике».
Математики могут как прийти к пониманию строительных блоков Вселенной в таких областях, как квантовая механика, так и получить образование в увлекательных теоремах и абстрактных концепциях, которые обучают студентов ряду применимых навыков, которые можно передавать другим профессионалам. поля.
Лучшие университеты мира по физике, химии и математике
Лучшие университеты по физике, химии и математике в Канаде
Что вы изучаете по математике?
В рамках математической степени студент может рассчитывать найти более высокий уровень контактных часов в первый год обучения, поскольку преподаватели работают со студентами, чтобы обеспечить понимание основных модулей и концепций, обсуждаемых на лекциях и семинарах.
Типичный курс для первого курса бакалавриата представляет собой введение в абстрактную алгебру, а также в такие области, как нелинейные дифференциальные уравнения. В более поздние годы обучения на степень будет больше свободы, поскольку студенты будут выбирать из более широкого набора модулей и более глубоко изучать области математики, которые им нравятся.
Математические степени все больше основываются на цифровых технологиях, связанных с информатикой через такие модули, как символьные вычисления и автоматическое доказательство теорем.
Математика также является идеальным предметом для совместных занятий с отличием, поскольку ее преподавание может стать основой для изучения информатики, инженерии и статистики среди других. Для курса бакалавриата типичная продолжительность курса составляет три года, хотя в образовательных системах, таких как Соединенные Штаты, это может быть четыре года, или если курс включает год обучения за границей или стажировку по сэндвич-работе.
Что мне нужно изучать, если я хочу изучать математику?
Математика не является предметом, в который можно просто попасть, и будет преподаваться при условии, что учащиеся будут иметь конкретное понимание основных понятий математики и прикладной математики до начала курса.
Университеты обычно принимают студентов, хорошо успевших по математике в школе и получивших дальнейшее образование перед подачей заявления. Университеты будут проверять способности по смежным школьным предметам, таким как традиционные науки (например, химия).
Также важно не упускать из виду языковые навыки и навыки письма, так как многие курсы будут включать в себя длительные задания на сочинение.
Другие тематические руководства
Чем можно заниматься со степенью искусства?
Что можно сделать со степенью архитектора?
Чем можно заниматься со степенью ветеринарной науки?
Что можно делать со степенью биологии?
Что вы можете делать со степенью в области спорта?
Что вы можете делать со степенью врача?
Что можно сделать со степенью дизайнера?
Что вы можете делать со степенью исполнительского искусства?
Чем можно заниматься со степенью в сфере бизнеса?
Чем занимаются люди, изучающие математику после выпуска?
В то время как выпускник математики может посвятить свою карьеру изучению и обучению других теоретическим математическим знаниям, квалификация по этому предмету также может открыть двери в широкий спектр профессиональных областей.
Работодатели ценят навыки анализа данных и новаторское, оригинальное мышление, которому можно научить на математике. Выпускники математики идеально подходят для работы в финансовом секторе, например, на должности инвестиционного аналитика или налогового консультанта.
На такой должности, как актуарий или дипломированный бухгалтер, степень по математике — это только первый шаг, поскольку для получения квалификации по этим профессиям требуются годы дальнейшего обучения и экзаменов.
Математика также является предметом, тесно связанным со статистическим анализом.Это открывает возможности для трудоустройства в социальных исследованиях, таких как сбор данных опросов и опросов, а также в научных исследованиях в таких областях, как география и медицинская статистика. Хотя эта работа может быть источником постоянной занятости после получения степени бакалавра, многие институты также предлагают постдокторские должности в качестве научного сотрудника или эквивалентного сотрудника.
Существует также четкий путь от навыков работы на компьютере, полученных на математике, до карьеры, основанной на ИТ или разработке программного обеспечения.Многие программисты видеоигр имеют математическое образование, сочетая творческий подход с техническими способностями для разработки продуктов в одной из самых быстрорастущих отраслей сегодня. Агентства безопасности также будут нанимать команду обученных математиков, которые будут использовать одни из самых мощных компьютеров в мире для разработки криптографии и интернет-безопасности.
Студенческий опыт изучения математики
Калифорнийский технологический институт: «уникально трудное, но прекрасное место для учебы»
Меньше — не значит меньше возможностей
Известные люди, изучавшие математику
Среди самых известных людей, когда-либо получивших математическую степень, является Альберт Эйнштейн, который в возрасте 17 лет уже учился по программе преподавания математики в Цюрихском политехническом институте.
Среди многих других выдающихся пионеров математики — Эмми Нётер, которая изучила этот предмет в Университете Эрлангена и внесла плодотворный вклад в физику и абстрактную алгебру.
Диплом по математике также может стать трамплином к предпринимательскому успеху, например, Сергей Брин, который учился в Университете Мэриленда, прежде чем стал соучредителем Google, и Рид Хастингс, соучредитель Netflix, имеющий степень бакалавра математики в Стэнфордском университете.
Среди других известных математиков модель Синди Кроуфорд, которая изучала этот предмет в Северо-Западном университете, а также бывший профессиональный рестлер и звезда команды The A Team, Mr.T, получил специальность по этому предмету в университете Prairie View A&M.
Подробнее: Лучшие университеты по физике, химии и математике
Снова в школу по математике, чтобы познакомиться со своими математиками
Большинство занятий по знакомству с вами в школе вращаются вокруг интересов и увлечений учащихся, их семей и культур, а также того, какие книги они читают за лето. Хотя эти задания — отличный способ узнать все о вашей новой группе студентов, не забудьте выделить время, чтобы познакомиться со своей новой группой студентов как математиков.
Задания по математике, которые я выполняю со своими учениками в течение первой недели школы, специально разработаны, чтобы помочь мне познакомиться с моими учениками как математиками. Это термин, который я использую со своими учениками в течение всего года. Так же, как я называю студентов читателями и писателями во время семинаров по чтению и письму, я называю их математиками во время занятий математикой. Это задает тон, что все ученики — математики и что во время обучения математике мы усердно работаем как математики.
Следующие ниже упражнения по математике — отличный способ с первого дня научить учеников глубоко погрузиться в математические задания и критическое мышление.Ваши ученики не только начнут учебный год с любовью ко всему, что связано с математикой, но и вы получите ценную информацию о том, как ваши ученики относятся к математике, столкнутся с трудными задачами по решению проблем, а также будут работать и обсуждать математику со своими сверстниками.
Эти задания проведут вас в течение первой недели в школе и дольше, если вы решите углубиться в каждую идею урока. БЕСПЛАТНЫЕ упражнения по решению математических задач и другие математические полезности внизу этого поста.
Давайте поговорим о математике
Нет лучшего способа узнать мысли и чувства ваших новых учеников о математике, чем поговорить о математике! Мне нравится использовать стартовые карточки для обсуждения математики, чтобы задавать вопросы по математике, чтобы мои дети рассказывали о своем математическом прошлом, о том, что они думают о решении задач, и о работе с партнерами во время урока математики.Ответы, которыми делятся ученики, содержат ценную информацию о них как об учениках-математиках.
После обсуждения в классе математики я предлагаю студентам работать самостоятельно, чтобы заполнить математический инвентарь. Это дает студентам возможность рассказать мне, что они думают о математике в частной обстановке. Я собираю их и храню в своих файлах. Я люблю повторять это упражнение в середине года, чтобы увидеть, изменились ли их представления о математике.
После того, как мы закончили обсуждение математики и инвентаризации, у меня есть ученики, которые выполнили достижимые математические цели, которых они хотели бы достичь.Я действительно использую метод постановки целей SMART, который, как я считаю, является отличным способом помочь студентам ставить цели, достигать их, а затем снова ставить новые цели.
Мы математики
Воспользуйтесь этим простым, но очень увлекательным заданием, чтобы ваши ученики привыкли к тому, что вы называете их математиками. Для начала вместе со своими учениками создайте якорную диаграмму о том, что делают хорошие математики. Поощряйте студентов делиться стратегиями и инструментами, которые необходимы при решении математических задач.Продемонстрируйте свою диаграмму привязки в классе и сделайте копии своего списка, чтобы учащиеся могли хранить их в своих тетрадях или папках по математике.
После того, как ваш список будет составлен, попросите учащихся создать красочную иллюстрацию себя как математиков. Где бы они работали? Какие инструменты они использовали бы? Будут ли они одни? Попросите учащихся обозначить свои иллюстрации, чтобы показать все, что они используют.
Мне особенно нравится это занятие, потому что работа, которую выполняют ученики, очаровательно вешается на доску объявлений или на дверь класса! Они всегда являются большим хитом для Meet the Teacher Night.
Прочтите книжку с картинками по математике
(или две) Каждый день идеально подходит для чтения книги, но эти первые две недели в школе часто заполнены потрясающими книжками с картинками! Почему бы не найти время, чтобы прочитать несколько удивительных математических книжек с картинками , чтобы вовлечь студентов в содержательную беседу о решении проблем, настойчивости и совершении ошибок. Вот три книжки с картинками по математике, которые я обязательно прочитаю в течение первых нескольких недель в школе.Мышление роста
Если вы преподаете математику, вы не можете начать учебный год, не углубившись в концепцию установки на рост вместе со своими учениками.Мне нравится показывать цитаты с установкой на рост и алфавитные таблицы в моем классе и использовать утреннее время для обсуждения концепции установки на рост, чтобы побудить учеников проявлять настойчивость и стойкость, особенно когда они сталкиваются со сложными математическими задачами.Но с годами я обнаружил, что нужно гораздо больше, чем просто повесить положительную цитату.
Проводя формальные уроки, читая книжки с картинками и просматривая видео о установке на рост, учащиеся гораздо лучше поймут концепцию установки на рост и быстро начнут применять некоторые стратегии установки на рост, которым я их научил. Вот почему я выделяю время в течение первой недели в школе, чтобы начать уроки установки на рост. Их можно легко вплести в первые десять минут уроков математики в начале года.
Решение проблем
Я люблю ставить ученикам задачи по решению проблем в течение первой недели учебы. Хотя я действительно считаю, что понимание основных математических навыков учащихся важно, мне нравится видеть, как они справляются с более сложными задачами.
Любая задача, состоящая из нескольких этапов решения проблем, в которой используются навыки предыдущего года, будет работать как неформальная оценка способностей учащихся.Дайте студентам один урок, чтобы завершить его, процесс важнее конечного продукта. Во время работы наблюдайте за их поведением и диалогом со студентами, задавая им вопросы о шагах и стратегиях, которые они используют для решения проблемы.
Собирайте работы студентов и сохраняйте их в качестве контрольных мероприятий, даже если учащиеся еще не закончили. Это отличная отправная точка, с которой можно будет сравнивать будущие оценки по ходу года. Он также показывает, что студенты могут выполнить за один урок.
Сыграть в математическую игру
Нет лучшего способа заставить детей полюбить математику, чем поиграть в математические игры. Мне нравится использовать математические игры в классе, чтобы помочь ученикам участвовать в содержательном обсуждении математики и делиться своим математическим мышлением со сверстниками. Игра в математические игры также заставляет учащихся отвечать за свою работу и сосредотачиваться на поставленной задаче.Эта БЕСПЛАТНАЯ математическая игра даст вам ценную информацию о том, как ваши ученики подходят как к вопросам навыков, так и к вопросам решения проблем.Если вам нужны более подробные игры или школьные тематические мероприятия, я могу поиграть в эти игры со студентами в течение первых нескольких недель в школе:
Сезон «Снова в школу» — это все о том, чтобы познакомиться с вашей новой группой учеников! Удостоверьтесь, что вы нашли время, чтобы узнать их как математиков. Он не только покажет студентам, насколько вы цените математику, но и позволит студентам развить позитивные отношения с математикой с первого дня обучения e.
Любите эти идеи? Закрепите, чтобы сохранить их!
Возможно, вас заинтересует этот математический алфавит:
* партнерских ссылок: «Think Grow Giggle является участником программы Amazon Services LLC Associates, партнерской рекламной программы, разработанной для предоставления сайтам средств для получения рекламных сборов за счет рекламы и ссылок на Amazon.