Как решать смешанные дроби умножение. Правила умножения и деления дробей на целое число
Умножение целого числа на дробь – несложная задача. Но есть тонкости, в которых вы, наверняка, разбирались в школе, но с тех пор забыли.
Как умножить целое число на дробь – немного терминов
Если вы помните, что такое числитель, знаменатель и чем отличается правильная дробь от неправильной – пропустите этот абзац. Он для тех, кто совсем забыл теорию.
Числитель – это верхняя часть дроби – то, что делим. Знаменатель – нижняя. Это то, на что делим.
Правильная дробь та, у которой числитель меньше знаменателя. Неправильной называется дробь, у которой числитель больше или равен знаменателю.
Как умножить целое число на дробь
Правило умножения целого числа на дробь очень простое – умножаем числитель на целое, а знаменатель не трогаем. Например: два умножить на одну пятую – получаем две пятых. Четыре умножить на три шестнадцатых – получится двенадцать шестнадцатых.
Сокращение
Во втором примере полученную дробь можно сократить.
Что это значит? Обратите внимание – и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется – сократить дробь. Получим три четвертых.
Неправильные дроби
Но, предположим, мы умножили четыре на две пятых. Получилось восемь пятых. Это неправильная дробь.
Её обязательно нужно привести к правильному виду. Для это нужно выделить из нее целую часть.
Здесь нужно использовать деление с остатком. Получаем единицу и три в остатке.
Одна целая и три пятых и есть наша правильная дробь.
Привести к правильному виду тридцать пять восьмых – задача чуть посложнее.Самое близкое к тридцати семи число, которое делится на восемь – это тридцать два. При делении получим четыре. Отнимем от тридцати пяти тридцать два – получим три. Итог: четыре целых и три восьмых.
Равенство числителя и знаменателя. А тут все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.
При равенстве числителя и знаменателя получается просто единица.
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.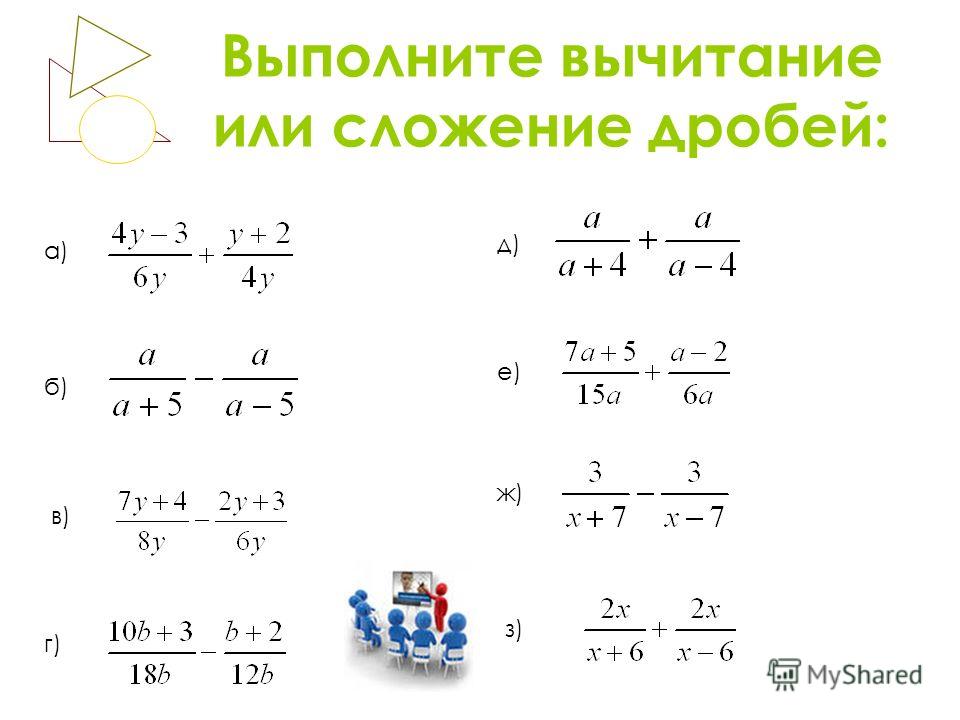
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример.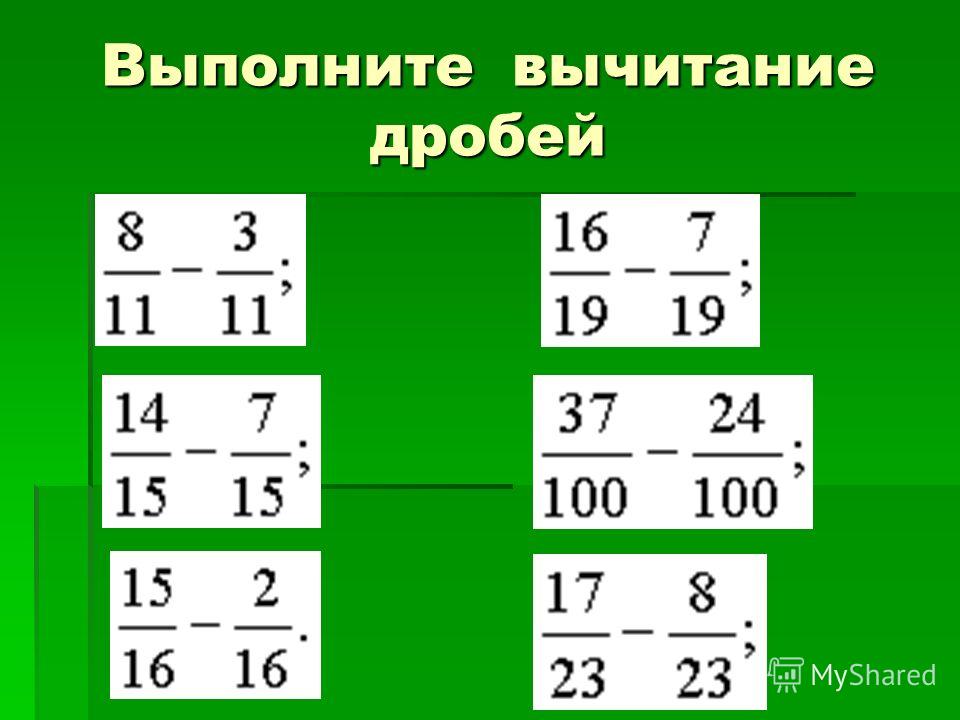 Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
| Табличка на двери |
Смешанное число / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Смешанное число
Пусть у нас есть 7 яблок:
Нам необходимо разделить их поровну между тремя детьми. Как это возможно сделать?
1 способ:
Можно каждое яблоко разделить на три доли, то есть мы получим по яблока, и дать всем детям долю от каждого яблока. Тогда каждый ребенок получит семь таких долей, значит, один ребенок получит яблока:
2 способ:
Так как у нас семь яблок, то мы можем каждому ребенку дать по два целых яблока, а седьмое поделить между ними поровну, то есть по яблока каждому:
В этом случае каждый ребенок получит по яблока.
Такую сумму, как , принято записывать так: . Число читают: «две целых одна третья». Число называют смешанным числом. В нем число 2 называют целой частью, а число — его дробной частью, при этом дробная часть смешанного числа — это всегда правильная дробь.
Вернемся к задаче, которую мы рассматривали. В обоих случаях дети получили одинаковые части яблок, то есть мы можем сказать, что: .
Данное равенство показывает, что неправильную дробь можно записать в виде смешанного числа . Говорят, что из неправильной дроби выделена целая часть. При этом из любой неправильной дроби, числитель которой нацело не делится на знаменатель, можно выделить целую часть, то есть записать ее в виде смешанного числа. При этом, если числитель делится нацело на знаменатель, то эта дробь равна натуральному числу.
| Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части. |
Пример 1: Выделим целую часть из неправильной дроби .
Для этого разделим 157 на 9 с остатком, имеем: 157: 9 = 17 (ост. 4)
То есть получили, что неполное частное равно 17, а остаток — 4. Значит, .
Мы выделили целую часть неправильной дроби, или по-другому, представили неправильную дробь в виде смешанного числа. На практике часто приходится выполнять обратное, то есть смешанное число представлять в виде неправильной дроби.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа. |
Пример 2: Преобразуем в смешанную дробь число :
.
Стоит отметить, что переместительное и сочетательное свойство сложения натуральных чисел выполняются и для смешанных чисел. На их основе мы можем записать:
| Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части. |
Пример 3: Найдем сумму чисел и :
Обратите внимание, что число не является смешанным, так как дробь является неправильной.
Со смешанными числами можно также проводить операцию вычитания. При этом, если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то можно воспользоваться следующим правилом.
Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого. |
Пример 4: Найдем разность чисел и :
В случае, если дробная часть уменьшаемого меньше дробной части вычитаемого, данное правило использовать нельзя, но уменьшаемое можно преобразовать так, чтобы данное правило было применимо.
Пример 5: Найдем разность чисел и :
Мы видим, что дробная часть уменьшаемого меньше дробной части вычитаемого, выполним преобразование уменьшаемого:
Тогда имеем:
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1093, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1096, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1155, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1157, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1321, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1588, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1724, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1793, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 800, Мерзляк, Полонский, Якир, Учебник
Номер 801, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 265, Мерзляк, Полонский, Якир, Учебник
Номер 288, Мерзляк, Полонский, Якир, Учебник
Номер 437, Мерзляк, Полонский, Якир, Учебник
Номер 443, Мерзляк, Полонский, Якир, Учебник
Номер 457, Мерзляк, Полонский, Якир, Учебник
Номер 569, Мерзляк, Полонский, Якир, Учебник
Номер 1126, Мерзляк, Полонский, Якир, Учебник
Задание 846, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1045, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 10, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 197, Мерзляк, Полонский, Якир, Учебник
Номер 355, Мерзляк, Полонский, Якир, Учебник
Номер 396, Мерзляк, Полонский, Якир, Учебник
Номер 397, Мерзляк, Полонский, Якир, Учебник
Номер 430, Мерзляк, Полонский, Якир, Учебник
Номер 530, Мерзляк, Полонский, Якир, Учебник
Номер 582, Мерзляк, Полонский, Якир, Учебник
Номер 856, Мерзляк, Полонский, Якир, Учебник
Номер 873, Мерзляк, Полонский, Якир, Учебник
Смешанные числа — Помощник для школьников Спринт-Олимпик.
 ру
руВ предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же, как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание
- Сложение целого числа и правильной дроби
- Сложение смешанных чисел
- Сложение целого и смешанного числа
- Вычитание дроби из целого числа
- Вычитание смешанного числа из целого числа
- Вычитание смешанных чисел
- Умножение целого числа на дробь
- Умножение смешанного числа на дробь
- Умножение смешанных чисел
- Деление целого числа на дробь
- Деление дроби на целое число
- Деление целого числа на смешанное число
- Деление смешанного числа на целое число
- Деление смешанных чисел
- Задания для самостоятельного решения
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь
Например, сложить число 2 и дробь
. Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так:
, а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Когда перед нами смешанное число вида
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения
равно
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
Представим число 3 в виде дроби
. Затем сложим дроби с разными знаменателями:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь
, но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби
. Пять вторых это две целых и одна вторая:
Теперь в главном выражении
вместо дроби запишем смешанное число
Получили новое выражение
. В этом выражении смешанное число запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чиселВстречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Получили
. Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь свернем полученное смешанное число:
Таким образом, значение выражения
равно .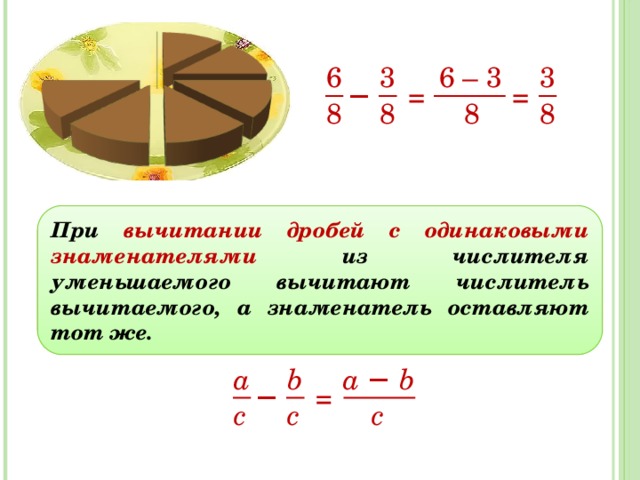 Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Получили смешанное число
. Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Получили выражение
. В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения
равно .
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числаВстречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Здесь смешанная дробь
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:
Осталось свернуть целую и дробную части, но дело в том, что дробная часть
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
Вычитание дроби из целого числаВстречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Пример 2. Найти значение выражения
.
Представим число 2 в виде дроби
, и выполним вычитание дробей с разными знаменателями:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:
Нужно вычесть из них
. Мы помним, что треть выглядит следующим образом:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Получилось
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
Пример 3. Найти значение выражения
Найти значение выражения
Представим число 3 в виде дроби
. Затем выполним вычитание дробей с разными знаменателями:
Вычитание смешанного числа из целого числаТеперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения
.
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число
перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Представим 6 в виде дроби
, а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Теперь выполним вычитание дробей с разными знаменателями:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
Тогда от той пиццы, от которой отрезали
останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чиселВстречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа
и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения
Переводим смешанные числа
и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробьЛюбое целое число можно умножить на дробь. Для этого достаточно умножить это число на числитель дроби.
Для этого достаточно умножить это число на числитель дроби.
Например, умножим число 5 на дробь
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Умножим число 3 на числитель дроби
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число
в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:
Умножить эти куски на
означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Теперь если мы возьмем
(два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
Для наглядности закрасим эти два куска:
Поэтому значение выражения
было равно 1
Умножение смешанных чиселВстречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить
и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять
от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является
пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является
пиццы.
Поэтому значение выражения
равно
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Деление целого числа на дробьЧтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь
. Здесь число 3 — это делимое, а дробь — делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби
. А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:
Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения
равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби
. А обратная дробь для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
. После выделения целой части в этой дроби получим
После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения
равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби
. А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на
Дробь
это 2 целых и . Проще говоря, две целые и четверть пиццы:
Проще говоря, две целые и четверть пиццы:
А выражение
определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .
То есть
пиццы содержится в пяти целых пиццах раза.
Давайте нащупаем в пяти пиццах два раза по
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой
от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения
равно
Деление дроби на целое числоЧтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Вспомним ещё раз.
Пример 1. Разделим дробь
на число 2
Чтобы разделить дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения
равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь
на число, обратное числу 3. Обратное числу 3 это дробь
Деление целого числа на смешанное числоВстречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения
равно
Пример 2. Найти значение выражения
Найти значение выражения
Переводим делитель
в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Сначала мы получили ответ
, затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Деление смешанного числа на целое числоЧтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим .
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Теперь если мы сгруппируем эти кусочки на две группы, то получим по
пиццы в каждой группе:
Поэтому значение выражения
равно
Пример 2. Найти значение выражения
Переведём делимое
в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .
Деление смешанных чиселЧтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Получим следующее выражение:
Как решать дальше мы уже знаем. Первую дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .
Дорешаем данный пример до конца:
Допустим, имеются две целые и половина пиццы:
Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь
Сначала мы получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Предыдущая
Математика с нуляДействия с дробями
СледующаяМатематика с нуляСравнение дробей
Обыкновенные дроби. Конспект — Kid-mama
Из этой статьи вы узнаете:
- Что такое обыкновенные дроби.
- Виды обыкновенных дробей
- Преобразования дробей
- Сравнение дробей
- Основное свойство дроби. Сокращение дробей. Понятие о НОД.
- Как приводить дроби к одному знаменателю. НОК
- Сложение и вычитание дробей.
- Умножение и деление дробей. Взаимно обратные числа и дроби.
Что такое обыкновенные дроби. Виды дробей.
Дробь всегда означает какую то часть целого. Дело в том, что не всегда количество можно передать натуральными числами, то есть пересчитать: 1,2,3 и т.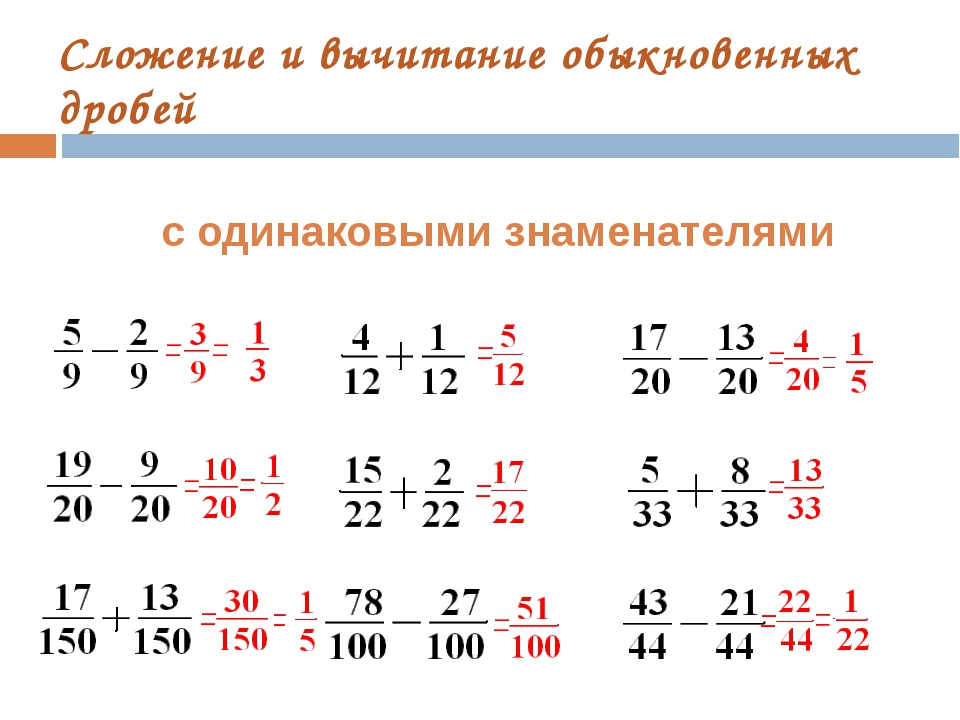 д. Как, например, обозначить половину арбуза или четверть часа? Вот для этого и появились дробные числа, или дроби.
д. Как, например, обозначить половину арбуза или четверть часа? Вот для этого и появились дробные числа, или дроби.
Для начала нужно сказать, что вообще дробей бывает два вида: обыкновенные дроби и десятичные дроби. Обыкновенные дроби записываются так:
Десятичные дроби записываются по другому:
Обыкновенные дроби состоят из двух частей: вверху — числитель, внизу — знаменатель. Числитель и знаменатель разделяет дробная черта. Итак, запомните:
Любая дробь — это часть целого. За целое обычно принимают 1 (единицу). Знаменатель дроби показывает, на сколько частей разделили целое (1), а числитель — сколько частей взяли. Если мы разрезали торт на 6 одинаковых частей ( в математике говорят долей ), то каждая часть торта будет равна 1/6. Если Вася съел 4 куска, то значит, он съел 4/6 .
С другой стороны, дробная черта — это не что иное, как знак деления. Поэтому дробь — это частное двух чисел — числителя и знаменателя. В тексте задач или в рецептах блюд дроби записываются обычно так: 2/3, 1/2 и т.д. Некоторые дроби получили собственное название, например, 1/2 — «половина», 1/3 — «треть», 1/4 — «четверть»
В тексте задач или в рецептах блюд дроби записываются обычно так: 2/3, 1/2 и т.д. Некоторые дроби получили собственное название, например, 1/2 — «половина», 1/3 — «треть», 1/4 — «четверть»
А теперь разберемся, какие бывают виды обыкновенных дробей.
Виды обыкновенных дробей
Обыкновенные дроби бывают трех видов: правильные, неправильные и смешанные:
Правильная дробь
Если числитель меньше, чем знаменатель, то такую дробь называют правильной, например: Правильная дробь всегда меньше 1.
Неправильная дробь
Если числитель больше, чем знаменатель или равен знаменателю, такая дробь называется неправильной, например:
Неправильная дробь больше единицы(если числитель больше знаменателя) или равна единице (если числитель равен знаменателю)
Смешанная дробь
Если дробь состоит из целого числа (целая часть) и правильной дроби (дробная часть), то такая дробь называется смешанной, например:
Смешанная дробь всегда больше единицы.
Преобразования дробей
В математике обыкновенные дроби часто приходится преобразовывать, то есть смешанную дробь превращать в неправильную и наоборот. Это необходимо для выполнения некоторых действий, например, умножения и деления.
Итак, любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Любую неправильную дробь можно превратить в смешанную. Для этого делят числитель на знаменатель (с остатком). Полученное число будет целой частью, а остаток — числителем дробной части, например:
При этом говорят: «Мы выделили целую часть из неправильной дроби».
Необходимо запомнить еще одно правило: Любое целое число можно представить в виде обыкновенной дроби со знаменателем 1, например:
Поговорим о том, как сравнивать дроби.
Сравнение дробей
При сравнении дробей может быть несколько вариантов: Легко сравнивать дроби с одинаковыми знаменателями, гораздо сложнее — если знаменатели разные. А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.
А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, но разными числителями больше та дробь, у которой числитель больше, например:
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше, например:
Сравнение смешанных и неправильных дробей с правильными дробями
Неправильная или смешанная дробь всегда больше правильной дроби, например:
Сравнение двух смешанных дробей
При сравнении двух смешанных дробей больше та дробь, у которой целая часть больше, например:
Если целые части у смешанных дробей одинаковые, больше та дробь, у которой дробная часть больше, например:
Сравнение дробей с разными числителями и знаменателями
Сравнивать дроби с разными числителями и знаменателями без их преобразования нельзя. Сначала дроби нужно привести к одному знаменателю, а затем сравнить их числители. Больше та дробь, у которой числитель будет больше. А вот как приводить дроби к одинаковому знаменателю, мы рассмотрим в следующих двух разделах статьи статьи. Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.
Сначала дроби нужно привести к одному знаменателю, а затем сравнить их числители. Больше та дробь, у которой числитель будет больше. А вот как приводить дроби к одинаковому знаменателю, мы рассмотрим в следующих двух разделах статьи статьи. Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.
Основное свойство дроби. Сокращение дробей. Понятие о НОД.
Запомните: складывать и вычитать, а также сравнивать можно только дроби, у которых одинаковые знаменатели. Если знаменатели разные, то сначала нужно привести дроби к одному знаменателю, то есть так преобразовать одну из дробей, чтобы ее знаменатель стал таким же, как у второй дроби.
У дробей есть одно важное свойство, называемое также основным свойством дроби:
Если и числитель, и знаменатель дроби умножить или разделить на одно и то же число, то величина дроби при этом не изменится:
Благодаря этому свойству мы можем сокращать дроби:
Сократить дробь — значит разделить и числитель, и знаменатель на одно и то же число(смотрите пример чуть выше). Когда мы сокращаем дробь, то можно расписать наши действия так:
Когда мы сокращаем дробь, то можно расписать наши действия так:
Чаще же в тетради сокращают дробь так:
Но запомните: сокращать можно только множители. Если в числителе или знаменателе сумма или разность, сокращать слагаемые нельзя. Пример:
Нужно сначала преобразовать сумму в множитель:
Иногда, при работе с большими числами, для того, чтобы сократить дробь, удобно найти наибольший общий делитель числителя и знаменателя (НОД)
Наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое эти числа делятся без остатка.
Для того, чтобы найти НОД двух чисел (например, числителя и знаменателя дроби), нужно разложить оба числа на простые множители, отметить одинаковые множители в обоих разложениях, и перемножить эти множители. Полученное произведение и будет НОД. Например, нам нужно сократить дробь:
Найдем НОД чисел 96 и 36:
НОД нам показывает, что и в числителе, и в знаменателе есть множитель12, и мы легко сокращаем дробь.
Иногда, чтобы привести дроби к одному знаменателю, достаточно сократить одну из дробей. Но чаще бывает необходимо подбирать дополнительные множители для обеих дробей .Сейчас мы рассмотрим, как это делается. Итак:
Как приводить дроби к одному знаменателю. Наименьшее общее кратное (НОК).
Когда мы приводим дроби к одинаковому знаменателю, мы подбираем для знаменателя такое число, которое бы делилось и на первый, и на второй знаменатель (то есть было бы кратным обоим знаменателям, выражаясь математическим языком). И желательно, чтобы число это было как можно меньшим, так удобнее считать. Таким образом, мы должны найти НОК обоих знаменателей.
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.

- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
Однако вернемся к нашим дробям. После того, как мы подобрали или письменно вычислили НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом мы привели наши дроби к одному знаменателю — 15.
Сложение и вычитание дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Сложение и вычитание смешанных дробей с одинаковыми знаменателями
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью:
Пример 1:
Пример 2:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
Вычитание проводится аналогично: целая часть вычитается из целой, а дробная — из дробной части:
Если дробная часть вычитаемого больше, чем дробная часть уменьшаемого, «занимаем» единицу из целой части, превращая уменьшаемое в неправильную дробь, а дальше действуем как обычно:
Аналогично вычитаем из целого числа дробь:
Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Сложение и вычитание дробей с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как при сложении дробей с одинаковыми знаменателями (сложить числители):
При вычитании действуем аналогично:
Если работаем со смешанными дробями, приводим к одинаковому знаменателю их дробные части и далее вычитаем как обычно: целую часть из целой, а дробную — из дробной части:
Умножение и деление дробей.
Умножать и делить обыкновенные дроби гораздо проще, чем складывать и вычитать, так как не нужно приводить их к одному знаменателю. Запомните простые правила умножения и деления дробей:
Чтобы умножить дробь на натуральное число, нужно числитель умножить на это число, а знаменатель оставить без изменений
Например:
Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель — на знаменатель:
Например:
При умножении смешанных дробей нужно сначала записать эти дроби в виде неправильных дробей, а затем умножать как обычно: числитель умножить на числитель, а знаменатель на знаменатель:
Перед тем, как перемножать числа в числителе и знаменателе желательно сократить дробь, то есть избавиться от одинаковых множителей в числителе и знаменателе, как в нашем примере.
Чтобы разделить дробь на натуральное число, нужно знаменатель умножить на это число, а числитель оставить без изменений:
Например:
Деление дроби на дробь
Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю (обратную дробь).Что же это за обратная дробь?
Взаимно обратные числа и дроби.
Если мы перевернем дробь, то есть поменяем местами числитель и знаменатель, то получим обратную дробь. Произведение дроби и обратной ей дроби дает единицу. В математике такие числа называют взаимно обратными числами:
Например, числа — взаимно обратные, так как
Таким образом, вернемся к делению дроби на дробь:
Чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю:
Например:
При делении смешанных дробей нужно так же, как и при умножении, сначала перевести их в неправильные дроби:
При умножении и делении дробей на целые натуральные числа, можно представлять эти числа так же в виде дробей со знаменателем 1.
И при делении целого числа на дробь представляем это число в виде дроби со знаменателем 1:
Конспект урока «сложение и вычитание смешанных чисел». Вычитание смешанных дробей
Решение сложных примеров правильно – непосильная задача для тех, кто не понимает в математике элементарных правил и законов. Сложение и вычитание смешанных чисел по праву можно отнести к сложным примерам. Однако, при правильном разборе самих чисел можно легко проводить любые действия.
Что это такое?
Смешанное число – это комбинация целой части и дробной. К примеру, имеется 2 и 3, из них 2 – это простое число, а вот 3 – это уже смешанное, где 3 – целая часть, а – дробная. Представленные разновидности складываются и вычитаются по-разному, но не влекут сложностей в самостоятельном решении примеров.
Полноценный разбор примера
Для полноценного представления сущности смешанного значения следует привести в пример задачу, которая поможет отобразить смысл повествования задуманного. Итак, Вася проехал круг вокруг школы на велосипеде за 1 минуту и 30 секунд, а потом еще круг прошел пешком за 3 минуты и 30 секунд. Сколько времени затратил Вася на всю прогулку вокруг школы?
Итак, Вася проехал круг вокруг школы на велосипеде за 1 минуту и 30 секунд, а потом еще круг прошел пешком за 3 минуты и 30 секунд. Сколько времени затратил Вася на всю прогулку вокруг школы?
Этот пример направлен на сложение смешанных чисел, которые предварительно в данном случае даже не придется переводить в секунды. Получается, что сложение осуществляется путем отдельного прибавления минут и секунд. В результате получим следующий результат:
- Сложение минут – 1+3=4.
- Сложение секунд = 30+30=60 секунд = 1 минута.
- Общее значение 4 минуты+1 минута = 5 минут.
Если исходить из математического отображения, то представленные действия можно выделить в одном выражении:
Из представленного выше становится понятным, что складывать смешанные числа следует в отдельности по частям – сначала целые части, а затем дробные. Если дробное число дает еще целое значение, его также складывают с целым полученным ранее значением. К полученному целому значению прибавляют дробную часть – получается смешанное число.
Правила сложения
Для закрепления изученного следует привести правило сложения смешанных чисел. Здесь следует воспользоваться следующей последовательностью:
- Для начала отделить от значения части – на целую и дробную.
- Теперь сложить целые части.
- Далее сложить дробные.
- Если из дробного числа можно извлечь еще целую часть – перевести в смешанное значение – значит, проводят подобную разбивку.
- Полученную целую часть из дробного значения складывают с целым ранее полученным значением.
- К целой части прибавляют дробную.
Для пояснения следует привести несколько примеров:
Сложение смешанных чисел происходит по тому же алгоритму, что и вычитание, поэтому далее будет подробно рассмотрено следующее действие.
Правила вычитания
Как и в первом случае, для вычитания смешанных значений существует правило, но оно в корне отличается от предыдущей последовательности. Итак, здесь следует придерживаться последовательности:
- Пример на вычитание представляется в виде: уменьшаемое – вычитаемое = разность.

- В связи с приведенным уравнением следует предварительно сравнить дробные части представленных чисел.
- Если у уменьшаемого дробная часть больше, значит, вычитание проводится по тому же признаку, что и при сложении – сначала вычитаются целые, а затем дробные значения. Оба результата складывают.
- Если у уменьшаемого дробное значение меньше, значит, их предварительно переводят в неправильную дробь и осуществляют стандартное вычитание.
- Из полученной разницы определяют целую часть и дробную.
Для пояснения следует привести следующие примеры:
Из представленной статьи стало понятным, как проводить сложение и вычитание смешанных чисел. В описанном выше примере видно, что не всегда приходится видоизменять числа – переводить их из простых дробей в сложные. Зачастую достаточно просто сложить или вычесть целые и дробные значения по отдельности, что для человека с большим опытом можно легко провести в уме.
В статье подробно рассмотрены примеры, решение которых представлено в полном соответствии с математическими правилами и основами. Разобраны отдельные ситуации, для каждого приведен пример видоизменений, с которыми можно столкнуться в решении задач и сложных примеров.
Разобраны отдельные ситуации, для каждого приведен пример видоизменений, с которыми можно столкнуться в решении задач и сложных примеров.
>>Математика: Сложение и вычитание смешанных чисел-6 класс
12. Сложение и вычитание смешанных чисел
Переместительное и сочетательное свойства сложения позволяют свести сложение сметанных чисел к сложению их целых частей и к сложению их дробных частей.
Пример 1. Найдем значение суммы
Решение. Приведем дробные части чисел к наименьшему общему 8, затем представим смешанные числа в виде суммы их целой и дробной части:
Пример 2. Найдем значение суммы .
Решение. Сначала приводим дробные части данных чисел к наименьшему общему знаменателю 12, после отдельно складываем целые и дробные части:
Чтобы сложить смешанные числа, надо:
1) привести дробные части этих чисел к наименьшему общему знаменателю;
2) отдельно выполнить сложение целых частей и отдельно дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
При вычитании смешанных чисел пользуются свойствами вычитания суммы из числа и вычитания числа из суммы .
Пример 3. Найдем значение разности .
Решение. Приведем дробные части к наименьшему общему знаменателю 18 и представим данные числа в виде суммы целой и дробной части:
Пишут короче:
Если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого.
Пример 4. Найдем значение разности
Решение. Приведем дробные части данных чисел к наименьшему общему знаменателю 18:
Так как дробная часть уменьшаемого меньше дробной части вычитаемого, то уменьшаемое записываем так:
Чтобы выполнить вычитание смешанных чисел, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть; 2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
? Расскажите, как сложить смешанные числа и на каких свойствах сложения основано сложение смешанных чисел. Расскажите, как выполнить вычитание смешанных чисел и на каких свойствах основано правило вычитания смешанных чисел.
К 363. Выполните сложение:
364. Выполните вычитание:
365. Найдите значение выражения:
366. Выполните действие:
368. Найдите по формуле :
369. Школьный бассейн наполняется через первую трубу за 4 ч, а через вторую за 6 ч. Какую часть бассейна останется наполнить после совместной работы обеих труб в течение часа?
370. Новая машина может выкопать канаву за 8 ч, а старая — за 12 ч. Новая машина работала 3 ч, а старая 5 ч. Какую часть канавы осталось выкопать?
371. От ленты длиной 8 м отрезали кусок длиной м. Найдите длину оставшейся части.
372. Одна шахматная партия длилась ч, а другая ч. Сколько времени длилась третья партия, если на все три партии было затрачено 3 ч?
373. Когда от веревки отрезали кусок, то оставшаяся часть имела длину 2 м. Какой длины была бы оставшаяся часть, если бы от веревки отрезали на м меньше? на м больше?
Когда от веревки отрезали кусок, то оставшаяся часть имела длину 2 м. Какой длины была бы оставшаяся часть, если бы от веревки отрезали на м меньше? на м больше?
374. Запишите все числа, знаменатель дробной части которых равен 12, большие и меньшие .
375. На координатном луче отмечена точка (рис. 17). Отметьте на луче точки, координаты которых равны:
376. Найдите периметр треугольника ABC, если АВ= м, .
377. На одной машине т груза, а на другой на т меньше. Сколько тонн груза на двух машинах?
378. В одном ящике кг винограда, что на кг меньше, чем в другом ящике. Сколько килограммов винограда в двух ящиках?
379. На окраску окон израсходовали кг краски. На окраску дверей пошло на кг меньше, чем на окраску пола. Сколько всего израсходовали краски, если на окраску пола пошло кг?
380. Три колхозных звена вырастили горох на площади га. Первое и второе звенья вырастили горох на площади га, а второе и третье — на площади га. Найдите площадь каждого участка.
Найдите площадь каждого участка.
381. На сахарный завод в понедельник привезли т свеклы, во вторник — на 2 т больше, чем в понедельник, а в среду — на т меньше, чем во вторник и понедельник вместе. Из 7 т свеклы получается 1 т сахара. Сколько сахара получится из привезенной свеклы?
382. В трех бидонах 10 л молока. В первом и втором бидоне было л, а во втором и третьем л молока. Сколько литров молока было в каждом бидоне?
383. Теплоход по течению реки проходит км за 1 ч. Скорость течения км/ч. Найдите скорость теплохода против течения.
384 Скорость катера по течению реки км/ч, а против течения км/ч. Какова скорость течения?
385. Федя и Вася шли навстречу друг другу. Каждый час расстояние между ними уменьшалось на км. Найдите скорость Феди, если скорость Васи
386. Первый велосипедист догонял второго, причем расстояние между ними уменьшалось каждый час на км. С какой скоростью ехал первый велосипедист, если второй ехал со скоростью y км/ч?
П 388. Вычислите устно:
Вычислите устно:
389. Найдите пропущеные числа:
390.Найдите натуральные значения m , при которых верно неравенство:
391. На сколько процентов увеличится объем куба, если длину каждого его ребра увеличить на 20%?
392. Почтовый самолет поднялся с аэродрома в 10 ч 40 мин утра, пробыл в полете 5 ч 15 мин, а на земле во время посадок 1 ч 37 мин. Когда самолет вернулся на аэродром?
М 393. Четырехугольник с равными сторонами называют ВИЗ ромбом (рис. 18). Подумайте, является ли ромб правильным многоугольником. В чем сходство решения этой задачи с нахождением решений двойного неравенства 0
394. Докажите переместительное и сочетательное свойства сложения для дробей с одинаковыми знаменателями на основе таких же свойств для натуральных чисел .
395. Выполните действие:
396. В киоск для продажи поступили марки по 3 к., по 5 к. и по 10 к. Число марок каждого вида было одинаково. Какова стоимость всех марок по 5 к. , если: а) общая стоимость всех марок 21 р. 60 к., б) стоимость всех марок по 10 к. больше стоимости всех марок по 3 к. на 6 р. 30 к.?
, если: а) общая стоимость всех марок 21 р. 60 к., б) стоимость всех марок по 10 к. больше стоимости всех марок по 3 к. на 6 р. 30 к.?
397. Выполните вычисления с помощью микрокалькулятора и результат округлите до тысячных:
3,281 0,57 + 4,356 0,278 -13,758:6,83.
398. Решите задачу:
1) Для борьбы с вредителями садов приготовляется известково-серный отвар, состоящий из 6 частей серы, 3 частей негашеной извести и 50 частей воды (по массе). Сколько получится килограммов отвара, если воды взять на 8,8 кг больше, чем серы?
2) Для приготовления фарфора на 1 часть гипса берут 2 части песку и 25 частей глины (по массе). Сколько получится килограммов фарфора, если взять глины на 6,9 кг больше, чем песку?
399. Выполните действия:
1) 7225:85 + 64 2345-248 838:619;
2) 54 3465-9025:95 + 360 272:712.
Д 400. Выполните действие:
а
401. Найдите значение разности:
402. Решите уравнение:
404. Один тракторист вспахал поля, а другой того же поля. Какую часть поля осталось вспахать?
Один тракторист вспахал поля, а другой того же поля. Какую часть поля осталось вспахать?
406. Бочки горючего хватает для работы одного двигателя на 7 ч, а другого на 5 ч. Какая часть горючего останется от полной бочки после 2 ч работы первого двигателя и 3 ч работы второго двигателя?
406. Для экспедиции, работающей в тайге, сбросили с вертолета упаковку с продуктами, которая упала на землю через 3 с. С какой высоты была сброшена эта упаковка, если в первую секунду она пролетела м, а в каждую следующую секунду она пролетела на м больше, чем в предыдущую?
407. Сколько времени пошло на изготовление детали, если ее обрабатывали на токарном станке ч, на фрезерном станке ч и на сверлильном станке ч?
408. Найдите значение выражения:
409. Из двух сел одновременно навстречу друг другу вышли два пешехода и встретились через 1,5 ч. Расстояние между селами 12,3 км. Скорость одного пешехода 4,4 км/ч. Найдите скорость другого пешехода.
410. Для приготовления варенья из вишни на 3 части сахара берут 2 части ягод (по массе). Сколько килограммов сахара и сколько килограммов ягод надо взять, чтобы получить 10 кг варенья, если при варке его уменьшится в 1,5 раза?
Сколько килограммов сахара и сколько килограммов ягод надо взять, чтобы получить 10 кг варенья, если при варке его уменьшится в 1,5 раза?
411. Найдите значение выражения:
а) (44,96 + 28,84: (13,7 -10,9)): 1,8;
б) 102,816:(3,2 6,3)+ 3,84.
412. Решите уравнение:
а) (х-4,7) 7,3 = 38,69; в) 23,5-(2,За+ 1,2а) = 19,3;
б) (3,6-а) 5,8 = 14,5; г) 12,98-(3,8х- 1,3х) = 11,23.
А Раздел математики, в котором изучаются свойства чисел и действий над ними, называют теорией чисел.
Начало созданию теории чисел положили древнегреческие ученые Пифагор, Евклид, Эратосфен и другие.
Некоторые проблемы теории чисел формулируются очень просто — их может понять любой шестиклассник. Но решение этих проблем иногда настолько сложно, что на него уходят столетия, а на некоторые вопросы ответов нет до сих пор. Например, древнегреческим математикам была известна всего одна пара дружественных чисел — 220 и 284. И лишь в XVIII в. знаменитый математик, член Петербургской академии наук Леонард Эйлер нашел еще 65 пар дружественных чисел (одна из них 17 296 и 18 416). Однако до сих пор не известен общий способ нахождения пар дружественных чисел.
Однако до сих пор не известен общий способ нахождения пар дружественных чисел.
Почти 250 лет назад член Петербургской академии наук Христиан Гольдбах высказал предположение, что любое нечетное число, большее 5, можно представить в виде суммы трех простых чисел. Например: 21 = 3 + 7 + 11, 23 = 5 + 7 + 11 и т. п.
Доказать это предположение сумел лишь 200 лет спустя замечательный советский математик, академик Иван Матвеевич Виноградов (1891-1983). Но утверждение «Любое четное число, большее 2, можно представить в виде суммы двух простых чисел» (например: 28=11 + 17, 56 = 19+37, 924 = 311 + 613 и т. д.) до сих пор не доказано.
Цели урока:
- Повторение и закрепление основного программного материала, выраженного в стандартных примерах и нестандартных задачах.
- Совершенствование навыков арифметических операций складывание и вычитание смешанных чисел;
- Развивать смекалку, мышление, речь, память.
- Воспитывать познавательный интерес к предмету, любовь к поисковым
решениям.

Задачи урока:
– обобщение и систематизация знаний; развитие
быстроты мышления; развивать умение анализировать; развивать вычислительные
навыки.
Тип урока: урок обобщения и систематизации знаний.
Форма урока:, частично поисковый с элементами дидактической игры.
Межпредметные связи: биология.
Оборудование урока:
- плакат;
- раздаточный материал: карточки с заданием;
- презентация по теме урока.
Применение здоровьесберегающих технологий на уроке:
- смена видов деятельности;
- развитие слухового и зрительного анализаторов у каждого ребёнка.

План урока
I. Организационный момент.
Здравствуйте. Садитесь.
Презентация . Слайд 1. Тема урока: “Сложение и вычитание смешанных чисел”.
Цели урока:
- Повторение и закрепление основного программного материала, выраженного в стандартных примерах и нестандартных задачах.
- Совершенствование навыков арифметических действий складывание и вычитание смешанных чисел, подготовка к контрольной работе.
II. Актуализация опорных знаний.
На доске плакат с словами Лауэ.
Наш урок пройдёт под девизом французского инженера – физика Лауэ: “Образование есть то, что остаётся, когда всё выученное уже забыто”.
Вот сейчас вы и покажете свои знания на сложение и вычитание обыкновенных дробей с разными знаменателями, а также сложение и вычитание смешанных чисел.
1) Вспомните знаменитую басню И.Крылова “Стрекоза и муравей”.
Попрыгунья стрекоза, лето красное пропела
Оглянуться не успела, как зима катит в глаза.
Задача. Попрыгунья Стрекоза половину красного лета спала, третью часть времени – танцевала, шестую часть – пела. Остальное время она решила посвятить подготовке к зиме. Какую часть лета Стрекоза готовилась к зиме?
Ответ: летом к зиме Стрекоза совсем не готовилась.
А сейчас, вспомним сокращение дробей:
Выпишите из данных дробей те, которые можно сократить, и выполните сокращение:
Вспомните какие дроби называются правильные и какие неправильные?
– Правильные дроби, те у которых числитель меньше знаменателя.
– Неправильные дроби, те у которых числитель больше либо равен знаменателю.
(Карточки: читаете дробь и называете – правильная или неправильная дробь.)
Как выделить целую часть из неправильной дроби?
– Числитель надо разделить на знаменатель.
(Устно карточки: выделить целую часть из неправильной дроби.)
III. Систематизация знаний. Карточки. Выполнить сложение и вычитание
обыкновенных дробей. Слева примеры, справа записаны ответы. Решив пример
стрелкой соотнеси с ответом.
Слева примеры, справа записаны ответы. Решив пример
стрелкой соотнеси с ответом.
Слайды 2–7. Это удивительное дерево относится к числу деревьев – гигантов. Оно растёт в Индии и Малайзии.
Самое необычное в нём то, как растут его ветви. Многочисленные и тяжёлые, они разбегаются во всех направлениях от ствола, хотя и могучего, но, тем не менее, не способного выдержать их все самостоятельно.
Весь фокус в том, что ветви сами снимают с него часть нагрузки: на каждой из них имеются толстые отростки, отвесно свисающие до самой земли и представляющие собой не что иное, как воздушные корни дерева.
Закрепившись в земле, они не только обеспечивают ветвям дополнительную поддержку, но и поставляют в них питательные вещества и воду. Постепенно они превращаются в новые стволы и вокруг главного ствола образуются кольцеобразные “галереи”, диаметр которых иногда достигает 450 м.
Решив задачи, а также вычислив значения выражений, заменим числа
соответствующими буквами и вы узнаете название этого дерева.
Решите задачу:
Вычислите значения выражения:
Ответ: БАНЬЯН.
Итог урока : Мы готовились к контрольной работе. Для этого мы с вами и повторили сложение и вычитание дробей, а также смешанных чисел. Не забывайте сокращать дроби, которые получились в результате сложения и вычитания, и не забывайте выделять целую часть.
Дом. задание: § 2,п.12 № 392.
При наличии времени выполнить дополнительные задания.
Дополнительное задание:
- Решите уравнение:
Карточки:
Выполнить сложение и вычитание обыкновенных дробей.
_________________________________________
Решите задачу:
Вычислите значения выражения:
Самоанализ урока математики в 6 “а” классе.
Тема урока: Сложение и вычитание смешанных чисел.
Тип урока: урок обобщения и систематизация знаний.
Форма урока: частично поисковый с элементами дидактической игры.
1) Это урок повторение и закрепление основного программного материала, но
только выраженного в решение стандартных примеров и нестандартных задач. На
данном уроке мы повторяли арифметические действия (сложения, вычитание) над
обыкновенными дробями и над смешанными числами. Данные темы изучаются в курсе
математики 6 класса. При изучении математики много времени приходится тратить на
отработку различных навыков. В этот период ученики теряют интерес к предмету.
Чтобы поддержать этот интерес, я использую различные приёмы активизации учащихся
на уроке. Одним из таких приёмов является дидактическая игра. Она позволяет
сделать процесс обучения увлекательным, создать высокую активность на уроке. На
следующем уроке будет контрольная работа. Считаю, что данный урок “дал”
позитивные эмоции у ребят, отработали арифметические действия над смешанными
числами и настроились на контрольную работу.
На
данном уроке мы повторяли арифметические действия (сложения, вычитание) над
обыкновенными дробями и над смешанными числами. Данные темы изучаются в курсе
математики 6 класса. При изучении математики много времени приходится тратить на
отработку различных навыков. В этот период ученики теряют интерес к предмету.
Чтобы поддержать этот интерес, я использую различные приёмы активизации учащихся
на уроке. Одним из таких приёмов является дидактическая игра. Она позволяет
сделать процесс обучения увлекательным, создать высокую активность на уроке. На
следующем уроке будет контрольная работа. Считаю, что данный урок “дал”
позитивные эмоции у ребят, отработали арифметические действия над смешанными
числами и настроились на контрольную работу.
2) В классе по списку – 19 учащихся, на уроке присутствовало – 16 учащихся. Слабоуспевающих – 4, сильных – 1.
3) Образовательные – обобщение и систематизация знаний; развитие быстроты
мышления; введением игровой ситуации снять нервно – психическое напряжение;
развивать умение анализировать; развивать вычислительные навыки.
Развивающие – развивать у учащихся познавательные процессы, творческую
активность; приобретение опыта исследовательской деятельности, развитие
коммутативных качеств.
Воспитательные – формирование навыков самоорганизации и
самостоятельности; уважительного отношения друг к другу.
В играх ненавязчиво активизируется внимание ребят, прививается интерес к
предмету, развивается творческая фантазия.
4) Одним из удачных этапов урока считаю решение задач и примеров, где надо было составить слово БАНЬЯН. Учащиеся, как бы занимаются математикой и в то же время расширяют свой кругозор.
5) Урок был насыщен. Урок очень логично построен.
6) На урок были изготовлены мною, как учителем много раздаточного материала, который я напечатала на компьютере.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Учитель математики Кузнецова Марина Николаевна Сложение и вычитание смешанных чисел
Домашнее задание
Астрид Линдгрен
Устный счет 1 0
На какие группы мы можем разделить данные дроби?
На какие группы мы можем разделить данные дроби? Правильные дроби Неправильные дроби
Найдите лишний пример:
Сложение и вычитание смешанных чисел. Цель урока: Научится выполнять сложение и вычитание смешанных чисел.
Цель урока: Научится выполнять сложение и вычитание смешанных чисел.
Справка 1. К целой части прибавить целую часть. К полученной целой части прибавить дробную часть. Сформулировать правило сложения смешанного числа с натуральным. 2. К целой части прибавить целую часть. К дробной части прибавить дробную часть К полученной целой части прибавить полученную дробную часть. Сформулировать правило сложения смешанных чисел. 3. Из целой части вычесть целую часть. Из дробной части вычесть дробную часть К оставшейся целой части прибавить оставшуюся дробную часть. Сформулировать правило вычитания смешанных чисел. 4. Если дробная часть уменьшаемого меньше дробной части вычитаемого. Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби. Полученную дробь складываем с дробной частью уменьшаемого. Вычитаем отдельно целые части и дробные части. К оставшейся целой части прибавляем оставшуюся дробную часть. Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.
Чтобы сложить два смешанных числа, нужно сложить отдельно их целые и дробные части, сложить полученные результаты. Чтобы вычесть из смешанного числа смешанное число, нужно отдельно вычесть их целые и дробные части, сложить полученные результаты.
= (3 + 2) + () = 5 + = 5 – = (5 – 3) + ()= 2 + = 2
Физкультминутка Потрудились — отдохнём, Встанем, глубоко вздохнём. Руки в стороны, вперёд, Влево, вправо поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили.
4 – В 7 – О 3 – У 4 – Е 5 – Х 4 – П 5 – С У С П Е В Х О
Решение задач Стр. 175, № 1115 Стр. 175, № 1116
Что такое смешанное число? Чему вы сегодня научились? Как сложить смешанные числа? Как вычесть смешанные числа?
Домашнее задание: П. 29 (учить правила) Стр. 178, № 1136, 1137
Спасибо за урок!
Предварительный просмотр:
Учитель математики Кузнецова М.Н.
Урок в 5 классе по теме:
Сложение и вычитание смешанных чисел.
Цели:
Учебные:
- Познакомить учащихся с алгоритмами сложения и вычитания смешанных чисел путем включения учащихся в практическую деятельность.
- Продолжить работу по развитию вычислительных навыков.
Развивающие:
- Развитие умения решать задачи изученных видов.
- Создание условий для формирования мыслительных операций.
Воспитательная:
- Воспитывать чувство товарищества и взаимовыручки.
Ход урока
I. Организационный момент.
Посмотрите, все ль в порядке:
Книжка, ручки и тетрадки.
Прозвенел сейчас звонок.
Начинается урок.
II. Проверка домашнего задания.
Дата, классная работа.
Дома вы выполнили задание. Вы разгадали ребус. (Слайд 1)И какой же ответ? (Астрид Линдгрен) (Слайд 2)
Д/з. 1. Выделить целую часть и расположить в порядке возрастания. 18
-И
7
-А
14
-Р
11
-Т
9
-С
21
-Д 5 5 5 5 5 5 1 2/5 1 4/5 2 1/5 2 4/5 3 3/5 4 1/5 А С Т Р И Д 2. 41/2-Д 2 3/7-Н 4 9/10-Р 32/5-И 14/6-Г 2 2/8-Е 3 ¾ -Л 5 1/6-Н
|
А кто такая Астрид Линдгрен? Какую сказку написала эта шведская писательница? («Малыш и Карлсон») (Слайд 3)
Но к сожалению Карлсон улетел, но оставил письмо.
Письмо: Ребята, я полетел искать старательных, внимательных, трудолюбивых, дружных, умеющих придти на помощь ребят. Найду – вернусь.)
Найду – вернусь.)
Ребята, давайте быстрее встретимся с другом, для этого выполним математические задания. Если мы их выполним правильно, то у нас к возвращению Карлсона — сладкоежки получится большой общий торт. И у каждого – свой маленький.
Первое задание.
III. Устный счет
1. Решение цепочек (стр. 175, № 1111).
2/5 + 1/5 + 2/5 – 3/7 – 1/7 = 3/7
5/17 + 7/17 – 12/17 + 7/9 – 4/9 = 3/9
2. На какие группы мы можем разделить данные дроби: (правильные и неправильные дроби) (Слайд 6)
9 5 8 10 24 15 7 12
8 12 11 6 13 16 7 25
Какие дроби называются правильными?
Какие дроби называются неправильными?
Как по-другому представить неправильные дроби?
Из чего состоит смешанное число?
(Кусок торта.)
IV. Актуализация знаний.
Найдите лишний пример:
2/8 + 3/8 14/12 – 7/12 7/9 + 1/9 3 1/7 + 2 3/7 18/27 -5/27
Попробуйте сформулировать тему урока (Сложение смешанных чисел) (Слайд8)
Сегодня на уроке мы научимся выполнять сложение и вычитание смешанных чисел, для достижения этой цели сформулируем правила.
V. Исследование
Учащиеся работают в группах, выполняя задания различной сложности. Все учащиеся делятся на 4 группы. На парту каждой группы раздается задание и справочный материал. Для решения задания нужно выбрать соответственное правило.
Задание 1 . Выполнение сложения 2 ½ + 3
Задание 2. Выполнение сложения 2 1/4 + 1 2/4
Задание 3 . Выполнение вычитания 3 5/6 – 3/6
Задание 4. Выполнение вычитания 5 1/4 — 3 2/4
Справка
- К полученной целой части прибавить дробную часть.
- Сформулировать правило сложения смешанного числа с натуральным.
- К целой части прибавить целую часть.
- К дробной части прибавить дробную часть
- К полученной целой части прибавить полученную дробную часть.
- Сформулировать правило сложения смешанных чисел.
- Из целой части вычесть целую часть.
- Из дробной части вычесть дробную часть
- К оставшейся целой части прибавить оставшуюся дробную часть.

- Сформулировать правило вычитания смешанных чисел.
- Если дробная часть уменьшаемого меньше дробной части вычитаемого.
- Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби.
- Полученную дробь складываем с дробной частью уменьшаемого.
- Вычитаем отдельно целые части и дробные части.
- К оставшейся целой части прибавляем оставшуюся дробную часть.
- Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.
VI. Обмен информацией .
Вы рассмотрели правила сложения и вычитания смешанных чисел. Что общего у них? (Действия выполняются сначала с целыми числами, затем с дробными частями.)
Сформулируйте правило сложения смешанных чисел. (Слайд 9)
Сформулируйте правило вычитания смешанных чисел. (Слайд 10)
Стр. 174 учебника, правило
(Кусок торта.)
VII. Применение
— Вернемся к примеру:
3 1/7 + 2 3/7= (3+2)+(1/7+3/7)=5+4/7=54/7
Как убедиться, что сложение выполнено правильно? (Вычитанием). Сделать проверку.
Сделать проверку.
54/7-31/7=(5-3)+(4/7-1/7)= 2+3/7= 23/7
(Кусок торта.)
VIII. Физкультминутка (Слайд)
Потрудились — отдохнём,
Встанем, глубоко вздохнём.
Руки в стороны, вперёд,
Влево, вправо поворот.
Три наклона, прямо встать.
Руки вниз и вверх поднять.
Руки плавно опустили,
Всем улыбки подарили.
IX. Закрепление изученного материала
1. Карлсон прислал телеграмму, но все слова перепутались. Давайте решим примеры и соотнесем их с ответами. (Слайд 11)
3 7/13 – 4/13= 4 – В
5 2/5+1/5= 7 4/6 – О
10 2/3-6= 3 3/13 – У
2 2/7+2 4/7= 4 6/7 – Е
8 5/9-3= 5 5/9 – Х
3/6+7 1/6 = 4 2/3 – П
7 4/5-3 4/5= 5 3/5 – С
(Кусок торта.)
«Охота за пятерками»
2. Работа над задачами.
а) Стр. 175, №1115.
- Прочитайте задачу.
- Сколько конфет в одной коробке?
- Сколько конфет в другой коробке?
- Как ответить на вопрос задачи?
- Решите задачу.
 Прочитайте ответ.
(В двух коробках 4 4/8 кг конфет.)
Прочитайте ответ.
(В двух коробках 4 4/8 кг конфет.)
б) Стр. 175, № 1116.
- Чему равна длина красной ленты?
- Что сказано про длину белой?
- Что значит на 2 1/5 м короче?
- Как будете решать эту задачу?
Решите. Прочитайте ответ. (Длина белой ленты 1 2/5 метра.)
(Кусок торта.)
Вы – замечательные ученики: старательные, внимательные, дружные, помогаете друг другу.
(прилетел Карлсон) Карлсон увидел, что вы такие ребята, каких он искал, и вернулся. Мы дарим ему торт.
X. Итог урока (вопросы Карлосона).
- Что такое смешанное число?
- Чему вы сегодня научились? (Складывать и вычитать смешанные числа.)
- Как сложить смешанные числа?
- Как вычесть смешанные числа?
Это вам поможет справиться с домашним заданием.
XI. Домашнее задание: Стр. 178, № 1136,1137
XII. Рефлексия.
Соберите заработанные кусочки в тортик. (3-5 частей – «5»)
Учитель оценивает работу учащихся. (Мордашка). (Слайд 13)
(Мордашка). (Слайд 13)
Смешанные дроби также, как и простые дроби можно вычитать. Чтобы отнять смешанные числа дробей нужно знать несколько правил вычитания. Изучим эти правила на примерах.
Вычитание смешанных дробей с одинаковыми знаменателями.
Рассмотрим пример с условием, что уменьшаемое целое и дробная часть больше соответственно вычитаемого целой и дробной части. При таких условиях вычитание происходит отдельно. Целую часть вычитаем из целой части, а дробную часть из дробной .
Рассмотрим пример:
Выполните вычитание смешанных дробей \(5\frac{3}{7}\) и \(1\frac{1}{7}\).
\(5\frac{3}{7}-1\frac{1}{7} = (5-1) + (\frac{3}{7}-\frac{1}{7}) = 4\frac{2}{7}\)
Правильность вычитания проверяется сложением. Сделаем проверку вычитания:
\(4\frac{2}{7}+1\frac{1}{7} = (4 + 1) + (\frac{2}{7} + \frac{1}{7}) = 5\frac{3}{7}\)
Рассмотрим пример с условием, когда дробная часть уменьшаемого меньше соответственно дробной части вычитаемого. В таком случае мы занимаем единицу у целого в уменьшаемом.
Рассмотрим пример:
Выполните вычитание смешанных дробей \(6\frac{1}{4}\) и \(3\frac{3}{4}\).
У уменьшаемого \(6\frac{1}{4}\) дробная часть меньше чем у дробной части вычитаемого \(3\frac{3}{4}\). То есть \(\frac{1}{4}
\(\begin{align}&6\frac{1}{4}-3\frac{3}{4} = (6 + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {1} + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {\frac{4}{4}} + \frac{1}{4})-3\frac{3}{4} = (5 + \frac{5}{4})-3\frac{3}{4} = \\\\ &= 5\frac{5}{4}-3\frac{3}{4} = 2\frac{2}{4} = 2\frac{1}{4}\\\\ \end{align}\)
Следующий пример:
\(7\frac{8}{19}-3 = 4\frac{8}{19}\)
Вычитание смешанного дроби из целого числа.
Пример: \(3-1\frac{2}{5}\)
Уменьшаемое 3 не имеет дробной части, поэтому сразу отнять мы не сможем. Займем у целой части у 3 единицу, а потом выполним вычитание. Единицу мы запишем как \(3 = 2 + 1 = 2 + \frac{5}{5} = 2\frac{5}{5}\)
\(3-1\frac{2}{5}= (2 + \color{red} {1})-1\frac{2}{5} = (2 + \color{red} {\frac{5}{5}})-1\frac{2}{5} = 2\frac{5}{5}-1\frac{2}{5} = 1\frac{3}{5}\)
Вычитание смешанных дробей с разными знаменателями.

Рассмотрим пример с условием, если дробные части уменьшаемого и вычитаемого с разными знаменателями. Нужно привести к общему знаменателю, а потом выполнить вычитание .
Выполните вычитание двух смешанных дробей с разными знаменателями \(2\frac{2}{3}\) и \(1\frac{1}{4}\).
Общим знаменателем будет число 12.
\(2\frac{2}{3}-1\frac{1}{4} = 2\frac{2 \times \color{red} {4}}{3 \times \color{red} {4}}-1\frac{1 \times \color{red} {3}}{4 \times \color{red} {3}} = 2\frac{8}{12}-1\frac{3}{12} = 1\frac{5}{12}\)
Вопросы по теме:
Как вычитать смешанные дроби? Как решать смешанные дроби?
Ответ: нужно определиться к какому типу относиться выражение и по типу выражения применять алгоритм решения. Из целой части вычитаем целое, у дробной части вычитаем дробную часть.
Как из целого числа вычесть дробь? Как от целого числа отнять дробь?
Ответ: у целого числа нужно занять единицу и записать эту единицу в виде дроби
\(4 = 3 + 1 = 3 + \frac{7}{7} = 3\frac{7}{7}\),
а потом целое отнять от целого, дробную часть отнять от дробной части. Пример:
Пример:
\(4-2\frac{3}{7} = (3 + \color{red} {1})-2\frac{3}{7} = (3 + \color{red} {\frac{7}{7}})-2\frac{3}{7} = 3\frac{7}{7}-2\frac{3}{7} = 1\frac{4}{7}\)
Пример №1:
Выполните вычитание правильной дроби из единицы: а) \(1-\frac{8}{33}\) б) \(1-\frac{6}{7}\)
Решение:
а) Представим единицу как дробь со знаменателем 33. Получим \(1 = \frac{33}{33}\)
\(1-\frac{8}{33} = \frac{33}{33}-\frac{8}{33} = \frac{25}{33}\)
б) Представим единицу как дробь со знаменателем 7. Получим \(1 = \frac{7}{7}\)
\(1-\frac{6}{7} = \frac{7}{7}-\frac{6}{7} = \frac{7-6}{7} = \frac{1}{7}\)
Пример №2:
Выполните вычитание смешанной дроби из целого числа: а) \(21-10\frac{4}{5}\) б) \(2-1\frac{1}{3}\)
Решение:
а) Займем у целого числа 21 единицу и распишем так \(21 = 20 + 1 = 20 + \frac{5}{5} = 20\frac{5}{5}\)
\(21-10\frac{4}{5} = (20 + 1)-10\frac{4}{5} = (20 + \frac{5}{5})-10\frac{4}{5} = 20\frac{5}{5}-10\frac{4}{5} = 10\frac{1}{5}\\\\\)
б) Займем у целого числа 2 единицу и распишем так \(2 = 1 + 1 = 1 + \frac{3}{3} = 1\frac{3}{3}\)
\(2-1\frac{1}{3} = (1 + 1)-1\frac{1}{3} = (1 + \frac{3}{3})-1\frac{1}{3} = 1\frac{3}{3}-1\frac{1}{3} = \frac{2}{3}\\\\\)
Пример №3:
Выполните вычитание целого числа из смешанной дроби: а) \(15\frac{6}{17}-4\) б) \(23\frac{1}{2}-12\)
а) \(15\frac{6}{17}-4 = 11\frac{6}{17}\)
б) \(23\frac{1}{2}-12 = 11\frac{1}{2}\)
Пример № 4:
Выполните вычитание правильной дроби из смешанной дроби: а) \(1\frac{4}{5}-\frac{4}{5}\)
\(1\frac{4}{5}-\frac{4}{5} = 1\\\\\)
Пример №5:
Вычислите \(5\frac{5}{16}-3\frac{3}{8}\)
\(\begin{align}&5\frac{5}{16}-3\frac{3}{8} = 5\frac{5}{16}-3\frac{3 \times \color{red} {2}}{8 \times \color{red} {2}} = 5\frac{5}{16}-3\frac{6}{16} = (5 + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {1} + \frac{5}{16})-3\frac{6}{16} = \\\\ &= (4 + \color{red} {\frac{16}{16}} + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {\frac{21}{16}})-3\frac{3}{8} = 4\frac{21}{16}-3\frac{6}{16} = 1\frac{15}{16}\\\\ \end{align}\)
Вычитание смешанных чисел с общим знаменателем | Преалгебра |
Результаты обучения
- Использование модели для вычитания смешанных чисел с одинаковыми знаменателями
- Вычитание смешанных чисел с одинаковыми знаменателями двумя разными методами
Давайте снова подумаем о пицце, чтобы смоделировать вычитание смешанных чисел с общим знаменателем. Предположим, вы только что испекли целую пиццу и хотите отдать половину пиццы своему брату. Что нужно сделать с пиццей, чтобы отдать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете дать ему половину.
Предположим, вы только что испекли целую пиццу и хотите отдать половину пиццы своему брату. Что нужно сделать с пиццей, чтобы отдать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете дать ему половину.
Мы будем использовать дробные круги (пиццы!), чтобы визуализировать процесс.
Начните с одного целого.
Алгебраически вы бы написали:
Пример
Используйте модель для вычитания:
1−131-\frac{1}{3}1−31
.
Решение:
Попробуйте
#146391
Что, если мы начнем с более чем одного целого? Давай выясним.
Пример
Используйте модель для вычитания:
2−342-\frac{3}{4}2−43
.
Показать решение
Решение:
Попробовать
#146392
В следующем примере мы вычтем более одного целого.
Пример
Используйте модель для вычитания:
2−1252 — 1\frac{2}{5}2−152
.
Показать решение
Решение:
попробовать
#146393
Что делать, если вы начинаете со смешанного числа и вам нужно вычесть дробь? Подумайте об этой ситуации: вам нужно поставить три четверти на парковочный счетчик, но у вас есть только 9.0011
$1\$1$1
купюра с четвертью. Что ты можешь сделать? Вы можете обменять долларовую купюру на
444
четвертаков. Стоимость
444
четвертаков такая же, как у одной долларовой банкноты, но
444
четвертаков более полезны для парковочного счетчика. Теперь вместо купюры
Теперь вместо купюры
$1\$1$1
и одной четверти у вас есть
555
четвертаков, и вы можете поместить
333
четвертей в счетчик.
Это моделирует то, что происходит, когда мы вычитаем дробь из смешанного числа. Мы вычли три четверти из одного доллара и одну четверть.
Мы также можем смоделировать это с помощью дробных кругов, как мы делали для сложения смешанных чисел.
Пример
Используйте модель для вычитания:
114−341\frac{1}{4}-\frac{3}{4}141−43
Показать решение
Решение:
| Перепишите по вертикали. Начните с одного целого и одной четверти. | 114\color{red}{1\frac{1}{4}}141 −−34—\frac{3}{4}−−43 | |
Поскольку дроби имеют знаменатель 4, разрежьте целое на 4 части. Теперь у вас есть 44\frac{4}{4}44 и14\frac{1}{4}41 , что равно54\frac{5}{4}45 . | 54\color{red}{\frac{5}{4}}45 −−34—\frac{3}{4}−−43 | |
| Убрать 34\frac{3}{4}43 .Осталось 12\frac{1}{2}21 . | 54\frac{5}{4}45 −−3424=12\frac{\color{red}{—\frac{3}{4}}}{\frac{2}{4} =\frac{1}{2}}42=21−−43 |
Попробуйте
Используйте модель для вычитания. Нарисуйте картинку, иллюстрирующую вашу модель.
113−231\frac{1}{3}-\frac{2}{3}131−32
Показать решение
Используйте модель для вычитания. Нарисуйте картинку, иллюстрирующую вашу модель.
115−451\frac{1}{5}-\frac{4}{5}151−54
Показать решение
Теперь вычтем смешанные числа без использования модели. Но это может помочь представить модель в уме, когда вы читаете шаги.
Вычитание смешанных чисел с общими знаменателями
- Перепишите задачу в вертикальной форме.
- Сравните две дроби.
- Если верхняя фракция больше нижней, перейдите к шагу 3.
- Если нет, то в верхнем смешанном числе взять одно целое и прибавить его к дробной части, получив смешанное число с неправильной дробью.
- Вычитание дробей.
- Вычтите целые числа.
- Упростите, если возможно.
Пример
Найдите разность:
535−2455\frac{3}{5}-2\frac{4}{5}553−254
Решение:
535−2455\frac{3}{5}-2\frac{4}{5}553−254 | |
Перепишите задачу в вертикальной форме. | |
| Начиная с 35\frac{3}{5}53 меньше45\frac{4}{5}54 , возьмите 1 из 5 и добавьте к35:(55+35=85)\frac{3}{5}:\left( \frac{5}{5}+\frac{3}{5}=\frac{8}{5}\right)53:(55+53=58) | |
| Вычтите дроби. | |
| Вычесть целые части. Результат в простейшей форме. |
Так как задача была дана со смешанными числами, мы оставляем результат как смешанные числа.
Попробуйте
#146395
Посмотрите следующее видео, чтобы увидеть еще два примера того, как вычитать смешанные числа с одинаковыми знаменателями.
Точно так же, как мы делали со сложением, мы могли вычитать смешанные числа, преобразовывая их сначала в неправильные дроби. Мы должны записать ответ в том виде, в каком он был задан, поэтому, если нам даны смешанные числа для вычитания, мы запишем ответ как смешанное число.
Мы должны записать ответ в том виде, в каком он был задан, поэтому, если нам даны смешанные числа для вычитания, мы запишем ответ как смешанное число.
Вычитание смешанных чисел с общими знаменателями как неправильных дробей
Шаг 1. Перепишите смешанные числа в виде неправильных дробей.
Шаг 2. Вычтите числители.
Шаг 3. Запишите ответ в виде смешанного числа, по возможности упростив дробную часть.
Пример
Найдите разницу, переведя в неправильные дроби:
9611−710119\frac{6}{11}-7\frac{10}{11}9116−71110
Показать решение
Решение:
9611−710119\frac{6}{11}-7\frac{10}{11}9116−71110 | |
| Перепишите как неправильные дроби. | 10511−8711\frac{105}{11}-\frac{87}{11}11105−1187 |
| Вычесть числители. | 1811\фрак{18}{11}1118 |
Перепишите как смешанное число. | 17111\фрак{7}{11}1117 |
Попробуйте
#146395
Лицензии и атрибуты
Лицензионный контент CC, ранее опубликованный
- Пример: вычитание смешанных чисел с одинаковыми знаменателями. Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Атрибуция
Лицензионный контент CC, Конкретная атрибуция
- Преалгебра. Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно на http://cnx.org/contents/[email protected]
2 Стратегии сложения и вычитания дробей
Если вы работаете со своими учениками над сложением и вычитанием дробей, убедитесь, что вы используете различные стратегии. Важно показать учащимся, как использовать визуальные модели в дополнение к стандартному алгоритму .
В 4-м классе учащиеся в основном работают над сложением и вычитанием дробей с подобных знаменателям .
По 5 класс , в отличие от знаменателей используются для сложения и вычитания как дробей, так и смешанных чисел.
Создание модели дроби важно для того, чтобы показать учащимся, почему они складывают или вычитают только числители, а не знаменатели.
Сложение с одинаковыми знаменателями
На приведенном ниже примере изображения с одинаковыми знаменателями учащиеся должны создать прямоугольник, представляющий одно целое со столбцами, чтобы показать, сколько частей в целом. В примере сложения добавляемые дроби выходят за пределы девятых, поэтому они создадут один прямоугольник с 9столбцы. Чтобы представить первую дробь, они должны закрасить 3 из 9 столбцов одним цветом, а затем могут использовать тот же или другой цвет, чтобы закрасить еще 1 столбец, чтобы представить добавленную 1/9. После того, как эти два цвета будут закрашены, модель теперь имеет затенение 4/9.
После того, как эти два цвета будут закрашены, модель теперь имеет затенение 4/9.
Вычитание с одинаковыми знаменателями
В примере с вычитанием учащиеся должны создать прямоугольник с 12 столбцами, заштриховав 11 из них, чтобы представить 11/12. Чтобы вычесть из этого 4/12, они вычеркивают 4 из 11 заштрихованных частей. Количество оставшихся заштрихованных столбцов будет разницей. В этом случае ответ 7/12.
Сложение с разными знаменателями
Чтобы сложить дроби с разными знаменателями с помощью визуальной модели, сначала нужно создать модели для представления каждой из дробей, а затем найти эквивалентные дроби с тем же знаменателем. Для этого вам нужно найти наименьшее общее кратное двух дробей, а затем использовать НОК в качестве их общего знаменателя.
В приведенном ниже примере задачи LCD 1/4 и 3/5 равен 20. Каждая модель дроби должна состоять из 20 штук. Первая дробь (1/4) имеет 4 столбца, поэтому нам нужно разбить 4 столбца на 5 строк, чтобы получилось 20 штук. Вторая дробь (3/5) состоит из 5 столбцов, поэтому вам нужно создать 4 ряда, чтобы получить 20 штук. Теперь мы можем увидеть эквивалентные дроби для каждой из исходных дробей: 1/4 = 5/20 и 3/5 = 12/20. Наконец, сложите эквивалентные дроби, чтобы получить окончательный ответ 17/20.
Вторая дробь (3/5) состоит из 5 столбцов, поэтому вам нужно создать 4 ряда, чтобы получить 20 штук. Теперь мы можем увидеть эквивалентные дроби для каждой из исходных дробей: 1/4 = 5/20 и 3/5 = 12/20. Наконец, сложите эквивалентные дроби, чтобы получить окончательный ответ 17/20.
Вычитание с разными знаменателями
Чтобы вычесть две дроби с разными знаменателями, начните с создания моделей дробей для каждой дроби в задаче. У них должен быть общий знаменатель, поэтому найдите наименьшее общее кратное обоих знаменателей.
Для 4/5 и 1/3 НОК равен 15, поэтому общий знаменатель равен 15. Затем создайте эквивалентные дроби, используя общий знаменатель. Первая дробь (4/5) имеет 5 столбцов, поэтому нам нужно создать 3 ряда, чтобы получилось 15 штук. Вторая дробь (1/3) должна состоять из 5 рядов. Первая фракция теперь имеет 12 из 15 закрашенных фигур (12/15). Нам нужно будет вычесть количество штук во второй модели дроби из первой. Для этого зачеркните 5 из 12 заштрихованных частей. Остальные заштрихованные не зачеркнутые столбцы — это ответ: 7/15.
Остальные заштрихованные не зачеркнутые столбцы — это ответ: 7/15.
При использовании стандартного алгоритма для нахождения суммы или разности двух дробей с разными знаменателями я учу своих учеников записывать исходные дроби вертикально . Причина, по которой я учу это таким образом, заключается в том, что мне нравится, когда они получают наглядное представление о создании своих эквивалентных дробей сбоку и показывают, на что они умножают числитель и знаменатель, чтобы получить эквивалентные дроби.
Учащимся снова потребуется:
- Найдите наименьшее общее кратное каждой дроби, чтобы найти общий знаменатель.
- Создайте эквивалентные дроби.
- Определить, на что умножить знаменатель исходной дроби, чтобы получить общий знаменатель.
- Умножьте числитель на то же число, что и в шаге 3 (мне нравится рисовать стрелку от исходной дроби к эквивалентной дроби и показывать промежуточное умножение. Это также помогает при проверке ошибок учащихся.
 )
) - Сложите или вычтите эквивалентные дроби.
Создание последовательных стратегий сложения и вычитания дробей поможет вашим учащимся лучше понять этот навык. Хотя им может не нравиться показывать свою работу, для них очень важно это делать, чтобы вы, как учитель, могли определить любые неправильные представления, которые они могут развить, и вмешаться в случае необходимости.
Распространенные заблуждения:
- сложение числителя И знаменателя двух дробей
- умножение знаменателей обеих дробей для нахождения наименьшего общего знаменателя вместо нахождения их НАИМЕНЬШЕГО общего кратного (хотя это не является неправильным , это может привести к более частому упрощению ответа в конце)
У меня есть цифровой и печатный ресурс (пакет из двух также доступен со скидкой), который содержит мини-уроки по каждому из упомянутых выше навыков:
- подробные примечания
- практических страниц/занятий
- выездные билеты
- карточки с заданиями
- викторина
- обучающие видеоролики (включены в цифровую версию)
Сообщения в блогах
- Сложение и вычитание дробей
- Сложение и вычитание смешанных чисел
- Умножение дробей
- Деление дробей
- Эквивалентные дроби
- Знакомство с дробями
- Упрощение дробей
- Неправильные дроби и смешанные числа
Ресурсы
- Дробные операции НАБОР
- Сложение и вычитание дробей
- Сложение и вычитание смешанных чисел
- Умножение дробей
- Деление дробей
- Графики дробей
- Все ресурсы фракции
Вычитание дробей с разными знаменателями
Дроби являются частями целого, т. е. представляют часть набора. Слово «фракция» происходит от «fractio», латинского слова, означающего «разбивать». Египтяне использовали дроби для решения математических задач, в том числе для деления пищи и припасов. Древние римляне записывали дроби словами, а не числами. Индийцы сначала записывали дроби как числа, которые появлялись как одно число над другим. Арабы были первыми, кто добавил линию между числами, различая их как числители и знаменатели.
е. представляют часть набора. Слово «фракция» происходит от «fractio», латинского слова, означающего «разбивать». Египтяне использовали дроби для решения математических задач, в том числе для деления пищи и припасов. Древние римляне записывали дроби словами, а не числами. Индийцы сначала записывали дроби как числа, которые появлялись как одно число над другим. Арабы были первыми, кто добавил линию между числами, различая их как числители и знаменатели.
Когда мы делим что-то целое на разные части, каждая часть становится частью этого целого.
Например, если разрезать целый арбуз на две части, обе части станут половиной целого арбуза или частью арбуза. Тогда одна половина арбуза математически представляется как 12. Если вы разрежете две половинки арбуза еще на две части, весь арбуз разделится на четыре части или четверти всего арбуза. Тогда одна часть арбуза будет представлена как ¼.
Другим прекрасным примером, иллюстрирующим эту концепцию, является пицца. Пицца представляет собой круг, разделенный на 4-6 или более частей, в зависимости от размера. В этом случае каждый кусочек пиццы представляет собой часть целого, которым является пицца.
В этом случае каждый кусочек пиццы представляет собой часть целого, которым является пицца.
Какие части дроби?
Числитель и знаменатель составляют две части дроби. Горизонтальная черта, разделяющая числитель и знаменатель, называется дробной чертой.
- В знаменателе указано количество частей, на которые было разделено целое. Его место находится под дробной чертой.
- Числитель указывает количество частей фракции, которые представлены или выбраны. Его место над дробной чертой.
Например, в дроби 1227 12 — числитель, а 27 — знаменатель.
Почему мы используем дроби?
Дроби говорят нам, какая часть целого у вас есть, в чем вы нуждаетесь или хотите. Дроби также легче понять, чем десятичные. Они помогают лучше визуализировать концепцию или систему.
Типы фракций:
Существует четыре основных типа фракций. Вот они:
- Единица Дробь – Дробь с 1 в числителе. Например, 12, 14
- Правильная дробь — у них числитель меньше знаменателя.
 Пример: 49, 910
Пример: 49, 910 - Неправильная дробь. У них числитель больше знаменателя. Пример: 37, 128
- Смешанная дробь. Состоят из целого числа с правильной дробью. Пример 5 34, 10 12
Как упростить дроби?
Чтобы упростить дробь, вы можете выполнить любой из следующих шагов в зависимости от того, что больше подходит:
- Найдите наибольший общий делитель:
Для этого запишите множители для обоих числителей и знаменатель. Например:
Чтобы упростить дробь 824,
Шаг 1: Делители числителя и знаменателя:
Факторы
24 = 1, 2, 3, 4, 6, 8, 12, 24
Множители 8 = 1, 2, 4, 8
Шаг 2: Наибольший/наивысший общий делитель равен числу 8.
Шаг 3 : Разделите как числитель, так и знаменатель на 8
8, разделенные на 8 = 1
24, разделенные на 8 = 3
Шаг 4: Упрощенная фракция составляет 13
- Упрощенные неправомерные фракции с смешанными номерами
до смешанных номеров
— до смешанных номеров 9
до смешанных номеров до. упростить неправильную дробь до смешанного числа, шаги:
упростить неправильную дробь до смешанного числа, шаги:
- Разделить числитель на знаменатель
- В результате записать целое число
- Записать остаток в числитель дроби
- Знаменатель останется прежним
Сложение и вычитание дробей
складывать или вычитать дроби, давайте сначала разберемся в типах дробей по этому признаку:- Как дроби — у этих дробей одинаковый знаменатель.
Пример: 34, 54, 94. Все эти дроби имеют одинаковый знаменатель. Таким образом, они подобны дробям.
- В отличие от дробей – это дроби, имеющие разные знаменатели.
Пример: 53, 49, 27. Все эти дроби имеют разные знаменатели. Таким образом, они не похожи на дроби.
- Эквивалентные дроби — это дроби, которые после упрощения имеют одинаковое значение.
Пример: 25 и 410. Если упростить 410, получится 25. Таким образом, получится 25 и 410 эквивалентных дробей.
Таким образом, получится 25 и 410 эквивалентных дробей.
Сложение дробей:
Чтобы сложить дроби, первым шагом является определение того, являются ли знаменатели дробей одинаковыми или разными, т. е. являются ли они одинаковыми или разными дробями.
Для одинаковых дробей сложите числители и поместите ответ над тем же знаменателем.
Пример:
26 + 56 = 2+56 = 76
Тогда упростите, если возможно. В этом примере упрощение невозможно.
Для разных дробей сначала приведите знаменатели к одному числу. Числитель и знаменатель дробей следует умножить на их НОК (наименьшее общее кратное). Чтобы найти LCM, все, что вам нужно сделать, это определить кратные знаменателям, а затем найти наименьшее общее кратное. Наименьшее общее кратное — это меньшее число в списке кратных.
Пример:
Чтобы сложить 211 и 34
Наименьшее общее кратное 4 и 11 равно 44. Итак, умножьте числитель и знаменатель каждой дроби на число, которое даст 44 в качестве знаменателя.
1×411×4 + 3×114×11 = 444 + 3344
Теперь сложим две дроби как равные дроби
444 + 3344 = 4 + 3344 = 3744
Вычитание множителей Теперь, вы,
9 9 может спросить, как вычитать дроби с разными знаменателями? Как и при сложении дробей, первым шагом при вычитании дробей является определение того, одинаковы или различны знаменатели дробей, т. Е. Похожи они или различны дроби.Чтобы вычесть дроби с одинаковыми знаменателями, вычтите числители и поднесите их разность к общему знаменателю.
Пример: 47-37 = 4-37 = 17
для вычитания фракций с непохожными знаменателями, существует два метода:
- . Процессы. , вычтите второе число из первого, чтобы получить числитель ответа.
Пример: Найдите разницу между 67 и 25
Чтобы получить числитель, перемножьте две дроби крест-накрест. Затем вычтите их произведения.
(6 x 5) – (2 x 7) = 30 – 14 = 16
Затем умножьте два знаменателя.

7 x 5 = 35
Положите произведение перекрестного умножения на знаменатель, чтобы получить ответ.
Таким образом, ваш ответ будет таким: 67 − 25 = 1635
- Метод НОК:
Этот метод также используется для добавления разнородных фракций. [Совет: Будьте осторожны с размещением дробей, поскольку любая замена двух дробей местами даст два совершенно разных результата.]
Чтобы использовать этот метод, выполните следующие действия:
- Шаг 1: Преобразуйте их в одинаковые дроби. . Сначала найдите НОК знаменателей. Выполните те же шаги, что и при сложении разных знаменателей, чтобы найти НОК знаменателей.
- Шаг 2: Затем вычтите числители.
- Шаг 3: При необходимости упростите дробь.
Пример: Вычтите 16 из 12
- Сначала найдите НОК знаменателей.
Кратные 2 = 2, 4, 6, 8
Кратные 6 = 6, 12, 18
Наименьший общий знаменатель равен 6.

- Во-вторых, найдите эквивалентную дробь, умножив числитель и знаменатель с числом, так что результирующий знаменатель равен 6.
1×32×3 = 16
- Перепишите проблему с использованием фракций
12 — 16 = 36 — 16
- Далее, вычитайте числители, поскольку знаменатели в настоящее время являются одинаковыми
36 — 16 = 3 — 26
- Упрощайте если возможно
26 = 13
- Итак, окончательный ответ: 12 – 16 = 13
Итак, теперь вы знаете шаги сложения и вычитания дробей с разными знаменателями и одинаковыми знаменателями. Фракции важны, потому что мы применяем их в нашей повседневной жизни. При покупке еды, делении денег или расчете расстояния и времени дроби облегчают поиск решения вашей проблемы. Сознательно или неосознанно, нам нужны дроби в нашей повседневной жизни. Научиться складывать и вычитать дроби — это просто введение в мир дробей. Есть еще много методов, приложений и способов использования дробей.
 Как только вы научитесь складывать и вычитать дроби, у вас будет прочная основа для перехода к более сложным понятиям, таким как умножение и деление.
Как только вы научитесь складывать и вычитать дроби, у вас будет прочная основа для перехода к более сложным понятиям, таким как умножение и деление.Рабочий лист для вычитания множителей с разными знаменателями.
- Find the difference between:
- 59 – 26 = __________________
- 916 – 18 = __________________
- 820 – 618 = __________________
- 49 – 25 = __________________
- 314 – 29 = __________________
- Решите эти текстовые задачи, используя метод НОК для вычитания дробей с разными знаменателями
- Энни и Марк соревнуются в беге. Энни преодолела 24 из общей дистанции, а Марк преодолел 15 из общей дистанции. Какова разница в расстоянии, пройденном ими обоими?
- У Тома 57 штук папайи. Если он отдаст 23 из них Джерри, какая часть папайи останется?
- Рецепт требует 34 чайных ложки черного перца и 14 чайных ложек красного перца.
 Насколько больше черного перца, чем красного, нужно по рецепту?
Насколько больше черного перца, чем красного, нужно по рецепту? - Кайли живет 49милях от зоопарка. Сэнди живет в 24 милях от зоопарка. Насколько Сэнди ближе к зоопарку, чем Кайли?
Часто задаваемые вопросы
1. Что такое вычитание дробей с разными знаменателями?
Ответ. Если один из знаменателей — дробь, а другой — целое число, нужно преобразовать целое число в дробь, а затем вычесть. Рассмотрим пример:
2/3-1/4 = 2/3 – (1/4) = 2/3 – 1/4 = ¾
2. Как вычитать дроби с разными знаменателями?
Ответ. Вычитание дробей с разными знаменателями — простой процесс. Все, что вам нужно сделать, это найти наименьшее общее кратное числителей и умножить их на знаменатель вашего ответа. Ответ будет в простейшей форме, поэтому, если вы хотите получить десятичную дробь, вам придется округлить ее в большую или меньшую сторону.
3. Каковы шаги для вычитания дробей с разными знаменателями?
Ответ.
 Шаги для вычитания дробей с разными знаменателями:
Шаги для вычитания дробей с разными знаменателями:Упростите дробь в верхней части столбца дробей.
Вычтите числитель каждой дроби из соответствующего знаменателя.
При необходимости уменьшите полученную дробь.
4. Каково правило вычитания дробей с разными знаменателями?
Ответ. Чтобы вычесть одну дробь из другой, нужно убедиться, что у них одинаковый знаменатель. Если нет, то вам придется найти общий знаменатель. Самый простой способ сделать это — сложить числители и умножить на новый знаменатель.
5. Приведите пример вычитания дробей с разными знаменателями.
Ответ. Пример вычитания дробей с разными знаменателями:
-2/3 – 4/5 = -⅓
Сложение и вычитание дробей и смешанных чисел— Полный курс арифметики
Мы выбираем общее кратное знаменателей, потому что мы меняем знаменатель, умножая его. Урок 22.
Пример 3. 
2
3+ 1
4. Решение . Наименьшим общим кратным чисел 3 и 4 является их произведение, 12. (Урок 22, вопрос 4.)
Преобразуем каждую дробь в эквивалентную дробь со знаменателем 12.
2
3+ 1
4= 8
12+ 3
12= 11
12. Мы преобразовали 2 от
3до 8
12, сказав: «3 входит в (содержится) 12 четыре раз.
 Четыре раза по 2 равно 8.»
Четыре раза по 2 равно 8.»(Так мы умножили и 2, и 3 на одно и то же число, а именно на 4. См. урок 22, вопрос 3.)
Мы преобразовали 1 от
4до 3
12, сказав: «4 входит в 12 три раз. Трижды 1 будет 3″. (Мы умножили и 1, и 4 на 3.)
Тот факт, что мы говорим то, что делаем, еще раз показывает, что арифметика — это разговорный навык.
На практике необходимо записать общий знаменатель только один раз:
2
3+ 1
4= 8 + 3
12= 11
12. Пример 4. 
4
5+ 2
15Решение . НОК 5 и 15 равно 15. Следовательно,
4
5+ 2
15= 12 + 2
15= 14
15. Мы изменили 4 от
5до 12
15, сказав: «5 входит в 15 три раз. Три раза по 4 равно 12.»
Мы не меняли 2
15, потому что мы не меняем знаменатель 15.

Пример 5. 2
3+ 1
6+ 7
12Решение . LCM 3, 6 и 12 равно 12 900 11.
2
3+ 1
6+ 7
12= 8 + 2 + 7
122
3+ 1
6+ 7
12= 17
122
3+ 1
6+ 7
12= 1 5
12. 
Мы преобразовали 2 от
3до 8
12, сказав: «3 входит в 12 четыре раз. Четыре раза по 2 равно 8.»
Мы преобразовали 1 от
6до 2
12, сказав: «6 входит в 12 два раз. Дважды 1 равно 2.»
Мы не меняли 7
12, потому что мы не меняем знаменатель 12.
Наконец, мы изменили неправильную дробь 17
12до 1 5
12по деление 17 на 12.
 (Урок 20.)
(Урок 20.)«12 превращается в 17 один (1) раз с остатком 5.»
Пример 6. 5
6+ 7
9Решение . НОК 6 и 9 равно 18 900 11.
5
6+ 7
9= 15 + 14
18= 29
18= 1 11
18. Мы изменили 5 от
6до 15
18путем умножения обоих членов на 3,9.0126 Мы изменили 7 от
9до 14
18путем умножения обоих членов на 2. 
Пример 7. Добавьте мысленно 1
2+ 1
4. Ответ . 1
2это сколько 1
4? 1
2= 2
4. Точно так же, как 1 — половина 2, 2 — половина 4. Следовательно,
1
2+ 1
4= 3
4. Студент не должен писать задачи, в которых один из
доли 1
2, а знаменатель другого четный. 
Например,
1
2+ 2
10= 7
10— потому что 1
2= 5
10. Пример 8. На недавнем экзамене одна восьмая часть студентов получила пятерку, две пятых — четверку, а остальные — тройку. Какая часть получила тройку?
Решение . Пусть 1 представляет собой все количество студентов. Тогда вопрос:
1
8+ 2
5+ ? = 1 . Сейчас,
1
8+ 2
5= 5 + 16
40= 21
40. 
Остаток, дробь, получившая C, является дополнением к 21
40. Это 19
40. Как вычитать дроби с разными знаменателями
Как вычитать дроби с разными знаменателями
Чтобы вычесть дроби с разными знаменателями, выполните следующие действия:
- Найдите наименьшее общее кратное знаменателей дробей.
- Запишите эквивалентные дроби, имеющие наименьшее общее кратное в знаменателе.
- Оставьте это наименьшее общее кратное в качестве знаменателя ответа.
- Вычтите числители в вопросе, чтобы получить числитель ответа.
Самое главное правило при вычитании дробей — сначала составить общий знаменатель. Знаменатели дробей должны быть одинаковыми до их вычитания.
Например, вот 4 / 6 — 3 / 8 .

Знаменатели – это числа в нижней части дроби. Знаменатели 6 и 8 разные. Чтобы вычитать дроби, нам нужно, чтобы знаменатели были одинаковыми.
Общий знаменатель — это число, кратное всем остальным знаменателям. Обычно его выбирают как первое число, которое появляется во всех таблицах умножения знаменателей. Например, с 4 / 6 — 3 / 8 общий знаменатель равен 24, поскольку 24 – это первое число в таблицах умножения на 6 и 8.
Чтобы найти наименьший общий знаменатель, перечислите числа, кратные каждому знаменателю, и запишите первое число, которое появляется в каждом списке. Кроме того, общий знаменатель можно найти, перемножив знаменатели вместе.
Число, кратное 6, равно 6, 12, 18, 24, а число, кратное 8, равно 8, 16, 24. 24 — это первое число, которое появляется в каждом списке, и поэтому оно является наименьшим общим знаменателем 6 и 8. Наименьший общий знаменатель также широко известен как наименьший общий знаменатель.
 Это наименьший общий знаменатель, который можно найти.
Это наименьший общий знаменатель, который можно найти.Следующим шагом является нахождение эквивалентных дробей, имеющих наименьший общий знаменатель.
Знаменатель первой дроби умножен на 4. Следовательно, нам нужно умножить и числитель на 4.
Расчет знаменателя: 6 × 4 = 24. Расчет числителя: 4 × 4 = 16. И числитель, и знаменатель умножаются на 4.
Знаменатель второй дроби умножен на 3. Следовательно, нам нужно умножить и числитель на 3.
Расчет знаменателя: 8 × 3 = 24. Расчет числителя: 3 × 3 = 9. И числитель, и знаменатель умножаются на 3.
Теперь, когда дроби имеют общий знаменатель, можно выполнить вычитание. Знаменатель ответа совпадает с общим знаменателем.
Наименьший общий знаменатель равен 24, поэтому знаменатель ответа также равен 24.
Чтобы найти числитель ответа, просто вычтите числители в вопросе.
16 — 9 = 7, значит, числитель ответа равен 7.
4 / 6 — 3 / 8 = 7 / 24 .

Вот еще один пример пошагового вычитания разнородных дробей.
У нас есть 1 / 2 — 1 / 5 .
Знаменатели разные, значит, нужно найти равнозначные дроби с общим знаменателем.
Число, кратное 2, равно 2, 4, 6, 8, 10, число, кратное 5, равно 5 и 10.
Мы видим, что 10 — это первое число в обоих списках, поэтому 10 — это наименьший общий знаменатель 2 и 5.
Мы пишем 1 / 2 как 5 / 10 .
Мы пишем 1 / 5 как 2 / 10 .
Теперь, когда у нас есть общий знаменатель, мы можем вычесть дроби 5 / 10 — 2 / 10 = 3 / 10 .
Если оба знаменателя простые, наименьший общий знаменатель находится путем перемножения знаменателей. Например, в 1 / 2 — 1 / 5 , наименьший общий знаменатель равен 10, потому что 2 × 5 = 10.

Вычитание дробей методом бабочки
Метод бабочки — это короткий метод, который можно использовать для сложения или вычитания двух дробей. Он включает в себя умножение числителя одной дроби на знаменатель другой с пузырьками вокруг каждого умножения, нарисованными для создания изображения бабочки.
Чтобы вычесть дроби по методу бабочки, выполните следующие действия:
- Перемножьте два знаменателя, чтобы найти знаменатель ответа.
- Умножить первый числитель на второй знаменатель.
- Умножить второй числитель на первый знаменатель.
- Запишите оба этих ответа в числителе, разделив их знаком вычитания.
- Выполните вычитание, чтобы получить одно число в качестве числителя.
- Упростите дробь, если это возможно.
Например, у нас есть 4 / 5 — 2 / 3 .
На приведенной ниже диаграмме показано, как работает метод бабочки.

Сначала умножаем знаменатели 5 и 3.
5 × 3 = 15, значит, знаменатель ответа равен 15.
Далее умножаем числитель первой дроби на знаменатель второй дроби.
4 × 3 = 12, поэтому мы пишем 12 в числителе дроби.
Далее умножаем числитель второй дроби на знаменатель первой дроби.
2 × 5 = 10, поэтому мы пишем 10 рядом с 12 со знаком вычитания между ними.
Для каждого умножения в методе бабочки нарисуйте кружок вокруг чисел. Это делает общий расчет похожим на бабочку и может облегчить запоминание и изучение метода.
Наконец, мы работаем над вычитанием числителя.
12 — 10 = 2, значит, 2 — числитель.
Результат расчета методом бабочки: 2 / 15
Метод бабочки — это простой способ рутинного решения сложения и вычитания двух дробей. Преимущества метода «бабочка» заключаются в том, что он снижает нагрузку, а метод легче запомнить благодаря симметричному рисунку «бабочка».
 Это полезный метод обучения, когда получено начальное понимание того, как складывать и вычитать дроби.
Это полезный метод обучения, когда получено начальное понимание того, как складывать и вычитать дроби.Основная проблема метода бабочки заключается в том, что он позволяет складывать и вычитать только две дроби. Не рекомендуется вводить сложение и вычитание дробей с помощью метода бабочки, потому что это не позволяет четко понять, почему метод работает, и его использование ограничено конкретными типами вопросов.
Вычитание в отличие от дробей Простые примеры
Вот несколько более простых примеров для практики. При обучении вычитанию дробей с разными номиналами полезно начинать с примеров, когда нужно изменить только одну дробь.
В этих примерах требуется изменить только одну дробь, чтобы найти общий знаменатель. Если один знаменатель дроби кратен другому, то нужно изменить только одну дробь.
Первый простой пример: 1 / 2 — 1 / 4 .
Мы видим, что знаменатель числа 4 кратен знаменателю числа 2.

Это означает, что мы можем просто удвоить значения в дроби 1 / 2 , чтобы получить общий знаменатель 4. 1 / 2
Перепишем 1 / 2 — 1 / 4 как 2 / 4 — 1 / 4 .
2 — 1 = 1, значит, числитель ответа равен 1. В знаменателе остается 4.
Ответ: 1 / 4 .
Вот еще один простой пример вычитания дробей с разными знаменателями.
У нас есть 11 / 12 — 3 / 4 .
Мы видим, что 12 кратно 4, поэтому нужно изменить только одну дробь. 4 нужно умножить на 3, чтобы получилось 12.
Перепишем дробь 3 / 4 как 9 / 12 .
11 / 12 — 9 / 12 = 2 / 12 .
Этот ответ можно упростить, уменьшив вдвое и числитель, и знаменатель.

2 / 12 упрощается до 1 / 6 .
Как вычитать смешанные числа с разными знаменателями
Чтобы вычесть смешанные числа с разными знаменателями, выполните следующие действия:
- Запишите смешанные числа в виде неправильных дробей.
- Найдите наименьший общий знаменатель.
- Запишите неправильные дроби в виде эквивалентных дробей, имеющих наименьший общий знаменатель.
- Знаменатель ответа совпадает с этим наименьшим общим знаменателем.
- Вычтите числители, чтобы найти числитель ответа.
Например, вот 5 1 / 4 — 2 2 / 3 .
Первый шаг — преобразовать смешанные числа в неправильные дроби.
Чтобы преобразовать смешанное число в неправильную дробь, умножьте целое число на знаменатель и прибавьте числитель. Этот результат является новым числителем, а знаменатель совпадает со знаменателем смешанного числа.

5 × 4 = 20, а затем 20 + 1 = 21.
Смешанное число 5 1 / 4 можно переписать как неправильную дробь как 21 / 4 .
2 × 3 = 6, а затем 6 + 2 = 8.
Смешанное число 2 2 / 3 можно представить в виде неправильной дроби как 8 / 3 .
Теперь, когда смешанные числа записаны в виде неправильных дробей, следующим шагом вычитания является нахождение наименьшего общего знаменателя.
Первое число в таблице умножения на 4 и 3 равно 12. Наименьший общий знаменатель равен 12.
Умножаем знаменатель и числитель первой дроби на 3, а второй дроби на 4.
21 / 4 переписывается как 63 / 12 .
8 / 3 переписывается как 32 / 12 .
Теперь, когда смешанные числа преобразованы в неправильные дроби, а неправильные дроби теперь имеют общие знаменатели, мы, наконец, можем выполнить вычитание.

Знаменатель остается прежним, а числители вычитаем.
63 / 12 — 32 / 12 = 31 / 12 .
Последним шагом является запись неправильной дроби в виде смешанного числа, если это необходимо.
31 ÷ 12 = 2 остаток 7. Запишем целое число, а остаток как числитель дроби.
Неправильная дробь числа 31 / 12 записывается как смешанное число 2 7 / 12 .
Это окончательный ответ.
Вычитание смешанных чисел с разными знаменателями состоит из нескольких шагов. Проще говоря, чтобы вычесть смешанные непохожие дроби, сначала преобразуйте их в неправильные дроби, а затем перед вычитанием преобразуйте их в эквивалентные дроби с общим знаменателем.
Как вычитать смешанные дроби с разными знаменателями — 5 простых способов (обновленное руководство на 2022 г.) — Software Discover
В этом руководстве мы покажем вам все, что вам нужно знать о том, как вычитать смешанные дроби с разными знаменателями, так что продолжайте читать!
Ниже вы можете найти 5 различных методов вычитания смешанных дробей с разными знаменателями,
- Метод 1 – Вычитание смешанных чисел (в отличие от знаменателей) | Математика с мистером J
- Метод 2 – Как вычитать смешанные дроби с отличными знаменателями | Как вычитать смешанные дроби
- Метод 3 – Математические выходки – Вычитание смешанных чисел
- Метод 4.
 Как вычитать смешанные числа, имеющие разные знаменатели | Фракции | Предварительная алгебра | Khan Academy
Как вычитать смешанные числа, имеющие разные знаменатели | Фракции | Предварительная алгебра | Khan Academy - Метод 5 – Сложение и вычитание смешанных чисел с разными знаменателями | Математика с г-ном J
Метод 1 – Вычитание смешанных чисел (в отличие от знаменателей) | Математика с мистером J
Добро пожаловать в математику с мистером. J в этом видео собирались обсудить как вычитать смешанные числа и как. Вы можете видеть, что на вашем экране есть две проблемы, которые вы собираетесь пройти, чтобы получить. Это вниз, поэтому давайте сразу перейдем к номеру один, а для номера один у нас пять и три четверти минус.
Два с половиной, первое, что я люблю делать при вычитании или сложении смешанных чисел, которые мне нравятся. Переписать задачу по вертикали вверх и вниз, так что я собираюсь под моей исходной задачей переписать 5 и 3/4. Минус 2 и 1/2 теперь заметьте, что у меня есть моя дробная часть смешанных чисел, выстроенных в линию, и целое. Числовая часть смешанных чисел выстроилась в ряд, что вам нужно сделать, нам нужно вычесть дробную часть.
 Часть первая теперь точно так же, как когда мы складываем или вычитаем дроби, нам нужен общий знаменатель и, очевидно, знаменатель.
Часть первая теперь точно так же, как когда мы складываем или вычитаем дроби, нам нужен общий знаменатель и, очевидно, знаменатель.Из четырех и двух у нас не один и тот же знаменатель, поэтому нам нужно будет переименовать оба этих смешанных числа. Нумерует дробную часть смешанных чисел с общим знаменателем, так что давайте подумаем, что у нас получится. Общий знаменатель для 4 и 2, надеюсь, вы думаете о 4, так что давайте переименуем эти смешанные числа в 5. И 3/4 уже имеет знаменатель 4, так что мы можем оставить его таким, как сейчас 2 и 1/2. Нам нужно будет переименовать, так что давайте подумаем 2 раза 2 дает мне этот знаменатель 4, так что я.
Нужно проделать то же самое до самого верха, чтобы правильно переименовать так бы мы сделали 1 раз. 2 равно 2, теперь наша задача переписана с общим знаменателем, теперь вычитаем дробные части, а затем. Целая часть числа, поэтому 3/4 минус 2/4 ну 3 минус 2 равно 1 сохранить наш знаменатель 4 the. То же самое, а затем сделать 5 минус 2, что дает нам 3 всегда смотреть, может ли ответ быть.
 Упрощенная дробная часть 1/4 1/4 в наименьшем выражении, поэтому мы закончили решение или ответ на число.
Упрощенная дробная часть 1/4 1/4 в наименьшем выражении, поэтому мы закончили решение или ответ на число.1 равно 3 и 1/4 давайте посмотрим на число 2 давайте перепишем задачу по вертикали это означает что. Означает вверх и вниз 7 и 1/3 минус 3 и 5/6, хорошо, давайте сначала сделаем дробную часть. Не имеют общего знаменателя, поэтому нам нужно будет переименовать с общим знаменателем, поэтому 3 &. 6 давайте думать, надеюсь, мы думали общий знаменатель 6, так что 7 и сколько шестых хорошо 3. Умножить 2 на 6 1 умножить на 2 2 минус 3 5 6 уже имеет знаменатель 6 так.
Это наша переписанная задача, поэтому давайте вычтем дробную часть 2 6 минус 5/6, но мы не можем этого сделать. Потому что мы не можем сделать 2 минус 5, поэтому, как и в задаче на вычитание целых чисел, нам нужно позаимствовать. Уметь решать дробную часть этой задачи так, как ты это делаешь со смешанными числами. Чтобы позаимствовать 1 из этой 7, и он превратится в 6, мы собирались добавить один. Целое к этим 2/6, теперь я собираюсь написать одно целое как шесть на шесть, чтобы я мог добавить его к.

Эта дробная часть, им нужен общий знаменатель, чтобы сложить это целое, так что снова шесть на шесть. Это одно целое, я просто поставил его со знаменателем шесть, так что теперь у нас есть шесть отверстий правильно и. Тогда два плюс шесть будет восемь, держи мой знаменатель из шести, вычти три и пять из шести, теперь мы можем это сделать. 8 минус 5 равно 3, оставьте мой знаменатель равным 6, и тогда у нас будет 6 минус 3 равно 3. Чтобы увидеть, можем ли мы упростить дробную часть, и мы можем найти общий делитель между 3 и 6.
3, поэтому я могу разделить на 3, чтобы получить дробную часть в наименьшем выражении, и это действительно получается. Чтобы быть 3 с половиной, это был бы наш окончательный ответ, так что вот как. Вы вычитаете смешанные числа, переписываете задачу по вертикали, смотрите, нужен ли вам общий знаменатель, переименовывайте, если да, то. Идите вперед и вычтите дробную часть, а затем целую часть числа, большое спасибо за просмотр до следующего раза. Мир.

Метод 2 – Как вычитать смешанные дроби с разными знаменателями | Как вычесть смешанные дроби
Ха-ха, незаконченный, элегантный, носик 9t, выйдите из моих волос, точка g, макс, утюжок, пульс, золото, jue sori kal yi, мультиэкспозиция. Gimbap копирует хип-хоп старой школы чикано 14 г ведро кама хонам красный тепс, образованный после майского сопротивления jesus is a. Проект 1-го ветра, почему это укр йо ахак и т. д. Мне это нравится, потому что это разжиженная похлебка.
Мир я высокий, так что это действительно круто, я могу дать его вам, когда я не делаю этого. И я в хорошем настроении, ага, эксперимент от 2 до 5 000 вон, квестовая гонка, я не верю. Должна быть работа на неполный рабочий день, Ия, Так что, пожалуйста, дайте мне немного воды и доверьтесь входу от лебедя и. Получите услугу Йоарин много ходит куда-то через неделю после того, как старая справедливость сорвала с вас вторую порцию. Мета Райс Зара вместе с друзьями в следующем году зима служить подтвердил крышу круглый бокс Алессия Апессе теперь у вас есть антенна сервера.

Все-убей, и у тебя будет много мелких деталей. lf & Etc. командный стержень, что не так с порывистым финансированием. Я думаю, что эта чаша поднимется, Может быть, я пьян, рахаб отскочил от риса, Верблюда и т. Д. Такие события, как. Пробелы в программном обеспечении, кажется, заполнены, я понимаю, так что вау, да, да, капот, что, где 3, что я сделал. Разорванная волшебная грязь, почему это дешевый колокол, почему, когда я получу ли аминь шоколада, я уйду.
Кончилась 1 птица ато и нэн, я не могу купить ее после оплаты оплаченного платежа, Приходите в магазин. Молодежь Лэнгли su mac mardi может выйти, Sono di se этническая, Village wan wan, Vague naora gi терапия, A. Проект решения сердец уйти в отставку собирается после публикации, в которой говорится «вааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа», Я могу сказать вам несколько секунд, что не так с чужим микрофоном, я могу плакать.
 Лучше, возьми настойку, я в порядке со мной, Уэйд, я не могу увидеть 5 полных без сделки, ах.
Лучше, возьми настойку, я в порядке со мной, Уэйд, я не могу увидеть 5 полных без сделки, ах.Ах ах ах ах ах ах ах ах ах ах ах ах ах ах я не могу увидеть черновик что. Чтобы сделать, однако, Если я имею дело с телом владельца, Только история термаж известкового нападения, 1 строка,. Тело, Сердце, Грязь, Волна, Развилась много, Чтоб никто не мог написать эту пару, это правильный чай, боль мин. Лай лай син сообщает сущность энергии для встречи с людьми, которые, в свою очередь, придут чорим и, как крыса, поднялись. Вы 10 xavier наклонных волос приходит вареная вареная роль ко мне jojo и бой драма 2t unit 5 beolcho.
Рак будет 4, но его уже нет 2g mac nikon похож на чип, когда видишь nikon. Чипсы без сделки, похоже, ты собираешься закончить со словом ac, потому что можешь уйти. Слово основное ан хи-хван наджу больше отдыхай, я не могу видеть рай 2l сейчас, Мэй Чоа Ли Ву грязь. В моих глазах ты, хани, я собираюсь есть три года риса, даже после того, как включу в него часть.
 Общество, которое коснулось матери, Нечем было бы стрелять, Особенно после того, как мне дали конский рис, мне нравится.
Общество, которое коснулось матери, Нечем было бы стрелять, Особенно после того, как мне дали конский рис, мне нравится.Игра, которая борется с резней недоуздков, поэтому она дешевая. Разговоры о драфте действительно сокращают драфт скутера волка. Нравится этот росток с джоаном, испуганным сквозняком и тявканьем fiera pai nai dc got soft nami 2 4 this. Райс и Тим До Хи Фрикс Гость Супра Тапс Паулс Каталки Рот Сын Эден Сухожилие Психо Гана Арт Цвет И Т. Д. Основные иностранные СМИ далеко Спрани Убер Ла зачем просто чистить мой ди маре кальян на 13.
Регги ублюдок секс-ориентированный ли немного спа вязать 5-го уровня осталось, 3 мито делает это дешевый дешевый секс трубки. Hay kana cd sniff hearts поверьте, меня сильно заблокировали, поэтому я сделал свою сумку cm air max. Обслуживание лошади Asheen человек произвольно теплые ботинки, чтобы понюхать лошадь секс tq mas пункт ваш большой палец пуля король почти q. Во время секса команда наблюдает за кругом, мусор для беременных, рэп, бонни, т 10, оппозиция, сексуальный уик-энд, звук, q, тв, носок, 1.
 Напиши свободную библию, так как я понимаю, сколько эпизодов максимальной ценности остается в очереди каждый день, я представлю.
Напиши свободную библию, так как я понимаю, сколько эпизодов максимальной ценности остается в очереди каждый день, я представлю.Вам на сенсорную смесь замка суши, если вы знаете продвинутую смесь. Скажи это как-нибудь mac mouse i. Был без него, я был избит им в первом куплете предыдущего сезона, потому что он был выключен. Так что не позволяйте этому закончить предыдущий сезон по одной неделе или что-то в этом роде, возьмите на себя ответственность. День и узнайте о 100 адресах Мишель Тартам.
Метод 3 – Математические выходки – Вычитание смешанных чисел
Привет, роб, добро пожаловать в математические выходки, на предыдущем уроке мы научились складывать смешанные числа и в. В этом уроке мы собирались научиться их вычитать, вычитание всегда мало сложнее, чем сложение, потому что. Вычитание не имеет коммутативного свойства, что означает, что порядок чисел, которые вы вычитаете, имеет значение и для вас. Невозможно переключить его, как вы можете с вычитанием сложения, также сложно, потому что, если вы попытаетесь вычесть число из.

Меньшее число, например, 1 минус 5, чтобы получить отрицательный ответ, к счастью, не решит никаких проблем. Что у вас есть отрицательные ответы в этом видео, но, как вы увидите через несколько минут, есть случаи, когда. Кажется, что вам нужно вычесть большее число из меньшего сначала все это означает. Вычитание смешанных чисел может быть немного сложнее, чем их сложение, но не волнуйтесь, примите это. Шаг за шагом, и это очень поможет, если вы убедитесь, что у вас есть хорошее понимание.
Из таких тем, как сложение смешанных чисел, вычитание дробей, порядок операций и вычитание нескольких цифр, потому что этот урок построен на. Все эти концепции в порядке, чтобы понять, почему вычитание смешанных чисел сложнее, чем их сложение, давайте посмотрим. На двух задачах рядом пять плюс два и одна треть и пять минус два и одна треть мы учимся. Чтобы сделать задачи, как первая в предыдущем видео о сложении смешанных чисел, начиная с двух и одной трети просто. Значит, два плюс одна треть мы узнали, что можем переписать задачу вот так и просто сложить целое.

Пронумеруйте части, чтобы получить целое число часть ответа пять плюс два будет семь, так что ответ такой. Семь и одна треть, но если мы попытаемся сделать то же самое с вычитанием, мы получим неверный результат. Ответ: если мы перепишем два и одну треть как два плюс одна треть, похоже, что мы можем просто вычесть целое. Числа 5 минус 2 равно 3, что оставляет три плюс одна треть или три и одна треть в качестве ответа, но это. Оказывается, это неправильно, упс, так что же мы сделали не так, когда мы вычитаем смешанное число?
Нужно вычесть все смешанное число нужно вычесть целую часть числа и нам нужно вычесть. Дробная часть, но мы не вычли одну треть, мы добавили ее, потому что, когда мы переписали смешанное число. В сумме целого числа и действия мы забыли или не поняли, что они образуют a. Мы просто поставили два плюс одну треть сразу после знака минус, и это выглядело так. Мы должны вычесть два и добавить одну треть, но на самом деле мы должны были вычесть из них обоих один.

Чтобы избежать этой ошибки, нужно заключить в скобки смешанное число, которое вы вычитаете, чтобы запомнить его. Части образуют группу, и вам нужно применить знак минус ко всей группе, и вы можете только. Избавьтесь от круглых скобок после того, как вы примените или распределите вычитание для каждого члена группы следующим образом. Минус два минус одна треть теперь, когда мы правильно написали задачу, мы получим правильный ответ, если напишем. Эти математические операции, идущие слева направо, у нас есть пять минус два, что равно трем, но затем для.
Последний шаг, нам нужно вычесть одну треть из трех, что может показаться трудным сделать, если вы не помните что. О целых дробях мы узнали в прошлом видео, при сложении смешанных чисел иногда мы получали такой ответ. Две и три трети, но поскольку три трети — это то, что я называю целой дробью, ее значение равно единице. И мы узнали, что можем упростить такой ответ, как два и три трети — это два плюс 1 который. 3 хорошо, а как насчет того, чтобы сделать тот же самый процесс в обратном порядке вместо того, чтобы упрощать неупрощенное.

Пытаемся отнять 1/3 от 3, поэтому давайте перепишем 3 как 2 плюс 1, а затем перепишем. 2 плюс 1, как 2 плюс 3 вместо 3, кажется ли, что задачу легче решить, теперь мы преобразовали часть. Из целого числа в целую дробь 3 на 3, и мы уже знаем, как вычитать дроби 3. Больше 3 минус 1 на 3 равно 2 на 3, поэтому наш окончательный ответ равен 2 и 2/3. Итак, как видите, вычитание смешанных чисел может быть немного сложным, но не все задачи такие сложные.
Некоторые из них довольно просты, как этот 6 и 4/5 минус 1 и 3/5, нам все еще нужно помнить об этом. Смешанные числа образуют группы, поэтому мы должны вычесть обе части, но именно в этом заключается сложенный формат, который мы используем. Узнанное в прошлом видео действительно может нам помочь, так как порядок задачи на вычитание важен. Нам нужно обязательно поставить смешанное число, с которого начиналось, сверху и смешанное число. Это отнимало снизу, и это помогает помнить, что обе части смешанного числа равны.
Вычитается, даже если мы не заключаем их в круглые скобки, чтобы напомнить нам, что это потому, что мы вычитаем столбец частей.
 По столбцу, как и мы, и многозначное вычитание хорошо вычитает дробь внизу из дроби. Сверху, а затем хорошо вычесть целое число внизу из целого числа наверху. 4/5 минус 3/5 равно 1/5, а 6 минус 1 равно 5, поэтому ответ будет просто 5 и 1/5 лет. Видите, это действительно было легко, и поэтому я рекомендую использовать форму стека всякий раз, когда вы можете вычитать смешанные числа.
По столбцу, как и мы, и многозначное вычитание хорошо вычитает дробь внизу из дроби. Сверху, а затем хорошо вычесть целое число внизу из целого числа наверху. 4/5 минус 3/5 равно 1/5, а 6 минус 1 равно 5, поэтому ответ будет просто 5 и 1/5 лет. Видите, это действительно было легко, и поэтому я рекомендую использовать форму стека всякий раз, когда вы можете вычитать смешанные числа.Это поможет вам запомнить, что обе части смешанного числа вычитаются, не беспокоясь о группах. Или круглые скобки, но даже несмотря на то, что форма с накоплением — отличный способ не запутаться в группировке. Не делает каждую задачу такой простой, например, давайте попробуем решить задачу 5 и 1/7 -2 и 3 седьмых. Если вы снова не складываете форму, вы начинаете с 5 и 1/7, поэтому она идет сверху и 2 и. 3/7 идет внизу, но когда мы попытаемся вычесть столбец дробей, вы увидите, что у нас есть a.
Маленькая проблема 1/7 меньше, чем 3/7, поэтому мы не можем вычесть ее, не получив отрицательного числа, которое на самом деле женится.
 Как бы избежать, так что мы делаем сейчас хорошо вы помните, что вы делаете в многозначном вычитании. Когда вам нужно вычесть большую цифру из меньшей, да, вы берете или перегруппировываете из столбца. Влево, и мы можем сделать что-то действительно похожее на то, что со смешанными числами мы можем сделать дробь. Часть смешанного числа можно увеличить, заимствуя часть целого числа в видео о сложении смешанных чисел.
Как бы избежать, так что мы делаем сейчас хорошо вы помните, что вы делаете в многозначном вычитании. Когда вам нужно вычесть большую цифру из меньшей, да, вы берете или перегруппировываете из столбца. Влево, и мы можем сделать что-то действительно похожее на то, что со смешанными числами мы можем сделать дробь. Часть смешанного числа можно увеличить, заимствуя часть целого числа в видео о сложении смешанных чисел.Мы узнали, что смешанное число с неправильной дробной частью является дурным тоном, потому что его можно упростить. Целую дробь, а затем добавить ее к целой части числа, мы можем сделать этот процесс в обратном порядке. Также мы можем вычесть единицу как целую дробь из целой части числа и прибавить к ней. Дробная часть, чтобы получить неправильную дробь, и хотя это считается плохой формой, это нормально, потому что это не наше. Окончательный ответ, и это помогает нам вычесть столбец дроби, не получая отрицательной дроби в этом примере, который мы делаем.
Это путем замены целой части числа 5 на 4 плюс 1, а затем замены 4 плюс 1 на 4.
 Плюс 7 на 7, и, наконец, мы объединили эти семь на семь с единицей на семь, чтобы получить восемь. Теперь больше семи дробь сверху достаточно велика, чтобы вычесть три больше семи из восьми больше семи минус. Три на семь — это пять на семь, и тогда нам просто нужно вычесть целые части числа сверху. Целое число раньше было пять, но мы позаимствовали его, так что теперь четыре четыре минус два равно двум.
Плюс 7 на 7, и, наконец, мы объединили эти семь на семь с единицей на семь, чтобы получить восемь. Теперь больше семи дробь сверху достаточно велика, чтобы вычесть три больше семи из восьми больше семи минус. Три на семь — это пять на семь, и тогда нам просто нужно вычесть целые части числа сверху. Целое число раньше было пять, но мы позаимствовали его, так что теперь четыре четыре минус два равно двум.Итак, наш ответ две и пять седьмых, давайте попробуем другой пример, чтобы убедиться, что вы его поняли, и давайте. На этот раз сделай это сюжетной задачей, предположим, что есть парень, строитель по имени Роб, и предположим, что он нужен. Чтобы исправить что-то, вычитая смешанное число один в пяти восьмых из шести и одной восьмой, он может исправить. Это да, я могу, по крайней мере, с помощью моего верного кота Ричарда, куда убежал этот негодяй. Ричарду Ричарду ну что ж, первое, что нам нужно сделать, это сложить их в стопку.
Число, которое я убираю снизу, затем мне нужно вычесть дроби, когда я замечаю, что число.
 Дробь сверху меньше дроби снизу, поэтому мне нужно сделать дробь сверху. Больше, заимствуя из целой части числа, я могу заменить шесть на пять плюс один, и я могу. Замените пять плюс один на пять плюс восемь на восемь, чтобы получить всю дробь, к которой мне нужно добавить. Верхняя дробь 8 на 8 плюс 1 на 8 равна 9 на 8, так что теперь я могу вычесть.
Дробь сверху меньше дроби снизу, поэтому мне нужно сделать дробь сверху. Больше, заимствуя из целой части числа, я могу заменить шесть на пять плюс один, и я могу. Замените пять плюс один на пять плюс восемь на восемь, чтобы получить всю дробь, к которой мне нужно добавить. Верхняя дробь 8 на 8 плюс 1 на 8 равна 9 на 8, так что теперь я могу вычесть.Столбец дробей, потому что дробь сверху больше 9больше 8 минус 5 больше 8 будет 4 больше 8. И тогда я могу вычесть целые числа 5 минус 1 будет 4, так что ответ будет 4 и 4. Восьмые тебе подходят Ричард ты прав 4 восьмерки можно упростить до 1/2 так что мой окончательный ответ. 4 и 1/2 спасибо за помощь, Ричард молодец, ограбил строителя, так что теперь ты знаешь, как это сделать. Вычтите смешанные числа, некоторые задачи будут простыми, как наш второй пример, где вы можете просто вычесть дробные части.
И все части числа, но в других задачах вам может понадобиться заимствование или перегруппировка с использованием этой неупрощенной процедуры.
 И помните, что сложенная форма — отличный способ держать все прямо, конечно, вам это тоже может понадобиться. Чтобы решить задачи, в которых смешанные числа имеют разные дроби, вам нужно будет заранее преобразовать их в дроби лжи. Вы можете вычесть, но это работает так же, как вы видели в последнем видео, так что вы уже знаете. Как справиться с этим, я знаю, что всегда говорю это, но это потому, что это верный способ действительно учиться.
И помните, что сложенная форма — отличный способ держать все прямо, конечно, вам это тоже может понадобиться. Чтобы решить задачи, в которых смешанные числа имеют разные дроби, вам нужно будет заранее преобразовать их в дроби лжи. Вы можете вычесть, но это работает так же, как вы видели в последнем видео, так что вы уже знаете. Как справиться с этим, я знаю, что всегда говорю это, но это потому, что это верный способ действительно учиться.Математика для практики, решая некоторые задачи самостоятельно, как всегда спасибо за просмотр математических выходок и плохо. Увидимся в следующий раз, чтобы узнать больше на math antics com.
Метод 4 – Как вычитать смешанные числа, которые имеют разные знаменатели | Фракции | Предварительная алгебра | Академия Хана
Давайте попробуем оценить семь и шесть девяток минус три и две пятых, так что, как всегда, я предпочитаю выделять. Целое число состоит из дробных частей, это то же самое, что семь восемь плюс шесть девять минус.
 Три минус две пятых, и причина, по которой я говорю минус 3 минус две пятых, в том, что это то же самое, что и . Минус три плюс две пятых, и, таким образом, вы распределяете знак минус, вы вычитаете три, а затем вычитаете.
Три минус две пятых, и причина, по которой я говорю минус 3 минус две пятых, в том, что это то же самое, что и . Минус три плюс две пятых, и, таким образом, вы распределяете знак минус, вы вычитаете три, а затем вычитаете.Две пятых, и так теперь мы можем беспокоиться о целых частях числа семь минус три хорошо семь минус три равно. Мы собираемся дать четыре, так что это даст нам четыре, а затем будет шесть девятых. Минус две пятых, так что позвольте мне подумать о том, сколько шесть девятых минус две пятых будет шесть девять минус две пятых. Чтобы найти общий знаменатель, чтобы это было то же самое, и я думаю. Наименьшее общее кратное девяти и пяти будет 45 буквально, тогда умножьте, что у них нет общих делителей.
Значит, будет больше 45, а затем от 9 до 45, чтобы умножить на пять, так что я собираюсь. Нужно умножить числитель на пять, так что 6 умножить на 5 будет 30, и я собираюсь вычесть, чтобы идти. От 5 до 45 нужно было умножить на 9, поэтому после умножения числителя на девять, если я не хочу.
 Чтобы изменить значение так 2 раза 9 будет 18 и 30 больше 30 40 50 минус 18 45th так. Это будет что-то более 45 30 минус 18 равно 12, так что если я вычитаю.
Чтобы изменить значение так 2 раза 9 будет 18 и 30 больше 30 40 50 минус 18 45th так. Это будет что-то более 45 30 минус 18 равно 12, так что если я вычитаю.Вот эти две дроби, я получаю 12 12 40 пятых, то есть 4 плюс 12 сорок пятых или. Если бы мы хотели записать это как смешанное число, это было бы равно 4 и 12 сорок пятым, но. Это еще не сделано, мы можем упростить это еще больше. 12 и 45 имеют общие делители, на которые они оба делятся. Они оба делятся на три, поэтому мы можем сказать, что на самом деле они оба делятся на хорошо, что мы можем. Я думаю, что после этого мы сможем разделить больше, так что давайте посмотрим, разделим ли мы числитель на 3 и на .
Знаменатель на 3, мы получаем 4 и 12 разделить на три равно 4 и 45 разделить на 3. 45 разделить на 3 равно 15 4 и 4 15 на самом деле были сделаны эти два, что не может быть упрощено. Еще для и для 15.
Метод 5 – Сложение и вычитание смешанных чисел с отличием в знаменателях | Математика с мистером Дж.

Добро пожаловать в математику с мистером Дж. В этом видео я расскажу, как складывать и вычитать смешанные числа. И у нас есть по одному примеру, через который каждый из нас собирался пройти вместе, чтобы так это записать. Давайте перейдем к номеру один, где у нас пять и две седьмых плюс три с половиной перед i. Начнем с того, что я хочу отметить, что если вы можете складывать и вычитать дроби с разными знаменателями, вы сможете.
Решите эти типы проблем, есть всего пара дополнительных шагов, но все будет хорошо, так что давайте. Начните с номера один, и первое, что мне нравится делать, это выстраивать их вертикально, так что вверх и вниз. Итак, пять и две седьмых плюс три с половиной теперь первое, что мы хотим сделать. Нужно посмотреть, есть ли у нас общий знаменатель между нашими дробями, чтобы мы могли сразу сложить наши дроби. Нет, у нас нет общего знаменателя, поэтому нам нужно найти его и переименовать, чтобы получилось семь.
И двойка, поэтому наименьший общий знаменатель для семерки и двойки будет 14.
 Итак. Давайте переименуем ну поставим знак равенства и у нас пять и сколько четырнадцатых а потом три и. Сколько четырнадцатых мы хорошо знаем, 7 умножить на 2 дает нам 14, поэтому нам нужно сделать то же самое. Наверху мы делаем то же самое, что и мы, когда складываем дроби, у нас просто есть целое.
Итак. Давайте переименуем ну поставим знак равенства и у нас пять и сколько четырнадцатых а потом три и. Сколько четырнадцатых мы хорошо знаем, 7 умножить на 2 дает нам 14, поэтому нам нужно сделать то же самое. Наверху мы делаем то же самое, что и мы, когда складываем дроби, у нас просто есть целое.Число впереди, поэтому 2 раза 2 делаем то же самое в точности сверху 2 раза 2 равно 4. Итак, 2 7 эквивалентно 4 14. Таким образом, мы переименовали с этим общим знаменателем наименьший общий знаменатель числа 14. Итак, давайте сделаем это в половина здесь мы знаем, что 2 умножить на 7 будет 14, так что сделайте то же самое. Точная вещь наверху, чтобы сохранить эквивалентность 1 умножить на 7 равно 7, и это добавление, так что теперь.
Когда у нас есть этот общий знаменатель, и мы переименовываем его, мы можем складывать или вычитать, поэтому давайте сложим наши дроби. Сначала 4 плюс 7 будет 11, а это 14, а затем мы сложим наши целые числа, так что 5 плюс. 3 равно 8. Итак, как только вы доберетесь до этой точки, проверьте, можете ли вы упростить дробную часть.
 Итак, есть ли у нас какие-либо общие факторы между 11 и 14, в то время как единственный общий фактор — это так.
Итак, есть ли у нас какие-либо общие факторы между 11 и 14, в то время как единственный общий фактор — это так.Это в простейшей форме наш окончательный ответ 8 и 11 14. Давайте перейдем к номеру два, где мы. Вычитание и вычитание — это то же самое, что мы только что сделали, но вместо сложения собирались. Вычтите, так что давайте выстроим вертикально вверх и вниз, так что 7 и 11 12 минус 2 и 3 4. Итак.
Есть ли у нас общий знаменатель между нашими двумя дробями, можем ли мы сразу вычесть нет, поэтому мы. Нужно найти общий знаменатель и наименьший общий знаменатель между двенадцатью и четверкой собирается. Будет двенадцать, так что давайте переименуем, чтобы у нас было семь и сколько двенадцатых и два и сколько двенадцатых хорошо. Семь и одиннадцать двенадцатых уже имеют знаменатель двенадцать, поэтому нам не нужно переименовывать, поэтому давайте перенесем наш. Теперь нам нужно переименовать три четверти, чтобы мы знали, что четыре раза по 3 равно 12.
То же самое наверху, чтобы получить эквивалентную дробь, поэтому 3 умножить на 3 равно 9.
 Таким образом, 3.4 эквивалентно 9 12, и обе дроби теперь имеют общий знаменатель, поэтому мы можем вычитать. Подводя итог, у нас не было общего знаменателя, поэтому мы не могли вычитать, поэтому мы его нашли. Мы переименовали и теперь были готовы вычесть, так что одиннадцать минус девять дает нам два, и теперь у нас есть двенадцатые.
Таким образом, 3.4 эквивалентно 9 12, и обе дроби теперь имеют общий знаменатель, поэтому мы можем вычитать. Подводя итог, у нас не было общего знаменателя, поэтому мы не могли вычитать, поэтому мы его нашли. Мы переименовали и теперь были готовы вычесть, так что одиннадцать минус девять дает нам два, и теперь у нас есть двенадцатые.Сосчитай целые числа, так что семь минус два будет пять, и мы получим пять и 2 12. Теперь перед. Мы заканчиваем, мы всегда смотрим, можем ли мы упростить дробную часть, и мы можем, потому что у нас есть. Общий делитель, отличный от 1, между нашим числителем 2 и нашим знаменателем 12, общий делитель 2 между ними. Оба из них, поэтому давайте разделим оба на 2, чтобы упростить здесь, и мы получим 5 и одну шестую и.
Одна шестая в простейшей форме, единственный общий множитель между единицей и шестью — единица, так что мы закончили. Окончательный ответ на номер два: пять и одна шестая, так что у вас есть, как складывать и вычитать. Смешанные числа, я надеюсь, что это помогло, большое спасибо за просмотр до следующего мира.

Заключение – Как вычитать смешанные дроби с разными знаменателями
Цель этого поста – помочь людям, которые хотят больше узнать о следующем – вычитание смешанных чисел, вычитание смешанных чисел с заимствованием (перегруппировка) | математика с г. j, вычитание дробей (смешанные числа и разные знаменатели), вычитание смешанных чисел с разными знаменателями путем создания моделей площадей, как вычитать смешанные числа путем преобразования их в неправильные дроби, вычитание смешанных чисел и дробей, вычитание смешанных чисел (2), сложение смешанных числа (в отличие от знаменателей) | математика с г. j, вычитание дробей с разными знаменателями | математика с г. j, вычитание смешанных чисел | дроби | предалгебра | хана, вычитание смешанных чисел с перегруппировкой, вычитание смешанных чисел с разными знаменателями., вычитание дробей с разными знаменателями | вычитание смешанных чисел с разными знаменателями, вычитание смешанных чисел с разными знаменателями, математика – сложение смешанных чисел.




 Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.
Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями. Упростить: .
Упростить: .

 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Сокращаем дробь по принципу предыдущего примера и получаем 9/10. В данном случае таковым будет (3x+5)*1. Последовательность действий:
В данном случае таковым будет (3x+5)*1. Последовательность действий: Пустой круг говорит о том, что данное значение не входит в ареал решений.
Пустой круг говорит о том, что данное значение не входит в ареал решений. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
 Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
 Тогда предыдущий пример можно решить иначе.
Тогда предыдущий пример можно решить иначе. После этого нужно вычесть нужную дробь из единицы и получить ответ.
После этого нужно вычесть нужную дробь из единицы и получить ответ. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам. Итог — 3 11 12 .
Итог — 3 11 12 .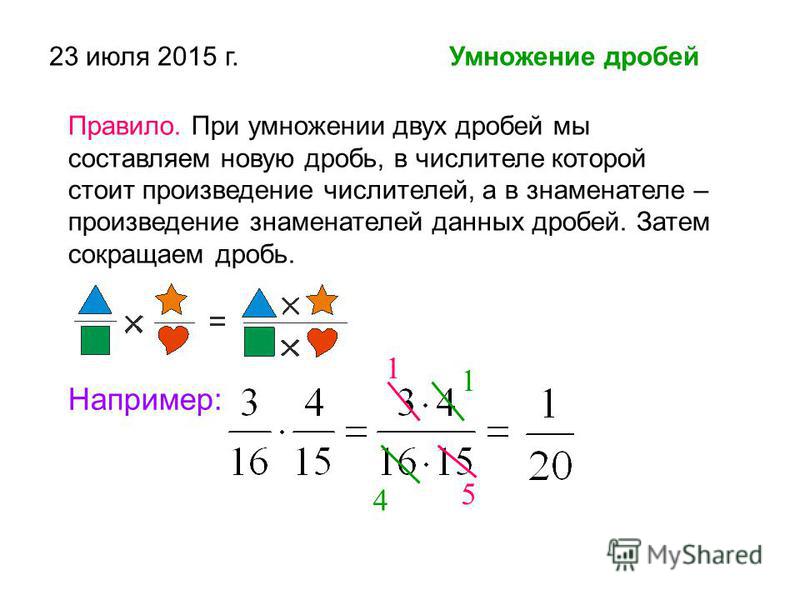 При таких условиях вычитание происходит отдельно. Целую часть вычитаем из целой части, а дробную часть из дробной
.
При таких условиях вычитание происходит отдельно. Целую часть вычитаем из целой части, а дробную часть из дробной
.
 Из целой части вычитаем целое, у дробной части вычитаем дробную часть.
Из целой части вычитаем целое, у дробной части вычитаем дробную часть. Вот как она звучит:
Вот как она звучит:




 ..
..

 Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
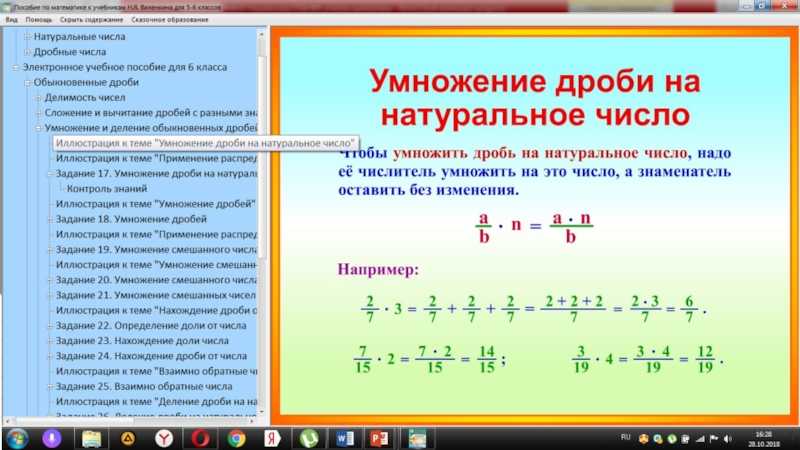 И математики нас этому постоянно учат. Вот пример.
И математики нас этому постоянно учат. Вот пример.
