3 класс. Математика. Умножение на однозначное число — Умножение двузначного числа на однозначное
Комментарии преподавателяУмножить многозначное число на однозначное можно с помощью правила умножения суммы на число, разложив при этом многозначное число на разрядные слагаемые. Но такой способ не всегда удобен.
При умножении многозначного числа на однозначное можно делать запись столбиком, как при сложении и вычитании. Такой способ очень помогает при умножении многозначных чисел. В этом уроке научимся находить значение произведения многозначного и однозначного чисел, выполняя запись столбиком.
Найдем значение произведения: 32 ∙ 2.
Запишем произведение столбиком.
Первый множитель 32 имеет два разряда: 3 десятка, 2 единицы.
Второй множитель 2 имеет один разряд – 2 единицы.
При записи в столбик записываем множители поразрядно: единицы под единицами.
При умножении столбиком знак умножения записываем крестиком «х».
Вместо знака равно проводим черту под вторым множителем.
Заметим, что при умножении многозначного числа на однозначное число умножаем число каждого разряда первого множителя на второй множитель.
Умножать начинаем с единиц: 2 умножить на 2 – равно 4.
4 единицы записываем под единицами.
Потом умножаем десятки первого множителя, 3 десятка умножить на 2 – равно 6 десятков.
6 записываем под десятками.
Читаем результат 64.
Аналогично можно умножить любое многозначное число на однозначное.
Например, 4211 умножить на 2.
Начинаем с единиц:
1 умножить на 2 – равно 2, 2 единицы записываем под единицами.
1 десяток умножить на 2 – равно 2 десятка, 2 записываем под десятками.
2 сотни умножить на 2 – равно 4 сотни, 4 записываем под сотнями.
4 единицы тысяч умножить на 2 – равно 8 единиц тысяч, 8 записываем под единицами тысяч.
Читаем результат: 8422.
А теперь рассмотрим произведения, в которых при умножении чисел разрядов получается двузначное число.
Например, 547 умножить на 4.
Начинаем умножать с единиц:
7 умножить на 4 – равно 28.
28 – это двузначное число, в нем 2 десятка и 8 единиц.
8 единиц записываем под единицами, 2 десятка запомним и прибавим к десяткам.
4 десятка первого множителя умножаем на 4 – равно 16, добавим 2 десятка, полученных при умножении единиц, получится 18 десятков.
8 записываем под десятками, а 1 запомним и прибавим к сотням.
Умножим 5 сотен на 4 – равно 20 сотен, прибавим 1 сотню от умножения десятков, получится 21.
1 записываем под сотнями, 2 являются единицами тысяч.
Читаем результат: 2 188.
Подведем итоги.
- При умножении столбиком записываем множители друг под другом поразрядно: единицы пишем под единицами.
- Умножать начинаем с разряда единиц.
- Если при умножении однозначного числа на значение разряда многозначного числа получается двузначное число, количество единиц этого двузначного числа записываем в разряд, который умножали, а количество десятков прибавляем к результату умножения однозначного числа на значение следующего разряда многозначного числа.

ИСТОЧНИКИ
http://znaika.ru/catalog/3-klass/matematika/Umnozhenie-na-odnoznachnoe-chislo-stolbikom
ФайлыНет дополнительных материалов для этого занятия.
«Умножение двузначного числа на однозначное в столбик» | План-конспект занятия по математике (3 класс):
Урок математики в 3 классе
Тема: «Умножение двузначного числа на однозначное в столбик»
Цель урока: познакомить с алгоритмом умножения двузначного числа на однозначное в столбик; повторить распределительное свойство умножения и свойство умножения суммы на число; закреплять умения решать задачи, находить площадь прямоугольника.
Задачи урока:
Личностные:
— прививать интерес к математике;
— уметь находить выход из спорных ситуаций при объяснении алгоритма умножения двузначного числа на однозначное в столбик;
— развитие способности к рефлексивной оценке собственных действий.
Предметные:
— уметь пользоваться: устной и письменной речью при объяснении алгоритма умножения двузначного числа на однозначное в столбик, основами логического мышления, исполнения алгоритмов при вычислении выражений;
— составлять последовательности (цепочки) предметов, чисел, фигур по заданному правилу;
— выполнять перебор всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям.
Метапредметные:
— умение выполнять заданное учебное действие, в случае неуспеха грамотно фиксировать своё затруднение, анализировать ситуацию, устранять причины затруднения;
— формирование специфических для математики логических операций (сравнение, анализ, аналогия).
Ход урока
I. Организационный момент.
— Здравствуйте, дети! Я очень рада вас видеть, начинаем наш урок!
Математика – королева наук!
Без нее не летят корабли,
Без нее не поделишь ни акра земли,
Даже хлеба не купишь, рубля не сочтешь,
Что почем, не узнаешь,
А узнав, не поймешь!
II. Устный счет, актуализация знаний:
— умножьте 78 на 8;
— умножьте 32 на 3;
— умножьте 14 на 6;
— умножьте 28 на 2.
— Удобно ли было умножать устно?
— Что нужно помнить, когда мы устно умножаем двузначное число на однозначное?
III. Открытие новых знаний. (Презентация.)
— Рассмотрим графическую модель распределительного свойства умножения – нахождение площади прямоугольника по известным его сторонам:
(a + b) ∙ c = a ∙ c + b ∙ c
— Как же можно выполнить умножение 24 на 8?
(Дети решают. Ответы фиксируются на доске.)
Ответы фиксируются на доске.)
24 х 8 = (20+4) х 8 = 20 х 8 + 4 х 8 = 160 + 32 = 192
Постановка проблемы:
— Запись решения громоздкая, неудобная. Существует ли другой способ умножения таких чисел? Сформулируйте задачи урока: (придумать более компактную, удобную запись по аналогии записи сложения в столбик).
Логика рассуждений:
— Произведение 24 и 8 равно площади прямоугольника со сторонами 24 ед. и 8 ед. Разбив большую сторону на части 20 ед. и 4 ед., видим, что вся площадь равна сумме площадей получившихся прямоугольников: 32 и 160 кв. ед. Записав сумму в столбик, приходим к более удобной записи умножения:
24
8
32
160
192
— Эту запись можно еще упростить, вычисляя число десятков «в уме». Тогда число десятков первого произведения удобно писать для памяти над числом десятков первого множителя.
3
24
8
192
Знакомство с алгоритмом:
— Чему мы будем учиться на уроке? (Выполнять умножение, записывая числа в столбик).
IV. Первичное закрепление знаний.
Работа по учебнику — № 2- 3 на странице 36.
(Коллективное выполнение с комментированием у доски).
14х2 21х4 32х3
11х9 13х3 42х3
VI. Самостоятельная работа.
Решение примеров:
26 х 3 44 х 5 73 х 4
(Самопроверка по образцу).
VII. Физкультминутка.
VIII. Закрепление изученного материала.
Работа по учебнику — №4, с.36 (самопроверка), №6, с.37 (работа в парах).
IX. Подведение итогов урока.
— Все ли было понятно сегодня на уроке?
— Кому было трудно?
— Расскажите алгоритм умножения двузначного числа на однозначное в столбик.
— Где можно применить полученные знания?
Х. Рефлексия.
— Кто доволен своей работой?
— Кому еще нужна помощь?
XI. Домашнее задание
№9, с.37, №15, 16, с.38
Выучить алгоритм умножения в столбик.
— Спасибо за работу! До свидания!
Как умножать двузначные числа: стратегии и идеи для игр
Когда я заканчивал учебный год с моим третьеклассником, мы потратили некоторое время, работая над умножением и пытаясь закрепить факты умножения. Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
Но наряду со знанием того, что означает умножение, и важностью знания фактов, я также хотел, чтобы он увидел, как мы можем распространить это знание на , умножая двузначные числа, и дальше . Хотя вид таких больших задач на умножение может пугать, это не обязательно. Узнать простые, но мощные стратегии для того, как с легкостью умножать двузначные числа . Затем вы можете применить эти идеи к еще большим числам и умножению десятичных дробей.
* Обратите внимание : Этот пост содержит партнерские ссылки, которые поддерживают работу этого сайта. Подробное описание читайте здесь.*
Как умножать двузначные числа: используйте модель площадиМой любимый метод умножения двузначных цифр — это нарисовать модель площади
0004 . Это полезно, потому что дает наглядное представление о том, что представляет собой проблема.
Кроме того, впоследствии его можно будет применить к более сложным задачам, включая многочлены умножения в алгебре.
Один из способов представить умножение как площадь прямоугольника. Это означает, что в любой заданной задаче на умножение вы можете думать о каждом множителе как о длине и ширине прямоугольника.
Допустим, мы хотим умножить 24 x 35. Вы можете начать с рисования прямоугольника шириной 24 и длиной 35.
В этот момент вы можете подумать: «Хорошо, отлично. Теперь это коробка, но как, черт возьми, это поможет мне ее решить??»
Ну, тогда вы можете разбить коробку на части , которые легче решить, как будто вы раскрашиваете область по одной небольшой секции .
Например, я могу разделить ширину на 20 и 4, затем я могу разделить 35 на 30 и 5, например:
Теперь у меня есть меньшие прямоугольные секции, которые мне легче умножать. Например, начиная с самого большого прямоугольника, мы имеем 30 х 20 = 600:9.0007
Затем я могу продолжить с остальными ячейками:
30 х 4 = 120,
И 5 х 20 = 100,
И, наконец, 5 х 4 = 20.
Теперь, когда я нашел площадь каждого маленького участка, я могу сложить их вместе , чтобы найти общую площадь (или окончательное решение исходной задачи умножения двузначного числа: 24 x 35): 600 + 120 + 100 + 20 = 840
Преимущества использования модели площадиЭто наглядное изображение также полезно, поскольку оно показывает, что умножение больших чисел дает более крупные ответы, что видно на рисунке (большие участки всего прямоугольника).
Другая замечательная особенность этого метода заключается в том, что дети могут разбить исходный прямоугольник на миллионами различных способов . Они могут делать то, что имеет для них наибольший смысл, или использовать любые задачи на умножение, которые им будет легче всего решить в уме.
Нет «правильного» или «неправильного» пути. Это дает детям свободу разобраться в проблеме самостоятельно и исследовать ее по-своему.
И если вы видите, что они склонны всегда выбирать одну и ту же стратегию (например, разделение десятков и единиц), попросите их решить ее другим способом. Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Это заставит их подумайте о других способах декомпозиции чисел , которые могли бы работать лучше или сделать решение проблемы проще и эффективнее.
Кроме того, это дает им дополнительную практику умножения. 😉
Чтобы узнать больше о настройке и решении с использованием моделей площадей, см. эту статью и скачайте бесплатный шаблон.
Как умножать двузначные числа: использовать разрядное значение для нахождения частичных произведенийЕще одна полезная стратегия, которую могут использовать дети, не обученные формальному алгоритму, — использовать 9.0003 поместите значение, чтобы разбить задачу на части и решить ее по частям .
Это похоже на использование модели области, но не включает визуал.
Это может быть особенно полезно, когда одно из чисел включает младшие, легко умножаемые цифры, такие как 2 или 3.
Например, предположим, что вы хотите умножить 78 x 12.
Вместо этого вы можете представить это как (78 х 10) + (78 х 2).
Умножить на десять несложно, и это даст вам 780.
Умножение на 2 равно удвоению, поэтому 78 x 2 = 156
Затем вы можете просто сложить частичные произведения вместе , чтобы получить 780 + 156 = 936
Вот еще один пример: 48 x 14
В этом примере мы можем думать об этом как (48 x 10) + (48 x 4)
Первая часть проста, давая нам 48 x 10 = 480
Умножение 48 x 4 не так просто сделать в уме, но затем его можно разбить на 48 x 2, а затем снова x 2.
Другими словами, 48 х 2 = 96 и тогда 96 х 2 = 192
Тогда снова мы можем сложите частичные произведения вместе , чтобы получить 480 + 192 = 672
Как умножать двузначные числа: используя формальный алгоритмпосредством задач умственного вычисления вы можете ввести формальный алгоритм .
Я предлагаю поделиться этим последним, потому что, если дети уже хорошо понимают, как работать с двузначными числами и умножать их, алгоритм не так страшен.
Если на самом деле, это, скорее всего, будет иметь смысл для большинства детей. Потому что теперь это не похоже на случайные правила, которым нужно следовать и помнить, а на удобный способ денди отслеживать то, что они раньше делали в своей голове.
Итак, если вы не знакомы, вот пошаговый пример умножения двузначных цифр с использованием традиционного алгоритма . Допустим, теперь мы хотим умножить 34 x 62.
Шаг первый: выровняйте все цифрыСначала выровняйте все числа в соответствии с их разрядностью.
Шаг второй: Умножьте на цифру единицЗатем начните с , умножая каждую цифру верхнего числа на цифру единиц (в данном случае 2). В этом примере у нас есть 4 x 2 = 8 (запишите это в единицах), а затем 3 (что на самом деле означает 30) x 2 = 6 (что на самом деле означает 60). Затем вы записываете 6 в разряде десятков.
Шаг третий: добавьте нулевой заполнитель Затем поместите ноль под столбцом единиц , когда вы начнете умножать 34 на 6 (что на самом деле означает 60).
Причина этого нуля в том, что вы не просто умножаете 34 на 6. Вы умножаете 34 x 60 . Другими словами, кратно десяти , поэтому мы знаем, что должны иметь этот ноль там .
Шаг четвертый: Умножение на десяткиЗатем вы можете умножить каждую цифру на 6 .
Это дает 6 х 4 (что на самом деле 60 х 4) = 24 (что на самом деле 240).
Поскольку это на самом деле представляет 240, 4 идет в столбце десятков в нашем решении, а затем мы «переносим» 2, то есть помещаем его в столбец десятков вверху.
Я обычно записываю это как «+2» , а не просто как 2, потому что часто дети забывают, должны ли они сложить это или умножить.
Затем мы умножаем 3 x 6 = 18 и к добавляем 2 , чтобы получить 20 (что на самом деле представляет собой 2000, потому что мы на самом деле умножили 30 x 60 и добавили к нему еще 200).
Следовательно, мы получаем 2040 во второй строке нашего ответа.
Затем, как и в случае с частичными произведениями, мы складываем вместе две строки решений , чтобы получить 68 + 2040 = 2,108
Когда я учу своих детей В этой процедуре я обычно записываю каждый шаг как частичный продукт по мере решения проблемы. Это позволяет им увидеть, откуда берутся все числа, почему мы добавляем ноль и почему мы складываем строки ответов вместе для окончательного ответа.
Затем я позволяю им практиковаться, используя любой метод или стратегию, которые наиболее эффективны и удобны для них!
Умножение двузначных чисел: идеи для игрЕсли вы хотите, чтобы ваши дети попрактиковались в умножении двузначных чисел, вот несколько игр, которые могут вам понравиться.
- Распечатанные настольные игры для тренировки двузначного умножения
- Многоразрядное умножение страниц вырезания и вставки
- Настольные игры с многозначным умножением
И обязательно ознакомьтесь с этой стратегией, которая поможет детям понять и увидеть закономерности при умножении больших чисел: Как умножать большие числа с помощью таблиц
Надеюсь, вы нашли это полезным и, возможно, даже узнали новых способа умножения двузначных чисел. числа !
числа !
Математические идеи никогда не заканчиваются
Если вам понравился этот пост, вам понравится быть частью сообщества Math Geek Mama! Каждую неделю я отправляю электронное письмо с забавными и увлекательными математическими идеями, бесплатными ресурсами и специальными предложениями. Присоединяйтесь к более чем 163 000 читателей, поскольку мы помогаем каждому ребенку добиться успеха и преуспеть в математике! ПЛЮС, получи мою БЕСПЛАТНУЮ электронную книгу, 5 математических игр, в которые можно играть СЕГОДНЯ , в подарок вам !
2-значное умножение — Шаги
2-значное умножение или двузначное умножение выполняется путем расположения чисел таким образом, что заданные числа располагаются одно под другим. Двузначное число можно умножить на однозначное, на другое двузначное число, на трехзначное число и так далее. Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
Давайте узнаем больше о двузначном умножении, шагах для умножения и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Что такое двузначное умножение? |
| 2. | 2-значное умножение на 2-значное |
| 3. | 2-значное умножение с перегруппировкой |
| 4. | Часто задаваемые вопросы по двузначному умножению |
Что такое двузначное умножение?
2-значное умножение — это метод умножения двузначных чисел, упорядоченных по двум разрядам, то есть единицам и десяткам. Способ умножения чисел такой же, как и умножения однозначных цифр. Однако в двузначных числах мы умножаем каждую цифру по одной на множитель. Это означает, что множитель сначала умножается на разряд единиц множимого, а затем на разряд десятков множимого. Давайте узнаем об умножении 2 цифр на 1 цифру и 2 цифры на 2 цифры умножения в следующих разделах.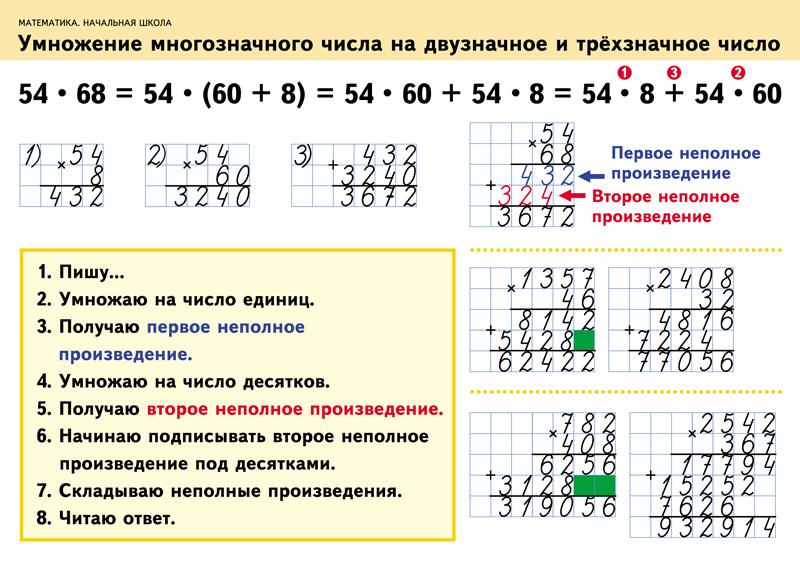
Умножение 2-значных чисел на 1-значное
Умножение 2-значных чисел на 1-значные очень просто. Давайте разберемся в этом, используя следующие шаги и пример.
Пример: Умножить 23 × 2
- Шаг 1: Поместите однозначное число под двузначным. Это делает однозначное число множителем. Умножьте однозначное число (множитель) на единицу множимого. Здесь 2 — это множитель, а единица множимого равна 3. Таким образом, 2 × 3 = 6. Это частичное произведение (6) будет помещено под колонку единиц.
- Шаг 2: Теперь умножьте множитель на разряд десятков множимого. Здесь 2 — это множитель, а цифра десятков множимого равна 2. Это означает, что 2 × 2 = 4. Это частичное произведение (4) будет помещено в столбец десятков. Следовательно, 23 × 2 = 46 .
Теперь давайте научимся умножать двузначные числа на двузначные числа.
2-значное умножение на 2-значное
Умножение 2 цифр на 2 цифры означает, что оба числа, которые нужно умножить, состоят из двух цифр. Умножение начинается с разряда единиц, а затем переходит к разряду десятков. Цифры располагаются одна под другой. Хотя любое из двух чисел можно поместить сверху или снизу, предпочтительнее поместить меньшее число снизу, потому что это облегчает умножение. Давайте разберемся с этим умножением с помощью следующего примера. Умножим 34 × 12. В этом случае пусть 34 будет множимым, а 12 — множителем.
Умножение начинается с разряда единиц, а затем переходит к разряду десятков. Цифры располагаются одна под другой. Хотя любое из двух чисел можно поместить сверху или снизу, предпочтительнее поместить меньшее число снизу, потому что это облегчает умножение. Давайте разберемся с этим умножением с помощью следующего примера. Умножим 34 × 12. В этом случае пусть 34 будет множимым, а 12 — множителем.
- Шаг 1: Поместите множимое (34) сверху, а множитель (12) под ним, как показано на рисунке выше. Умножьте цифру единиц множителя на множимое. Здесь 34 — множимое, а цифра единиц 12 — 2. Это даст 34 × 2 = 68. Это первое частичное произведение, которое будет помещено в одну строку.
- Шаг 2: Умножьте множимое на разряд десятков множителя. Здесь 34 — это множимое, а цифра десятков множителя равна 1. Это будет 34 × 1 = 34. Следует отметить, что нам нужно поместить ноль под цифрой единиц частичного произведения, а затем записать второе частичное произведение.
 продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.
продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь. - Шаг 3: Добавьте оба частичных продукта, чтобы получить конечный продукт. Это будет 68 + 340 = 408.
Теперь давайте узнаем о двузначном умножении, в котором у нас есть переносы.
2-значное умножение с перегруппировкой
Двузначное умножение с перегруппировкой или переносом происходит при переносе числа вперед. Давайте поймем это на следующем примере и шагах. Умножим 45 × 6,
- Шаг 1: Умножьте множитель на единицу множимого. Здесь множимое равно 45, цифра единиц в числе 45 равна 5, а множитель равен 6. Таким образом, это будет 6 × 5 = 30.
- Шаг 2: Поскольку произведение, полученное на шаге 1, равно 30, мы перенесем 3 в предыдущий столбец десятков и запишем 0 под столбцом единиц как частичное произведение.
- Шаг 3: Теперь мы умножим множитель на разряд десятков множимого.
 Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221
Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221
Двузначное умножение с десятичными дробями очень похоже на обычное умножение с использованием нескольких правил десятичных чисел. Давайте узнаем больше об этом в следующем разделе.
Двузначное умножение с десятичными дробями
Двузначное умножение с десятичными дробями выполняется так же, как и обычное умножение двузначных цифр с учетом правил десятичных чисел. При умножении таких чисел мы можем игнорировать десятичную точку, пока не получим окончательный результат. После получения окончательного результата подсчитываем количество знаков после запятой в обоих числах, складываем их и в соответствии с этим ставим запятую. Разберем это на примере и умножим 2,5 × 1,1
- Шаг 1: Расположите числа вертикально в соответствии со значением разряда.
 Не выравнивайте числа по десятичной точке.
Не выравнивайте числа по десятичной точке. - Шаг 2: Умножьте разряд единиц множителя на множимое. Здесь 25 × 1 = 25, .
- Шаг 3: Поместите ноль под цифрой единиц частичного произведения.
- Шаг 4: Умножьте разряд десятков множителя на множимое. Это будет 25. Поместите это рядом с 0 под частичным произведением.
- Шаг 5: Добавьте два продукта, чтобы получить конечный продукт. Здесь 25 + 250 = 275, .
- Шаг 6: Поместите десятичную точку через 2 знака справа в конечном продукте. Поскольку множимое и множитель имеют по 1 десятичному знаку, получается 1 + 1 = 2 десятичных знака. Поэтому ставим запятую через 2 знака справа и получаем 2,5 × 1,1 = 2,75
☛ Связанные темы
- Вычитание 2 цифр
- 2-значное дополнение
- 3-значное дополнение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Умножение и деление целых чисел
Примеры двузначного умножения
Пример 1: Найдите произведение 67 × 20.

Решение: Давайте разберемся с этим двузначным умножением, используя следующие шаги.
- Умножить 0 на 7 и 6.
- Поместите ноль под цифрой единиц частичного произведения.
- Умножить 2 на 7 и 6.
- Добавьте продукты, чтобы получить окончательный ответ.
Следовательно, 67 × 20 = 1340.
Пример 2: Умножить 31 × 7
Решение: Выполним это двузначное умножение, используя следующие шаги.
- Умножить 7 на 1, то есть 7 × 1 = 7
- Теперь умножьте 7 на 3, то есть 7 × 3 = 21
- Запишите их вместе как 217
- Следовательно, 31 × 7 = 217
Пример 3: Укажите истинное или ложное значение умножения 2-значного числа.
а.) 10 × 11 = 110
б.) 20 × 20 = 40
Решение:
а.) Верно, 10 × 11 = 110
б.) Ложь, 20 × 20 = 400
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.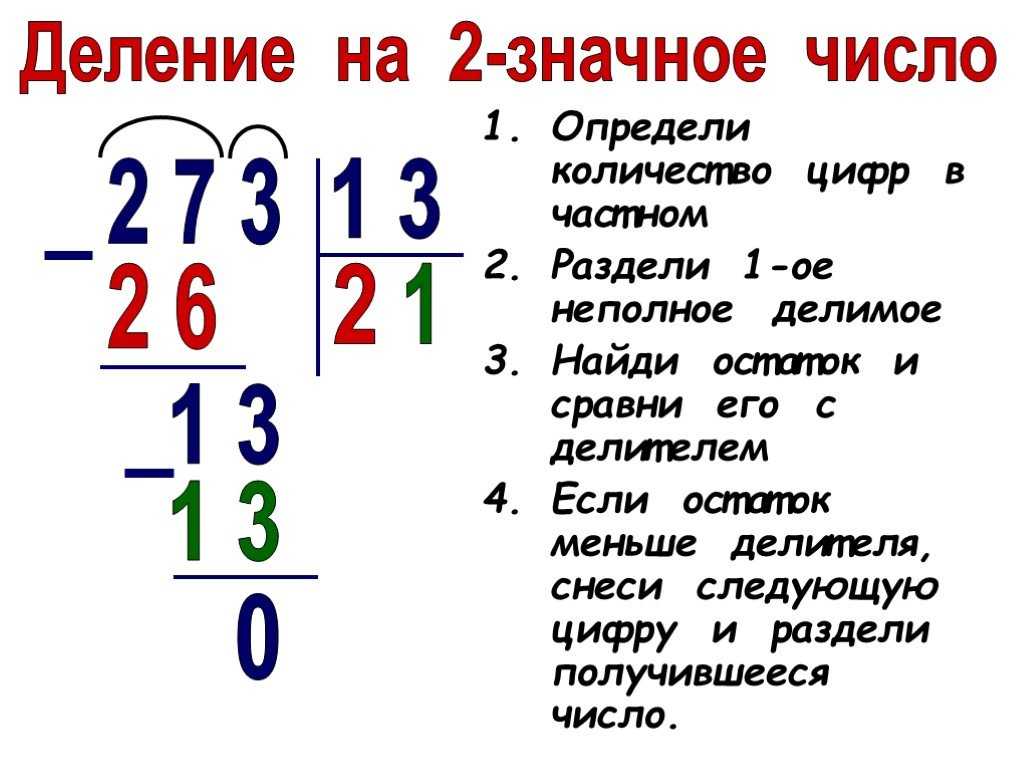
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению двузначных чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о двузначном умножении
Что такое двузначное умножение?
Двузначное умножение — это метод умножения двузначного числа на другое число. Числа располагаются друг под другом для выполнения умножения. Число, написанное сверху, называется множимым, а число, написанное ниже, — множителем. Двузначные числа можно умножать на однозначные числа, двузначные числа и так далее.
Как выполнить двузначное умножение?
Следующие шаги объясняют процесс двузначного умножения. Например, давайте умножим 42 × 3
- Расположите числа одно под другим так, чтобы большее число (42) было сверху, а меньшее (3) — под ним. Итак, 3 становится множителем, а 42 — множимым.

- Начните умножать множитель с разряда единиц множимого. Здесь 3 будет умножено на 2, что даст 3 × 2 = 6. Это 6 будет записано как частичное произведение.
- Затем умножьте 3 на разряд десятков множимого, то есть 4, что будет 3 × 4 = 12. Теперь, записав оба произведения вместе, конечный продукт будет 42 × 3 = 126
Как выполнить двузначное умножение с переносом?
Двузначное умножение с переносом выполняется, когда произведение одного столбца больше 9. Лишняя цифра переносится в следующий столбец и прибавляется к этому конкретному произведению. Например, давайте умножим 45 × 7.
- Поместите 45 сверху и 7 под ним, чтобы 45 стало множимым, а 5 стало множителем.
- Умножьте 7 на 5, и вы получите 7 × 5 = 35. Поскольку произведение представляет собой двузначное число 35, мы перенесем 3 в столбец десятков и запишем 5 под столбцом единиц как частичное произведение.
- Теперь умножьте множитель на разряд десятков множимого.
 Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Как умножить 2-значное на 1-значное?
Умножение 2 цифр на 1 цифру выполняется так же, как и умножение одной цифры. Например, умножим 13 × 2,9.0007
- Двузначное число (13) записывается сверху, а однозначное (2) — снизу, поэтому 13 становится множимым, а 2 — множителем.
- Начинаем умножать младшую цифру (множитель) на единицу множимого. Здесь мы умножим 2 на 3, что будет 2 × 3 = 6. Мы запишем это 6.
- Затем мы идем дальше и умножаем нижнюю цифру (множитель) на разряд десятков множимого. Здесь 2 × 1 = 2. Это также будет записано вместе с произведением, полученным на предыдущем шаге. Итак, это даст произведение 13 × 2 = 26,9.0221
Как выполнить двузначное умножение на двузначное?
Умножение двух цифр на две цифры — это процесс умножения, при котором двузначное число умножается на другое двузначное число. Например, умножим 23 × 14.
Например, умножим 23 × 14.
- Поместите 23 сверху и 14 под ним, чтобы 23 стало множимым, а 14 — множителем.
- Умножьте разряд единиц множителя на множимое. Здесь 23 — множимое, а цифра единиц 14 — 4. После умножения 23 на 4 мы получаем 23 × 4 = 9.2. Это первый неполный товар, который будет размещен в одной строке.
- Умножьте множимое на разряд десятков множителя. Это означает, что мы умножим 23 на 1, и получится 23 × 1 = 23. Следует отметить, что нам нужно поставить ноль под цифрой единиц частичного произведения, а затем написать рядом с ним второе частичное произведение. (Этот 0 помещен здесь, потому что мы фактически умножаем 23 на 10 на этом шаге.) Таким образом, мы получаем здесь 230.
- Теперь мы добавим оба частичных продукта, чтобы получить конечный продукт. это будет 92 + 230 = 322.
- Следовательно, конечный продукт равен 23 × 14 = 322.
Как умножить 3-значное на 2-значное?
Умножение 3-значного на 2-значное означает, что мы умножаем 3-значное число на 2-значное число.

 продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.
продукт. (Этот 0 помещен здесь, потому что мы на самом деле умножаем 34 на 10 на этом шаге). Таким образом, мы получаем 340 здесь.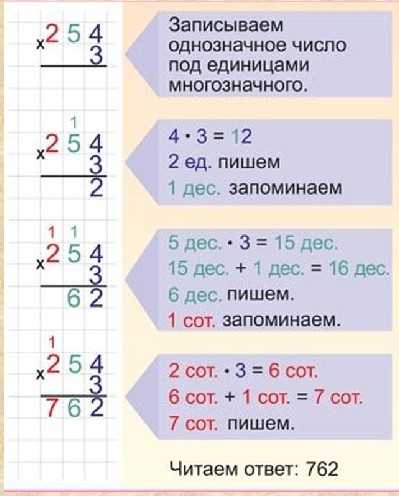 Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221
Здесь разряд десятков множимого равен 4, а множитель равен 6. Таким образом, это будет 6 × 4 = 24. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 24 + 3 = 27. Таким образом, конечный продукт равен 270,9.0221 Не выравнивайте числа по десятичной точке.
Не выравнивайте числа по десятичной точке.

 Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.
Здесь разряд десятков множимого равен 4, а множитель равен 7. Таким образом, это будет 7 × 4 = 28. На этом этапе нам нужно добавить число, которое было перенесено на предыдущем шаге. Это означает 28 + 3 = 31. Таким образом, конечный продукт равен 315.