Свойства деления натуральных чисел: формулировки, примеры

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Арифметика Свойства деления чисел с примерами

В данной публикации мы рассмотрим 8 основных свойств деления натуральных чисел, сопроводив их примерами для лучшего понимания теоретического материала.

• Свойства деления чисел
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
  • Свойство 5
  • Свойство 6
  • Свойство 7
  • Свойство 8

Свойство 1

Частное от деления натурального числа на само себя равняется единице.

a : a = 1

Примеры:

• 9 : 9 = 1
• 26 : 26 = 1
• 293 : 293 = 1

Свойство 2

Если натуральное число разделить на единицу, то в результате получится это же самое число.

a : 1 = a

Примеры:

• 17 : 1 = 17
• 62 : 1 = 62
• 315 : 1 = 315

Свойство 3

При делении натуральных чисел нельзя применять переместительный закон, действующий при сложении.

a : b ≠ b : a

Примеры:

• 84 : 21 ≠ 21 : 84
• 440 : 4 ≠ 4 : 440

Свойство 4

Если требуется разделить сумму чисел на заданное, то нужно сложить частное от деления каждого слагаемого на данное число.

(a + b) : c = a : c + b : c

Свойство в обратную сторону:

c : (a + b) = c : a + c : b

Примеры:

• (45 + 18) : 3 = 45 : 3 + 18 : 3
• (28 + 77 + 140) : 7 = 28 : 7 + 77 : 7 + 140 : 7
• 120 : (6 + 20) = 120 : 6 + 120 : 20

Свойство 5

При делении разности чисел на заданное нужно вычесть частное от деления вычитаемого на данное число из частного от деления уменьшаемого на это число.

(a – b) : c = a : c – b : c

Свойство в обратную сторону:

c : (a – b) = c : a – c : b

Примеры:

• (60 – 30) : 2 = 60 : 2 – 30 : 2
• (150 – 50 – 15) : 5 = 150 : 5 – 50 : 5 – 15 : 5
• 360 : (90 – 15) = 360 : 90 – 360 : 15

Свойство 6

Разделить произведение чисел на заданное – это то же самое, что разделить на это число один из сомножителей, затем результат умножить на другой.

(a ⋅ b) : c = (a : c) ⋅ b = (b : c) ⋅ a

Если число, на которое выполняется деление, равно одному из сомножителей:

• (a ⋅ b) : a = b
• (a ⋅ b) : b = a

Свойство в обратную сторону:

c : (a ⋅ b) = c : a : b = c : b : a

Примеры:

• (90 ⋅ 36) : 9 = (90 : 9) ⋅ 36 = (36 : 9) ⋅ 90
• 180 : (90 ⋅ 2) = 180 : 90 : 2 = 180 : 2 : 90

Свойство 7

Если требуется частное от деления чисел a и b разделить на число c, это означает, что a можно разделить на произведение b и c.

(a : b) : c = a : (b ⋅ c)

Свойство в обратную сторону:

a : (b : c) = (a : b) ⋅ c = (a ⋅ c) : b

Примеры:

• (16 : 4) : 2 = 16 : (4 ⋅ 2)
• 96 : (80 : 10) = (96 : 80) ⋅ 10

Свойство 8

При делении нуля на натуральное число в результате получится ноль.

0 : a = 0

Примеры:

• 0 : 17 = 0
• 0 : 56 = 56

Примечание: делить число на ноль нельзя.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

5.

5.6. Деление на десятичную дробь.

Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 14.2k. Опубликовано 7 февраля 2013

I.  Чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число.

Примеры.

Выполнить деление: 1) 16,38:0,7;   2) 15,6:0,15;    3) 3,114:4,5;   4) 53,84:0,1.

Решение. 

Пример 1)  16,38:0,7.

В делителе 0,7 после запятой стоит одна цифра, поэтому, перенесем запятые в делимом и делителе на одну цифру вправо.

Тогда нам нужно будет разделить 163,8 на 7.

Выполним деление по правилу деления десятичной дроби на натуральное  число.

Делим так, как делят натуральные числа. Как снесем цифру 8 — первую цифру после запятой (т.е. цифру в разряде десятых), так сразу поставим в частном запятую и продолжим деление.

Ответ: 23,4.

 

Пример 2) 15,6:0,15.

Переносим запятые в делимом (15,6) и делителе (0,15) на две цифры вправо, так как в делителе 0,15 после запятой стоят две цифры.

Помним, что справа к десятичной дроби можно приписать сколько угодно нулей, и от этого десятичная дробь не изменится.

Тогда:

15,6:0,15=1560:15.

Выполняем деление натуральных чисел.

Ответ: 104.

 

Пример 3) 3,114:4,5.

Перенесем запятые в делимом и делителе на одну цифру вправо и разделим 31,14 на 45 по правилу деления десятичной дроби на натуральное число.

Итак:

3,114:4,5=31,14:45.

В частном поставим запятую сразу, как сносим цифру 1 в разряде десятых. Затем продолжаем деление.

Чтобы закончить деление нам пришлось приписать нуль к числу 9 — разности чисел 414 и 405. (мы знаем, что справа к десятичной дроби можно приписывать нули)

 

Ответ: 0,692.

Пример 4)  53,84:0,1.

Переносим запятые в делимом и делителе на 1 цифру вправо.

Получаем: 538,4:1=538,4. 

Проанализируем равенство: 53,84:0,1=538,4. Обращаем внимание на запятую в делимом в данном примере и на запятую в полученном частном. Замечаем, что запятая в делимом перенесена на 1 цифру вправо, как если бы мы умножали 53,84 на 10. (Смотрите видео «Умножение десятичной дроби на 10, 100, 1000 и т. д.») Отсюда правило деления десятичной дроби на 0,1; 0,01; 0,001 и т.д.

II. Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001 и т. д., нужно перенести запятую вправо на 1, 2, 3 и т. д. цифр. (Деление десятичной дроби на 0,1; 0,01; 0,001 и т. д. равносильно умножению этой десятичной дроби на 10, 100, 1000 и т.д.)

Примеры.

Выполнить деление: 1) 617,35:0,1;  2) 0,235:0,01;  3) 2,7845:0,001;  4) 26,397:0,0001.

Решение.

Пример 1) 617,35:0,1.

Согласно правилу II деление на 0,1 равносильно умножению на 10, и запятую в делимом перенесем на 1 цифру вправо:

1) 617,35:0,1=6173,5.

Пример 2) 0,235:0,01.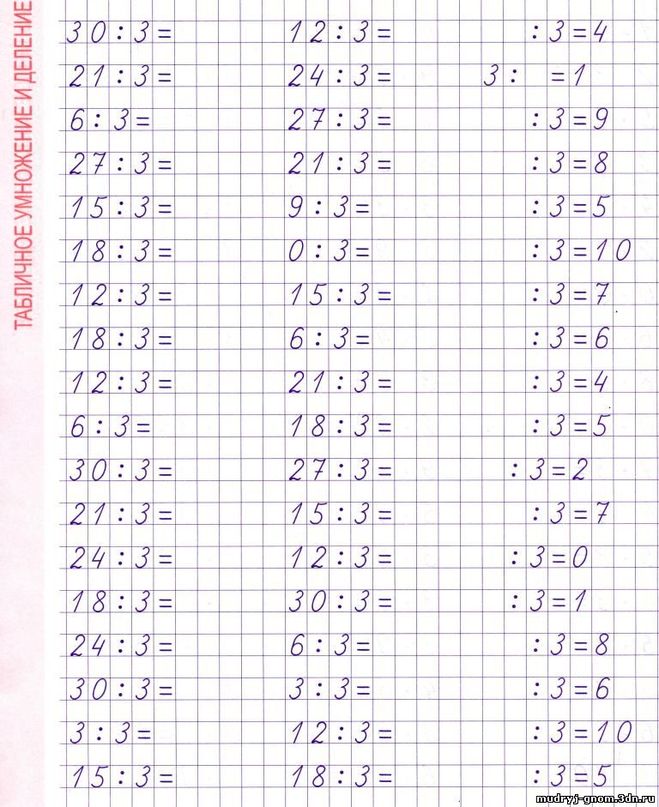

Деление на 0,01 равносильно умножению на 100, значит, запятую в делимом перенесем на 2 цифры вправо:

2) 0,235:0,01=23,5.

Пример 3) 2,7845:0,001.

Так как деление на 0,001 равносильно умножению на 1000, то перенесем запятую на 3 цифры вправо:

3) 2,7845:0,001=2784,5.

Пример 4) 26,397:0,0001.

Разделить  десятичную дробь на 0,0001 — это все равно, что умножить ее на 10000 (переносим запятую на 4 цифры вправо). Получаем:

4) 26,397:0,0001=263970.

Смотрите видео «Деление на десятичную дробь»

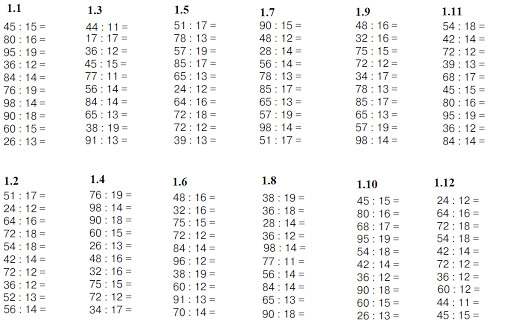
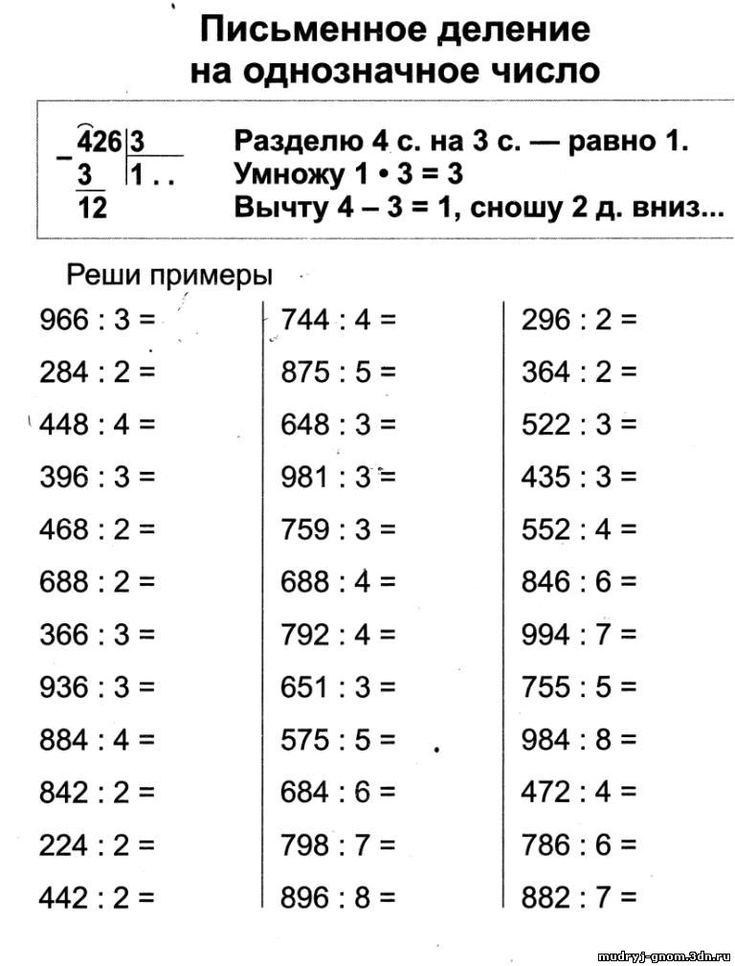
Деление для 2 класса: определение, факты и примеры

Обычно дети начинают углубленно изучать деление в третьем классе; однако в первый и второй годы дети познакомятся с понятиями, которые ведут к делению в полных формах и простому делению с использованием методов и игр. Ожидается, что дети будут работать с числами, намного большими, чем те, которые они могут физически сосчитать, поскольку математические концепции становятся более сложными. Понимание деления будет проще, если изучать его на примерах из реальной жизни. Давайте рассмотрим деление для детей 2 года в этой статье.

Что такое определение подразделения?

Деление — это процесс многократного вычитания. Это действие, обратное умножению. Считается формированием равных групп. Когда мы делим числа, мы разбиваем их на меньшие числа, так что умножение этих меньших чисел равняется взятому большему числу.

Примеры из повседневной жизни

1. У Нирмала есть 12 сладостей, и он хочет разделить их поровну между тремя своими друзьями. Давайте начнем с создания трех групп, затем добавляйте по одной сладости в каждую группу, пока все двенадцать сладостей не будут разделены поровну. Подсчитаем, сколько конфет в каждой группе, чтобы получить ответ: Двенадцать конфет, разделенных поровну между друзьями, равны 4.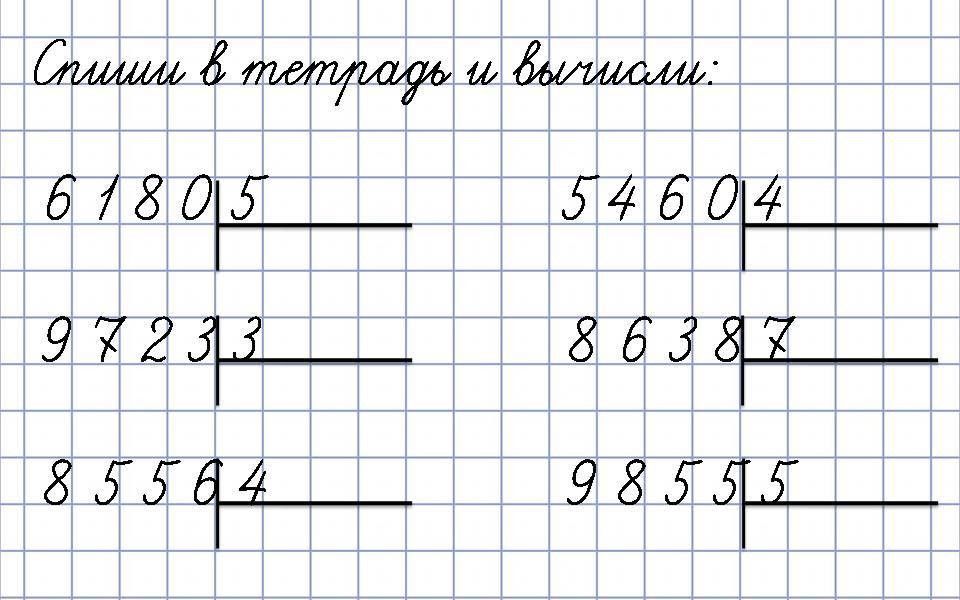

Деление обозначается математическим символом, состоящим из небольшой горизонтальной линии с точками над и под линией. Есть два основных символа деления, которые обозначают деление двух чисел.

Условные обозначения раздела

Другие слова для раздела: «разделить между» и «разделить». Наш решенный пример можно записать так: 12 разделить на 3 равно 4.

Изображение показывает деление 12/3

2. У Махимы 16 яблок, и она хочет разделить их поровну между своими 4 друзьями. Это можно записать как 16 разделить на 4.

Изображение показывает деление 16/4

Чтобы найти ответ, нам нужно разделить 16 поровну между 4 группами. Давайте посчитаем, сколько яблок в каждой группе, чтобы получить ответ.

На изображении показано, что 16 яблок делятся поровну между 4 людьми с делением 16/4

Таким образом, 16 яблок, разделенных поровну между друзьями, равно 4.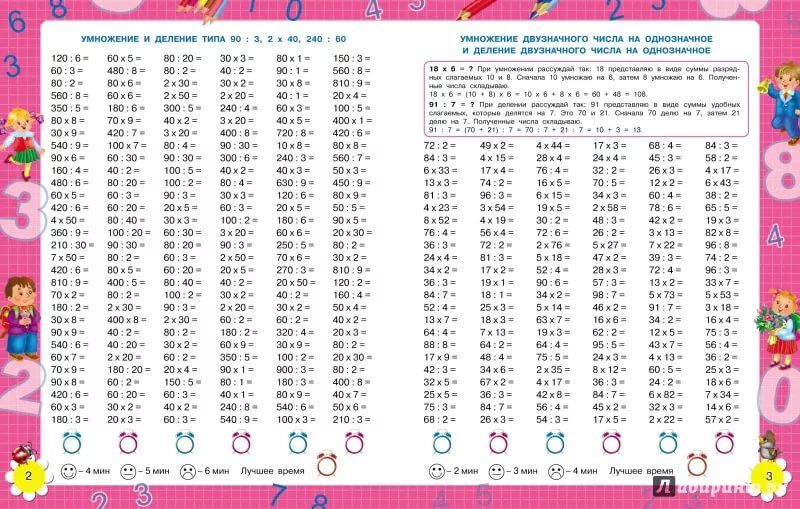

3. Мы можем разделить, разделив предметы на равные группы. Итак, если мы произведем расчет для 10, разделенного на 2, мы можем получить ответ, разделив десять предметов поровну на две группы.

На изображении показана группа из 10 объектов

В каждой из двух групп по пять шариков.

На изображении показаны 10 объектов, которые поровну разделены на 2 группы. Каждая из 5 объектов

Итак, десять разделить на два равно пяти.

Деление на группировку

Деление на группировку показывает, сколько одинаковых групп содержится в числе. Итак, если мы возьмем вычисление, как в примере истории 3,

10 разделить на 2.

Мы можем посмотреть на это как на то, сколько групп по 2 есть в 10.

На изображении показаны 10 объектов, которые поровну разделены на 5 групп. Каждый из 2 объектов

Равные группы по 2 из 10 составляют 5 (см. изображение выше). Таким образом, 10, деленное на 2, равно 5.

Важные термины деления

• Число, которое нужно разделить при делении суммы, называется делимым.

• Делитель — это число, на которое мы делим.

• Результат деления известен как частное.

Изображение показывает условия деления на примере

Умножение и деление

На приведенном ниже рисунке показаны 12 конфет, сгруппированных по 4.

Изображение показывает три группы, каждая из четырех конфет

показывает факт умножения: 3 x 4 = 12, а также факт деления: 12 ÷ 4 = 3. 12 конфет также можно расположить группами по 3. Это показано ниже.

На изображении показаны четыре группы по три конфеты

Здесь мы имеем факт умножения: 4 x 3 = 12 и факт деления: 12 ÷ 3 = 4.

Таким образом, мы можем заметить, что,

Помощь детям с делением дома

Игрушки, немного винограда, бумага зажимы и пуговицы — отличные предметы для практики. Попросите ребенка сосчитать количество предметов для начала. Могут ли они поровну распределить предметы между вами двумя? Помогите им по очереди делиться предметами между двумя группами. Когда все предметы будут разделены, спросите ребенка, сколько их в каждой группе. Если у вас одинаковые числа, объясните, что ваш ребенок разделил предметы поровну на две группы, что равносильно делению на два.

Заключение

Деление — это разбиение большой группы на более мелкие таким образом, чтобы в каждой группе было равное количество вещей. В математике это операция, используемая для равного группирования и равного распределения. В этой статье мы подробно обсудили процесс деления в математике с некоторыми примерами.

7.3: Отделение на других базах

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

70325

• Джули Харланд
• Колледж МираКоста

Вам потребуется: Базовые блоки (карты материалов 3–15)

Теперь мы будем работать над делением по другим основаниям. Во-первых, мы будем делить, используя повторное вычитание с фактическими базовыми блоками. Позже мы воспользуемся тем же алгоритмом, что и в предыдущем упражнении, для решения задач с повторным вычитанием с частичной таблицей умножения и скаффолдом.

Достаньте базовые блоки Base Three. Мы собираемся использовать их с методом повторного вычитания, чтобы разделить \(221_{\text{три}} \div 21_{\text{три}}\). Делимое равно \(221_{\text{три}}\), которое состоит из 2 плоских, 2 длинных и 1 единицы. Нам нужно выяснить, сколько раз мы можем повторно вычесть делитель \(21_{\text{три}}\) из делимого. Для этого мы можем преобразовать дивиденд только в лонги и единицы, сделав несколько обменов, а затем сформировать как можно больше подмножеств, содержащих 1 лонг и 2 единицы. Количество образовавшихся подмножеств — это то, сколько раз можно вычесть делитель из делимого. Убери свои блоки, чтобы решить эту проблему со мной.

Шаг 1: Сформируйте делимое по основанию три. На самом деле вы должны достать свои базовые три блока и решить задачи с блоками. Я буду использовать инициалы для базовых блоков (U, L, F, B и т. д.), чтобы показать, что происходит. Дивиденд можно показать так:

Ф Ф Л Л У

Шаг 2: Сделайте обмены, чтобы можно было сформировать как можно больше подмножеств, каждое из которых содержит делитель, который равен 2 длинным и 1 единице. Каждую квартиру можно обменять на 3 лонга, чтобы получить:

Л Л Л Л Л Л Л Л У

Затем один из лонгов можно обменять на 3 единицы, чтобы получить L L L L L L L U U U U. Давайте посмотрим, сможем ли мы вычесть некоторые равные подмножества из 2 лонгов и 1 единицы из делимого. По мере того, как вы вынимаете каждые 2 лонга и единицу, сформируйте их в подмножество.

Я могу взять и сформировать из делимого 3 равных подмножества по 2 лонга и по 1 юниту. В делимом остается одна длинная и 1 единица. Сформированные подмножества выглядят так:

ЛЛУ

ЛЛУ

ЛЛУ

Часть, оставшаяся в делимом, то есть остаток выглядит так:

Шаг 3: Каждое равное подмножество из 2 длинных позиций и 1 единицы, которое было вычтено из дивиденда, считается равным 1 для частного. Дайте себе единицу для каждого равного подмножества, которое вы сформировали, это частное. Оставшиеся длинные и единичные числа являются остатком, потому что они меньше делителя.

Коэффициент: U U U

Остаток: L U

Шаг 4: В частном и/или остатке сделайте необходимые замены, чтобы частное и остаток можно было записать по основанию три.

Коэффициент: L

Остаток: L U

Шаг 5: Запишите частное и остаток по основанию три: \(10_{\text{три}}r. 11_{\text{три}}\).

Следовательно, \(221_{\text{три}} \div 21_{\text{три}} = 10_{\text{три}}r. 11_{\text{три}}\)

Шаг 6: Проверьте ответ. Это показано справа.

Упражнение 1

Следуя примеру на предыдущей странице, шаг за шагом выполните следующее деление. Используйте базовые три блока, чтобы сделать это упражнение. Вы можете использовать инициалы или нарисовать блоки, чтобы показать, как вы делаете деление.

Выполните следующее деление: \(222_{\text{три}} \div 12_{\text{три}}\)

а. Сформируйте делимое по основанию три. Нарисуйте, как выглядит дивиденд:

b. Сделайте обмены, чтобы можно было сформировать как можно больше подмножеств, каждое из которых содержит делитель, равный 1 длине и 2 единицам. Вычтите из делимого несколько равных подмножеств из 1 длинной и 2 единиц. По мере того, как вы вынимаете каждое длинное и 2 единицы, сформируйте их в подмножество. Нарисуйте рисунок всех равных подмножеств, которые вы смогли сформировать, вычитая из делимого, затем нарисуйте отдельно то, что осталось в делимом, которое будет остаток (это должно быть меньше, чем 1 длинный и 2 единицы).

i) Показать все сформированные одинаковые подмножества:

ii) Остаток:

c. Для каждого из равных подмножеств из 1 длинной и 2 единиц, которые были вычтены из делимого и сформированы (показаны в b.i.), присвойте себе единицу — это частное. Изобразите частное в единицах:

d. В частном (часть c) и/или в остатке (часть b.ii) сделайте необходимые замены, чтобы частное и остаток можно было записать по основанию три. Нарисуйте картину того, как выглядят частное и остаток после того, как сделали возможными любые обмены.

Частное:

Остаток:

Проверить: \(\begin{align} 21_{\text{three}} \\ \underline{\times 10_{\text{three}}} \\ 210_{\text{three}} \\ \ подчеркивание {+ 11 _ {\ text {три}}} \\ 221 _ {\ text {три}} \ end {выровнено} \)

e. Запишите частное и остаток по основанию три: ________________________

f. Проверьте ответ.

Упражнение 2

Используйте базовые блоки в указанных базах, чтобы найти частное и остаток для каждой задачи. Затем проверьте свой ответ в базе данных. Показать свою работу. Вы можете умножать, используя любой алгоритм умножения, который вы предпочитаете — вы можете попробовать решетку.

а. \(1204_{\text{пять}} \div 42_{\text{пять}}\) = Чек:	в. \(1345_{\text{шесть}} \div 25_{\text{шесть}}\) = Чек:
б. \(323_{\text{четыре}} \div 23_{\text{четыре}}\) = Чек:	д. \(11111_{\text{два}} \div 101_{\text{два}}\) = Чек:

Вы, возможно, заметили в частях c и d, что вам приходилось делать много стопок и что многократное вычитание было несколько утомительным, когда вы могли вычесть из делимого только одно подмножество делителей за раз. Здесь полезно использовать идею о том, что делитель, умноженный на длинное, аналогичен умножению на 10 в десятичной системе счисления. Помните, что 10b — это длинное число для некоторого основания, b. Например, если вы умножите 25 на 10, вы получите 250. В системе счисления \(25_{\text{шесть}}\) означает 2 длинных числа и 5 единиц. Когда вы умножаете это на длинное (\(10_{\text{шесть}}\)), вы получаете \(250_{\text{шесть}}\), что составляет 2 плоских и 5 длинных — каждая часть сдвигается вверх на позицию. ценить. Мы можем использовать это в упражнении 2с, чтобы ускорить вычитание. Мы выполним упражнение 2с, используя эту идею на следующей странице.

Упражнение 2c, \(1345_{\text{шесть}} \div 25_{\text{шесть}}\), можно выполнить более эффективным методом. Вот шаги:

Нарисуйте делимое \(1345_{\text{шесть}}\), используя блоки с основанием шесть.

Б Ф Ф Ф Л Л Л Л У У У У У

Вы хотите вычесть из делимого как можно больше подмножеств делителя \(25_{\text{шесть}}\). Это потребует много шагов. Вам придется разбить блок и три квартиры на множество длинных и юнитов. Теперь \(25_{\text{шесть}}\) означает 2 длинных числа и 5 единиц. Если вы умножите это на длинное, вы получите \(250_{\text{шесть}}\), что составляет 2 квартиры и 5 длинных чисел. Если вы вычтете из дивиденда сразу 2 флета и 5 лонгов, это будет то же самое, что шесть раз вычесть из дивиденда 2 лонга и 5 юнитов! А можно вычесть сразу 2 бемоля и 5 лонгов.

Давайте обменяем некоторые части делимого на более мелкие части, чтобы можно было вычесть и сделать подмножества из 2 плоских и 5 длинных. Я начал с обмена блока на 6 флетов и двух флетов на 12 длинных позиций:

.

F F F F F F F L L L L L L L L L L L L L L L U U U U U

Теперь я сформирую как можно больше подмножеств из 2 плоских и 5 длинных.

Ф Ф Л Л Л Л Л

Ф Ф Л Л Л Л Л

Ф Ф Л Л Л Л Л

У меня все еще остается F L U U U U U в делимом, и я не могу больше брать подмножества из 2 плоских и 5 длинных позиций. Итак, теперь я пытаюсь вычесть подмножества делителя из того, что осталось в делимом. Опять же, мне нужно совершить несколько сделок. Обменяю флет на 5 лонгов и 6 юнитов, так что у меня есть:

Л Л Л Л Л Л У У У У У У У У У У У

Можно сформировать две подгруппы:

Л Л У У У У У

Л Л У У У У У

Все, что осталось в делимом, это единица и 2 лонга, что меньше делителя и является остатком. Таким образом, остаток, LLU, равен \(21_{\text{шесть}}\).

Теперь нам нужно вычислить частное. Каждое из первых 3 сформированных подмножеств было длинной, умноженной на делитель, поэтому для частного я вставил длинное значение для каждого из сформированных подмножеств. Я добавляю единицу для каждого из следующих двух сформированных подмножеств. Итак, у меня есть 3 длинных и 2 единицы для частного, и никаких обменов делать не нужно.

Частное равно L L L U U, или \(32_{\text{шесть}}\), а остаток равен \(21_{\text{шесть}}\).

Следовательно, \(1345_{\text{шесть}} \div 25_{\text{шесть}} = 32_{\text{шесть}}\)r. \(21_{\text{шесть}}\)

Вы должны были получить тот же ответ, когда выполняли упражнение 2с, но вы должны были вычесть и образовать 13 подмножеств делителя, а затем обменять 13 единиц на ответ с основанием шесть.

(Кстати, если делитель \(25_{\text{шесть}}\) умножить на плоскость, то получится 2 квадрата и 5 плоскостей, что больше, чем делимое, поэтому мы не можем отнять столько делителей за один раз, поэтому мы начинаем с вычитания подмножеств длинного числа, умноженного на делитель, по одному.)

Упражнение 3

Разделите следующее, используя базовые блоки. Вы можете использовать метод, описанный на предыдущей странице, или вычитать по одному подмножеству делителя за раз. Объясните или нарисуйте блоки, чтобы показать, как вы решали задачу. Проверьте свои ответы, используя любой алгоритм умножения.

а. \(1046_{\text{семь}} \div 31_{\text{семь}}\) = _________________________________________________ Чек:

б. \(10021_{\text{три}} \div 22_{\text{три}}\) = _________________________________________________ Чек:

Теперь мы собираемся поработать над делением по разным основаниям, используя тот же алгоритм повторного вычитания, что и в Упражнении 2. Поскольку большинство, если не все из нас, недостаточно знакомы с разными основаниями, чтобы оценивать в уме , составление частичной таблицы умножения становится чрезвычайно полезным для решения этих задач.

Поскольку каждое основание имеет разное количество цифр, мы можем выбрать метод удвоения или некоторую частичную таблицу для больших оснований, таких как 11, 12 и 13. Для меньших оснований вы можете подумать о создании полной таблицы. В базе пять вам нужно будет только вычислить 2, 3 и 4 делителя (поскольку 4 — это самая старшая цифра в базе пять). Изучите следующие примеры использования метода лесов в других базах.

Пример 1

Задача о делении по основанию пять: \(200_{\text{пять}} \div 24_{\text{пять}}\). Я прекращаю писать «пять», кроме ответа (в рамке) и чека. Вы должны быть очень осторожны, чтобы помнить, что вы находитесь в базе пять, когда вы складываете (подготовительная работа в начале и сложение в конце проверки, когда вы добавляете остаток), вычитаете (выполняете повторное вычитание) и умножение (в чеке). Для проверки вы можете использовать метод решетки или любой другой метод, который вы предпочитаете.

Пример 2

Задача о делении по основанию два: \(1001011_{\text{два}} \div 111_{\text{два}}\). На самом деле здесь нет никакой подготовительной работы, потому что единственными цифрами по основанию 2 являются 0 и 1.

Для примеров 3 и 4 я решил создать для каждого из них свой тип частичной таблицы умножения.

Пример 3

Задача о делении по основанию восемь: \(2155_{\text{восемь}} \div 61_{\text{восемь}}\). Поскольку это проблема с основанием восемь, я решил составить неполную таблицу, чтобы вычислить делитель, умноженный на 1, 2, 4 и 6. Другой человек может решить составить таблицу только для 1, 2 и 4. Помните, что 7 — старшая цифра в основании восемь. Еще один учащийся может составить полную таблицу для всех цифр по основанию восемь: 1, 2, 3, 4, 5, 6 и 7.

Пример 4

Задача о делении по основанию тринадцать: \(1046_{\text{тринадцать}} \div T2_{\text{тринадцать}}\). Поскольку это проблема в системе счисления тринадцать, я решил составить неполную таблицу, чтобы вычислить делитель, умноженный на 1, 2, 4 и 8. Помните, что W — это старшая цифра в системе счисления восемь. Другой человек может составить таблицу для 1, 2, 4, 6, 8, T и W. Помните, что W — это старшая цифра в базе тринадцати. Другой учащийся мог бы составить полную таблицу для всех цифр по основанию тринадцать, но это большая подготовительная работа, которая обычно не окупается.

Убедитесь, что вы попрактиковались в предыдущих четырех примерах, прежде чем выполнять упражнения, которые следуют на следующих страницах.

Для каждой из задач на деление в оставшейся части этого раздела продемонстрируйте свою работу, используя модель, аналогичную последним четырем примерам. Сначала составьте частичную или полную таблицу умножения (подготовьтесь к делению с помощью многократного вычитания). Затем разделите с помощью метода лесов с методом повторного вычитания. Напишите свой ответ в рамке над эшафотом. Затем проверьте свой ответ, умножив делитель на частное и прибавив остаток. Убедитесь, что вы внимательно следите за тем, с какой базой вы работаете, когда складываете, вычитаете и/или умножаете эту базу. Не забудьте написать основание, когда вы пишете частное и остаток.

Упражнение 4

\(222_{\text{три}} \div 12_{\text{три}}\)

Упражнение 5

\(1204_{\text{пять}} \div 42_{\text{ пять}}\)

Упражнение 6

\(323_{\text{четыре}} \div 23_{\text{четыре}}\)

Упражнение 7

\(1345_{\text{шесть}} \ div 25_{\text{шесть}}\)

Упражнение 8

\(11111_{\text{два}} \div 101_{\text{два}}\)

Упражнение 9

\(1046_{\ text{семь}} \div 31_{\text{семь}}\)

Упражнение 10

\(10021_{\text{три}} \div 22_{\text{три}}\)

Упражнение 11

\(200_{\text{пять}} \div 3_{\text{пять}} \)

Упр.