Как быстро умножать двузначные числа в уме?

Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Например, для умножения 38 на 57 необходимо:

• разложить число на (30+8)*(50+7);
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Реклама

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:
  (100 — 13)*(100 — 9)
  Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
  
  87 – 9 = 78
  91 – 13 = 78
• Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

Поделитесь этим постом с друзьями

Источник

Мария

Читайте Также

ещё больше интересных новостей:

Как быстро умножать числа без калькулятора

Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.

Умножай на пальцах, как купец

Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.

Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.

Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.

Умножай, как Ферроль

Этот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.

Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.

Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!

Умножай, как японец

Этот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.

Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.

Умножай, как итальянец

Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.

Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.

Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.

Вот как мы умножили 639 на 12.

Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!

длинное умножение? Определение, методы, шаги, примеры, факты

Что такое длинное умножение?

Длинное умножение — это простой способ умножения больших чисел. Это упрощает процесс умножения двух чисел, которые иначе умножить непросто.

Например, мы можем легко найти произведение 55$ \умножить на 20$, умножив 55 на 2, а затем добавив 0 в самом правом месте ответа.

55$ х 2 = 110$ и 55$ х 20 = 1100$

Однако иногда найти товар не так просто. В таких случаях мы используем метод длинного умножения. Его часто называют длинным ручным умножением (длинное умножение вручную).

Длинное умножение: определение

Длинное умножение — это метод умножения, с помощью которого упрощается умножение двух больших чисел, состоящих из двух или более цифр.  

Например, мы можем легко найти произведение 55 долларов США на 20 долларов, умножив 55 на 2, а затем добавив 0 в самом правом месте ответа.

55$\умножить на 2 = 110$ и 55$\умножить на 20 = 1100$

Но как умножать большие числа? Много раз найти продукт не так просто. В таких случаях мы используем длинный метод умножения.

Например: $47 \times 63 =$ ?

Мы можем найти ответ простыми шагами, используя длинное умножение. Давайте подробно обсудим этот метод в следующем разделе.

Связанные игры

Как умножать, используя длинное умножение

Давайте обсудим шаги по умножению двузначного числа на двузначное, используя метод длинного умножения.

Умножим 47 на 63, используя метод длинного умножения .

Шаг 1: Сначала запишите два числа, одно под другим, так, чтобы их разряды совпадали. Обычно мы пишем большее число сверху, а знак умножения слева и рисуем линию под числами, как показано ниже.

Важное примечание:  

• В методе длинного умножения число вверху (63) называется множимым . Число, на которое оно умножается, то есть число внизу (43), называется множителем .

• Если вы напишете маленькое число сверху и выполните умножение, ответ останется тем же, поскольку при умножении двух чисел порядок не имеет значения.

Шаг 2: Умножьте разряд единиц верхнего числа на разряд единиц нижнего числа.

Напишите товар, как показано на картинке. Не забывайте о переносе, который идет в следующем месте!

Шаг 3: Умножьте разряд десятков верхнего числа на разряд единиц нижнего числа. Добавьте перенос.

Это наш первый неполный продукт, который мы получили путем умножения верхнего числа на единицу нижнего числа.

Шаг 4: Теперь поместим 0 под цифрой единиц, как показано на рисунке. Это потому, что теперь мы будем умножать цифры верхнего числа на разряд десятков нижнего числа.

Шаг 5: Умножьте разряд единиц верхнего числа на разряд десятков нижнего числа.

Шаг 6: Умножьте разряд десятков верхнего числа на разряд десятков нижнего числа.

Это второе частичное произведение, полученное путем умножения верхнего числа на разряд десятков нижнего числа.

Шаг 7: Теперь добавьте два частичных произведения.

Подведем итоги.

Вышеупомянутые длинных шагов умножения выполняются только для умножения чисел больше двух цифр.

Связанные рабочие листы

Метод длинного умножения в столбце

Длинное умножение также известно как метод умножения в столбце, поскольку мы выполняем умножение по вертикали или по столбцу.

Давайте рассмотрим еще один пример, чтобы лучше понять это.

Умножьте 321 на 23.

Посмотрите на длинную таблицу умножения, которая шаг за шагом показывает длинное умножение. Вы можете обращаться к нему, чтобы избежать ошибок при решении длинных задач на умножение.

Умножение десятичных дробей с помощью длинного умножения

Давайте разберемся, как умножать десятичных знаков с помощью метода длинного умножения .

Пример: Умножьте $3,6 \times 5,5$

Шаг 1 : Сначала мы помещаем меньшее число из двух в правую часть и меняем десятичное число на дробь.

$5,5 \times 3,6 = \frac{55}{10} \times \frac{36}{10}$

Шаг 2 : Затем мы умножаем числители, используя шаги метода длинного умножения. Оставим пока знаменатель как есть.

Шаг 3 : Теперь мы делим ответ (который мы получили на шаге 2) на знаменатель, чтобы получить окончательный ответ.

$\frac{1980}{100} = 19,80$

Длинное умножение с использованием горизонтального метода

Давайте теперь поймем, как использовать горизонтальный метод с помощью длинного примера умножения. Как следует из названия, мы умножаем числа по горизонтали, но выполняем те же шаги, что и ранее.

Пример: умножьте 48 на 24.

Шаг 1 : Сначала мы пишем числа рядом друг с другом и располагаем их горизонтально.

$48 \times 24$

Шаг 2 : Теперь умножаем второе число (число справа) на разряд единиц первого числа.

Здесь мы умножаем 24 на 8, так как 8 стоит на месте единиц в 48.

$24 \times 8 = 192$

Шаг 3 : Теперь умножаем второе число на разряд десятков первого число.

Здесь мы умножаем 24 на 40, так как 4 стоит на десятках числа 48.

$24 \times 40 = 960$

Шаг 4 : Наконец, мы добавляем частичные произведения, полученные на шагах 2 и 3, к получить окончательный ответ.

Таким образом, $48 \times 24 = 1152$

Длинное умножение с отрицательными числами

Умножение отрицательных чисел методом длинного умножения выполняется так же, как указано выше. Однако мы должны тщательно рассмотреть знаки двух чисел, чтобы определить знак произведения.

Например, когда мы умножаем два отрицательных числа друг на друга, знак результата остается положительным. С другой стороны, оно становится отрицательным при перемножении отрицательного числа и положительного числа.

На рисунке ниже показано, как меняется знак при умножении отрицательных чисел:

Забавные факты о длинном умножении

• Длинное умножение также известно как метод умножения столбцом.

• Всякий раз, когда любое число умножается на ноль, ответ также равен нулю.

• При умножении числа 9 на любое другое число сумма цифр в произведении всегда равна 9.

Например, 9$ \умножить на 25 = 225$ и 2$ + 2 + 5 = 9$;

                              9 долл.

• Длинное умножение также может называться повторным сложением, потому что умножение любого числа — это просто альтернатива его многократному сложению.

• Всякий раз, когда любое четное число от 0 до 9 умножается на 6, произведение имеет такое же четное число в разряде единиц.

Например, $6 \times 4 = 24,\; 6 х 2 = 12$

• Всякий раз, когда перемножаются два больших числа (скажем, трехзначные или четырехзначные числа), процесс длинного умножения остается прежним. Например:

Заключение

Длинное умножение — метод, упрощающий умножение больших чисел, в том числе двузначных, трехзначных и т. д., друг на друга. Давайте решим несколько примеров и попрактикуемся в задачах на длинное умножение!

Решенные примеры на длинное умножение

1. Умножьте 38 на 91, используя метод столбца.

Решение: 

2. Умножьте 72 на 44, используя метод столбца.

Решение :

3. Умножьте — 58 на 30.

Решение:

. Спинка продукта. -\;58) \times (30)$ будет отрицательным.

Так как 58 имеет отрицательный знак, окончательный ответ будет $ – 1740$.

$(\;-\;58) \times (30) = \;-\;1740$

4. Алия купила 42 тетради, каждая стоит $\$9,6$ . Сколько она потратила?

Решение:

Чтобы найти сумму, которую потратила Алия, умножьте 9,6 на 42. 10, чтобы получить окончательный ответ, который составляет $403,2$.

9,6$ \умножить на 42 = 403,2$

Таким образом, Алия потратила 403,2$ на ноутбуки.

5. Умножьте $-70$ на и $-15$ на .

Решение:

Найдем $(70) \times (15)$.

Поскольку оба числа отрицательные, окончательный ответ останется положительным, $1050$.

$(70) \times (15) = 1050$

Практические задачи на длинное умножение

1

Умножение 95 на 13, используя метод столбцов.

1125

1235

1545

1425

Правильный ответ: 1235
$ 95 \ Times13 = 1235 $

2

Multiply Decimals 1.2 и 6.7.

9,05

13,5

8,04

6,08

Правильный ответ: 8,04
$6,7\times1.2=\frac{67}{10}\times\frac{12}{23} числители.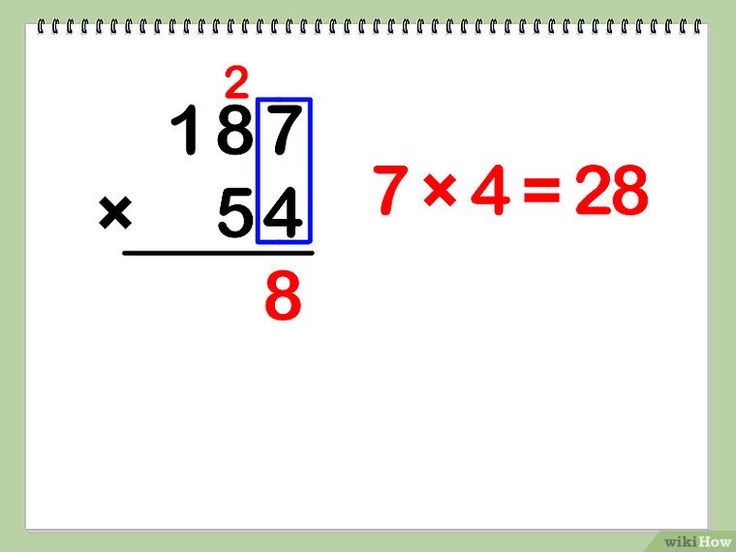 Затем мы делим их произведение на знаменатели, чтобы получить окончательный ответ.

3

Перемножьте отрицательные числа $(-\;89)$ и $(-\;61)$.

5429

3489

5299

4529

Правильный ответ: 5429
Поскольку оба числа отрицательные, окончательный ответ останется положительным.
$(-\;89)\times(-\;61) = 5429$.

4

Умножьте 45 на 21, используя горизонтальный метод.

645

745

845

945

Правильный ответ: 945
$21\times5=105$ __(i)
$21\times4=84$ __(ii)
Складывая (i) и (ii), получаем
$105\;+\;84=945$.

5

Умножение 530 на 22.

12600

13550

11660

14650

Правильный ответ: 11660
$ 530 \ Times22 = 11660 $

. числа?

Отрицательные числа — это числа, значение которых меньше нуля и поэтому перед ними стоит знак минус (-).

Что такое положительные числа?

Положительные числа — это числа, значение которых больше нуля.

Что такое десятичная дробь?

Десятичное число представляет собой число, которое отделяет целое число от дробного числа. Он представлен знаком точки (.).

В чем смысл горизонтального метода умножения?

Горизонтальный метод относится к методу, в котором числа расположены в горизонтальной строке слева направо.

Что означает столбчатый метод умножения?

Метод столбцов относится к методу, в котором числа располагаются одно под другим сверху вниз.

Что такое короткое умножение?

Сокращенное умножение — это метод умножения, обычно используемый при умножении трехзначного или большего числа на однозначное число.

Как умножать в Excel: пошаговое руководство

Вы когда-нибудь застревали, пытаясь выполнить сложное умножение в Excel? Вы хотите научиться умножать в Excel как профессионал, даже если вы новичок? Если да, то вы пришли в нужное место.

Независимо от того, являетесь ли вы студентом, работающим специалистом или просто хотите лучше управлять своими финансами, этот навык будет полезен вам сейчас и в будущем.

Excel предлагает три различных способа умножения чисел за считанные секунды. Итак, давайте узнаем, как создавать и легко применять формулы умножения в Excel.

В этом пошаговом руководстве мы объясним, как:

• Умножать числа в Excel, используя базовую формулу
• Умножение чисел в Excel с использованием формулы ПРОИЗВЕД
• Умножение чисел в Excel с использованием константы

Умножение чисел в Excel с использованием базовой формулы

Первые два метода позволяют быстро умножать числа как в одной, так и в нескольких ячейках с использованием базовой формулы.

Умножение чисел в одной ячейке

1. Откройте Microsoft Excel и выберите любую пустую ячейку.

 

Выберите любую пустую ячейку для начала

2. Введите знак равенства (=) в выбранную ячейку, а затем числа, которые вы хотите умножить, со звездочкой между ними.

 

Введите знак равенства, а затем числа, которые вы хотите умножить, разделенные звездочкой

3. Нажмите «Ввод» на клавиатуре. В выбранной ячейке ваше уравнение исчезнет, ​​и отобразится ответ.

 

Нажмите клавишу «Ввод», чтобы умножить ваши коэффициенты, и ответ появится в ячейке

Умножение числового содержимого разных ячеек

Если вы хотите умножить две или более ячеек в Excel, следуйте этим инструкциям:

1. Откройте электронную таблицу Microsoft Excel, содержащую числа, которые вы хотите умножить, и введите знак равенства в любую пустую ячейку.

 

Введите знак равенства в любую пустую ячейку, чтобы начать создание формулы

2. Нажмите на первую ячейку, которую вы хотите умножить, и имя ячейки появится рядом со знаком равенства. Введите звездочку рядом с появившимся именем ячейки.

 

Нажмите на первую ячейку, которую вы хотите умножить; после того, как имя ячейки появится рядом со знаком равенства, введите звездочку

3. Нажмите на вторую ячейку, которую вы хотите умножить, чтобы добавить ее в формулу. Повторите звездочку и нажмите на дополнительные ячейки, чтобы добавить больше факторов в уравнение.

 

Нажмите на вторую ячейку, содержащую число, которое вы хотите умножить; добавьте дополнительные звездочки и ячейки по желанию, чтобы завершить уравнение

4. Нажмите клавишу «Ввод», появится ответ.

Нажмите кнопку «Ввод», чтобы активировать формулу и просмотреть ответ. для умножения до 255 значений одновременно.

1. Откройте Microsoft Excel и выберите любую пустую ячейку. Введите знак равенства, а затем слово ПРОДУКТ, написанное заглавными буквами. Затем добавьте открывающую скобку.

 

В пустой ячейке введите знак равенства, ПРОИЗВЕД заглавными буквами и открывающую скобку

2. Чтобы умножить отдельные ячейки , введите имена ячеек и разделите их запятыми без пробелов.

 

Введите имена отдельных ячеек, которые вы хотите умножить, внутри открывающей скобки и разделите их запятыми

3. Чтобы умножить ряд ячеек , введите двоеточие между двумя именами ячеек, чтобы указать, что все ячейки в этом диапазоне должны быть умножены. Например, «=PRODUCT(A2:A5)» указывает, что ячейки A2, A3, A4 и A5 должны быть перемножены.

 

Чтобы умножить ряд ячеек, введите имя первой и последней ячейки ряда, разделенные двоеточием

4. Если вы хотите добавить число к уравнению, просто введите запятую, а затем это число.

 

Чтобы добавить одно число в диапазон или список отдельных ячеек, введите запятую, затем это число и закрывающую скобку

5. Закончив ввод формулы, поместите в конце закрывающую скобку и нажмите кнопку «Ввод» на клавиатуре. Ответ уравнения появится в ячейке.

Умножение чисел в Excel с использованием константы

В Excel константа — это заданное число, значение которого сохраняется на всем листе. Вы используете константу для создания формулы, которую можно применить к нескольким ячейкам.

Пользователи могут умножать набор чисел/ячеек на одно и то же число/ячейку без создания нескольких формул. Вот как:

1. Откройте Microsoft Excel. В пустой ячейке в верхней части столбца введите число, на которое вы хотите умножить ряд чисел/набор ячеек. Это ваш постоянный номер .

 

В пустой ячейке в верхней части столбца введите число, на которое вы хотите умножить каждую ячейку в выбранном вами наборе

2. Определите столбец чисел, которые вы хотите умножить на вашу константу. В пустой ячейке над другим пустым столбцом введите знак равенства.

 

В этом примере столбец A — это набор чисел/ячеек, которые вы хотите умножить на вашу константу — число 20 в верхней части столбца B. Затем введите знак равенства в верхней части пустого столбца (здесь мы используйте колонку C)

3. Нажмите на первую ячейку, которую вы хотите умножить на постоянное число. Имя ячейки появится рядом со знаком равенства. Далее введите звездочку.

 

Нажмите на первую ячейку в столбце чисел, которые вы хотите умножить на постоянное число; имя ячейки появится рядом со знаком равенства. Введите звездочку рядом с именем ячейки

.

4. В той же ячейке (после звездочки) введите знак доллара ($), а затем букву столбца ячейки, содержащей ваш постоянный номер. Добавьте еще один знак доллара, а затем номер строки ячейки, содержащей ваш постоянный номер.

Знак доллара превращает вашу константу в абсолютную ссылку, которую можно скопировать и вставить в любую ячейку электронной таблицы Excel.

 

После звездочки введите «$», затем букву столбца ячейки с вашим постоянным номером. Затем введите еще один знак доллара и номер строки ячейки, содержащей ваш постоянный номер

.

5. Нажмите кнопку «Ввод» на клавиатуре, и появится ответ.

 

Нажмите кнопку «Ввод» и ответ появится в ячейке, где вы набрали формулу

6. Чтобы применить формулу ко всем ячейкам в нужном столбце, дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, содержащей ваш результат/ответ. Excel автоматически запустит уравнение и заполнит столбец вашим ответом.

 

Дважды щелкните маленький зеленый квадратик в правом нижнем углу ячейки с вычисленным ответом, и Excel применит формулу ко всем числам в выбранном столбце

7.