Шестаков 1994 с 8 9 умножение дробей. Умножение простых и смешанных дробей с разными знаменателями

Умножение обыкновенных дробей

Рассмотрим пример.

Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.

Умножение двух обыкновенных дробей

Правило умножения обыкновенных дробей:

Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:

Пример 1

Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.

Решение.

Воспользуемся правилом умножения обыкновенных дробей:

\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]

Ответ: $\frac{15}{77}$

Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.

Пример 2

Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.

Решение.

Используем правило умножения обыкновенных дробей:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]

В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:

\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]

Краткое решение:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]

Ответ: $\frac{1}{24}.$

При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.

Пример 3

Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.

Решение.

Воспользуемся формулой умножения обыкновенных дробей:

\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]

Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$.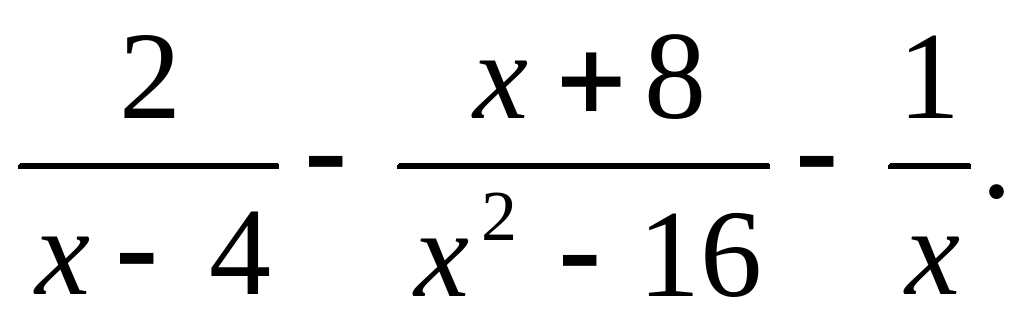 Разложим числитель и знаменатель на простые множители и произведем сокращение:

\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]

Ответ: $\frac{1}{20}.$

При умножении дробей можно применять переместительный закон:

Умножение обыкновенной дроби на натуральное число

Правило умножения обыкновенной дроби на натуральное число:

Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:

где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.

Пример 4

Выполнить умножение дроби $\frac{3}{17}$ на $4$.

Решение.

Воспользуемся правилом умножения обыкновенной дроби на натуральное число:

\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]

Ответ: $\frac{12}{17}.

$

Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.

Пример 5

Умножить дробь $\frac{7}{15}$ на число $3$.

Решение.

Воспользуемся формулой умножения дроби на натуральное число:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]

По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:

\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]

В результате получили неправильную дробь. Выделим целую часть:

\[\frac{7}{5}=1\frac{2}{5}\]

Краткое решение:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]

Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]

Ответ: $1\frac{2}{5}. $

При умножении дроби на натуральное число можно использовать переместительный закон:

Деление обыкновенных дробей

Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.

Деление двух обыкновенных дробей

Правило деления обыкновенных дробей: Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:

\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]

В результате получили неправильную дробь, из которой выделим целую часть:

\[\frac{14}{9}=1\frac{5}{9}\]

Ответ: $1\frac{5}{9}.$

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками.

Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей

:

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c

= a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5

= 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей.

Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Умножение и деление дробей

Необходимым навыком для каждого ученика пятого класса является умение выполнять умножение и деление дробей.

Разберём каждую тему подробнее.

Умножение обыкновенных дробей

Рассмотрим две обыкновенные дроби и выполним их умножение:

Сначала смотрим, можно ли сократить числители дробей со знаменателями. В нашем случае 3 и 4 не имеют общих делителей и с числами 5 и 7, поэтому сократить дроби невозможно.

Значит, начинаем умножать в лоб, числитель на числитель, знаменатель на знаменатель

Числитель меньше знаменателя, а значит, целую часть выделить невозможно,

Это окончательный ответ.

Разберём еще один пример:

В этой ситуации можно сократить числа 7 и 14, 10 и 5. Поэтому в первую очередь сокращаем дроби, чтобы упростить будущие вычисления

В итоге мы получили:

Задание для самопроверки:

Умножение смешанных дробей

Согласно правилам, умножение смешанных дробей выполнить невозможно, поэтому в первую очередь переводим каждую смешанную дробь и неправильную.

*см. перевод смешанной дроби в неправильную

Рассмотрим пример,

        

Мы получили:

Выполняем сокращение дробей, а затем умножаем их

Так как 52 > 15, выделяем целую часть

Задание выполнено

 

Задание для самопроверки:

 Умножение десятичных дробей

Выполним умножение десятичных дробей: 2,7 * 1,5.

Для этого умножим данные числа «столбиком», не обращая внимания на запятую.

При умножении, количество знаков после запятой складывается. У первого и у второго числа  по одной цифре после запятой, значит при их умножении у числа будет уже 2 знака после запятой, так как 1+1 = 2

Ставим запятую в нужное место

Мы получили, что 2,7 * 1,5 = 4,05

Задание для самопроверки:

• 8,7 : 0,3
• 1,24 : 3,1
• 51,2: 0,64

Деление обыкновенных дробей

При делении обыкновенных дробей действуем следующим образом, деление заменяем на умножение, при этом переворачиваем вторую дробь.

Умножаем дроби по правилам умножения обыкновенных дробей.

Сокращаем числитель со знаменателем, 3 и 9 сокращаются на 3, а 4 и 8 на 4 соответственно

Умножаем верх на верх, а низ на низ у каждой дроби

Умножение выполнено.

Деление смешанных дробей

Ни умножение, ни  деление смешанных дробей выполнить невозможно, поэтому переводим смешанную дробь в неправильную.

А затем выполняем замену деления на умножение, переворачивая вторую дробь

Сокращаем числитель со знаменателем, а зачем умножаем дроби, верх на верх, низ на низ соответственно

Получили  в ответе.

Задание для самопроверки:

 Деление десятичных дробей

• Рассмотрим деление десятичных дробей на примере чисел 2,6 : 0,2

По правилу, делить на дробь нельзя, поэтому переносим запятую у делителя в конец числа, то есть на один знак вправо, при этом у делимого она также перенесется на знак в правую сторону.

И делим целые числа, будто запятой и не было вовсе.

Ответ готов, это число 13.

• Разделим 25,6 на 0,04

У делителя 2 знака после запятой, поэтому переносим ей вправо на 2 знака и у делимого и у делителя. Но, так как у делимого был всего 1 число после «,» , а нам необходим перенос на 2 знака,  в конец этого числа припишем недостающее число 0. В нашем случае ровно один.

• Попробуем решить следующий пример с делением десятичных дробей: 0,315 : 0,9

У делителя 1 цифра после запятой, переносим её ровно на один знак у делимого и у делителя, получаем:

В этом случае сначала делим целую часть у делимого, то есть 3 на делитель, т. е. на 9. Но 3 < 9, поэтому берём по 0. После 0 в значении частного ставим запятую, списываем 1 и делим уже 31 на 9. Подбираем такое число, которое при умножении на 9 даёт число, близкое к 31, но чуть меньше, 9 * 3 = 27, берём по 3. 31-27 = 4, списываем 5, делим уже 45 на 9, получаем 5

В итоге наш ответ – 0,35.

 

 

Дроби и десятичные числа — Умножение дробей и смешанных чисел

Предыдущий Следующий

Умножение дробей и смешанных чисел

Умножение дробей довольно просто по сравнению со сложением и вычитанием. И угадайте, что? Нам не нужно находить общий знаменатель. Мы 9Однако от 0008 до необходимо убедиться, что каждое число является дробью: смешанные числа или целые числа не допускаются. Это клуб элитной фракции.

Просто выполните следующие четыре простых шага:

1. Преобразуйте все смешанные числа или целые числа в неправильные дроби.
2. Умножьте числители.
3. Умножьте знаменатели.
4. Сократите окончательный ответ и при необходимости преобразуйте его обратно в смешанное число.

Пример умножения 1

	Умножьте числители, затем умножьте знаменатели.
	Сократите дробь. 12 и 72 имеют GCF, равный 12, поэтому разделите верхнюю и нижнюю часть на 12.
	Бум, вот и наш ответ.

Пример умножения 2

	Сначала преобразуем это второе смешанное число в неправильную дробь:
	Есть один ответ, но мы также можем превратить его в смешанное число.
	Здравствуйте, окончательный ответ.

Ярлык: кросс-отмена

Вместо сокращения дроби в конце задачи мы можем перекрестно отменить перед умножением . Это не обязательно, но сэкономит несколько шагов.

Сокращение означает, что при умножении дробей мы можем уменьшить любой числитель с любой знаменатель . В этом примере 5 и 10 можно разделить на 5, даже если они не в одной и той же дроби.

Давайте еще раз посмотрим на пример 1 и посмотрим, как использовать этот метод.

Пример перекрестного исключения 1

	Здесь мы можем уменьшить 3 и 9 (на 3), а также уменьшить 4 и 8 (на 4). Да, давайте так.
	Теперь умножаем верх на верх и низ на низ, как обычно.
	Эй, окончательный ответ такой же, как и в Примере 1. Хороший.

Вот еще один пример, который включает почти все, что мы сделали до сих пор.

Пример 2 с перекрестным сокращением

	Сначала преобразуйте каждое число в неправильную дробь.
	14 и 7 можно уменьшить на 7, поэтому мы можем взаимно отменить.
	Умножение.
	Вот ответ.
	Если хотите, вы можете превратить его обратно в смешанное число

Умножение целого числа на дробь

Помните, что все действительные числа можно записать в виде дробей. Все, что нам нужно сделать с целым числом, это поставить его над знаменателем 1.

Давайте посмотрим на пример, не так ли?

Предыдущий Следующий

Подробнее о дробях и десятичных дробях Навигация

Это продукт премиум-класса

Разблокировать эти функции

Устали от рекламы?

Присоединяйтесь сегодня и никогда больше их не увидите.

Начало работы

Почему работает взаимное сокращение дробей при умножении?

$\begingroup$

Я просматриваю свою арифметику, и сейчас я занимаюсь дробями, у меня просто небольшая проблема с «визуализацией», почему сокращение работает при умножении дробей, я знаю, как это работает, это просто почему. Возьмем, к примеру.

$$\frac{2}{3}\cdot\frac{3}{4}=\frac{1}{3}\cdot\frac{3}{2}=\frac{1\cdot1}{ 1\cdot2}=\frac{1}{2}. $$ Благодаря сокращению мы знаем, что это заканчивается на 1/2, потому что общий делитель числителя «2» и знаменателя «4» равен 2, поэтому мы делим оба на «2» и заканчиваем с новыми числами на месте, мы также знаем, что общий множитель числителя «3» и знаменателя «3» равен «3», что равно «1» в обоих местах, поэтому он делает работу по «приведению к наименьшим терминам» несуществующей, поскольку этот метод уже является кратчайший путь к этому.

Но я просто не могу представить себе, как это работает. Не могли бы вы, ребята, дать мне наглядную модель, которая поможет мне понять это? благодарю вас.

• дроби

$\endgroup$

3

$\begingroup$

Просто напишите $$\frac{2}{3}:\frac{3}{4}=\frac{2}{3}\cdot\frac{4}{3}=\frac{2\cdot4} {3\cdot3}=\frac{8}{9}.$$

$\endgroup$

$\begingroup$

Если вы умножаете верхнюю и нижнюю части дроби на одно и то же число, это не меняет своего значения, например. $$\frac{1}{2} = \frac{1\times 2}{2\times 2} = \frac{2}{4}$$ Сделайте то же самое для вашей задачи 3\times 3}{4}} = \frac{2}{\frac{9}{4}}=\frac{2\times 4}{\frac{9 \times 4}{4}} = \frac{8}{9}$$

$\endgroup$

1

$\begingroup$

Это не совсем наглядно, но самый простой способ увидеть, как работает взаимное сокращение, состоит в том, что умножение является коммутативным: вы можете умножать числа в любом порядке (например, $2 \cdot 4 = 4 \cdot 2 $). Умножение на $\frac{a}{b}$ всегда равносильно умножению на $a$, а затем на $\frac{1}{b}$. Итак, $$\frac{2}3 \cdot \frac34 = 2 \cdot \frac13 \cdot 3 \cdot \frac14 = 2 \cdot\frac14 \cdot 3 \cdot \frac13 = \frac24 \cdot \frac33 = \frac24 \ cdot 1 = \frac24$$

Вот наглядное изображение, которое может помочь: вы можете представить $\frac23 \cdot \frac34$, взяв прямоугольник, разделив его по длине на $3$ и по ширине на $4$, а затем взяв подпрямоугольник длины $2$ вдоль длины и $3$ по ширине.