Раскрытие скобок: правила, примеры, решения

Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.

Что называется раскрытием скобок?

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2·(3+4) на выражение вида 2·3+2·4без скобок. Этот прием носит название раскрытия скобок.

Определение 1

Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:

• знаки «+» или «-» перед скобками, в которые заключены суммы или разности;
• произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.

Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5+(−3)−(−7) к 5−3+7. Фактически, это тоже раскрытие скобок.

Точно также мы можем заменить произведение выражений в скобках вида (a+b)·(c+d) на сумму a·c+a·d+b·c+b·d. Такой прием также не противоречит смыслу раскрытия скобок.

Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x2·1a-x+sin(b)  будет соответствовать выражение без скобок вида x2·1a-x2·x+x2·sin(b) .

Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5−(3−(2−1))=5−(3−2+1)=5−3+2−1 или 5−(3−(2−1))=5−3+(2−1)=5−3+2−1.

Правила раскрытия скобок, примеры

Приступим к рассмотрению правил раскрытия скобок.

У одиночных чисел в скобках

Отрицательные числа в скобках часто встречаются в выражениях. Например, (−4) и 3+(−4). Положительные числа в скобках тоже имеют место быть.

Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, +(а) на +а, -(а) на –а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5, выражение 3+(5) без скобок примет вид 3+5, так как +(5) заменяется на +5, а выражение 3+(−5) эквивалентно выражению 3−5, так как +(−5) заменяется на −5.

Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.

Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. +(−a) мы заменяем на −a,  −(−a) заменяется на +a. Если выражение начинается с отрицательного числа (−a), которое записано в скобках, то скобки опускаются и вместо (−a) остается −a.

Приведем примеры:  (−5) можно записать как  −5,  (−3)+0,5 принимает вид −3+0,5,  4+(−3) превращается в 4−3, а −(−4)−(−3) после раскрытия скобок принимает вид 4+3, так как −(−4) и −(−3) заменяется на +4 и +3.

Следует понимать, что записать выражение 3·(−5) как 3·−5 нельзя. Об этом речь пойдет в следующих пунктах.

Давайте посмотрим, на чем основываются правила раскрытия скобок.

Согласно правилу разность a−b равна a+(−b). На основе свойств действий с числами мы можем составить цепочку равенств (a+(−b))+b=a+((−b)+b)=a+0=a, которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a+(−b)  — это разность a−b.

Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что −(−a)=a, a−(−b)=a+b.

Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть −(−((−(5)))). Раскроем скобки, продвигаясь изнутри наружу: −(−((−(5))))=−(−((−5)))=−(−(−5))=−(5)=−5. Также этот пример можно разобрать и в обратном направлении: −(−((−(5))))=((−(5)))=(−(5))=−(5)=−5.

Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком «+» впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.

К примеру, после раскрытия скобок выражение −(−2·x)−(x2)+(−1x)−(2·x·y2:z) примет вид 2·x−x2−1x−2·x·y2:z. Как мы это сделали? Мы знаем, что −(−2·x) есть +2·x, а так как это выражение стоит вначале, то +2·x можно записать как 2·x, −(x2)=−x2, +(−1x)=−1x и −(2·x·y2:z)=−2·x·y2:z.

В произведениях двух чисел

Начнем с правила раскрытия скобок в произведении двух чисел.

Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел −a и −b вида (−a)·(−b) мы можем заменить на (a·b), а произведения двух чисел с противоположными знаками вида (−a)·b и a·(−b) заменить на (−a·b). Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.

Рассмотрим несколько примеров.

Пример 1

Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел -435 и -2, вида(-2)·-435 . Для этого заменим исходное выражение на 2·435 . Раскроем скобки и получим 2·435 .

А если мы возьмем частное отрицательных чисел (−4):(−2), то запись после раскрытия скобок будет иметь вид 4:2

На месте отрицательных чисел −a и −b могут быть любые выражения со знаком минус впереди, которые  не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.

Раскроем скобки в выражении  -3·xx2+1·x·(ln5). Согласно правилу, мы можем произвести следующие преобразования:   -3·xx2+1·x·(ln5)=-3·xx2+1·x·ln5=3·xx2+1·x·ln5.

Выражение (−3)·2 можно преобразовать в выражение (−3·2). После этого можно раскрыть скобки: −3·2.

 23·-45=-23·45=-23·45

 Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок:  

(−5):2=(−5:2)=−5:2 и  234:(-3,5)=-234:3,5=-234:3,5.

Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два  примера.

-1x+1:x-3=-1x+1:x-3=-1x+1:x-3

и 

sin(x)·(-x2)=(-sin(x)·x2)=-sin(x)·x2

В произведениях трех и большего количества чисел

Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.

Пример 2

Для примера, возьмем выражение 5·(−3)·(−2), которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как

 (5·3·2) и затем окончательно раскрыть скобки, получив выражение 5·3·2.

В произведении (−2,5)·(−3):(−2)·4:(−1,25):(−1)  пять чисел являются отрицательными. поэтому (−2,5)·(−3):(−2)·4:(−1,25):(−1)=(−2,5·3:2·4:1,25:1). Окончательно раскрыв скобки, получаем  −2,5·3:2·4:1,25:1.

Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и -1 или -1 заменяем на (−1)·a.

Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные −1, в начало выражения. Произведение четного числа минус единиц равно 1, а нечетного – равно 

−1, что позволяет нам использовать знак минус.

Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении -23:(-2)·4:-67 выглядела бы следующим образом:

-23:(-2)·4:-67=-23·-12·4·-76==(-1)·23·(-1)·12·4·(-1)·76==(-1)·(-1)·(-1)·23·12·4·76=(-1)·23·12·4·76==-23·12·4·76

Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение

 x2·(-x):(-1x)·x-3:2.

Его можно привести к выражению без скобок  x2·x:1x·x-3:2 .

Раскрытие скобок, перед которыми стоит знак «+»

Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.

Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.

Пример 3

Для примера приведем выражение (12−3,5)−7.  Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12−3,5)−7=+12−3,5−7. В приведенном примере знак перед первым слагаемым ставить не обязательно, так как +12−3,5−7=12−3,5−7.

Пример 4

Рассмотрим еще один пример. Возьмем выражение  x+2a-3×2+1-x2-4+1x и проведем с ним действия  x+2a-3×2+1-x2-4+1x==x+2a-3×2+1-x2-4+1x

Вот еще один пример раскрытия скобок:

Пример 5

2+x2+1x-x·y·z+2·x-1+(-1+x-x2)==2+x2+1x-x·y·z+2·x-1-1+x+x2

Как раскрываются скобки, перед которыми стоит знак минус

Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение.

Согласно правилу раскрытия скобок, перед которыми стоит знак «-», скобки со знаком «-» опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.

Пример 6

К примеру:

—12=12,-1x+1=-1x+1,-(-x2)=x2

Выражения с переменными могут быть преобразованы с использованием того же правила:

—x+x3-3—2·x2+3·x3·x+1x-1-x+2,

получаем x-x3-3+2·x2-3·x3·x+1x-1-x+2.

Раскрытие скобок при умножении числа на скобку, выражения на скобку

Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a1±a2±…±an)·b=(a1·b±a2·b±…±an·b) или b·( a1±a2±…±an)=(b·a1±b·a2±…±b·an), где a1, a2, …, an и b – некоторые числа или выражения.

Пример 7

Например, проведем раскрытие скобок в выражении (3−7)·2. Согласно правилу, мы можем провести следующие преобразования: (3−7)·2=(3·2−7·2). Получаем 3·2−7·2.

Раскрыв скобки в выражении 3·x2·1-x+1x+2, получаем  3×2·1-3·x2·x+3·x2·1x+2.

Умножение скобки на скобку

Рассмотрим произведение двух скобок вида (a1+a2)·(b1+b2). Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.

Для того, чтобы решить приведенный пример, обозначим выражение (b1+b2) как b. Это позволит нам использовать правило умножения скобки на выражение. Получим (a1+a2)·(b1+b2)=(a1+a2)·b=(a1·b+a2·b)=a1·b+a2·b. Выполнив обратную замену b на (b1+b2), снова применим правило умножения выражения на скобку:  a1·b+a2·b==a1·(b1+b2)+a2·(b1+b2)==(a1·b1+a1·b2)+(a2·b1+a2·b2)==a1·b1+a1·b2+a2·b1+a2·b2

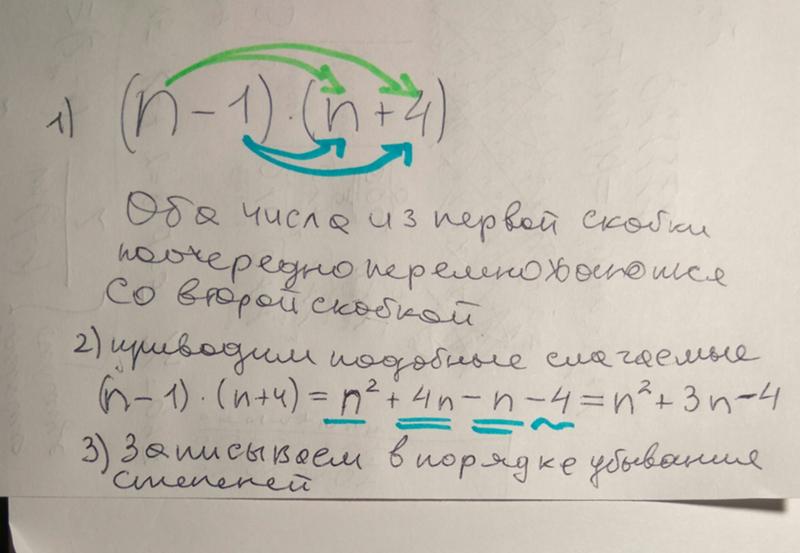
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.

Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.

Формула будет иметь вид:

(a1+a2+…+am)·(b1+b2+…+bn)==a1b1+a1b2+…+a1bn++a2b1+a2b2+…+a2bn++…++amb1+amb1+…ambn

Проведем раскрытие скобок в выражении (1+x)·(x2+x+6) Оно представляет собой произведение двух сумм.  Запишем решение: (1+x)·(x2+x+6)==(1·x2+1·x+1·6+x·x2+x·x+x·6)==1·x2+1·x+1·6+x·x2+x·x+x·6

Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение  (1−x)·(3·x·y−2·x·y3).

Сначала представим выражения в скобках в виде сумм: (1+(−x))·(3·x·y+(−2·x·y3)). Теперь мы можем применить правило: (1+(−x))·(3·x·y+(−2·x·y3))==(1·3·x·y+1·(−2·x·y3)+(−x)·3·x·y+(−x)·(−2·x·y3))

Раскроем скобки: 1·3·x·y−1·2·x·y3−x·3·x·y+x·2·x·y3.

Раскрытие скобок в произведениях нескольких скобок и выражений

При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2+4)·3·(5+7·8).

В выражении содержится сразу три множителя (2+4), 3 и (5+7·8). Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2+4)·3·(5+7·8)=((2+4)·3)·(5+7·8).

В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2+4)·3)·(5+7·8)=(2·3+4·3)·(5+7·8).

Умножаем скобку на скобку: (2·3+4·3)·(5+7·8)=2·3·5+2·3·7·8+4·3·5+4·3·7·8.

Скобка в натуральной степени

Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.

Рассмотрим процесс преобразования выражения  (a+b+c)2. Его можно записать в виде произведения двух скобок  (a+b+c)·(a+b+c).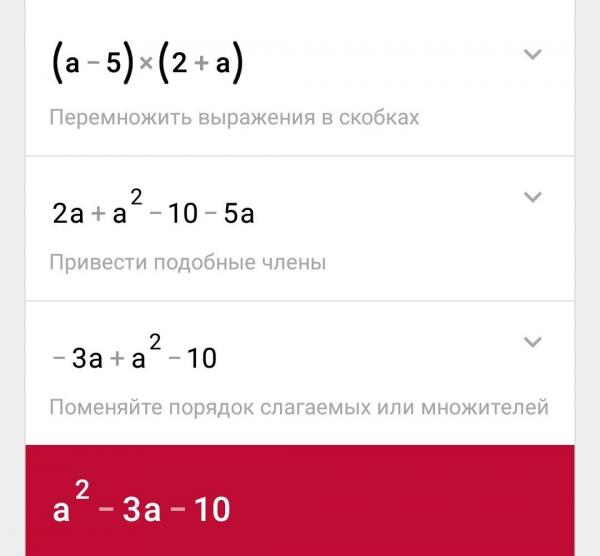  Произведем умножение скобки на скобку и получим a·a+a·b+a·c+b·a+b·b+b·c+c·a+c·b+c·c.

Разберем еще один пример:

Пример 8

1x+23=1x+2·1x+2·1x+2==1x·1x+1x·2+2·1x+2·2·1x+2==1x·1x·1x+1x·2·1x+2·1x·1x+2·2·1x+1x·1x·2++1×2·2+2·1x·2+2·2·2

Деление скобки на число и скобки на скобку

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x2-x):4=x2:4-x:4 .

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x+2):23 . Для этого сначала заменим деление умножением на обратное число (x+2):23=(x+2)·23. Умножим скобку на число (x+2)·23=x·23+2·23.

Вот еще один пример деления на скобку:

Пример 9

1x+x+1:(x+2) .

Заменим деление умножением: 1x+x+1·1x+2.

Выполним умножение:  1x+x+1·1x+2=1x·1x+2+x·1x+2+1·1x+2.

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок выполнения действий:

• первым делом необходимо выполнить возведение скобок в натуральную степень;
• на втором этапе производится раскрытие скобок в произведениях и частных;
• заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения  (−5)+3·(−2):(−4)−6·(−7). Намнем преобразование с выражений 3·(−2):(−4) и 6·(−7), которые должны принять вид (3·2:4) и (−6·7). При подстановке полученных результатов в исходное выражение получаем: (−5)+3·(−2):(−4)−6·(−7)=(−5)+(3·2:4)−(−6·7). Раскрываем скобки:−5+3·2:4+6·7.

Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.

как перемножить две, три, примеры

Содержание:

• Как умножать выражения в скобках
• Как вынести общий множитель за скобки
• Примеры вынесения общего множителя за скобки
• Раскрытие скобок при умножении числа на скобку, выражения на скобку

Содержание

• Как умножать выражения в скобках
• Как вынести общий множитель за скобки
• Примеры вынесения общего множителя за скобки
• Раскрытие скобок при умножении числа на скобку, выражения на скобку

Как умножать выражения в скобках

Умножение — операция над аргументами в математике: множимым и множителем. 2\end{array}.\)

Если выражение в скобках содержит сумму или разность переменных, то такое выражение называют многочленом. Каждый компонент многочлена является одночленом. Число перед одночленом — коэффициент. Если перед одночленом не указано число, то подразумевают один или минус один — зависит от знака.

Как вынести общий множитель за скобки

Общий множитель — наибольший общий делитель.

Операцию вынесения общего множителя за скобки используют при разложении многочлена на множители. Разложение многочлена на множители подразумевает его преобразование в равное этому многочлену произведение.

Правило вынесения общего множителя за скобки:

Чтобы вынести общий множитель, записывают исходное выражение в виде произведения общего множителя и суммы, заключенной в скобки, без общего множителя.

Для вынесения общего множителя за скобки используют распределительный закон или распределительное свойство умножения справа налево:

Формула

\(ab\pm ac=a(b\pm c)\) — сумма преобразуется в произведение.

Алгоритм нахождения общего множителя для членов многочлена:

1. Найти для каждого коэффициента делители.
2. Выбрать делитель, на который делится каждый коэффициент одночленов в многочлене.
3. Вынести этот делитель за скобки.
4. Найти переменные, которые встречаются в каждом члене многочлена.
5. Вынести за скобки эти переменные в наименьшей степени из встречающихся.
6. Разделить каждый член многочлена на полученный за скобками одночлен.

В многочлене в скобках должно остаться столько членов, сколько было в исходном.

Метод вынесения общего множителя за скобки на примере числового выражения:

Пример 1

\(5\times{\color[rgb]{1.0, 0.0, 0.0}\mathbf3}+{\color[rgb]{1.0, 0.0, 0.0}\mathbf3}\times8={\color[rgb]{1.0, 0.0, 0.0}\mathbf3}(5+8)\).

В этом выражении выносят за скобки общий множитель 3. Исходное выражение записывается как произведение общего множителя и суммы всех исходных слагаемых, кроме

общего множителя.

Дано числовое выражение \(5\ast2-4\ast2+2\ast3\). Это сумма трех слагаемых.

Есть общий множитель 2. По правилу получают: \(2\ast(5-4+3)\).

Полная запись решения: \(5\ast2-4\ast2+2\ast3=2\ast(5-4+3)\).

Примеры вынесения общего множителя за скобки

Пример 2

Вынести общий множитель: \(abc-ab\).

Алгоритм:

1. Раскладываем каждый одночлен на множители:

\(abc=a\times b\times c; ab=a\times b\).

2. Находим одинаковые множители: \( abc+ab=a\times b\times c+a\times b=\boldsymbol a\times\boldsymbol b\times c+\boldsymbol a\times\boldsymbol b\).
3. Одинаковые множители выносим за скобку и перемножаем, а каждый компонент в скобках делим на это произведение:\( \boldsymbol a\times\boldsymbol b\times c+\boldsymbol a\times\boldsymbol b=\boldsymbol a\boldsymbol b(\frac{\boldsymbol a\times\boldsymbol b\times c}{\boldsymbol a\boldsymbol b}+\frac{\boldsymbol a\times\boldsymbol b}{\boldsymbol a\boldsymbol b}). {\mathit2}.\)

   Пример 7

   Решите уравнение: \(3(x-4x)=0\).

   Чтобы решить уравнение, нужно найти все его корни или доказать, что корней нет.

   Корень уравнения — значение переменной, при которой получается верное равенство.

   Объяснение решения.

   1. Раскрываем скобки: умножаем 3 на каждый компонент в скобках.

   \(\begin{array}{l}3(x-4x)=0\\3\ast x-3\ast4x=0\\\end{array}.\)

   2. Перемножаем:\( \begin{array}{l}3\ast x-3\ast4x=0\\3x-12x=0\\\end{array}.\)
   3. В выражении есть подобные слагаемые\( ‒ 3x и (-12x)\).
   4. Упрощаем:\( \begin{array}{l}3x-12x=0\\-9x=0\\\end{array}.\)
   5. Осталось найти икс:

   Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель:

   \(\begin{array}{l}x=0\div(-9)\\x=0\end{array}.\)

   6. Выполняем проверку. Для этого найденное значение подставляем в исходное выражение и сравниваем правую и левую части: \(\begin{array}{l}3(0-4\ast0)=0\\0=0\end{array}. \)
   7. Получаем верное равенство, значит, \(x=0\) — корень уравнения.
   8. Записываем ответ: 0.

   Насколько полезной была для вас статья?

   Рейтинг: 4.00 (Голосов: 1)

   Поиск по содержимому

   Как умножать скобки?

   Учебные курсы

   Хотите посмотреть анимационные видеоролики и решить интерактивные упражнения на раскрытие скобок с помощью переменных?

   Нажмите здесь, чтобы попробовать учебные курсы!

   Здесь вы научитесь умножать две скобки друг на друга. Самое важное, что нужно помнить, это то, что каждый член в каждой скобке должен быть умножен на все члены в другом наборе скобок.

   Правило

   Умножение двух скобок друг на друга

   (a+b)(c+d)=ac+ad+bc+bd

   (a + b)(c + d) = ac + ad + bc + b d

   Пример 1

   Раскройте скобки (x+2)(x+3)

   (x+2)(x+3)=x⋅x+x⋅3+2⋅x+2⋅3 =x2+3x+2x+6=x2+5x+6

   (x+2)(x+3)=x⋅x+x⋅3+2⋅x+2⋅3=x2+3x+2x+6 =x2+5x+6

   Порядок умножения не имеет значения, пока вы выполняете все операции. Когда вы пишете, сколько у вас есть каждой переменной, число ставится перед переменной. Когда вы представляете свой ответ, вы пишете сначала термины высшей степени, а затем остальные в порядке убывания.

   В данном случае это означает, что x2 идет первым, так как это термин с наивысшим порядком. Если бы у вас был термин с x3, он шел бы перед x2.

   Подумайте об этом

   Как вы думаете, что произойдет, если в скобках будут отрицательные члены?

   Порядок действий прост. Когда вы умножаете два термина друг на друга, вы всегда должны сосредотачиваться на ЗНАКЕ, ЧИСЛЕ и ПЕРЕМЕННОЙ. Если вы сделаете это для каждого термина, вы получите правильный ответ.

   Пример 2

   Раскройте скобки (x−2) (x+3)

   = (x−2) (x+3)=x⋅x+x⋅3+ (−2)⋅x+ ( −2)⋅3=x2+3x−2x−6=x2+x−6

   (x−2) (x+3)=x⋅x+x⋅3+ (−2)⋅x+ (−2) ⋅3=x2+3x−2x−6=x2+x−6

   Пример 3

   Раскройте скобки (x−2)(x−3)

   = (x−2) (x−3) =x⋅x+x⋅ (−3)+ (−2)⋅x+ (−2)⋅ (−3)=x2−3x−2x+6=x2−5x+6

   (x−2) (x −3)=x⋅x+x⋅ (−3)+ (−2)⋅x+ (−2)⋅ (−3)=x2−3x−2x+6=x2−5x+6

   Пример 4

   Раскройте скобки (−x−2) (x−3)

   = (−x−2) (x−3)= (−x)⋅x+ (−x)⋅ (−3)+ (− 2)⋅x+ (−2)⋅ (−3)=−x2+3x−2x+6=−x2+x+6

   (−x−2) (x−3)= (−x)⋅x+ ( −x)⋅ (−3)+ (−2)⋅x+ (−2)⋅ (−3)=−x2+3x−2x+6=−x2+x+6

   Пример 5

   Раскройте скобки (−x−2) (−x−3)

   = (−x−2) (−x−3)= (−x)⋅ (−x)+ (−x)⋅ (−3)+ ( −2)⋅ (−x)+ (−2)⋅ (−3)=x2+3x+2x+6=x2+5x+6

   (−x−2) (−x−3)= (−x )⋅ (−x)+ (−x)⋅ (−3)+ (−2)⋅ (−x)+ (−2)⋅ (−3)=x2+3x+2x+6=x2+5x+6

   Хотите узнать больше? Зарегистрируйтесь. Это бесплатно!

   Предварительные алгебраические практические вопросы: FOILing с двумя наборами скобок с онлайн-практикой

   Рабочая тетрадь по основам математики и предварительной алгебры для чайников с онлайн-практикой

   Explore Book Купить на Amazon

   Если в выражении есть два набора скобок, расположенных рядом друг с другом, вам нужно умножить каждый член внутри первого набора скобок. каждым членом второго множества. Этот процесс называется FOILing.

   Слово FOIL — это запоминающее устройство для слов First, Outside, Inside, Last, , которое помогает отслеживать умножение, когда оба набора скобок содержат по два термина.

   Практические вопросы

   1. Упростите выражение ( x + 7)( x – 2).
   2. Упростите выражение 6 x – ( x – 2)( x – 4) + 7 x ² .

   Ответы и пояснения

   1. Ответ: x ² + 5 x – 14.

      Начните с того, что закройте круглые скобки. Начните с умножения двух первых членов:

      Умножьте два внешних члена:

      Умножьте два внутренних члена:

      Наконец, умножьте два последних члена:

      Сложите эти четыре произведения вместе и упростите, объединив одинаковые члены:

   2. Ответ: 6 x ² + 12 x – 8.

      Начните с круглых скобок: Умножьте первый, внешний, внутренний и последний члены:

      Сложите эти четыре продукта вместе и поместите результат в один набор скобок, заменив два набора скобок, которые были там изначально:

      6 x – ( x – 2)( x – 4) + 7 x ² = 6 x – ( x ² – 4 x – 2 x + 8) + 7 x ²

      The remaining set of parentheses is preceded знаком минус, поэтому измените знак каждого члена на противоположный и опустите круглые скобки:

      = 6 x — x ² + 4 x + 2 x — 8 + 7 x ²

      Теперь упростите выражение, как комбинация, такие как термины и повторно,

      .