Умножение в столбик. Умножение и деление столбиком
В третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
Что является основой умножения
Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное. Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Дробь. Умножение дробей обыкновенных, десятичных, смешанных
«Обыкновенные и десятичные дроби», «Смешанные числа» — все эти темы преподаются. ..
..
Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.
Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.
Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.
В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Вычитание дробей с разными знаменателями. Сложение и…
Для того чтобы произвести сложение или вычитание дробей с различными знаменателями, их необходимо…
Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)
Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
Исследовательская работа детей
Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Волшебная математика, или Как умножают японцы
Нации, использующие иероглифы, имеют другой тип мышления. Влияет ли это на их жизни? Сложно…
Этапы изучения умножения на многозначное число.
В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:
- самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
- для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
- отработка навыка умножения на круглые числа;
- использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
- операции с многозначными числами и умножение в столбик.

Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Задачи изучения умножения в курсе начальной школы
Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.
Какие же задачи ранее были решены учениками и их преподавателем?
- Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.

- Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
- Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2. Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Использование свойств умножения
Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.
Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.
Распределительное свойство умножения в этом случае выступает как универсальное.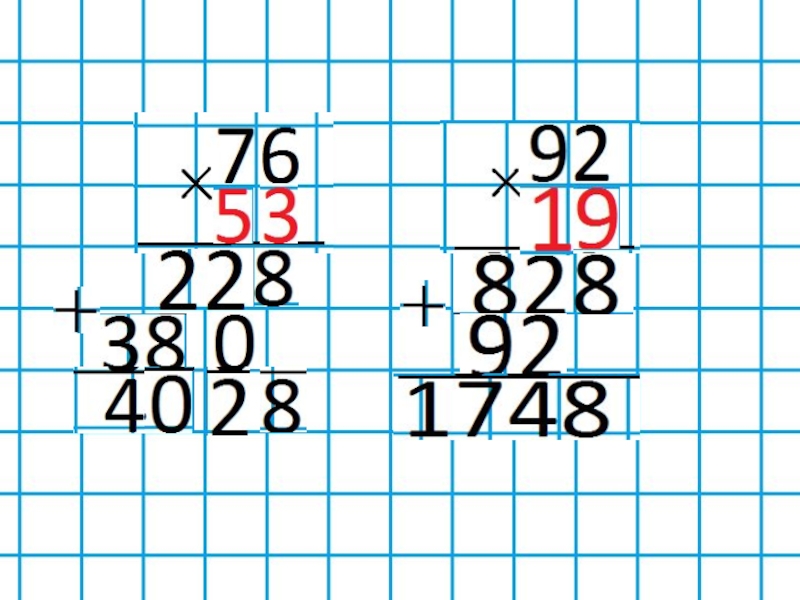 Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Алгоритм записи действия умножения в столбик
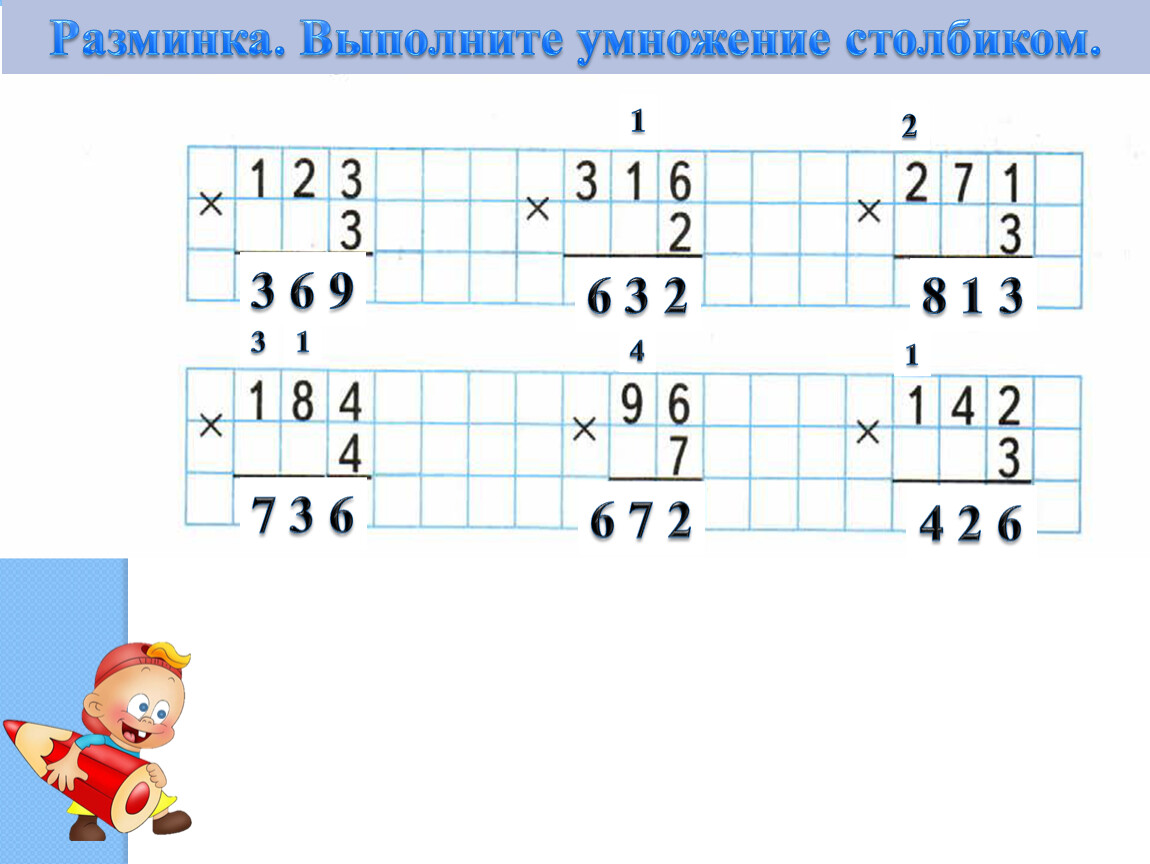
Запись умножения столбиком является самой компактной из всех существующих. Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».
Упражнения для формирования навыка
Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.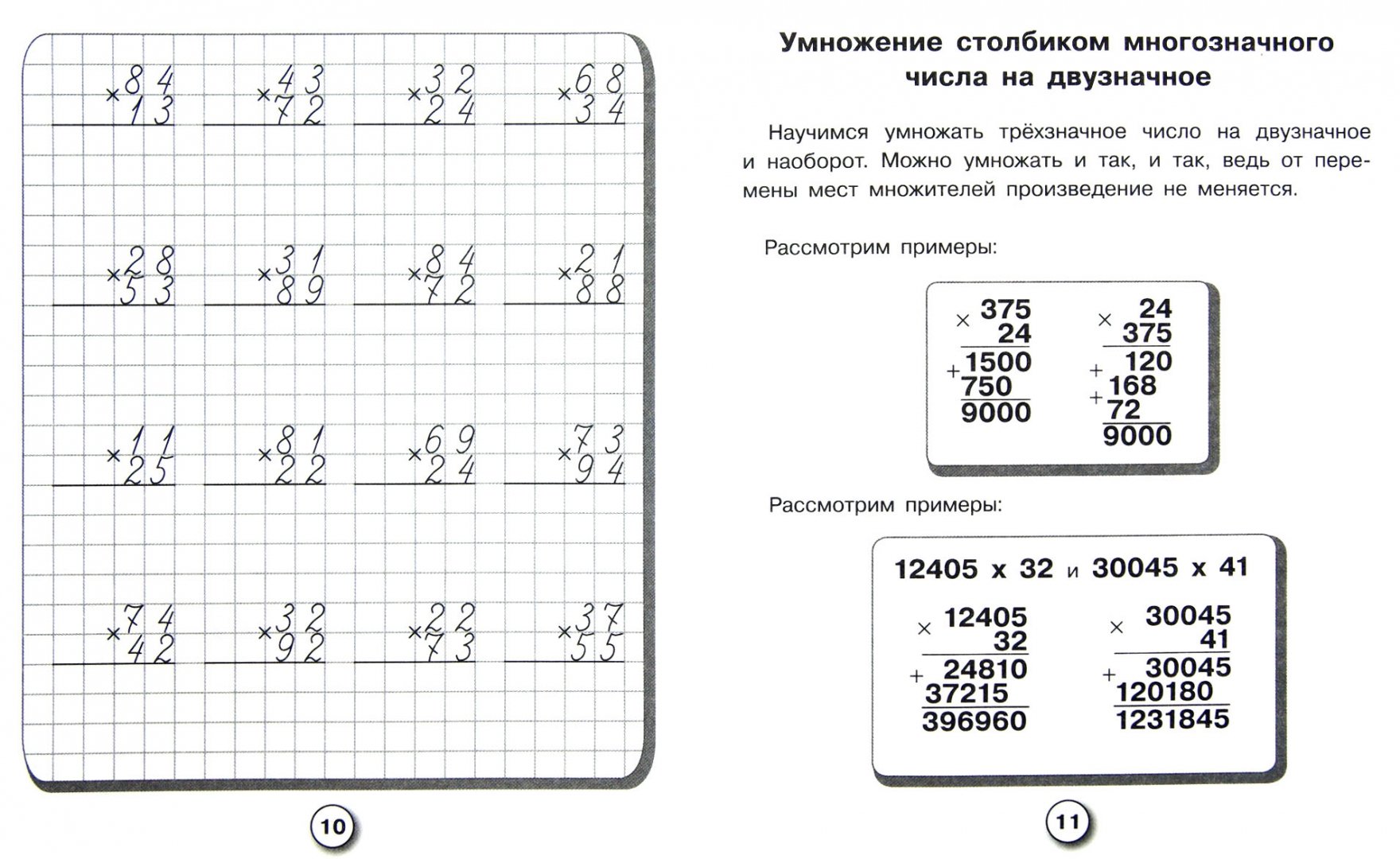
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.
Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.
Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»
Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.
Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».
Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.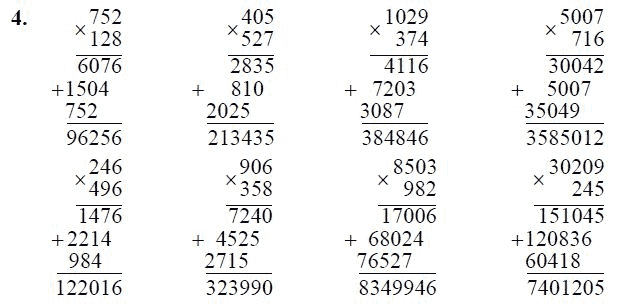
Калькулятор уравнений, интегралов, производных, пределов и пр.
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками ab и √ соответственно.

Вычисление выражений с логарифмами
В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$
$$\log _3\left(5x-1\right)=2$$ преобразуем в $$\frac{\log \left(5x-1\right)}{\log \left(3\right)}=2$$ (решить уравнение)
$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)
Вычисление пределов функций
Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim.
 7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)
7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)Что такое массив умножения в математике? Определение, примеры
Что такое массив умножения?
Чтобы понять концепцию массива умножения, давайте сначала разобьем концепцию на два слова и разберем их по отдельности.
Умножение — это математическая концепция, которая позволяет нам умножать одно число на другое. Например, 3 x 5 — это три раза по пять, то есть 15 .
Массив представляет собой таблицу, представляющую числа или данные в виде столбцов и строк.
Массив умножения создает механизм, в котором мы отображаем данные в виде массива, чтобы найти произведение любого вопроса на умножение. Массив обычно создается с использованием небольших объектов, форм или точек, чтобы сделать его интерактивным.
Например, чтобы умножить 3 x 5, тот же пример, что и выше, мы создадим следующий массив умножения.
Совет.
 Хотя вы можете использовать любое количество объектов в строке или столбце, в начале используйте один метод для каждой проблемы, чтобы избежать путаницы. Итак, будем представлять первое число в виде строк, а второе — в виде столбцов.
Хотя вы можете использовать любое количество объектов в строке или столбце, в начале используйте один метод для каждой проблемы, чтобы избежать путаницы. Итак, будем представлять первое число в виде строк, а второе — в виде столбцов.В приведенном выше массиве умножения мы можем найти ответ, подсчитав количество кругов, которое равно 15.
Связанные игры
Как представить массив умножения?
Возьмем пример 2 x 7, также называемый 2 на 7.
Это означает, что у нас есть 2 строки и 7 столбцов.
В этом массиве каждая строка и столбец содержат одинаковое количество объектов.
Другой способ взглянуть на это состоит в том, что у нас есть равные группы в виде строк или столбцов. Когда вы берете эти равные группы и упорядочиваете их как столбцы или строки, мы получаем массивы.
Например, равные группы по две звезды, расположенные в столбцах, создали приведенный выше массив звезд.
Связанные рабочие листы
Что такое множители и произведения в массиве умножения?
Мы используем специальные термины для чисел, участвующих в умножении:
- Множители — это числа, на которые умножаются
- Продукт – это результат, полученный в результате действия, которое представляет собой умножение
Что произойдет, если мы изменим порядок множителей в уравнении умножения?
В приведенном выше примере у нас было 2 строки и 7 столбцов.
 Что, если мы сделаем 2 столбца и 7 строк?
Что, если мы сделаем 2 столбца и 7 строк?Ответ остается прежним; оно по-прежнему равно 14.
Ситуация одинакова, независимо от того, сохраняете ли вы первое число в виде строки или столбца, и это справедливо для любого математического уравнения.
Если в проблеме задействовано более двух факторов, мы можем изменить порядок, но все равно получим точно такой же ответ. Это называется свойством коммутативного умножения.
Решенные примеры
Пример 1: Нам нужно создать массив умножения 5 на 6. Как мы его создадим?
Возьмем 5 строк и 6 столбцов.
Это означает, что нам нужно сделать 5 рядов по горизонтали и 6 столбцов по вертикали.
Когда вы посчитаете эти объекты, вы получите следующее:
5 x 6 = 30
Пример 2: Узнайте коэффициенты умножения в данном массиве умножения:
Сначала мы посчитаем количество строк: 2
Затем подсчитываем количество столбцов: 4
Таким образом, коэффициенты умножения равны 2 x 4, что также можно записать как 4 x 2.

Пример 3: Найдите ответ или произведение для данного массива умножения:
Сначала мы посчитаем объекты в каждой строке, что даст нам произведение = 12.
Если нам также нужно найти множители, то мы посчитаем строки (3) и столбцы (4).
3 x 4 = 12
Практические задачи
1
Какая из следующих цифр является массивом умножения?
A
B
Оба A и B
Ничего из вышеперечисленного
Правильный ответ: A
A образует массив, а B не образует массив. Это помогает считать и находить ответ, но формирует другую форму, например треугольник, а не массив.2
Как мы создадим массив умножения для следующего уравнения? 3 x 5
A
B
Оба A и B
Ничего из вышеперечисленного
Правильный ответ: Оба A и B
Оба A и B представляют массив умножения для задачи (свойство коммутативного умножения)3
Найдите произведение для данного массива умножения:
11
9
12
15
Правильный ответ: 12
У нас есть 4 строки и 3 столбца, 4 x 3, то есть 12.
Часто задаваемые вопросы
Как мы можем использовать массив s для умножения?
Чтобы использовать массив умножения, нам нужно присвоить коэффициенты строкам и столбцам, нарисовать их, а затем подсчитать. Это самый простой способ использования массива умножения.
Вам нужна фиксированная длина массива в массиве умножения?
Нет. У нас не может быть фиксированной длины массива умножения перед созданием массива.
Но после создания его длина фиксируется, и каждый столбец имеет одинаковую длину.
Обязательно ли иметь массив с четными строками и столбцами?
У нас могут быть четные строки и столбцы, но это не обязательно и не обязательно. Например, 4 х 4 может образовывать четный массив, а 4 х 5 — нет.
Как найти решение неравенства с умножением
Все математические ресурсы GRE
13 Диагностических тестов 452 практических теста Вопрос дня Карточки Learn by Concept
GRE Math Help » Алгебра » Уравнения / Неравенства » Неравенства » Как найти решение неравенства с умножением на
Количественное сравнение
Столбец A:Колонка B:
Возможные ответы:
Количество A больше.

Количества равны.
Связь не может быть определена на основании предоставленной информации.
Количество B больше.
Правильный ответ:
Связь не может быть определена на основании предоставленной информации.
Объяснение:
Для вопросов количественного сравнения, включающих общую переменную между величинами, лучше всего проверить положительное целое число, отрицательное целое число и дробь. Однако половина нашей работы исключается, потому что в вопросе указано, что x > 0. Нам нужно только проверить положительное целое число и положительную дробь между 0 и 1. Подставляя 2, мы видим, что количество A больше, чем количество B. Однако, проверяя 1/2, мы находим, что количество В больше, чем количество А. Таким образом, связь не может быть определена.
Сообщить об ошибке
Если –1 < n < 1, все следующие утверждения могут быть верными, КРОМЕ:
Возможные ответы:
|n 2 — 1| > 1
(n-1) 2 > n
16n 2 — 1 = 0
n 2 < 2n
n 90 205 2 < n
Правильный ответ:
| п 2 — 1| > 1
Объяснение:
Сообщить об ошибке
(√(8) / -x ) < 2.
 Какое из следующих значений может быть x?
Какое из следующих значений может быть x?Возможные ответы:
-4
Все варианты ответов верны.
-1
-2
-3
Правильный ответ:
-1
Пояснение:
Уравнение упрощается до x >
Сообщить об ошибке
Решить для x
Возможные ответы:
Правильный ответ: 900 05
Объяснение:
Сообщить об ошибке
У нас есть , найдите набор решений для этого неравенства.
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Заполните кружок символами , , или:
для .

Возможные ответы:
Ни один из других ответов не является правильным.Рациональное выражение не определено.
Правильный ответ:
Пояснение:
Упростим второе выражение. Мы знаем, что:
Таким образом, мы можем сократить следующим образом:
Сообщить об ошибке
Решить неравенство .
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с упрощения выражения, распределив через круглые скобки до .
Вычтите с обеих сторон, чтобы получить .
Затем вычтите 9 с обеих сторон, чтобы получить .

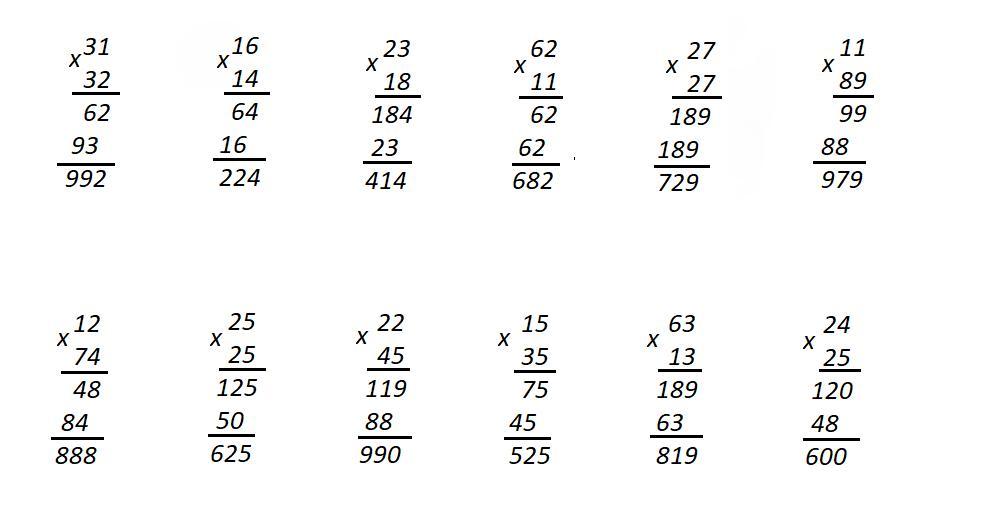

 7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)
7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами) Хотя вы можете использовать любое количество объектов в строке или столбце, в начале используйте один метод для каждой проблемы, чтобы избежать путаницы. Итак, будем представлять первое число в виде строк, а второе — в виде столбцов.
Хотя вы можете использовать любое количество объектов в строке или столбце, в начале используйте один метод для каждой проблемы, чтобы избежать путаницы. Итак, будем представлять первое число в виде строк, а второе — в виде столбцов.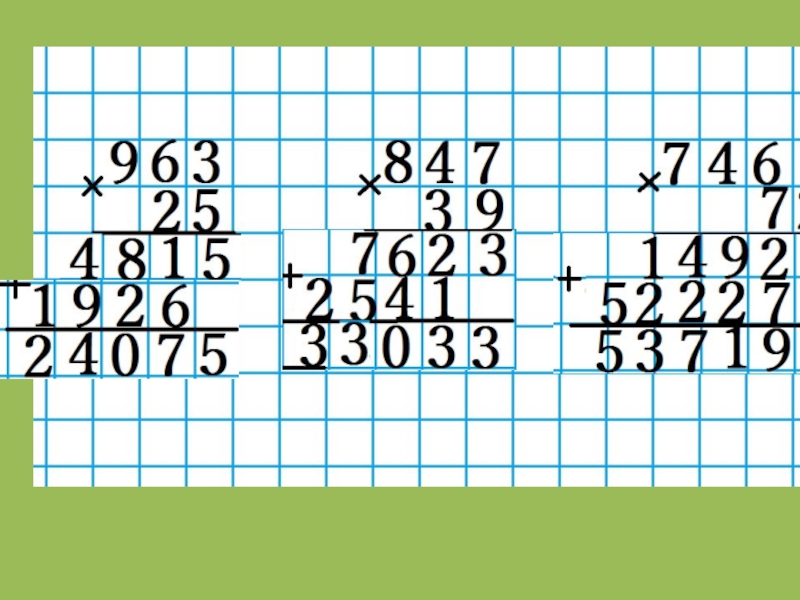 Что, если мы сделаем 2 столбца и 7 строк?
Что, если мы сделаем 2 столбца и 7 строк?


 Какое из следующих значений может быть x?
Какое из следующих значений может быть x?
