Как объяснить ребенку деление?

Конечно же, прежде чем ваш ребенок отправится в первый класс ему необходимо освоить азы арифметики.

Первоначально ему необходимо научиться правильно, понимать задание, а так же решать его в необходимой последовательности. Лучше всего изначально научить ребенка складывать, вычитать и умножать, а уж только потом делить. Самое главное вы должны понимать, что для того чтобы ребенок понимал как выполнить то или иное действие ему необходимо все демонстрировать наглядно. В данной статье мы подробно поговорим о том, как объяснить ребенку деление.

Как объяснить ребенку деление?

На самом деле, делить ребенок начинает еще в самом маленьком возрасте. Просто он еще до конца не осознает, что он участвует в данном процессе. Вы должны изначально объяснить ребенку, что такое целое, больше, меньше и т.д.,  он должен начать понимать каких игрушек больше, а каких меньше.

1. Поиграйте с малышом в деление

Для этого возьмите, к примеру, конфеты и попросите его поделиться с вами поровну. Изначально конечно ребенок будет действовать самым простым способом, он будет перекладывать конфетки по одной. В этом нет ничего страшного ведь малыш еще совсем маленький. После того как ребенок закончит делить конфеты помогите ему сосчитать сколько всего изначально их было.

Вы можете предложить малышу взять яблоки и угостить каждого члена семьи. Так же необходимо пояснить своему чаду, что не всегда, получается, разделить предметы поровну. Приведите ему пример, что у вас есть пять подушек и вам необходимо поделить их между двумя людьми поровну. Такое попросту не возможно, потому что кому-то достанется три подушки, а кому-то две.

2. Как объяснить ребенку деление Вам подскажут обычные примеры

Объясните ребенку, что первое число это и есть те самые конфеты, а вот второе это вы и он (или еще больше участников). И главное скажите ему, что абсолютно неважно, какие именно предметы он будет делить, самое главное узнать, сколько предметов в итоге окажется у каждого из участников.

Из всего вышесказанного можно сделать вывод о том, что для того чтобы ребенок как можно быстрее понял как делить предметы, ему нужно все наглядно демонстрировать. Приводите ему как можно больше примеров, рисуйте с ним, берите какие-либо предметы и делите их. Если вы будете следовать всем перечисленным рекомендациям, то будьте уверены, ваш ребенок очень скоро сможет без труда делить числа.

Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенных в стопки по 2 монеты, дадут 5 стопок.

Как выполняется деление?

Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 4 на 2 мы находим, сколько чисел 2 содержится в числе 4. Результат деления называется частным.

 

Как деление связано с умножением?

Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.

 

 

Возврат к исходному значению

Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного
делимого (10).

Другой подход к делению

Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное.
В этом примере 30 футбольных мячей делятся на группы по 3 мяча.

Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10.

Схема деления деления на однозначное число

 

Деление с остатком

Если одно число не делится на другое нацело, возникает остаток. Его можно преобразовать в десятичную дробь, как показано ниже.

 

Упрощение деления

Иногда делитель можно представить как произведение нескольких сомножителей. Тогда процедура деления сводится к нескольким более простым делениям.

Этим методом можно пользоваться и в более сложных задачах.

Деление на 4 с остатком и без остатка. Примеры на порядок действий. Геометрический материал. Решение задач.

Урок математики в 3 классе. Учитель: Шпанко И.Г.

Тема урока: Деление на 4 с остатком и без остатка. Примеры на порядок                    действий. Геометрический материал. Решение задач.

Цель урока: 1) закрепить умение делить числа на 4 без остатка; совершенствовать умение решать примеры на порядок действий;закреплять умения решать задачи на сравнение.

                        2)развивать навыки контроля и самоконтроля; умение и навыки устных и письменных вычислений; математические способности и интерес к предмету через доказательства и обоснования ответов учащихся.

                        3) Способствовать созданию условий обучения, при которых каждый ученик будет чувствовать свою успешность. Формировать культуру межличностных отношений, культуру умственного труда через формы организации обучения, способы взаимодействия учащихся учителя на уроке, контроль и  коррекцию ответов детей.

                                                Ход  урока:

1. Оргмомент ( создать положительный настрой на работу). Слайд №1 «Звонок»№1.

   Прозвенел уже звонок,

   Он позвал нас на урок.

   Мы все дружная семья –

   Он и ты, она и я.

   Время зря сам не теряй

   И соседу помогай.

— Как вы думаете, почему так написано в последней строчке?

— Мы сегодня много будем работать в парах.

— Значит нам понадобятся дружба, взаимопомощь, выручка, поддержка.

  2) Целеполагание. Мотивация.

           — Прочитайте название темы урока. Так что мы будем делать  сегодня на уроке? Зачем нам учиться  считать?

 3) Устный счет.

 — На прошлом уроке мы научились находить четверть от числа.                                                      — Другими словами, что мы повторяли на прошлом уроке?                                                     — Сегодня мы проверим свои знания и будем находить четверть от чисел, которые вы будете видеть на экране.

(На экране через каждые 12 секунд появляются числа. Дети находят четверть от них и записывают результаты в тетрадь.)

Слайды №2 на экране «20, 4, 24, 8, 32, 12, 36, 16, 40, 28»

  — Ответы деления будете записывать в тетрадь, а потом проверите друг друга.

( 2 минуты дети пишут ответы, затем меняются тетрадями и проверяют друг друга с помощью слайда « ответы» №3

«5, 1, 6, 2, 8, 3, 9, 4, 10, 7». Затем с помощью слайда « Как оценить работу»№4 оценивают своих товарищей.)

                                                «Без ошибок   — 12 баллов

                                                               1 ош.   —  9

                                                              2 ош.  —  6

                                                             3 ош.  – 2»

— Ребята, кто справился с работой на отлично? ( показывают зелёный сигнал) А кто допустил 1 ошибку? (те, кто не справился с работой – показывают красный  си гнал).

— Если вы не справились с работой, не отчаивайтесь. У вас будет время поработать дома самостоятельно над своими ошибками, а также в классе вам помогут ваши одноклассники – консультанты.

— Итак, что мы сейчас повторили? Сегодня нам пондобятся знания этой таблицы, мы будем использовать их на уроке при решении примеров.

— Давайте вспомним, как называются числа при делении?

( на экране слайд «компоненты»№5  «32     :     4      =       8»)

«делимое» «делитель» «частное»

4). Работа в парах. Решение примеров на порядок действий. ( время работы 3 минуты)

А) – Сейчас вы будете работать самостоятельно на своих карточках, но если понадобится помощь, обращайтесь к соседу по парте. Помните слова « Уча – учусь». Помогая товарищу, вы укрепляете свои знания. На каждой карточке есть памятка «Как оценить свою работу». Она поможет вам при оценке работы. (Карточек 4 варианта, примеры разные, но у всех получается в результате одно слово – «успех!» Если слово получилось, работа выполнена без ошибок. Т. К. дети работают в парах работу они заканчивают приблизительно одновременно.  )

 — Кто справился с заданием самостоятельно? Получают отличный результат. – Тот, кому помогали – оценку пока не получает.

Б) В это же время у компьютера работает один ученик. Он выполняет похожее задание. Слайд «Тропка»№6. 

   24 : 4 * 1 = 6    т

   1 * (36 : 4) = 9  р

  12 + 8 : 4 = 14   о

 32 : 4 + 8 = 16    п

 36 : (16 : 4) = 9  к

 1 * (20 : 4) = 5   а

В) Через 3 минуты учитель вызывает к доске двух, справившихся с работой учеников. На доске примеры:

16 : 4 = 4                                                           17 : 4 = 4 (ост. 1)

36 : 4 = 9                                                           37 : 4 = 9 (ост. 1)

20 : 4 = 5                                                            21 : 4 = 5 (ост. 1)

28 : 4 = 7                                                             29 : 4 = 7(ост. 1)

— Правильно ли решены примеры?

— Чем они отличаются?

— Почему появился остаток?

— Что мы должны помнить при решении примеров с остатком?

(остаток не должен быть больше делителя)

5). Творческая работа над задачей учебника ст.       №     .

А) Дети читают задачу про себя.

Б) Повторяют условие  задачи по слайдам№7 «2 палатки»

                                                                                 №8 «3 палатки».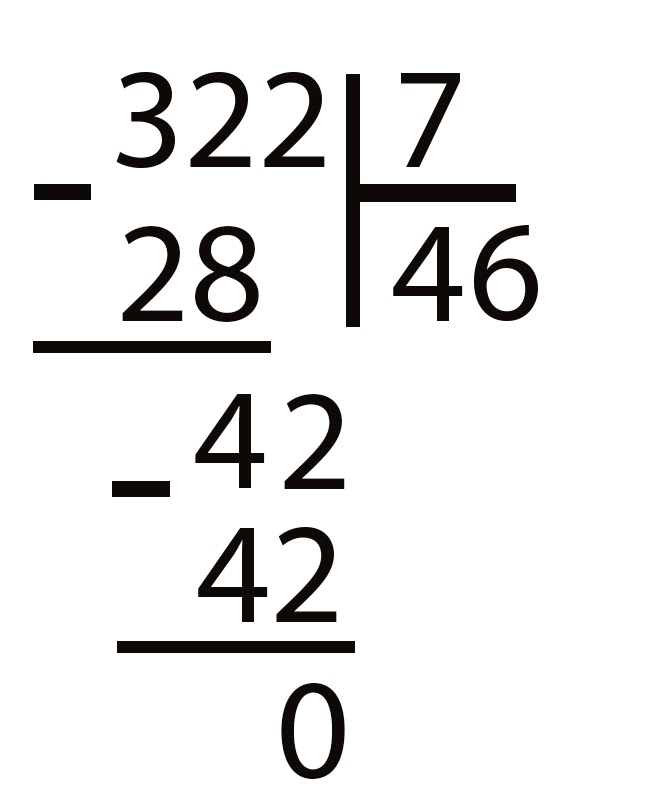

В) –Какой вопрос поставлен в задаче?

Г) запись краткой записи в тетрадях и на доске:

  2 палатки по 7 человек  на ? больше (меньше) человек в одной                       

  3 палатки по 4 человека палатке

— А какой ещё ворос можно поставить к задаче?

— Какие это задачи? Почему так думаете?  Какого типа первая задача? А вторая?  (Первый вариант записывает задачу на сравнение, а второй – на нахождение суммы).

6) Самостоятельная работа по решению задачи по краткой записи. Задачу решают по выбору. Слайд №9

«   3 коробки по 4 яблока           на ?

                                                       2 коробки по 7 яблок

                                                            3 коробки по 4 яблока       ?

             2 коробки по 7 яблок                                         

7). Рефлексия

— Как вы оцениваете свою работу на уроке? 

— Кто сам может оценить свои ответы? (показывают зелёные сигналы)

-А кто может объяснить, как выполнял свои задания? ( показать)

Узнайте, как решить деление с десятичными числами

В этом посте мы узнаем, как решить деление с десятичными числами. Мы увидим различные примеры.

Наконец, мы увидим, как решать задачи на деление до тех пор, пока остаток не станет равным нулю.

Деление десятичного числа на целое

Вы делите, как если бы они были целыми числами. Просто поместите десятичную точку в частное прямо над ее позицией в делимом.

Мы рассмотрим пример деления 77,5 на 25.

77 разделить на 25 равно 3 с остатком 2.

Теперь выпадаем следующая цифра. Поскольку 5 — это первое десятичное число, мы запишем десятичную точку в частном и разделим 25 на 25, что равно 1.

1 x 25 = 25, таким образом, 25 входит один раз без остатка.

Результат этого десятичного деления на целое число равен 3,1, а остаток равен нулю.

Деление целого числа на десятичное число

Например, мы собираемся разделить 278 на 3,6.

В делителе не может быть десятичных знаков; поэтому у делителя убираем запятую и прибавляем к делимому столько нулей, сколько цифр после запятой.

В этом случае мы должны добавить только один ноль. Итак, теперь мы должны разделить 2780 на 36.

36 входит в число 278 семь раз с остатком 26.9.0005

Теперь опустите 0, чтобы мы могли разделить 260 на 36, что равно 7 с остатком 8.

Решение деления 77 с остатком 8.

Деление d десятичное число на десятичное число

Удалить десятичную точку из делителя и переместить десятичную точку делимого вправо на столько знаков, сколько делитель имеет после запятой. При необходимости добавьте к делимому нули.

Теперь мы собираемся разделить 278,1 на 2,52.

Сначала удалите десятичную точку из делителя, и, поскольку делитель имеет два десятичных знака, вы должны переместить десятичную точку делимого на две позиции. Если делимое имеет только один десятичный знак, добавьте столько нулей, сколько осталось позиций. В этом случае мы добавляем один ноль и делим 27810 на 252. на 252, что входит один раз, с остатком 9.

Мы опускаем следующее число, равное 0, так что теперь нам нужно разделить 90 на 252. Поскольку 90 меньше 252, мы должны записать 0 в частном и опустить следующую цифру.

Мы уже решили деление, потому что цифр больше нет. Решением будет 110 с остатком 90.

Теперь мы увидим как вынуть десятичные дроби . Если в конце деления остался остаток, то в частном пишем десятичную точку, а к делимому прибавляем ноль. Если мы хотим продолжать вычитать десятичные дроби, нам придется продолжать добавлять нули к делимому.

Мы увидим пример удаления десятичных дробей, деление 33 на 6.

6 входит в 33, 5 раз с остатком 3.

Итак, если мы хотим сложить десятичные дроби, мы должны поставить десятичную точку в частном после 5.

Затем мы можем добавить ноль к остатку.

Теперь нам нужно разделить 30 на 6, что равно 5.

И решение 33 разделить на 6 равно 5,5.

Кроме того, теперь вы можете узнать больше о делении десятичных дробей!

• Изучите и попрактикуйтесь в делении десятичных дробей
• Как решить задачу, связанную с делением двухзначных чисел

Подпишитесь на бесплатную пробную версию Smartick уже сегодня!

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

Методы деления: изучите важные понятия

• Автор Шротасвини Мохапатра
• Последнее изменение 24-01-2023

Методы деления: Значение деления состоит в разделении числа на две или более равных частей, классов, областей, групп и категорий. Простыми словами, смысл деления в том, чтобы разделить целое число на группу равными частями или сделать равными части. Предположим, что диагональ прямоугольника делит его на два равных треугольника. Результат деления всегда может быть или не быть целым числом. Иногда результат деления будет в виде дроби или десятичной дроби.

Способ деления чего-либо называется способом деления. Способы деления бывают трех видов по уровню сложности. Это метод фрагментации или деления повторным вычитанием, метод короткого деления или метод автобусной остановки и метод длинного деления. В этой статье будет подробно рассмотрена одна из самых важных арифметических операций под названием «Деление или деление» и ее методы.

В математике есть четыре основных арифметических действия. Это сложение, вычитание, умножение и деление. Исходя из задач, которые мы собираемся решить, в соответствии с этим должен быть выбран тип арифметической операции.

Пример 1: Чтобы поровну разделить \(50\) карандашей между \(25\) детьми, нужно разделить \(50\) на \(25\). Таким образом, каждый ребенок получит \(2\) карандаша.

Пример 2: \(20\) разделить на \(4\).

Если мы возьмем \(20\) объектов и разделим их на четыре равные группы, то в каждой группе будет \(5\) объектов.

Таким образом, \(20÷4=5\).

Изучение концепций 11-го экзамена CBSE

Символ деления

Разделение может быть представлено символом \( \div \), косой чертой (/) или горизонтальной линией (_). Эти символы используются для удобства при решении различных задач и расчетов. Кроме того, \(\frac{a}{b}\) можно прочитать как «\(a\) через \(b\)».

Например, деление \(60\) на \(12\) может быть выражено следующим образом:

\(60 \div 12 = 5\)

Или \(\frac{{60}}{{ 12}} = 5\)

Таким образом, результат деления одинаков во всех приведенных выше представлениях.

Терминология, используемая в подразделе

Терминология означает термин. В делении используются четыре важных термина. Это делимое, делитель, частное и остаток.

Делимое: Число, которое нужно разделить на другое число, называется делимым.

Делитель: Число, на которое мы делим другое число (делимое) на равные части, называется делителем.

Частное: Результат деления называется частным.

Остаток: Число, оставшееся после деления, называется остатком.

Ниже приводится графическое представление вышеуказанной терминологии.

Деление по числовой строке

Деление — это процесс многократного вычитания.

Пример: \(18 \div 3\)

В этом методе начните с числа (делимое) в числовой строке и продолжайте вычитать число (делитель), пока не достигнете \(0\) (остаток), и количество шагов, которые мы идем в обратном счете, является частным (или результатом деления).

\(3\) многократно вычитается из 18 с использованием числовой строки.

Если \(3\) вычесть \(6\) раз из \(18\) в числовой строке, то мы получим остаток \(0\).

Таким образом, \(3\) вычитается из \(18\) шесть раз.

Следовательно, \(18÷3=6\), частное равно \(6\).

Формула деления

\({\bf{Дивиденд}} = {\bf{Делитель}} \times {\bf{Частное}} + {\bf{Остаток}}.\)

После деления мы можем поместите все значения в формулу, чтобы проверить или проверить правильность нашего деления или нет.

Пример: \(200÷25=8\)

Здесь делимое \(=200\), делитель \(=25\), частное \(=8\) и остаток \(=0\)

Подставим все вышеперечисленные значения в формулу

\({\rm{Дивиденд = Делитель \умножить на Частное + Остаток}}\)

\(⇒200=25×8+0\)

\(⇒200÷25=8\)

Следовательно, наше деление правильное.

Определить методы деления

Методы деления можно определить как то, как мы выполняем операцию деления. Существует три типа методов. Давайте обсудим каждый из них.

Метод фрагментации

Метод фрагментации также известен как метод повторного вычитания. Этот метод используется в младших классах при обучении базовому разделу. В методе фрагментации дети будут неоднократно вычитать делитель из делимого, пока мы не получим 0 или число меньше делителя.

Метод короткого деления (метод автобусной остановки)

Метод деления на автобусной остановке также известен как метод короткого деления. Он получил свое название от идеи, что дивиденд находится внутри автобусной остановки, а делитель ждет снаружи.

Короткое деление — это быстрый и эффективный метод деления больших чисел. После того, как дети освоятся с методом фрагментации, они перейдут к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым на однозначный делитель.

Метод длинного деления

Метод длинного деления — это наиболее распространенный метод, используемый для решения задач, основанных на делении. В этом методе делитель записывается за пределами правой скобки или левой боковой панели, в то время как делимое помещается внутри, а частное записывается над чертой над делимым.

Это метод, который используется при делении большого числа (обычно двузначного, трехзначного и более) на однозначное, двузначное (или большее) число.

Пример методов раздела

Пример метода фрагментации

Разделить \(12÷3\).

Давайте поймем это по некоторым картинкам,

\(12÷3\) означает, что нам нужно разделить \(12\) яблок на \(3\) в каждой группе.

Шаг 1: Вычтите или вычеркните \(3\) яблок, теперь осталось \(9\) яблок, т.е. \(12-3=9\).

Практические экзаменационные вопросы

Шаг 2: Вычтите или вычеркните еще \(3\) яблок, теперь осталось \(6\) яблок, т. е. \(12-6=3\).

Шаг 3: Вычтите или зачеркните еще \(3\) яблок, теперь осталось \(3\) яблок, т.е. \(12-9=3\).

Шаг 4: Вычтите или вычеркните еще \(3\) яблок, теперь осталось \(0\) яблок, т. е. \(12-12=0\).

Чтобы получить результат в виде \(0\), мы выполнили четыре шага или вычитали \(3\) несколько раз четыре раза. Итак, становится ясно, что ответ равен \(4\).

Следовательно, \(12÷3=4\).

Пример метода короткого деления

Пример: \(90÷6\)

Здесь нам нужно разделить \(90\) на \(6\) в методе короткого деления.

Теперь \(6×1=6\) и остается остаток \(3\).

Остаток затем передается следующему числу, т. е. \(0\), чтобы получилось \(30\).

Теперь, \(6×5=30\), остается остаток \(0\).

 Итак, при суммировании ответ будет \(15\).

Следовательно, результат равен \(15\).

Примеры длинного деления

Пример, \(436÷4\)

1. Здесь \(4\) — первая цифра делимого, равная делителю. Итак, \(4 \div 4 = 1.\) Итак, \(1\) написано сверху.
2. Теперь вычтите: \(4-4=0\),
3. Сократите вторую цифру делимого и поместите ее справа от \(0\).
4. Теперь \(3<4\). Таким образом, мы можем записать \(0\) как частное и уменьшить следующую цифру делимого и поместить ее справа от \(3\).
5. Теперь у нас есть \(36\) в качестве нового делимого. \(36>4\) и \(36\) делится на \(4\). Как, \(4×9=36\).
6. Запишите \(9\) как частное.
7. Теперь вычтите: \(36-36=0\).
8. Таким образом, остаток равен \(0,\), а частное равно \(109.\)

Методы деления Примечание

1. Если число разделить на \(1\), то частное будет таким же, как делимое.

Пример: \(98÷1=98\)

2. Если делимое и делитель совпадают, то частное будет \(1\).

Пример: \(45÷45=1\)

3. Если \(0\) разделить на любое число, то получится \(0\).

Пример: \(0÷13=0\)

4. Если делимое разделить на \(0\), то результат не определен.

Пример, \(106÷0=∞\) (не определено)

Деление дроби

Дроби можно разделить. При делении дробей оператор деления нужно преобразовать в умножение.

Пример: Разделите \(\frac{3}{5}\) на \(\frac{7}{5}\).

Здесь числитель равен \(\frac{3}{5}\), а знаменатель равен \(\frac{7}{5}\).

Теперь \(\frac{3}{5} \div \frac{7}{5}\) можно записать как \(\frac{3}{5} \times \frac{5}{7} \) 

Таким образом, \(\frac{3}{5} \times \frac{5}{7} = \frac{3}{7}\)

Следовательно, результат равен \(\frac{3}{7}\).

Десятичное деление

В математике десятичное деление можно наблюдать во многих понятиях, таких как алгебра, геометрия и другие числовые понятия. Деление десятичных дробей очень похоже на дроби.

Пример: Разделите \(0,2\) на \(0,3\).

Сначала преобразуем заданную десятичную дробь \(0,2\) на \(0,3\) в виде дроби.

\(0,2 = \frac{2}{{10}}\)

\(0,3 = \frac{3}{{10}}\)

Теперь \(\frac{{0.2}}{{0.3}} = \frac{2}{{10}} \div \frac{3}{{10}}\)

\( = \frac {2}{{10}} \times \frac{{10}}{3}\)

\( = \frac{2}{3}\)

\(=0,666\).

Следовательно, результат равен \(0,666\)

Деление многочлена

В отличие от чисел и дробей, многочлены также можно разделить на другой многочлен. Полиномиальное деление можно выполнить двумя способами. Одним из них является полиномиальное длинное деление, которое похоже на деление чисел, но вместо чисел будут появляться полиномиальные выражения. Другой метод деления многочленов — метод синтетического деления.

Решенные примеры – методы разделения

Q.1. Разделите \(125\) на \(5\) методом короткого деления.
Ответ: Здесь нам нужно разделить \(125\) на \(5\) методом короткого деления.

Теперь \(5×2=10\) и остается остаток \(2\).
Остаток затем передается следующему числу, т. е. \(5\), чтобы получилось \(25\).
Теперь, \(5 × 5 = 25\), остается остаток \(0\).
Таким образом, при суммировании ответ будет \(25\).
Следовательно, результат равен \(25\).

Q.2. Найдите значение: \([32 + 2 \times 17 + ( – 6)] \div 15\)
Ответ:
Дано, \([32 + 2 \times 17 + ( – 6)] \div 15 \)
Теперь, \([32 + 34 + ( – 6)] \div 15\)
\( = (66 – 6) \div 15\)
\( = 60 \div 15 = \frac{{60 }}{{15}} = 4\)
Следовательно, искомый ответ равен \(4\).

Q.3. Разделите \(0,214\) на \(0,02\).
Ответ: Сначала преобразуем заданную десятичную дробь \(0,214\) на \(0,02\) в виде дроби.
\(0,214 = \frac{{214}}{{1000}}\)
\(0,02 = \frac{2}{{100}}\)
Теперь \(\frac{{0,214}}{{0,02}} = \frac{{214}}{{1000}} \div \ frac{2}{{100}}\)
\( = \frac{{214}}{{1000}} \times \frac{{100}}{2}\)
\( = \frac{{214 }}{{20}} = \frac{{107}}{{10}}\)
\(= 10.7\)
Следовательно, результат равен \( 10.7.\)

Q.4. Разделите \(\frac{2}{5}\) на \(\frac{5}{7}\)
Ответ: Здесь числитель равен \(\frac{2}{5}\), а знаменатель равно \(\frac{5}{7}\).
Теперь \(\frac{2}{5} \div \frac{5}{7}\) можно записать как \(\frac{2}{5} \times \frac{7}{5}\ ) 92} + 3x + 1 = (x + 2)(2x – 1) + 3\)
Следовательно, \({\rm{Дивиденд = Делитель \умножить на частное + остаток}}\)
Следовательно, ответ правильный

Попытка пробных тестов

Резюме

В этой статье было рассмотрено, что такое деление, различные методы деления, формулы для проверки правильности деления, терминология, используемая при делении, примеры различных методов, деление по числовой прямой, некоторые решенные примеры и т. д. Это развеет все ваши сомнения, связанные с делением.

Часто задаваемые вопросы о методах деления

Q.1. Сколько существует способов деления?
Ответ: Существует три типа методов деления в зависимости от уровня сложности.
(i) Метод деления на части или метод многократного вычитания
(ii) Метод короткого деления или метод автобусной остановки
(iii) Метод длинного деления

Q.2. Какой метод деления предпочтительнее?
Ответ: Метод длинного деления предпочтительнее для лучшего понимания деления любого числа, особенно когда результат частного не является целым числом.

Q.3. Что такое метод короткого деления?
Ответ: В кратком делении шаги выполняются в уме и не записываются. Короткое деление обычно используется в задачах на деление, имеющих однозначные делители.

Q.4. Как сделать простое деление шаг за шагом?
Ответ: Давайте воспользуемся каким-нибудь трюком, чтобы запомнить все шаги, используемые при делении в большую сторону.