деление и умножение смешанных дробей

Вы искали деление и умножение смешанных дробей? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как дробь умножить на дробь с разными знаменателями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «деление и умножение смешанных дробей».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как деление и умножение смешанных дробей,как дробь умножить на дробь с разными знаменателями,как дробь умножить на другую дробь,как перемножать дроби с разными знаменателями,как перемножить дроби с разными знаменателями,как решать дроби с разными знаменателями на умножение и деление,как умножать дроби неправильные,как умножать дроби с разными знаменателями,как умножать дроби с разными знаменателями и целыми числами,как умножать дроби с разными знаменателями и числителями,как умножать дроби с целыми числами и разными знаменателями,как умножать и делить дроби с разными знаменателями и числителями,как умножать смешанные числа с разными знаменателями,как умножаются дроби с разными знаменателями,как умножить две дроби с разными знаменателями,как умножить дроби с разными знаменателями,как умножить дроби с разными знаменателями и целыми числами,как умножить дроби с разными знаменателями и числителями,как умножить дробь на дробь с разными знаменателями,как умножить дробь на дробь с разными знаменателями и числителями,как умножить дробь на неправильную дробь,как умножить неправильную дробь на дробь,перемножение дробей с разными знаменателями,правило умножения дробей с разными знаменателями,при умножении дробей с разными знаменателями,произведение дробей с разными знаменателями,смешанную дробь умножить натуральное число на дробь,сокращение дробей умножение дробей,умножение дробей с неизвестными,умножение дробей с разным знаменателем,умножение дробей с разными,умножение дробей с разными знаменателями,умножение дробей с разными знаменателями примеры с решением,умножение дробей с разными знаменателями с целыми числами,умножение дробей с целыми числами и разными знаменателями,умножение и деление дробей с разными знаменателями умножение и деление,умножение и деление смешанных дробей,умножение неправильных дробей,умножение с дробей,умножение смешанных дробей,умножение смешанных дробей с разными знаменателями,умножения дробей с разными знаменателями,умножить дроби.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и деление и умножение смешанных дробей. Просто введите задачу в окошко и нажмите «решить» здесь (например, как дробь умножить на другую дробь).

Решить задачу деление и умножение смешанных дробей вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Умножение дробей. Возведение дроби в степень

Урок 5. Алгебра 8 класс ФГОС

На этом уроке мы закрепим представления о рациональных выражениях.

Введем правило умножения и возведения рациональных дробей в степень.

Конспект урока «Умножение дробей. Возведение дроби в степень»

Для начала давайте вспомним правило умножения обыкновенных дробей.          

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.

Иначе говоря, докажем, что произведение двух

рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:  

Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

Пример 2: умножить дроби.

Решение:

Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

Пример 4: выполнить умножение.

Решение:

Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.

Проверим это

равенство на конкретных примерах.

   

Правило возведения рациональной дроби в степень:

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Пример 5: возвести в третью степень дробь.

       

Пример 6: возвести во вторую степень дробь.  

 

Пример 7:

     

Итоги

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

Чтобы возвести дробь в степень, надо возвести в эту степень

числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Предыдущий урок 4 Сложение и вычитание дробей с разными знаменателями

Следующий урок 6 Деление дробей

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 8 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Умножение дробей | Магазин развивающей математики

Результаты обучения

• Умножение двух или более дробей
• Умножить дробь на целое число

Модель может помочь вам понять умножение дробей.

Мы будем использовать дробные плитки для моделирования [латекс]\большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]. Чтобы умножить [латекс]\большой\фракция{1}{2}[/латекс] и [латекс]\большой\фракция{3}{4}[/латекс], подумайте [латекс]\большой\фракция{1}{ 2}[/latex] из [latex]\Large\frac{3}{4}[/latex].
Начните с тайлов дроби на три четверти. Чтобы найти половину от трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три плитки [latex]\Large\frac{1}{4}[/latex] поровну на две части, мы обмениваем их на плитки меньшего размера.

Мы видим, что [latex]\Large\frac{6}{8}[/latex] эквивалентен [latex]\Large\frac{3}{4}[/latex]. Взяв половину из шести плиток [latex]\Large\frac{1}{8}[/latex], мы получим три плитки [latex]\Large\frac{1}{8}[/latex], то есть [латекс] \Large\frac{3}{8}[/latex].

Следовательно,

[латекс]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]

Пример

Используйте диаграмму к модели [латекс]\Большой\фрак{1}{2}\cdot \фрак{3}{4}[/латекс]

Решение:
Первый оттенок в [латекс]\Большой\фрак{3}{4} [/latex] прямоугольника.

Мы возьмем [латекс]\Большой\фрак{1}{2}[/латекс] из этого [латекса]\Большой\фрак{3}{4}[/латекс], поэтому сильно заштрихуем [латекс] \Large\frac{1}{2}[/latex] заштрихованной области.

Обратите внимание, что [латекс]3[/латекс] из [латекс]8[/латекс] сильно затенены. Это означает, что [latex]\Large\frac{3}{8}[/latex] прямоугольника сильно затенены.
Следовательно, [latex]\Large\frac{1}{2}[/latex] из [latex]\Large\frac{3}{4}[/latex] равно [latex]\Large\frac{3}{ 8}[/латекс], или [латекс]{\большой\гидроразрыв{1}{2}\cdot \гидроразрыва{3}{4}}={\большой\гидроразрыва{3}{8}}[/латекс] .

Посмотрите на результат, который мы получили от модели в примере выше. Мы обнаружили, что [latex]\Large\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}[/latex]. Вы заметили, что мы могли бы получить один и тот же ответ, перемножив числители и умножив знаменатели?

	[латекс]\Большой\фракция{1}{2}\cdot \фракция{3}{4}[/латекс]
Умножьте числители и умножьте знаменатели.	[латекс]\Большой\фракция{1}{2}\cdot \фракция{3}{4}[/латекс]
Упрощение.	[латекс]\большой\фрак{3}{8}[/латекс]

Это приводит к определению дробного умножения. Чтобы умножить дроби, мы умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.

Умножение дроби

Если [latex]a,b,c,\text{ и }d[/latex] являются числами, где [latex]b\ne 0\text{ и }d\ne 0[/latex], затем

[latex]\Large\frac{a}{b}\cdot \frac{c}{d}=\frac{ac}{bd}[/latex]

Пример

Умножьте и запишите ответ в упрощенной форме: [latex]\Large\frac{3}{4}\cdot \frac{1}{5}[/latex]

Показать решение

Попробуйте

Чтобы умножить более двух дробей, у нас есть аналогичное определение. Мы по-прежнему умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.

Умножение более двух дробей

Если [latex]a,b,c,d,e \text{ и }f[/latex] числа, где [latex]b\ne 0,d\ne 0\text{ и }f\ne 0[/latex], затем

[латекс]\Large\frac{a}{b}\cdot\Large\frac{c}{d}\cdot\Large\frac{e}{f }=\Large\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]

 

Подумайте об этом

Умножьте [латекс]\Large\frac{2}{3 }\cdot\Large\frac{1}{4}\cdot\Large\frac{3}{5}[/latex]. Упростите ответ.

Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.

Показать решение

 

При умножении дробей сохраняются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак произведения. В следующем примере мы умножим два отрицательных значения, поэтому произведение будет положительным.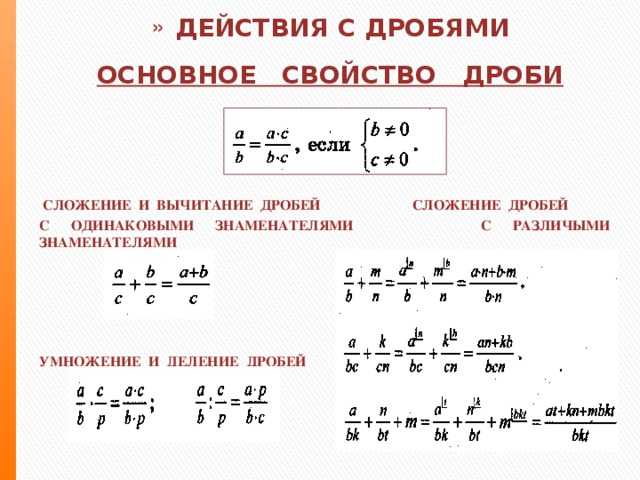

Пример

Умножьте и запишите ответ в упрощенной форме: [латекс]\большой-\frac{5}{8}\left(-\frac{2}{3}\right)[/latex]

Показать решение

Попробуй

Пример

Умножьте и запишите ответ в упрощенной форме: [latex]\Large-\frac{14}{15}\cdot \frac{20}{21}[/latex]

Показать решение

 

Попробуйте

В следующем видео показан еще один пример умножения отрицательных дробей.

При умножении дроби на целое число может быть полезно записать целое число в виде дроби. Любое целое число, [латекс]а[/латекс], может быть записано как [латекс]\большой\фрак{а}{1}[/латекс]. Например, [latex]3=\Large\frac{3}{1}[/latex].

пример

Умножьте и запишите ответ в упрощенной форме:

1. [латекс]\Large{\frac{1}{7}}\normalsize\cdot 56[/latex]
2. [латекс]\Large{\frac{12}{5}}\normalsize\left(-20x\right)[/latex]

Показать раствор

Попробуйте

Посмотрите следующее видео, чтобы увидеть больше примеров умножения дроби и целого числа.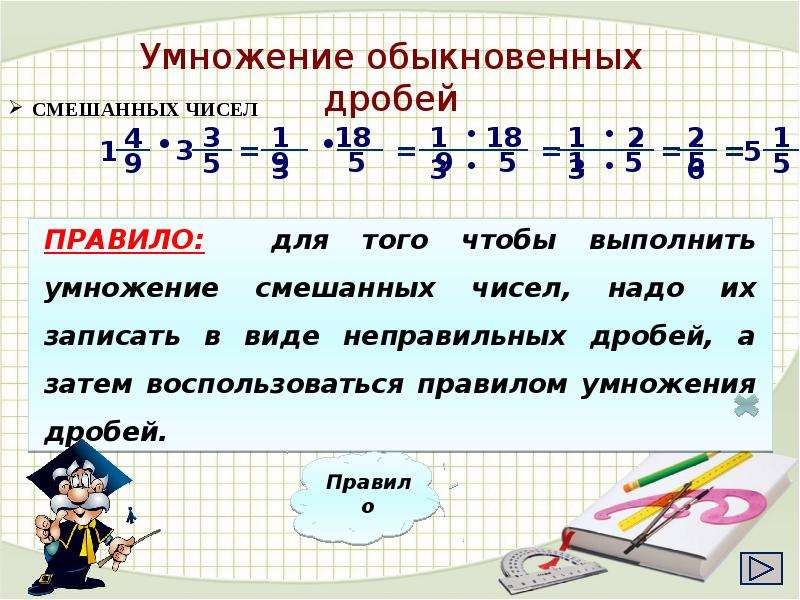

У вас была идея улучшить этот контент? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Умножение и деление дробей – Easy Peasy All-in-One Homeschool

Умножение дробей

При умножении дробей сначала умножаются числители, а затем знаменатели. Тогда вам нужно написать ответ в самых низких терминах. Вы также можете уменьшить дроби и исключить общие множители перед умножением. Это лучший метод, когда вы используете большие числа. Например, при умножении я могу упростить дроби перед умножением.

Умножение смешанных чисел

При умножении смешанных чисел их нужно записывать в виде неправильных дробей. Затем следуйте процессу умножения и при необходимости измените его обратно на смешанное число.

Например:

два с половиной умножить на три и две трети равно пять половин умножить на одиннадцать третей

Обратите внимание, как я заменил смешанные числа неправильными дробями. Это облегчит умножение дробей! Теперь поговорим о делении дробей.

Деление дробей

Обратные числа

Прежде чем говорить о делении, нам нужно определить обратное число. Обратная дробь находится путем замены числителя и знаменателя.

Деление дробей

Когда вы делите дроби, вы берете обратную делителю и заменяете задачу на задачу на умножение.

Вот общая формула:

А на В разделить на С на D равно А на В умножить на D на С

Деление смешанных чисел

При делении смешанных чисел применяются те же правила. Замените смешанные числа неправильными дробями и следуйте правилам деления.

Практика

Решить.

1. две трети умножить на одну четвертую
2. половина, разделенная на пять шестых
3. восемь двенадцатых умножить на девять десятых
4. десять четырнадцатых разделить на тридцать пять
5. четырнадцать раз восемь двадцать первый
6. шестнадцать разделить на сорок восемь сорок девятых
7. четыре и одна четвертая умножить на три и семь восьмых
8. двенадцать и три четвертых разделить на два с половиной
9. пять и три пятых умножить на одну и две пятых
10. восемь и одна четвертая разделить на четыре и одна восьмая

(источник)

Искать:

Задать вопрос

Пожалуйста, проверьте страницу часто задаваемых вопросов, прежде чем задавать вопрос! Группа поддержки Или найдите определенное место или группу уровня Список групп facebook

EP Gear

Большое разнообразие дизайнов и продуктов

Следите за EP на Facebook

EP на других языках

Kinderleicht Lernen

Использование EP для говорящих по-испански

Следите за блогом по электронной почте

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.