| Табличка на двери |
Урок 16. Вычитание дробей | Уроки математики и физики для школьников и родителей
Урок 16.
 Вычитание дробей
Вычитание дробейВИДЕО УРОК
Вычитание дробей определяется так же, как и вычитание целых чисел. Это есть действие, с помощью которого по данной сумме двух слагаемых и одному из них отыскивается другое слагаемое. Вычитание дробей можно представить как действие, обратное сложению дробей. Вычесть из одного дробного числа второе – значит найти третье число, которое в сумме со вторым дат первое.
Вычитание дробей с одинаковыми знаменателями.
Для начала приведём
пример, который позволит нам выяснить, как проводится вычитание дробей с
одинаковыми знаменателями.
ПРИМЕР:
Пусть на тарелке находилось пять восьмых долей яблока, то есть, 5/8 яблока. После чего две восьмых доли забрали. По смыслу вычитания, указанное действие можно записать так:
Понятно, что при этом на тарелке остаётся
5 – 2
= 3 восьмых доли яблока, то есть
Рассмотренный пример иллюстрирует правило вычитания дробей с одинаковыми знаменателями.
Чтобы вычесть дробь из дроби с одинаковыми знаменателями, нужно вычесть числитель вычитаемого из числителя уменьшаемого и оставить прежний знаменатель.
Озвученное правило с помощью букв записывается так:
Эту
формулу и будем использовать при вычитании дробей с одинаковыми знаменателями.
ПРИМЕР:
Выполните вычитание обыкновенной дроби 17/15 из обыкновенной дроби 24/15.
РЕШЕНИЕ:
Знаменатели вычитаемых дробей равны. Числитель уменьшаемого равен 34, а числитель вычитаемого равен 17, их разность равна:
24 – 17 = 7.
Поэтому вычитание дробей с одинаковыми знаменателями24/15 и 17/15 даёт дробь 7/15.
Краткий вариант решения выглядит так:
ОТВЕТ: 7/15
При
возможности нужно проводить сокращение дроби и (или) выделение целой части из
неправильной дроби, которая получается при вычитании дробей с одинаковыми
знаменателями.
ПРИМЕР:
Вычислите разность:
РЕШЕНИЕ:
Воспользуемся
формулой вычитания дробей с одинаковыми знаменателями.
Очевидно, что числитель и знаменатель
полученной дроби делятся надва, то есть дробь 22/12 – сократимая дробь. Выполнивсокращение этой
дроби на 2, приходим
к дроби 11/6.
Дробь 11/6 неправильная, поэтому из неё
нужно выделить целую часть.
Итак, вычисляемая разность дробей с
одинаковыми знаменателями равна 15/6.
Краткий
вариант решения выглядит так:
ОТВЕТ: 15/6
ПРИМЕР:
Вычитание дробей с разными
знаменателями.
Вычитание дробей с разными знаменателями сводится к вычитанию дробей с одинаковыми знаменателями. Для этого дроби с разными знаменателями достаточно привести к общему знаменателю.
Чтобы вычесть дробь из дроби с разными знаменателями, нужно предварительно привести их к наименьшему общему знаменателю, затем из числителя уменьшаемого вычесть числитель вычитаемого и под их разностью подписать общий знаменатель.
ПРИМЕР:
Отнимите от обыкновенной дроби 2/9 обыкновенную дробь 1/15.
РЕШЕНИЕ:
Так как знаменатели вычитаемых дробей разные, то сначала
выполним приведение дробей к наименьшему общему знаменателю. Так как
Так как
НОК (9; 15) = 45,
то дополнительным множителем дроби 2/9 является число
45 : 9 = 5,
а дополнительным множителем дроби 1/15 является число:
45 : 15 = 3,
тогда
Осталось вычесть из дроби 10/45 дробь 3/45, получаем
что и даёт нам искомую разность дробей с разными
знаменателями.
Краткое решение записывается так:
ОТВЕТ: 7/45
Не следует забывать
про сокращение полученной после вычитания дроби, а также про выделение целой части.
ПРИМЕР:
Вычтите из дроби 19/9 дробь 7/36.
РЕШЕНИЕ:
После приведения дробей с разными знаменателям к наименьшему общему знаменателю 36, получим дроби 76/36 и 7/36. Находим их разность:
Полученная дробь сократима, после её сокращения на 3, получаем 23/12. А эта дробь неправильная, поэтому, выделив из неё целую часть, получим 111/12. Краткое решение записывается так:
ОТВЕТ: 111/12
ПРИМЕР:
Вычитание смешанных
дробей.
Чтобы вычесть смешанные числа, сначала приведём дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю. Затем вычтем целое из целого и дробь из дроби.
ПРИМЕР:
Найти разность:
РЕШЕНИЕ:
ОТВЕТ: 413/22
ПРИМЕР:
Но бывают случаи,
когда дробная часть вычитаемого больше дробной части уменьшаемого. В таких
случаях нужно взять одну единицу из целой части уменьшаемого, раздробить её в
те доли, в каких выражена дробная часть, и прибавить к дробной части
уменьшаемого. А затем вычитание будет выполняться так же, как вычитание
смешанных чисел.
ПРИМЕР:
В случае, когда
дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом:
берут одну единицу (целое) из целого числа уменьшаемого, записывают его как
неправильную дробь, числитель и знаменатель которой равны между собой и равны
знаменателю дробной части, и прибавляют к дробной части, далее отнимают две
смешанные дроби.
ПРИМЕР:
Выполнить вычитание:
РЕШЕНИЕ:
Дробь 4/9 меньше чем дробь 11/12 так как
4 ∙ 12 = 36 < 9 ∙ 11 = 99,
тогда
ОТВЕТ: 319/36
Вычитание обыкновенной дроби из натурального числа.
Вычитание обыкновенной дроби из натурального числа можно свести к вычитанию обыкновенных дробей, представив натуральное число как дробь.
ПРИМЕР:
Отнимите обыкновенную дробь 5/3 от натурального числа 7.
РЕШЕНИЕ:
Представим число 7 как дробь 7/1, после чего выполним вычитание:
Выделив целую часть из полученной дроби, получаем окончательный ответ.
ОТВЕТ: 51/3
Рассмотрим ещё пример на вычитание смешанного числа из натурального числа.
ПРИМЕР:
Но существует более
рациональный способ вычитания дроби из натурального числа. Его преимущества
заметны тогда, когда уменьшаемое натуральное число и знаменатель вычитаемой
дроби являются большими числами. Если вычитаемая дробь правильная, то
уменьшаемое натуральное число можно заменить суммой двух чисел, одно из которых
равно единице, отнять правильную дробь от единицы, после чего завершить
вычисления.
ПРИМЕР:
Найти разность:
РЕШЕНИЕ:
Выполним вычитание дробей по описанному выше
правилу:
ОТВЕТ: 2/5
ПРИМЕР:
Выполните вычитание обыкновенной дроби 13/62 из натурального числа 1065.
РЕШЕНИЕ:
Вычитаемая обыкновенная дробь – правильная. Заменим число 1065 суммой
1064 + 1,
При этом получим:
Осталось вычислить
значение полученного выражения. В силу свойств вычитания, полученное выражение
можно переписать так:
В силу свойств вычитания, полученное выражение
можно переписать так:
Вычислим значение разности в скобках, заменив единицу дробью, 1/1:
Краткое решение записывается так: ОТВЕТ: 106449/62
Рассмотрим ещё пример на вычитание смешанного числа из целого числа.
ПРИМЕР:
Если же вычитаемая дробь неправильная, то её можно заменить смешанным числом, после чего провести вычитание смешанного числа из натурального числа.
ПРИМЕР:
Отнимите обыкновенную дробь 73/5 от натурального числа 644.
РЕШЕНИЕ:
Выделим целую часть из неправильной дроби:
Тогда
ОТВЕТ: 6292/5
Вычитание натурального числа из обыкновенной дроби.
Вычитание натурального числа из дроби можно свести к вычитанию обыкновенных дробей. Для этого достаточно представить натуральное число в виде дроби со знаменателем 1.
ПРИМЕР:
Выполните вычитание числа 3 из обыкновенной дроби 83/21.
РЕШЕНИЕ:
Так как число 3 = 3/1 то:
ОТВЕТ: 20/21
Вычитание натурального
числа из неправильной дроби удобнее проводить, представив дробь в виде
смешанного числа.
ПРИМЕР:
Отнимите число 3 от дроби 83/21.
РЕШЕНИЕ:
Сначала выделим целую часть из неправильной дроби 83/21, получим:
тогда
Осталось провести вычитание натурального числа из смешанного числа:
ОТВЕТ: 20/21
Распространение свойств вычитания на дробные числа.
Все законы и
свойства вычитания натуральных чисел справедливы и для дробных чисел. Их
применение во многих случаях значительно упрощает процесс вычисления.
Вместо того, чтобы вычесть сумму дробей, можно вычесть каждое слагаемое последовательно, и обратно: вместо того, чтобы вычитать каждое число последовательно, можно вычесть сразу их сумму.
ПРИМЕР:
Вычислите значение выражения:
РЕШЕНИЕ:
Сначала вычислим разность
после чего от неё отнимем дробь 5/6. после выделения целой части из полученной неправильной дроби получим:
ОТВЕТ: 311/12
ПРИМЕР:
Здесь использовано правило вычитания из чисел разности.
Когда выражение
содержит и натуральные числа и дроби, то при вычислении удобно группировать
числа с числами, а дроби с дробями.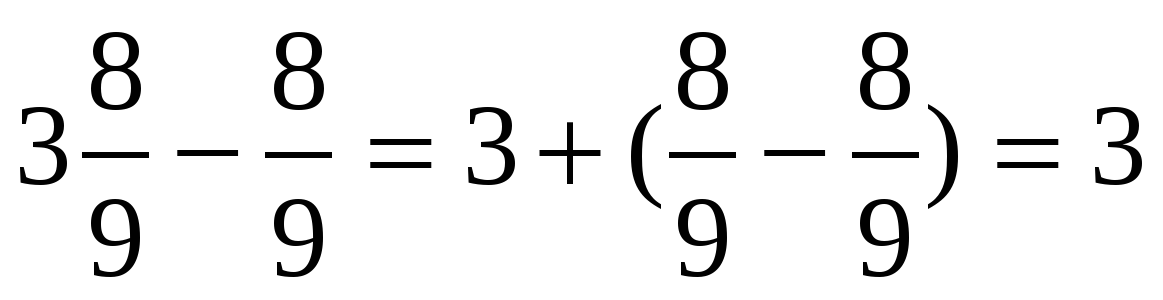
ПРИМЕР:
Выполните вычитание суммы натурального числа и обыкновенной дроби
из суммы натурального числа и дроби
РЕШЕНИЕ:
Нам нужно вычислить разность
Свойства сложения и вычитания позволяют нам провести следующую группировку что упрощает вычисления. Осталось лишь закончить вычисления:
ОТВЕТ: 931/4
Если уменьшаемое уменьшим на какое-нибудь число, не изменяя вычитаемого, то разность уменьшится на то же самое число.
Если вычитаемое
увеличим на какое-нибудь число, то разность уменьшится на то же число.
Если вычитаемое уменьшим на какое-нибудь число, то разность увеличится на то же число.
Если уменьшаемое и вычитаемое увеличим или уменьшим на одно и то же число, то разность не изменится.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Нумерация
- Урок 2. Сложение натуральных чисел
- Урок 3. Вычитание натуральных чисел
- Урок 4. Таблица умножения
- Урок 5. Умножение натуральных чисел
- Урок 6. Деление натуральных чисел
- Урок 7. Степень числа
- Урок 8. Измерение величины
- Урок 9. Деление с остатком
- Урок 10. Делимость натуральных чисел
- Урок 11. Наибольший общий делитель (НОД)
- Урок 12. Наименьшее общее кратное (НОК)
- Урок 13. Обыкновенные дроби
- Урок 14. Преобразование дробей
- Урок 15.
 Сложение дробей
Сложение дробей - Урок 17. Умножение дробей
- Урок 18. Деление дробей
- Урок 19. Нахождение дроби от числа (задачи)
- Урок 20. Нахождение числа по известной его части (задачи)
- Урок 21. Конечные десятичные дроби
- Урок 22. Сложение десятичных дробей
- Урок 23. Вычитание десятичных дробей
- Урок 24. Умножение десятичных дробей
- Урок 25. Деление десятичных дробей
- Урок 26. Округление чисел
Вычитание обыкновенных дробей объяснение и примеры кратко…
Привет, мой друг, тебе интересно узнать все про вычитание обыкновенных дробей , тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое вычитание обыкновенных дробей , настоятельно рекомендую прочитать все из категории Арифметика.
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную дробь 7/7 и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем ее в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.
Пример.
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
При подобных расчетах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).
Пример.
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведем обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3 < 14
Поэтому, вспомнив вычитание правильной дроби из целого числа, займем единицу из целой части и представим эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
Сложим полученную неправильную дробь 18/18 и дробную часть уменьшаемого и получим:
Все рассмотренные случаи можно описать с помощью правилвычитания смешанных чисел.
- Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
- Если дробная часть уменьшаемого меньше дробной части вычитаемого, то занимаем у целой части уменьшаемого единицу . Об этом говорит сайт https://intellect.icu . Эту единицу превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю.
- Прибавляем полученную неправильную дробь к дробной части уменьшаемого.

- Вычитаем из целой части целую, а из дробной — дробную.
- Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.
См. также
- десятичные дроби ,
- как читать десятичные дроби ,
- перевод обыкновенной дроби в десятичную ,
- нахождение обыкновенной дроби от числа ,
- деление обыкновенных дробей ,
- умножение обыкновенных дробей ,
- взаимно обратные числа , взаимно обратные дроби ,
- сравнение обыкновенных дробей ,
- периодическая дробь ,
- сложение обыкновенных дробей , общий знаменатель ,
- сокращение обыкновенных дробей ,
- смешанные числа , выделение целой части обыкновенной дроби ,
- сокращение обыкновенных дробей ,
Как ты считаеешь, будет ли теория про вычитание обыкновенных дробей улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое вычитание обыкновенных дробей
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Из статьи мы узнали кратко, но емко про вычитание обыкновенных дробей
Сложение и вычитание дробей: сходство и отличие знаменателей
Основные математические процедуры сложения и вычитания также применимы к дробям. Поскольку в каждой ситуации мы предпринимаем разные шаги, очень важно понять, имеют ли дроби одинаковые или разные знаменатели, чтобы легко складывать и вычитать дроби. При решении задач, связанных с дробями на сложение и вычитание, связь этих понятий является ключевым критерием для получения правильного решения.
Дроби являются составной частью большего целого. Дроби можно решать с помощью основных арифметических методов. В результате дроби можно складывать, вычитать, умножать и делить. Давайте рассмотрим дроби, прежде чем переходить к сложению дробей.
Подобные дроби: Две или более дроби, в которых один и тот же знаменатель, известны как «подобные дроби». Например, 3/7, 4/7, 8/7 и т. д. похожи на дроби. Обратите внимание, что 7/7 не является подобной дробью, потому что ее можно упростить до . В отличие от дробей: . Когда знаменатель между 2 или более дробями не совпадает, дроби называются, в отличие от дробей. Например, 1/7, 5/6, ⅔ и т. д. не похожи на дроби.
Например, 3/7, 4/7, 8/7 и т. д. похожи на дроби. Обратите внимание, что 7/7 не является подобной дробью, потому что ее можно упростить до . В отличие от дробей: . Когда знаменатель между 2 или более дробями не совпадает, дроби называются, в отличие от дробей. Например, 1/7, 5/6, ⅔ и т. д. не похожи на дроби.
В этой статье мы научимся складывать и вычитать похожие и разные дроби.
Как складывать и вычитать дроби с одинаковыми знаменателями Сложение одинаковых дробейСкладывать дроби с одинаковыми дробями очень просто и точно так же, как складывать целые числа. Прочтите приведенные ниже шаги, чтобы узнать, как складывать дроби:
Шаг 1: Правильно запишите одинаковые дроби с помощью символа «+».
Шаг 2: Так как знаменатель у сложенных дробей один и тот же, то и в полученной дроби будет тот же знаменатель.
Шаг 3: Добавьте числители.
Шаг 4: Запишите ответ в форме a/b.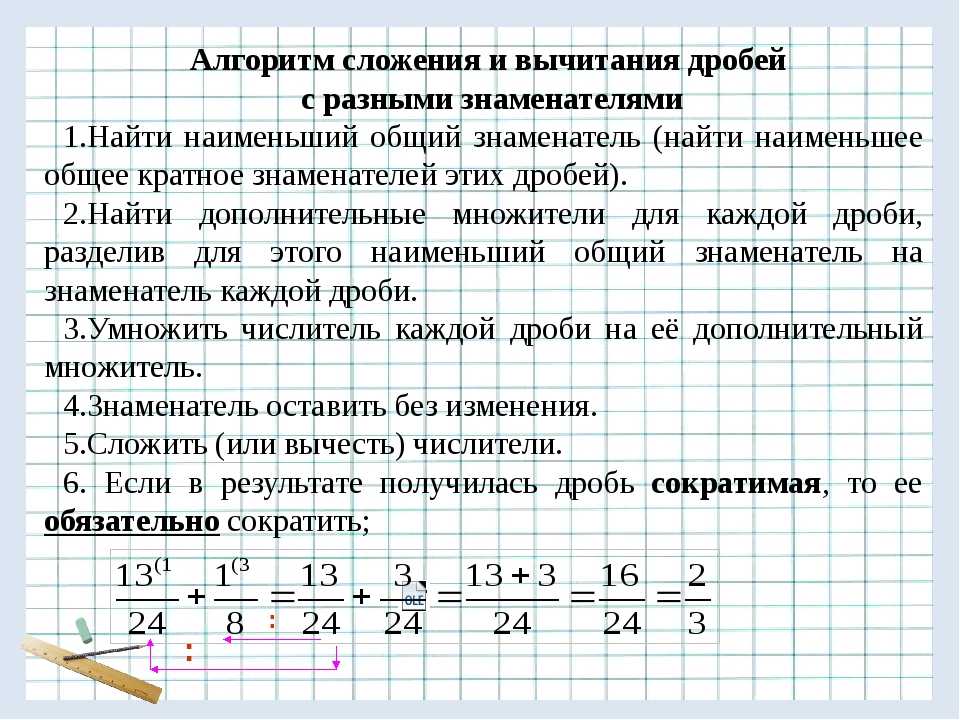 Где а — сумма числителя, а b — знаменатель слагаемых.
Где а — сумма числителя, а b — знаменатель слагаемых.
Пример: Добавить 11/3 к 4/3
Решение: Внимательно прочитав шаги и применив их к этому вопросу, мы получим:
Шаг 1: 11/3 + 4/3
3
3 : Знаменатель ответа будет 3. Так как они как функции.
Шаг 3: 11 + 4 = 15 (добавление числителя)
Шаг 4: Запишем результирующую дробь: 15/3
Мы видим, что в 15/3 15 можно разделить 5 раз на 3. Таким образом, результат равен 5. Если возможно, всегда упрощайте свои ответы.
Вычитание одинаковых дробейВычитание двух или более дробей с одинаковыми знаменателями осуществляется аналогично описанному выше подходу к сложению дробей. Шаги, связанные с вычитанием дробей с одинаковыми знаменателями, следующие:
Шаг 1: Запишите одинаковые дроби по порядку с символами «-» между ними.
Шаг 2: Знаменатель результата будет таким же, как знаменатель вычитаемых дробей.
Шаг 3: Соответственно вычтите числа в числителях.
Шаг 4: Запишите ответ в форме a/b. Где а — разность числителя, а b — знаменателя.
Пример: Вычесть 3/7 на 9/7.
Решение: Внимательно выполните описанные выше шаги→
Шаг 1: 07.09 – 07.03
Шаг 2: Поскольку они подобны функциям, знаменатель ответа будет равен 7.
Шаг 3: 9 – 3 = 6 (вычитание числителя)
Шаг 4: Запись результирующей дроби: 6/7.
Если разность числителей отрицательное число, то дробь записывается в виде -a/b.
На этом заканчивается понятие о том, как складывать и вычитать дроби, когда знаменатели одинаковы. Далее мы научимся складывать и вычитать дроби с разными знаменателями.
Как складывать и вычитать дроби с разными знаменателями Складывание дробей с разными знаменателями Сложение дробей с разными знаменателями — довольно сложная задача.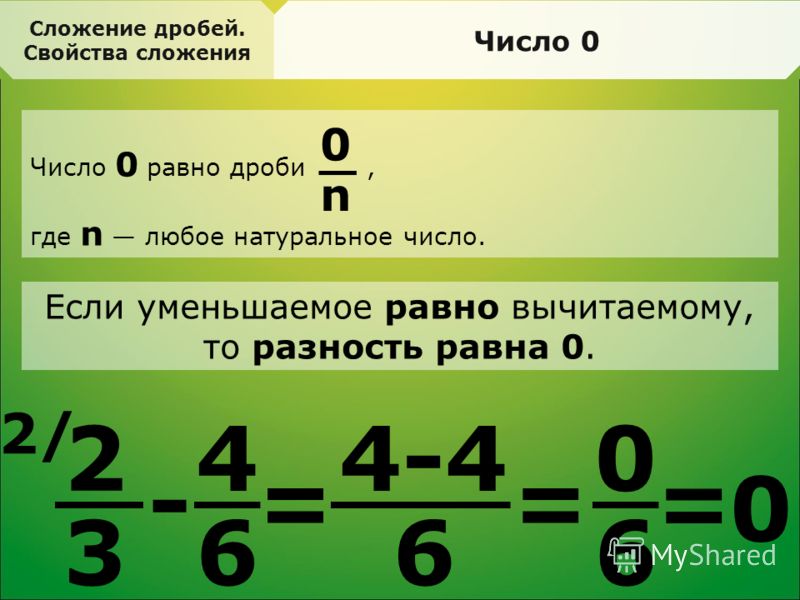 Это не так просто, как сложение «подобных дробей», потому что знаменатели здесь имеют разную величину. Результирующий знаменатель в этом случае представляет собой LCM (наименьшее общее кратное) знаменателей. См. шаги ниже, чтобы понять, как решать разные дроби:
Это не так просто, как сложение «подобных дробей», потому что знаменатели здесь имеют разную величину. Результирующий знаменатель в этом случае представляет собой LCM (наименьшее общее кратное) знаменателей. См. шаги ниже, чтобы понять, как решать разные дроби:
Шаг 1: Запишите одинаковые дроби правильно со знаком «+».
Шаг 2: Найдите результирующий знаменатель, найдя НОК знаменателей.
Шаг 3: Умножьте числители в соответствии с НОК. Сложите соответствующие числа, чтобы получить значение результирующего числителя.
Шаг 4: Запишите результат в форме a/b. Где a — это сумма числителя, а b — знаменатель (НОК).
Пример: Сложите дроби 5/4 и 2/9..
Решение: Мы решим это, используя пошаговый подход, упомянутый выше:
Шаг 1: 5/4 + 2/9
Шаг 2: Поскольку они не являются дробями, мы должны найти НОК 4 и 9 36 — это НОК 4 и 9.
Шаг 3: Теперь умножим числители соответственно. Для 5/4 4 делится на 36 девяток; следовательно, мы умножим 5 на 9 = 45. Точно так же для 2/9 9 делит 36 четыре раза; следовательно, 2 умножается на 4 = 8. Теперь мы добавляем 45 и 8 = 45 + 8 = 53.
Точно так же для 2/9 9 делит 36 четыре раза; следовательно, 2 умножается на 4 = 8. Теперь мы добавляем 45 и 8 = 45 + 8 = 53.
Шаг 4: Таким образом, полученная дробь равна 53/36. Его нельзя упростить; следовательно, дробь остается 53/36.
НОК берется для превращения непохожих дробей в подобные дроби. В остальном процедура остается прежней.
Вычитание дробей с разными знаменателямиВычитание, в отличие от дробей, является еще одним сложным, но важным арифметическим понятием дробей. Это следует той же процедуре, что и сложение, в отличие от дробей. Единственное изменение состоит в том, что здесь мы находим разницу, а не суммируем. Пошаговый подход к вычитанию двух разных дробей:
Шаг 1: Запишите одинаковые дроби правильно, используя знак вычитания «-».
Шаг 2: Результирующий знаменатель вычисляется путем нахождения НОК знаменателей.
Шаг 3: Соответственно умножьте числители на НОК. Сложите результаты, чтобы найти значение получившихся числителей.
Шаг 4: Результат должен быть записан в форме a/b. Где a — разница числителя, а b — НОК знаменателя.
Пример: Вычтите дроби 3/4 и 1/8
Решение: Мы решим это, используя пошаговый подход, упомянутый выше:
Шаг 1: 3/4 – 1/8
Шаг 2: Поскольку они в отличие от дробей, мы должны найти НОК 4 и 8. 8 — это НОК, потому что 4 x 2 = 8 и 8 x 1 = 8.
Шаг 3: Теперь умножим числители соответственно. Для 3/4 4 делит 8 два раза; следовательно, мы умножим 3 на 2 = 6. Точно так же для 1/8 8 делится на 1 раз; следовательно, 1 умножается на 1 = 1. Теперь мы вычитаем 6 и 1 = 6 – 1 = 5,
Шаг 4: Таким образом, полученная дробь равна 5/8.
Иногда вы можете обнаружить, что LCM является одним из знаменателей. Это возможно, когда знаменатели кратны друг другу. Наибольшее кратное становится знаменателем.
Сложение и вычитание дробей с целыми числами Мы научились складывать или вычитать дроби с помощью других дробей. Теперь давайте научимся складывать и вычитать дроби с целыми числами. Старайтесь всегда составлять дроби в форме, неподходящей для арифметических операций. Хитрость сложения или вычитания дроби и целого числа заключается в том, чтобы преобразовать целое число в дробь. Это можно сделать, поставив 1 в знаменателе целого числа.
Теперь давайте научимся складывать и вычитать дроби с целыми числами. Старайтесь всегда составлять дроби в форме, неподходящей для арифметических операций. Хитрость сложения или вычитания дроби и целого числа заключается в том, чтобы преобразовать целое число в дробь. Это можно сделать, поставив 1 в знаменателе целого числа.
Целое число и дробь можно складывать или вычитать, используя процедуру, описанную для разных дробей .
Пример: Сложите 6/5 и 11
Решение: Шаг 1. Преобразуйте 11 в дробную форму как 11/1.
Шаг 2. НОК 6/5 и 11/1 равен 5. Поскольку 5 кратно 1. Сложите числители
6 + 55 = 61,
Шаг 4. Полученная дробь равна 61/5.
Обратите внимание, что НОК в случае сложения и вычитания двух дробей всегда является большим числом. Это связано с тем, что каждое число кратно 1.
Важные напоминания:- Чтобы сложить разные дроби, выполните следующие действия:
а) Используя НОК знаменателя, преобразуйте данные дроби в подобные дроби.
b) Определите соответствующие дроби следующих дробей с НОК в качестве знаменателя.
c) Сложите числители, не изменяя знаменатель.
- Никогда по отдельности не вычитайте и не суммируйте числители и знаменатели разных дробей. Это приведет к ошибочному результату. Следуйте правилам, упомянутым в каждом разделе этой статьи.
- Не обязательно находить НОК знаменателей при сложении или вычитании, в отличие от дробей. Подойдет любой стандартный множитель. Таким образом, мы можем получить общее кратное, перемножив два знаменателя. Хотя это дает более крупные числа, его можно свести к простейшей форме.
Часто задаваемые вопросы
1. Как складывать и вычитать дроби?
Ответ. Чтобы сложить дробь, просто сложите числители. Чтобы вычесть дробь, нужно просто вычесть знаменатели. Например: чтобы сложить одну треть и две трети, умножьте 1 на 2, а затем умножьте 3 на 3. Сложите эти два числа вместе, чтобы получить 7/9. Если вы хотите вычесть одну треть из двух третей, умножьте 1 на 2, а затем снова умножить 3 на 3. Затем вычтите два числа, которые вы только что перемножили, — в данном случае 6/9..
Если вы хотите вычесть одну треть из двух третей, умножьте 1 на 2, а затем снова умножить 3 на 3. Затем вычтите два числа, которые вы только что перемножили, — в данном случае 6/9..
2. Как складывать и вычитать дроби с разными знаменателями?
Ответ. Сложение и вычитание дробей с разными знаменателями — это простой процесс, который требует сложения или вычитания числителей, умножения знаменателей на одно и то же число, а затем повторного сложения или вычитания полученных числителей.
3. Как складывать и вычитать дроби с целыми числами?
Ответ. Чтобы складывать и вычитать дроби с целыми числами, сначала нужно преобразовать каждую дробь в дробь с тем же знаменателем. Например, если бы вам нужно было сложить 1/2 + 1/4, вы бы преобразовали их оба в 3/4, разделив оба на 2. Затем вы бы сложили их вместе, как если бы они были целыми числами. Чтобы вычесть одну дробь из другой, это похоже — просто убедитесь, что знаменатели для обеих одинаковы для начала!
4.
 Как складывать и вычитать дроби со смешанными числами?
Как складывать и вычитать дроби со смешанными числами?Ответ. Чтобы складывать или вычитать дроби со смешанными числами, сначала нужно преобразовать их в неправильные дроби. Для этого вы просто берете большую дробь, делите ее на меньшую, а затем умножаете результат на 100%. Затем вы можете добавить или вычесть, как обычно.
5. Каковы правила сложения и вычитания дробей?
Ответ. Правило сложения и вычитания дробей довольно простое:
1) Если знаменатели одинаковые, сложите числители и напишите это над знаменателем первой дроби.
2) Если знаменатели не равны, нужно их умножить на какое-то общее число (то есть на такое число, на которое оба знаменателя делятся без остатка). Затем добавьте или вычтите, как обычно.
Как складывать и вычитать дроби: 3 простых шага
Сложение и вычитание дробей на первый взгляд может показаться пугающим. Мало того, что вы работаете с дробями, которые, как известно, сбивают с толку, так еще и внезапно вам приходится бороться с преобразованием числителей и знаменателей.
А вот складывать и вычитать дроби — полезный навык. Как только вы освоите словарный запас и основы, вы сможете с легкостью складывать и вычитать дроби. Это руководство познакомит вас со всем, что вам нужно знать для сложения и вычитания дробей , включая несколько примеров задач для проверки ваших навыков.
Ключевой словарь для сложения и вычитания дробей
Прежде чем мы приступим к математике сложения и вычитания дробей, вам нужно знать терминологию. Мы будем использовать эти термины на протяжении всего , так что освежите их в памяти, чтобы всегда знать, какую часть дроби мы имеем в виду.
Дробь : Число, не являющееся целым; часть целого. Для наших целей дробь будет относиться к числу, записанному с числителем 9.0008 и знаменатель , например 1/5$ или 147/4$.
Числитель : Верхнее число в дроби, отражающее количество частей целого, например 1 в $1/5$.
Знаменатель : Нижнее число в дроби, представляющее общее количество частей, например, 5 в $1/5$.
Общий знаменатель : Когда две дроби имеют одинаковый знаменатель, например, $1/3$ и $2/3$.
Наименьший общий знаменатель : Наименьший знаменатель, который могут разделить две дроби. Например, наименьший общий знаменатель $1/2$ и $1/5$ равен 10, потому что наименьшее число, в которое входят 2 и 5, равно 10.
Из пирогов получаются большие дроби.
Как складывать и вычитать дроби?
Теперь, когда у вас есть словарный запас, пришло время применить его на практике. Вы не можете просто складывать или вычитать дроби, как, например, целое число $1/4 — 1/2$ не равно $0/2$.
Вместо вам нужно будет найти общий знаменатель, прежде чем прибавлять или вычитать . Есть много способов найти общий знаменатель, некоторые из которых проще или эффективнее других.
Один из самых простых способов найти общий знаменатель, хотя и не обязательно лучший, — это просто перемножить два знаменателя.
Например, возможный наименьший общий знаменатель для $1/2$ и $1/12$ будет равен 24, что вы найдете, умножив знаменатель 2 на знаменатель 12. Вы можете решить задачу, используя общий знаменатель 24, используя приведенные ниже шаги, но если вы это сделаете, вы столкнетесь с проблемой — вашу дробь нужно будет уменьшить.
Чтобы избавиться от необходимости уменьшать после сложения или вычитания, вместо этого попытайтесь найти наименьший общий знаменатель. Иногда это равносильно умножению двух знаменателей, но чаще всего это не так.
Однако найти наименьший общий знаменатель несложно — вам просто нужно знать таблицу умножения . Например, попробуем найти наименьший общий знаменатель, а не просто общий знаменатель, для тех же дробей, которые мы использовали выше:
$$1/2\: \and \: 1/12$$.
Для этого перечислите несколько кратных каждого знаменателя
Кратные 2 : 2, 4, 6, 8, 10, 12 , 14, 16, 18, 20, 22, 24
2 Кратные числа 12
: 12 , 24, 36, 48, 60Затем просмотрите оба списка кратных чисел и найдите наименьшее число, которое они разделяют. В этом случае и 2, и 12 разделяют кратное 12. Если мы продолжим, мы получим другие кратные, которые они разделяют, например 24, но 9.0007 12 — наименьшее, то есть это наименьшее общее кратное .
Вы можете сделать это с любой парой чисел, хотя большие числа могут представлять большую проблему. Для сложения или вычитания вы всегда можете вернуться к простому умножению одного знаменателя на другой, если у вас возникли проблемы с поиском наименьшего общего знаменателя , но имейте в виду, что вам, вероятно, придется уменьшать.
Дроби — самая вкусная часть математики.
Как складывать дроби — метод 1
Теперь, когда вы знаете, как найти общий знаменатель, вы готовы приступить к сложению и вычитанию.
Вернемся к примеру с $1/2$ и $1/12$ — в этом случае давайте рассмотрим эту задачу: через; $1/2 + 1/12$ не равняется $2/14$.
#1: Найдите общий знаменатель
Сначала мы найдем наименьший общий знаменатель, так как обычно это лучший способ.
Мы уже проделали вышеописанную работу, но напомню, что вам нужно выписать ряд кратных каждому числу, пока не найдете совпадение . В этом случае и 2, и 12 кратны 12.
#2: Умножьте, чтобы получить каждый числитель с одним и тем же знаменателем
Всегда помните, что все, что вы делаете со знаменателем, должно быть сделано и с числителем. Итак, давайте посмотрим на эти две дроби, которые нам нужны, чтобы получить знаменатель 12.
$1/12$ легко — это уже больше знаменателя 12, поэтому нам не нужно ничего с ним делать.
$1/2$ нужно немного поработать. Какое число, умноженное на 2, будет равно 12?
Перефразируя этот вопрос как проблему, которую мы можем решить, $2*?=12$. Или, еще проще, мы можем инвертировать операцию , чтобы получить $12/2=?$, что мы можем легко решить.
Или, еще проще, мы можем инвертировать операцию , чтобы получить $12/2=?$, что мы можем легко решить.
Итак, теперь мы знаем, что чтобы перейти от знаменателя 2 к знаменателю 12, нам нужно умножить на 6. Опять же, помните, что все, что вы делаете со знаменателем, нужно делать и с числителем, поэтому умножьте сверху и снизу на 6, чтобы получить $6/12$.
#3: Сложите числители, но оставьте знаменатели в покое
Теперь, когда у вас одинаковые знаменатели, вы можете сложить числители.
В данном случае это будет означать, что $6/12 + 1/12 = 7/12$. Спросите себя, сможете ли вы уменьшить дробь, соединив и числитель, и знаменатель на одно и то же число. В этом случае вы не можете, поэтому ваш ответ прост: $7/12$.
Как складывать дроби — метод 2
В качестве альтернативы мы можем просто перемножить два знаменателя, чтобы найти другой общий знаменатель. Это другой способ решения проблемы, но ответ будет тот же.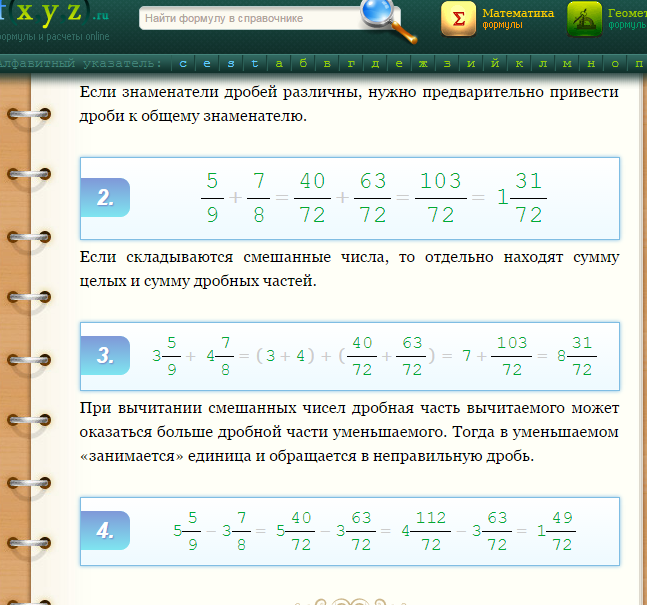
#1: Умножьте знаменатели вместе
Здесь нет никаких хитростей — просто умножьте 2 на 12, чтобы получить 24. Это будет ваш общий знаменатель.
#2: Умножьте, чтобы получить каждый числитель при одном и том же знаменателе
Как и при нахождении наименьшего общего знаменателя, нам нужно умножить как верхнее, так и нижнее число каждой дроби. В этом случае используйте обратные операции, чтобы узнать, какое число нужно умножить.
Если $1/2$ должно быть $?/24$, вы можете сделать $24÷2$, чтобы выяснить, какое число нужно умножить на 12. Умножьте верх и низ на 12, чтобы получить $12/24$.
Повторите процесс с $1/12$. Если $1/12$ должно быть $?/24$, решите $24÷12$, чтобы получить 2. Теперь умножьте числитель и знаменатель $1/12$ на 2, чтобы получить $2/24$.
#3: Сложите числители вместе
Теперь вы можете просто складывать прямо. $12/24 + 2/24 = 14/24$$.
#4: Уменьшить
Вот здесь и появляется дополнительный шаг. $14/24$ не является дробью в самой низкой форме, поэтому нам нужно ее уменьшить. Чтобы уменьшить, нужно разделить и числитель, и знаменатель на одно и то же число.
$14/24$ не является дробью в самой низкой форме, поэтому нам нужно ее уменьшить. Чтобы уменьшить, нужно разделить и числитель, и знаменатель на одно и то же число.
Для этого нам нужно найти наибольший общий делитель. Подобно поиску наименьшего общего кратного, это означает перечисление чисел до тех пор, пока мы не найдем два множителя, которые являются общими для числителя и знаменателя, за исключением 1, например:
14 : 2 , 7
24 : 2 , 3, 4, 6, 8, 12
Какое число у них общее? 2. Это означает, что 2 — это наш наибольший общий множитель, и, следовательно, число, на которое мы будем делить числитель и знаменатель.
$14÷2=7$ и $24÷2=12$ дают нам ответ $7/12$.
Ответ такой же, как и при решении с использованием наименьшего общего кратного, и его нельзя уменьшить дальше, так что это наш окончательный ответ!
Если вы когда-нибудь обнаружите, что записываете множество факторов без особой удачи, есть несколько быстрых способов вычислить потенциальные факторы.
- Если число четное, его можно разделить на 2.
- Если вы можете сложить цифры числа, которое делится на 3, число делится на 3, например, 96 ($9+6=15$ и $1+5=6$, которое делится на 3).
- Если число оканчивается на 5 или 0, оно делится на 5.
- Если вы не знаете, когда прекратить поиск факторов, вычтите меньшее число из большего. Это число будет наибольшим возможным общим делителем, но не самим наибольшим общим делителем.
Например, давайте возьмем 50 и 32. Конечно, мы могли бы просто разделить оба числа на 2 и продолжать уменьшать оттуда, но если вы сделаете $50-32$, вы получите 18, что говорит нам перестать искать наибольший общий множитель, как только мы найдем 18.
На практике это выглядит так:
50 : 2 , 5, 10
32 : 2 , 3 4, 90, 80002 Вместо того, чтобы продолжать, мы знаем, что должны остановиться, когда следующий фактор будет равен 18 или выше, что не позволит нам тратить больше времени на выяснение факторов, которые нам не нужны.
 Мы гораздо быстрее увидим, что наибольший общий делитель равен 2, и продолжим решать задачу!
Мы гораздо быстрее увидим, что наибольший общий делитель равен 2, и продолжим решать задачу!
$1/1 — 1/? = yum$
Как вычитать дроби
Как только вы научитесь складывать дроби, вычитание дробей станет легкой задачей! Процесс точно такой же, только вы, естественно, будете вычитать, а не складывать.
#1: Найдите общий знаменатель
Давайте рассмотрим следующий пример: вот так:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
10 : 10, 20 30 0 30 первое число в общем равно 30, поэтому мы прибавим оба числителя к знаменателю, равному 30.
#2: Умножьте, чтобы получить оба числителя при одном и том же знаменателе
Во-первых, нам нужно выяснить, на сколько нам нужно умножить числитель и знаменатель каждой дроби, чтобы получить знаменатель 30. Для $2/3$ какое число, умноженное на 3, равно 30? В форме уравнения:
$$30÷3=?$$
Наш ответ равен 10, поэтому мы умножим и числитель, и знаменатель на 10, чтобы получить $20/30$.
Далее мы повторим процесс для второй фракции. Какое число нужно умножить на 10, чтобы получить 30? Что ж, $30÷10=3$, поэтому мы умножаем верх и низ на 3, чтобы получить 9 долларов./30$.
Это делает нашу задачу $20/30-9/30$, а это значит, что мы готовы продолжить!
#3: Вычтите числители
Как и в случае сложения, мы вычтем один числитель из другого, но оставим знаменатели в покое.
$20/30-9/30=11/30$$.
Поскольку мы нашли наименьшее общее кратное, мы уже знаем, что задачу нельзя уменьшить дальше.
Однако предположим, что мы только что умножили 3 на 10, чтобы получить знаменатель 30, поэтому нам нужно проверить, можем ли мы уменьшить. Давайте воспользуемся этим маленьким трюком, который мы изучили, чтобы найти самые лучшие возможно общий делитель. Каковы бы ни были общие факторы 11 и 30, они не могут быть больше, чем 30-11 долларов или 19. у них нет общих множителей, ответ нельзя сократить дальше.
$1/10$ пицца по-прежнему стоит $10/10$ вкусная.
Сложение и вычитание дробей Примеры
Давайте рассмотрим еще несколько примеров задач!
$$ 8/15-4/9 $$
#1: Найдите общий знаменатель
15 : 15, 30, 45 , 60
: 9, 27, 27, 27, 26, 45
#2: Умножьте оба числителя на один и тот же знаменатель $$
$$24/45$$
$$45÷9=\bo5$$
$$4*5=20$$ 9#3: Вычтите числители $$6/11+3/4$$
№1: Найдите общий знаменатель 24, 28, 32, 36, 40,
44
#2: Умножьте оба числителя на один и тот же знаменатель
$$44÷11=\bo4$$
$$6*4=24
$11*4=44$$
$24/44$$
$44÷4=\bo11$$
$3*11=33$$
$$4*11=44$$
$$33/44$$
#3: Добавьте числители
$$ 4/7-11/21 $$
#1: Найти общий знаменатель
7 : 7, 14, 21
21 : 21 , 42, 63
#2: Умножьте, чтобы получить оба числителя на один и тот же знаменатель
$$21÷7=\bo3$$
$$3*4=12$$
$$3*7=21$$
$$12/21$$
$11/2$ уже старше 21 года, так что нам ничего не нужно делать.
#3: Вычтем числители
9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117
13 5, 57, 28, 13, 2 , 91, 104, 117
#2: Умножьте оба числителя на один и тот же знаменатель
$104/117$$
$117÷13=\bo9$$
$7*9=63$$
$13*9=117$$
$63/117$0 3
#3: Добавьте числители
$$104/117+63/117=\bo167/\bo117$$
Что дальше?
Сложение и вычитание дробей станет еще проще, если вы начнете преобразовывать десятичные дроби в дроби!
Если вы не знаете, какие уроки математики в средней школе вам следует посещать, это руководство поможет вам составить расписание, чтобы быть уверенным, что вы готовы к поступлению в колледж!
Теперь, когда вы стали экспертом в сложении и вычитании дробей, испытайте себя, научившись переводить градусы Цельсия в градусы Фаренгейта!
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша база данных проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Мелисса Бринкс
Об авторе
Мелисса Бринкс окончила Вашингтонский университет в 2014 году со степенью бакалавра по английскому языку с упором на творческое письмо. Она провела несколько лет, репетируя учеников K-12 по многим предметам, в том числе по подготовке к SAT, чтобы помочь им подготовиться к поступлению в колледж.
Сложение и вычитание дробей — математический обзор (видео)
TranscriptFAQsPracticeWorksheets
Привет! Добро пожаловать в это видео о сложении и вычитании дробей!
Прежде чем мы углубимся в это, давайте рассмотрим некоторую терминологию, необходимую для понимания концепций.
Дробь — это отношение значений, которые отражают «часть» к «целому». «Часть» называется числителем и пишется над чертой деления. «Целое» обозначается как в знаменателе и записывается под чертой деления:
| числитель | ||
| знаменатель |
Знаменатель не меняется. Например, предположим, что на обеденном столе в корзине стоит семь булочек. Ты съел один, а твой брат съел два. Какая дробь представляет собой количество булочек, съеденных вами и вашим братом?
Возможно, вы довольно быстро сможете осмыслить этот пример сложения дробей. Вы просто складываете количество булочек, съеденных вами и вашим братом, и делите на общее количество булочек, которые были на столе в начале ужина. Помните, знаменатель остается прежним. \(\frac{1}{7}+ \frac{2}{7}\), что можно рассматривать как \(\frac{1+2}{7}\), равно \(\frac{3} {7}\). Дробь \(\frac{3}{7}\) представляет собой количество булочек, съеденных вами и вашим братом.
Дробь \(\frac{3}{7}\) представляет собой количество булочек, съеденных вами и вашим братом.
\(\frac{1}{7}+\frac{2}{7}=\frac{1+2}{7}=\frac{3}{7}\)
Таким же образом можно рассматривать вычитание дробей.
Допустим, вы с друзьями играете в карты. Вы держите трех из четырех королей в колоде карт. Вы сбрасываете Короля Червей при следующей игре. Какая дробь представляет собой количество королей в вашей руке сейчас?
Поскольку в колоде карт всего четыре короля, дробь 34 представляет трех королей, которые были у вас в руке в начале игры. Если отдать Короля червей, то числитель этой дроби уменьшится на единицу. Доля королей в вашей руке изменяется следующим образом: \(\frac{3}{4}- \frac{1}{4}\), что можно увидеть как \(\frac{3-1 {4}\), равно \(\frac{2}{4}\), что упрощается до половины.
\(\frac{3}{4}-\frac{1}{4}=\frac{3-1}{4}=\frac{2}{4} \text{ или } \frac{ 1}{2}\)
Эти примеры довольно просты, потому что знаменатели складываемых и вычитаемых дробей одинаковы.
Как складывать дроби с разными знаменателями
Если знаменатели не совпадают, требуется немного больше работы. В частности, одна или обе дроби должны быть алгебраически скорректированы, чтобы получить общих знаменателей 9.0008 .
Пример:
\(\frac{2}{5}+\frac{3}{10}\)
Как я уже говорил, эти дроби нельзя складывать, пока они не имеют общий знаменатель. На самом деле знаменатель должен быть наименьшим значением, на которое оба знаменателя могут делиться поровну. Это значение известно как наименьший общий знаменатель (LCD) .
При рассмотрении знаменателей 5 и 10 становится ясно, что 10 — это наименьшее число, на которое можно разделить без остатка и 5, и 10. Это означает, что нам придется алгебраически подогнать первую дробь так, чтобы знаменатель стал равен 10. Мы делаем это, умножая и числитель, и знаменатель. Правила умножения дробей требуют умножения числителя на числитель и знаменателя на знаменатель: \(2 \times 2=4\) и \(2 \times 5=10\).
\(\frac{2}{2}\times \frac{2}{5}=\frac{4}{10}\)
Эта работа создает дробь \(\frac{4 {10}\), что эквивалентно исходной дроби \(\frac{2}{5}\). На этом этапе можно сложить дроби с общими знаменателями: \(\frac{4}{10}+ \frac{3}{10}\), что можно увидеть как \(\frac{4+3}{ 10}\), равно \(\frac{7}{10}\).
\(\frac{4}{10}+\frac{3}{10}=\frac{4+3}{10}=\frac{7}{10}\)
Это Последний пример требует от вас привести обе дроби к общему знаменателю. Давайте поработаем над этим вместе, а потом я дам вам попробовать самостоятельно.
Как вычитать дроби с разными знаменателями
\(\frac{5}{8}-\frac{1}{6}\)
Итак, обо всем по порядку: какое число встречается реже всего кратное из 6 и 8? 24. Так как 24 разделить на 8 равно 3, нам придется скорректировать первую дробь, умножив и числитель, и знаменатель на 3. \(24 \div 6=4\), поэтому нам придется умножить числитель и знаменатель вторую дробь на четыре.
\(\frac{3}{3} \times \frac{5}{8}-\frac{4}{4} \times \frac{1}{6}\)
Эти корректировки создают эквивалентные дроби с общим знаменателем 24. После этого числители можно вычесть следующим образом:
\(\frac{15}{24}-\frac{ 4}{24}=\frac{11}{24}\)
Хорошо, а теперь попробуйте. Поставьте видео на паузу и посмотрите, сможете ли вы его решить.
\(\frac{3}{5}+\frac{3}{7}\)
Как дела? Давайте пройдемся по нему. Наименьшее общее кратное 5 и 7 равно 35. Скорректируйте первую дробь, умножив числитель и знаменатель на 7, и скорректируйте вторую дробь, умножив числитель и знаменатель на 5. Когда знаменатели совпадут, сложите числители. Это дает нам \(\frac{36}{35}\)!
\(\frac{7}{7} \times \frac{3}{5}+\frac{5}{5} \times \frac{3}{7}\) \(\frac{21 }{35}+\frac{15}{35}=\frac{36}{35}\)
Давайте подведем итоги, прежде чем идти дальше.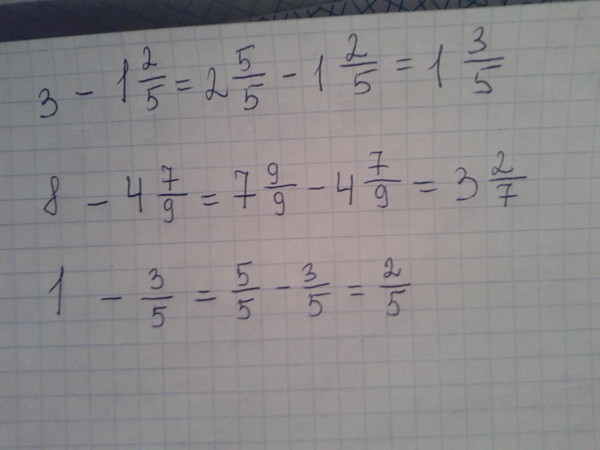 Складываете ли вы или вычитаете дроби, помните, что знаменатель всегда остается одним и тем же, и иногда вам придется создать общий знаменатель и найти наименьшее общее кратное, прежде чем вы сможете приступить к решению задачи.
Складываете ли вы или вычитаете дроби, помните, что знаменатель всегда остается одним и тем же, и иногда вам придется создать общий знаменатель и найти наименьшее общее кратное, прежде чем вы сможете приступить к решению задачи.
Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!
Сложение дробей с целыми числами | Умножение и деление дробей
Часто задаваемые вопросы
Q
При сложении дробей вы добавляете знаменатель?
A
Нет, при сложении дробей необходимо сначала найти общий знаменатель и привести обе дроби к этому знаменателю. Затем добавьте числители и сохраните знаменатель.
Пример. \(\frac{1}{3}+\frac{1}{2}=\frac{1}{3}×\frac{2}{2}+\frac{1}{2}×\frac{ 3}{3}=\frac{2}{6}+\frac{3}{6}=\frac{5}{6}\)
Q
Как складывать дроби с разными знаменателями?
A
Чтобы сложить дроби с разными знаменателями, сначала приведите обе дроби к общему знаменателю. Затем сложите числители и оставьте знаменатель прежним.
Затем сложите числители и оставьте знаменатель прежним.
Пример. \(\frac{1}{3}+\frac{3}{4}=\frac{1}{3} (\frac{4}{4})+\frac{3}{4} (\frac {3}{3})=\frac{4}{12}+\frac{9}{12}=\frac{13}{12}=1 \frac{1}{12}\)
Q
Что означает добавление похожих дробей?
A
Сложение одинаковых дробей означает сложение дробей с одинаковым знаменателем.
Пример. \(\frac{1}{4}+\frac{2}{4}=\frac{3}{4}\)
Q
Можете ли вы отменить перекрестную отмену при добавлении дробей?
A
Нет, при добавлении дробей нельзя отменять. Взаимная отмена работает только с умножением дробей.
Q
Как вычитать дроби?
A
Чтобы вычесть дроби, приведите обе дроби к общему знаменателю. Затем вычтите числители и оставьте знаменатель прежним.
пр. \(\frac{4}{5}-\frac{1}{3}=\frac{4}{5} (\frac{3}{5})-\frac{1}{3} (\frac {5}{5})=\frac{12}{15}-\frac{5}{15}=\frac{7}{15}\)
Q
Как вычитать дроби с целыми числами ?
A
Вычитание дробей с целыми числами путем преобразования целого числа в дробь, приведения к общему знаменателю, вычитания и упрощения, если это необходимо.
Пример. \(4-\frac{5}{7}=\frac{4}{1}-\frac{5}{7}=\frac{4}{1} (\frac{7}{7})- \frac{5}{7}=\frac{28}{7}-\frac{5}{7}=\frac{23}{7}=3 \frac{2}{7}\)
Q
Как вычитать дроби с разными знаменателями?
A
Чтобы вычесть дроби с разными знаменателями, сначала преобразуйте дроби в дроби с общими знаменателями, а затем вычтите числители, оставив знаменатель одинаковым.
Пример. \(\frac{4}{7}-\frac{1}{3}=\frac{4}{7} (\frac{3}{3})-\frac{1}{3} (\frac {7}{7})=\frac{12}{21}-\frac{7}{21}=\frac{5}{21}\)
Практические вопросы
Вопрос №1:
Добавьте следующие дроби: \(\frac{1}{5}+\frac{3}{5}=\)
\(\frac{4}{10}\)
\(\ frac{4}{5}\)
\(\frac{5}{5}\)
\(\frac{5}{4}\)
Показать ответ
Ответ:
правильный ответ: \(\frac{4}{5}\). При сложении дробей с одинаковым знаменателем просто сложите числители и оставьте знаменатель одинаковым. В этом случае сложение числителей дает сумму 4, а знаменатель остается равным 5. Результат равен \(\frac{4}{5}\).
В этом случае сложение числителей дает сумму 4, а знаменатель остается равным 5. Результат равен \(\frac{4}{5}\).
Скрыть ответ
Вопрос № 2:
Добавьте следующие дроби: \(\frac{12}{15}+\frac{2}{15}=\)
\(\frac{10 {15}\)
\(\frac{15}{14}\)
\(\frac{14}{15}\)
\(\frac{14}{30}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{14}{15}\) . При сложении дробей с одинаковым знаменателем просто сложите числители и оставьте знаменатель одинаковым. В этом случае сложение числителей дает сумму 14, а знаменатель остается равным 15. Результатом является \(\frac{14}{15}\) .
Скрыть ответ
Вопрос № 3:
Добавьте следующие дроби: \(\frac{2}{3}+\frac{1}{4}=\)
\(\frac{11 {12}\)
\(\frac{3}{7}\)
\(\frac{3}{12}\)
\(\frac{6}{11}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{11}{12}\). Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 3 и 4. Наименьшее общее кратное 3 и 4 равно 12, поэтому дроби следует переписать с 12 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{2}{3}\) знаменатель был умножен на 4, поэтому числитель также должен быть умножен на 4, что равно \(\frac{8}{12}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 3, поэтому числитель также должен быть умножен на 3, что равно \(\frac{3}{12}\). Наконец, добавьте \(\frac{8}{12}+\frac{3}{12}\), чтобы получить \(\frac{11}{12}\).
Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 3 и 4. Наименьшее общее кратное 3 и 4 равно 12, поэтому дроби следует переписать с 12 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{2}{3}\) знаменатель был умножен на 4, поэтому числитель также должен быть умножен на 4, что равно \(\frac{8}{12}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 3, поэтому числитель также должен быть умножен на 3, что равно \(\frac{3}{12}\). Наконец, добавьте \(\frac{8}{12}+\frac{3}{12}\), чтобы получить \(\frac{11}{12}\).
Скрыть ответ
Вопрос № 4:
Добавьте следующие дроби: \(\frac{3}{7}+\frac{2}{5}=\)
\(\frac{5 {35}\)
\(\frac{6}{35}\)
\(\frac{29}{35}\)
\(\frac{5}{12}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{29}{35}\). Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 7 и 5. Наименьшее общее кратное 7 и 5 равно 35, поэтому дроби следует переписать с 35 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{3}{7}\) знаменатель был умножен на 5, поэтому числитель также следует умножить на 5, что равно \(\frac{15}{35}\). Для дроби \(\frac{2}{5}\) знаменатель был умножен на 7, поэтому числитель также должен быть умножен на 7, что равно \(\frac{14}{35}\). Наконец, добавьте \(\frac{15}{35}+\frac{14}{35}\), чтобы получить \(\frac{29{35}\).
Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 7 и 5. Наименьшее общее кратное 7 и 5 равно 35, поэтому дроби следует переписать с 35 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{3}{7}\) знаменатель был умножен на 5, поэтому числитель также следует умножить на 5, что равно \(\frac{15}{35}\). Для дроби \(\frac{2}{5}\) знаменатель был умножен на 7, поэтому числитель также должен быть умножен на 7, что равно \(\frac{14}{35}\). Наконец, добавьте \(\frac{15}{35}+\frac{14}{35}\), чтобы получить \(\frac{29{35}\).
Скрыть ответ
Вопрос № 5:
Добавьте следующие дроби: \(\frac{5}{6}+\frac{1}{4}=\)
\(\frac{3) {5}\)
\(\frac{6}{10}\)
\(\frac{12}{13}\)
\(\frac{13}{12}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{13}{12}\). Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 6 и 4. Наименьшее общее кратное 6 и 4 равно 12, поэтому дроби следует переписать с 12 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{5}{6}\) знаменатель был умножен на 2, поэтому числитель также должен быть умножен на 2, что равно \(\frac{10}{12}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 3, поэтому числитель также должен быть умножен на 3, что равно \(\frac{3}{12}\). Наконец, добавьте \(\frac{10}{12}+\frac{3}{12}\), чтобы получить \(\frac{13}{12}\).
Чтобы сложить эти дроби, должен быть общий знаменатель. Общий знаменатель будет наименьшим общим кратным 6 и 4. Наименьшее общее кратное 6 и 4 равно 12, поэтому дроби следует переписать с 12 в качестве нового знаменателя. Теперь отрегулируйте числители. Для дроби \(\frac{5}{6}\) знаменатель был умножен на 2, поэтому числитель также должен быть умножен на 2, что равно \(\frac{10}{12}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 3, поэтому числитель также должен быть умножен на 3, что равно \(\frac{3}{12}\). Наконец, добавьте \(\frac{10}{12}+\frac{3}{12}\), чтобы получить \(\frac{13}{12}\).
Скрыть ответ
Вопрос № 6:
Вычтите следующие дроби: \(\frac{3}{4}-\frac{1}{4}\)
\(\frac{2} {4}\)
\(\frac{4}{2}\)
\(\frac{4}{5}\)
\(\frac{1}{4}\)
Показать Ответ:
Ответ:
Правильный ответ: \(\frac{2}{4}\). При вычитании дробей с одинаковым знаменателем просто вычтите числители и оставьте знаменатель прежним. В этом случае вычтите 1 из 3 и сохраните знаменатель равным 4. Результат будет \(\frac{2}{4}\).
При вычитании дробей с одинаковым знаменателем просто вычтите числители и оставьте знаменатель прежним. В этом случае вычтите 1 из 3 и сохраните знаменатель равным 4. Результат будет \(\frac{2}{4}\).
Скрыть ответ
Вопрос № 7:
Вычтите следующие дроби: \(\frac{5}{6}-\frac{2}{6}=\)
\(\frac{7 {12}\)
\(\frac{3}{4}\)
\(\frac{3}{6}\)
\(\frac{3}{36}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{3}{6}\). При вычитании дробей с одинаковым знаменателем просто вычтите числители и оставьте знаменатель прежним. В этом случае вычтите 2 из 5 и сохраните знаменатель равным 6. Результат будет \(\frac{3}{6}\).
Скрыть ответ
Вопрос № 8:
Вычтите следующие дроби: \(\frac{5}{9}-\frac{1}{4}=\)
\(\frac{11 {36}\)
\(\frac{36}{11}\)
\(\frac{4}{5}\)
\(\frac{5}{11}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{11}{36}\). Прежде чем эти дроби можно будет вычесть, знаменатели должны быть одинаковыми. Наименьшее общее кратное для 9 и 4 равно 36, поэтому измените оба знаменателя на 36. Для дроби \(\frac{5}{9}\), знаменатель был умножен на 4, чтобы получить 36, поэтому числитель также необходимо умножить на 4. Это дает нам \(\frac{20}{36}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 9, чтобы получить 36, поэтому числитель необходимо умножить на 9. Это дает нам \(\frac{9}{36}\ ). Теперь просто вычислите \(20-9\), чтобы получить \(\frac{11}{36}\).
Прежде чем эти дроби можно будет вычесть, знаменатели должны быть одинаковыми. Наименьшее общее кратное для 9 и 4 равно 36, поэтому измените оба знаменателя на 36. Для дроби \(\frac{5}{9}\), знаменатель был умножен на 4, чтобы получить 36, поэтому числитель также необходимо умножить на 4. Это дает нам \(\frac{20}{36}\). Для дроби \(\frac{1}{4}\) знаменатель был умножен на 9, чтобы получить 36, поэтому числитель необходимо умножить на 9. Это дает нам \(\frac{9}{36}\ ). Теперь просто вычислите \(20-9\), чтобы получить \(\frac{11}{36}\).
Скрыть ответ
Вопрос № 9:
Вычтите следующие дроби: \(\frac{1}{2}-\frac{2}{5}=\)
\(\frac{3}{10}\)
\(\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{1 }{10}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{1}{10}\). Для начала необходимо найти общий знаменатель, прежде чем эти дроби можно будет вычесть. Наименьшее общее кратное для 2 и 5 равно 10, поэтому измените оба знаменателя на 10. Для дроби \(\frac{1}{2}\) знаменатель был умножен на 5, чтобы получить 10, поэтому числитель должен быть также умножается на 5. Это дает нам \(\frac{5}{10}\). Для дроби \(\frac{2}{5}\) знаменатель был умножен на 2, чтобы получить 10, поэтому числитель необходимо умножить на 2. Это дает нам \(\frac{4}{10}\ ). Теперь просто посчитайте 5-4, чтобы получить \(\frac{1}{10}\).
Для начала необходимо найти общий знаменатель, прежде чем эти дроби можно будет вычесть. Наименьшее общее кратное для 2 и 5 равно 10, поэтому измените оба знаменателя на 10. Для дроби \(\frac{1}{2}\) знаменатель был умножен на 5, чтобы получить 10, поэтому числитель должен быть также умножается на 5. Это дает нам \(\frac{5}{10}\). Для дроби \(\frac{2}{5}\) знаменатель был умножен на 2, чтобы получить 10, поэтому числитель необходимо умножить на 2. Это дает нам \(\frac{4}{10}\ ). Теперь просто посчитайте 5-4, чтобы получить \(\frac{1}{10}\).
Скрыть ответ
Вопрос №10:
Вычтите следующие дроби: \(\frac{10}{12}-\frac{1}{6}=\)
\(\frac{3) {7}\)
\(\frac{8}{12}\)
\(\frac{9}{6}\)
\(\frac{1}{6}\)
Показать ответ
Ответ:
Правильный ответ: \(\frac{8}{12}\).
 Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;

 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.  Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
 В данном случае НОК равно 45 . Для первой дроби необходим дополнительный множитель 5 , а для второй – 3 .
В данном случае НОК равно 45 . Для первой дроби необходим дополнительный множитель 5 , а для второй – 3 .


 Рассмотрим, как использовать их при решении примеров.
Рассмотрим, как использовать их при решении примеров. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.
Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.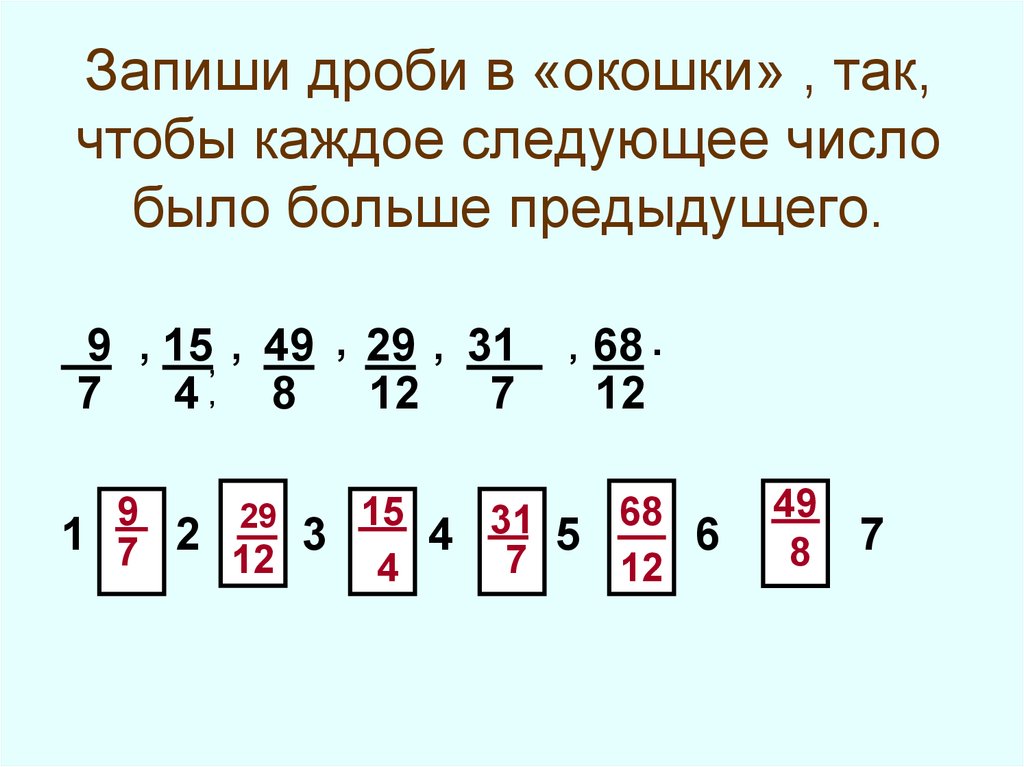
 Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.
Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них. Вычесть дроби: .
Вычесть дроби: .

 Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями. .. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если время останавливается, Ахиллес уже не может перегнать черепаху. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
 Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет? Сложение дробей
Сложение дробей
 Мы гораздо быстрее увидим, что наибольший общий делитель равен 2, и продолжим решать задачу!
Мы гораздо быстрее увидим, что наибольший общий делитель равен 2, и продолжим решать задачу!