Сложение дробей с разными знаменателями

Цели:

• научить складывать и вычитать дроби с разными знаменателями несколькими способами;
• развивать мышление, сообразительность.

Тип урока: урок-игра.

Оборудование: мультимедиа проектор, презентация «Сложение дробей с разными знаменателями», тест на компьютере (Приложение 1).

ХОД УРОКА

1. Организационный момент. Постановка целей урока

Учитель: Ребята! Сегодня мы с вами будем учиться складывать и вычитать дроби с разными знаменателями.

2. Повторение (разминка)

Учитель: Давайте сначала повторим, как сложить дроби с одинаковыми знаменателями и как сократить их. И заодно узнаем, что нам поможет понять эту тему.

Слайд №2

Ответ: СКАЗКА

Слайд №3

Сказка ложь,
Но в ней намёк,
Добрым молодцам
И красным девицам урок.

3. Объяснение нового материала

Слайд №4

В 3/9 царстве, в 3/9 государстве жили –  были обыкновенные дроби. Были они разные.

• Египтяне употребляли только дроби с числителем единица и дробь .
• В древнем Вавилоне наоборот предпочитали постоянный знаменатель, равный 60.
• Римляне тоже  пользовались одним знаменателем, равным 12.
• Дроби в древней Руси назывались долями, позднее «ломаными числами».

 – полтина,  – четь,  – полчеть, – треть,  – полтреть,  полполтреть.

Слайд №5

Действия с дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».

Слайд №6

Поставил царь перед своими подданными проблему: найти интересные способы сложения дробей. И дал на раздумье одну ночь.

Слайд №7

Первым вышел простак и предложил складывать дроби так:

Загудели дроби. Как же так?

Слайд №8

Вторым вышел Тугодум. Он изобрел оригинальный способ:  

Сократим  . Восхитился царь!

Учитель: Научить складывать дроби этим способом можно любого: просто меняй знаменатели и подписывай их как дополнительные множители.

Учитель: А теперь попробуем сами выполнить сложение дробей этим способом. Какой способ сложения и вычитания дробей предложил Тугодум?

Слайд №9

Слайд №10

Чем хорош способ? Просто меняем знаменатели – легкий!
Чем плох? Сокращать ответ приходится.

Слайд №11

А Зануда прочитал в умной книге, что сначала нужно найти НОК знаменателей.

НОК (8, 6) = 2 * 2 * 2 * 3 = 24

24 : 3
24 : 6 = 4

Не по душе пришелся подданным этот способ.

Учитель: Потренируемся

4. Физкультминутка

Раз – подняться, потянуться
Раз – подняться, потянуться,
Два – нагнуть, разогнуться,
Три – в ладоши, три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – на место тихо сесть. (Можно повторить)

5. Объяснение нового материала (продолжение)

Слайд №12

Тогда Умник говорит: 8 и 6 делятся на 2.

8 : 2 = 4, 6 : 2 = 3

Поменяем местами.

Вот увидите: этот способ в XXI веке будет самым удобным у шестиклассников!

Учитель: Действительно, это самый удобный способ нахождения дополнительных множителей: находим общий делитель знаменателей, делим на него знаменатели и подписываем результаты дополнительными множителями, меняя местами.

Учитель: Ребята! А вам понятен способ Умника? Давайте разберёмся, как находит дополнительные множители Умник. Потренируемся:

Слайд №13

= (знаменатели делятся на 2)
 = (знаменатели делятся на 4)

Слайд №14

А царь спросил у Умника: «Как сложить три дроби?».

Задумались подданные…

Учитель: А как вы предлагаете сложить эти дроби?

Слайд №15

Но тут вышли три мудреца и предложили свой способ:

 

Делим больший знаменатель на два других:

12 : 6 = 2      12 : 8 = ? (неудача!)

Тогда 12 + 12 = 24 и проверяем снова.

24 : 6 = 4    24 : 8 = 3     24 : 12 = 2

Учитель: А сейчас потренируемся

Слайд №16

6.

Закрепление

Затем ученики выполняют тест (Приложение 1). Если тест по техническим причинам не работает (это может случиться в Office – 2003), то можно выполнить следующие действия:

1) Правой кнопкой мыши кликнуть на тест
2) Появится меню
3) Выбрать: свойства – безопасность – изменить – полный доступ – пользователь – полный доступ.

Если тест не работает, то учащимся предлагается выполнить самостоятельную работу.

Самостоятельная работа

Ответы: 

Получится слово «УМНИКИ»

7. Итог урока

Слайд №17

Итак:

Если ты ленишься думать – пользуйся способом Тугодума (просто меняй знаменатели).
Если ты посообразительней – твой способ Умника.

Если ты – творец, то НОК дробей возникает у тебя в голове сразу.

Слайд №18

Вот и сказочке конец, а кто слушал и понял – молодец!

8. Рефлексия

Учитель: А сейчас, отметьте пожалуйста, насколько был Вам полезен и интересен наш урок. Выберите нужный смайлик (предлагаются разные смайлики) и закрепите на доске.

– Урок окончен, всего вам доброго!

правила с разными и одинаковыми знаменателями, как происходит, примеры с решениями

Вычитание дробей является важной темой при изучении арифметических операций. Чтобы его выполнять, нужно понять и изучить несколько простых правил, которые изложены далее. Знания о вычитании дробей могут пригодиться не только на уроке математики, но и в повседневной жизни. Например, при расчете процента за кредит или при разделении объекта на несколько частей.

Особенности темы дробей в программе обучения

Вычитание – действие в арифметике, когда от одного числа (не обязательно большего) отнимают второе. Его на практике применяют очень часто, и не только в отношении дробей, но и простых цифр. Проводить подобную операцию учат еще в младших классах школы, постепенно совершенствуя навыки. Но с вычитанием дробей не все так просто. Мало просто понять одно число от другого. Нужно понять принципы этого процесса и выучить правила.

Дробь – термин, который обозначает количество, определяемое как доля от некоторого числа. Дробное число состоит из числителя и знаменателя. Его можно выразить несколькими способами: 1/2 = 2/4 = 3/6. Если оба умножить на одно и то же, то изменений не произойдет. Для этого может быть использован десятичный вид – 0,5 = 1/2.

В некоторых случаях для выражения потребуется десятичная форма с бесконечным количеством цифр после запятой.

Если необходимо вычитать дроби с разными знаменателями, вместо них используют эквивалентные, но с одинаковыми нижними показателями.

Как происходит вычитание

Эта операция обратна по отношению к сложению. Проще всего осуществлять вычитание обыкновенных дробей, нижние значения которых равны. Для решения подобных уравнений достаточно от первого числителя отнять второй. Можно рассмотреть это на примере:

7/15 — 3/15 = 4/15

Отнимая 3 из 7 получают числитель.

Если нижние части различаются, следует сделать так, чтобы свести вычисления к первому случаю. Для этого используют тот факт, что для каждой ситуации существуют эквивалентные варианты. Умножая верхнюю и нижнюю часть на одно и то же число, значение изменить нельзя. Вычитание дробей с разными знаменателями основано на правильном выполнении эквивалентных преобразований уменьшаемого и вычитаемого.

Воспользовавшись этим правилом, можно привести дробные числа к виду, когда нижние показатели у них равны. После этого осуществляют действие обычным образом. Сказанное можно лучше понять, решив простое задание – сколько будет из 2/3 вычесть 4/7?

Для того, чтобы привести их к эквивалентному виду, оба числа умножают одинаковым образом. Вот несколько возможных вариантов:

2/3 = 4/6 = 6/9 = 8/12 = 10/15= 12/18 = 14/21

Теперь проводят аналогичные действия со вторым операндом. Здесь получают:

4/7= 8/14 = 12/21

Сравнивая полученные показатели видно, что в обоих случаях есть величины с использованием 21. После эквивалентного преобразования ранее сформулированное задание получило следующую формулировку – сколько будет из 14/21 вычесть 12/21?

Чтобы получить числитель, надо от первого отнять второй: 14 — 12 = 2. Результат равен 2/21.

Можно решать такие уравнения и не обязательно искать эквивалентные значения до тех пор, пока не получиться наткнуться на подходящее. Нужный цифры получают перемножением.

Для решения предложено задание – сколько будет из 15/17 вычесть 5/7?

Нужный ответ получается при умножении 17 на 7. Он равен 119. Таким образом, выражение преобразуется:

15/17 — 5/7 = 15х7/17х7 — 5х17/7х17 = 105/119 — 85/119 = (105 — 85)/119 = 20/119

Если делается вычитание десятичных дробей, то действия происходят аналогичным способом. У них знаменатель равен 10, 100, 1000 или аналогичным значениям.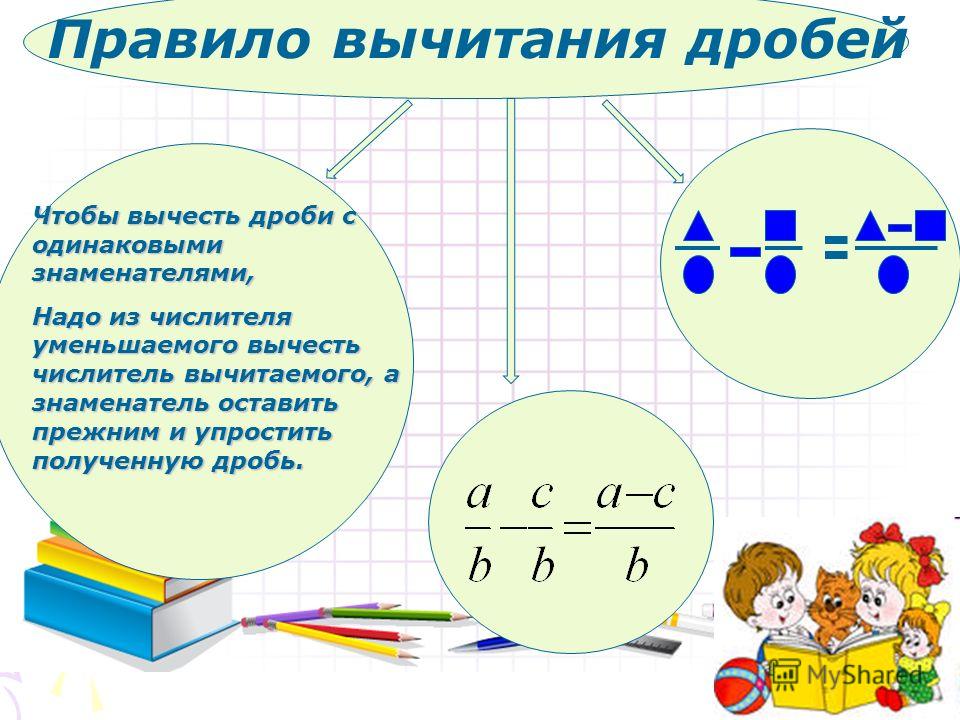 Работа с ними будет рассмотрена в задании – чему равно 0,56 — 0,32?

Здесь речь идет о 56/100и 32/100. В этом случае выполняют вычитание величин, у которых одинаковая нижняя часть. Осуществляется это так:

0,56 — 0,32 = 56/100 — 32/100 = (56 — 32)/100 = 24/100 = 0,24

Иногда используется различное количество цифр после запятой. Вот пример – сколько будет из 0,71 вычесть 0,335 ?

Для начала надо преобразовать десятичные величины в обычные. При этом будет результат такой: 0,71 = 71/100, 0,335 = 335/1000. Здесь поступают в соответствии с правилами работы с величинами с различными знаменателями. Однако нужное значение определяется более легким способом. Если первый операнд умножить на 10, то будет использована 1000.

Теперь делают подсчеты так:

0,71 — 0,335 = 71х10/100х10 — 335/1000 = 710 — 335/1000 = 375/1000 = 0,375

С десятичными дробными величинами работают обычным способом. При этом ту, в которой меньше знаков после запятой, дополняют нужным количеством нулей, чтобы уравнять количество цифр после запятой. Операцию выполняют приведенным ранее способом.

В рассмотренном выше примере решение будет выглядеть та:

0,71 — 0,335 = 0,710 — 0,335 = 0,375

Если в результате подсчета требуется получить положительное значение, необходимо сделать так, чтобы уменьшаемое было больше вычитаемого. Это проверяют, приведя обе цифры к обычной форме. У уменьшаемого числитель должен быть больше.

При выполнении операций при наличии целого и дробного значения, их сначала преобразуют в неправильную дробь, затем поступают так, как указано выше. Чтобы их вычитать, нужно сначала привести к общему знаменателю. Затем от одного числителя отнимают второй.

Вычитание дробей – не слишком легкая и доступная тема в математике. Чтобы понять, как проводить подобные подсчеты, следует потренироваться сначала на более простых примерах и обязательно изучить правила. Тогда никаких проблем точно не возникнет. Случаются ли у вас проблемы при вычитании? С чем они были связаны? Напишите в комментариях. Поделитесь статьей в социальных сетях и сохраните ее в закладках, чтобы не потерять полезную информацию и основные правила.

Также рекомендуем посмотреть подобранные видео по нашей теме.

Вычитание дробей с разными знаменателями

Сложение и вычитание дробей с одинаковыми знаменателями.

Как складывать дроби с одинаковыми знаменателями. Сложение и вычитание алгебраических дробей с разными знаменателями (основные правила, простейшие случаи)

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ .

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ .

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры:

50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

=> НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

в разложении большего числа не хватает двойки и тройки

=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17 119 = 7∙17

в разложении большего числа не хватает тройки

=> НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

На данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с разными знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.

Рассмотрим простейший пример для обыкновенных дробей.

Пример 1. Сложить дроби: .

Решение:

Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю. В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.

Определение

Наименьшее натуральное число, которое делится одновременно на числа и .

Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.

; . Тогда в НОК чисел должны входить две двойки и две тройки: .

После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).

Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.

Получаем: .

Ответ: .

Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.

Пример 2. Сложить дроби: .

Решение:

Алгоритм решения абсолютно аналогичен предыдущему примеру.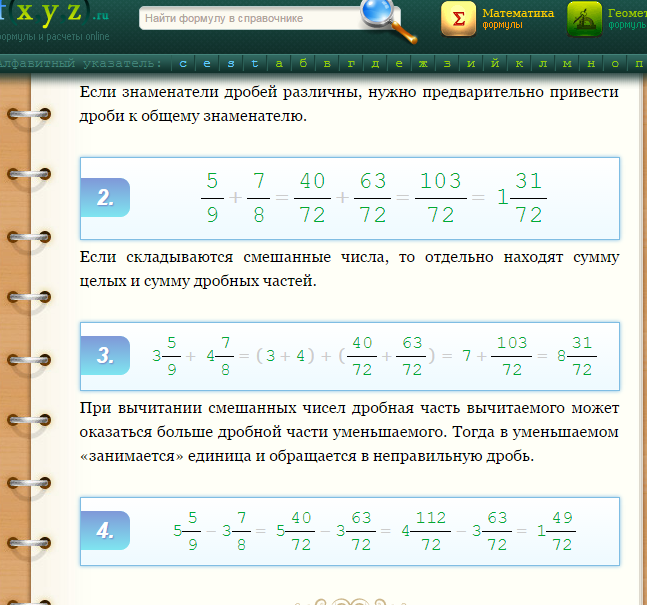 Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.

.

Ответ: .

Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями :

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).

3. Домножить числители на соответствующие дополнительные множители.

4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.

Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.

Пример 3. Сложить дроби: .

Решение:

Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел . Итоговый общий знаменатель будет иметь вид: . Таким образом, решение данного примера имеет вид:.

Ответ: .

Пример 4.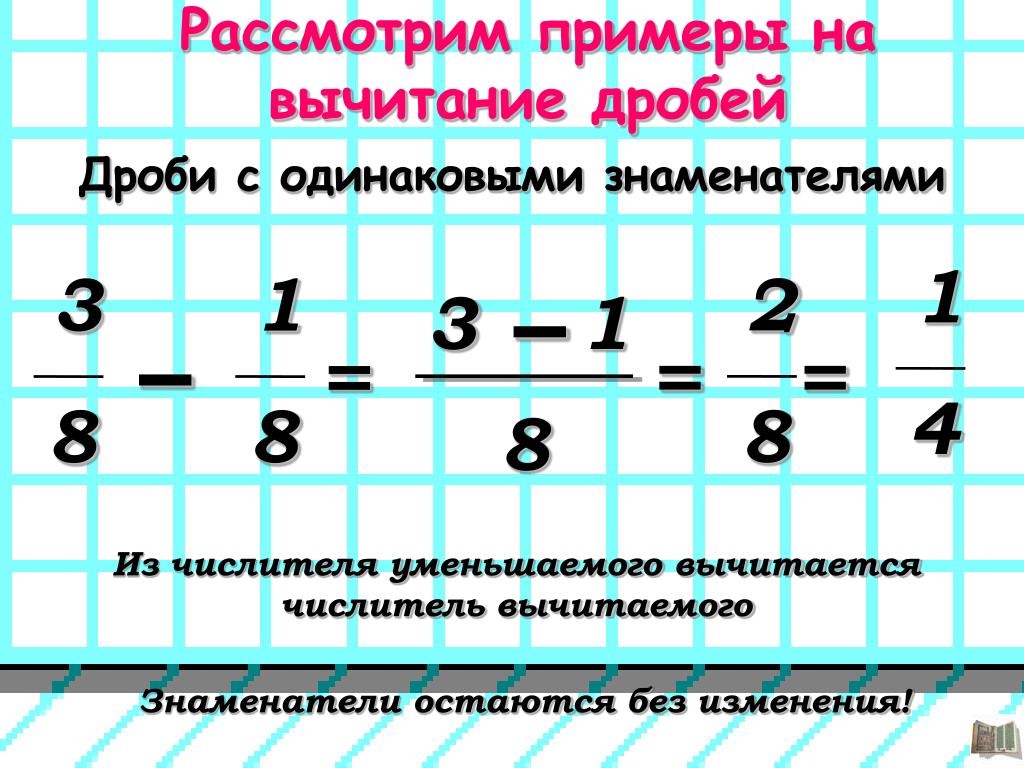 Вычесть дроби: .

Решение:

Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.

Ответ: .

Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.

Рассмотрим более сложный пример.

Пример 5. Упростить: .

Решение:

При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).

В данном конкретном случае:

Тогда легко определить общий знаменатель: .

Определяем дополнительные множители и решаем данный пример:

Ответ: .

Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.

Пример 6. Упростить: .

Решение:

Ответ: .

Пример 7. Упростить: .

Решение:

.

Ответ: .

Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).

Пример 8. Упростить: .

Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь

1 Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:

Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,

Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:

2 Сложение и вычитание дробей с разными знаменателями

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.

3 Наименьшее общее кратное (НОК)

Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:

Для того, чтобы найти НОК нескольких чисел, нужно:

1. Разложить эти числа на простые множители
2. Взять самое большое разложение, и записать эти числа в виде произведения
3. Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
4. Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:

4Приведение дробей к одному знаменателю

Вернемся к сложению дробей с разными знаменателями.

Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:

Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.

5Как сложить целое число и дробь

Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.

В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему — сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров

Правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями

Сфор-му-ли-ру-ем пра-ви-ло сло-же-ния (вы-чи-та-ния) ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми (оно сов-па-да-ет с ана-ло-гич-ным пра-ви-лом для обык-но-вен-ных дро-бей): То есть для сло-же-ния или вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми необ-хо-ди-мо со-ста-вить со-от-вет-ству-ю-щую ал-геб-ра-и-че-скую сумму чис-ли-те-лей, а зна-ме-на-тель оста-вить без из-ме-не-ний.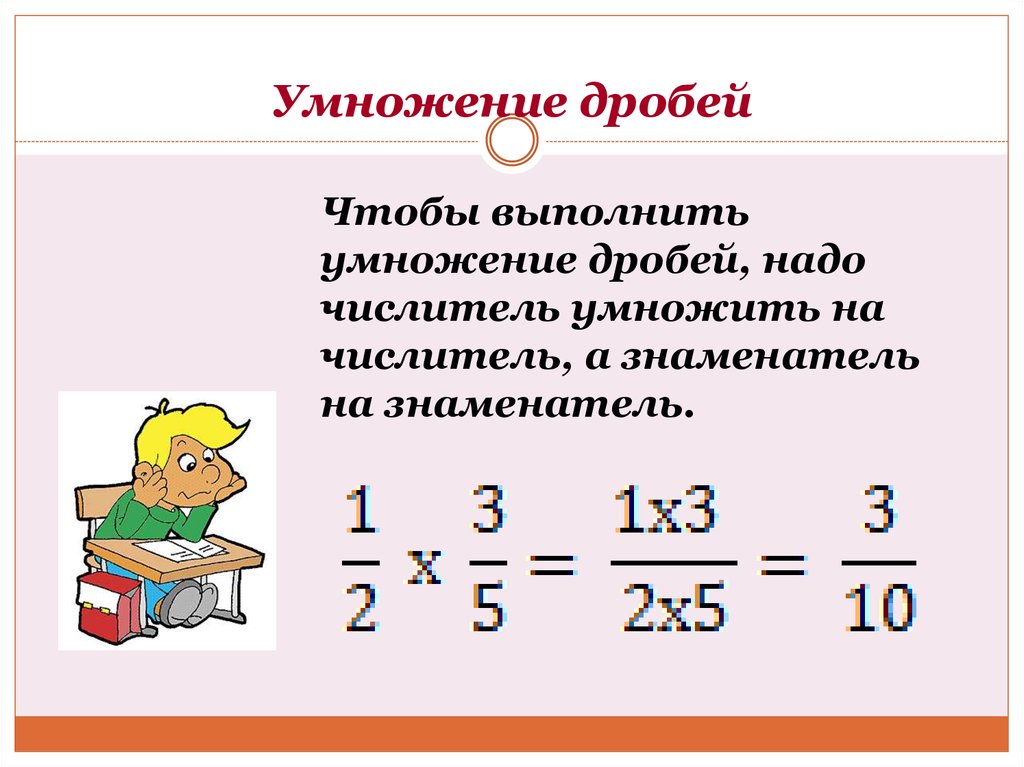

Это пра-ви-ло мы раз-бе-рём и на при-ме-ре обык-но-вен-ных дро-бей, и на при-ме-ре ал-геб-ра-и-че-ских дро-бей.

Примеры применения правила для обыкновенных дробей

При-мер 1. Сло-жить дроби: .

Ре-ше-ние

Сло-жим чис-ли-те-ли дро-бей, а зна-ме-на-тель оста-вим таким же. После этого раз-ло-жим чис-ли-тель и зна-ме-на-тель на про-стые мно-жи-те-ли и со-кра-тим. По-лу-чим: .

При-ме-ча-ние: стан-дарт-ная ошиб-ка, ко-то-рую до-пус-ка-ют при ре-ше-нии по-доб-но-го рода при-ме-ров, за-клю-ча-ет-ся в сле-ду-ю-щем спо-со-бе ре-ше-ния: . Это гру-бей-шая ошиб-ка, по-сколь-ку зна-ме-на-тель оста-ёт-ся таким же, каким был в ис-ход-ных дро-бях.

При-мер 2. Сло-жить дроби: .

Ре-ше-ние

Дан-ная за-да-ча ничем не от-ли-ча-ет-ся от преды-ду-щей: .

Примеры применения правила для алгебраических дробей

От обык-но-вен-ных дро-бей пе-рей-дём к ал-геб-ра-и-че-ским.

При-мер 3. Сло-жить дроби: .

Ре-ше-ние:как уже го-во-ри-лось выше, сло-же-ние ал-геб-ра-и-че-ских дро-бей ничем не от-ли-ча-ет-ся от сло-же-ния обык-но-вен-ных дро-бей. По-это-му метод ре-ше-ния такой же: .

При-мер 4. Вы-честь дроби: .

Ре-ше-ние

Вы-чи-та-ние ал-геб-ра-и-че-ских дро-бей от-ли-ча-ет-ся от сло-же-ния толь-ко тем, что в чис-ли-тель за-пи-сы-ва-ет-ся раз-ность чис-ли-те-лей ис-ход-ных дро-бей. По-это-му .

При-мер 5. Вы-честь дроби: .

Ре-ше-ние: .

При-мер 6. Упро-стить: .

Ре-ше-ние: .

Примеры применения правила с последующим сокращением

В дроби, ко-то-рая по-лу-ча-ет-ся в ре-зуль-та-те сло-же-ния или вы-чи-та-ния, воз-мож-ны со-кра-ще-ния. Кроме того, не стоит за-бы-вать об ОДЗ ал-геб-ра-и-че-ских дро-бей.

При-мер 7. Упро-стить: .

Ре-ше-ние: .

При этом . Во-об-ще, если ОДЗ ис-ход-ных дро-бей сов-па-да-ет с ОДЗ ито-го-вой, то его можно не ука-зы-вать (ведь дробь, по-лу-чен-ная в от-ве-те, также не будет су-ще-ство-вать при со-от-вет-ству-ю-щих зна-че-ни-ях пе-ре-мен-ных). А вот если ОДЗ ис-ход-ных дро-бей и от-ве-та не сов-па-да-ет, то ОДЗ ука-зы-вать необ-хо-ди-мо.

При-мер 8. Упро-стить: .

Ре-ше-ние: . При этом y (ОДЗ ис-ход-ных дро-бей не сов-па-да-ет с ОДЗ ре-зуль-та-та).

Сложение и вычитание обыкновенных дробей с разными знаменателями

Чтобы скла-ды-вать и вы-чи-тать ал-геб-ра-и-че-ские дроби с раз-ны-ми зна-ме-на-те-ля-ми, про-ве-дём ана-ло-гию с обык-но-вен-ны-ми дро-бя-ми и пе-ре-не-сём её на ал-геб-ра-и-че-ские дроби.

Рас-смот-рим про-стей-ший при-мер для обык-но-вен-ных дро-бей.

При-мер 1. Сло-жить дроби: .

Ре-ше-ние:

Вспом-ним пра-ви-ло сло-же-ния дро-бей. Для на-ча-ла дроби необ-хо-ди-мо при-ве-сти к об-ще-му зна-ме-на-те-лю. В роли об-ще-го зна-ме-на-те-ля для обык-но-вен-ных дро-бей вы-сту-па-ет наи-мень-шее общее крат-ное (НОК) ис-ход-ных зна-ме-на-те-лей.

Опре-де-ле-ние

Наи-мень-шее на-ту-раль-ное число, ко-то-рое де-лит-ся од-но-вре-мен-но на числа и .

Для на-хож-де-ния НОК необ-хо-ди-мо раз-ло-жить зна-ме-на-те-ли на про-стые мно-жи-те-ли, а затем вы-брать все про-стые мно-жи-те-ли, ко-то-рые вхо-дят в раз-ло-же-ние обоих зна-ме-на-те-лей.

; . Тогда в НОК чисел долж-ны вхо-дить две двой-ки и две трой-ки: .

После на-хож-де-ния об-ще-го зна-ме-на-те-ля, необ-хо-ди-мо для каж-дой из дро-бей найти до-пол-ни-тель-ный мно-жи-тель (фак-ти-че-ски, по-де-лить общий зна-ме-на-тель на зна-ме-на-тель со-от-вет-ству-ю-щей дроби).

Затем каж-дая дробь умно-жа-ет-ся на по-лу-чен-ный до-пол-ни-тель-ный мно-жи-тель. По-лу-ча-ют-ся дроби с оди-на-ко-вы-ми зна-ме-на-те-ля-ми, скла-ды-вать и вы-чи-тать ко-то-рые мы на-учи-лись на про-шлых уро-ках.

По-лу-ча-ем: .

Ответ: .

Рас-смот-рим те-перь сло-же-ние ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми. Сна-ча-ла рас-смот-рим дроби, зна-ме-на-те-ли ко-то-рых яв-ля-ют-ся чис-ла-ми.

Сложение и вычитание алгебраических дробей с разными знаменателями

При-мер 2. Сло-жить дроби: .

Ре-ше-ние:

Ал-го-ритм ре-ше-ния аб-со-лют-но ана-ло-ги-чен преды-ду-ще-му при-ме-ру. Легко по-до-брать общий зна-ме-на-тель дан-ных дро-бей: и до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из них.

.

Ответ: .

Итак, сфор-му-ли-ру-ем ал-го-ритм сло-же-ния и вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми :

1. Найти наи-мень-ший общий зна-ме-на-тель дро-бей.

2. Найти до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из дро-бей (по-де-лив общий зна-ме-на-тель на зна-ме-на-тель дан-ной дроби).

3. До-мно-жить чис-ли-те-ли на со-от-вет-ству-ю-щие до-пол-ни-тель-ные мно-жи-те-ли.

4. Сло-жить или вы-честь дроби, поль-зу-ясь пра-ви-ла-ми сло-же-ния и вы-чи-та-ния дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми.

Рас-смот-рим те-перь при-мер с дро-бя-ми, в зна-ме-на-те-ле ко-то-рых при-сут-ству-ют бук-вен-ные вы-ра-же-ния.

Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.

Yandex.RTB R-A-339285-1

Как найти разность дробей с одинаковыми знаменателями

Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:

В итоге у нас осталось 3 восьмых доли, поскольку 5 − 2 = 3 . Получается, что 5 8 — 2 8 = 3 8 .

Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.

Определение 1

Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде a b — c b = a — c b .

Такую формулу мы будем использовать и в дальнейшем.

Возьмем конкретные примеры.

Пример 1

Вычтите из дроби 24 15 обыкновенную дробь 17 15 .

Решение

Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24 . Мы получаем 7 и дописываем к ней знаменатель, получаем 7 15 .

Наши подсчеты можно записать так: 24 15 — 17 15 = 24 — 17 15 = 7 15

Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.

Пример 2

Найдите разность 37 12 — 15 12 .

Решение

Воспользуемся описанной выше формулой и подсчитаем: 37 12 — 15 12 = 37 — 15 12 = 22 12

Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 11 6 . Это неправильная дробь, из которой мы выделим целую часть: 11 6 = 1 5 6 .

Как найти разность дробей с разными знаменателями

Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:

Определение 2

Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.

Рассмотрим на примере, как это делается.

Пример 3

Вычтите из 2 9 дробь 1 15 .

Решение

Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45 . Для первой дроби необходим дополнительный множитель 5 , а для второй – 3 .

Подсчитаем: 2 9 = 2 · 5 9 · 5 = 10 45 1 15 = 1 · 3 15 · 3 = 3 45

У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 10 45 — 3 45 = 10 — 3 45 = 7 45

Краткая запись решения выглядит так: 2 9 — 1 15 = 10 45 — 3 45 = 10 — 3 45 = 7 45 .

Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.

Пример 4

Найдите разность 19 9 — 7 36 .

Решение

Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 76 9 и 7 36 .

Считаем ответ: 76 36 — 7 36 = 76 — 7 36 = 69 36

Результат можно сократить на 3 и получить 23 12 . Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 1 11 12 .

Краткая запись всего решения — 19 9 — 7 36 = 1 11 12 .

Как вычесть из обыкновенной дроби натуральное число

Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.

Пример 5

Найдите разность 83 21 – 3 .

Решение

3 – то же самое, что и 3 1 . Тогда можно подсчитать так: 83 21 — 3 = 20 21 .

Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.

Из дроби 83 21 при выделении целой части получится 83 21 = 3 20 21 .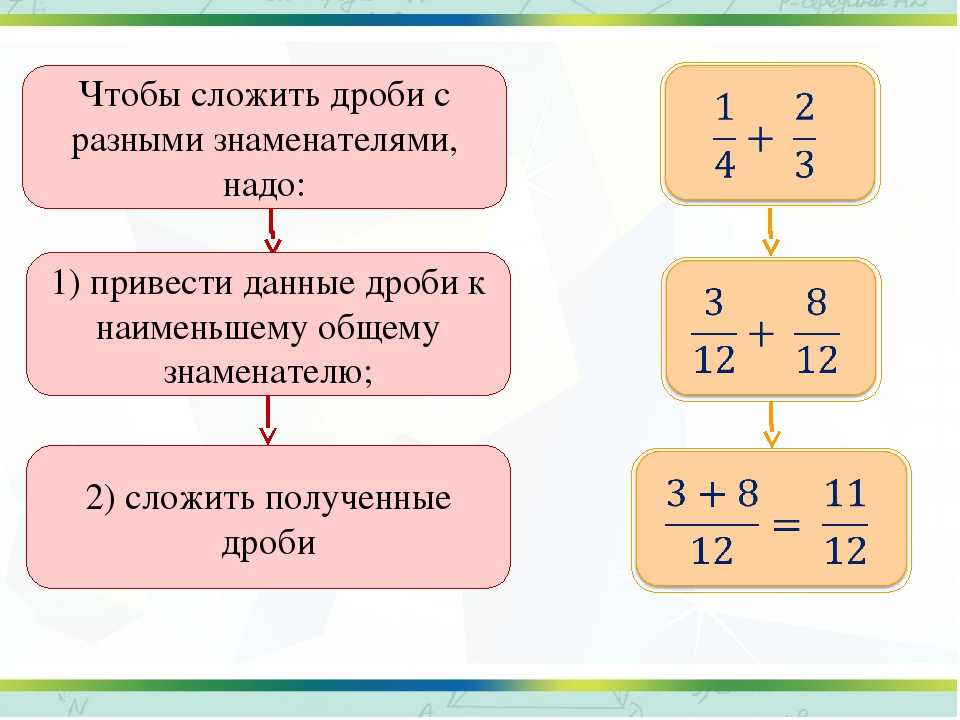

Теперь просто вычтем 3 из него: 3 20 21 — 3 = 20 21 .

Как вычесть обыкновенную дробь из натурального числа

Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.

Пример 6

Найдите разность: 7 — 5 3 .

Решение

Сделаем 7 дробью 7 1 . Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7 — 5 3 = 5 1 3 .

Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.

Определение 3

Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1 . После этого нужно вычесть нужную дробь из единицы и получить ответ.

Пример 7

Вычислите разность 1 065 — 13 62 .

Решение

Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065 — 13 62 = (1064 + 1) — 13 62

Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064 + 1 — 13 62 . Подсчитаем разность в скобках. Для этого единицу представим как дробь 1 1 .

Получается, что 1 — 13 62 = 1 1 — 13 62 = 62 62 — 13 62 = 49 62 .

Теперь вспомним про 1064 и сформулируем ответ: 1064 49 62 .

Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:

1065 — 13 62 = 1065 1 — 13 62 = 1065 · 62 1 · 62 — 13 62 = 66030 62 — 13 62 = = 66030 — 13 62 = 66017 62 = 1064 4 6

Ответ тот же, но подсчеты, очевидно, более громоздкие.

Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.

Пример 8

Вычислите разность 644 — 73 5 .

Решение

Вторая дробь – неправильная, и от нее надо отделить целую часть.

Теперь вычисляем аналогично предыдущему примеру: 630 — 3 5 = (629 + 1) — 3 5 = 629 + 1 — 3 5 = 629 + 2 5 = 629 2 5

Свойства вычитания при работе с дробями

Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.

Пример 9

Найдите разность 24 4 — 3 2 — 5 6 .

Решение

Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 25 4 — 3 2 , а потом отнимем от нее последнюю дробь:

25 4 — 3 2 = 24 4 — 6 4 = 19 4 19 4 — 5 6 = 57 12 — 10 12 = 47 12

Преобразуем ответ, выделив из него целую часть. Итог — 3 11 12 .

Краткая запись всего решения:

25 4 — 3 2 — 5 6 = 25 4 — 3 2 — 5 6 = 25 4 — 6 4 — 5 6 = = 19 4 — 5 6 = 57 12 — 10 12 = 47 12 = 3 11 12

Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.

Пример 10

Н айдите разность 98 + 17 20 — 5 + 3 5 .

Решение

Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98 + 17 20 — 5 + 3 5 = 98 + 17 20 — 5 — 3 5 = 98 — 5 + 17 20 — 3 5

Завершим расчеты: 98 — 5 + 17 20 — 3 5 = 93 + 17 20 — 12 20 = 93 + 5 20 = 93 + 1 4 = 93 1 4

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сложение и вычитание дробей с разными знаменателями | Преалгебра |

Результаты обучения

• Сложение или вычитание дробей с разными знаменателями
• Сложение или вычитание дробей, которые содержат переменные и имеют разные знаменатели

После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем складывать или вычитать их, добавляя или вычитая числители.

Сложение или вычитание дробей с разными знаменателями

1. Найдите ЖК-дисплей.
2. Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
3. Сложение или вычитание дробей.
4. Запишите результат в упрощенной форме.

Пример

Добавить:

12+13\frac{1}{2}+\frac{1}{3}21​+31​

Решение:

	12+13\frac{1}{2}+\frac{1}{3}21​+31​
Найти ЖК-дисплей 222 , 333 .
Преобразование в эквивалентные дроби с помощью ЖКИ 666 .	1⋅32⋅3+1⋅23⋅2\frac{1\cdot\color{red}{3}}{2\cdot\color{red}{3}} + \frac{1\cdot\color {red}{2}}{3\cdot\color{red}{2}}2⋅31⋅3​+3⋅21⋅2​
Упростите числители и знаменатели.	36+26\frac{3}{6}+\frac{2}{6}63​+62​
Доп.	56\фрак{5}{6}65​

Помните, всегда проверяйте, можно ли упростить ответ. Поскольку

555

и

666

не имеют общих делителей, дробь

56\frac{5}{6}65​

не может быть сокращена.

Попробуйте

#146262

Посмотрите следующее видео, чтобы увидеть больше примеров и пояснений о том, как сложить две дроби с разными знаменателями.

Пример

Вычесть:

12−(−14)\frac{1}{2}-\left(-\frac{1}{4}\right)21​−(−41​)

Показать решение

Решение:

The next line says, » data-label=»»>

	12−(−14)\frac{1}{2}-\left(-\frac{1}{4}\right)21​−(−41​)
Найдите ЖК-дисплей 222 и 444 .
Перепишите в виде эквивалентных дробей с помощью ЖК-дисплея 444 .	1⋅22⋅2−(−−14)\frac{1\cdot\color{red}{2}}{2\cdot\color{red}{2}} — (—\frac{1} {4})2⋅21⋅2​−(−−41​)
Упростите первую дробь.	24−(−14)\frac{2}{4}-\left(-\frac{1}{4}\right)42​−(−41​)
Вычесть.	2−(−1)4\frac{2-\left(-1\right)}{4}42−(−1)​
Упрощение.	34\фрак{3}{4}43​

У одной из дробей уже был наименьший общий знаменатель, поэтому нам оставалось только преобразовать другую дробь.

Попробуй

#146264

В следующем видео представлены еще два примера того, как вычесть две дроби с разными знаменателями.

Пример

Добавить:

712+518\frac{7}{12}+\frac{5}{18}127​+185​

Показать решение

Решение:

	712+518\frac{7}{12}+\frac{5}{18}127​+185​
Найдите ЖК-дисплей 121212 и 181818 .
Перепишите эквивалентные дроби с помощью ЖК-дисплея.	7⋅312⋅3+5⋅218⋅2\frac{7\cdot\color{red}{3}}{12\cdot\color{red}{3}} + \frac{5\cdot\color {red}{2}}{18\cdot\color{red}{2}}12⋅37⋅3​+18⋅25⋅2​
Упростите числители и знаменатели.	2136+1036\frac{21}{36}+\frac{10}{36}3621​+3610​
Доп.	3136\фрак{31}{36}3631​

Поскольку

313131

является простым числом, оно не имеет общих делителей с

363636

. Ответ упрощен.

Попробуйте

#146265

Когда мы используем свойство Equivalent Fractions, есть быстрый способ найти число, на которое нужно умножить, чтобы получить LCD. Запишите множители знаменателей и LCD так же, как вы это делали, чтобы найти LCD. «Недостающие» множители каждого знаменателя — это числа, которые вам нужны.

LCD,

363636

, имеет

222

Факторы

222

и

222

Факторы

333

.

Двенадцать имеет два множителя

222

, но только один из

333

— так что «отсутствует» один

333

. Мы умножили числитель и знаменатель

712\frac{7}{12}127​

на

333

, чтобы получить эквивалентную дробь со знаменателем

363636

.

Восемнадцать не хватает одного множителя

222

— таким образом, вы умножаете числитель и знаменатель

518\frac{5}{18}185​

на

222

1 дробь, эквивалентную 1 100261 90.

363636

. Мы будем применять этот метод при вычитании дробей в следующем примере.

Пример

Вычесть:

715−1924\frac{7}{15}-\frac{19}{24}157​−2419​

Показать решение

Решение:

The next line says » data-label=»»>

	715−1924\frac{7}{15}-\frac{19}{24}157​−2419​
Найдите ЖК-дисплей. 151515 «отсутствует» три множителя из 222 242424 «отсутствует» множитель из 555
Перепишите эквивалентные дроби с помощью ЖК-дисплея.	7⋅815⋅8−19⋅524⋅5\frac{7\cdot\color{red}{8}}{15\cdot\color{red}{8}} — \frac{19\cdot\color {red}{5}}{24\cdot\color{red}{5}}15⋅87⋅8​−24⋅519⋅5​
Упростите каждый числитель и знаменатель.	56120−95120\frac{56}{120}-\frac{95}{120}12056​−12095​
Вычесть.	−39120-\frac{39}{120}−12039​
Перепишите, указав общий делитель числа 333 .	−13⋅340⋅3-\frac{13\cdot 3}{40\cdot 3}−40⋅313⋅3​
Удалите общий множитель для упрощения.	−1340-\frac{13}{40}−4013​

Попробуйте

#146266

Пример

Добавить:

−1130+2342-\frac{11}{30}+\frac{23}{42}−3011​+4223​

Показать решение

Решение:

−14230+23 -\frac{11}{30}+\frac{23}{42}−3011​+4223​
Найдите ЖК-дисплей.
Перепишите эквивалентные дроби с помощью ЖК-дисплея.	−11⋅730⋅7+23⋅542⋅5-\frac{11\cdot\color{red}{7}}{30\cdot\color{red}{7}} + \frac{23\cdot \color{red}{5}}{42\cdot\color{red}{5}}−30⋅711⋅7​+42⋅523⋅5​
Упростите каждый числитель и знаменатель.	−77210+115210-\frac{77}{210}+\frac{115}{210}−21077​+210115​
Доп.	38210\фрак{38}{210}21038​
Перепишите, указав общий делитель числа 222 .	19⋅2105⋅2\frac{19\cdot 2}{105\cdot 2}105⋅219⋅2​
Удалите общий множитель для упрощения.	19105\фрак{19}{105}10519​

Попробуйте

#146267

В следующем примере одна из дробей имеет переменную в числителе. Выполняем те же действия, что и в случае, когда оба числителя являются числами.

Пример

Добавить:

35+x8\frac{3}{5}+\frac{x}{8}53​+8x​

Показать решение

Решение:

У дробей разные знаменатели.

	35+x8\frac{3}{5}+\frac{x}{8}53​+8x​
Найдите ЖК-дисплей.
Перепишите эквивалентные дроби с помощью ЖК-дисплея.	3⋅85⋅8+x⋅58⋅5\frac{3\cdot\color{red}{8}}{5\cdot\color{red}{8}} + \frac{x\cdot\color {red}{5}}{8\cdot\color{red}{5}}5⋅83⋅8​+8⋅5x⋅5​
Упростите числители и знаменатели.	2440+5×8\frac{24}{40}+\frac{5x}{8}4024​+85x​
Доп.	24+5×40\frac{24+5x}{40}4024+5x​

Мы не можем добавить

242424

и

5x5x5x

, поскольку они не похожи на термы, поэтому мы не можем еще больше упростить выражение.

Попробуйте

#146268

Посмотрите следующее видео, чтобы увидеть больше примеров сложения и вычитания дробей с разными знаменателями, которые содержат переменные.

Лицензии и атрибуты

Контент с лицензией CC, совместно используемый ранее

• Пример: добавление дробей с отличающимися знаменателями (базовый с моделью). Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Attribution
• Пример: вычитание дробей с разными знаменателями. Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Атрибуция
• Пример: Сложение и вычитание дробей, содержащих переменные. Автор : Джеймс Соуза (mathispower4u.com). Лицензия : CC BY: Атрибуция

Лицензионный контент CC, Конкретная атрибуция

• Преалгебра. Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии.0594
  

  Учащиеся должны продемонстрировать понимание одинаковых и разных знаменателей, чтобы уметь складывать и вычитать дроби. Когда дроби имеют , как знаменатели , они имеют тот же самый знаменатель. Когда дроби имеют , а знаменатели не равны , их знаменатели различны. Знаменатели должны быть одинаковыми или общими, чтобы складывать или вычитать дроби.

   Дроби с одинаковыми знаменателями разбиваются на одинаковое количество частей, поэтому их части имеют одинаковый размер и их можно складывать или вычитать.
  Например:

  В приведенном выше примере детали можно легко складывать вместе, поскольку все они имеют одинаковый размер. Как видите, знаменатели не складываются. На самом деле возникает вопрос: Одна пятая плюс две пятых равно количеству пятых? Ответом на этот вопрос будет три пятых , поэтому знаменатель не изменится.

  
  

  Складывать дроби с разными знаменателями, к сожалению, не так просто. При сложении дробей с разными знаменателями необходимо, чтобы знаменатели были одинаковыми. Мы делаем это, находя LCD или Наименьший общий знаменатель . Наименьший общий знаменатель – это наименьшее общее кратное знаменателей. В приведенном ниже примере ЖК-дисплей равен 6,
  . Затем две дроби складываются в пропорции , чтобы найти эквивалентные дроби с одинаковыми знаменателями. Чтобы найти эквивалентную дробь, нужно умножить числитель и знаменатель на одно и то же. В этом случае одна половина умножается на 3. Затем одна треть умножается на 2. Получаются эквивалентные дроби три шестых и две шестых. Это значительно упрощает их добавление. Что делает нашу сумму пятью шестыми.

  Понедельник: ЧЕРНЫЙ
  Цели обучения: Я могу решать реальные задачи на сложение и вычитание дробей с разными знаменателями.
  (5.NF-1. Сложите дроби с разными знаменателями)
  (5.NF-2. Решить текстовые задачи на сложение дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями)
  Критерии успеха:   Я могу складывать дроби с разными знаменателями, заменяя заданную дробь эквивалентными дробями.
  Я могу решать текстовые задачи на сложение дробей с одинаковыми/непохожими знаменателями, используя визуальную модель дроби.
  Процедуры:

  ·         Продемонстрируйте сложение дробей с одинаковыми знаменателями, используя модели.

  ·         Используйте модели для обсуждения сложения дробей с разными знаменателями.

  o   Вопросы:

  §  В чем разница между сложением дробей с разными/одинаковыми знаменателями.

  §  Что сложнее складывать, одинаковые или разные знаменатели?

  §  Как вы думаете, какое решение можно использовать, чтобы упростить сложение дробей с разными знаменателями?

  ·         Используйте изображения/модели для добавления дробей с одинаковыми/непохожими знаменателями в их группу.

  ·         Проверьте практические вопросы в группе.

  FLEX: учащиеся выполняют тест «Простые решения №7». Завершите Урок 29 после прохождения викторины «Простые решения №7».

  Оценка: Анкетирование, групповая работа, наблюдение за разговорами учащихся. Викторина для оценки сохранения учащимися предыдущих стандартов.
  Вторник: ЗОЛОТО
  Цели обучения: Я могу решать реальные задачи на сложение и вычитание дробей с разными знаменателями.
  (5.NF-1. Складывать и вычитать дроби с разными знаменателями)
  (5.NF-2. Решить текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями)
  Критерии успеха: Я могу складывать и вычитать дроби с разными знаменателями, заменяя данную дробь эквивалентными дробями.
  Я могу решать текстовые задачи на сложение дробей с одинаковыми/непохожими знаменателями, используя визуальную модель дроби.
  Процедуры:  

  ·         Просмотрите сложение дробей с одинаковыми знаменателями и сложность сложения дробей с разными знаменателями.

  ·         Продемонстрируйте использование ЖК-дисплея и эквивалентных дробей, чтобы складывать дроби с разными знаменателями. (с использованием моделей/числовых представлений)

  ·         Учащиеся отвечают на практические вопросы вместе с партнером.

  ·         Обсудите практические вопросы всем классом. Учащиеся демонстрируют, как они справились с каждой задачей.

  FLEX: учащиеся выполняют тест «Простые решения №7». Завершите Урок 29 после прохождения викторины «Простые решения №7».

  Оценка: Практика с партнером, наблюдение за студентами. Самооценка с партнером на красной, желтой, зеленой доске. Викторина для оценки сохранения учащимися предыдущих стандартов.
  Среда: ЧЕРНЫЙ
  Цели обучения: Я могу решать реальные задачи на сложение и вычитание дробей с разными знаменателями.
  (5.NF-1. Складывать и вычитать дроби с разными знаменателями)
  (5.NF-2. Решить текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями)
  Критерии успеха: Я могу складывать и вычитать дроби с разными знаменателями, заменяя данную дробь эквивалентными дробями.
  Я могу решать текстовые задачи на сложение дробей с одинаковыми/непохожими знаменателями, используя визуальную модель дроби.
  Процедуры:  

  ·         ДАМП ДАННЫХ: учащиеся пишут все, что могут вспомнить, о сложении дробей с разными знаменателями.

  o   Поделитесь/объясните ДАМП ДАННЫХ с партнером.

  o   Создайте DATA DUMP как класс.

  ·         Учащиеся самостоятельно решают 5 практических задач.

  o   Вызов учащихся, которые вчера поставили свои инициалы на «красный» или «желтый» на красной, желтой, зеленой доске, для индивидуального обучения/вмешательства.

  ·         Вместе решите практические задачи всем классом. Учащиеся демонстрируют работу на доске.

                 FLEX: Компенсация для учащихся, пропустивших контрольную оценку Discovery Education.

  Пройдите Урок 29. Учащиеся завершат Урок 30. Попрактикуйтесь в математических фактах (5 минут). Учащиеся решают предыдущую математическую задачу OAA с партнером, используя контрольный список для решения задач.

  Вызов отдельных учащихся на основе результатов Discovery Ed для отработки задач в тех направлениях, в которых учащиеся испытывают трудности.

  Оценка: Дамп данных — самооценка усвоения материала, практические задачи демонстрируют понимание учащимися. Индивидуальная конференция для оценки понимания учащимися.
  Четверг: ЗОЛОТО
  Цели обучения: Я могу решать реальные задачи на сложение и вычитание дробей с разными знаменателями.
  (5.NF-1. Складывать и вычитать дроби с разными знаменателями)
  (5.NF-2. Решить текстовые задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями)
  Критерии успеха: Я могу складывать и вычитать дроби с разными знаменателями, заменяя данную дробь эквивалентными дробями.
  Я могу решать текстовые задачи на сложение дробей с одинаковыми/непохожими знаменателями, используя визуальную модель дроби.
  Процедуры:  

  ·         Напишите абзац, объясняющий, как складывать дроби с разными знаменателями.

  ·         Поделитесь/сравните абзац с партнером.

  ·         Студенты разделены на 3 группы (группы поддержки)

  o   Учащимся предоставляется работа на уровне: группе вмешательства предоставляется дополнительная поддержка/инструкция.

  FLEX: компенсация для учащихся, пропустивших контрольную оценку Discovery Education.

  Пройдите Урок 29. Учащиеся завершат Урок 30. Попрактикуйтесь в математических фактах (5 минут). Учащиеся решают предыдущую математическую задачу OAA с партнером, используя контрольный список для решения задач. Привлекайте отдельных учащихся на основе результатов Discovery Ed, чтобы отрабатывать задачи из тех направлений, с которыми учащиеся борются.

  Оценка:   Уровневая работа для оценки уровня разочарования учащихся, параграф для оценки знаний учащихся о стратегии LCD.
  Пятница: ДЕНЬ НАДЕЖДЫ. НЕТ КЛАССОВ СЕГОДНЯ
  

  Одинаковые и разные Знаменатели ｜ Hatsudy

  При вычислении дробей мы часто делаем сложение и вычитание. Когда дело доходит до вычисления дробей, сложение и вычитание являются самыми трудными. Они сложнее, чем умножение.

  Способ сложения и вычитания дробей отличается от обычного. Также метод расчета меняется в зависимости от того, совпадают знаменатели или нет. Если знаменатели разные, нам нужно найти общий знаменатель, чтобы знаменатели были одинаковыми.

  Итак, как складывать и вычитать дроби?

  Как при сложении, так и при вычитании дробей знаменатели должны быть одинаковыми. Итак, давайте посмотрим, как складывать и вычитать дроби. 9

  • 1.1 Вычитание, когда знаменатели одинаковы то же самое и выполнение сложения и вычитания
• 3 Сложение и вычитание смешанных дробей: перенос и заимствование
• 4 Какой ответ лучше, неправильные дроби или смешанные дроби?
• 5 Как складывать и вычитать дроби

Сложение с одинаковым знаменателем

При сложении дробей не добавляйте и числитель, и знаменатель. Например, следующий расчет неверен.

• $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}$

Почему этот расчет неверен? $\displaystyle\frac{1}{2}$ – это число, делящее 1 пополам, а $\displaystyle\frac{1}{3}$ – это число, которое делит 1 на три равные части.

С другой стороны, $\displaystyle\frac{2}{5}$ — это число, полученное путем деления 1 на пять равных частей и последующего сложения двух из них. Следовательно, вычисление $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}=\displaystyle\frac{2}{5}$ меньше реального ответа.

Глядя на рисунок, мы видим, что этот расчет явно неверен.

Почему мы совершаем такую ​​ошибку? Причина в том, что мы добавили знаменатель. Как было сказано выше, знаменатель — это число, которое делит 1 на равные части. Таким образом, вы не должны добавлять знаменатели. Когда знаменатели одинаковы, знаменатель не менять.

Для дробей с одинаковым знаменателем не меняйте знаменатель, а просто добавляйте числитель. Например, $\displaystyle\frac{3}{4}$ содержит три $\displaystyle\frac{1}{4}$. Кроме того, в $\displaystyle\frac{2}{4}$ есть два $\displaystyle\frac{1}{4}$. Поэтому имеем следующее.

• $\displaystyle\frac{3}{4}+\displaystyle\frac{2}{4}=\displaystyle\frac{5}{4}$

Как видите, знаменатель имеет не изменился. При сложении дробей меняется только число числителя. Знаменатель имеет свойство того, сколько в нем равных частей числа 1. Кроме того, мы не должны изменять природу числа в дополнение. Поэтому знаменатель не меняем, только числитель.

Вычитание, когда знаменатели одинаковы

С другой стороны, как мы можем вычитать дроби? Как и раньше, рассмотрим случай, когда знаменатели совпадают.

Принцип тот же, что и при добавлении. Знаменатель представляет свойство дроби. Поэтому при вычитании число в знаменателе не меняется. Вместо этого вы должны вычесть число из числителя. Например, мы можем рассчитать следующим образом.

• $\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}$

Несложно понять вычитание дробей, если умеешь складывать. При вычитании дробей с одинаковым знаменателем знаменатель не менять; только числитель вычесть.

Если знаменатели разные, вы не можете складывать или вычитать

С другой стороны, если знаменатели разные, как мы можем складывать или вычитать? Как упоминалось выше, знаменатель представляет собой свойство дроби. Кроме того, если числа имеют разные свойства, их нельзя ни сложить, ни вычесть. Например, как мы вычисляем следующее?

• $\displaystyle\frac{3}{4}+\displaystyle\frac{1}{3}$

С этими дробями нельзя выполнять сложение. Поскольку знаменатели разные, однозначного ответа получить невозможно.

Итак, приравняем знаменатели. Когда знаменатели различны, свойства чисел различны, поэтому вы не можете складывать или вычитать. С другой стороны, если знаменатели совпадают, вы можете складывать или вычитать. При сложении или вычитании дробей знаменатели должны совпадать.

Приведение знаменателей дробей к одному и тому же называется нахождением общего знаменателя. Итак, давайте найдем общий знаменатель.

Нахождение общего знаменателя, чтобы сделать знаменатели одинаковыми и выполнить сложение и вычитание

Чтобы найти общий знаменатель в дробях, используйте общие кратные. У двух дробей проверьте знаменатели. Например, как мы вычисляем следующие дроби?

• $\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}$

Чтобы сделать это вычисление, давайте найдем общий знаменатель. Проверяя знаменатели, числа равны 2 и 3, а наименьшее общее кратное 2 и 3 равно 6. Итак, мы находим наименьший общий знаменатель и устанавливаем знаменатели равными 6 следующим образом.

• $\displaystyle\frac{1}{2}=\displaystyle\frac{1×3}{2×3}=\displaystyle\frac{3}{6}$
• $\displaystyle\frac{1 }{3}=\displaystyle\frac{1×2}{3×2}=\displaystyle\frac{2}{6}$

Таким образом, мы можем изменить $\displaystyle\frac{1}{2} $ в $\displaystyle\frac{3}{6}$ и $\displaystyle\frac{1}{3}$ в $\displaystyle\frac{2}{6}$. Поскольку знаменатели одинаковы, мы можем сделать сложение. Итак, давайте сложим дроби следующим образом.

• $\displaystyle\frac{3}{6}+\displaystyle\frac{2}{6}=\displaystyle\frac{5}{6}$

Тот же метод используется для вычитания. Например, в следующем вычислении давайте найдем общий знаменатель так же, как и раньше.

• $\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}$

Как объяснялось ранее, $\displaystyle\frac{1}{2}$ равно $\displaystyle\ дробь{3}{6}$. Кроме того, $\displaystyle\frac{1}{3}$ равно $\displaystyle\frac{2}{6}$. Следовательно, мы можем изменить уравнение на следующее.

• $\displaystyle\frac{3}{6}-\displaystyle\frac{2}{6}=\displaystyle\frac{1}{6}$

Как при сложении, так и при вычитании знаменатели должны быть то же самое для выполнения расчета. Поэтому, если знаменатели разные, обязательно найдите общий знаменатель.

Сложение и вычитание смешанных дробей: перенос и заимствование

До сих пор мы использовали правильные дроби и неправильные дроби.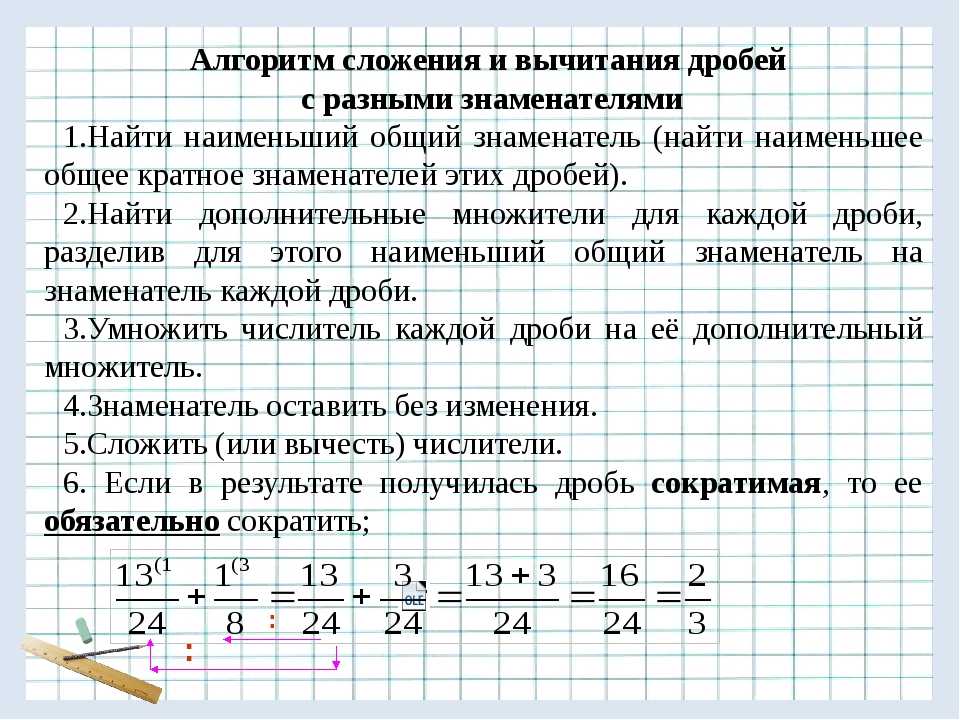 Метод расчета тот же, что и для смешанных фракций. Если знаменатели совпадают, вы можете добавить или вычесть. Например, как мы вычисляем следующее?

• $1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}$

$1\displaystyle\frac{3}{4}$ означает $1+\displaystyle\frac{ 3}{4}$. А $2\displaystyle\frac{2}{4}$ означает $2+\displaystyle\frac{2}{4}$. Итак, давайте разделим целые числа и дроби и выполним сложение. Результат следующий.

• $1\displaystyle\frac{3}{4}+2\displaystyle\frac{2}{4}=3\displaystyle\frac{5}{4}$

Таким образом, мы можем вычислить смешанные дроби . Обратите внимание, что число в числителе $3\displaystyle\frac{5}{4}$ больше, чем в знаменателе. Следовательно, нам нужно уменьшить число в числителе. $3\displaystyle\frac{5}{4}$ становится следующим.

• $3\displaystyle\frac{5}{4}=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$

Важно отметить, что $\ displaystyle\frac{4}{4}=1$. Поэтому мы можем заменить $3\displaystyle\frac{5}{4}$ на $4\displaystyle\frac{1}{4}$. Чтобы увидеть это в деталях, расчет выглядит следующим образом.

$3\displaystyle\frac{5}{4}$

$=3+\displaystyle\frac{4}{4}+\displaystyle\frac{1}{4}$

$=3+1+ \displaystyle\frac{1}{4}$

$=4\displaystyle\frac{1}{4}$

Таким образом, в смешанных дробях вам, возможно, придется рассчитывать перенос.

— Вычитание смешанных дробей

С другой стороны, как мы вычитаем смешанные дроби? В качестве примера рассчитаем $3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}$. Поскольку смешанные дроби содержат целые числа, отделим целые числа от дробей. Результат следующий.

• $3\displaystyle\frac{3}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{1}{4}$

Вычисляя целые числа, получаем $3-1=2$. Следовательно, целая часть смешанной дроби равна 2. Также имеем $\displaystyle\frac{3}{4}-\displaystyle\frac{2}{4}=\displaystyle\frac{1}{4}$. Следовательно, дробная часть этой смешанной дроби равна $\displaystyle\frac{1}{4}$.

С другой стороны, как рассчитать следующее?

• $3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}$

При вычитании дробей мы не можем вычислить $\displaystyle\frac{1}{4}-\ displaystyle\frac{2}{4}$. Итак, давайте позаимствуем число из целого числа. В смешанных дробях иногда приходится брать взаймы для расчета. Другими словами, мы меняем $3\displaystyle\frac{1}{4}$ на следующее.

$3\displaystyle\frac{1}{4}$

$=2+1+\displaystyle\frac{1}{4}$

$=2+\displaystyle\frac{4}{4}+ \displaystyle\frac{1}{4}$

$=2\displaystyle\frac{5}{4}$

В этом случае мы можем вычесть дроби. Это происходит следующим образом.

• $3\displaystyle\frac{1}{4}-1\displaystyle\frac{2}{4}=2\displaystyle\frac{5}{4}-1\displaystyle\frac{2}{4} =1\displaystyle\frac{3}{4}$

Если вы не можете вычесть, одолжите целое число для вычисления.

Какой ответ лучше: неправильные дроби или смешанные дроби?

Какой ответ лучше для дробей, неправильных дробей или смешанных дробей? Ответ на этот вопрос однозначен: считать следует с использованием неправильных дробей. Если ответ не указан, вместо смешанных дробей следует писать неправильные дроби.

Причина в том, что смешанные дроби используются только в начальной школе. В высшей математике, такой как математика в средней школе, средней школе и колледже, смешанные дроби никогда не используются. В высшей математике вы всегда будете использовать неправильные дроби.

Хорошо знать смешанные дроби как знания, но они редко используются в реальной жизни.

Математика используется во многих областях, таких как программирование, архитектура и космос. Хотя мы часто используем неправильные дроби, мы никогда не используем смешанные дроби. Поэтому попробуйте считать с неправильными дробями вместо смешанных дробей.

Как складывать и вычитать дроби

Дроби трудно вычислять, пока вы к ним не привыкнете. Особенно, когда дело доходит до сложения и вычитания, вы должны научиться делать это. Чтобы выполнять сложение и вычитание, знаменатели должны быть одинаковыми.

Кроме того, знаменатель не меняется при сложении или вычитании.