Вычитание ⭐ дробей с разными знаменателями: правило, способы решения

Что такое дробь? Какие бывают дроби

Определение 1

Дробь является одним из вариантов записи числа в математике.

Дробь бывает:

• обыкновенная, как 12  или ab;
• десятичная, например, 0,5.

В простой записи дроби над чертой записывают делимое, то есть числитель. Под чертой расположен делитель, то есть знаменатель. Черта в дроби, разделяющая делитель и знаменатель, обозначает, что необходимо сделать, то есть выполнить деление.

Пример 1

В качестве примера можно рассмотреть следующее выражение:

7÷8=78

В левой части равенства 7 является делимым, а 8 — делителем. В правой части уравнения записана дробь. Здесь 7 играет роль числителя, а 8 представляет собой знаменатель.

Основная классификация дробей:

1. Числовые дроби, в состав которых входят числа, к примеру, 59, (1,5-0,2)15.
2. Алгебраические дроби, состоящие из переменных, например(x+y)(x-y).

Значение алгебраических дробей определяется значением букв в выражении.

Определение 2

Правильная дробь — это дробь с числителем, который по значению меньше, чем знаменатель.

Пример 2

В качестве примеров правильных дробей можно привести следующие записи:

37

3145

Определение 3

Неправильная дробь — это дробь с числителем, который больше, либо равен знаменателю.

Пример 3

Пример неправильной дроби:

214

Данное число является смешанным. Читать его необходимо таким образом: пять целых одна четвертая. Запись числа имеет следующий вид: 514.

Использование свойств вычитания при вычитании дробей

Свойство дробей:

1. В том случае, когда делитель дроби является нулем, такая дробь не имеет значения.
2. Дробь равна нулю при условии, что числитель обладает нулевым значением, а знаменатель не равен нулю.
3. Дроби ab и cd равны друг другу, если a×d=b×c.
4. В процессе деления или умножения числителя и знаменателя дроби на одно и то же натуральное число получается равная ей дробь.

Определение 4

Вычитание является действием в арифметике, когда одно число отнимают от другого числа.

При вычитании справедливо использовать следующие свойства чисел:

• при вычитании суммы из числа из него допускается вычесть одно слагаемое, а затем результат уменьшить на значение второго слагаемого:

a — (b + c) = (a — b) — c,

a — (b + c) = (a — с) — b.

• скобки в выражении ((a — b) – c) не имеют смыслового значения, допустимо исключить их из выражения:

(a — b) — c = a — b — c.

• для вычитания числа из суммы необходимо воспользоваться рациональным способом решения, то есть вычесть его из одного слагаемого, а результат увеличить на значение оставшегося:

(a + b) — c = (a — c) + b, если a > c или а = с,

(a + b) — c = (b — c) + a, если b > c или b = с.

• когда из числа, в том числе, отрицательного, вычитают нуль, получается то же самое число:

a — 0 = a.

• при вычитании числа из аналогичного числа получается нуль:

a — a = 0.

Вычитание дробей с одинаковыми знаменателями

Правило 1

При вычитании различных дробей с одинаковыми знаменателями требуется из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить без изменений.

Таким образом, чтобы из одной дроби вычесть дробь с аналогичным знаменателем, необходимо вычитать числители, а одинаковые знаменатели оставить прежними. Используя буквы, можно представить наглядную запись этого правила:

ac-bc=a-bc

Пример 4

В качестве примеров можно решить следующие выражения:

79-59

79-59=7-59=29

1517-317

1517-317=15-317=1217

2735-1135

2735-1135=27-1135=1635

4863-2563

4863-2563=48-2563=2363

Вычитание смешанных дробей с одинаковыми знаменателями 

Правило 2

При вычитании смешанных дробей требуется выполнить отдельно вычитание их целых частей и отдельно вычитание их дробных частей.

В том случае, когда дробная часть уменьшаемого меньше, чем дробная часть вычитаемого, следует выполнить следующие действия:

• сначала нужно занять 1 у целой части;
• единицу необходимо представить, как дробь с числителем, равным знаменателю;
• выполнить сложение этой дроби и дробной части уменьшаемого.

Используя буквы, данное правило вычитания смешанных дробей можно записать с помощью формулы:

amc-bnc=(a-b)+m-nc

При m<n имеем:

amc-bnc=(a-1)m+cc-bnc=(a-1-b)+m+c-nc

Пример 5

На нескольких примерах можно рассмотреть правило вычитания смешанных дробей:

845-235

845-235=(8-2)+4-35=615

Допустимо записать менее сложное решение:

845-235=64-35=615

527-167

527-167=42+77-167=497-167=39-67=337

1529-649

1529-649=142+99-649=14119-649=811-49=879

17323-21023

17323-21023=163+2323-21023=162623-21023=1426-1023=141623

54227-20927

54227-20927=532+2727-20927=532927-20927=3329-927=332027

Вычитание дробей с разными знаменателями

Правило 3

Вычитание дробей, которые обладают разными знаменателями, выполняют путем приведения их к общему знаменателю и вычисления разности числителей.

Применение озвученного правила на практике можно рассмотреть на примере дробей, разность которых требуется определить:

29

115

В процессе решения задачи можно использовать следующий алгоритм:

1. В связи с тем, что знаменатели не одинаковые, нужно определить самое маленькое общее кратное (НОК), чтобы найти единый делитель. Следует записать в колонку числа, составляющие в сумме значения делителей. Затем необходимо перемножить полученные значения и вычислить НОК.

НОК(9,15)=3×3×5=45

1. На следующем этапе следует определить дополнительные множители. При этом НОК нужно поделить на каждый из знаменателей.

459=5

4515=3

1. Числа, которые были получены в результате действий, требуется умножить на соответствующие дроби:

29=2×59×5=1045

115=1×315×3=345

1. В завершении алгоритма можно выполнить вычитание заданных чисел:

1045-345=10-345=745

29-115=745

Как вычесть из обыкновенной дроби натуральное число

При вычитании натурального числа из обыкновенной дроби следует выполнить ряд действий:

• перевод натурального числа в дробь;
• перевод всех элементов выражения к единому знаменателю;
• определение разности.

Пример 6

Рассмотреть принцип вычитания натурального числа из обыкновенной дроби можно на примере:

8321–3

Запишем:

3=31

Таким образом:

8321-31=8321-6321=2021

В качестве альтернативного варианта решения этого примера можно записать 8321, как смешанную дробь. В процессе необходимо разделить делитель на делимое:

8321=3×2021

После вычитания получим:

3×2021–3=2021

Как вычесть обыкновенную дробь из натурального числа

Уменьшить обыкновенную дробь на натуральное число можно путем перевода данного действия к вычитанию обыкновенных дробей. Принцип решения подобной задачи можно рассмотреть на конкретном примере:

3-67

В первую очередь следует записать натуральное число, как смешанное. Для этого нужно занять единицу и перевести ее в неправильную дробь с тем же знаменателем, что у вычитаемой:

3=2×77

3=2×1

3=2×77

Таким образом:

3-67=2×77-67=2×17

Ответ прозвучит таким образом: две целых одна седьмая.

Как из единицы вычесть дробь

Если по условиям задачи из единицы нужно вычесть дробь, то в этом случае следует выполнить ряд последовательных действий:

1. Перевод единицы в дробь с числителем и знаменателем, которые будут равны знаменателю вычитаемого;
2. Вычитание дробей, которые обладают аналогичными знаменателями.

Используя буквы, можно записать алгоритм:

1-ab=bb-ab=b-ab

Пример 7

1-38=88-58=8-58=38

Если найти сумму числителя разности и числителя вычитаемого, получится в результате знаменатель вычитаемого. Таким образом, при вычитании дроби из единицы итогом является  дробь с числителем, который равен разности знаменателя и числителя вычитаемой дроби, а знаменатель — остается таким же. На основании этого заключения можно упростить вычитание дроби из единицы, то есть:

1-ab=b-ab

Поэтому:

1-718=1818-718=18-718=1118

1-153200=200200-153200=200-153200=47200

1-45=5-45=15

1-316=16-316=1316

1-2531=31-2531=631

Сокращенная запись имеет вид:

1-29=79

1-911=211

1-2150=2950

Вычитание смешанного числа из целого числа

Операция вычитания из целого числа смешанного числа (смешанной дроби) выполняется по принципу, аналогичному вычитанию дроби из целого числа. При уменьшении целого числа на значение смешанного следует выполнить несколько действий:

1. Перевод целого числа в смешанную дробь. Нужно занять единицу у целой части и перевести ее в дробь с числителем и знаменателем, которые аналогичны знаменателю дробной части вычитаемого.
2. Вычитание смешанных чисел. Вычитание вычитаемого из уменьшаемого: отдельно — целые части, отдельно — дробные.

Используя буквы, можно записать правило вычитания смешанного числа из целого:

a-bmc=(a-1)cc-bmc=(a-1-b)c-mc

Пример 8

8-125

8-125=755-125=65-25=635

11-378

11-378=1088-378=78-78=718

33-20211

33-20211=321111-20211=1211-211=12911

40-9750

40-9750=395050-9750=3050-750=304350

28-10514

28-10514=271414-10514=1714-514=17914

Вычитание смешанных чисел

Алгоритм действий при вычитании одного смешанного числа из другого:

1. Приведение дробных частей к самому маленькому единому знаменателю.
2. В том случае, когда дробная часть уменьшаемого меньше, чем дробная часть вычитаемого, следует перевести ее в вид неправильной дроби путем уменьшения на единицу целой части. При этом числитель уменьшаемого увеличивают на значение знаменателя.
3. Отдельно вычесть целые части и отдельно вычесть дробные части.
4. Выполнить проверку полученной дроби на возможность сокращения.

Пример 9

7512-329

716-234

10-347

379-1518

В первую очередь при вычитании смешанных чисел следует найти самый маленький единый знаменатель дробных частей:

12 на 9 не делится;

12∙2=24 на 9 не делится;

12∙3=36 на 9 делится.

Таким образом, минимальный единый знаменатель этих дробей соответствует 36. Для поиска дополнительного множителя к каждой из дробей необходимо новый знаменатель разделить на старый знаменатель. Отдельно следует вычитать целые части, отдельно — дробные. В итоге получится дробная часть, которая является правильной и несокращаемой. Можно сделать вывод о том, что ответ является окончательным.

71\26-23\34=52-912=42+12-912=4512

Для вычитания смешанных чисел необходимо найти минимальный единый знаменатель для дробных частей:

6 на 4 не делится;

6∙2=12 на 4 делится.

Таким образом, 12 является минимальным единым знаменателем. Дробная часть уменьшаемого меньше по сравнению с дробной частью вычитаемого. Нужно позаимствовать единицу у целой части. В связи с тем, что знаменатель соответствует 12, единицу допустимо расписать, как 1212, то есть к числителю дробной части уменьшаемого следует прибавить знаменатель. Итоговым результатом будет дробная часть в виде правильной несократимой дроби.

10-347=977-347=637

В том случае, когда в процессе вычитания смешанных чисел в уменьшаемом нет дробной части, следует занять единицу у целой части. В связи с тем, что значение знаменателя вычитаемого соответствует 7, единицу можно представить в виде 77. В результате получена дробь, которая является правильной и не подлежит сокращению.

37\29-15\118=214-518=2918=212

Начать вычитание смешанных чисел целесообразно с определения минимального единого знаменателя. В связи с тем, что 18 делится на 9, то 18 является самым маленьким общим знаменателем. Дробь, которая получилась в результате, сокращается на 9.

Как перевести смешанную дробь в обыкновенную

Смешанная дробь обладает целыми числами:

113

В обычной дроби знаменатель больше, чем числитель:

13

В действительности невозможно перевести обычную дробь в смешанную дробь и наоборот.

Неправильная дробь, в которой числитель больше по сравнению со знаменателем, имеет вид:

43

Неправильную дробь можно записать в виде смешанной дроби. Возможен и обратный перевод.

К примеру, имеется некая неправильная дробь:

173

В результате деления 17 на 3 получится 5 с каким-то остатком. Выяснять значение остатка не обязательно, так как для последующих расчетов необходимо только целое число. Затем нужно 5 умножить на 3. Из 17 следует отнять полученный результат 15. В итоге получится 2, что позволит записать 23. В результате получится 5 целых 23:

173=523

Смешанная дробь может быть преобразована в неправильную дробь. Для этого следует выполнить действия в обратном порядке:

(5×3+2)3=173

Таким образом:

523=173

примеры методик операций с дробными выражениями и решения задач

Математика

12. 11.21

14 мин.

Ученики изучают на уроках математики в 5 классе смешанные дроби и примеры работы с ними. Однако не всегда усваивают теоретический материал, а на практике не могут решать задачи с обыкновенными дробными величинами. Специалисты нашли выход с этой ситуации, предложив специальные алгоритмы для оптимизации вычислений без ошибок. Для их изучения необходимы определенные базовые знания.

Оглавление:

• Общие сведения
• Конвертация смешанного числа
• Приведение к единому знаменателю
• Вычитание и суммирование
• Произведение и частное
• Возведение в степень и корень

Общие сведения

Запись чисел не всегда выполняется с применением целых значений. Иногда величина может выражаться обыкновенными или десятичными дробными выражениями. Первая может преобразовываться во вторую. Допустима также и обратная операция.

Следует отметить, что обыкновенные дроби бывают трех типов:

1. Правильными.
2. Неправильными.
3. Смешанными.

Для объяснения различия между ними необходимо записать величину в математической форме «w/v». В первом случае, когда дробное выражение является правильным, его числитель «w» меньше знаменателя «v» (w<v). Если оно считается неправильным, то величина числителя «v» всегда будет больше, чем «w», т. е. v>w. При этом дробное число нужно «превратить» в смешанное.

Смешанной называется обыкновенная дробь, состоящая из целого компонента и дробной части. Она имеет такой вид: 3[2/7]. Следует отметить, что любое дробное тождество обыкновенного вида может быть записано в виде десятичного. Для этого достаточно просто разделить числитель на знаменатель, т. е. ½=0,5.

Кроме того, над смешанными числами можно совершать любые арифметические операции.

К последним относятся следующие:

1. «*» — произведение. (1/n)» — извлечение корня.

Для совершения любой операции рекомендуется преобразовать смешанное число в неправильное дробное выражение. Далее необходимо разобрать подробно методику выполнения этой операции.

Конвертация смешанного числа

Конвертация смешанной дроби в обыкновенную применяется для оптимизации вычислений при выполнении арифметических операций. Она выполняется по следующей методике:

1. Записать величину: С[w/v].
2. Перемножить знаменатель и целую часть, а затем прибавить числитель: (vC+w)/v.
3. Выполнить математические операции по расчету знаменателя, записав окончательный результат.

На практике необходимо разобрать реализацию методики в математике для 5 класса на примере смешанной дроби «3[2/7]». Конвертация выглядит таким образом:

1. 3[2/7].
2. (7*3+2)/7.
3. 23/7.

Однако существует обратная операция по преобразованию неправильного дробного числа в смешанное. Она применяется для решения заданий, в которых нужно записать окончательный ответ. Оставлять его в виде неправильной дроби не рекомендуется, т. к. за это могут снизить оценку. Алгоритм имеет следующий вид:

1. Записать искомое число.
2. Разделить числитель на знаменатель, выделив целую часть.
3. Преобразовать числитель, воспользовавшись формулой: w’=w-vС.
4. Записать результат: w’/v.

Однако при изучении конкретного алгоритма рекомендуется разобрать его на примере. Для этого нужно взять число «23/7», и представить его в виде неправильного дробного тождества:

1. 23/7.
2. С=23/7=3.
3. w’=w-Cv=23−3*7=2/7
4. 3[2/7].

Используя алгоритмы преобразования смешанного числа, можно сравнивать, приводить к общему знаменателю, делить, перемножать, складывать и вычитать дроби, а также возводить в степень и извлекать корень.

Приведение к единому знаменателю

Операцию приведения смешанных чисел к общему знаменателю рекомендуется выполнять только при сравнении, сложении и вычитании.

Существует три способа выполнения этого действия, перед которым обязательно следует конвертировать смешанное число в неправильную дробь.

Методика зависит от знаменателей дробей (w/v и u/z):

1. v/z — целое число, при условии, что v>z.
2. Знаменатели v и z cодержат общие множители.
3. Невыполнение первого и второго правил.

В первом случае приводить дроби к единому знаменателю очень просто. Для этого нужно записать общее значение «v», а над числителем второго выражения — коэффициент «v/z». Выполнить арифметические преобразования, и написать искомое дробное тождество. Математическая форма имеет следующий вид: [w+u*v/z]/v.

Если знаменатели содержат общие множители, то нужно найти наименьшее общее кратное (НОК). Для этого необходимо разложить их на простые множители. Далее требуется выделить один или совокупность общих элементов. Затем перемножить их с сомножителями, которые не повторяются. Полученный результат и будет общим знаменателем.

Однако бывает случай, когда первые два метода применить невозможно. Для получения единого знаменателя достаточно перемножить v и z между собой, записав коэффициенты над числителями «крест-накрест». Математическая запись операции сложения имеет следующий вид: [wz+vu]/(vz). Следует отметить, что вместо суммирования дробных величин, значения можно сравнивать или вычитать друг с друга.

Изучив вспомогательные операции над смешанными величинами (конвертации и приведения к единому знаменателю), можно переходить к методикам выполнения арифметических действий. Сначала следует рассмотреть сумму и разность.

Вычитание и суммирование

Для сложения двух смешанных дробей необходимо руководствоваться определенной методикой.

Она имеет такой вид:

1. Преобразовать обе величины в неправильные дроби.
2. Привести к общему знаменателю.
3. Выполнить сложение числителей, записав окончательный результат.

Операция вычитания выполняется по такому же алгоритму, что и сложение. Однако используется знак вычитания, а не суммирования. Следует отметить, что при сложении и вычитании смешанные числа можно не преобразовывать в неправильные дробные выражения при эквивалентности их знаменателей одному значению.

В этом случае методика будет выглядеть немного по-другому:

1. Записать два выражения дробного типа.
2. Отнять из одной целой части другую.
3. Выполнить операцию разности числителей.
4. Написать результат.

Следует отметить, что специалисты рекомендуют сразу ознакомиться с оптимизацией решения. Это значит, что при равенстве знаменателей нет необходимости преобразовывать смешанные числа в неправильные дроби.

Задания должны решаться простыми способами, которые позволяют избежать множества ошибок.

Далее можно перейти к более сложным операциям произведения и деления смешанных выражений дробного типа.

Произведение и частное

Для операций умножения и деления нет необходимости приводить смешанные выражения к единому знаменателю. Арифметические действия выполняются по различным алгоритмам. Методика определения результата произведения выглядит таким образом:

1. Написать смешанные величины.
2. Преобразовать значения в первом пункте в неправильные дробные выражения.
3. Перемножить числители между собой, а затем знаменатели.
4. При необходимости вынести общий множитель, и сократить дробь на него.

Операция получения частного похожа на произведение, но существует некоторая особенность.

Последнюю часто забывают выполнить начинающие математики.

Алгоритм деления смешанных величин имеет такой вид:

1. Записать смешанные значения, и переконвертировать их в неправильные дробные тождества.
2. Поменять местами числитель и знаменатель второй дроби.
3. Выполнить операцию умножения, записав результат.

Следует отметить, что обязательным условием при делении является «переворот» второй дроби, а также замена знака деления «:» на умножение «*». Это правило не нужно забывать, поскольку только его соблюдение позволит решить пример без ошибок. Следующими операциями являются возведение в степень и извлечение корня.

Возведение в степень и корень

Операции возведения в степень и изъятия корня похожи между собой, поскольку последний можно записать в виде первой, которая представлена обыкновенной дробью. Например, кубический радикал (корень) имеет математическую форму записи в виде «(8)^(1/3)».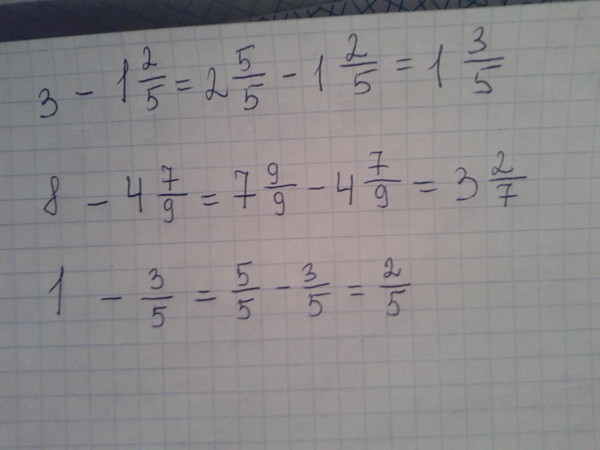 (½)=4.

Методики возведения смешанного тождества в степень и извлечения радикала похожи между собой.

Алгоритм выглядит следующим образом:

1. Преобразовать смешанное выражение в неправильное дробное.
2. Возвести числитель и знаменатель в заданную степень или извлечь из них корень.
3. Записать результат.

Следует отметить, что после получения результата дробь можно сократить, а затем преобразовать в смешанную. Этот прием является правилом «хорошего тона» в математике. Математическим «этикетом» пользуются во всем мире. Это свидетельствует о том, что каждый ученый приводит свои исследования или расчеты к читабельной форме представления, чтобы его наработками могли воспользоваться и другие специалисты.

Таким образом, при выполнении различных операций над смешанными дробными числами необходимо руководствоваться специальными алгоритмами, а также знать, как производятся операции конвертирования в неправильные дробные формы.

Как вычитать смешанные числа

Независимо от того, имеют ли смешанные числа одинаковые знаменатели или разные знаменатели, их вычитание очень похоже на вычитание целых чисел: вы складываете их одно над другим, рисуете линию и вычитаете. По этой причине некоторые учащиеся чувствуют себя более комфортно при вычитании смешанных чисел, чем при вычитании дробей.

1. Найдите разность дробных частей.

2. Найдите разность двух целых частей числа.

Однако по пути вы можете столкнуться с еще парочкой поворотов. Следующие инструкции помогут вам в решении любой задачи на вычитание смешанных чисел.

Вычитание смешанных чисел с одинаковыми знаменателями

Вычитание намного проще, когда знаменатели совпадают. Например, предположим, что вы хотите вычесть 7 3/5 – 3 1/5. Вот как проблема выглядит в виде столбца:

В этой задаче вы вычитаете 3/5 – 1/5 = 2/5. Затем вы вычитаете 7 – 3 = 4. Не так уж и страшно, согласитесь?

Одна сложность возникает, когда вы пытаетесь вычесть большую дробную часть из меньшей. Предположим, вы хотите найти 11 1/6 – 2 5/6. На этот раз, если вы попытаетесь вычесть дроби, вы получите

.

Очевидно, вы не хотите, чтобы в вашем ответе оказалось отрицательное число. Вы можете решить эту проблему, позаимствовав из столбца слева. Эта идея очень похожа на заимствование, которое вы используете при обычном вычитании, с одним ключевым отличием.

При заимствовании при вычитании смешанных чисел,

1. Заимствуйте 1 из целочисленной части и прибавьте ее к дробной части, превратив дробь в смешанное число.

   Чтобы найти 11 1/6 – 2 5/6, одолжите 1 из 11 и прибавьте к 1/6, получив смешанное число 1 1/6:

2. Замените это новое смешанное число неправильной дробью.

   Вот что получится, если заменить 1 1/6 на неправильную дробь:

   Результат равен 10 7/6. Этот ответ представляет собой странную смесь смешанного числа и неправильной дроби, но это то, что вам нужно для выполнения задания.

3. Используйте результат при вычитании.

   В этом случае нужно уменьшить дробную часть ответа:

Вычитание смешанных чисел с разными знаменателями

Вычитание смешанных чисел при разных знаменателях — едва ли не самое сложное, что вам когда-либо приходилось делать в предварительной алгебре. Предположим, вы хотите вычесть 15 4/11 — 12 3/7. Поскольку знаменатели разные, вычитание дробей усложняется. Но у вас есть еще один вопрос для размышления: в этой задаче вам нужно брать взаймы? Если 4/11 больше, чем 3/7, вам не нужно брать взаймы. Но если 4/11 меньше 3/7, то да.

Поскольку 28 меньше 33, 4/11 меньше 3/7, так что вам придется брать взаймы. Сначала избавьтесь от займа:

Теперь проблема выглядит так:

Первый шаг, вычитание дробей, будет самым трудоемким, так что вы можете позаботиться об этом на стороне:

Хорошая новость заключается в том, что эту дробь нельзя уменьшить. (Они не могут быть уменьшены, потому что 72 и 77 не имеют общих делителей: 72 = 2 2 2 3 3, а 77 = 7 11.) Таким образом, трудная часть задачи решена, а остальное следует за ней легко:

Эта задача не уступает по сложности задаче на вычитание смешанных чисел. Посмотрите на это шаг за шагом. Или, что еще лучше, скопируйте задачу, а затем попытайтесь выполнить шаги самостоятельно. Если вы застряли, это нормально. Лучше сейчас, чем на экзамене!

Об этой статье

Эту статью можно найти в категории:

• Предварительная алгебра,

Дроби — Сложение и вычитание смешанных чисел

Дроби — Сложение и вычитание смешанных чисел — Первый взгляд

Дом | Учитель | Родители | Глоссарий | О нас

Шаги то же самое, если вы добавляете или вычитаете смешанные числа:

1. Найти Наименее Общий знаменатель (ЖК-дисплей)
2. Найдите эквивалентные дроби.