Умножение и деление натуральных чисел – Документ 1 – УчМет
Фамилия, имя, отчество автора: Чойна Анна Игоревна
Квалификационная категория (по желанию): молодой специалист
Место проживания (город, поселок), область, край, регион: Хабаровский край, г.Комсомольск-на-Амуре
Название учебного заведения: МОУ Лицей №33
Дисциплина: математика
Учебник, по которому ведется обучение: Математика. 5класс: учебник для общеобразовательных учреждений; под ред. Г.В. Дорофеева, И.Ф. Шарыгин; Рос. акад. Наук, Рос. акад. образования, изд-во «Просвещение». – 11-е изд. – М.: Просвещение, 2010. – 303с.: ил. – (Академический школьный учебник). ISBN 978-5-09-022248-8
Тема (для материалов типа «Урок», «Мероприятие», «Обобщение опыта» (при необходимости)): «Урок»
Тема: Умножение и деление натуральных чисел.
Класс (курс): 5
Продолжительность урока: 45минут
Использование информационных технологий: использование проектора или интерактивной доски
Цели:
дидактические:
— формирование навыков нахождения неизвестных компонентов умножения и деления;
— закрепление и развитие навыков умножения и деления натуральных чисел;
— отработка навыков решения текстовых задач арифметическим способом;
развивающие:
— развитие внимательности, быстроты мысли;
— развитие умения делать выводы и культуры речи;
— развитие и укрепление интереса к математике;
воспитательные:
— воспитание у учащихся аккуратности при оформлении;
— воспитание стремления к непрерывному совершенствованию своих
знаний;
— содействовать формированию дружеских отношений, умению
работать
командой.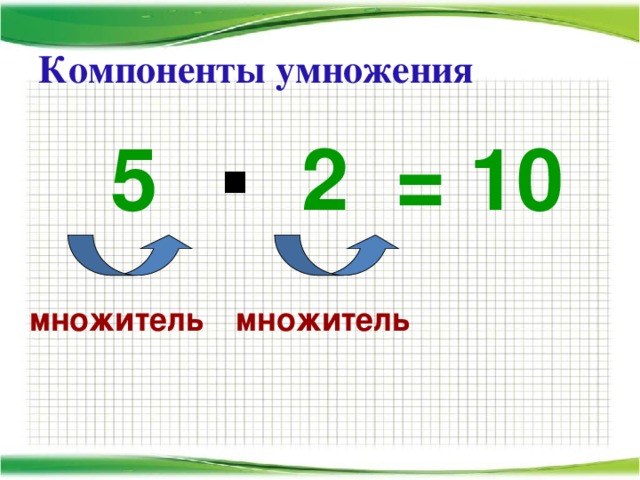
Задачи:
— закрепить умение выполнять умножение и деление натуральных чисел;
— совершенствовать навыки письменного умножения и деления, умение решать задачи;
— развивать творческое воображение, логическое мышление.
Оснащение урока:
— проектор или интерактивная доска;
— жетоны;
— раздаточный материал для команд.
Ход урока
I Организационный момент (2мин) Учитель: Здравствуйте, ребята! Рада вас снова всех видеть. У
нас сегодня гости, давайте поприветствуем
их. Садитесь, пожалуйста, мы начинаем
нашу работу. О чём мы с вами говорили на предыдущих уроках? Предполагаемый ответ: об умножение и деление натуральных чисел. II Постановка проблемы (4мин) Учитель: Открываем свои тетрадки и записываем на полях число «14.10», «Классная работа» и тему урока «Умножение и деление натуральных чисел». Сегодня у нас необычный урок повторения темы «Умножения и деления натуральных чисел», урок-соревнование, участниками которого будут пять команд во главе со своими капитанами (на команды учащиеся разделились заранее, по желанию). Цель сегодняшнего урока: обобщить знания по данной теме и научиться их применять при решении различных заданий. Познакомлю вас с правилами состязания. Правила:
Необычность урока состоит и в том, что это будет урок-сказка. А наш урок хотелось бы начать со следующих строк.
Если
вы отгадаете загадку, то узнаете
главного героя нашего урока. У
отца был мальчик странный, Предполагаемый ответ: Буратино! Учитель: Буратино по-итальянски – деревянная кукла. Ребята, как называется сказка, и кто ее написал? Предполагаемый ответ: Алексей Толстой. «Золотой ключик, или Приключения Буратино». Учитель: Сегодня я вас познакомлю с математической версией этой сказки. Надеюсь, вы поможете, Буратино выпутаться из тех трудных ситуаций, в которые он постоянно попадает. III Вычислить (5мин) Учитель: Итак, каморка папы Карло… Сверчок
поведал Буратино о том, что в каморке
кроется какая-то тайна, и чтобы ее
узнать, надо правильно ответить на
вопросы, которые, оказывается, записаны
на холсте. Каждый участник нашего урока выполняет в своей тетрадке задание для своей команды. Копии заданий лежат на партах у команд. I Задание. I команда: а) 1456*12= Ответ: 17472 б) 6363:21= Ответ: 303 II команда: а) 4321*13= Ответ: 56173 б) 2954:14= Ответ: 211 III команда:а) 2346*15= Ответ: 35190 б) 1968:16= Ответ: 123 IV команда: а) 3457*18= Ответ: 62226 б) 4752:11= Ответ: 432 V команда: а) 2453*13= Ответ: 31889 б) 4806:18= Ответ: 267 Учитель: А сейчас каждый передаст свою тетрадку
соседу слева для проверки. Учитель: Выполнено первое задание, и вам открывается тайна — за холстом есть потайная дверь. А что за этой дверью — не знает никто. Дверь можно открыть только золотым ключиком, который хранится у старой черепахи Тортилы. Узнав об этом, Буратино решил утром отправиться на поиски ключика. Внимание! IV Групповая работа — Решить задачу (3мин) II Задание. Учитель: Буратино лег спать пораньше — в 19.00, предварительно заведя будильник на 9.00. Обычно Буратино спит 7часов в сутки. Подскажите Буратино, во сколько раз больше он проспал в этот день? Ответ: В этот день Буратино проспал в 2раза
больше, чем в обычный день. (Команда, участник которой первый ответит правильно, получает жетон.) V Групповая работа — Решить задачу (4мин) III Задание. Учитель: Дождавшись
утра, Буратино отправился в путь.
Дорога предстояла трудная и далекая.
На окраине города внимание Буратино
привлекла харчевня «Три пескаря».
Проголодавшийся Буратино решил
подкрепиться. Войдя в харчевню, он
увидел Карабаса Барабаса, лису Алису
и кота Базилио. На вертеле готовилось
фирменное блюдо — жарилась утка. У
Буратино совсем не было денег, тогда
коварный и злой Карабас Барабас
предложил ему пойти на сделку. Если
Буратино правильно ответит на вопрос,
то он его не только накормит, но даст
еще 7 золотых монет в придачу. Если же
Буратино неправильно ответит на
вопрос, то его кинут в огонь для
приготовления очередного фирменного
блюда. Сколько трехлитровых банок понадобится, чтобы перелить весь апельсиновый сок из полного 40-литрового бидона? Ответ: Чтобы перелить весь апельсиновый сок понадобится 14 трехлитровых банок. (Команда, участник которой первый ответит правильно, получает жетон.) Физкультминутка Мы считали и устали, Дружно все мы тихо встали, Ручками похлопали, Раз, два, три. (Хлопки в ладоши под счет учителя.) Ножками потопали, Раз, два, три. (Шаги ногами на месте.) Сели, встали, встали, сели, И друг друга не задели. (Приседания.) Ах, как долго мы писали, Поморгаем
глазками. Посмотрим влево-вправо. Посмотрим вверх. Глазки мы сейчас закроем, (Закрыть глаза ладошками.) В классе радугу построим, Вверх по радуге пойдем, Посмотрим по дуге вверх-вправо и вверх-влево. Жмурься сильно, но держись. А сейчас опять считать начнем. VI Решить уравнение, устный опрос (5мин) IV Задание. Учитель: Все
обошлось как нельзя лучше. Сытый
Буратино с семью золотыми монетами
продолжил путь. За городом Буратино
увидел красивую лужайку и посреди нее
— маленький домик. В нем жила Мальвина
— девочка с голубыми волосами. За ее
домиком дорога разветвляется на пять
частей. Поможем Буратино справиться с этим трудным заданием. Капитаны команд самостоятельно решают уравнения в своих тетрадях, а затем выписывают полученные ответы на доске для проверки. I команда: (х+3)*7=133 Ответ: х=16 II команда: 124:(х-14)=31 Ответ: х=18 III команда: (х-9)*12=132 Ответ: х=20 IV команда: 224:(х+5)=16 Ответ: х=9 V команда: 18*(х-9)=216 Ответ: х=21 (За правильный ответ команды получают жетон.) Остальные отвечают на вопросы: 1)
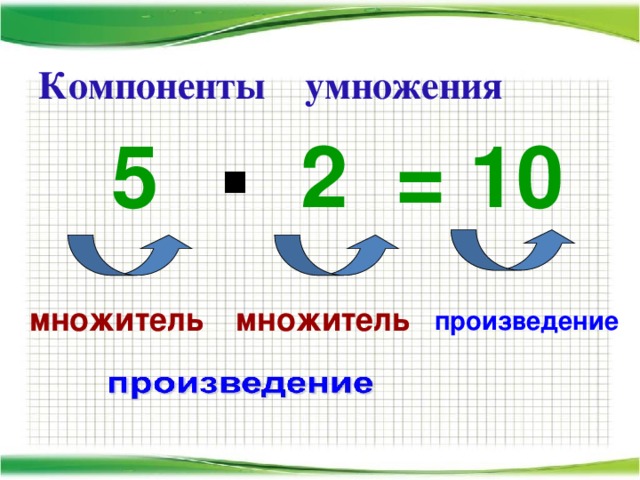
Как называются компоненты действия
умножения? 2) Если один из множителей равен 0, то чему равно произведение? (Произведение будет равно 0) 3) Если один из множителей равен 1, чему равно произведение? (Произведение равно второму множителю) 4) Как найти неизвестный множитель? (Необходимо произведение разделить на второй множитель) 5) Как называются компоненты действия деления? (Число,
которое мы делим называется делимое. 6) Как найти неизвестный делитель? (Необходимо делимое разделить на частное) 7) Как найти неизвестное делимое? (Необходимо делитель умножить на частное) 8) Если число разделить на 1, то чему будет равно частное? (Частное будет равно делителю) 9) Если число разделить на тоже число, то чему будет равно частное? (Частное будет равно 1) 10) Если число разделить на 0, то чему будет равно частное? (На 0 делить нельзя) (За каждый правильный ответ команда получает жетон.) VII Групповая работа — Составление уравнения (3мин) V Задание. Учитель: К
пруду Тортилы вел указатель с числом
18, поэтому Буратино пошел по второй
дороге. Оказывается, лиса Алиса и кот Базилио были свидетелями всего происходящего. Они решили заманить Буратино в Страну Дураков. Как вы знаете, лиса Алиса и кот Базилио убедили Буратино зарыть свои 7 монет в землю. Они ему посоветовали вырыть три ямки, в первую ямку положить х монет, во вторую — на три монеты меньше, чем в первую, а в третью — в два раза больше, чем во вторую. Составьте к сформулированной задаче уравнение и запишите его в своих тетрадях. А капитаны запишите получившиеся уравнения своих команд на доске. Ответ: х+(х-3)+2(х-3)=7 (За правильный ответ команды получают жетон.) VIII Групповая работа – Вычислить (10мин) VI Задание. Учитель: Лиса
Алиса и кот Базилио обманули Буратино. Если вы хотите узнать, чем это путешествие закончилось, вам придется последовать за Буратино по математическим кочкам. Не торопитесь при выполнении вычислений, а то можете соскользнуть с кочки и увязнуть в болоте. (Цепочкой, по одному, выходят к доске и записывают ответы.) Если увидели, что предыдущий участник команды допустил ошибку, можете ее исправить. I команда: 27 * 20 = 540 ____ + 160 = 700 ____ — 250 = 450 ____ : 5 = 90 ____ * 30 = 2700 ____ + 300 = 3000 II команда: 37 * 20 = 740 ____ + 160 = 900 ____ — 450 = 450 ____ : 9 = 50 ____ * 40 = 2000 ____ + 200 = 2200 III команда: 34 * 20 = 680 ____ + 120 = 800 ____ — 350 = 450 ____ : 5 = 90 ____ * 30 = 2700 ____ + 300 = 3000 IV команда: 26 * 20 = 520 ____ + 280 = 800 ____ — 150 = 650 ____ : 5 = 130 ____ * 20 = 2600 ____ + 400 = 3000 V команда: 42 * 20 = 840 ____ + 160 = 1000 ____ — 550= 450 ____ : 9 = 50 ____ * 30 = 1500 ____ + 500 = 2000 (Каждая
команда выписывает свои ответы на
доске. Учитель: Очередное препятствие преодолено, хотя некоторых оступившихся пришлось вытягивать из болота. Наконец-то, Буратино подошел к пруду, в котором живут черепаха Тортила и много-много зеленых лягушек. Квакушки со всех сторон окружили Буратино и рассказали ему о своей мечте. IX Групповая работа — Решить задачу (3мин) VII Задание. Учитель: В окрестностях пруда четыре болота. В каждом болоте по 58 кочек, а на каждой кочке живет по шесть лягушек. Каждая лягушка мечтает стать лягушкой-путешественницей. Сколько нужно уток, чтобы осуществилась их мечта? Надеюсь, вы не забыли способ передвижения лягушки-путешественницы по воздуху! Ответ: Чтобы мечта лягушек осуществилась необходимо 4
* 58 * 6 * 2 = 2784 утки. Учитель: Благодарные лягушки на кувшинке довезли Буратино до черепахи. (За правильный ответ команды получают жетон.) X Групповая работа – Решить задачу (3мин) VIII Задание. Учитель: Оказывается, Тортила отдала золотой ключик Буратино не просто, как рассказал Алексей Толстой, а совсем иначе. Она вынесла три коробочки: красную, синюю и зеленую. На красной коробочке было написано «Здесь лежит золотой ключик», на синей — «Непустая коробочка», на зеленой — «Здесь сидит змея». Тортила прочла надписи и сказала: «Действительно, в одной коробочке лежит золотой ключик, в другой — змея, а одна коробочка пуста, но все надписи неверны. Если отгадаешь, в какой коробочке лежит золотой ключик, он твой». Так где же лежит золотой ключик? Кто
первым объяснит решение задачи —
принесет команде один балл. Ответ: Золотой ключик лежит в третьей (зеленой) коробочке. (За правильный ответ команды получают жетон.) XI Подведение итогов урока (2мин) Учитель: Получив ключик, довольный Буратино вернулся домой. С какими результатами каждая команда пришла к концу путешествия? Право прочитать надпись за потайной дверью предоставляется капитану победившей команды. (Учащиеся видят четверостишье).
За помощь Буратино всем большое спасибо! О чем на уроке мы сегодня с вами говорили? Назовите компоненты действия умножения? (Числа, которые перемножают, называют множителями, результат умножения называют произведением) Назовите
компоненты действия деления? (Число,
которое мы делим называется делимое. Если один из множителей равен 0, то чему равно произведение? (Произведение будет равно 0) Если число разделить на 0, то чему будет равно частное? (На 0 делить нельзя) Участники победившей команды за урок получают пятерки. XII Домашнее задание (1мин) Читать п. 3.2, №226, №248. | Цели: 1. Снять напряжение. 2. Мотивировать учащихся на работу. Цели: 1. 2. Развитие внимательности. Цели: 1. Отработка навыков решения текстовых задач арифметическим способом. 2. Содействовать умению работать командой. Цели: 1. Отработка навыков решения текстовых задач арифметическим способом. 2. Содействовать умению работать командой. 3. Развитие внимательности, быстроты мысли. Цели: 1. Формирование навыков нахождения неизвестных компонентов умножения и деления. 2.
Воспитание усидчивости, целеустремленности,
самостоятельности. 3. Воспитание усидчивости, целеустремленности, самостоятельности. 4. Воспитание у учащихся аккуратности при оформлении. Цели: 1. Отработка навыков составления уравнений. 2. Развитие внимательности, быстроты мысли. Цели: 1. Закрепление и развитие навыков умножения и деления натуральных чисел. 2. Содействовать формированию дружеских отношений, умению работать командой. Цели: 1.
Развитие внимательности, быстроты
мысли. 2. Развитие умения делать выводы и культуры речи. Цели: 1. Воспитание усидчивости, целеустремленности, самостоятельности. 2. Развитие умения делать выводы и культуры речи. Цель: 1. Развитие и укрепление интереса к математике. 2. Воспитание стремления к непрерывному совершенствованию своих знаний. |
Рекомендуемая литература
Умножение и деление положительных отрицательных чисел правило. Умножение и деление чисел с разными знаками
Главная > ВПР > Умножение и деление положительных отрицательных чисел правило. Умножение и деление чисел с разными знаками
На этом уроке мы повторим правила сложения положительных и отрицательных чисел. Также научимся умножать числа с разными знаками и узнаем правила знаков для умножения. Рассмотрим примеры умножения положительных и отрицательных чисел.
Свойство умножения на ноль остается верным и в случае отрицательных чисел. Ноль умножить на любое число — будет ноль.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
Домашнее задание
- Интернет-портал Mnemonica.ru ().
- Интернет-портал Youtube.com ().
- Интернет-портал School-assistant.
 ru ().
ru (). - Интернет-портал Bymath.net ().
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число с называется частным от деления чисел a и b , если верно произведение c · b = a . При этом, a ÷ b = c .
Правило деления отрицательных чисел
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Пусть a и b — отрицательные числа. Тогда
a ÷ b = a ÷ b .
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа a на число undefined умножить на число b — 1 , обратное числу b .
a ÷ b = a · b — 1 .
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
Равенство a ÷ b = a · b — 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел. Запишем равенства:
a · b — 1 · b = a · b — 1 · b = a · 1 = a .
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.
Перейдем к рассмотрению примеров.
Начнем с простых случаяв, переходя к более сложным.
Пример 1. Как делить отрицательные числа
Разделим — 18 на — 3 .
Модули делителя и делимого соответственно равны 3 и 18 . Запишем:
18 ÷ — 3 = — 18 ÷ — 3 = 18 ÷ 3 = 6 .
Пример 2. Как делить отрицательные числа
Разделим — 5 на — 2 .
Аналогично, записываем по правилу:
5 ÷ — 2 = — 5 ÷ — 2 = 5 ÷ 2 = 5 2 = 2 1 2 .
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
5 ÷ — 2 = — 5 · — 1 2 = 5 · 1 2 = 5 2 = 2 1 2 .
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Пример 3. Как делить отрицательные числа
Разделим — 0 , 004 на — 0 , 25 .
Сначала записываем модули этих чисел: 0 , 004 и 0 , 25 .
Теперь можно выбрать один из двух способов:
- Разделить десятичные дроби столбиком.
- Перейти к обыкновенным дробям и выполнить деление.
Разберем оба способа.
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
Ответ: — 0 , 004 ÷ 0 , 25 = 0 , 016
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
0 , 004 = 4 1000 ; 0 , 25 = 25 100 0 , 004 ÷ 0 , 25 = 4 1000 ÷ 25 100 = 4 1000 · 100 25 = 4 250 = 0 , 016
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Пример 4. Как делить отрицательные числа
Вычислим частное от деления чисел — 0 , 5 и — 5 .
0 , 5 ÷ — 5 = — 0 , 5 ÷ — 5 = 0 , 5 ÷ 5 = 1 2 · 1 5 = 1 2 5 = 5 10 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки
(1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить. Также в формуле
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
§ 1 Умножение положительных и отрицательных чисел
В этом уроке познакомимся с правилами умножения и деления положительных и отрицательных чисел.
Известно, что любое произведение можно представить в виде суммы одинаковых слагаемых.
Cлагаемое -1 нужно сложить 6 раз:
(-1)+(-1)+(-1) +(-1) +(-1) + (-1) =-6
Значит произведение -1 и 6 равно -6.
Числа 6 и -6 -противоположные числа.
Таким образом, можно сделать вывод:
При умножении -1 на натуральное число получится противоположное ему число.
Для отрицательных чисел, так же как для положительных, выполняется переместительный закон умножения:
Если натуральное число умножить на -1, то также получится противоположное число
При умножении любого неотрицательного числа на 1 получится это же число.
Например:
Для отрицательных чисел данное утверждение тоже верно: -5 ∙1 = -5; -2 ∙ 1 = -2.
При умножении любого числа на 1 получится это же число.
Мы уже убедились, что при умножении минус 1 на натуральное число получится противоположное ему число. При умножении отрицательного числа данное утверждение тоже справедливо.
Например: (-1) ∙ (-4) = 4.
Также -1 ∙ 0 = 0, число 0 противоположно само себе.
При умножении любого числа на минус 1 получится противоположное ему число.
Перейдем к другим случаям умножения. Найдем произведение чисел -3 и 7.
Отрицательный множитель -3 можно заменить произведением -1 и 3. Тогда можно применить сочетательный закон умножения:
1 ∙ 21 = -21, т. е. произведение минус 3 и 7 равно минус 21.
е. произведение минус 3 и 7 равно минус 21.
При умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей.
А чему равно произведение чисел с одинаковыми знаками?
Мы знаем, что при умножении двух положительных чисел получится положительное число. Найдем произведение двух отрицательных чисел.
Заменим один из множителей произведением с множителем минус 1.
Применим выведенное нами правило, при умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей,
получится -80.
Сформулируем правило:
При умножении двух чисел с одинаковыми знаками получается положительное число, модуль которого равен произведению модулей множителей.
§ 2 Деление положительных и отрицательных чисел
Перейдем к делению.
Подбором найдем корни следующих уравнений:
y ∙ (-2) = 10. 5 ∙ 2 = 10, значит х = 5; 5 ∙ (-2) = -10, значит а = 5; -5 ∙ (-2) = 10, значит y = -5.
Запишем решения уравнений. В каждом уравнении неизвестен множитель. Неизвестный множитель находим, разделив произведение на известный множитель, значения неизвестных множителей мы уже подобрали.
Проанализируем.
При делении чисел с одинаковыми знаками (а это первое и второе уравнения) получается положительное число, модуль которого равен частному модулей делимого и делителя.
При делении чисел с разными знаками (это третье уравнение) получается отрицательное число, модуль которого равен частному модулей делимого и делителя. Т.е. при делении положительных и отрицательных чисел знак частного определяется по тем же правилам, что знак произведения. А модуль частного равен частному модулей делимого и делителя.
Таким образом, мы сформулировали правила умножения и деления положительных и отрицательных чисел.
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина.
 – Мнемозина, 2009.
– Мнемозина, 2009. - Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений./Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Определение 1
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел – a , — b данное равенство считается верным.
(- а) · (- b) = a · b .
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (- а) · (- b) = a · b . Статья умножение чисел с разными знаками рассказывает о том, что равенств а · (- b) = — a · b справедливое, как и (- а) · b = — a · b . Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
(- a) · (- b) = (- a · (- b)) = — (- (a · b)) = a · b .
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Пример 1
Произвести умножение чисел — 3 и — 5 .
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5 . Их произведение дает в результате 15 . Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
(- 3) · (- 5) = 3 · 5 = 15
Ответ: (- 3) · (- 5) = 15 .
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Пример 2
Вычислить произведение (- 0 , 125) · (- 6) .
Решение.
Используя правило умножения отрицательных чисел, получим, что (− 0 , 125) · (− 6) = 0 , 125 · 6 . Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид (− 0 , 125) · (− 6) = 0 , 125 · 6 = 0 , 75 .
Ответ: (− 0 , 125) · (− 6) = 0 , 75 .
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Значение вычисляется только по необходимости.
Пример 3
Необходимо произвести умножение отрицательного — 2 на неотрицательное log 5 1 3 .
Решение
Находим модули заданных чисел:
2 = 2 и log 5 1 3 = — log 5 3 = log 5 3 .
Следуя из правил умножения отрицательных чисел, получим результат — 2 · log 5 1 3 = — 2 · log 5 3 = 2 · log 5 3 . Это выражение и является ответом.
Ответ: — 2 · log 5 1 3 = — 2 · log 5 3 = 2 · log 5 3 .
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
3.3.3 Математические термины умножения и деления
Перейти к основному содержанию
Путь к странице
Давайте рассмотрим части задачи на умножение или деление, чтобы убедиться, что мы используем правильный словарь. Все слова, выделенные жирным шрифтом, являются важной математической лексикой, поэтому добавляйте их в свою тетрадь по математике вместе со своими определениями по мере их появления.
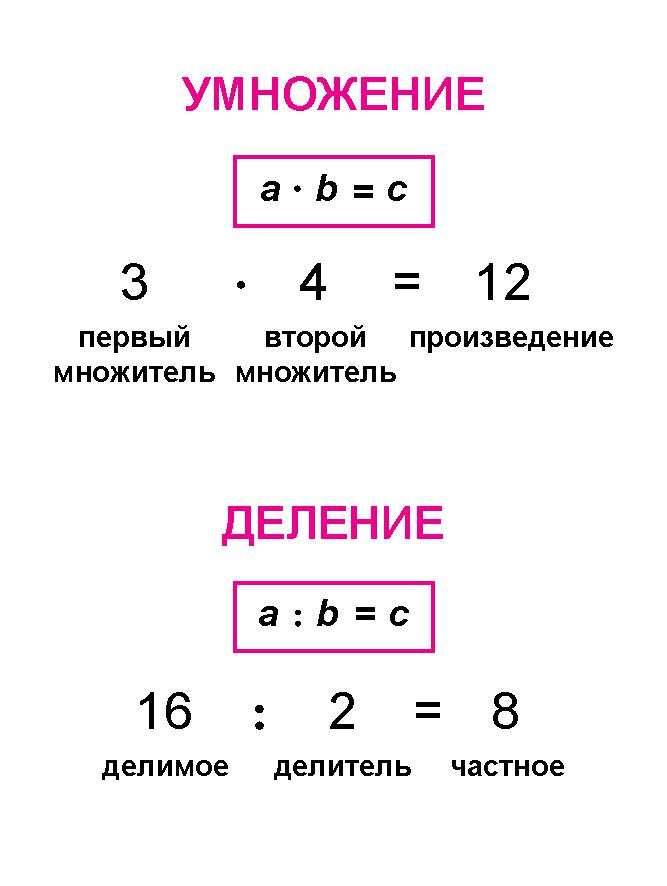
Предположим, что у нас есть шесть умноженных на норму x умножить на четыре равно 24. 6 и 4 называются делителями , а 24 равно называется продукт . Перемножение чисел равно делят на , и ответом на задачу умножения является произведение на . Так, коэффициент умножения равен произведению.
Теперь предположим, что у нас есть 56 деление семь равняется восьми. Имя для числа 56 в этом примере — делимое , 7 делитель , а 8 частное . Число разделить, или разбить, дивидендов . Число, на которое мы делим, делитель , а ответом на задачу деления будет частное . Так, делитель деления дивиденда равен частному.
Остаток в задаче на деление — это число, «оставшееся», которое
делитель больше не может делиться на. Мы говорим, что делитель делит нацело
делимое, если остаток равен нулю. Однако, если есть остаток, то
обычно пишут частное, затем R , а затем
ценность. Например, левая часть уравнения восемь, деление пять, равняется правой части один раз, умноженный на r, умноженный на три, потому что 5 входит в число 8 один раз, что дает нам 3 слева.
над.
Например, левая часть уравнения восемь, деление пять, равняется правой части один раз, умноженный на r, умноженный на три, потому что 5 входит в число 8 один раз, что дает нам 3 слева.
над.
Мы также можем связать деление с умножением. Мы говорим, что 56 деление семь равно восьми, потому что восемь умножить семь равно 56. Это показывает, что деление отменяет умножение или является противоположностью умножения. Мы можем использовать это правило, чтобы показать, что деление является единственным основным арифметическим действием. операция, имеющая ограничение. Рассмотрим шесть делений ноль. Допустим, шесть делений на ноль равно a. Это эквивалентно утверждению, что умножение нуля равно шести, но 0, умноженное на любое число, дает 0, поэтому умножение нуля равно шести невозможно. Таким образом, деление на ноль не определено; Это не существует.
Однако ноль можно разделить на любое ненулевое число. Например, нулевое деление восемь равно нулю, потому что
восемь умножение ноль равно нулю точка Ноль может быть делимым или частным, но не
делитель.
(a) Чему равно частное 30 третьего деления?
а.
А. 27
б.
Б. 10
в.
К. 6
г.
Д. 9
Правильный ответ: б.
Ответ
(a) Поскольку три умножения на 10 равно 30, правильный ответ — 10, то есть буква B.
(b) Чему равно частное 12 деления четыре?
а.
А. 8
б.
Б. 10
в.
С. 3
d.
D. 2
Правильный ответ c.
Ответ
(b) Так как четыре умножить на три равно 12, правильный ответ — буква С.
Распечатать
стр.Для получения дополнительной информации ознакомьтесь с нашими часто задаваемыми вопросами, которые могут оказать вам необходимую поддержку.
Есть вопрос?
Если вас что-то беспокоит на этом сайте, пожалуйста, свяжитесь с нами здесь.
Сообщить о проблеме
Терминология, используемая в отделе вычитания и умножения
| Операции | Словарь | Пояснение | Пример |
|---|---|---|---|
| Дополнение | Август | Номер, к которому добавляется другой. | |
| Дополнение | Номер, который добавляется к другому. | ||
| Сумма | Сумма является результатом сложения | ||
| Вычитание | Минуэнд | Первое число в вычитании | |
| Вычитаемое | Число, которое необходимо вычесть. 2-й номер в вычитании | ||
| Разница | Разница является результатом задачи на вычитание. | ||
| Умножение | Множимое | Число, которое умножается на другое число | |
| Множитель | Число, с которым умножается, называется множителем | ||
| Продукт | Продукт является результатом умножения. | ||
| Подразделение | Дивиденд | Число делится | |
| Делитель | Число, которое делит делимое ровно на | ||
| Частное | Результат деления | ||
| Остаток | Число «осталось» после деления одного числа на другое |
Работает на mymathtables.com
Дополнение Пример:
3 + 2 = 5,
Здесь, 3 IS Agend
2 — Приложение
5 — сумма
Пример вычитания:
23 — 2 = 21,
здесь, 23 — Minuend
2 IS Subtrahend
21 — Разница
Пример умножения:
5 x 1 = 5,
Здесь 5 — умноженность
1 IS Multiplier
5 — продукт
Пример дивизии:
10. = 5 ,
Здесь 10 — это делимое
2 — это делитель
5 — частное
0 — это остаток (после деления не остается)
Этот словарь сложения, вычитания, умножения и деления — это основные вещи в целом.


 Будьте
внимательными, так как некоторые из
них адресованы всему классу. В этом
случае отвечает та команда, участники
которой первыми поднимут руки.
Будьте
внимательными, так как некоторые из
них адресованы всему классу. В этом
случае отвечает та команда, участники
которой первыми поднимут руки.
 Буратино — мальчик шустрый,
но деревянный, поэтому ему нужна ваша
помощь.
Буратино — мальчик шустрый,
но деревянный, поэтому ему нужна ваша
помощь. На экране
вы видите правильные ответы. Проверьте
результаты своего соседа. Обменяйтесь
тетрадками обратно. Поднимите руки
те, кто выполнил вычисления без ошибок.
Эти ребята приносят своим командам
по одному баллу!
На экране
вы видите правильные ответы. Проверьте
результаты своего соседа. Обменяйтесь
тетрадками обратно. Поднимите руки
те, кто выполнил вычисления без ошибок.
Эти ребята приносят своим командам
по одному баллу!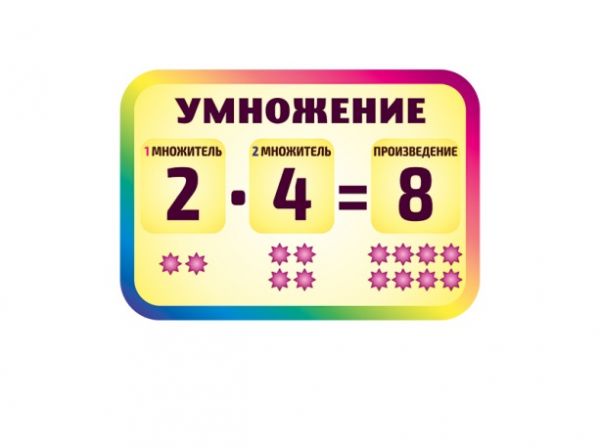

 Мальвина рассказала Буратино
о том, что вдоль каждой дороги написано
уравнение. Нужно найти корни уравнений
и по указателю направлений определить
путь, ведущий к пруду черепахи Тортилы.
Мальвина рассказала Буратино
о том, что вдоль каждой дороги написано
уравнение. Нужно найти корни уравнений
и по указателю направлений определить
путь, ведущий к пруду черепахи Тортилы.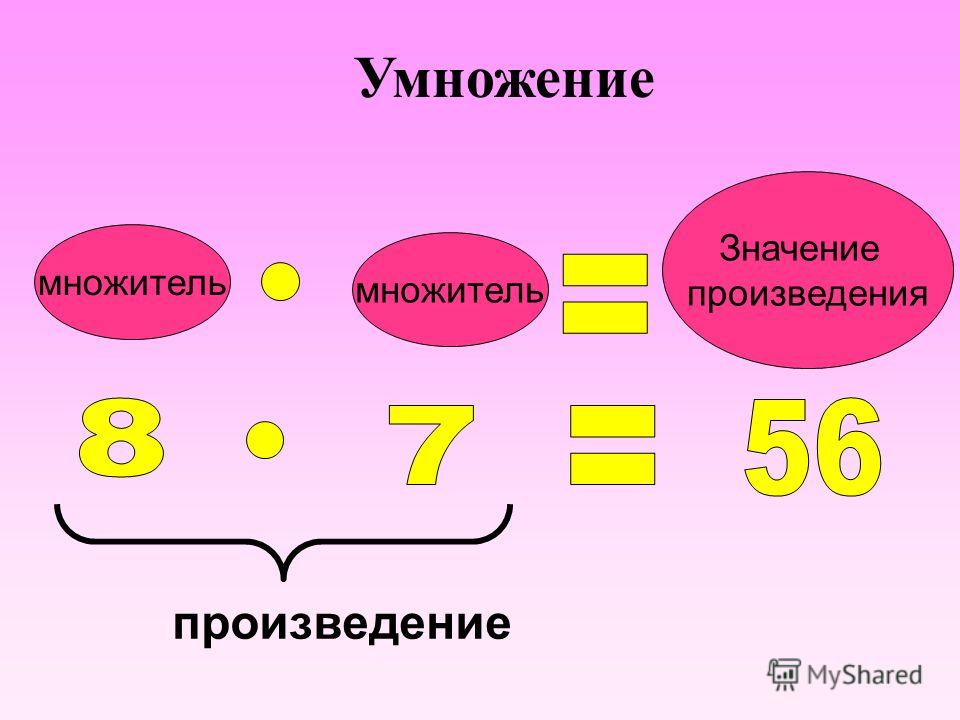 Число, на которое делим, называется
делителем. А результат действия деления
называется частным)
Число, на которое делим, называется
делителем. А результат действия деления
называется частным)
 Они направили на него сыщиков, и он,
бросив свои монеты, бежал из Страны
Дураков. Чтобы вернуться на правильный
путь, ведущий к пруду, Буратино пришлось
идти через топкое болото.
Они направили на него сыщиков, и он,
бросив свои монеты, бежал из Страны
Дураков. Чтобы вернуться на правильный
путь, ведущий к пруду, Буратино пришлось
идти через топкое болото. За каждый правильный ответ
команда получает жетон.)
За каждый правильный ответ
команда получает жетон.)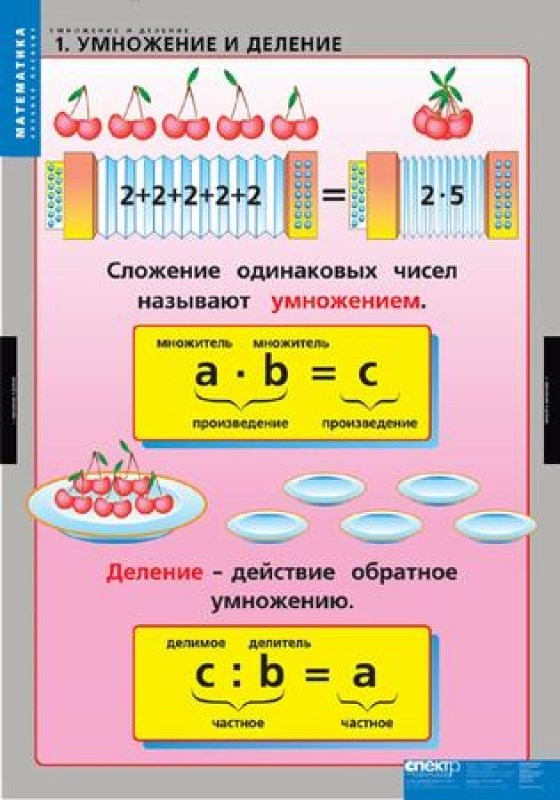

 Число, на которое делим, называется
делителем. А результат действия деления
называется частным)
Число, на которое делим, называется
делителем. А результат действия деления
называется частным) Отработка навыков умножения и деления
натуральных чисел.
Отработка навыков умножения и деления
натуральных чисел.
 ru ().
ru ().