Сложение и вычитание обыкновенных дробей
Главная » Дроби онлайнСложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Исследуй дальше: Понятие Дроби- наглядное объяснение
Сложение и вычитание обыкновенных дробей
Ключевые слова: дроби, сложение, вычитание
Цели урока:
- систематизация знаний учащихся по данной теме;
- закрепление знаний правил сложения и вычитания обыкновенных дробей ;
- развитие интереса учащихся к изучению математики.
Оборудование:
Ход урока
Добрый день! Добрый час!
Как я рада видеть вас!
Встали все у парт красиво,
Поздоровались учтиво.
Друг на друга посмотрели,
Улыбнулись, тихо сели!
Начнем работу с чтения стихотворения с пропущенными словами. Вставьте пропущенное:
Каждый может за версту
Видеть дробную … (черту)
Над чертой … (числитель)
Знайте!
Под чертою … (знаменатель)
Дробь такую непременно
Надо звать … (обыкновенной)
В древности учение о дробях считалось самым трудным разделом арифметики. Римский писатель Цицерон говорил, что без знаний дробей никто
Как вы думаете, что нам сегодня необходимо сделать на уроке? Наша задача сегодня повторить правила и закрепить умение выполнять эти действия при решении примеров, уравнений, задач.
А свои знания, смекалку и находчивость покажете, во время путешествия в страну Дроби. В этой стране мы сделаем несколько остановок: в Поле цветов, на берегу озера Ребусного, посетим Замок Кроссвордный, отдохнем на поляне Отдыха, попробуем преодолеть высокие горы Ума. Свой труд вы будете оценивать сами. Для этого у вас на столах лежат листы с таблицей самооценивания. После каждого задания вы будете ставить себе оценку по 5 бальной шкале.
Пойдем пешком или поедем? Поскольку мы хотим отправиться в путешествие, то что нам необходимо? Нам необходимо найти транспорт. Давайте соберем поезд.
На каждой парте перед вами лежат разноцветные фигуры, ножницы, линейка, карандаш и задание: на слайде по очереди
- Синий квадрат разделите на две доли и возьмите половину – это будет носовая часть паровоза
- Большой красный квадрат разделите на 4 доли и возьмите 2 доли – кабина паровоза
- Возьмите 3 целых зеленых круга – колеса паровоза
- Из синего прямоугольника возьмите четверть – окно кабины
- Зеленый прямоугольник разделите на 3 доли и возьмите треть – дымовая труба
- Красный квадрат разделите на четыре доли в виде треугольников и возьмите четверть – путеочиститель
Что мы повторили, вырезая фигуры? (Доли, дроби, сложение и вычитание дробей).
Поставьте оценку на листе самооценвания.
Молодцы! Поехали.
Мы сядем в поезд и — вперёд!
Помчим по рельсам быстро-быстро.
А кто же поезд поведёт?
Им управляют машинисты
Попасть в страну Дроби, минуя поле Ромашек, нельзя. Здесь мы вспомним о дробях.
Поле цветов «Цветик-семицветик»Давайте-ка дружно
Мы вспомним ребята
О чём говорили на прошлом занятии.
Пройденный материал повторим,
В голове у себя закрепим.
На каждом лепестке цветика-семицветика написано по одному вопросу. Каждый выбирает цвет и отвечает на вопрос, написанный на нём.
- Что показывают знаменатель и числитель дроби?
- Какая дробь называется правильной?
- Какая дробь называется неправильной?
- Какая дробь равна единице?
- Какая дробь больше единицы?
- Какая их двух дробей с равными знаменателями меньше?
- Какая из двух дробей с одинаковыми знаменателями больше?
- Как из одной дроби вычесть другую, если знаменатели одинаковые?
- Как сложить дроби с одинаковыми знаменателями?
- Как из одной дроби вычесть другую, если знаменатели разные?
- Как сложить дроби с разными знаменателями?
Поставьте оценку на листе самооценвания
Ребята, мы вспомнили о дробях, а теперь нам пора продолжить путешествие.
Наш путь к озеру Ребусному.
Здесь задания, реши,
Думай лучше не спеши.
Если смысл разберешь,
Ответ быстро ты найдешь.
Здесь ребятам предлагается решить ребус и расшифровать коды.
Проверка: ответы закодированы. Расшифровав код, составить слово.
Поставьте оценку на листе самооценвания.
Замок КроссвордныйНа вопросы отвечай,
и быстрей кроссворд решай.
Ты кроссворд любой решишь,
Если думать поспешишь.
Следующая остановка «Замок Кроссвордный», здесь учащимся нужно отгадать кроссворд.
По вертикали:
- Как называется дробь, записанная в виде ?
По горизонтали:
- Как называется дробь, у которой числитель и знаменатель делятся на одно и то же число?
- Как называется дробь, у которой числитель больше или равен знаменателю?
- На какое число можно сократить дробь 12/24
- Как называется, записанное над чертой дроби?
- Дробная черта – это знак …
- Как называется, записанное под чертой дроби?
- Как по-другому называют дробь 1 /2
- Как называется дробь, у которой числитель меньше знаменателя?
Поставьте оценку на листе самооценвания.
Пришло время отдохнуть на поляне Отдыха
Поляна ОтдыхаМы поставили пластинку
И выходим на разминку.
Песня из мультсериала «Фиксики». Молодцы. Похлопали себе.
Итак, на нашем пути горы Ума
Горы УмаТест по теме: «Сравнение, сложение и вычитание обыкновенных дробей»А теперь все ручки взяли,
вместе дружно замолчали.
Вы примеры запишите
И самостоятельно их решите
Вариант I
1. Что больше: ?
а) ; б) .
2. Сократите дробь:
а) б) в) г)
3. Чему равна сумма чисел ?
а) ; б) ; в) ; г) .
4. Чему равна разность ?
а) ; б) ; в) ; г) .
5. Решением уравнения является:
а) ; б) ; в) ; г) .
6. В книге 100 страниц. Саша прочитал всех страниц. Сколько страниц прочитал Саша.?
а) 50; б) 60; в) 15; г) 45.
Вариант II
1. Что меньше: ?
а) ; б) .
2. Сократите дробь:
а) б) в) г)
3.Чему равна разность чисел ?
а) ; б) ; в) ; г) .
4. Чему равна сумма ?
а) ; б) ; в) ; г) .
5. Решением уравнения является:
а) ; б) ; в) ; г) .
6. На выполнение домашнего задания Вите нужно 150 минут. всего времени Витя тратит на математику. Сколько минут Витя тратит на математику?
а) 50; б) 60; в) 15; г) 45.
Ключи на слайде:
Вариант I | Вариант II |
1-а | 1-а |
Поменялись тетрадями и проверяем.
Поставьте оценку на листе самооценвания.
Станция КонечнаяНу что, вот закончена игра
Результат узнать пора
Кто же лучше всех трудился?
Кто в путешествии отличился?
Сегодня на уроке мы повторили сложение и вычитание дробей. Скажите, что вам запомнилось и понравилось на сегодняшнем уроке? Какие трудности и при выполнении каких заданий вы испытывали? Посещение каких станций запомнилось вам больше всего? Пришла пора подводить окончательный итог.
Количество баллов | 16-17 | 13-15 | 10-12 | меньше 10 |
Оценка | 5 | 4 | 3 | 2 |
По листам самооценивания за каждый вид работы вы себе ставили балл.
Учитывая все результаты поставьте общую отметку за урок. Покажите ее руками.
Хорошо работали следующие учащиеся…..
Порадовали своими ответами такие учащиеся как….
Оценки за урок….
Д/З. Составить кроссворд или сказку о дробях.
РефлексияСейчас я попрошу каждого из вас выбрать по смайлику, который соответствует вашему состоянию и приклеить к своему поезду.
Спасибо за урок ребята!
Приложения:
- Лист самооценивания
- Презентация
Калькулятор вычитания дробей
GENERATE WORK
сообщите об этом объявлении $ и $\frac{c}{d}$ для $b,d\ne0$ и вычисляет их разницу.
Это онлайн-инструмент для нахождения разницы в простейшей форме двух правильных или неправильных дробей.
Необходимо выполнить следующие шаги:
- Введите в поле две дроби $\frac{a}{b}$ и $\frac{c}{d}$. Числа $a,b,c$ и $d$ должны быть целыми числами, так что $b$ и $d$ должны быть ненулевыми.
- Нажмите кнопку «СОЗДАТЬ РАБОТУ» , чтобы выполнить расчет;
- Калькулятор вычитания дробей покажет разницу между первой дробью и второй дробью.
Ввод: Две дроби;
Результат: Простейшая дробь.
Правило вычитания дробей:
- Если знаменатели равны, $b=d$:
$$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}, \quad \mbox{for}\;b\ne0$$
- Если знаменатели разные, $b\ne d$:
$$\frac{a}{b}-\frac{c}{d}= \frac{a\times d-c\times b}{b\times d},\quad \mbox{for}\;b,d\ne0$$
или эквивалентно,$$\frac{a}{b}- \frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b}-c\times \frac{LCM(b,d)}{d}}{LCM(b ,d)},\quad \mbox{for}\;b,d\ne0$$
, где $LCM(b,d)$ — наименьшее общее кратное $b$ и $d$.
Как вычитать дроби?
Результатом вычитания чисел является \underline{разность}. Разница двух чисел зависит от их порядка, т.е.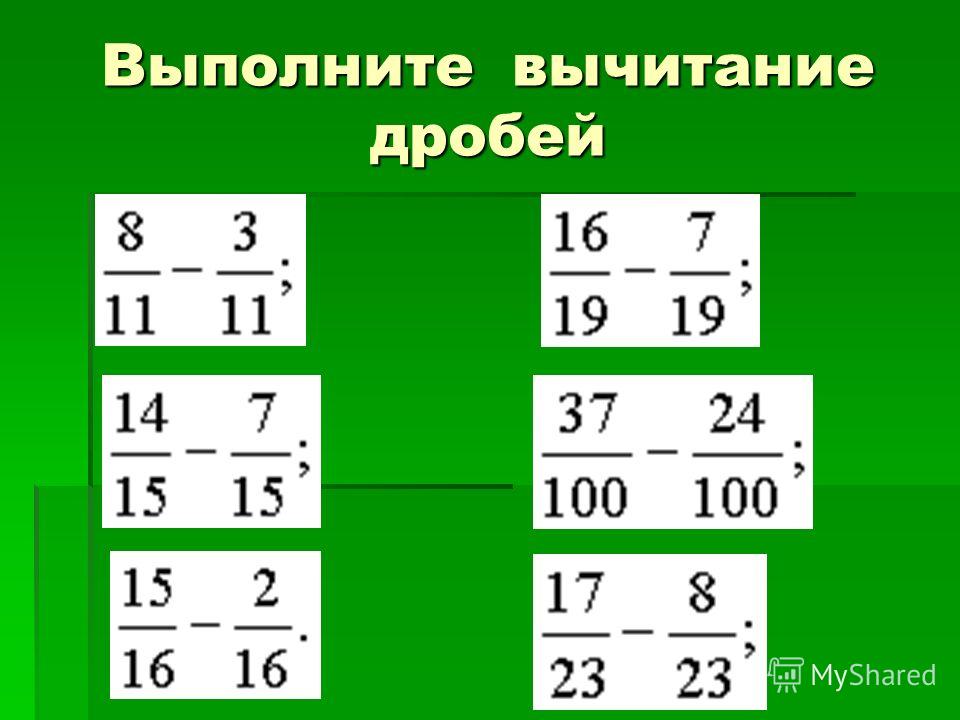
вычитание является некоммутативной операцией. Например, $\frac 53-\frac 13\ne \frac 13-\frac 53$.
Подобно коммутативному свойству, ассоциативное свойство не выполняется для вычитания чисел.
Когда мы имеем дело с дробями, есть два типа вычитания:
- Когда знаменатели равны
При равенстве знаменателей дробей их разность будет разностью числителей над общим знаменателем. При необходимости результат может быть упрощен. Это можно выразить алгебраически:
$$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b},\quad \mbox{for}\;b\ne0$ $
- При разных знаменателях
При разных знаменателях дробей, чтобы вычесть две такие дроби, необходимо выполнить следующие шаги:
- Найти НОК знаменателей;
- Переписать дроби по НОК;
- Вычесть новые числители;
- Результатом является разница числителей по LCM;
- При необходимости упростите результат.
Этот метод можно выразить алгебраически:
$$\frac{a}{b}-\frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b }-c\times \frac{LCM(b,d)}{d}}{LCM(b,d)},\quad \mbox{for}\;b,d\ne0$$
Если $LCM( b,d)=b\times d$, то предыдущая формула принимает вид
$$\frac{a}{b}-\frac{c}{d}=\frac{a\times d-c\times b}{b\times d},\quad \mbox{for}\;b ,d\ne0$$
Например, найдем разницу между $\frac 76$ и $\frac 3 4$. Поскольку $LCM(6,4)=12$, то
$$\frac 76-\frac 3 4=\frac {7\times 2-3\times 3}{12}=\frac {8}{12 }$$
Чтобы записать разницу в простейшей форме, найдите GCF числителя и знаменателя разницы. $GFC(8,12)=4$, поэтому при делении числителя и знаменателя разницы на 4 окончательный результат равен
$$\frac{8\div4}{12\div 4}=\frac 23$$
Аналогичное рассмотрение можно применить при вычитании алгебраических дробей.
Работа по вычитанию дробей с шагами показывает полный пошаговый расчет для нахождения разности двух дробей $\frac{7}{6}$ и $\frac{3}{4}$ с использованием правила вычитания дробей. Для любых других дробей просто введите две правильные или неправильные дроби и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор вычитания, как или в отличие от дробей, для выполнения работы, проверки результатов вычитания двух или более чисел, полученных вручную, или эффективного решения домашних задач.
Реальные задачи с использованием дробей на вычитание
Поскольку во многих реальных ситуациях приходится иметь дело с дробями, вычитание дробей очень полезно. Вычитание дробей можно представить моделью площади. Например, найдем разность $\frac 2 5-\frac 16$.
Если мы разделим квадрат на пять конгруэнтных прямоугольников, $\frac 25$ означает $2$ прямоугольников квадрата.
Кроме того, если тот же самый квадрат разделить на $30$ прямоугольников, $12$ общих прямоугольников будут иметь такую же площадь, что и $2$ ранее общих прямоугольников.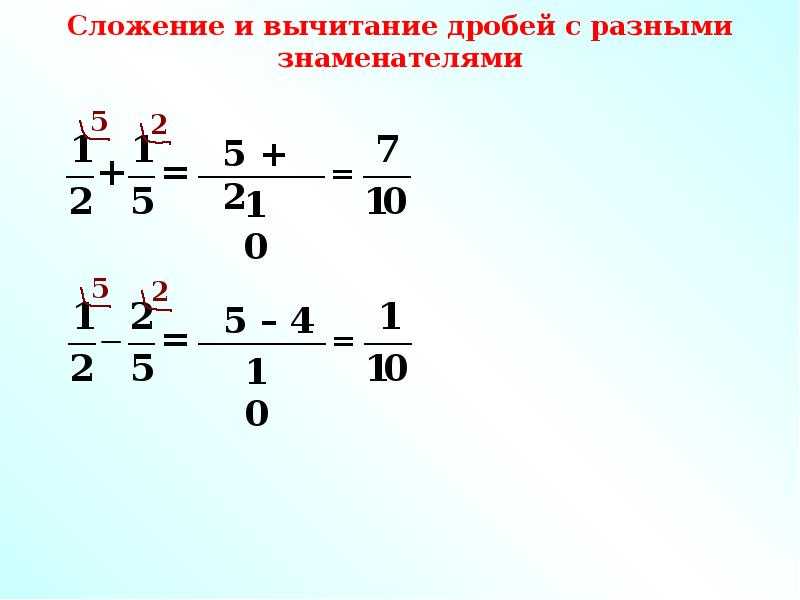
Итак, $\frac 2 5$ равно $\frac {12} {30}$.
Таким же образом мы можем переписать дробь $\frac 16$ как $\frac 5{30}$.
Так как обе дроби имеют общий знаменатель, мы можем найти разницу между первой дробью $\frac{12}{30}$ и второй дробью $\frac {5}{30}$. Если вычесть прямоугольники на первом изображении с прямоугольником на втором изображении, мы получим $7$ общих прямоугольников. Таким образом, разница составляет $\frac {7}{30}.$
Практические задачи на вычитание дробей
Практическая задача 1:
Джон прошел $\frac {6}{15}$ пути, а затем пробежал $\frac 13$ пути. Насколько дальше он прошел, чем пробежал?
Практическая задача 2:
У нас было $\frac {185}3$ грамма сахара. Затем мы использовали $\frac{123}{5}$ граммов, чтобы испечь торт. Сколько сахара у нас осталось?
Калькулятор вычитания дробей, формулы, примеры вычислений (работа с шагами), задачи из реальной жизни и практические задачи будут очень полезны учащимся начальных классов (K-12 образование), чтобы понять вычитание двух чисел, представленных в виде дробей.
Используя эту концепцию, они могут решать сложные алгебраические задачи и уравнения, а также задачи из реальной жизни.
| Like & Unlike Fractions Subtraction | ||
|---|---|---|
| Fractions | Difference | |
| 9/4 — 9/8 | 9/8 | |
| 5/6 — 5/9 | 5/18 | |
| 7/9 — 7/2 | -49/18 | |
| 3/5 — 1/7 | 16/35 | |
| 29.4141414145. | ||
| 2/9 — 1/4 | -1/36 | |
| 7/9 — 3/7 | 22/63 | |
| 4/9 — 4/3 | -8/9 | |
| 8/5 — 9/5 1 5 5 — 9/5 16 | ||
| 5/7 — 2/5 | 11/35 | |
| 4/5 — 7/8 | .7/9 — 1/2 | 5/18 |
| 5/9 — 4/3 | -7/9 | |
| 3/5 — 1/6 | 13/30 | |
| 5/6 — 5/3 | -5/6 | |
| 7/6 — 7/3 | -7/6 | |
| 4/7 — 7/8 | ||
| 8/5 — 7/4 | -3/20 | |
| 7/4 — 8/5 | 3/20 | |
| 7/2 — 1/2 | 3/1 | |
| 1/6 — 3/4 | -7/12 | |
| 1/7 — 7/2 | -47/14 | |
| 3/4 — 5/7 | ||
| 3/4 — 5/7 | ||
| . | 9/8 — 9/4 | -9/8 |
| 9/8 — 3/2 | -3/8 | |
| 1/8 — 1/4 | 5 91435 | |
| 5/6 | ||
| 2/7 — 2/5 | -4/35 | |
| 4/7 — 3/8 | 11/56 | |
| 7 /5 — 5/4 | 3/20 | |
| 1/9 — 8/9 | -7/9 | |
| 8/9 — 7/8 | 1/72 | |
| 1/ 3 — 7/5 | -16/15 | |
| 8/7 — 7/4 | -17/28 | |
| 8/7 — 7/9 | 23/63 | |
| 5/8 — 5/3 | -25/24 | |
| 4/5 — 3/7 | . | -7/12 |
| 1/3 — 7/4 | -17/12 | |
| 6/5 — 6/7 | 12/35 7/4 | |
| 20/63 | ||
| 4/7 — 2/9 | 22/63 | . 38/45|
| 2/3 — 8/5 | -14. 44/21 | |
| 9/7 — 1/9 | 74/63 | |
| 1/5 — 2/7 | -3/35 | 23/72 |
| 8/5 — 5/7 | 31/35 | |
| 2/5 — 7/8 | -19/40 | |
| 5/6 — 5/2 | -5/3 | |
| 7/5 — 7/9 | 28/45 | |
| 3/2 — 6/5 | 3/10 | |
| 3/10 | ||
| 3/10 | 3/10 | 3/10 | 3/10 | .
| 2/9 — 4/5 | -26/45 | |
| 4/7 — 9/8 | -31/56 | 2 3/56 | 20146 | 5/24 |
| 2/5 — 4/3 | -14/15 | |
| 9/7 — 4/5 | 17/35 | |
| 2/9 — 1/3 | -1/9 | |
| 3/4 — 1/3 | 5/12 | |
| 8/9 — 6/7 | . 17/15 | |
| 2/3 — 1/2 | 1/6 | |
| 7/8 — 4/3 | -11/24 | 8/21 |
| 7/6 — 5/8 | 13/24 | |
| 1/5 — 3/4 | -11/20 | |
| -11/20 | -11/20 | 9 | -11/20 | — -1/2 |
| 7/2 — 2/9 | 59/18 | |
| 6/5 — 1/9 | 49/45 | 4/91432 5 1/28 |
| 2/7 — 8/9 | -38. 3/4 | |
| 9/4 — 1/6 | . 9 | |
| 7/3 — 6/7 | 31/21 | |
| 1/7 — 5/6 | -29/42 | |
| 8/3 — 1/7 | 53/21 | |
| . | 31/24 | |
| 9/4 — 8/3 | .-59/36 | |
| 2/5 — 1/9 | 13/45 | |
| 1/7 — 5/3 | -32/21 | -32/21 | -32/21 | -32/21 | -32/21 | -32.0146 | 3/2 |
| 3/8 — 1/3 | 1/24 | . 1/3|
37/35Калькулятор вычитания дробей | Шаги по вычитанию дробей
Используйте онлайн-калькулятор вычитания дробей, чтобы легко вычитать две дроби. Все, что у тебя есть нужно ввести дроби в указанные поля ввода и нажать на кнопку расчета, чтобы узнать вычитание дробей как ответ в мгновение ока.
Калькулятор вычитания дробей: Этот удобный инструмент ускоряет вычисления и дает
вывод в кратчайшие сроки с подробным объяснением.
В следующих разделах мы также предоставляем пошаговый процесс вычитания дробей и решенные примеры.
- Добавление дроби
- Умножение дроби
- Дробный отдел
- Упрощение дробей
- Эквивалент дроби
- Десятичная дробь
- Проценты в дроби
- Дробь до десятичной дроби
- Доля в процентах
Вот шаги для вычитания дробей с одинаковыми знаменателями и разными знаменатели.
Шаги для вычитания одинаковых дробей
- Возьмите любые две дроби с одинаковыми знаменателями.
- Просто вычтите числители.
- Запишите полученную дробь в виде нового числителя, за которым следует исходный знаменатель.
Вычитание разных дробей
- Рассмотрим любые 2 дроби с разными знаменателями.
- Возьмите НОК знаменателей.
- Теперь сделайте знаменатель обеих дробей как значение НОК, умножив число.
- После этого дроби становятся как дроби. Итак, вычитаем числители.
- Запишите полученный числитель как верхнюю часть, а НОК как нижнюю часть результирующей дроби.
Вопросы по вычитанию дробей
Вопрос 1:
Вычесть 2/9 и 1/7?
Решение:
Даны дроби 2/9 и 1/7
Это разные дроби
НОК 9, 7 равно 63
Сделайте знаменатели дробей равными 63, умножив 7/7 на 2 /9и 9/9 с 1/7
7/7 x 2/9 = 14/63
9/9 x 1/7 = 9/63
2/9 — 1/7 = 14/63 — 9/63
= ( 14 — 9)/63 = 5/63
Вопрос 2:
Вычесть неправильные дроби 15/23 и 2/23?
Решение:
Даны дроби 15/23 и 2/23
Дроби похожи на дроби.
Вычесть числители дробей.
15/23 — 2/23 = (15 — 2)/23
= 13/23
Примеры вычитания фракции
