Математика Деление как арифметическое действие. Письменные приемы деления многозначного числа на однозначное
Материалы к уроку
33. Деление как арифметическое действие. Письменные приемы деления многозначного числа на однозначное.ppt
7.22 MBСкачать33. Деление как арифметическое действие. Письменные приемы деления многозначного числа на однозначное.doc
87.5 KBСкачать
Конспект урока
|
33. Деление как арифметическое действие. Письменные приемы деления многозначного числа на однозначное
|
|
Организационный этап
|
|
Всем, всем добрый день!
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
|
|
Сегодня на уроке мы вспомним, что такое деление.
|
|
|
|
Задание Назовите неизвестное число. Проверьте себя. Чтобы узнать неизвестное число, надо определить закономерность. В центре треугольника должна быть сумма трёх чисел, так как семь, три и шесть в первом случае дают в сумме шестнадцать. Четыре, девять и пять во втором случае дают в сумме восемнадцать. Значит, в третьем треугольнике должно быть число пятнадцать, так сумма шести, пяти и четырёх равна пятнадцати.
|
|
Задание Из палочек составьте такую же стрелку. Переложите четыре палочки так, чтобы получились четыре равных треугольника. Проверьте себя. Убираем четыре палочки: три в начале и одну в конце. Докладываем ими недостающие стороны треугольников.
Задание Поставьте арифметические знаки и скобки между данными цифрами так, чтобы равенства стали верными. 2 2 2 2 2 = 7 3 3 3 3 3 3 = 0
2 : 2 + 2 + 2 + 2 = 7 (3 — 3) ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 0
|
|
Этап усвоения новых знаний
|
|
Деление – это действие, обратное умножению. Компоненты при делении называются: делимое, делитель, значение частного.
Вспомним свойства деления: 1. Например, надо разделить сумму чисел двенадцати и сорока восьми на шесть. По очереди делим на шесть каждое слагаемое, а затем складываем результаты. Получаем 10. 2. Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе. Например, надо разность сорока восьми и двенадцати разделить на шесть. Сначала по очереди делим на шесть уменьшаемое и вычитаемое, а затем из первого частного восемь вычитаем второе частное два. Получаем 6. Эти свойства деления помогают нам делить многозначное число на однозначное устно. Чтобы разделить многозначное число на однозначное устно, нужно заменить делимое суммой удобных слагаемых.
Число три тысячи двести шестнадцать при делении на восемь заменили суммой удобных слагаемых: три тысячи двести и шестнадцать. Теперь мы можем разделить каждое из слагаемых в отдельности. А затем сложить результаты деления: три тысячи двести при делении на восемь даёт четыреста, а при делении шестнадцати на восемь, получим два. Складываем четыреста и два, получаем четыреста два.
Однако не всегда удобно пользоваться этим способом. Тогда на помощь нам приходит деление столбиком. Мы уже умеем делить трёхзначное число на однозначное. Давайте вспомним алгоритм.
Деление многозначного числа на однозначное выполняется по этому же алгоритму. Рассмотрим пример. Четыре тысячи семьсот тридцать один надо разделить на три. Сначала нужно выделить первое неполное делимое. Надо, начиная с высшего разряда (у нас это тысячи) найти такое число, которое при делении на три даст однозначное число. Теперь определим количество цифр в значении частного. Так как первое неполное делимое единицы тысяч, то в записи частного будет четыре цифры. Ставим в частном четыре точки. Начнём деление. Разделим четыре тысячи на три. Получится один. Это количество единиц тысяч в частном. Теперь найдём остаток. Один умножить на три – три. Столько единиц тысяч разделили. Четыре минус три, будет один. Столько единиц тысяч ещё надо разделить. Сравниваем остаток один с делителем три. Остаток меньше делителя. Значит, деление выполнено верно. Запишем цифры следующего разряда делимого рядом с остатком. Получили число семнадцать. Число семнадцать показывает количество сотен. Делим сотни. Семнадцать разделить на три – пять. Находим остаток. Пять умножить на три – пятнадцать. Столько сотен разделили. Семнадцать минус пятнадцать, остаток – два. Столько сотен осталось ещё разделить. Запишем цифру следующего разряда рядом с остатком. Мы получили число двадцать три. Оно показывает количество десятков. Продолжаем деление. Двадцать три разделить на три – семь. Находим остаток. Семь умножить на три – двадцать один. Столько десятков разделили. Двадцать три минус двадцать один – два. Столько десятков ещё осталось разделить. Сравниваем остаток с делителем: два меньше трёх. Деление выполнено верно. Записываем следующую цифру делимого рядом с остатком. Делим единицы. Двадцать один разделить на три – семь. Находим остаток: семь умножить на три – двадцать один. Столько единиц разделили.
Рассмотрим ещё один пример. Две тысячи пятьсот восемьдесят три разделить на три.
|
|
Этап закрепления знаний
|
|
Задание Назовите, сколько цифр будет в каждом частном. Обоснуйте своё решение. 2 736 : 6 4820 : 2
Во втором выражении в частном будет четыре цифры, так как первое неполное делимое 4 тыс.
Задание Проверьте начало решения и закончите деление. Проверим.
Задание 532 : 2 = 266 3192 : 6 = 532 920 : 5 = 184 1472 : 8 = 184
Первое неполное делимое… Разделю… Умножу … Вычту… Сравню остаток с делителем… Второе неполное делимое…
Задача В магазине было 1327 кг конфет. В первый день продали 156 кг, во второй в 3 раза меньше, чем в первый день. Сколько конфет продали в третий день, если осталось 600 кг конфет. Решение: 1) 156 : 3 = 52 (кг) – продали во второй день 2) 156 + 52 = 208 (кг) – продали в первый и второй день 3) 1327 — 600 = 727 (кг) – продали за три дня 4) 727 — 208 = 519 (кг) – продали в третий день. Ответ: 519 килограммов.
|
|
Этап подведения итогов
|
|
Сегодня на уроке я узнал… На уроке я научился… Мне легко далось… У меня вызвало затруднение…
Рефлексия
|
|
Нарисуйте в тетради маленький круг. |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Урок математики 4 класс — математика, уроки
Откройте учебники на маршрутных листах и посмотрите какие темы вы уже изучили?
Какие единицы массы вы знаете?
А назовите их в порядке увеличение?
Молодцы.
Какая следующая тема, которую вы изучили?
Чему вы учились на уроке при изучение этой темы?
Какая же следующая тема?
А какие единица S вы знаете?
А какое правило вы знаете для единицы S?
Правильно.
А сегодня на уроке мы с вами будем изучать, новый большой который называется ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ.
И первая наша тема будет Деление- действия, обратное умножению.
Как вы думаете, чему мы будем учиться сегодня на уроке?
Правильно, делить многозначные числа и результат записывать уголком т.е. письменно.
Но сначала повторим связь между умножение и делением.
Откроем учебник на странице 48.
Прочитайте про себя задание №1 (а) и рассмотрите схему № 1.
Давай те рассмотри схему. Какие величины даны в схеме?
Как связаны величины между собой?
Сколько в день состоялось матчей чемпионата по футболу?
Сколько команд принимало участие во встрече?
А если у нас состоялось 8 матчей, то значит сколько команд принимало участие в первый день.?
Сколько игроков в одной команде?
Как же нам узнать общее количество игроков?
Запишите в тетрадях и скажите ответ.
Прочитайте задачу под буквой (б)
Какие величины даны в этой схеме?
Что нам известно?
Сколько?
Сколько игроков в команде?
Как получим число команд?
Запишите в тетрадях.
Как записали ответ?
Итак, посмотрите еще раз на схемы, и скажите, как же связаны умножение и деление?
Выполним №2.(а) (устно)
68:17=4 Как проверим?
Верно.
75:15=7 Проверим.
Неверно.
140:28=5 Верный ли это ответ.
Верно.
204:6=36 Проверим.
Ответ не верен.
Решим под буквой (б) письменно. Методом подбора.
63:21=
72:18=
92:23=
98:14=
74:37=
А теперь давайте немного отдохнем.
Если вам трудно делить, то делить можно выполнить уголком.
Разделим вместе с вами 154:22. Записываем уголком так как записано на доске.
Давайте попробуем определить цифру в частном.
Какой вычислительный разряд в числе 154?
Можем ли мы одну сотню разделить на 22?
Значит делить будем все число 154, и в ответе поставим точку, это значит, что будем однозначное число.
Чтобы удобнее подобрать цифру в частном, округлим 154 до 150, а 22 до 20. Чтобы разделить 150 на 20 достаточно 15:2, это примерно получится 7.
Цифра 7 и будет нашем пробным числом. Проверим ее. Для этого 22*7=20*7 получим, и 2*7 получим 14, 140+14= 154. Вычислим остаток 154-154=0. Закончили деление.
А теперь таким же способом выполним №3.
133:19
Делить будем всё число.
133 округляем до…
19 округлим до……
Значит 130:20, для этого 13:2 получим примерно 6.
Проверим. 19*6= 10*6=60+9*6=54. Значит 60+54=124.
Не правильно. Попробуем число 7. 19*7=10*7=70+9*7=63. 70+63=133. Записываем в частном 7. Делаем проверку 133-133=0. Деление закончили.
Смотри далее.
108:18.
Делить будем все число.
108 округляем до
18 округлим до
100:20, для этого 10:2=5. Проверим .18*5=10*5=50+8*5=40=50+40=90. Неправильно
Возьмем цифру 6.18*6=10*6+8*6=60+48=108.
Делаем проверку. В частном записываем 6. Деление закончено.
Рассмотрим следующий пример.
279:31. Делить будем всё число.
279 округлим до
31 округлим до
200:30=20:3=6. Проверим. 31*6=30*6+1*6=180+6=186.
Проверим. 31*6=30*6+1*6=180+6=186.
Неправильно. Возьмем 7. Проверим.31*7=30*7+1*7=210+7=217. Не подходит. Возьмем 9. Проверим. 31*9=30*9+1*9=270+9=279.
В частном запишем 9. Проверим остаток 0. Деление закончено.
Следующий пример попробуйте решить самостоятельно.
Проверим.
168:24=160:20=16:2=8.24*8=20*8+4*8=160+32=192. Много возьмем 7.
24*7=20*7+4*7=140+28=168.
243:27=240:30=24:3=8. Проверим.27*8=20*8+7*8=160+56=216. Не подходит. Берем по 9.27*9=20*9+7*9=180+63=243. Деление закончено.
464:58=400:50=40:5=8. Проверим. 58*8=50*8+8*8=400+64=464.
292:73=200:70=290:7=4. Проверим. 73*4=70*4+3*4=280+12=292.
390:65=300:60=30:6=5. Проверим.65*5=60*5+5*5=300+25=325. Не подходит берем по 6. Проверим. 65*6=60*6+6*5=360+30=390.
420:84=400:80=40:8=5. Проверим. 84*5=80*5+4*5=400+20=420.
Молодцы.
Итак наш урок подошел к концу, давай те вспомним чему мы с вами учились?
Грамм, килограмм, тонна, центнер.
Гр, кг ,ц, т.
Умножать многозначные числа столбиком.
Делить многозначные числа.
Число команд, число игроков в команде, общее число игроков.
8
2
16
11
16*11=176(и)
Ответ: общее кол-во игроков 176
Читают
общее число игроков. Число игроков в команде, число команд.
Общее кол-во игроков
352
11
352:11=32(к)
Число команд=32
4*17=68
7*15=105
5*28=140
36*6=216
3
Сотни.
Нет
130
20
100
20
200
30
336:42. Делим полное
число. Для этого 336
округлим до 300, а 42
до 40. 300: 40=
30: 4=7.Проверим.
42*7=40*7+2*7=
280+14=294.
Не подходит. Возьмем 8. Проверим.42*8=40*8+2*8
=320+16=336. В частном пишем 8. Делаем проверку. Деление закончено.
Делить многозначные числа уголком.
«Деление. Деление многозначных чисел столбиком»
В этом уроке мы изучим деление чисел. Деление чисел считается непростой операцией, как в освоении, так и в использовании. Рекомендуем набраться терпения и осилить этот урок до конца.
Содержание урока
Что такое деление?
Деление — это операция, позволяющая разделить числа. Деление состоит из трёх параметров: делимого, делителя и частного.
- Делимое — это число, которое делят.
- Делитель — это число, которое указывает на сколько частей надо разделить делимое.
- Частное — это собственно результат.
Например в выражении 10: 2 = 5
10 это делимое (число, которое делят).
2 — делитель (показывает на сколько частей надо разделить делимое, т.е. десятку)
5 — частное (результат деления 10 на 2).
Если мы представим десятку в виде десяти единичек:
и разделим эти единички поровну на две группы:
то получим по пять единичек в каждой группе. Так можно понять суть выражения 10: 2 = 5 и вообще суть деления в общем.
Так можно понять суть выражения 10: 2 = 5 и вообще суть деления в общем.
Говоря о делении, можно рассуждать и по-другому. Например, вернёмся к предыдущему выражению 10: 2 = 5. Можно посмотреть на делитель и задать вопрос: сколько двоек в десятке? И ответить: пять двоек. Действительно, если сложить подряд пять двоек, мы получим число десять:Еще один пример на подобное рассуждение. Найти значение выражения 8:4. Смотрим на делитель и спрашиваем: сколько четвёрок в восьмёрке? Отвечаем: две четверки. Действительно, если сложить две четвёрки, получим число 8:
С помощью переменных деление можно записать так:
Чтобы научиться быстро делить надо в первую очередь знать наизусть таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это обратная операция умножению. Например, если 5 × 5 = 25, то 25: 5 = 5.
Видно, что второе выражение записано в обратном порядке. Единственное отличие — это знак деления. Знак деления выглядит в виде двоеточия: но также можно встретить знак ÷ (двоеточие и чёрточка).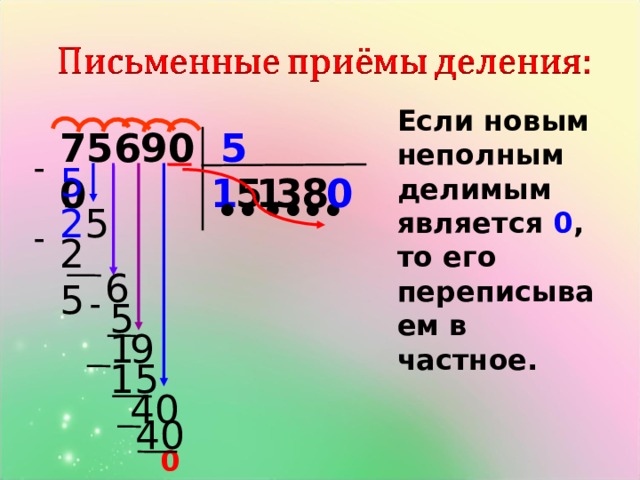 Какой из значков использовать человек решает сам. Мы советуем использовать двоеточие, поскольку оно выглядит аккуратнее и красивее.
Какой из значков использовать человек решает сам. Мы советуем использовать двоеточие, поскольку оно выглядит аккуратнее и красивее.
Деление с остатком
Остаток — это то, что осталось от операции деления неразделённым. Например, девять разделить на два будет четыре и один в остатке:
9: 2 = 4 (1 в остатке)
Можно проверить это умножением вот так:
(4 × 2) + 1 = 9
Если мы представим девятку как девять единичек:
И разделим эти единички поровну на две группы:
то получим по четыре единички в каждой группе, и одну единичку в остатке. Так можно понять суть выражения 9: 2 = 4 (1 в остатке) и вообще суть деления с остатком в общем.
Деление уголком
Когда требуется разделить большое число, то прибегают к такому способу, как деление уголком. Прежде чем делить уголком, человек должен понимать:
- обычное деление маленьких чисел
- деление с остатком
- умножение в столбик
- вычитание в столбик
Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9: 3. Уголком это выражение записывается следующим образом:Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Пусть требуется найти значение выражения 9: 3. Уголком это выражение записывается следующим образом:Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:
Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель, и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:
Теперь от делимого отнимаем девятку, которую мы под ним написали: 9 — 9 = 0. Остаток равен нулю. Другими словами, остатка нет. Значит деление успешно завершено:
Пример 2 . Найти значение выражение 8: 3
Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. Очевидно, здесь будет присутствовать остаток от деления. Сначала записываем данное выражение уголком:
Теперь надо задать вопрос: сколько троек в восьмёрке? В восьмёрке две тройки. Это можно увидеть даже воочию, если представить восьмёрку как восемь единичек:
В школе частное подбиралось путем подбора. Наверное, вы тоже слышали такие слова как «берём по-одному» , «берём по два» или «берём по три». Это как раз тот случай. Мы с вами взяли «по два», ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
Наверное, вы тоже слышали такие слова как «берём по-одному» , «берём по два» или «берём по три». Это как раз тот случай. Мы с вами взяли «по два», ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:
Теперь «вынимаем» остаток. Для этого, умножаем частное на делитель (2 на 3) и записываем полученное число под делимым (под восьмёркой):
Далее, из 8 вычитаем 6. Полученное число и будет остатком:
8: 3 = 2 (2 в остатке)
Проверка: (3 × 2) + 2 = 6 + 2 = 8
Деление многозначного числа на однозначное
Сразу предупреждаем, данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать изучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.
В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.
Если непонятно, что такое однозначные и многозначные числа, советуем изучить . Там написано об этом коротко и без воды.
Там написано об этом коротко и без воды.
Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить делится ли оно на делитель. Если делится — разделить, если нет, то посмотреть делятся ли на делитель первые две цифры многозначного числа. Если первые две цифры делятся на делитель — разделить, если нет, то проверить делятся ли первые три цифры многозначного числа на делитель. И так до тех пор, пока не будет осуществлено первое деление.
Сложно? Ни чуть, если мы разберём несколько примеров.
Пример 1 . Найти значение выражения 25: 3
25 это многозначное число. 3 — однозначное. Применяем правило. Смотрим на первую цифру многозначного числа. Первая цифра это 2. Два делится на три? Нет. Значит смотрим первые две цифры многозначного числа. Первые две цифры это 25. Двадцать пять можно разделить три? Да, хоть и с остатком, но можно. Записываем в столбик данное выражение и начинаем делить:
Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему. Если найдем такое произведение, то необходимо «забрать» оттуда множитель, который дал такое произведение:
Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему. Если найдем такое произведение, то необходимо «забрать» оттуда множитель, который дал такое произведение:
Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему. Очевидно, это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.
Данная восьмёрка и отвечает на наш вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:
Теперь вынимаем остаток. Для этого, умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:
Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:
25: 3 = 8 (1 в остатке)
(3 × 8) + 1 = 24 + 1 = 25
Есть и второй метод. Точнее тот же метод, но немного проще. В выражении 25: 3 мы смотрели делится ли первая цифра числа 25 на 3. Если делится, то делили, а если нет — смотрели две цифры. Две цифры вместе разделились, и мы продолжили решать наш пример.
Если делится, то делили, а если нет — смотрели две цифры. Две цифры вместе разделились, и мы продолжили решать наш пример.
Но можно сделать и так: сначала посмотреть на первую цифру делимого и проверить больше ли она делителя. Если больше, то разделить, а если нет — посмотреть сразу две цифры. Если две цифры больше делителя, то разделить, а если нет — посмотреть сразу три цифры.
Например, разделим 326 на 4.
Смотрим на первую цифру числа 326. Первая цифра 3. Она больше делителя 4? Нет. Значит смотрим сразу две цифры делимого. Две цифры делимого это число 32. Больше ли оно делителя 4? Да. Значит делим. Записываем в столбик данное выражение:
Теперь задаём вопрос: сколько четвёрок в числе 32. В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:
Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:
Теперь как обычно умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Пока пример не завершен, ноль не пишут:
Далее вычитаем это число из 32. Получим 0. Пока пример не завершен, ноль не пишут:
Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:
Теперь делим 6 на 4. Для этого задаём вопрос: сколько четвёрок в шестёрке? В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть единичек:
Записываем единицу в правом уголке нашего ответа:
Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:
Затем из 6 вычитаем 4, получаем число 2, которое является остатком:
Получили 326: 4 = 81 (2 в остатке)
Проверка: (81 × 4) + 2 = 324 + 2 = 326
Процедура в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого .
Например, вернёмся к предыдущему примеру 326: 4. Первое неполное делимое в данном выражении было число 32, т.к. его мы разделили в первую очередь.
А в выражении 25: 3, первое неполное делимое было 25.
Пример 3 . Найти значение выражения 384: 5
Записываем данное выражение в столбик:
Сначала находим первое неполное делимое . Первая цифра меньше делителя, значит смотрим сразу две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет нашим первым неполным делимым . Его и будем делить на делитель:
Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему. Найдя такое произведение, нужно «забрать» оттуда множитель, который будет отвечать на наш вопрос:
Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему. Очевидно, это произведение 35, которое выделено синим. Из этого выражения «забираем» множитель, который дал такое произведение. Это множитель 7, который выделен красным.
Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:
Записываем эту семёрку в правом уголке нашего примера:
Умножаем 7 на 5, получаем 35 и записываем его под 38:
Теперь из 38 вычитаем 35, получим 3:
Эта тройка является остатком, которая осталась неразделенной в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе тройкой:
Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого, снова спрашиваем себя сколько пятёрок в числе 34. Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему:
Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения «забираем» множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:
Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:
Теперь вычитаем из 34 число 30, получим 4. Эта четвёрка будет остатком от деления 384 на 5
Эта четвёрка будет остатком от деления 384 на 5
384: 5 = 76 (и 4 в остатке)
Проверка: (76 × 5) + 4 = 380 + 4 = 384
Пример 4. Найти значение выражения 8642: 4
Этот пример немного посложнее. Записываем в столбик данное выражение:
Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2:
Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под нашим первым неполным делимым:
8 — 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не пишем. Далее сносим 6 и делим его на делитель, получаем 1:
Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:
Получили остаток 2. Это остаток, который остался от деления 6 на 4.
Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6:
Умножаем 6 на 4, получаем 24. Записываем это число под 24:
Записываем это число под 24:
24 — 24 = 0. Ноль это остаток от деления 24 на 6. Ноль как мы уже договорились — не пишем. Далее, сносим последнюю цифру 2:
Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Поэтому, два разделить на четыре это ноль:
Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:
Теперь находим остаток: 2 — 0 = 2. Двойка это остаток от деления 8648 на 4. Таким образом, пример завершён:
8642: 4 = 2160 (2 в остатке)
Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642
Деление чисел у которых на конце 0
Чтобы разделить число у которого на конце ноль, нужно временно отбросить этот ноль, осуществить обычное деление, и приписать этот ноль в ответе.
Например, разделим 120: 3
Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:
И дописываем этот ноль в частном. В итоге получаем 40:
Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее как обычно находим остаток 120 — 120 = 0. Остаток равен нулю. Пример завершён.
Проверка 40 × 3 = 120.
Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:
12: 3 = 4 (делимое без нулей на конце)
120: 3 = 40 (здесь у делимого один ноль)
1200: 3 = 400 (здесь у делимого два нуля)
12000: 3 = 4000 (здесь у делимого три нуля)
В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.
Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5:
Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:
Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.
Например, найдём значение выражения 1400: 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком, или собрать ответ подобно конструктору. Давайте рассмотрим второй способ.
Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:
1000 + 400 = 1400
Можно отдельно разделить 1000 на 5 и отдельно разделить 400 на 5:
1000: 5 = 200
400: 5 = 80
И полученные частные сложить:
200 + 80 = 280
Итого: 1400: 5 = 280
Решим этот же пример уголком:
Деление многозначного числа на многозначное
Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так просто.
Чтобы разделить многозначное число на многозначное, нужно в первую очередь хорошенько разобраться в . Если забыли, советуем повторить — мы изучали это ранее.
Если забыли, советуем повторить — мы изучали это ранее.
Принцип деления остаётся тем же, что и раньше. Здесь также надо находить первое неполное делимое. Здесь также могут присутствовать остатки от деления.
Для начала введём новое понятие — круглое число . Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 500, 600, 1000, 13000 и т.д.
Любое число можно превратить в круглое. Для этого, первые цифры образующие старший разряд, оставляют без изменений, а остальные цифры заменяют нулями. Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10
Еще пример. Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.
Еще пример. Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.
Еще пример. Превратим число 13 735 в круглое число. Первые две цифры 13 образуют старший разряд (разряд десятков тысяч) — эти две цифры оставляем без изменений, а остальные цифры 735 заменяем нулями. В итоге получаем 13 000.
Как видите, ничего сложного нет. Главное, хорошо разбираться в разрядах.
Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное приходится находить методом «подбора». Для этого, прибегают к различным техникам, например, превращают делимое и делитель в круглое число.
Пример 1. Найти значение выражения 88: 12
Записываем данное выражение уголком:
Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.
Если вы помните, то в школе частное подбиралось методом угадывания, говоря «берем по два» или «берем по три». Не все помнят, что на это уходило много времени и нервов.
Не все помнят, что на это уходило много времени и нервов.
Давайте и мы попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число, которое меньше делимого, но очень близко к нему или равно ему.
Давайте, предположим, что частное равно 2. Умножаем это частное на делитель 12:
Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка, как частное не подходит. Угадываем следующее число. Допустим частное равно 5:
Что это нам дало? Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит. Попробуем сразу взять по 8:
На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять 7:
Наконец-то нашли подходящее частное. Умножим частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого, из 88 вычитаем 84, получаем 4.
Умножим частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого, из 88 вычитаем 84, получаем 4.
88: 12 = 7 (4 в остатке)
Проверка: (12 × 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.
Чтобы сэкономить время, надо делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел, и просто разделить 9 на 1. В итоге получим 90: 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, потому что у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90: 9 = 10. В итоге получаем 900: 90 = 10.
В итоге получаем 900: 90 = 10.
В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.
Ещё примеры где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:
800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)
800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)
900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)
400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)
320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)
Если вы заметили, всё в конечном итоге сводится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.
Теперь давайте решим предыдущий пример 88: 12 где мы бились, находя частное методом угадывания. Для начала превращаем делимое и делитель в круглые числа.
Круглое число для 88 будет число 80.
А круглое число для 12 будет число 10.
А затем делим полученные круглые числа:
80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:
Теперь проверяем, верно ли подобралось частное. Для этого, умножаем частное на делитель (8 на 12). Восьмёрку, как частное мы уже проверяли, когда решали этот пример методом угадывания. Если помните, она не подошла, т.к. после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.
Отсюда можно сделать вывод, что в выражении 88: 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача — уменьшить это частное на единицу.
Так и сделаем уменьшим 8 на единицу: 8 — 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:
Как видите, этим способом мы решили этот пример намного быстрее.
Пример 2. Найти значение выражения 1296: 144
Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:
Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.
Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.
Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144:
Десятка не подходит, т.к. при умножении получается число, которое больше делимого.
Попробуем «взять по 9», уменьшив десятку на единицу.
Теперь проверяем девятку. Для этого умножаем её на делитель:
Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что данное деление осуществилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296:
1296: 144 = 9
Проверка: 144 × 9 = 1296
Пример 3 . Попробуем решить большой и сложный пример 227 492: 331
Записываем уголком данное выражение.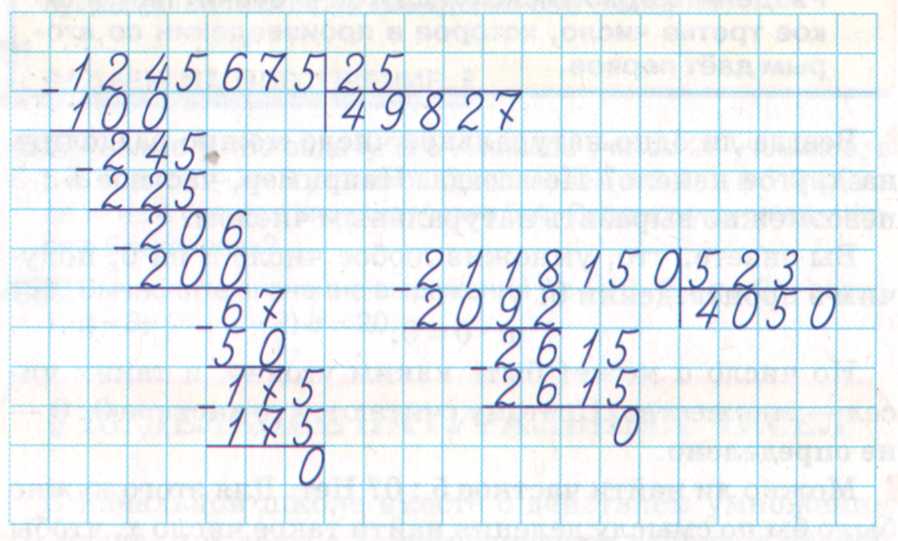 Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит, сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит, сначала будем делить 2274 на 331. Их же превратим в круглые числа.
Для 2274 круглым числом будет 2000. А для 331 круглым числом будет 300:
Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:
Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы «взяли по семь», то получилось бы следующее:
Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.
Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:
Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и сразу же делим их. Сразу же проверяем полученное таким способом частное:
Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придется проводить методом угадывания частного:
Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придется проводить методом угадывания частного:
Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:
Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли «по девять», то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.
Теперь, как обычно вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241:
241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:
Теперь делим 2412 на 331. Возьмём «по семь»:
Теперь находим последний остаток. Для этого, из 2412 вычитаем 2317, получаем 95. На этом пример завершается.
227 492: 331 = 687 (95 в остатке)
Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492
На этом данный урок завершаем. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается не сразу, а со временем. Самое главное понимать.
Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается не сразу, а со временем. Самое главное понимать.
Для закрепления материала разберите следующие примеры, которые уже решены. Можете воспользоваться калькулятором.
Пример 1 . Найти значение выражения: 325: 5
Решение:
Проверка 65 × 5 = 325
Пример 2. Найти значение выражения 16 250: 25
Решение:
16 250: 25 = 650
Проверка : 650 × 25 = 16 250
Пример 3. Найти значение выражения 1257: 79
Решение:
1575: 79 = 15 (72 в остатке)
Проверка: (15 × 79) + 72 = 1185 + 72 = 1257
Пример 4 . Найти значение выражения 165 325: 425
Решение:
165325: 425 = 389
Проверка : 389 × 425 = 165 325
Пример 5. Найти значение выражения 328 911 256: 4523
328 911 256: 4523 = 72 719 (3 219 в остатке)
Проверка : (72 719 × 4 523) + 3 219= 328 908 037 + 3 219
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Прием деления в столбик прост и удобен в случае, если под рукой не оказалось калькулятора, а в уме рассчитать частное сложно.
В дальнейшем мы будем оперировать следующими понятиями:
- делимое — это то число, которое мы делим;
- делитель — то, на что делим;
- частное — результат операции деления.
Для деления столбиком запись необходимо переписать таким образом, чтобы «уголок» отделял делимое и делитель, как показано на рисунке. В свободный угол будем вписывать частное.
Смотрим на первую цифру делимого. Если оно меньше делителя, сравниваем с делителем двузначное число, состоящее из первых двух цифр делимого. Мы нашли, что в рассматриваемом примере как раз такой случай. Двузначное число превышает делитель. Находим их частное, записываем под уголок. Затем перемножаем частное и делитель и полученный результат подписываем под наше двузначное делимое. Вычитаем из большего меньшее, подводим горизонтальную черту, под нее записываем результат (это остаток от деления).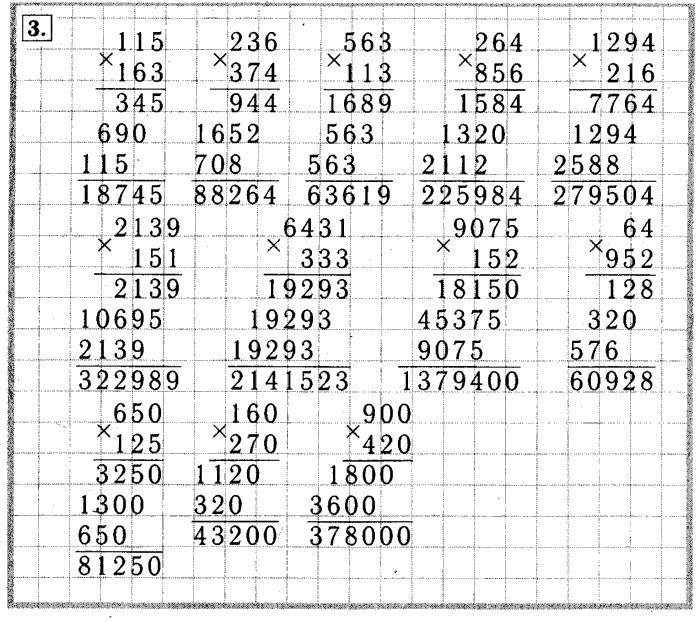 Если остаток больше делителя, ищите ошибку!
Если остаток больше делителя, ищите ошибку!
Теперь спускаем к нашему остатку следующую цифру делимого. Опять сравниваем получившееся число с делителем, если меньше — добавляем следующую, но в частное при этом приписываем 0. Итак, мы вычленили из делимого число, превышающее делитель. Повторяем действия предыдущего пункта.
Повторяем алгоритм 4-го пункта до тех пор, пока не будут «спущены» все цифры делимого. Если последний остаток меньше делителя — решение завершено. Если остаток равен нулю, значит, делимое делится на делитель нацело. В итоге получаем в качестве частного число под «уголком». Не забудьте выполнить проверку: перемножьте частное с делителем, если результат равен делимому, значит, решение найдено верно.
Не пугайтесь вида записи, разобравшись один раз в делении столбиком, вы поймете, насколько легко и удобно считать именно так.
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.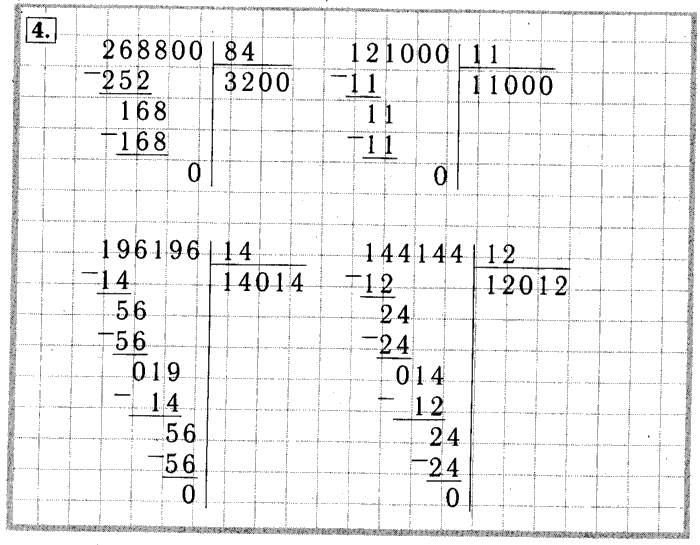
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.
Пошаговая инструкция обучения делению столбиком
Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8. Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211. Результат необходимо перепроверить обратным умножением.
Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211. Результат необходимо перепроверить обратным умножением.
В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:
- Берем первую цифру числа, делим ее на делитель. Сколько раз делитель может содержаться в делимом?
- Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
- Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.

- Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
- Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.
На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.
Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки.
Для того чтобы в школе у ребенка не было проблем с уроками, необходимо давать ему базовые знания с самого раннего возраста.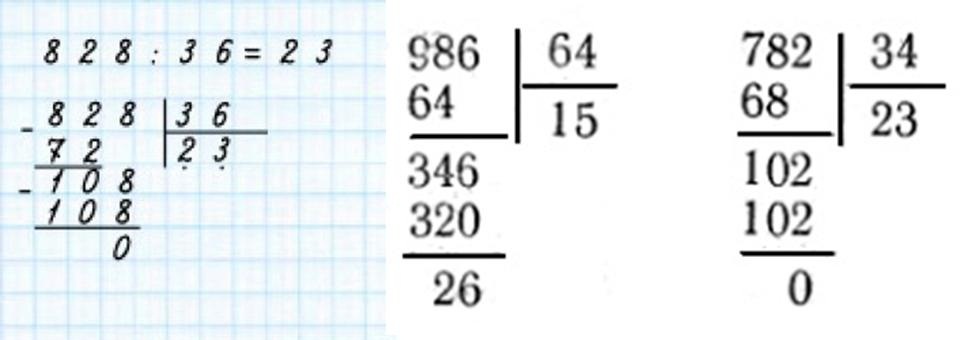 Ведь намного проще объяснить ему некоторые вещи в процессе игры, а не во время строгого школьного урока.
Ведь намного проще объяснить ему некоторые вещи в процессе игры, а не во время строгого школьного урока.
Принцип деления для детей
Ребенок часто сталкивается со многими математическими понятиями, даже не догадываясь о них. Ведь все мамы, играя с малышом, рассказывают о том, что у папы супа налито больше, к бабушке идти дольше, чем до магазина и прочие простые примеры. Все это дает малышу начальное представление о математике.
Стоит попробовать предложить ребенку поиграть в игры с делением. Поделите яблоки (груши, вишни, конфеты) между мамой и ребенком, постепенно добавляя и других участников: папу, игрушку, кошку. В начале малыш будет делить, раздавая всем по одному предмету. А вы потом подведите итог. Скажите ему, что было всего 6 яблок, вы разделили их на троих человек, и каждому досталось по два. Объясните, что слово разделить – это значит раздать всем поровну.
Если вам нужно объяснить деление с цифрами, то также можно привести игровой пример. Скажите, что цифры – это те же яблоки. Расскажите, что то число яблок, которое нужно разделить – это делимое. А то число человек, на которых нужно поделить эти яблоки – это делитель. Покажите несколько примеров наглядно. В игровой форме ребенок обязательно все поймет.
Скажите, что цифры – это те же яблоки. Расскажите, что то число яблок, которое нужно разделить – это делимое. А то число человек, на которых нужно поделить эти яблоки – это делитель. Покажите несколько примеров наглядно. В игровой форме ребенок обязательно все поймет.
Как научить ребенка делению столбиком?
Если вы учите ребенка делить столбиком, то, скорее всего сложение, вычитание и умножение в столбик он уже освоил. Если нет, то обязательно подтяните эти знания, иначе, добавив еще и деление, ребенок вообще запутается.
Итак, делим в столбик. Возьмем не сложный пример: 110 нужно поделить на 5.
- Запишем делимое — 110, а рядом с ним делитель – 5.
- Разделим все это уголком.
- Начинаем объяснять, вот пример диалога:
-Первая цифра 1. 1 на 5 делится?
-Нет.
-Значит, берем следующую самую маленькую возможную цифру, которая делится на 5 – это 11. Сколько раз цифра 5 может поместиться в 11?
-Два раза.
— Записываем цифру 2 в уголке под пятеркой. Проверяем, умножаем 5 на 2.
— Получается 10.
— Записываем это число под 11. Делаем вычитание. 11 минус 10?
— Равно 1.
— Пишем 1 и рядом сносим 0 из делимого (110 которое). Получилось 10. 10 на 5 делится?
— Да, получается 2.
— Записываем 2 под 5.
Для того чтобы облегчить изучение деления, сейчас появились таблицы деления для детей. Принцип действия у них тот же, что и у таблицы умножения. Вот только надо ли учить таблицу деления, если уже выучил умножение? Это будет зависеть от школы и преподавателя.
просмотров
Разделяй многозначные числа
ЕЖЕДНЕВНЫЕ УПРАЖНЕНИЯ ДЛЯ МОЗГА
🤔 Угадай год исторического события
PLAY YEARLE
Интерактивные упражнения
Результаты
Обучение
Интерактивные упражнения — Деление многозначных чисел
Интерактивные упражнения являются общими, приложение составляет новую серию задачи при каждом запуске.

ИНТЕРАКТИВНЫЕ УПРАЖНЕНИЯ
| Интерактивные упражнения: | {{восстановить}} |
| Имя: | |
| Виртуальная клавиатура: |
| Количество задач: | {{(плинум)}} |
| Сложность: | {{ресдифи}} |
СТОП УПРАЖНЕНИЯ
{{$индекс+1}}. задача
{{one.qins}}
{{one.qtxt.rsT}} | {{one.qtxt.rsS}} | {{один.qtxt.rsD}} | {{один.qtxt.rsE}} | : | {{один.qtxt.nuB}} | = | ||||
7
8
9
←
→
4
5
6
↑
1
2
3
. Правильный ответ
Правильный ответ
CE
.
{{shareResHtml.length}}
КОПИРОВАТЬ
РЕЗУЛЬТАТ
| Интерактивные упражнения: | {{восстановить}} |
| Имя: | |
| Дата: | {{время * 1000 | дата:’дд.мм.гггг ЧЧ:мм:сс’}} |
| Номер. задач: | {{(ответ+ответ)}} |
| Сложность: | {{ресдифи}} |
| Правильный ответ: | {{анскор}} |
| Неправильные ответы: | {{ответ}} |
| Эффективность: | {{анскор/(анскор+ответ)*100|число:0}} % |
| Время: | {{tmdur}} с |
| Время на задачу: | {{tmdur / (anscor+answer)|номер:1}} с |
Сохраните результат и отслеживайте свой прогресс.
Авторизуйтесь, если у вас еще нет профиля, создайте свой профиль.
КОЛИЧЕСТВО ЗАДАЧ
6
10
15
Сложность
Easy
Средняя
Трудно
Выберите Тип задач
Разделите многочисленные номера
. ЗАДАЧА
ЗАДАЧА
1 7 1 3 : 3 =
Это не ваши результаты.
Войти
чтобы увидеть ваши результаты.
Если у вас еще нет профиля,
создайте свой профиль.
Производительность — Деление многозначных чисел
Доля правильных ответов (в %) для последних {{chrAnum}} упражнений.
Показать: последние 10 упражненийпоследние 20 упражненийпоследние 30 упражнений
ПОКАЗАТЬ
Решаемые по месяцам задачи — Разделить многозначные числа
Количество выполненных задач по месяцам. Одно упражнение обычно содержит от 6 до 15 заданий.
Показать сложность: alleasymediumdifficult
SHOW
Производительность по месяцам — Разделить многозначные числа
Доля правильно решенных задач (в %) по месяцам.
Показать сложность: alleasymediumdifficult
ПОКАЗАТЬ
Задания по сложности — Разделить многозначные числа
Количество решенных задач по сложности в каждом месяце.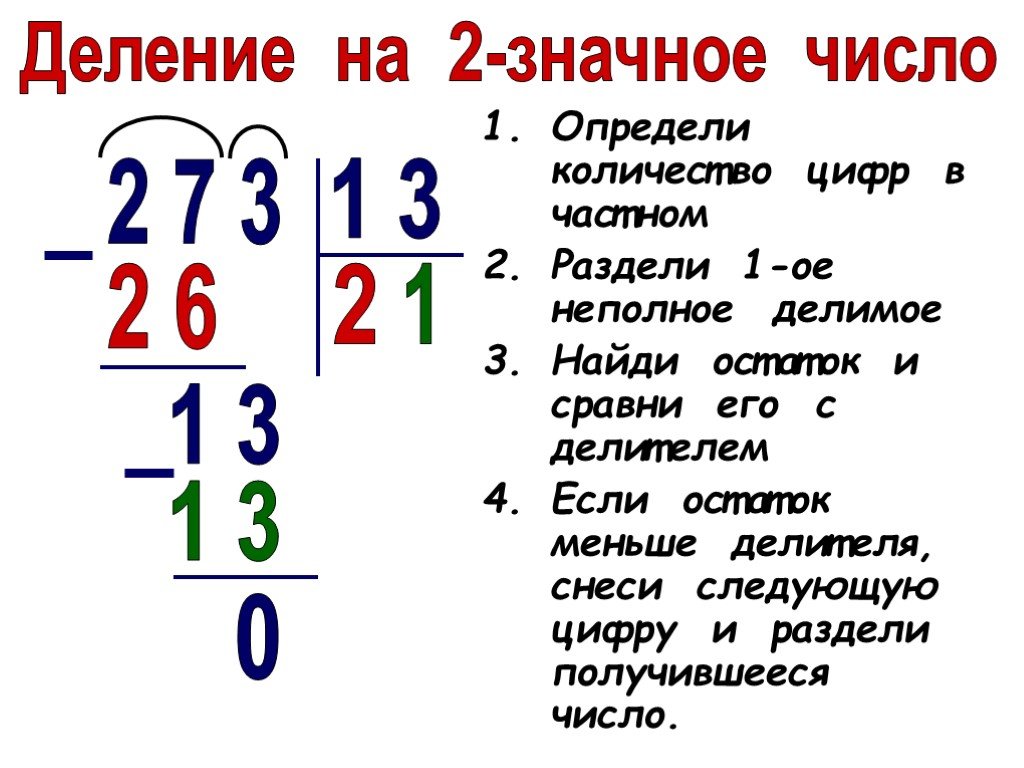
Показать месяц: ЯнварьФевральМартАпрельМайИюньИюльАвгустСентябрьОктябрьНоябрьДекабрь
ПОКАЗАТЬ
Научиться делить многозначные числа
Вводить числа.
РАСЧЕТ
Поделитесь ссылкой на страницу с друзьями.
https://kveez.com/en/math/divide-multi-digit-numbers/
КОПИРОВАТЬ
ИНТЕРАКТИВНЫЕ УПРАЖНЕНИЯ, РАБОЧИЕ ТАБЛИЦЫ – 4 ГОД
Рабочие листы – Разделение многозначных чисел
Создание рабочих листов и ПЕЧАТЬ Спаси их. Вы можете создавать неограниченное количество различных рабочих листов.
1. ВЫБЕРИТЕ НАСТРОЙКИ :: Выберите количество заданий, сложность и тип заданий.
2. СОЗДАТЬ ЗАДАЧИ :: Используйте кнопку СОЗДАТЬ, чтобы создать новую серию задач
если вам не нравится рабочий лист, вы можете легко создать другой.
3. СОЗДАТЬ PDF :: Рабочий лист (PDF) открывается в новой вкладке, вы можете РАСПЕЧАТАЙТЕ или СОХРАНИТЕ на свой компьютер.
КОЛИЧЕСТВО ЗАДАЧ
{{one.num}}
СЛОЖНОСТЬ
{{one.text}}
ВЫБЕРИТЕ ТИП ЗАДАНИЯ
ПРИМЕР ЗАДАНИЯ
СОЗДАТЬ
РАБОЧИЙ ЛИСТ
СОЗДАТЬ PDF
Отзывы
Напишите свое мнение, оценку, критику или предложение.
Пожалуйста
авторизуйтесь, если у вас еще нет профиля,
создайте свой профиль.
Мы используем файлы cookie, чтобы предоставить вам лучший опыт на нашем веб-сайте и персонализировать контент. Пожалуйста, дайте нам знать, если вы согласны.
ДА, СОГЛАСЕН
Свободно делите многозначные числа по стандартному алгоритму.
Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого контрольного показателя для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом тесте.
Уроки STEM — Активность по моделированию
Я хочу сотовый телефон:
Учащиеся разрабатывают процедуру выбора сотового телефона на основе качеств, которые, по их мнению, ценят в сотовом телефоне их родители. Учащиеся представляют свое решение в письменном виде маркетинговой компании, которая хочет использовать результаты для продажи сотовых телефонов родителям учеников начальной школы.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Длинное деление — 1:
Учащихся просят решить три задачи на деление (без остатка), чтобы проверить беглость выполнения стандартного алгоритма деления.
Длинное деление — 2:
Учащихся просят решить три задачи на деление на длинное (одну с остатком), чтобы проверить беглость выполнения стандартного алгоритма на деление на длинное.
Длинное деление — 3:
Учащихся просят решить три задачи на деление на длинное (каждая с остатком), чтобы проверить беглость выполнения стандартного алгоритма деления.
Оригинальные учебные пособия для студентов по информатике
Ферма MacCoder, часть 1. Объявление переменных:
Изучите компьютерное программирование на ферме, объявляя и инициализируя переменные в этом интерактивном учебном пособии. Вы также получите возможность попрактиковаться в своих навыках длинного дивизиона.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом тесте.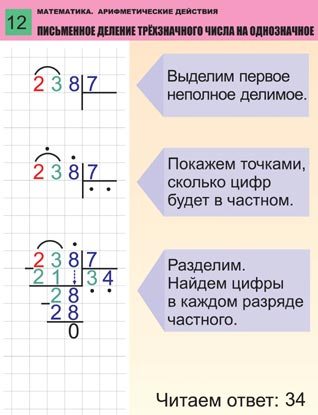
Оригинальный учебник для студентов
Ферма MacCoder, часть 1. Объявление переменных:
Изучите компьютерное программирование на ферме, объявляя и инициализируя переменные в этом интерактивном учебном пособии. Вы также получите возможность попрактиковаться в своих навыках длинного дивизиона.
Тип: оригинальное учебное пособие для учащихся
Задачи решения проблем
Рассуждения об умножении и делении и разрядном значении, часть 2:
Учащихся просят рассуждать и объяснять размещение десятичных знаков в частных.
Тип: Задание на решение задач
Постановка целей:
Целью этого задания является решение учащимися задач на умножение и деление десятичных дробей в реальном контексте постановки финансовых целей. Основное внимание в задании уделяется моделированию и пониманию концепции постановки финансовых целей, поэтому свободное владение вычислениями позволит учащимся сосредоточиться на других аспектах задания.
Основное внимание в задании уделяется моделированию и пониманию концепции постановки финансовых целей, поэтому свободное владение вычислениями позволит учащимся сосредоточиться на других аспектах задания.
Тип: Задача решения проблем
Деятельность студенческого центра
Edcite: Математика 6 класс:
Учащиеся могут практиковаться в ответах на математические вопросы по различным темам. Имея учетную запись, учащиеся могут сохранять свою работу и отправлять ее учителю по завершении.
Тип: Деятельность студенческого центра
Руководство
Процентное слово Проблема:
Используйте длинное деление, чтобы найти проценты в этом уроке.
Тип: Учебное пособие
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Рассуждения об умножении, делении и разрядном значении, часть 2:
Учащихся просят рассуждать и объяснять размещение десятичных знаков в частных.
Тип: Задание на решение задач
Постановка целей:
Целью этого задания является решение учащимися задач на умножение и деление десятичных дробей в реальном контексте постановки финансовых целей. Основное внимание в задании уделяется моделированию и пониманию концепции постановки финансовых целей, поэтому свободное владение вычислениями позволит учащимся сосредоточиться на других аспектах задания.
Тип: Задание на решение задач
2 простых способа обучения многозначному делению
Полное деление для начинающих может быть сложным и разочаровывающим для некоторых учащихся. Но это не обязательно должно быть связано с несколькими умными и привлекательными стратегиями. Мы все знаем, что наши ученики учатся по-разному, поэтому для нас, как для учителей, важно убедиться, что мы представляем много дифференцированного обучения, когда знакомим наших детей с новой концепцией. Я рад поделиться с вами некоторыми из моих самых успешных стратегий обучения делению в столбик, которые вам и вашим ученикам наверняка понравятся.
Мы все знаем, что наши ученики учатся по-разному, поэтому для нас, как для учителей, важно убедиться, что мы представляем много дифференцированного обучения, когда знакомим наших детей с новой концепцией. Я рад поделиться с вами некоторыми из моих самых успешных стратегий обучения делению в столбик, которые вам и вашим ученикам наверняка понравятся.
Стратегия частичного частного для многозначного длинного деления
Хотя эта стратегия может показаться странной на первый взгляд, многие из моих учеников 4-го класса в конечном итоге предпочли эту стратегию деления.
Эта стратегия состоит в том, чтобы разбивать числа на более мелкие и думать о «дружественных числах». Это облегчает учащимся понимание процесса шаг за шагом. Поскольку проблема разбита на части, эта стратегия частичного частного помогает учащимся не чувствовать себя перегруженными.
Посмотрите этот пример с числом 520. Это отличный наглядный пример для учащихся, который поможет им понять, как разбить 520 на более мелкие, более понятные числа.
Разделение процесса на четыре этапа действительно помогает учащимся легко понять концепцию.
Я использую следующие шаги:
- Переименуйте номер и разбейте его на более удобные номера.
- В этом примере переименуйте 520 в 400.
- Начните новую задачу на деление, используя дружественное число 100 вместо 120.
- Повторите и сложите три частных, чтобы получить окончательный ответ.
Готовы попробовать эту технику в своем классе сегодня? Проверьте это частичные коэффициенты БЕСПЛАТНО!
Традиционная стратегия длинного деления
Это также то, что мы называем способом «мама и папа», потому что в целом это то же самое, как нас учили наши родители, когда мы были в начальной школе. Я знаю, что это та же старая стратегия длинного дивизиона, которую я использовал, когда был моложе.
Прежде чем приступить к задаче, я предлагаю учащимся сгенерировать первые 9кратные делителю. Когда я был ребенком, я потратил много времени, пытаясь выяснить, какие мультипликаторы близки к дивиденду. Из-за этого я знаю, что создание списка заранее и обращение к нему на протяжении всей задачи поможет облегчить задачу вашим ученикам.
Из-за этого я знаю, что создание списка заранее и обращение к нему на протяжении всей задачи поможет облегчить задачу вашим ученикам.
Затем мы проводим линии между разрядами делимого. Таким образом, это поможет учащимся увидеть значение каждого разряда и правильно выстроить числа в частном.
Это простое изменение в способе обучения длинному делению четвероклассников, но это ОДНА вещь, которая полностью изменит игру! Каждый раз, когда ваши ученики начинают решать задачу, они тренируются с множителями и распознают закономерности.
Длинное деление может быть забавным и легким
Длинное деление может быть простым для новичков, если вы используете один из этих двух проверенных методов! Я хотел бы знать, используете ли вы одну из этих стратегий или что-то еще! Оставьте комментарий ниже, чтобы рассказать нам о своем любимом способе научить детей делению на две части!
Если вам нужны готовые к печати задания, вам понравится этот длинный набор! Там даже есть специальное место для ваших студентов, чтобы отслеживать кратные в стороне. (Любой, кто преподает в 3, 4 и 5 классах, знает, как важно дать учащимся достаточно ПРОСТРАНСТВА для работы!)
(Любой, кто преподает в 3, 4 и 5 классах, знает, как важно дать учащимся достаточно ПРОСТРАНСТВА для работы!)
Этот комплект дивизии содержит 2 БУМАЖНЫХ пакета дивизии для длинной дивизии для начинающих. Один пакет представляет собой длинное деление без остатков, а второй пакет включает в себя простые остатки.
Используйте эти страницы для быстрых контрольных оценок, занятий по математике, занятий с друзьями, взаимного обучения, небольших групп, домашних заданий, независимого анализа или даже для обогащения.
Long Division Made Easy
Вы всегда можете «РАСЧИТАТЬСЯ НА МЕНЯ» в увлекательных, дифференцированных математических ресурсах, которые помогут каждому учащемуся проявить себя!
Приколи!
Обязательно закрепите эти длинные стратегии деления на своей любимой учительской доске Pinterest, чтобы вы могли вернуться в любое время.
Поделиться:
Почтовые теги: #Длинное деление#Математические факты
Похожие сообщения
Математика для 3 класса | 4-й класс математики | Факт Fun | халява | Умножение
Умножение на 12 с играми, заданиями и песнями
После того, как учащиеся освоили базовое сложение и вычитание, они готовы к забавным занятиям. Одно слово, умножение. Это концепция, которая, как мне кажется, может иметь двоякое значение для студентов. Они либо в восторге от того, что узнают что-то новое, либо сильно беспокоятся о неизвестном умножении. Из-за этого это…
Подробнее Практика умножения на 12 с играми, заданиями и песнямиПродолжить
Дополнение | Мартин Лютер Кинг младший | Умножение
Мартин Лютер Кинг-младший. БЕСПЛАТНЫЕ ПРИЗЫ, книги и ресурсы
День Мартина Лютера Кинга-младшего не за горами, а это значит, что мы должны быть готовы! Этот человек заслуживает нашей чести и уважения, так что что может быть лучше, чем отпраздновать его с Мартином Лютером Кингом-младшим БЕСПЛАТНО, книгами и ресурсами?! И, конечно же, мы не можем забыть о Месяце черной истории в целом! Первый…
Читать дальше Мартин Лютер Кинг-младший БЕСПЛАТНЫЕ ДОМА, Книги и ресурсыПродолжить
Математика для 4 класса | халява
Преобразование десятичных дробей и процентов
 Познакомимся с письменными приёмами деления многозначного числа на однозначное число.
Познакомимся с письменными приёмами деления многозначного числа на однозначное число.


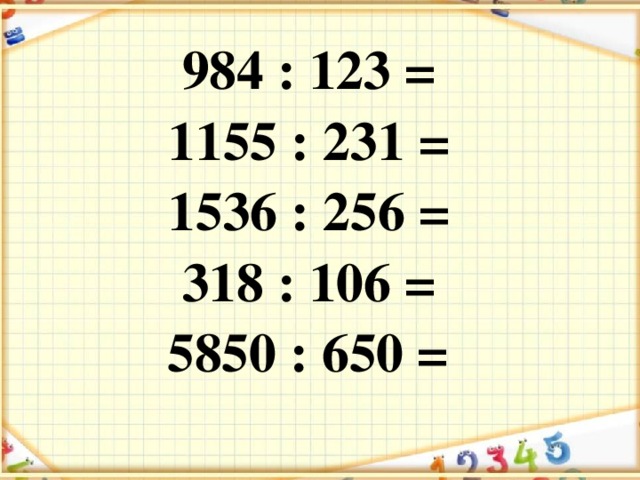 У нас это четыре. Оно показывает количество единиц тысяч в делимом.
У нас это четыре. Оно показывает количество единиц тысяч в делимом. Сравниваем остаток с делителем. Два меньше трёх. Деление выполнено верно.
Сравниваем остаток с делителем. Два меньше трёх. Деление выполнено верно. Это и есть первое неполное делимое.
Это и есть первое неполное делимое. От трёх вычесть три – нуль. Единицы разделили полностью. Деление окончено. Получилось восемьсот шестьдесят один.
От трёх вычесть три – нуль. Единицы разделили полностью. Деление окончено. Получилось восемьсот шестьдесят один.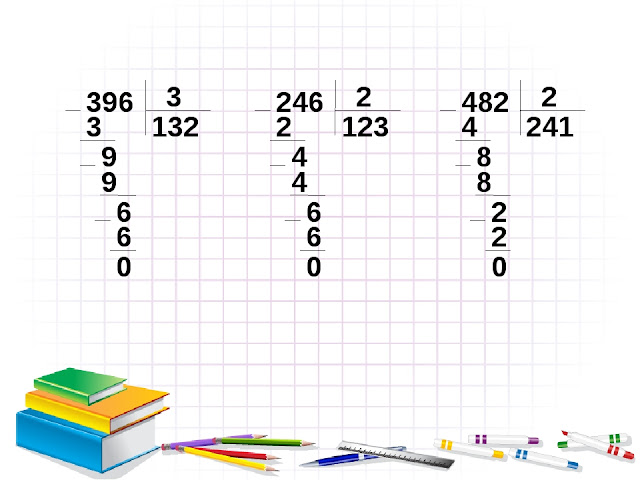 Один на семь не делится. Значит, берём семнадцать. Это единицы тысяч.
Один на семь не делится. Значит, берём семнадцать. Это единицы тысяч.

 Закрасьте его тем цветом, который соответствует вашему настроению.
Закрасьте его тем цветом, который соответствует вашему настроению.