Как умножить обыкновенную дробь: на число, другую дробь

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Умножение обыкновенных дробей

В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь умножить на число или другую дробь, и как найти произведение смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

• Умножение дроби
  • На число
  • На другую дробь
• Произведение смешанных дробей
• Примеры задач

Умножение дроби

На число

Умножение обыкновенной дроби на число n равно сумме, слагаемыми которой является данная дробь n-ое количество раз.

Другими словами, числитель дроби умножается на данное число n, а знаменатель остается тем же.

Примечание: дробь, полученную в результате умножения, следует проверить на предмет того, можно ли ее сократить.

На другую дробь

В результате умножения одной дроби на другую получается новая дробь, числитель которой равняется произведению числителей исходных дробей, а знаменатель – произведению знаменателей.

a/b

⋅

c/d

=

a⋅b/c⋅d

Произведение смешанных дробей

Чтобы умножить смешанные дроби, необходимо их сперва представить в виде неправильных дробей, и только после этого выполнить умножение.

X

a/b

 ⋅ Y

c/d

 = 

X ⋅ b + a/b

 ⋅ 

Y ⋅ d + c/d

Примеры задач

Задание 1

Умножьте дробь 

3/15

 на число 5.

 
Решение

3/15

⋅ 5 =

3⋅5/15

=

15/15

=1

 
Задание 2

Найдите произведение дробей 

9/17

 и 

4/7

.

 
Решение

9/17

⋅

4/7

=

9⋅4/17⋅7

=

36/119

 
Задание 3

Найдите произведение дробей 3

3/8

 и 7

1/9

.

Решение

Т.к. мы имеем дело со смешанными дробями, сперва представим их в виде неправильных, затем выполним умножение.

3

3/8

⋅ 7

1/9

=

3⋅8+3/8

⋅

7⋅9+1/9

=

27/8

⋅

64/9

=

27⋅64/8⋅9

=

1728/72

=24

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Произведение алгебраических дробей квадрат бинома.

Умножение, деление и сокращение алгебраических дробей

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе

упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или, скажем, квадрата суммы, просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,16 2 — 2 3,16 1,16 + 1,16 2 . Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!

Итак, семь формул «школьной» алгебры, которые должны знать все:

Название	Формула
Квадрат суммы	(A + B) 2 = A 2 + 2AB + B 2
Квадрат разности	(A — B) 2 = A 2 — 2AB + B 2
Разность квадратов	(A — B)(A + B) = A 2 — B 2
Куб суммы	(A + B) 3 = A 3 + 3A 2 B + 3AB 2 + B 3
Куб разности	(A — B) 3 = A 3 — 3A 2 B + 3AB 2 — B 3
Сумма кубов	A 3 + B 3 = (A + B)(A 2 — AB + B 2)
Разность кубов	A 3 — B 3 = (A — B)(A 2 + AB + B 2)

Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.

Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).

Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.

Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B) 4 , (A + B) 5 и даже (A + B) n , где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?

Да, подобная закономерность существует. Выражение вида (A + B) n называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B) 4 и (A + B) 5 , а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах.

Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:

(A + B) n = A n + C n 1 A n-1 B + C n 2 A n-2 B 2 + … + C n k A n-k B k + … + B n .

Здесь C n k = n!/(k! (n-k)!).

Напоминаю, что n! — это 1 2 … n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n . Например, 4! = 1 2 3 4 = 24. Факториал нуля считается равным единице!

А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для A n — B n ?

Да, можно. Вот эта формула:

A n — B n = (A — В)(A n-1 + A n-2 B + A n-3 B 2 + … + B n-1).

Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:

A n + B n = (A + В)(A n-1 — A n-2 B + A n-3 B 2 — … + B n-1).

Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.

Обыкновенных дробей.

Сложение алгебраических дробей

Запомните!

Складывать можно только дроби с одинаковыми знаменателями!

Нельзя складывать дроби без преобразований

Можно складывать дроби

При сложении алгебраических дробей с одинаковыми знаменателями :

1. числитель первой дроби складывается с числителем второй дроби;
2. знаменатель остаётся прежним.

Рассмотрим пример сложения алгебраических дробей.

Так как знаменатель у обеих дробей «2а », значит, дроби можно сложить.

Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним. При сложении дробей в полученном числителе приведем подобные .

Вычитание алгебраических дробей

При вычитании алгебраических дробей с одинаковыми знаменателями :

1. из числителя первой дроби вычитается числитель второй дроби.
2. знаменатель остаётся прежним.

Важно!

Обязательно заключите в скобки весь числитель вычитаемой дроби.

Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель «2с », значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби «(a + d) » числитель второй дроби «(a − b) ». Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем правило раскрытия скобок .

Приведение алгебраических дробей к общему знаменателю

Рассмотрим другой пример. Требуется сложить алгебраические дроби.

В таком виде сложить дроби нельзя, так как у них разные знаменатели.

Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю .

Правила приведения алгебраических дробей к общему знаменателю очень похожи на правила приведения к общему знаменателю обыкновенных дробей. .

В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.

Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.

1. Работаем с числовыми коэффициентами. Определяем НОК (наименьшее общее кратное) для всех числовых коэффициентов.
2. Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
3. Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
4. Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.

Вернемся к нашему примеру.

Рассмотрим знаменатели «15a » и «3 » обеих дробей и найдем для них общий знаменатель.

1. Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка делится на каждый числовый коэффициент). Для «15 » и «3 » — это «15 ».
2. Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях. В знаменателях «15a » и «5 » есть только
   один одночлен — «а ».
3. Перемножим НОК из п.1 «15 » и одночлен «а » из п.2. У нас получится «15a ». Это и будет общим знаменателем.
4. Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a »?».

Рассмотрим первую дробь. В этой дроби и так знаменатель «15a », значит, ее не требуется ни на что умножать.

Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3 », чтобы получить «15a »?» Ответ — на «5a ».

При приведении к общему знаменателю дроби умножаем на «5a » и числитель, и знаменатель .

Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через «домики» .

Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.

Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.

Рассмотрим пример вычитания дробей с разными знаменателями.

Рассмотрим знаменатели «(x − y) » и «(x + y) » обеих дробей и найдем для них общий знаменатель.

У нас есть два различных многочлена в знаменателях «(x − y) » и «(x + y) ». Их произведение будет общим знаменателем, т.е. «(x − y)(x + y) » — общий знаменатель.

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать формулы сокращенного умножения .

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

В первой алгебраической дроби знаменатель «(p 2 − 36) ». Очевидно, что к нему можно применить формулу разности квадратов .

После разложения многочлена «(p 2 − 36) » на произведение многочленов
«(p + 6)(p − 6) » видно, что в дробях повторяется многочлен «(p + 6) ». Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6) ».

В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему — сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров

Правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями

Сфор-му-ли-ру-ем пра-ви-ло сло-же-ния (вы-чи-та-ния) ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми (оно сов-па-да-ет с ана-ло-гич-ным пра-ви-лом для обык-но-вен-ных дро-бей): То есть для сло-же-ния или вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми необ-хо-ди-мо со-ста-вить со-от-вет-ству-ю-щую ал-геб-ра-и-че-скую сумму чис-ли-те-лей, а зна-ме-на-тель оста-вить без из-ме-не-ний.

Это пра-ви-ло мы раз-бе-рём и на при-ме-ре обык-но-вен-ных дро-бей, и на при-ме-ре ал-геб-ра-и-че-ских дро-бей.

Примеры применения правила для обыкновенных дробей

При-мер 1. Сло-жить дроби: .

Ре-ше-ние

Сло-жим чис-ли-те-ли дро-бей, а зна-ме-на-тель оста-вим таким же. После этого раз-ло-жим чис-ли-тель и зна-ме-на-тель на про-стые мно-жи-те-ли и со-кра-тим. По-лу-чим: .

При-ме-ча-ние: стан-дарт-ная ошиб-ка, ко-то-рую до-пус-ка-ют при ре-ше-нии по-доб-но-го рода при-ме-ров, за-клю-ча-ет-ся в сле-ду-ю-щем спо-со-бе ре-ше-ния: . Это гру-бей-шая ошиб-ка, по-сколь-ку зна-ме-на-тель оста-ёт-ся таким же, каким был в ис-ход-ных дро-бях.

При-мер 2. Сло-жить дроби: .

Ре-ше-ние

Дан-ная за-да-ча ничем не от-ли-ча-ет-ся от преды-ду-щей: .

Примеры применения правила для алгебраических дробей

От обык-но-вен-ных дро-бей пе-рей-дём к ал-геб-ра-и-че-ским.

При-мер 3. Сло-жить дроби: .

Ре-ше-ние:как уже го-во-ри-лось выше, сло-же-ние ал-геб-ра-и-че-ских дро-бей ничем не от-ли-ча-ет-ся от сло-же-ния обык-но-вен-ных дро-бей. По-это-му метод ре-ше-ния такой же: .

При-мер 4. Вы-честь дроби: .

Ре-ше-ние

Вы-чи-та-ние ал-геб-ра-и-че-ских дро-бей от-ли-ча-ет-ся от сло-же-ния толь-ко тем, что в чис-ли-тель за-пи-сы-ва-ет-ся раз-ность чис-ли-те-лей ис-ход-ных дро-бей. По-это-му .

При-мер 5. Вы-честь дроби: .

Ре-ше-ние: .

При-мер 6. Упро-стить: .

Ре-ше-ние: .

Примеры применения правила с последующим сокращением

В дроби, ко-то-рая по-лу-ча-ет-ся в ре-зуль-та-те сло-же-ния или вы-чи-та-ния, воз-мож-ны со-кра-ще-ния. Кроме того, не стоит за-бы-вать об ОДЗ ал-геб-ра-и-че-ских дро-бей.

При-мер 7. Упро-стить: .

Ре-ше-ние: .

При этом . Во-об-ще, если ОДЗ ис-ход-ных дро-бей сов-па-да-ет с ОДЗ ито-го-вой, то его можно не ука-зы-вать (ведь дробь, по-лу-чен-ная в от-ве-те, также не будет су-ще-ство-вать при со-от-вет-ству-ю-щих зна-че-ни-ях пе-ре-мен-ных). А вот если ОДЗ ис-ход-ных дро-бей и от-ве-та не сов-па-да-ет, то ОДЗ ука-зы-вать необ-хо-ди-мо.

При-мер 8. Упро-стить: .

Ре-ше-ние: . При этом y (ОДЗ ис-ход-ных дро-бей не сов-па-да-ет с ОДЗ ре-зуль-та-та).

Сложение и вычитание обыкновенных дробей с разными знаменателями

Чтобы скла-ды-вать и вы-чи-тать ал-геб-ра-и-че-ские дроби с раз-ны-ми зна-ме-на-те-ля-ми, про-ве-дём ана-ло-гию с обык-но-вен-ны-ми дро-бя-ми и пе-ре-не-сём её на ал-геб-ра-и-че-ские дроби.

Рас-смот-рим про-стей-ший при-мер для обык-но-вен-ных дро-бей.

При-мер 1. Сло-жить дроби: .

Ре-ше-ние:

Вспом-ним пра-ви-ло сло-же-ния дро-бей. Для на-ча-ла дроби необ-хо-ди-мо при-ве-сти к об-ще-му зна-ме-на-те-лю. В роли об-ще-го зна-ме-на-те-ля для обык-но-вен-ных дро-бей вы-сту-па-ет наи-мень-шее общее крат-ное (НОК) ис-ход-ных зна-ме-на-те-лей.

Опре-де-ле-ние

Наи-мень-шее на-ту-раль-ное число, ко-то-рое де-лит-ся од-но-вре-мен-но на числа и .

Для на-хож-де-ния НОК необ-хо-ди-мо раз-ло-жить зна-ме-на-те-ли на про-стые мно-жи-те-ли, а затем вы-брать все про-стые мно-жи-те-ли, ко-то-рые вхо-дят в раз-ло-же-ние обоих зна-ме-на-те-лей.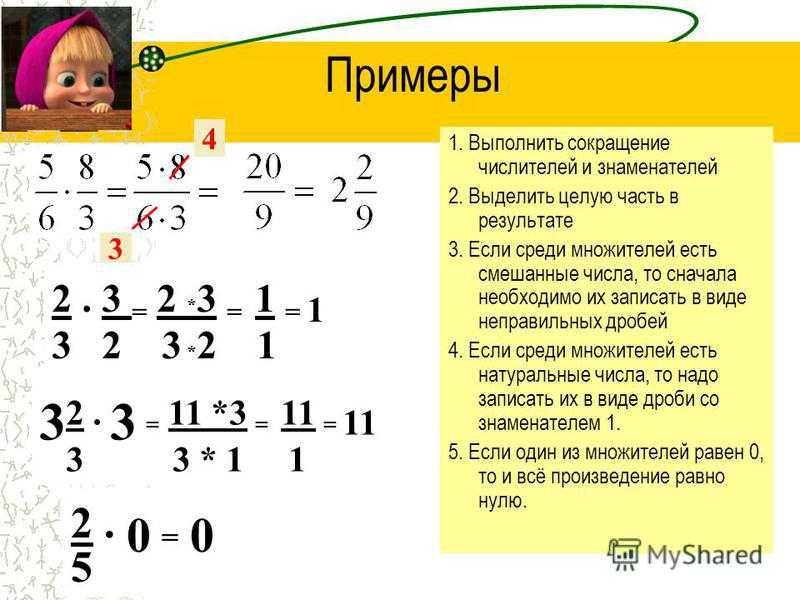

; . Тогда в НОК чисел долж-ны вхо-дить две двой-ки и две трой-ки: .

После на-хож-де-ния об-ще-го зна-ме-на-те-ля, необ-хо-ди-мо для каж-дой из дро-бей найти до-пол-ни-тель-ный мно-жи-тель (фак-ти-че-ски, по-де-лить общий зна-ме-на-тель на зна-ме-на-тель со-от-вет-ству-ю-щей дроби).

Затем каж-дая дробь умно-жа-ет-ся на по-лу-чен-ный до-пол-ни-тель-ный мно-жи-тель. По-лу-ча-ют-ся дроби с оди-на-ко-вы-ми зна-ме-на-те-ля-ми, скла-ды-вать и вы-чи-тать ко-то-рые мы на-учи-лись на про-шлых уро-ках.

По-лу-ча-ем: .

Ответ: .

Рас-смот-рим те-перь сло-же-ние ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми. Сна-ча-ла рас-смот-рим дроби, зна-ме-на-те-ли ко-то-рых яв-ля-ют-ся чис-ла-ми.

Сложение и вычитание алгебраических дробей с разными знаменателями

При-мер 2. Сло-жить дроби: .

Ре-ше-ние:

Ал-го-ритм ре-ше-ния аб-со-лют-но ана-ло-ги-чен преды-ду-ще-му при-ме-ру. Легко по-до-брать общий зна-ме-на-тель дан-ных дро-бей: и до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из них.

.

Ответ: .

Итак, сфор-му-ли-ру-ем ал-го-ритм сло-же-ния и вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми :

1. Найти наи-мень-ший общий зна-ме-на-тель дро-бей.

2. Найти до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из дро-бей (по-де-лив общий зна-ме-на-тель на зна-ме-на-тель дан-ной дроби).

3. До-мно-жить чис-ли-те-ли на со-от-вет-ству-ю-щие до-пол-ни-тель-ные мно-жи-те-ли.

4. Сло-жить или вы-честь дроби, поль-зу-ясь пра-ви-ла-ми сло-же-ния и вы-чи-та-ния дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми.

Рас-смот-рим те-перь при-мер с дро-бя-ми, в зна-ме-на-те-ле ко-то-рых при-сут-ству-ют бук-вен-ные вы-ра-же-ния.

В этой статье мы рассмотрим основные действия с алгебраическими дробями :

• сокращение дробей
• умножение дробей
• деление дробей

Начнем с сокращения алгебраических дробей .

Казалось бы, алгоритм очевиден.

Чтобы сократить алгебраические дроби , нужно

1. Разложить числитель и знаменатель дроби на множители.

2. Сократить одинаковые множители.

Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.

Рассмотрим примеры:

1. Сократить дробь:

1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов

2. Разделим числитель и знаменатель на

2. Сократить дробь:

1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.

2. Разложим на множители знаменатель. Так же применим группировку.

3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:

Умножение алгебраических дробей.

При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.

Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.

Рассмотрим примеры:

3. Упростите выражение:

1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:

2. Разложим каждую скобку на множители:

Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.

Итак,

Деление алгебраических дробей мы выполняем по такому правилу:

То есть чтобы разделить на дробь, нужно умножить на «перевернутую».

Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.

Рассмотрим пример:

4. Упростите выражение:

Умножение и деление дробей — Алгебра II

Все ресурсы по Алгебре II

10 Диагностические тесты 630 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →

Алгебра II Помощь » Математические отношения и основные графики » Фракции » Умножение и деление дробей

Решите следующее уравнение, чтобы найти .

Возможные ответы:

Правильный ответ:

Объяснение:

Первым шагом в решении этого уравнения является сложение дробей, что дает нам:

Чтобы найти , нам нужно разделить обе части на .

Помните: Когда мы делим число на дробь, мы «переключаем» (находим обратную) дробь и умножаем ее на число.

Правая часть уравнения сокращается, если не учитывать: 

Обратите внимание: И числитель, и знаменатель делятся на , поэтому мы можем упростить это еще больше.

Сообщить об ошибке

Упрощение .

Возможные ответы:

Правильный ответ:

Объяснение:

Задачу можно упростить, если сначала упростить каждую дробь:  и .

Это подводит нас к новой проблеме .

Теперь числители умножаются друг на друга, затем знаменатели умножаются друг на друга: .

Сообщить об ошибке

Упростить .

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы решить, мы должны превратить задачу деления в задачу умножения, «перевернув» вторую дробь (деление на дробь равносильно умножению на обратную):

 .

Затем умножаем числители, за которыми следуют знаменатели:

.

Наконец, дробь должна быть упрощена в 3 раза:

, что дает нам окончательный ответ.

Сообщить об ошибке

Умножить:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы умножить дроби, просто умножьте числители, затем знаменатели, а затем упростите.

Сообщить об ошибке. Пояснение:

Чтобы умножить дроби, умножьте числители и знаменатели, а затем упростите.

Сообщить об ошибке

Умножить:

Возможные ответы:

Правильный ответ:

Пояснение:

Умножьте числители и знаменатели. Тогда упрости.

Сообщить об ошибке

Умножить:

Возможные ответы:

Правильный ответ:

5

4

6 Пояснение:

Умножьте числители и знаменатели, затем упростите.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.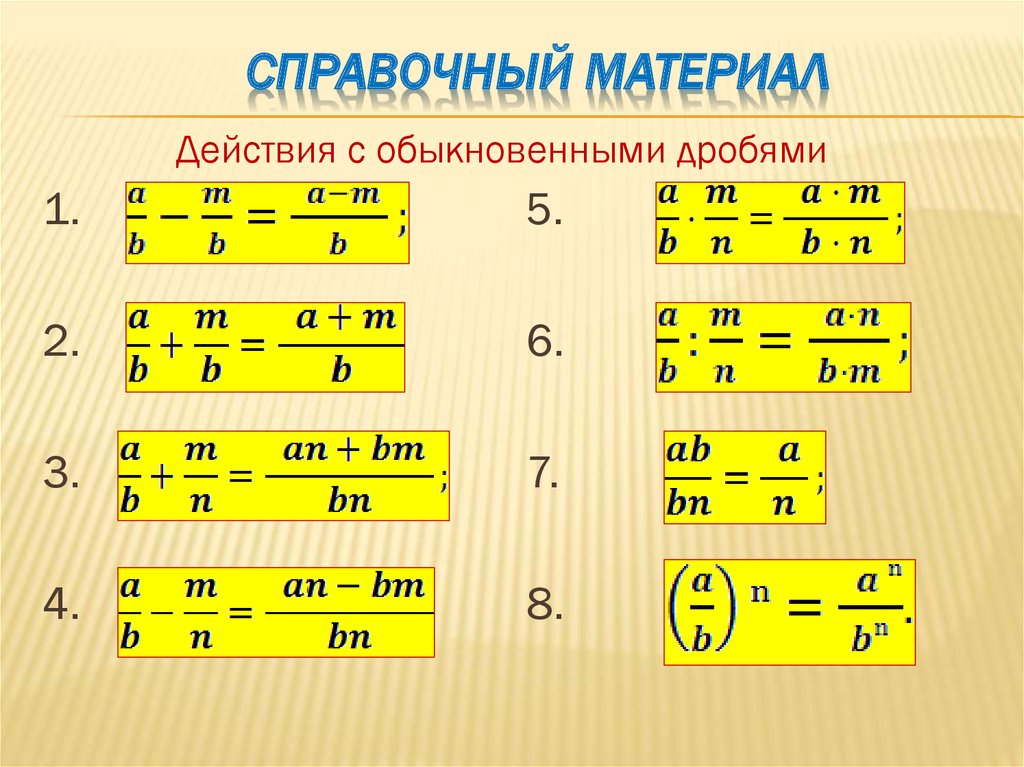

Теперь умножьте числители и знаменатели вместе, затем упростите.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели вместе, затем упростите.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

4

6 Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели, затем упростите.

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →

Уведомление об авторских правах 630 практических тестов Вопрос дня Карточки Learn by Concept

Как умножать дроби? Определение, примеры, факты

Перекрестное умножение: Введение

Мы обычно используем метод перекрестного умножения, чтобы найти неизвестные значения в любом алгебраическом уравнении. Давайте посмотрим на эти повседневные математические вопросы. Если один батончик стоит $\$$2, сколько будут стоить 10 таких батончиков?

Перекрестное умножение, как следует из названия, относится к умножению чисел, стоящих на перекрестных позициях.

Скрещиваем дроби $\frac{1}{10}$ и $\frac{2}{?}$.

$? \times 1= $\$$10$ $\times 2$ 

$? =$ $\$$20

Итак, 10 батончиков будут стоить $\$$20.

Давайте узнаем больше об этом методе и его применении.

Что такое перекрестное умножение?

Для любого алгебраического уравнения типа $\frac{a}{b}=\frac{c}{d}$ , метод перекрестного умножения использует следующую формулу:

$a\times d = b\times c $

Чтобы скрестить умножить дроби, мы умножаем числитель первой дроби на знаменатель второй дроби и числитель второй дроби на знаменатель первой дроби.

Перекрестное умножение можно использовать для сравнения дробей, сложения или вычитания разных дробей, поиска неизвестного значения в выражении и сравнения отношений.

Как скрестить дроби?

Давайте разберемся, как скрестить дроби на примере.

Мы знаем, что $\frac{3}{4} = \frac{6}{8}$  

Перемножить дроби $\frac{3}{4}$ и $\frac{6}{8}$ .

Умножьте числитель первой дроби на знаменатель второй дроби.

Умножьте числитель второй дроби на знаменатель первой дроби.

Получаем

$3\times8=24$

$6\times4=24$

Итак, перемножая дроби $\frac{a}{b} = \frac{c}{d}$  , мы get $a\times d = b\times c$

Перекрестное умножение дробей для сравнения в отличие от дробей

Мы только что научились скрещивать умножающие дроби. Когда вы скрещиваете умножение дробей? В отличие от дробей можно сравнивать путем перекрестного умножения. Отличие от дробей — это дроби с разными знаменателями.

Пример :  

Сравните $\frac{3}{7}$ и  $\frac{5}{8}$  , используя перекрестное умножение.

Чтобы сравнить две дроби с разными знаменателями, мы делаем их знаменатели одинаковыми.

Мы делаем это, заменяя знаменатели произведением обоих знаменателей.

Итак, знаменатель обеих дробей становится $7 \times 8 = 56$

Теперь мы скрестим и умножим дроби , чтобы найти числители.

• Сначала умножаем числитель первой дроби на знаменатель второй дроби.

$3 \times 8 = 24$           

Таким образом, первая дробь принимает вид: $\frac{24}{56}$

• Далее умножаем числитель второй дроби на знаменатель первой дроби.

$5 \times 7 = 35$

Таким образом, вторая дробь становится: $\frac{35}{56}$

Так как  $\frac{24}{56} \lt \frac{35}{56 }$ , можно сказать, что $\frac{3}{7} \lt \frac{5}{8}$.

Перекрестное умножение для сравнения отношений

Если два отношения равны, т. е. $\frac{a}{b} = \frac{c}{d}$, (где b и d не равны нулю), то произведение после перекрестного умножения также равно.

• $\frac{a}{b} \lt \frac{c}{d}$, если $a\times d \lt b\times c$.

Пример: $\frac{1}{2} \lt \frac{3}{4}$, начиная с $4 \lt 6$.

• $\frac{a}{b} \gt \frac{c}{d}$, если $a \times d \gt b \times c$.

Пример: $\frac{1}{10} \gt \frac{1}{100}$ начиная со 100 $\gt 10$.

Мы можем использовать перекрестное умножение , чтобы найти значение переменной в уравнении, содержащем соотношения. Давайте лучше поймем это на примере.

Пример : Если 8 подсвечников стоят $\$$40. Сколько будут стоить 12 таких подсвечников?

Стоимость 8 подсвечников = $\$$40

Стоимость 1 подсвечника $= \frac{40}{8}$                                                          …………(i)

Пусть стоимость 12 подсвечников равна Икс.

Следовательно, стоимость 1 подсвечника составит $\frac{x}{12}$. …………..(ii)

Приравнивая (i) и (ii), получаем

$\frac{40}{8} = \frac{x}{12}$

Перемножить, чтобы получить

$40 \times 12 = 8 \times x$

$\frac{480}{8}=$ x 

x $=60$

Следовательно, стоимость 12 подсвечников составляет $\$$60.

Перекрестное умножение с одной переменной

Метод перекрестного умножения в основном используется для нахождения неизвестной переменной в уравнении. Давайте посмотрим на пример.

$\frac{4}{9} = \frac{x}{45}$

Когда мы пересекаем умножение:

$4 \times 45 = 180$ и $9 \times x = 9x$

Теперь, $9 x = 180$

x$ = \frac{180}{9} = 20$

Отсюда получаем $x = 20$

Решенные примеры

1. Сравните дроби 57 и 17 49 перекрестным умножением.

Решение: Пересекая умножение, мы находим

$5 \times 9 = 45$ и $4 \times 7 = 28$

Так как $45 \gt 28, 57$ больше, чем 49.

2. Джимми хочет найти значение x в заданном уравнении. Вы можете помочь ему?

$\frac{12}{15} = \frac{x}{10}$

Решение:

$\frac{12}{15} = \frac{x}{10} $ (дано)

При перекрестном умножении:

$12 \times 10 = 15 \times x$

$\frac{120}{15} =$ x 

$8 =$ x 

Итак, значение x равно 8.

3. Что больше, $\frac{7}{12}$ или $\frac{6}{11}$ ?

Решение :

Когда мы перекрестно размножаемся, мы обнаружим

$ 7 \ Times 11 = 77 $ и 6 $ 12 = 72 $

AS, $ 77 \ GT 72 $

. $\frac{7}{12} \gt \frac{6}{11}$.

Практические задачи

40

5

15

10

Правильный ответ: 10
Поскольку данные дроби равны, мы можем перекрестно умножить и сказать, что $4x= 8 \times 5 = 40$
Таким образом, x $=$ 10

$\$$30

$\$ $48

$\$$40

$\$$36

Правильный ответ: $\$$30
Стоимость 4 кексов $\$$12.
Пусть стоимость 10 кексов равна x. Если мы представим это как уравнение, мы получим:
$\frac{12}{4} = \frac{x}{10}$
При перекрестном умножении мы получим
$12 \times 10 = 4 \times x$
$\frac{120}{4} = x$
$30 = x$
Следовательно, стоимость 10 кексов составляет $\$$30.