Переместительное свойство умножения – определение (5 класс, математика)

4.6

Средняя оценка: 4.6

Всего получено оценок: 78.

4.6

Средняя оценка: 4.6

Всего получено оценок: 78.

Переместительное свойство умножения очень похоже по своей сути на такое же свойство умножения. Тем не менее, часто ученики 5 класса, которые полностью овладели свойствами сложения, допускают ошибку в таких же по сложности законах умножения. Чтобы избежать этого разберемся подробнее в теме вопроса.

Что такое умножение?

Умножение это сокращенное сложение, базовые элементы которого принято знать наизусть. Под базовыми элементами понимается таблица умножения. Под упрощенным сложением имеется в виду то, что первый множитель показывает число, а второй сколько раз это число было сложено с самим собой.

В математике 3 ступени подобных упрощений. На первой стоит сложение, на второй умножение, а третьей возведение в степень. Возведение в степень это умножение числа на себя самого какое-то количество раз.

Сколько раз нужно повторить умножение отражает показатель степени.

Закон или свойство?

Для того, чтобы не путаться, нужно разобраться, как правильно называть законы умножения. Законами или все же свойствами?

Проблема в том, что закон это непреложное правило, а свойство это некоторая особенность действия. И то, и другое верно для свойств умножения. Поэтому никакой разницы в названиях нет. Но принято говорить свойства сложения и законы умножения. Однако ошибкой не будет назвать свойства сложения законами сложения и наоборот.

Свойства умножения

Распределительное свойство может применяться и относительно вычитания или деления. С помощью этого свойства раскрывают скобки в примерах при необходимости.

Переместительное свойство

Правильное использование определения переместительного свойства умножения может увеличить скорость счета. К сожалению, специальных правил группировки нет. Нужно полагаться только на собственный опыт и логику. Рассмотрим небольшой пример, чтобы показать применение свойства на практике:

((15*25*7*3:125)-3):12 – в этом примере упростить можно только правильно сгруппировав произведение в скобках для ускорения деления. Для этого представим число 15 в виде произведения 3*5

((15*25*7*3:125)-3):12=((5*3*25*7*3:125)-3):12 теперь перемножим 5 и 25, выполним деление произведения на число. Для этого можно только один из множителей разделить на это число, а потом результат использовать, как один из множителей.

(((5*25)*3*7*3:125)-3):12=((125*3*7*3:125)-3):12=(3*3*7-3):12=(9*7-3):12=(63-3):12=60:12=5

Без переместительного свойства не удалось бы правильно сгруппировать множители, а значит пришлось бы считать пример полностью, что отняло бы большое количество времени.

Что мы узнали?

Мы поговорили о том, что такое умножение. Решили, что понятия свойств и законов умножения одинаковы. Выделили свойства умножения и рассмотрели примеры переместительного свойства умножения. Сказали об особенностях этого свойства и его практическом значении.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 78.

---

А какая ваша оценка?

§ Свойства умножения и деления

Свойства сложения и вычитания Свойства умножения и деления

Свойства умножения

Переместительное свойство умножения

Запомните!

От перестановки множителей произведение не меняется.

a · b = b · a

Сочетательное свойство умножения

Запомните!

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

a · (b · c) = (a · b) · c

Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.

Запомните!

При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.

Свойство нуля при умножении

Запомните!

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

a · 0 = 0

0 · a · b · c = 0

Распределительное свойство умножения относительно сложения

Запомните!

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

(a + b) · c = a · c + b · c

Это свойство справедливо для любого количества слагаемых.

(a + b + с + d) · k = a · k + b · k + c · k + d · k

Распределительное свойство умножения относительно вычитания

Запомните!

Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.

В буквенном виде свойство записывается так:

(a − b) · c = a · c − b · c

Запомните!

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Свойства деления

• Ни одно число нельзя делить на ноль.
• При делении нуля на число получается ноль.

  0 : a = 0

• При делении любого числа на 1 получается это же число.

  b : 1 = b

Запомните!

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

a : b = (a · k) : (b · k)

, где «k» — любое натуральное число.

Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.

Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.

Свойства сложения и вычитания Свойства умножения и деления

Ассоциативные и перестановочные свойства умножения

••• Jupiterimages/Photos.com/Getty Images

Обновлено 26 октября 2020 г. Прибавление одного и того же числа несколько раз даст тот же результат, что и умножение числа на количество повторений сложения, так что 2 + 2 + 2 = 2 × 3 = 6.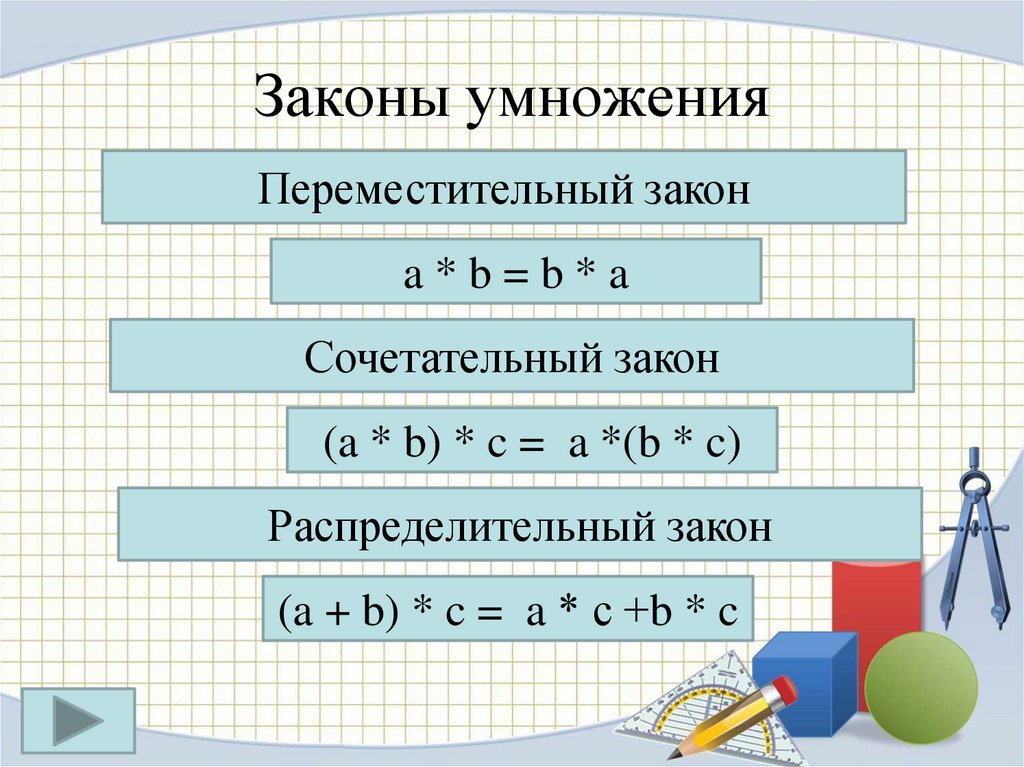 Эта взаимосвязь далее иллюстрируется сходством между ассоциативным и коммутативные свойства умножения и ассоциативные и коммутативные свойства сложения. Эти свойства связаны с тем, что порядок чисел в числе сложения или умножения не меняет результат уравнения. Важно отметить, что эти свойства применяются только к сложению и умножению, а не к вычитанию или делению, где изменение порядка чисел в уравнении изменит результат.

Коммутативное свойство умножения

При умножении двух чисел изменение порядка чисел в уравнении на противоположное приводит к тому же произведению. Это известно как коммутативное свойство умножения и очень похоже на ассоциативное свойство сложения. Например, умножение трех на шесть равно шестикратному трем (3 × 6 = 6 × 3 = 18). Выраженное в алгебраических терминах, коммутативное свойство:

a × b = b × a

или просто

ab = ba

Ассоциативное свойство умножения

Ассоциативное свойство умножения можно рассматривать как расширение коммутативного свойства умножения и параллельно ассоциативному свойству сложения. При умножении более двух чисел изменение порядка умножения чисел или способа их группировки приводит к тому же произведению. Например, (3 × 4) × 2 = 12 × 2 = 24. Изменение порядка умножения на 3 × (4 × 2) дает 3 × 8 = 24. В алгебраических терминах ассоциативное свойство можно описать как:

(a + b) + c = a + (b + c)

Коммутативное свойство сложения

Может быть полезно помнить ассоциативные и коммутативные свойства сложения в отношении ассоциативных и коммутативных свойств умножения . Согласно коммутативному свойству сложения, два числа, сложенные вместе, дают одну и ту же сумму независимо от того, сложены ли они вперед или назад. Другими словами, два плюс шесть равно восьми, а шесть плюс два также равно восьми (2 + 6 = 6 + 2 = 8) и напоминает коммутативное свойство умножения. Опять же, это может быть выражено алгебраически как

a + b = b + a

Ассоциативное свойство сложения

В ассоциативном свойстве сложения порядок сложения более трех или более наборов чисел не изменяет сумму чисел. Таким образом, (1 + 2) + 3 = 3 + 3 = 6. Как и в ассоциативном свойстве умножения, изменение порядка не меняет результат, поскольку 1 + (2 + 3) = 1 + 5 = 6. Алгебраически, ассоциативность сложения

(a + b) + c = a + (b + c)

Статьи по теме

Ссылки

• Йельский педагогический институт Нью-Хейвена: использование основных свойств для решения задач по математике; К. Киндер; 2011
• Сиракузский университет: Математические свойства действительных чисел

Об авторе

Дэвид Чандлер с 2006 года является внештатным писателем, чьи работы публиковались в различных печатных и онлайн-изданиях. Бывший морской пехотинец-разведчик, он активный путешественник, ныряльщик, байдарочник, моряк и рыболов. Он много путешествовал и имеет степень бакалавра Университета Южной Флориды, где он получил образование в области международных исследований и микробиологии.

Photo Credits

Jupiterimages/Photos.com/Getty Images

Свойства умножения — Элементарная математика

Свойства умножения: распределительное, коммутативное, ассоциативное, удаление общего множителя и нейтрального элемента.

Мы посвящаем этот пост изучению свойств умножения, а именно:

• Распределяющее свойство: Умножение числа на сумму равно сумме произведений этого числа на каждое из суммы, которые необходимо добавить.

Возьмем, к примеру: 2 x (3 + 5)

Согласно свойству распределения 2 x (3 + 5) будет равно 2 x 3 + 2 x 5.

Проверим, так ли это .

2 х (3 + 5) = 2 х 8 = 16

2 х 3 + 2 х 5 = 6 + 10 = 16

Оба дают в результате 16, что показывает, что распределительное свойство умножения работает.

• Переместительное свойство: Порядок множителей не меняет произведение.

Рассмотрим на примере свойство коммутативности:

Результат умножения 10 х 3 будет равен умножению 3 х 10. Хотя мы меняем порядок множителей, результат по-прежнему равен 30.

• Ассоциативное свойство: Способ группировки множителей не изменяет результат умножения.

Давайте рассмотрим пример ассоциативного свойства умножения:

В этом случае, как показано на рисунке, мы получим тот же результат, если умножим 3 x 2, а затем умножим результат на 5, как если бы мы умножьте 2 x 5, а затем умножьте результат на 3.

• Удаление общего множителя:
  Это свойство, обратное распределительному свойству. Если различные слагаемые имеют общий множитель, мы можем преобразовать сумму в произведение, вычитая этот множитель.

Рассмотрим пример удаления общего множителя. Если у нас есть операция (2 х 7) + (3 х 7), которая имеет 7 в качестве общего делителя, мы можем преобразовать эту операцию в 7 х (2 + 3).

Проверим, что удаление общего множителя дает тот же результат:

(2 x 7) + (3 x 7) = 14 + 21 = 35

7 x (2 + 3) = 7 x 5 = 35

Это показывает, что это свойство умножения работает.

• Нейтральный элемент: 1 называется тождеством умножения, потому что каждое число, умноженное само на себя, является одним и тем же числом.