Основные арифметические операции с дробями
Главная / i / t
- Умножение дробей
- Деление дробей
- Сложение и вычитание дробей
Дроби в математике будут всегда и везде, и с ними будут производиться самые разнообразные действия, поэтому нам для начала следует познакомиться с самыми базовыми из них.
Умножение дробей
Умножение является наиболее простой операцией, производимой с дробями.
Чтоб умножить одну дробь на другую, достаточно просто умножить числитель на числитель, а знаменатель на знаменатель:
Например:
Проверим результат, умножив эти числа другим способом: одна вторая – это один, деленый на два. А один, деленый на два, равно 0.5:
А три пятых – это три, деленое на пять, которое равно 0.6:
И умножим не эти две дроби, а равные им числа:
Получился такой же результат – значит все правильно
Еще пример:
Нельзя забывать и об упрощающем арифметику основном свойстве дроби: в следующем примере в процессе умножения можно заменить на равное ему, но более простое , что сильно упростит расчеты:
Применим основное свойство дроби еще раз, уменьшив числитель в 7 раз: для этого достаточно разделить 21 на 7 (разумеется, при этом с двойкой в числителе ничего делать не надо).
Тогда и числитель, равный 42 (2∙21=42), уменьшится в 7 раз и станет равным 6 (2∙3=6). Точно таким же образом разделим на 7 и знаменатель:
А что делать, если потребуется умножить дробь на число?
Тогда надо свести эту задачу к предыдущей, и сделать так, чтобы число x стало дробью, значение которой будет равно x. Например, если x разделить на 1, то получится дробь, равная x:
Или так:
Действительно, два икса разделить на два – будет икс
Тогда заменим x на равную ему дробь:
А как умножаются дроби уже известно:
Например:
Деление дробей
Следует иметь ввиду, что в математике прежде всего ценится способность выводить правила и закономерности, а не способность эти правила запоминать! Поэтому попробуем именно вывести правило, по которому следует делить дроби. Тем более, что нижеописанная операция с многоэтажными дробями будет очень часто использоваться в математике далее.
Деление одной дроби на другую можно представить в виде четырехэтажной дроби, в которой числителем будет , а знаменателем :
Воспользуемся основном свойстве дроби и умножим числитель и знаменатель на число b:
Теперь в числителе число a делится на b, а затем умножается на b. А что будет с числом, которое уменьшили в b раз и потом увеличили в b раз? Естественно число a от этого не изменится. Поэтому можно заменить на a, потому что это одно и то же число:
Дробь уже стала трехэтажной. Что бы сделать еще, чтоб она стала двухэтажной? Домножим опять, но уже на число y:
Получившееся выражение будет равно произведению двух дробей:
Так как к изначальному выражению мы применяли основное свойство дроби, которое не изменяет ее значение, то мы получили то же самое выражение только в другом виде:
Вот таким образом из ничего благодаря логике мы вывели следующее правло:
Чтоб одну дробь разделить на другую, надо вторую дробь перевернуть, заменить деление умножением и умножить образававшиеся дроби:
Пример:
Ну а умножать дроби мы уже умеем:
Проверить это можно, заменив дроби на равные им числа:
Еще пример:
Упростим выражение, сократив с помощью основного свойства дроби:
Деление дроби на число, которое дробью не является, происходит просто — x заменяется на равное ему число :
Приведем пример:
Сложение и вычитание дробей
Еще в математике очень полезным качеством является способность воспринимать один и тот же объект по-разному.
Например, число можно воспринимать как количество кругов, изображенных на следующем рисунке.
Тогда какое количество кругов будет соответствовать числу ? Это количество можно представить следующим образом: мысленно делим один круг на 4 равные части, и одну часть убираем. Таким образом, останутся только 3 части из 4. То есть это будет меньше одного круга.
Числу будет соответствовать окружность, поделенная на 3 равные части, из которых будет присутствовать только одна
Сложим эти дроби:
Количественно эту сумму можно изобразить в графическом виде:
Теперь разделим каждую из присутствующих и отсутствующих долей первого круга на 3 равные части, а во втором круге каждую долю разделим на 4 равные части
Такое преобразование равносильно применению основного свойства дроби: количество кругов и значения дробей не изменилось, а вид дробей стал другой – у них сейчас одинаковые знаменатели:
Каждый круг теперь поделен на 12 равных частей: 3 – в первом, и 4 – во втором.
А значит, их можно сложить
Таким образом, мы опять вывели новое правило:
Чтобы сложить дроби, нужно с помощью основного свойства дроби изменить вид дробей так, чтобы их знаменатели стали одинаковыми:
затем сложить числители, а новый общий знаменатель оставить тем же:
Применим на практике это правило:
Легко можно заметить, что достаточно только домножить только первую дробь на 2, чтоб знаменатели стали одинаковыми:
Осталось лишь сложить числители:
Так выглядет количественная аналогия
Чтобы отнять одну дробь от другой, сначала нужно тоже привести их к общему знаменателю:
Первую дробь домножим на 2, вторую – на 3:
После чего отнимем от первого числителя второй:
Все остальные действия с дробями будут основываться на вышеописанных правилах, поэтому не следует недооценивать их важность.
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | 93/8 | ||
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Вычитание дробей с общими знаменателями
Результаты обучения
- Используйте круги дробей, чтобы найти разницу между двумя дробями с одинаковыми знаменателями
- Вычитание дробей с одинаковыми знаменателями без дробных кругов
- Вычитание дробей с одинаковыми знаменателями, которые содержат переменные
Модель Вычитание дробей
Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей.
Представьте себе пиццу, нарезанную на [латекс]12[/латекс] кусочков. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или [латекс]{\большой\фрак{7}{12}}[/латекс] пиццы). Если Леонардо съест [латекс]2[/латекс] из этих оставшихся кусков (или [латекс]{\большой\фрак{2}{12}}[/латекс] пиццы), сколько останется? Осталось [латекс]5[/латекс] кусочков (или [латекс]{\большой\фрак{5}{12}}[/латекс] пиццы).
[латекс] {\ Большой \ гидроразрыва {7} {12}} — {\ Большой \ гидроразрыва {2} {12}} = {\ Большой \ гидроразрыва {5} {12}} [/латекс]
Давайте используйте дробные круги для моделирования того же примера, [латекс] {\ большой \ гидроразрыв {7} {12}} — {\ большой \ гидроразрыва {2} {12}} [/латекс].
Начните с семи [латексных] {\ больших \ гидроразрывов {1} {12}} [/ латексных]. Уберите два куска [латекс]{\Large\frac{1}{12}}[/latex]. Сколько двенадцатых осталось?
Опять же, у нас есть пять двенадцатых, [латекс] {\ большой \ гидроразрыв {5} {12}} [/латекс].
Пример
Используйте дробные круги, чтобы найти разницу: [латекс] {\ большой \ гидроразрыв {4} {5}} — {\ большой \ гидроразрыва {1} {5}} [/латекс]
Решение:
Начните с четырех [латексных] {\ больших \ гидроразрывов {1} {5}} [/латексных] частей. Уберите один кусок [латекса]{\Large\frac{1}{5}}[/latex]. Посчитайте, сколько пятых осталось. Осталось три куска [латекс]{\большой\фрак{1}{5}}[/латекс].
Попробуйте
Вычитание дробей с общим знаменателем
Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.
Вычитание дроби
Если [latex]a,b,\text{ и }c[/latex] — числа, где [latex]c\ne 0[/latex], то
[latex]{\Large\frac{a}{ c}}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}[/latex]
Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разность над общим знаменателем.
Пример
Найдите разницу: [латекс]{\Large\frac{23}{24}}-{\Large\frac{14}{24}}[/latex]
Показать решение
Попробуйте
Посмотрите следующее видео, чтобы увидеть больше примеров вычитания дробей с одинаковыми знаменателями.
Пример
Найдите разницу: [латекс]{\Large\frac{y}{6}}-{\Large\frac{1}{6}}[/latex]
Показать решение
Попробуйте
Пример
Найдите разницу: [латекс]{\Large-\frac{10}{x}-\frac{4}{x}}[/latex]
Показать решение
Попробуйте
Теперь давайте сделаем пример, который включает в себя сложение и вычитание.
Пример
Упрощение: [латекс]{\Large\frac{3}{8}}+\left(-{\Large\frac{5}{8}}\right)-{\Large\frac{1 {8}}[/latex]
Показать решение
Попробуйте
В следующем видео мы покажем больше примеров вычитания дробей с общим знаменателем. Обратите внимание на второй пример, он устраняет распространенную ошибку, допускаемую учащимися при упрощении дробей с переменными.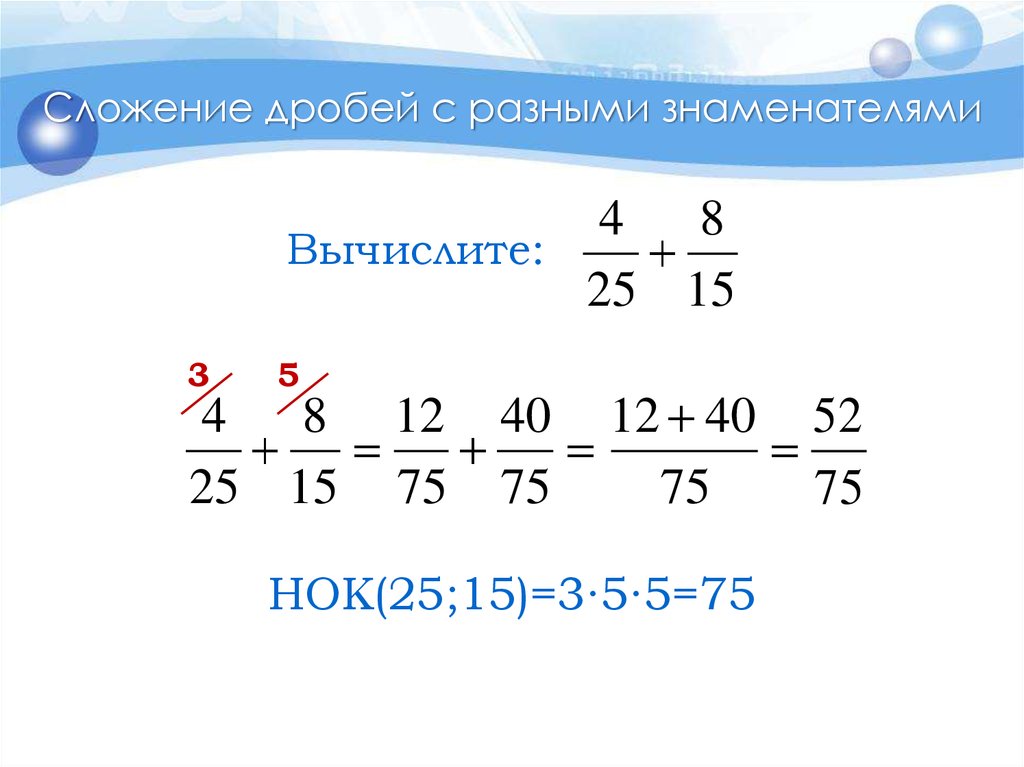
Видеоурок: Вычитание дробей из смешанных чисел: без перегруппировки
Стенограмма видео
Вычитание правильных дробей Где Знаменатели кратны
В этом видео мы узнаем
как вычесть родственные дроби в пределах одного целого, найдя общую
знаменатель. Как бы мы вычли треть из
семь девятых? Когда мы вычитаем дроби,
обе дроби должны иметь одинаковый знаменатель. Мы не можем отнять треть у
девятые. Это не одно и то же. Давайте воспользуемся моделью, которая поможет нам
представляют этот расчет. Знаменатель в нашем первом
дробь — девятка. Это означает, что нам нужно разделить
всю сумму на девять равных частей. Один два три четыре пять шесть,
семь, восемь, девять.
Мы разделили всю сумму на
девять равных частей. Каждая часть стоит одну девятую.
Числитель, который является верхним
число в дроби равно семерке. Итак, мы должны выбрать
семь девятых. Ну вот. Мы заштриховали семь девятых. Итак, как бы мы вычли
одна третья? Давайте нарисуем модель для представления
одна третья. Эта полоса представляет собой одно целое. А поскольку знаменатель нашего
дробь это тройка, нам нужно разделить наше целое на три равные части: один, два,
три. Каждая часть представляет одну треть. И поскольку наш числитель равен единице,
нам нужно заштриховать одну из наших частей. Эти две модели помогают нам увидеть
что одна треть равна трем девятым. Таким образом, чтобы вычесть одну треть из
семь девятых, нам просто нужно вычесть три из наших девятых. Сколько у нас девятых
левый? Четыре девятых. Таким образом, семь девятых вычитают одну треть
равняется четырем девятым.
Мы использовали модель, чтобы помочь нам работать
получается, что одна треть равна трем девятым.
Есть еще один способ выяснить, как многие девятые равны одной трети. Чтобы преобразовать трети в девятые, мы можно умножить на три, потому что трижды три девять. И что бы мы ни делали с знаменатель, то же самое нужно сделать с числителем, чтобы сохранить дроби равный. И мы знаем, что один раз три три. Как только мы узнаем, что одна треть равно трем девятым, мы можем вычесть. Семь девятых вычесть три девятых составляет четыре девятых. Если у нас есть семь девятых и мы возьмем три из них, мы останемся с четырьмя девятыми. Давайте попробуем ответить на вопрос сейчас, чтобы мы могли применить на практике то, что мы узнали до сих пор.
Используя данную модель, найти
пять восьмых вычесть одну четверть. Дайте ответ в самом простом
форма.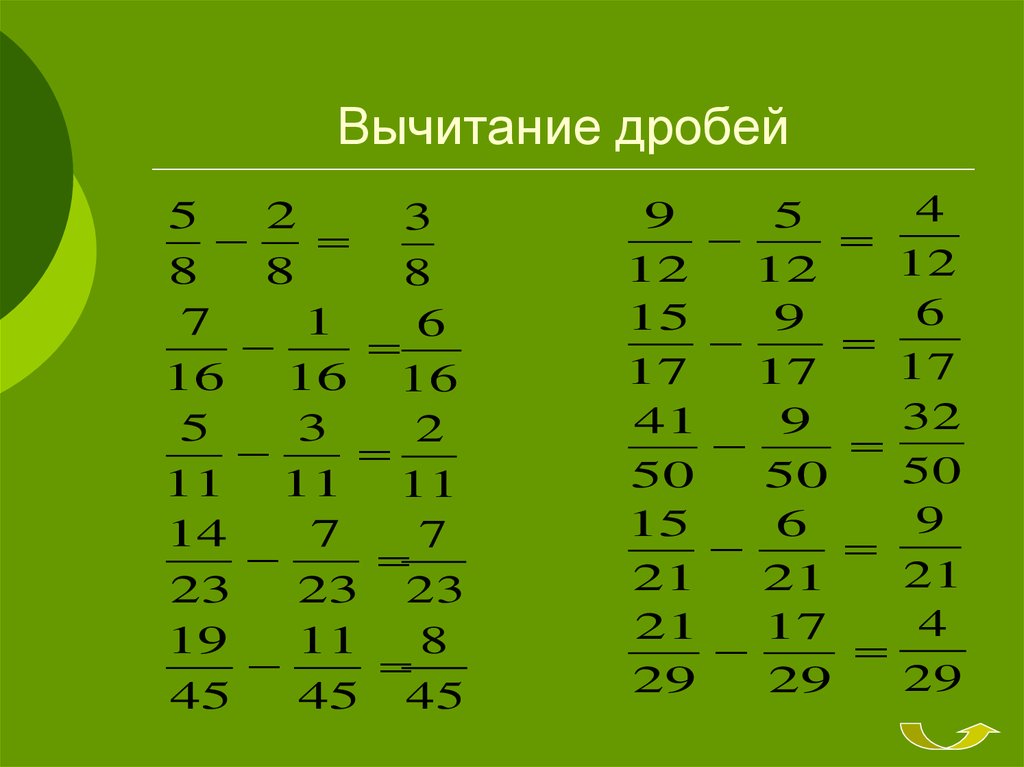
В этом вопросе мы должны найти пять восьмых вычитают одну четверть, и нам в помощь дана модель. Первая модель представляет пять восьмых. Вся сумма разделена на восемь равных частей, и пять из этих восьми частей заштрихованы. Мы должны вычесть одну четверть из этих пяти восьмых. Наша вторая модель представляет одна четверть. Вся сумма разделена на четыре равные части, и одна из этих четырех частей заштрихована.
Сравнивая эти две модели, мы
можно увидеть, что одна четверть равна двум восьмым. Итак, чтобы вычесть четверть из нашего
пять восьмых, нам нужно убрать две восьмых. Один два. Сколько у нас восьмых
левый? Есть три. Итак, пять восьмых забрать
одна четверть равна пяти восьмым отнять две восьмых. Итак, если у нас есть пять восьмых и мы
убери два, останется три восьмых. И вопрос говорит, что мы должны
дайте наш ответ в его простейшей форме.
Мы не можем упростить
три восьмых. Пять восьмых отнимают четверть
равняется трем восьмым.
На данный момент в этом видео мы узнали как вычитать дроби с разными знаменателями с помощью моделей. Давайте попробуем вычитать эти дроби без модели.
Что такое пять шестых забрать две трети?
Сразу видно, что
знаменатели у этих двух дробей разные. Прежде чем мы сможем вычесть две трети
из пяти шестых нам нужно сделать оба знаменателя одинаковыми. Другими словами, нам нужно сделать
обе наши дроби на количество шестых. Мы знаем, что шесть кратно
три. Если умножить три на два, то получим
шесть. И что бы мы ни делали с
знаменатель, то же самое нужно сделать с числителем. Итак, нам нужно умножить два на
два. Итак, две трети равны
четыре шестых. Теперь обе наши фракции имеют
тот же знаменатель.
У нас есть пять шестых, и нам нужно убрать четыре. И мы знаем, что пять отнять четыре оставляет нас с одним. Пять шестых забирают четыре шестых равняется одной шестой. Чтобы помочь нам вычесть пять шестых из двух третей нам пришлось сделать оба знаменателя одинаковыми. Мы знаем, что шесть кратно три. Итак, мы умножили три на два, чтобы дайте нам наш знаменатель шесть. Затем мы умножаем числитель на два, что дало нам четыре шестых. Когда знаменатели совпадают, мы можем вычесть.
Давайте попробуем ответить на несколько вопросов теперь, когда нам нужно вычесть две дроби с разными знаменателями без используя модель.
У Джексона половина плитки шоколада и он съедает одну шестую его часть. Сколько стоит плитка шоколада осталось?
Если у Джексона половина
плитка шоколада и он съедает шестую часть, чтобы узнать, сколько в плитке шоколада
осталось, нужно от половины отнять одну шестую.
Прежде чем мы сможем вычесть, оба
знаменатели должны быть одинаковыми. Шесть кратно двум, поэтому
может сделать оба знаменателя шестью. Скольким шестым равны
одна половина? Как мы получаем от двух до шести? Дважды три шесть. Мы умножили знаменатель на
три. Теперь нам нужно умножить
числитель на три, и мы знаем, что один раз три равно три. Теперь, когда мы знаем, что половина равна
три шестых, мы можем вычесть. Три шестых вычесть одну шестую
равняется двум шестым.
Если у нас есть три шестых и мы возьмем один прочь, у нас останется две шестых. Но нам нужно дать ответ в его простейшая форма. Две шестых равны одна третья. Если разделить два на два, то получим один. И если мы разделим шесть на два, мы получим три. Половина вычесть одну шестую равно две шестых или одну треть.
Бутылка Софии содержит
три четверти литра воды.
Если она выпьет одну восьмую литра
из ее бутылки, сколько воды в литрах осталось?
Мы знаем, что бутылка Софии содержит три четверти литра воды. Если она выпьет еще одну восьмую литр, сколько воды у нее останется? Мы должны найти три четверти дубля от одной восьмой. Прежде чем мы сможем вычесть, оба знаменатели должны быть одинаковыми. Мы знаем, что восемь кратно четыре, так что давайте посмотрим, сколько восьмых равны трем четвертям. Восьмерка — это общее знаменатель. Как мы получаем от четырех до восемь? Мы знаем, что четырежды два равно восемь, поэтому нам нужно умножить наш числитель на два. И мы знаем, что трижды два шесть.
Теперь, когда мы это знаем
три четверти равны шести восьмым, мы можем вычесть. Если у нас есть шесть восьмых и мы
убери один из них, у нас останется пять восьмых.