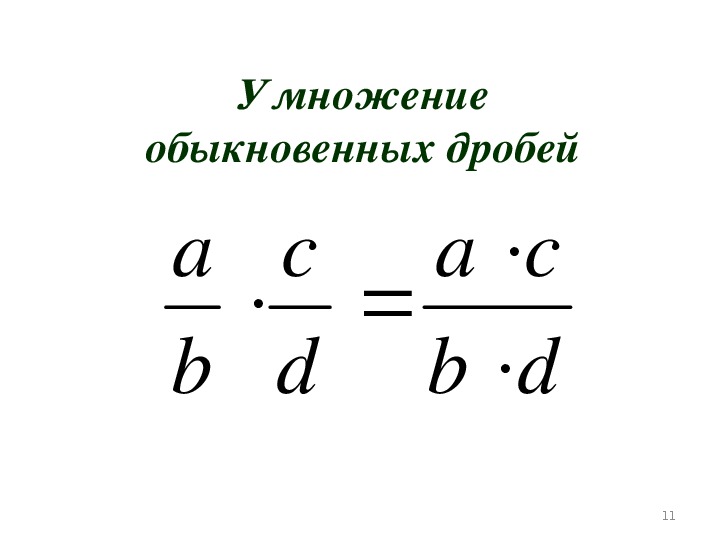Урок 62. умножение натурального числа на дробь — Математика — 5 класс

Математика

5 класс

Урок № 62

Умножение натурального числа на дробь

Перечень рассматриваемых вопросов:

– произведение двух дробей;

– взаимно обратные дроби;

– умножение натурального числа на дробь.

Тезаурус

Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Взаимно обратные дроби – это дроби, произведение которых равно единице.

Обязательная литература

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС./ С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017, стр. 272.

Теоретический материал для самостоятельного изучения

Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Например,

Можно ли умножить дробь на натуральное число n? Конечно, да! Натуральное число n можно представить в виде обыкновенной дроби n/1 и применить правило умножения дробей. Итак, чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же.

Например:

Вычислим произведение четырёх пятых и трёх. Умножение можно заменить сложением, то есть три раза сложить дробь четыре пятых. Применяем правило сложения обыкновенных дробей и получаем:

Если произведение дробей равно единице, то такие дроби называют взаимно обратными.

Например,

Дроби ¼ и 4/1 называются взаимно обратными.

Чтобы умножить простую и смешанную дробь, можно записать последнюю в виде неправильной дроби и выполнить умножение обыкновенных дробей.

Например,

Перед возведением в степень смешанную дробь записывают в виде неправильной, и эту дробь возводят в степень.

Решим задачу: в равностороннем треугольнике длина стороны равна 4/7 м. Найдите периметр треугольника.

Решение. Как мы знаем, периметр – это сумма длин всех сторон. В треугольнике три стороны, а т. к. треугольник равносторонний – стороны равны. Получается, что сумму длин всех сторон можно представить как произведение натурального числа 3 на обыкновенную дробь

Разбор решения заданий тренировочного модуля

№ 1. Вычислите значение выражения, результат запишите в виде смешанной дроби.

Переведём смешанные дроби в неправильные, после чего перемножим числители и знаменатели, а результат запишем в виде смешанной дроби. Получим:

№ 2. Вычислите значение произведения, результат сократите.

Умножим числитель первой дроби на числитель второй дроби, знаменатели тоже перемножим. Получим:

Ответ:

Калькулятор дробей

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i nd = i · d + nd

Например,

5 34 = 5 · 4 + 34 = 234

Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную или смешанную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная дробь1
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Например, переведем 0.36 в обыкновенную дробь:

1. Записываем дробь в виде: 0.361
2. Умножаем на 10 два раза, получим 36100
3. Сокращаем дробь 36100 = 925

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Как умножать дроби с разными и одинаковыми знаменателями

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.

Дроби могут быть двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя:

Неправильной — ту, у которой числитель больше знаменателя или равен ему:

Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.

Основные правила дробей Если делитель равен нулю — у дроби нет значения Дробь равна нулю, если числитель равен нулю, а знаменатель — нет Две дроби a/b и c/d называют равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число — получится равная ей дробь.

Умножение дробных чисел

Рассмотрим несколько вариантов умножения обыкновенных дробей.

Как умножить дробь на дробь

Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:

Важно проверить возможность сокращения — так решать будет легче:

Как умножить смешанные дроби

Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.

Как умножить дробь на натуральное число

Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.

Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.

Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.

 

Решение задач

Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.

Задание 1. Выполнить умножение 2/17 на 5.

Как решаем: перемножим делимое и натуральное число.

Ответ: 

Задание 2. Выполнить умножение 4/15 и 55/6.

Как решаем:

• перемножим числители между собой и знаменатели соответственно
  

• сократим полученное
  

• выделим целую часть
  

Ответ:

Задание 3. Выполнить умножение одной целой трех седьмых на шесть.

Как решаем:

• переводим смешанное число в неправильную дробь,
• умножаем делимое на натуральное число,
• сократим полученное,
• преобразуем в смешанное число.

Ответ: 

Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Умножение дробей, формулы и примеры решений

Содержание:

Умножение дроби на число

Умножение дроби $\frac{a}{b}$ на число $n$ равносильно сложению одинаковых слагаемых:

Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой дроби умножить на это число, а знаменатель оставить без изменения.

Пример

Задание. Найти произведение  $\frac{1}{3} \cdot 4$

Решение. Выполним умножение по описанному выше правилу

$\frac{1}{3} \cdot 4=\frac{1 \cdot 4}{3}=\frac{4}{3}=1 \frac{1}{3}$

Ответ.   $\frac{1}{3} \cdot 4=1 \frac{1}{3}$

Аналогично выполняется умножения числа на дробь.

Слишком сложно?

Умножение дробей не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Найти произведение  3$\cdot \frac{1}{4}$

Решение. Выполним умножение по описанному выше правилу

$3 \cdot \frac{1}{4}=\frac{3 \cdot 1}{4}=\frac{3}{4}$

Ответ.   $3 \cdot \frac{1}{4}=\frac{3}{4}$

Умножение дробей

Определение

Произведением дробей называется такая дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель — произведению их знаменателей:

$\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}$

Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.

Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.

Пример

Задание. Найти произведение дробей  $\frac{1}{3}$  и  $\frac{4}{5}$ 

Решение. Выполним умножение дробей по описанному выше правилу

$\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}$

Ответ.   $\frac{1}{3} \cdot \frac{4}{5}=\frac{4}{15}$

Пример

Задание. Умножить  $\frac{13}{14}$  на  $\frac{14}{39}$ 

Решение. Необходимо найти произведение $\frac{13}{14} \cdot \frac{14}{39}$ . Как видим, числа 13 и 39 можно сократить на общее число 13. Для этого сами указанные величины зачеркиваем, а над ними пишем число, которое получается после деления. Аналогично поступает со знаменателем первой дроби и числителем второй:

Ответ.   $\frac{13}{14} \cdot \frac{14}{39}=\frac{1}{3}$

Умножение смешанных дробей

Чтобы перемножить смешанные дроби, нужно представить их в виде неправильных дробей, а затем уже выполнить умножение как обыкновенных дробей.

Пример

Задание. Найти произведение дробей 3$\frac{1}{3} \cdot 4 \frac{2}{5}$

Решение. Выполним умножение смешанных дробей по описанному выше правилу

$3 \frac{1}{3} \cdot 4 \frac{2}{5}=\frac{3 \cdot 3+1}{3} \cdot \frac{4 \cdot 5+2}{5}=\frac{10}{3} \cdot \frac{22}{5}=$

Ответ.   $3 \frac{1}{3} \cdot 4 \frac{2}{5}=14 \frac{2}{3}$

Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число, либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.

Пример

Задание. Умножить смешанную дробь 3$\frac{3}{4}$ на 2

Решение. Выполним умножение смешанной дроби на число по описанному выше правилу

Либо

$=(6+1)+\frac{1}{2}=7+\frac{1}{2}=7 \frac{1}{2}$

Ответ.   $3 \frac{3}{4} \cdot 2=7 \frac{1}{2}$

Читать следующую тему: деление дробей.

Умножение и деление обыкновенных дробей. Онлайн калькулятор

Умножение дробей

Чтобы умножить одну обыкновенную дробь на другую, нужно умножить числитель первой дроби на числитель второй дроби (это произведение будет числителем результата), и знаменатель первой дроби на знаменатель второй дроби (это произведение будет знаменателем результата):

Правило умножения обыкновенных дробей в виде формулы:

Для упрощения вычислений, ещё до выполнения умножения дробей, можно сокращать любой множитель числителя с любым множителем знаменателя на общий делитель.

При сокращении числителей со знаменателями их обычно зачёркивают и рядом пишут число, которое получилось после сокращения:

В примере мы сократили  25  и  20  на общий делитель —  5,  а  27  и  12  на общий делитель —  3.

Умножение дроби на натуральное число

Чтобы умножить натуральное число на обыкновенную дробь или наоборот — умножить дробь на натуральное число, можно числитель дроби умножить на это натуральное число, а знаменатель оставить без изменений:

Пример.

Деление дробей

При делении одной обыкновенной дроби на другую, нужно перевернуть вторую дробь и после этого умножить первую дробь на вторую, т. е. нужно числитель первой дроби умножить на знаменатель второй (это произведение будет числителем результата), а знаменатель первой дроби умножить на числитель второй (это произведение будет знаменателем результата):

Для проверки правильности выполненного деления, можно полученное частное умножить на делитель и посмотреть, получится ли у нас делимое, если делимое получено верно, значит деление было выполнено правильно:

Теперь осталось только сократить полученную дробь:

Правило деления обыкновенных дробей в виде формулы:

Иногда могут встретиться записи такого вида:

Так как дробная черта означает деление, то такие записи можно переписать в более удобном виде:

В записях, в которых дробная черта используется несколько раз, знак = ставится у дробной черты, означающей последнее по порядку действие деления:

Деление дроби на натуральное число

Чтобы обыкновенную дробь разделить на натуральное число или наоборот — натуральное число разделить на дробь, нужно просто представить натуральное число в виде дроби.

Примеры.

Калькулятор умножения и деления дробей

Данный калькулятор поможет вам выполнить умножение или деление обыкновенных дробей. Просто введите две дроби, выберите нужную операцию и нажмите кнопку Вычислить.

правила, примеры, решения, умножение дробей с разными знаменателями

Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.

Как умножить одну обыкновенную дробь на другую

Запишем сначала основное правило:

Определение 1

Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.

Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.

Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:

У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.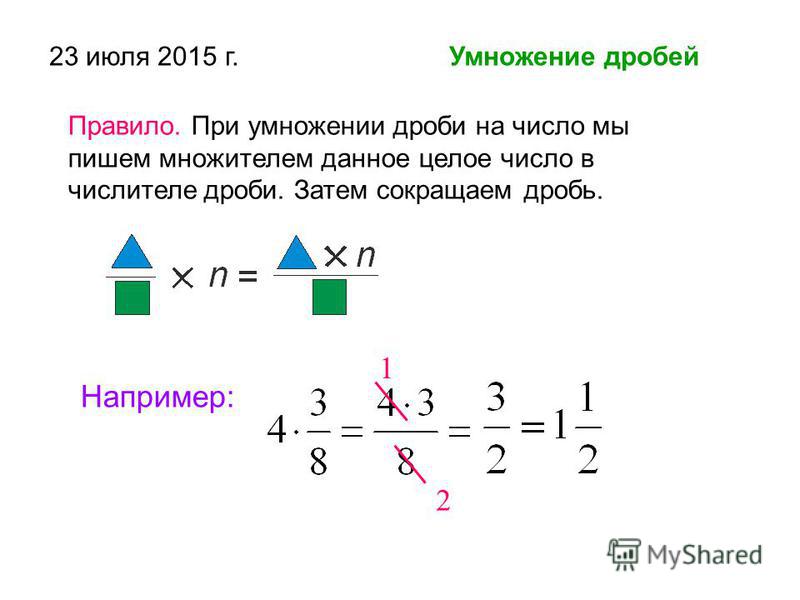

Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:

58·34=5·38·4=1532

Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.

Разберем решения нескольких задач на умножение обыкновенных дробей.

Пример 1

Умножьте 711 на 98.

Решение

Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.

Все решение можно записать так:

711·98=7·911·8=6388

Ответ: 711·98=6388. 

Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.

Пример 2

  Вычислите произведение дробей 415 и 556.

Решение

Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:

415·556=4·5515·6=22090

Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.

Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.

Ответ: 415·556=249.

  

Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.

Поясним, как это выглядит, используя данные конкретной задачи.

Пример 3

Вычислите произведение 415·556.

Решение

Запишем вычисления, исходя из правила умножения. У нас получится:

415·556=4·5515·6

Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.

Далее мы можем просто сократить некоторые множители и получить следующее: .

Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:

2·113·3=229=249

Ответ: 415·556=249. 

Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:

ab·cd=cd·ab=a·cb·d

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Как перемножить обыкновенную дробь с натуральным числом

Запишем сразу основное правило, а потом попробуем объяснить его на практике.

Определение 2

Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n  можно записать в виде формулы ab·n=a·nb.

Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:

ab·n=ab·n1=a·nb·1=a·nb

Поясним нашу мысль конкретными примерами.

Пример 4

Вычислите произведение 227 на 5.

Решение 

В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:

227·5=2·527=1027

Ответ: 227·5=1027 

Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.

Пример 5

Условие: вычислите произведение 8 на 512.

Решение

По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:

НОК(40, 12)=4, значит, 4012=40:412:4=103

Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.

В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.

Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.

Ответ: 512·8=313.

Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:

ab·n=n·ab=a·nb

Как выполнить умножение трех и более обыкновенных дробей

Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.

Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.

Покажем на примере, как это делается.

Пример 6

Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.

Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.

Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.

1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280

Ответ: 1·12·3·520·5·7·8=9280.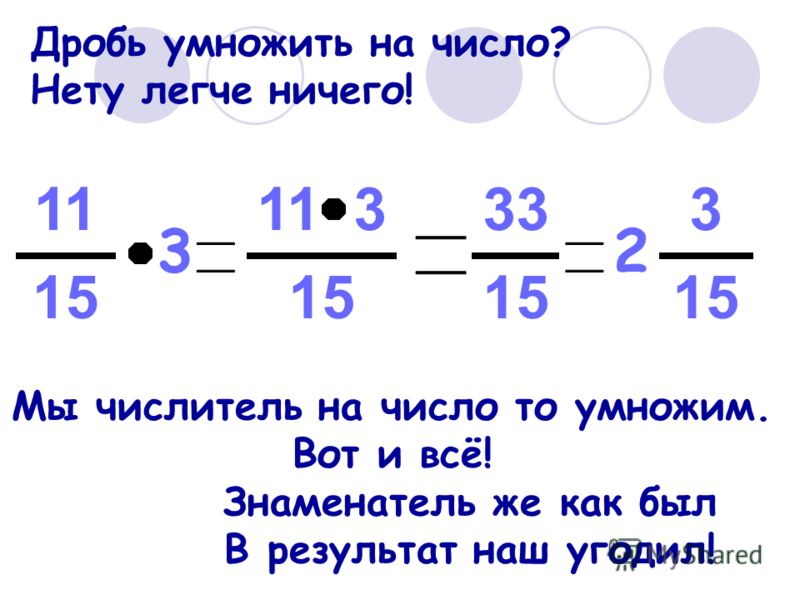

Пример 7

Перемножьте 5 чисел 78·12·8·536·10.

Решение

Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623

Ответ: 78·12·8·536·10=11623.

Правила умножения дробей

 

 

Для того чтобы произвести арифметические действия умножения над дробями, следует перемножить их числители и знаменатели, а результат записать в соответствующей форме.

Умножение простой дроби на число

При умножении простой дроби на натуральное число, ее числитель следует умножить на этот множитель, а знаменатель оставить без изменения.

3 8

×

4

=

3 × 4 8

=

12 8

=

1

4 8

=

1

1 2

Умножение смешанной дроби на число

При необходимости умножения смешанной дроби на натуральное число следует произвести данное арифметическое действие с целым числом этой дроби и её числителем.

1

2 5

×

3

=

1 × 3

+

2 × 3 5

=

3

6 5

=

4

1 5

Умножение дроби на дробь

Когда нужно умножить простую дробь на простую дробь, следует перемножить числители, а затем знаменатели.

3 6

×

4 8

=

3 × 4 6 × 8

=

12 48

=

1 4

Умножение смешанной дроби на смешанную дробь

При выполнении операции умножения смешанных чисел, их следует записать в виде неправильных дробей, после чего перемножить их по соответствующим правилам.

2

1 3

×

4

3 5

=

7 3

×

23 5

=

7 × 23 3 × 5

=

161 15

=

10

11 15

Калькулятор дробей

Использование калькулятора

Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей. Ответы представляют собой дроби в наименьшем значении или смешанные числа в сокращенном виде.

Введите правильные или неправильные дроби, выберите математический знак и нажмите Рассчитать. Это калькулятор дробей с шагами, указанными в решении.

Если у вас отрицательные дроби, вставьте знак минус перед числителем.Итак, если одна из ваших дробей -6/7, вставьте -6 в числитель и 7 в знаменатель.

Иногда в математических задачах используется слово «из», например Что такое 1/3 от 3/8? Of означает, что вам нужно умножить, поэтому вам нужно решить 1/3 × 3/8.

Для математических вычислений со смешанными числами (целыми и дробными) используйте Калькулятор смешанных чисел.

Математика в дробях с разными знаменателями

Есть 2 случая, когда вам нужно знать, имеют ли ваши дроби разные знаменатели:

• если складываете дроби
• , если вы вычитаете дроби

Как сложить или вычесть дроби

1. Найдите наименьший общий знаменатель
2. Вы можете использовать ЖК-калькулятор, чтобы найти наименьший общий знаменатель для набора дробей
3. Для первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель.
4. Умножьте числитель и знаменатель вашей первой дроби на это число
5. Повторите шаги 3 и 4 для каждой фракции
6. Для сложения уравнений добавьте числители дробей
7. Для уравнений вычитания вычтите числители дробей
8. Преобразовать неправильные дроби в смешанные числа
9. Уменьшить дробь до наименьшего значения

Как умножать дроби

1. Умножить все числители вместе
2. Умножить все знаменатели вместе
3. Уменьшить результат до минимума

Как разделить дроби

1. Перепишите уравнение, как в «Сохранить, изменить, перевернуть»
2. Оставить первую дробь
3. Поменять знак деления на умножение
4. Переверните вторую дробь, переключив верхнее и нижнее числа
5. Умножить все числители вместе
6. Умножить все знаменатели вместе
7. Уменьшить результат до минимума

Формулы фракций

Есть способ складывать или вычитать дроби, не находя наименьший общий знаменатель (ЖКД). Этот метод предполагает перекрестное умножение дробей. См. Формулы ниже.

Вы можете обнаружить, что проще использовать эти формулы, чем производить математические вычисления, чтобы найти наименьший общий знаменатель.

Формулы для умножения и деления дробей следуют тому же процессу, что и описанный выше.

Формула сложения дробей:

\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {ad + bc} {bd} \)

Пример шагов:

\ (\ dfrac {2} {6} + \ dfrac {1} {4} = \ dfrac {(2 \ times4) + (6 \ times1)} {6 \ times4} \)

\ (= \ dfrac {14} {24} = \ dfrac {7} {12} \)

Формула вычитания дробей:

\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {ad — bc} {bd} \)

Пример шагов:

\ (\ dfrac {2} {6} — \ dfrac {1} {4} = \ dfrac {(2 \ times4) — (6 \ times1)} {6 \ times4} \)

\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)

Формула умножения дробей:

\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {ac} {bd} \)

Пример шагов:

\ (\ dfrac {2} {6} \ times \ dfrac {1} {4} = \ dfrac {2 \ times1} {6 \ times4} \)

\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)

Формула деления дробей:

\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {ad} {bc} \)

Пример шагов:

\ (\ dfrac {2} {6} \ div \ dfrac {1} {4} = \ dfrac {2 \ times4} {6 \ times1} \)

\ (= \ dfrac {8} {6} = \ dfrac {4} {3} = 1 \ dfrac {1} {3} \)

Сопутствующие калькуляторы

Для выполнения математических операций над смешанными дробями чисел используйте нашу Калькулятор смешанных чисел. Этот калькулятор также может преобразовывать неправильные дроби в смешанные числа и показывает проделанную работу.

Если вы хотите упростить отдельную дробь до наименьших значений, используйте наш Упростите калькулятор дробей.

Для объяснения того, как множить числа, чтобы найти наибольший общий множитель (GCF), см. Калькулятор наибольшего общего коэффициента.

Если вы вручную упрощаете большие дроби, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целые числа и остатки.

Банкноты

Этот калькулятор выполняет вычисление сокращения быстрее, чем другие калькуляторы, которые вы можете найти. Основная причина в том, что он использует алгоритм Евклида для уменьшения дробей, который можно найти на Математический форум.

Умножение дробей

Умножьте вершины, умножьте основания.

Есть 3 простых шага для умножения дробей

1.Умножьте верхние числа (числители , ).

2. Умножьте нижние числа (знаменатели ).

3. При необходимости упростите дробь.

Пример:

1 2 × 2 5

Шаг 1 . Умножьте верхние числа:

1 2 × 2 5 знак равно 1 × 2 знак равно 2

Шаг 2 .Умножаем нижние числа:

1 2 × 2 5 знак равно 1 × 2 2 × 5 знак равно 2 10

Шаг 3 . Упростим дробь:

2 10 знак равно 1 5

С пиццей

Вот с пиццей …

Вы видите, что половина двух пятых — это две десятых?
Вы также видите, что две десятых проще одной пятой?

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

Другой пример:

1 3 × 9 16

Шаг 1 .Умножьте верхние числа:

1 3 × 9 16 знак равно 1 × 9 знак равно 9

Шаг 2 . Умножаем нижние числа:

1 3 × 9 16 знак равно 1 × 9 3 × 16 знак равно 9 48

Шаг 3 .Упростим дробь:

9 48 знак равно 3 16

(На этот раз мы упростили, разделив верхнюю и нижнюю части на 3)

Рифма

♫ «Умножение дробей: нет большой проблемы,
Верхнее умножение сверху на нижнее умножение на низ.
« И не забудьте упростить,
Прежде, чем пришло время прощаться »♫

Дроби и целые числа

А как насчет умножения целых чисел на дроби и ?

Превратите целое число в дробь, поставив его над единицей.

Затем продолжайте, как прежде.

Пример:

2 3 × 5

Превратите 5 в 5 1 :

2 3 × 5 1

А теперь как обычно.

Умножение вершин и оснований:

2 3 × 5 1 знак равно 2 × 5 3 × 1 знак равно 10 3

Дробь уже настолько проста, насколько это возможно.

Ответ = 10 3

Или вы можете просто представить себе целое число как «верхнее» число:

Пример:

3 × 2 9

Умножение вершин и оснований:

3 × 2 9 знак равно 3 × 2 9 знак равно 6 9

Упростить:

6 9 знак равно 2 3

Смешанные фракции

Вы также можете прочитать, как умножить смешанные дроби

Умножение дробей — методы и примеры

Как умножать дроби?

В этой статье обсуждаются все шаги, которые необходимо знать при умножении дробей, включая умножение правильных и неправильных дробей, смешанную дробь и умножение дроби на целое число.Вот шаги для умножения дробей:

• Умножьте числители вместе и поместите произведение поверх полученной дроби
• Умножьте знаменатели вместе и запишите результат внизу новой дроби
• Уменьшите или упростите результат, если возможно

Пример 1:

1/2 × 2/5

Шаг 1. Умножьте числители:

1/2 × 2/5 = 1 × 2 = 2

Шаг 2 .Умножьте знаменатели:

2 x 5 = 10

Шаг 3. Упростите дробь:

2/10 = 1/5

Пример 2:

1/3 × 9/16

Шаг 1. Умножьте числители:

1/3 × 9/16 = 1 × 9 = 9

Шаг 2. Умножьте знаменатели:

3 × 16 = 48
Шаг 3. Упростите дробь:

9 / 48 = 3/16

Пример 3:

Умножение: 4/5 x 7/6

Сначала умножьте числители, чтобы получить: 4 × 7 = 28.

Затем умножьте знаменатели, чтобы получить: 5 × 9 = 45.

Результат = 28/45

Поскольку нет общих делителей 28 и 45, эта дробь уже находится в самом низком выражении. Окончательный ответ — 28/45.

Пример 4:

Умножение: 9/4 x 14/15

Вы можете выполнить все операции в одной математической строке. Не забудьте поставить числитель вверху, а знаменатели — внизу.

9/4 x 14/15 = (9 x 14) / (4 x 15) = 126/60

Умножение более чем на 2 дроби

Отмена — отличный способ умножения с более чем двумя множителями.

Пример 5:

Умножение (1/2) × (2/3) × (3/4) × (4/5).

Начните с исключения общих факторов.

(1/2) × (2/3) × (3/4) × (4/5).

= 1/5

Как умножить дроби на целые числа?

Дроби можно умножать на целые числа точно так же, как умножаются другие дроби.Самая важная процедура состоит в том, чтобы переписать целое число как дробь, введя знаменатель 1. Затем можно применить те же методы умножения дроби.

Целое число N можно преобразовать в дробь со знаменателем 1 следующим образом:

N = N / 1

Пример 6:

Умножение: 3/5 × 60.

3/5 × 60 = 3/5 x 60/1

Умножьте числители:

3 x 60 = 180

Умножьте знаменатели:

1 x 5 = 5

Результат — 180/5, упростите ответ до минимально возможного термины.

180/5 = 36.

Как умножить смешанные дроби?

Смешанная фракция — это фракция, состоящая из целой и дробной части. Например, 7½ — это смешанная дробь, состоящая из целого числа 7 и дробной части ½.

Ниже приведены ключевые шаги при умножении смешанных дробей или смешанной дроби на правильную или неправильную дробь:

• Первым шагом является преобразование всех дробей в неправильную дробь.
• Умножьте числители и поместите произведение вверху.
• Умножьте знаменатели и поместите произведение внизу.
• По возможности упростите результат.

Пример 7:

Умножение: 2 ⁵ / ₆ x 3 ¹ / ₄

Начните с преобразования каждой смешанной дроби в эквивалентную неправильную дробь.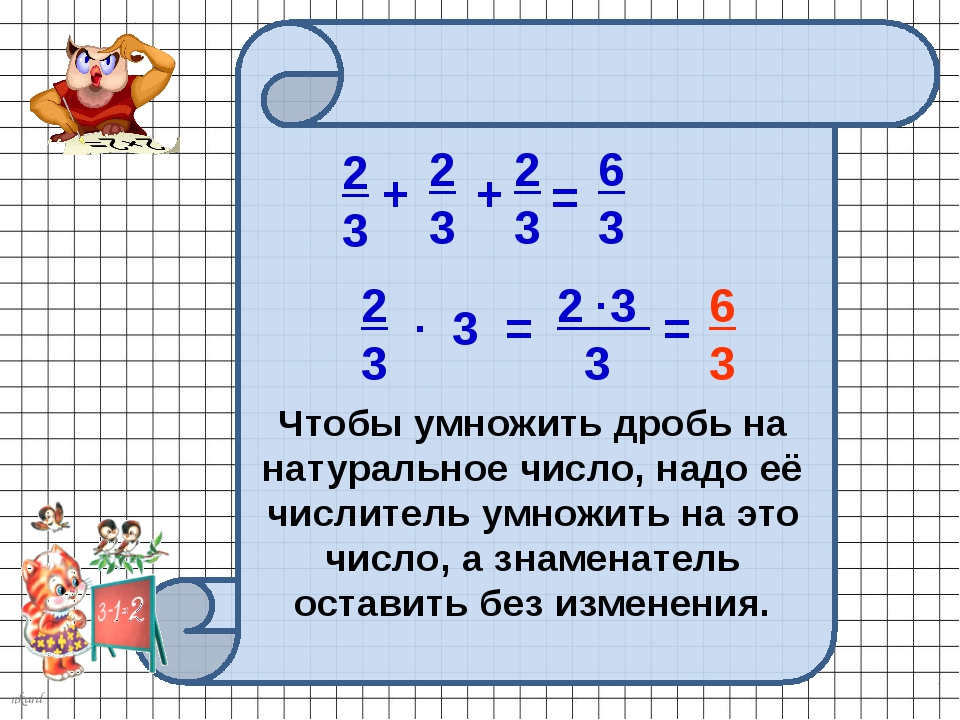

2 ⁵ / ₆ x 3 ¹ / ₄ = 17/6 x 13/4 = 221/24

Окончательный ответ можно упростить или преобразовать обратно в смешанное число путем деления.Преобразование обратно в смешанную дробь похоже на деление с остатком. Частное становится целой частью, а остаток становится новым числителем.

Как умножить отрицательные дроби?

Те же правила умножения отрицательных чисел применяются при умножении дробей:

• + x + = +
• + x — = —
• — x — = +

Пример 8:

Умножение : 2/3 × (–3/4)

2/3 × (–3/4) = –6/12 = –1/2.

Пример 9:

Умножение: (–4/3) × (–7/5)

(–4/3) × (–7/5) = 28/15.

Практические вопросы

Умножьте следующие дроби:

1. 1/3 × 4/5
2. –3/7 × 2/11
3. 9/10 × 35/36
4. 3/8 × 10
5. 5 / 3 × 7/2 × 6/7
6. 6 × 4¾
7. –11/3 × (–3/11)
8. Мой грузовик проезжает 10 ² / ₃ миль на галлон. Предположим, что бак пуст и я заправляю его 5 ¹ / ₂ галлонов, как далеко я могу уехать с грузовиком?
9. Для рецепта требуется 1/2 столовой ложки соли.Сколько нужно соли, чтобы приготовить 20 подобных рецептов?

Предыдущий урок | Главная страница | Следующий урок

Что такое умножение дробей? — Определение, факты и примеры

Умножение дробей

Дробь — это часть целого .

Яблочный пирог, разрезанный на 4 равных ломтика и один ломтик, отделенный друг от друга, как показано на рисунке.

Здесь яблочный пирог разрезан на 4 равные части, каждая из которых составляет одну четвертую часть пирога. Сколько будет яблочного пирога в 5 таких кусочках?

Это будет произведение 5 × 1 4. Мы также можем оценить умножение как повторное сложение, и это проще.

5 × 1 4 = 1 4 + 1 4 + 1 4 + 1 4 + 1 4 = 5 4

Мы также можем преобразовать это в смешанное число, 5 4 = 1 1 4. Следовательно, из 5 кусочков пирога будет одна с четвертью яблочного пирога.

Но повторное сложение — не всегда более простой метод, особенно когда множитель также является дробью.

Рассмотрим произведение 2 5 × 3 4.

Дробь 3 4 может быть представлена ​​следующим образом:

Теперь требуемый продукт составляет две пятых этой заштрихованной части.

Чтобы найти это, вам нужно разделить эти три заштрихованные части на 5 равных частей. Более простой способ сделать это — разделить каждую из этих 4 частей на 5 равных частей.

Итак, две пятых от трех четвертых — это две заштрихованные части из каждой из этих трех частей, то есть 6 заштрихованных частей из 20, как показано.

Другой способ геометрического представления:

В дроби, представляющей произведение, целое делится на 20 равных частей, и заштрихованные части, общие для обоих факторов, являются знаменателем, а 6 представляет числитель произведения.

Алгебраически правило умножения двух дробей:

Шаг 1 : Умножьте числители дробей множителя.

Шаг 2 : Умножьте знаменатели.

Шаг 3 : При необходимости упростите продукт.

Пример:

5 6 x 3 8 = 5 x 3 6 x 8 = 15 48

Здесь 3 — общий множитель числителя и знаменателя. Итак, чтобы упростить дробь, разделите числитель и знаменатель на 3.

15 ÷ 3 48 ÷ 3 = 5 6

Таким образом, 5 6 x 3 8 = 5 16.

Правило:

Если a b и c d дроби с b, d ≠ 0, то a b x c d = ac bd

Интересные факты Слово «дробь» происходит от латинского слова «fractio», что означает «разбивать». При умножении двух дробей, если одна из дробей больше 1, это увеличивает размер второй дроби как произведения. Если оно меньше 1, это уменьшит размер второй фракции как продукта.

Обзор дробей: умножение и деление дробей

Purplemath

Умножать дроби просто: вы умножаете верхние числа и умножаете нижние числа.Например:

Когда это возможно, вы уменьшаете дробь, отбрасывая общие множители; то есть вы вычеркиваете любые множители с одной стороны дробной линии, которые дублируются с другой стороны линии. Однако в приведенном выше примере ничего не уменьшается, потому что 8 и 45 не имеют общих множителей.

MathHelp.com

Если вы не уверены, можно ли что-то отменить, вы всегда можете разложить числитель и знаменатель на множители и проверить наличие повторяющихся множителей:

Ничего не дублируется между верхом и низом, поэтому ничего не отменяется.

Однако часто что-то отменяется:

• Упростить

Для умножения я умножаю все верхние числа (числители) друг на друга и умножаю все нижние числа (знаменатели) друг на друга. Однако, чтобы немного облегчить себе жизнь, я сначала исключу все факторы, общие как для числителей, так и для знаменателей:

Тогда упрощенный продукт —

⁷ / ₂ .

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в умножении дробей. Попробуйте введенное упражнение, введите свое упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

---

Разделить дроби так же просто, как и умножить их; есть только один дополнительный шаг.Когда вы делите на дробь, первое, что вы делаете, — это «перевернуть-п-умножить». То есть вы берете вторую дробь, переворачиваете ее вверх ногами (то есть «находите обратную»), а затем умножаете первую дробь на эту перевернутую дробь.

• Упростить

Моим первым шагом будет преобразовать это в умножение, перевернув ⁹ / ₄ , чтобы получить ⁴ / ₉ .Затем я могу продолжить простое умножение, исключив все повторяющиеся множители:

Тогда мой упрощенный ответ:

⁴ / ₁₅ .

• Упростить

Это немного сложно, но я могу справиться с целым числом 5, преобразовав его в дробь.Помните, что любое целое число является дробью, если вы поставите его над «1». Итак, я преобразовываю 5 в дробь ⁵ / ₁ и переверну с умножением:

Тогда мой упрощенный ответ:

¹ / ₆ .

• Упростить

Для этого упражнения мне сначала нужно преобразовать смешанные числа в (неправильную) дробную форму.(Умножение и деление дробей — это места, где дроби оооочень намного лучше, чем смешанные числа!) Как только у меня есть дроби, я могу перевернуть-n-умножить.

Тогда мой ответ смешанный:

1 ³⁷ / ₆₈ .

Примечание. Когда входные данные представляют собой смешанные числа, как в последнем примере выше, книга (или преподаватель, или оценщик) обычно также ожидает смешанные числа на выходе. Итак, если ваш ответ является неправильной дробью, вам нужно будет преобразовать ее обратно в форму смешанного числа.Не забывайте этот шаг!

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в делении дробей. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

Далее мы переходим к гораздо более сложному сложению и вычитанию дробей …

---

URL: https://www.purplemath.com/modules/fraction3.htm

Каковы правила умножения дробей?

Обновлено 21 декабря 2020 г.

Лиза Мэлони

Умножение — одна из самых простых операций, которые вы можете выполнять с дробями, потому что вам не нужно беспокоиться о том, имеют ли дроби одинаковый знаменатель или нет; просто умножьте числители вместе, умножьте знаменатели вместе и, если необходимо, упростите полученную дробь.Однако есть несколько вещей, на которые следует обратить внимание, включая смешанные числа и отрицательные знаки.

Умножение прямо через

Первое и самое важное правило умножения дробей состоит в том, что вы умножаете только числитель на числитель и знаменатель на знаменатель. Если у вас есть две дроби 2/3 и 4/5, их умножение даст новую дробь:

\ frac {2 × 4} {3 × 5}

\ frac {8} {15}

При этот момент вы бы упростили, если бы могли, но, поскольку 8 и 15 не имеют общих множителей, эту дробь нельзя упростить дальше.

Чтобы увидеть больше примеров, включая умножение дробей, которые необходимо уменьшить, посмотрите видео ниже:

Следите за отрицательными знаками

Если вы умножаете дроби с отрицательными членами, убедитесь, что у вас есть эти отрицательные знаки через ваши расчеты. Например, если вам даны две дроби -3/4 и 9/6, вы должны умножить их вместе, чтобы получить новую дробь:

\ frac {-3 × 9} {4 × 6}

\ frac {-27} {24}

Поскольку -27 и 24 имеют общий делитель 3, вы можете вынести 3 из числителя и знаменателя, в результате получится:

\ frac {-9} {8}

Обратите внимание, что -9/8 представляет собой значение, сильно отличающееся от 9/8.Если бы этот отрицательный знак потерялся по пути, ваш ответ был бы неправильным.

Да, неправильные дроби можно умножать

Еще раз взгляните на только что приведенный пример. Вторая дробь, 9/6, неправильная дробь. Или, другими словами, его числитель был больше, чем знаменатель. Это никак не меняет способ работы вашего умножения, хотя в зависимости от вашего учителя или ограничений задачи, над которой вы работаете, вы можете предпочесть упростить результат последнего примера, который сам является неправильной дробью, до смешанное число:

\ frac {-9} {8} = -1 \, \ frac {1} {8}

Умножение смешанных чисел

Это прекрасно ведет к обсуждению того, как умножать смешанные числа: Преобразование смешанное число на неправильную дробь и умножьте как обычно, как описано в последнем примере.Например, если вам нужно умножить дробь 4/11 и смешанное число 5 2/3, вы сначала умножите целое число 5 на 3/3 (это число 1 в виде дроби знаменатель которого совпадает со знаменателем дробной части смешанного числа), чтобы преобразовать его в дробь:

5 × \ frac {3} {3} = \ frac {15} {3}

Затем добавьте дробную часть смешанного числа, что дает вам:

5 \, \ frac {2} {3} = \ frac {15} {3} + \ frac {2} {3} = \ frac {17} {3}

Теперь вы готовы умножить две дроби вместе:

\ frac {17} {3} × \ frac {4} {11}

Умножение числителя и знаменателя дает:

\ frac {17 × 4} { 3 × 11}

\ frac {68} {33}

Вы не можете больше упрощать члены этой дроби, но при желании можете преобразовать ее обратно в смешанное число:

2 \, \ frac {2} {33}

Умножение — это обратное деление

Вот удобный Уловка: если вы знаете, как умножать на дроби, вы уже знаете, как делить на дроби.Просто переверните вторую дробь вверх дном и умножьте ее, вместо того чтобы делить. Итак, если у вас есть:

\ frac {3} {4} ÷ \ frac {2} {3}

Это то же самое, что писать:

\ frac {3} {4} × \ frac {3} { 2}

, которые затем можно умножить как обычно.

Умножение дробей — ChiliMath

Чтобы умножить дроби, достаточно выполнить 3 предложенных ниже шага. Понятно, что ни одна дробь не может иметь знаменатель \ color {red} 0, потому что это будет неопределенный член.

Шаги в умножении дробей

Даны две дроби с ненулевыми знаменателями:

Шаг 1: Умножьте числители.

• Это будет числитель «новой» дроби.

Шаг 2: Умножьте знаменатели.

• Это будет знаменатель «новой» дроби.

Шаг 3: Упростите полученную дробь, уменьшив ее до наименьшего члена, если необходимо.

---

Прежде чем мы рассмотрим некоторые примеры, есть другие способы обозначить умножение.

• Точечный символ как оператор умножения

• Скобка как оператор умножения

---

Примеры умножения дробей

Пример 1 : Умножение.

Умножьте числители дробей.

Аналогичным образом умножьте знаменатели.

Результирующая дробь после умножения уже имеет уменьшенную форму, поскольку наибольший общий делитель числителя и знаменателя равен \ color {blue} +1.Это и станет нашим окончательным ответом!

---

Пример 2 : Умножение.

Шаг 1. Умножьте верхние числа.

Шаг 2: Умножьте нижние числа.

Шаг 3. Упростите ответ, сократив его до наименьшего члена.

Разделите верхнюю и нижнюю на наибольший общий коэффициент (GCF), равный 10.

---

Пример 3 : Умножьте.

Вы можете столкнуться с проблемой, когда вам будет предложено умножить три дроби.

Общая идея остается такой же, как и при умножении двух дробей, как показано в предыдущих примерах.

Шаг 1. Рассчитайте произведение числителей.

Шаг 2: Вычислите произведение знаменателей.

Шаг 3. Уменьшите дробь до ее простейшего вида.

Разделите числитель и знаменатель на наибольший общий делитель, равный 12.

---

Пример 4 : Умножьте целое число на дробь.