Также читайте о Self в Python здесь!

Существует много типов систематических ошибок, таких как систематическая ошибка отбора, систематическая ошибка отчетности, систематическая ошибка выборки и так далее. Точно так же смещение округления связано с числовыми данными. В этой статье мы увидим следующее:

• Почему важно знать способы округления чисел
• Как использовать различные стратегии округления чисел
• Как округление влияет на данные
• Как использовать массивы NumPy и Pandas DataFrames для округления чисел

Давайте сначала узнаем о встроенном в Python процессе округления.

О встроенной в Python функции round()

Программирование на Python предлагает встроенную функцию round(), которая округляет число до заданного количества цифр и упрощает округление чисел. Функция round() принимает два числовых аргумента, n и n цифр, а затем возвращает число n после округления до цифр. Если количество цифр для округления не указано, функция округляет число n до ближайшего целого числа.

Предположим, вы хотите округлить число, скажем, 4,5. Оно будет округлено до ближайшего целого числа, равного 5. Однако число 4,74 будет округлено до одного десятичного знака, чтобы получить 4,7.

Очень важно быстро и легко округлять числа, когда вы работаете с числами с плавающей запятой, имеющими много десятичных разрядов. Встроенная функция Python round() делает это простым и легким.

Синтаксис

 round(число, количество цифр) 

Параметры функции round():

1. число — число, которое нужно округлить
2. количество цифр (необязательно) — количество цифр, до которого нужно округлить данное число.

Второй параметр является необязательным. В случае, если он отсутствует, функция round() возвращает:

• Для целого числа 12 оно округляется до 12
• Для десятичного числа, если последняя цифра после запятой >=5, оно округляется до следующего целого числа, а если <5, оно будет округлено до целого числа пола

Рассмотрим пример, в котором отсутствует второй параметр.

 # Для целых чисел
печать (круглый (12))

# Для плавающей запятой
печать (округление (21,7))
print(round(21.4)) 

Вывод будет:

 12
22
21 

Теперь, если присутствует второй параметр.

 # когда (nцифра+1)я цифра =5
печать (округление (5,465, 2))

# когда (ndigit+1)я цифра >
 =5
печать (округление (5,476, 2))

# когда (ndigit+1)я цифра <5
печать (округление (5.473, 2)) 

Вывод будет:

 5,46
5,48
5.47 

Практическое применение функции round()
Между дробями и десятичными дробями всегда есть несоответствие. Для обработки таких случаев можно использовать округление функций. При преобразовании дробей в десятичные мы обычно получаем много цифр после запятой, например, для ⅙ мы получаем 0,166666667, но мы используем либо две, либо три цифры справа от десятичной точки. Здесь функция раунда спасает положение.

Например:

 х = 1/3
печать (х)
print(round(x, 2)) 

Вывод будет:

 0.3333333333333333
0,33 

Некоторые ошибки и исключения, связанные с этой функцией
Например,

print(round("x", 2))

Вывод будет:

 ----------- -------------------------------------------------- --------------
TypeError                                 Traceback (самый последний вызов последним)
  в ()
----> 1 print(round("x", 2))
TypeError: тип str не определяет метод __round__ 

Другой пример,

 print(round(1.5))
печать (круглый (2))
print(round(2.5)) 

Вывод будет:

 2
2
2 

Функция round() округляет 1,5 до 2 и 2,5 до 2. Это не ошибка, так ведет себя функция round(). В этой статье вы узнаете еще несколько способов округления числа. Рассмотрим различные способы округления числа.

Различные методы округления

Существует множество способов округления чисел со своими преимуществами и недостатками. Чтобы лучше понять эти разнообразные методы округления, учащиеся-новички могут также пройти расширенный курс Python. Но перед этим здесь мы изучим некоторые приемы округления числа.

Усечение

Усечение, как следует из названия, означает сокращение. Это один из самых простых методов округления числа, который включает в себя усечение числа до заданного количества цифр. Этот метод заменяет каждую цифру после заданной позиции на 0. Давайте рассмотрим несколько примеров.

Value	Truncated To	Result
19.345	Tens place	10
19. 345	Ones place	19
19.345	Tenths place	19.3
19.345	Сотые доли	19.34

Функция truncate() может использоваться как для положительных, так и для отрицательных чисел:

 >>> обрезать (19.5)
19,0
>>> обрезать(-2,852, 1)
-2,8
> >> обрезать(2.825, 2)
2.82 

Функцию truncate() также можно использовать для усечения цифр слева от десятичной точки путем передачи отрицательного числа.

 >>> усечение (235,7, -1)
230,0
>>> обрезать(-1936.37, -3)
-1000.0 

Когда положительное число усекается, мы обычно округляем его в меньшую сторону. Точно так же, когда мы усекаем отрицательное число, оно округляется в большую сторону. Рассмотрим различные методы округления.

Округление в большую сторону

Существует еще одна стратегия, называемая «округлением в большую сторону», при которой число округляется до определенного количества цифр. For example:

Термин потолок используется в математике для объяснения ближайшего целого числа, которое больше или равно заданному числу. В Python для «округления» мы используем две функции, а именно функцию

1. ceil() и функцию
2. math()

Нецелое число лежит между двумя последовательными целыми числами. Например, учитывая число 5,2, оно будет лежать между 4 и 5. Здесь потолок — это верхняя конечная точка интервала, а пол — нижняя. Следовательно, потолок 5.2 равен 5, а пол 5.2 равен 4. Однако потолок 5 равен 5.

В Python функцией для реализации функции потолка является функция math.ceil(). Он всегда возвращает ближайшее целое число, которое больше или равно его входу.

 >>> импорт математики
>>> math.ceil(5.2)
6
>>> math.ceil(5)
5
>>> math.ceil(-0,5)
0 

Если вы заметили, то увидите, что потолок -0,5 равен 0, а не -1.
Давайте посмотрим на короткий код для реализации стратегии «округления» с помощью функции round_up():

 def round_up(n, десятичные числа=0):
множитель = 10 ** десятичных знаков
return math.ceil(n * multiplier) / multiplier 

Давайте посмотрим, как функция round_up() работает с различными входными данными:

 >>> round_up(3.1)
4.0
>>> round_up(3.23, 1)
3.3
>>> round_up(3,543, 2)
3.55 

Вы можете передавать отрицательные значения десятичным дробям, как мы это делали при усечении.

 >>> round_up(32.45, -1)
40,0
>>> round_up(3352, -2)
3400 

Вы можете следовать приведенной ниже диаграмме, чтобы понять округление в большую и меньшую сторону.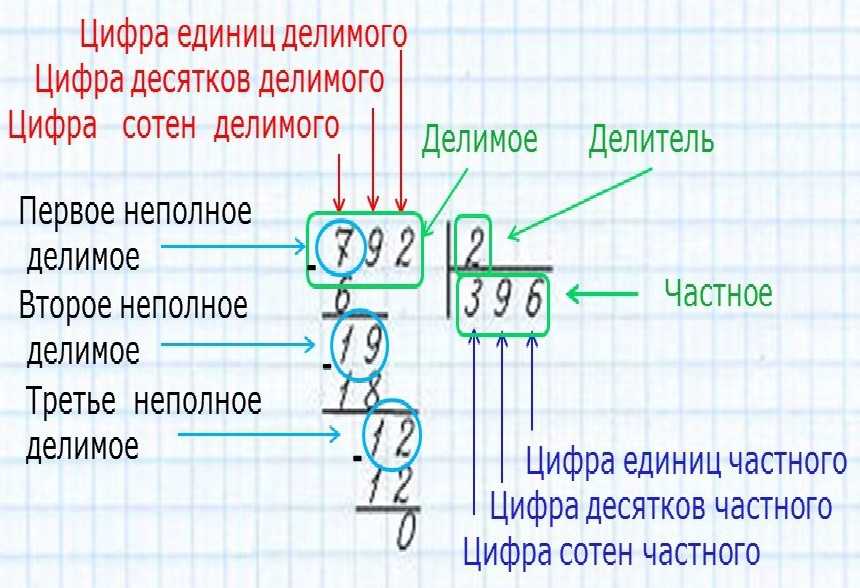

Округление всегда округляет число вправо в числовой строке, а округление в меньшую сторону всегда округляет число влево в числовой строке.

Rounding Down

Similar to rounding up we have another strategy called rounding down where

In Python, rounding down can be implemented using a similar algorithm as we truncate or round up . Сначала вам нужно будет сдвинуть десятичную точку, а затем округлить целое число. Наконец, сдвиньте запятую назад.

Math. ceil() используется для округления до максимального числа после сдвига десятичной точки. Для «округления в меньшую сторону» нам сначала нужно округлить пол числа после смещения десятичной точки.

 >>> мат.пол(1.2)
1
>>> math.floor(-0,5)
-1 

Вот определение round_down():

 def round_down(n, decimals=0):
множитель = 10 ** десятичных знаков
return math.floor(n * multiplier) / multiplier 

Это очень похоже на функцию round_up(). Здесь мы используем math.floor() вместо math.ceil().

 >>> round_down(1.5)
1
>>> round_down(1,48, 1)
1,4
>>> round_down(-0,5)
-1 

Округление числа в большую или меньшую сторону сильно влияет на большой набор данных. После округления вверх или вниз вы можете удалить много точности, а также изменить вычисления.

Округление наполовину в большую сторону

Стратегия «округление наполовину в большую сторону» округляет каждое число до ближайшего числа с заданной точностью и устраняет неравенство путем округления в большую сторону. Here are some examples:

В этом случае вам нужно будет определить, является ли цифра после сдвинутой запятой меньше или больше равной 5.

Вы можете добавить 0,5 к смещенному значению, а затем округлить его в меньшую сторону с помощью math.floor( ) функция.

 по определению round_half_up(n, десятичные знаки=0):
множитель = 10 ** десятичных знаков
return math.floor(n*multiplier + 0.5) / multiplier 

Если вы заметили, то можете заметить, что round_half_up() похож на round_down. Единственное отличие состоит в том, что после смещения запятой нужно добавить 0,5, чтобы результат округления в меньшую сторону совпал с ожидаемым значением.

 >>> round_half_up(19.23, 1)
19.2
>>> round_half_up(19.28, 1)
19,3
>>> round_half_up(19.25, 1)
19.3 

Округление наполовину вниз

В этом методе округления округление производится до ближайшего числа, аналогичного методу «округление наполовину в большую сторону», отличие состоит в том, что при этом округление выполняется до меньшего из двух чисел. Here are some examples:

в Питкене, «Функциональный» (Flationfed) (Flationfed). с помощью math.ceil(), а затем путем вычитания 0,5 вместо добавления:

 def round_half_down(n, decimals=0):
множитель = 10 ** десятичных знаков
return math. ceil(n*multiplier - 0.5) / multiplier 

Давайте рассмотрим несколько тестов.

 >>> round_half_down(1.5)
1,0
>>> round_half_down(-1,5)
-2,0
>>> round_half_down(2.25, 1)
2.2 

В общем, для round_half_up() и round_half_down() нет смещения. Однако округление данных с большим количеством связей приводит к систематической ошибке. Давайте рассмотрим пример, чтобы лучше понять.

 >>> data = [-2,15, 1,45, 4,35, -12,75] 

Вычислим среднее значение этих чисел:

 >>>statistics.mean(data)
-2,275 

Теперь давайте вычислим среднее значение данных после округления до одного десятичного знака с помощью round_half_up() и round_half_down():

 >>> rhu_data = [round_half_up(n, 1) для n в данных]
>>>statistics.mean(rhu_data)
-2,2249999999999996
>>> rhd_data = [round_half_down(n, 1) для n в данных]
>>>statistics.mean(rhd_data)
-2,325 

Функция round_half_up() приводит к округлению в сторону положительной бесконечности, а round_half_down() приводит к округлению к отрицательной бесконечности.

Округление до половины от нуля

Если вы внимательно заметили, проходя через round_half_up() и round_half_down(), ни один из них не является симметричным относительно нуля:

 >>> round_half_up(1.5)
2.0
>>> round_half_up(-1,5)
-1,0
>>> round_half_down(1.5)
1,0
>>> round_half_down(-1,5)
-2.0 

Чтобы ввести симметрию, вы всегда можете округлить ничью от нуля. Приведенная ниже таблица ясно иллюстрирует это:

Реализация стратегии «округления до половины от нуля» для числа n очень проста. Все, что вам нужно сделать, это начать, как обычно, сдвинув десятичную точку вправо на заданное количество знаков, а затем заметить цифру d сразу справа от десятичной точки в этом новом числе. Здесь необходимо рассмотреть четыре случая:

1. Если n положительно и d >= 5, округлить в большую сторону
2. Если n положительно и d < 5, округлить до
3. Если n отрицательное и d >= 5, округлить в меньшую сторону
4. Если n отрицательное и d < 5, округлить в большую сторону

После округления в соответствии с указанными выше правилами вы можете сдвинуть десятичный разряд обратно влево.

У вас может возникнуть вопрос: как вы справляетесь с ситуациями, когда количество положительных и отрицательных связей резко различается? Ответ на этот вопрос возвращает нас к функции, которая обманула нас в начале этой статьи: встроенной в Python функции round().

Округление от половины до четного

Существует способ уменьшить погрешность округления при округлении значений в наборе данных. Вы можете просто округлить связи до ближайшего четного числа с нужной точностью. Let us look at some examples:

 >>> круглый(4.5)
4
>>> раунд(3,5)
4
>>> раунд(1,75, 1)
1,8
>>> раунд(1,65, 1)
1.6 

Десятичный класс

Десятичный модуль в Python — это одна из тех особенностей языка, о которых вы могли не знать, если только начали изучать Python. Десятичная система «основана на модели с плавающей запятой, которая была разработана для людей и обязательно имеет первостепенный руководящий принцип — компьютеры должны обеспечивать арифметику, которая работает так же, как арифметика, которую люди изучают в школе». – кроме десятичной арифметической спецификации.

Ниже перечислены некоторые преимущества десятичного модуля:

• Точное десятичное представление: 0,1 на самом деле равно 0,1, а 0,1 + 0,1 + 0,1 - 0,3 возвращает 0, как и ожидалось.

• Сохранение значащих цифр: при сложении 1,50 и 2,30 получается 3,80 с сохранением нуля в конце для обозначения значимости.

• Изменяемая пользователем точность: Точность десятичного модуля по умолчанию составляет двадцать восемь цифр, но это значение может быть изменено пользователем в соответствии с поставленной задачей.

Давайте посмотрим, как работает округление в десятичном модуле.

 >>> импорт десятичного
>>> десятичный.getcontext()
Контекст(
прец=28,
округление=ROUND_HALF_EVEN,
Эмин=-999999,
Emax=999999,
столицы = 1,
зажим=0,
флаги=[],
ловушки=[
неверная операция,
Деление на ноль,
Переполнение
]
) 

Функция decimal. getcontext() возвращает объект контекста, который представляет контекст по умолчанию десятичного модуля. Он также включает точность по умолчанию и стратегию округления по умолчанию.

В приведенном выше примере вы увидите, что стратегия округления по умолчанию для десятичного модуля — ROUND_HALF_EVEN. Это позволяет выполнить выравнивание со встроенной функцией round()

. Давайте создадим новый экземпляр Decimal, передав строку, содержащую желаемое значение, и объявив число с помощью класса Decimal модуля decimal.

 >>> из десятичного импорта Десятичный
>>> Десятичное ("0,1")
Decimal('0.1') 

Вы можете создать экземпляр Decimal из числа с плавающей запятой, но в этом случае возникнет ошибка представления с плавающей запятой. Например, вот что происходит, когда вы создаете экземпляр Decimal из числа с плавающей запятой 0,1

 >>> Десятичный (0,1)
Decimal('0.1000000000000000055511151231257827021181583404541015625') 

Вы можете создавать экземпляры Decimal из строк, содержащих нужные вам десятичные числа, чтобы поддерживать точную точность.

Округление десятичного числа с использованием метода .quantize():

 >>> Decimal("1,85").quantize(Decimal("1,0"))
Decimal('1.8') 

Аргумент Decimal("1.0") в .quantize() позволяет определить количество знаков после запятой для округления числа. Поскольку 1,0 имеет один десятичный знак, число 1,85 округляется до одного десятичного знака. Округление от половины до четного является стратегией по умолчанию, поэтому результат равен 1,8.

Десятичный класс:

 >>> Decimal("2,775").quantize(Decimal("1,00"))
Decimal('2.78') 

Десятичный модуль дает еще одно преимущество. После выполнения арифметических операций округление выполняется автоматически, а также сохраняются значащие цифры.

 >>> decimal.getcontext().prec = 2
>>> Десятичный ("2,23") + Десятичный ("1,12")
Decimal('3.4') 

Чтобы изменить стратегию округления по умолчанию, вы можете установить для свойства decimal. getcontect().rounding любой из нескольких флагов. В следующей таблице приведены эти флаги и стратегии округления, которые они реализуют:

Rounding NumPy Arrays

In Data Science and scientific computation , мы обычно храним данные в виде массива NumPy. Одной из самых мощных функций NumPy является использование векторизации и широковещательной рассылки для применения операций ко всему массиву сразу, а не к одному элементу за раз.

Давайте сгенерируем некоторые данные, создав массив 3×4 NumPy из псевдослучайных чисел:

 >>> import numpy as np
>>> np.random.seed(444)
>>> данные = np.random.randn(3, 4)
>>> данные
массив([[ 0,35743992, 0,3775384, 1,38233789, 1,17554883],
[-0,9392757, -1,14315015, -0,54243951, -0,54870808],
       [ 0.20851975, 0.21268956, 1.26802054, -0.80730293]]) 

Здесь сначала мы задаем модуль np.random, чтобы легко воспроизвести вывод. Затем с помощью np.random.randn() создается массив чисел с плавающей запятой 3×4 NumPy.

Не забудьте установить pip3 перед выполнением кода, упомянутого выше. Если вы используете Anaconda, все готово.

Чтобы округлить все значения в массиве данных, передайте данные в качестве аргумента функции np. around(). Желаемое количество знаков после запятой задается аргументом ключевого слова decimals. В этом случае используется стратегия округления от половины до чета, аналогичная встроенной в Python функции round().

Чтобы округлить данные в вашем массиве до целых чисел, NumPy предлагает несколько вариантов, которые упомянуты ниже:

• numpy.ceil()
• numpy.floor()
• numpy.trunc()
• numpy.rint()

Функция np.ceil() округляет каждое значение в массиве до ближайшего целого числа больше больше или равно исходному значению:

 >>> np.ceil(data)
массив([[ 1.,  1.,  2.,  2.],
[-0., -1., -0., -0.],
       [ 1., 1., 2., -0.]]) 

Внимательно посмотрите на код; у нас новый номер! Отрицательный ноль! Давайте теперь посмотрим на библиотеку Pandas, широко используемую в науке о данных с Python.

Округление серий Pandas и DataFrame

Pandas изменили правила игры для анализа данных и науки о данных. Две основные структуры данных в Pandas — Dataframe и Series. Dataframe работает как электронная таблица Excel, тогда как вы можете рассматривать ряды как столбцы в электронной таблице. Методы Series.round() и DataFrame.round(). Давайте посмотрим на пример.

Не забудьте установить pip3 перед выполнением кода, упомянутого выше. Если вы используете Anaconda, все готово.

 >>> импортировать панд как pd
>>> # Повторное заполнение np.random, если вы закрыли свой REPL после последнего примера
>>> np.random.seed(444)
>>> series = pd.Series(np.random.randn(4))
>>> серия
0    0,357440
1    0,377538
2    1,382338
3     1.175549
тип: float64
>>> series.round(2)
0    0,36
1    0,38
2    1,38
3    1.18
тип: float64
>>> df = pd.DataFrame(np.random.randn(3, 3), columns=["A", "B", "C"])
>>> дф
А         Б         С
0 -0,939276 -1,143150 -0,542440
1 -0,548708 0,208520 0,212690
2  1,268021 -0,807303 -3,303072
>>> df.round(3)
А      В      С
0 -0,939 -1,143 -0,542
1 -0,549 0,209 0,213
2  1,268 -0,807 -3,303
Метод DataFrame. round() также может принимать словарь или ряд, чтобы указать разную точность для каждого столбца. Например, в следующих примерах показано, как округлить первый столбец df до одного знака после запятой, второй — до двух, а третий — до трех знаков после запятой:
>>> # Укажите точность столбца за столбцом со словарем
>>> df.round({"A": 1, "B": 2, "C": 3})
А     Б      С
0 -0,9-1,14 -0,542
1 -0,5 0,21 0,213
2  1,3 -0,81 -3,303
>>> # Укажите точность столбца за столбцом с помощью Series
>>> decimals = pd.Series([1, 2, 3], index=["A", "B", "C"])
>>> df.round(десятичные числа)
А     Б      С
0 -0,9 -1,14 -0,542
1 -0,5 0,21 0,213
2  1,3 -0,81 -3,303
Если вам нужна большая гибкость округления, вы можете применить функции NumPy floor(), ceil() и print() к объектам Pandas Series и DataFrame:
>>> np.floor(df)
А    В    С
0 -1,0 -2,0 -1,0
1 -1,0  0,0  0,0
2  1,0 -1,0 -4,0
>>> np.ceil(df)
А    В    С
0 -0,0 -1,0 -0,0
1 -0,0  1,0  1,0
2  2,0 -0,0 -3,0
>>> np.rint(df)
А    В    С
0 -1,0 -1,0 -1,0
1 -1,0  0,0  0,0
2  1,0 -1,0 -3,0
Здесь также будет работать модифицированная функция round_half_up() из предыдущего раздела:
>>> round_half_up(df, десятичные числа=2)
А     Б     С
0 -0,94 -1,14 -0,54
1 -0,55 0,21 0,21
2 1,27 -0,81 -3,30 

Передовой опыт и приложения

Теперь, когда вы познакомились с большинством методов округления, давайте изучим некоторые передовые методы, позволяющие правильно округлять числа.

Сгенерировать больше данных и округлить позже

Предположим, вы имеете дело с большим набором данных, хранение которых иногда может быть проблемой. Например, в промышленной печи вы хотели бы измерять температуру каждые десять секунд с точностью до восьми знаков после запятой с помощью датчика температуры. Эти показания помогут избежать больших колебаний, которые могут привести к выходу из строя любого нагревательного элемента или компонентов. Мы можем написать скрипт Python для сравнения показаний и проверки больших колебаний.

Будет большое количество показаний, так как они записываются каждый день. Вы можете рассмотреть возможность сохранения трех знаков после запятой. Но опять же, удаление слишком большой точности может привести к изменению расчета. Однако, если у вас достаточно места, вы можете легко хранить все данные с полной точностью. При меньшем объеме памяти всегда лучше хранить как минимум два или три десятичных разряда с точностью, необходимой для вычислений.

В конце концов, как только вы закончите вычисление среднесуточной температуры, вы можете вычислить ее с максимально доступной точностью и, наконец, округлить результат.

Обмен валюты и правила

Всякий раз, когда мы покупаем товар в определенном месте, сумма налога, уплачиваемая в отношении стоимости товара, во многом зависит от географических факторов. Товар, который стоит вам 2 доллара США, может стоить вам меньше (скажем, 1,8 доллара США), если вы покупаете тот же товар в другом штате. Это связано с правилами, установленными местными властями.

В другом случае шведское округление выполняется, когда минимальная единица валюты на уровне учета в стране меньше самой низкой единицы физической валюты. Список таких методов округления, используемых в разных странах, можно найти в Интернете.

Если вы хотите разработать какое-либо подобное программное обеспечение для расчета валюты, не забудьте проверить местные законы и правила, применимые в вашем текущем местоположении.

Уменьшить ошибку

Поскольку вы округляете числа в большом наборе данных, используемом в сложных вычислениях, вашей главной задачей должно быть ограничение роста ошибки из-за округления.

Резюме

В этой статье мы рассмотрели несколько методов округления чисел, из которых стратегия «округления от половины до четного» лучше всего минимизирует погрешность округления. Нам повезло, что Python, NumPy и Pandas уже имеют встроенные функции округления для использования этой стратегии. Здесь мы узнали о -

• Несколько стратегий округления и как их реализовать на чистом Python.
• Каждая стратегия округления по своей сути вводит смещение округления, и стратегия «округления от половины до четного» в большинстве случаев хорошо смягчает это смещение.
• Вы можете округлять массивы NumPy и объекты Pandas Series и DataFrame.

Если вам понравилось читать эту статью и она показалась вам интересной, оставьте комментарий.