Индивидуальные задания по математике, 4 класс
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
432:2 588:4 748:4
675:5 396:3 968:4
924:2 258:2 753:3
444:2 384:2 524:4
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Выполни деление столбиком
658:2 576:3 196:2
453:3 954:3 332:4
688:4 146:2 291:3
585:5 219:3 455:7
Реши примеры, правильно их запиши и прочитай
№1
60 000 + 3 = 301 000 + 45 =
20 000 + 54 = 29 000 + 702 =
71 000 + 246 = 930 000 + 5 =
57 000 + 1 = 1 000 + 237 =
802 000 + 26 = 2 000 + 2 =
746 000 + 529 = 893 000 + 58 =
607 000 + 435 = 248 000 + 52 =
№2
247 000 + 2 000 + 31 =
103 000 + 5000 + 586 =
721 000 + 4 000 + 3 =
350 000 + 1 000 + 15 =
285 000 + 3 000 + 645 =
915 000 + 4 000 + 2 =
302 000 + 6 000 + 37 =
400 000 + 5 000 + 625 =
Реши примеры, правильно их запиши и прочитай
№1
60 000 + 3 = 301 000 + 45 =
20 000 + 54 = 29 000 + 702 =
71 000 + 246 = 930 000 + 5 =
57 000 + 1 = 1 000 + 237 =
802 000 + 26 = 2 000 + 2 =
746 000 + 529 = 893 000 + 58 =
607 000 + 435 = 248 000 + 52 =
№2
247 000 + 2 000 + 31 =
103 000 + 5000 + 586 =
721 000 + 4 000 + 3 =
350 000 + 1 000 + 15 =
285 000 + 3 000 + 645 =
915 000 + 4 000 + 2 =
302 000 + 6 000 + 37 =
400 000 + 5 000 + 625 =
Реши примеры, правильно их запиши и прочитай
№1
60 000 + 3 = 301 000 + 45 =
20 000 + 54 = 29 000 + 702 =
71 000 + 246 = 930 000 + 5 =
57 000 + 1 = 1 000 + 237 =
802 000 + 26 = 2 000 + 2 =
746 000 + 529 = 893 000 + 58 =
607 000 + 435 = 248 000 + 52 =
№2
247 000 + 2 000 + 31 =
103 000 + 5000 + 586 =
721 000 + 4 000 + 3 =
350 000 + 1 000 + 15 =
285 000 + 3 000 + 645 =
915 000 + 4 000 + 2 =
302 000 + 6 000 + 37 =
400 000 + 5 000 + 625 =
Замени каждое число суммой разрядных слагаемых
207 301 =… + … + … + …
892 040 = … + … + … + …
504 678 = … + … + … + … + …
925 002 = … + … + … + …
2 546 = … + … + … + …
130 042 = … + … + … + …
Реши примеры
200 000 + 3 000 + 12 =
893 000 – 800 000 – 3 =
400 000 + 50 000 + 728 =
702 564 – 700 000 – 64 =
645 080 – 600 000 – 80 =
326 976 – 300 000 – 900 =
182 003 – 100 000 – 3 =
246 070 – 200 000 – 70 =
700 000 + 3 000 + 267 =
Замени каждое число суммой разрядных слагаемых
207 301 =… + … + … + …
892 040 = … + … + … + …
504 678 = … + … + … + … + …
925 002 = … + … + … + …
2 546 = … + … + … + …
130 042 = … + … + … + …
Реши примеры
200 000 + 3 000 + 12 =
893 000 – 800 000 – 3 =
400 000 + 50 000 + 728 =
702 564 – 700 000 – 64 =
645 080 – 600 000 – 80 =
326 976 – 300 000 – 900 =
182 003 – 100 000 – 3 =
246 070 – 200 000 – 70 =
700 000 + 3 000 + 267 =
Замени каждое число суммой разрядных слагаемых
207 301 =… + … + … + …
892 040 = … + … + … + …
504 678 = … + … + … + … + …
925 002 = … + … + … + …
2 546 = … + … + … + …
130 042 = … + … + … + …
Реши примеры
200 000 + 3 000 + 12 =
893 000 – 800 000 – 3 =
400 000 + 50 000 + 728 =
702 564 – 700 000 – 64 =
645 080 – 600 000 – 80 =
326 976 – 300 000 – 900 =
182 003 – 100 000 – 3 =
246 070 – 200 000 – 70 =
700 000 + 3 000 + 267 =
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
82 000 : 10 63 000 • 10
7 600 • 100 985 000 : 1000
42 000 : 100 64 800 • 10
900 000 :10 205 • 1000
450 000 : 1000 79 800 : 100
80 200 • 10 850 • 10
725 000 : 10 982 • 1000
568 000 : 100 50 800 : 10
Реши примеры
№1
9 999 + 1 = 98 999 + 1 = 1 999 + 1 = 35 909 + 1 =
8 899 + 1 = 100 000 – 1 =
10 000 — 1 = 50 000 – 1 =
2 999 + 1 = 80 200 – 1 =
7 000 — 1 = 3 700 – 1 =
49 099 + 1 = 6 000 – 1 =
№2
10 000 — 1000 = 4 000 + 2000 =
50 000 — 1000 = 30 000 + 50 000 =
7 000 – 3 000 = 100 000 – 20 000 =
№3
3 630 + 70 = 2 000 + 500 =
4 920 – 20 = 6 540 — 40 =
2 610 + 90 = 4 640 — 640 =
9 800 – 9 000 = 3 620 + 80 =
5 700 + 300 = 2 500 + 200 =
6 760 – 760 = 9 500 + 500 =
Реши примеры
№1
9 999 + 1 = 98 999 + 1 = 1 999 + 1 = 35 909 + 1 =
8 899 + 1 = 100 000 – 1 =
10 000 — 1 = 50 000 – 1 =
2 999 + 1 = 80 200 – 1 =
7 000 — 1 = 3 700 – 1 =
49 099 + 1 = 6 000 – 1 =
№2
10 000 — 1000 = 4 000 + 2000 =
50 000 — 1000 = 30 000 + 50 000 =
7 000 – 3 000 = 100 000 – 20 000 =
№3
3 630 + 70 = 2 000 + 500 =
4 920 – 20 = 6 540 — 40 =
2 610 + 90 = 4 640 — 640 =
9 800 – 9 000 = 3 620 + 80 =
5 700 + 300 = 2 500 + 200 =
6 760 – 760 = 9 500 + 500 =
Реши примеры
№1
9 999 + 1 = 98 999 + 1 = 1 999 + 1 = 35 909 + 1 =
8 899 + 1 = 100 000 – 1 =
10 000 — 1 = 50 000 – 1 =
2 999 + 1 = 80 200 – 1 =
7 000 — 1 = 3 700 – 1 =
49 099 + 1 = 6 000 – 1 =
№2
10 000 — 1000 = 4 000 + 2000 =
50 000 — 1000 = 30 000 + 50 000 =
7 000 – 3 000 = 100 000 – 20 000 =
№3
3 630 + 70 = 2 000 + 500 =
4 920 – 20 = 6 540 — 40 =
2 610 + 90 = 4 640 — 640 =
9 800 – 9 000 = 3 620 + 80 =
5 700 + 300 = 2 500 + 200 =
6 760 – 760 = 9 500 + 500 =
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Начерти схемы и реши задачи
№1
Из двух городов, расстояние между которыми 810 км, вышли навстречу друг другу два автомобиля. Один проехал 302 км, а другой -118 км. На каком расстоянии друг от друга находятся поезда?
№2
От двух остановок, расстояние между которыми 600 км, выехали два автобуса в противоположном направлении. Один из них проехал 130 км, а другой – 270 км. На каком расстоянии друг от друга находятся автобусы?
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
737246 + 54337 358219 + 12275
28238 + 5468 516739 + 175152
392476 + 1346 485754 + 334674
600010 – 25086 877223 — 412667
9652311 – 329864 700100 — 4345
500000 – 453644 500010 — 14075
175216 + 419335 427753 + 16824 238624 + 316376 958432 – 431764 500000 – 13777 801300 – 239005
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Вычисли примеры столбиком
357846 + 485329 429875 + 378159
780300 – 596248 930170 — 785356
513201 – 427365 800020 — 597816
720300 – 568472 600000 — 295386
600001 – 526345 612340 — 578427
856348 – 579199 66540 — 8988
623105 – 357829 81152 + 3247
768594 + 175843 361487 + 452663
570020 – 483697 807000 — 651972
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
х – 80= 280 + 2
55 + х = 4352 – 2398
х + 39= 786 • 4
899 + х= 4532 – 631
600 – х= 802 : 2
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни сложные уравнения
940 + х=843 : 3
х + 78= 1800 + 350
х – 54= 506 -102
703 – х= 135 • 5
80962 + х= 678956 — 237908
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
43127 ∙ 6 36039 ∙ 4
7 ∙ 23844 95136 ∙ 3
391005 ∙ 4 9 ∙ 12543
56482 ∙ 3 341008 ∙ 6
4 ∙ 81429 9 ∙ 930700
719806 ∙ 4 903040 ∙ 3
9 ∙ 24845 5 ∙ 120605
25482 ∙ 2 374006 ∙ 7
5 ∙ 93748 7 ∙ 31476
15213 ∙ 6 65080 ∙ 4
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
Выполни умножение столбиком
23452 ∙ 7 36008 ∙ 9
6 ∙ 32749 4 ∙ 82190
36193 ∙ 5 670032 ∙ 8
9 ∙ 56492 7 ∙ 420080
68715 ∙ 4 90048 ∙ 7
7 ∙ 49873 6 ∙ 72680
84308 ∙ 6 536937 ∙ 4
7 ∙ 403900 5 ∙ 971680
3968719 ∙ 7 130704 ∙ 6
6 ∙ 109765 9 ∙ 700200
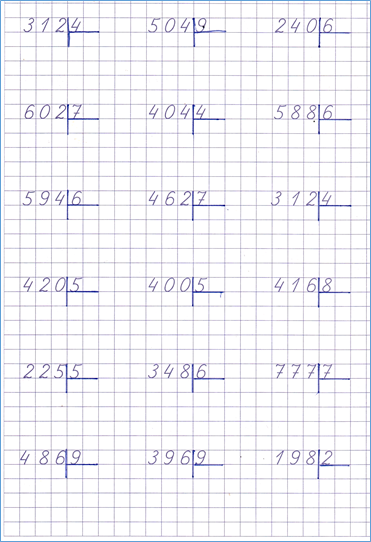
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Выполни деление столбиком
5922 : 9 7896 : 8
4375 : 5 5460 : 4
4734 : 6 8638 : 7
2604 : 4 9855 : 5
6180 : 5 1024 : 4
9723 : 3 2840 : 5
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
Организационный этап.
Сообщение темы урока.
Целеполагание.
Составление плана работы.
Мотивационная беседа. |
Здравствуйте, ребята! Садитесь. Я рада вас видеть, мне приятно с вами общаться. Покажите вашими улыбками ваше настроение. Я вижу, что настроение у вас хорошее, надеюсь, что таким оно сохранится до конца урока. А теперь поприветствуйте своего соседа по парте.
Прочитайте тему урока. Тема записана на доске. Эта тема новая для нас? Что нам уже известно из этой темы, что мы уже умеем? Мы уже многое знаем и умеем по теме «Деление». Почему же нам вновь предлагают изучать эту тему? Давайте составим план, т. е. наметим вопросы, на которые нужно ответить при рассмотрении нового случая деления. Учитель записывает вопросы на доске. Для чего нам нужно рассматривать новый случай деления? Мы и так уже много знаем и умеем, может быть и не нужно это знать? |
Дети здороваются, садятся на места.
Дети поворачиваются друг к другу, улыбаются друг другу и говорят по очереди слова: «Я рад тебя видеть, мне приятно с тобой общаться». После того, как закончат приветствие, берутся за руки и, подняв их вверх, показывают учителю готовность работать.
Дети читают Нет. Мы уже умеем делить на однозначное число тремя способами: два способа устных и один способ письменный, деление столбиком. Мы уже умеем выполнять деление столбиком, когда в частном получают нуль в середине. Чтобы изучить новый случай деления, когда в частном получается нуль в конце. Для чего нужно это знать? В чем заключается суть этого случая? Чем он отличается от других случаев деления?Нет, нужно. Вдруг нам встретится такое деление, и мы не будем знать, как выполнить деление и решим неправильно.
|
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
Актуализация знаний:
0:5= 72:4=18
|
На первый вопрос ответили. Ставит возле первого вопроса знак +. Какие знания нам понадобятся, чтобы выполнять деление столбиком? Давайте все это повторим. Возьмите таблицы «Стосчет» (см. Приложение № 2), работаем с таблицей № 3. Считаете в парах в течение двух минут, затем оцениваете друг друга. Ставит песочные часы. Возьмите магнитные досточки. Мы решим примеры, записанные на доске. Учитель показывает пример. Какие правила вспомнили, решая примеры первого столбика?
Какой прием использовали? В ходе объяснения подчеркивает числа, которые делили (здесь они подчеркнуты синим цветом), и дугой показывает, как поступали с нулем |
Дети в парах, по очереди говорят ответы и проверяют друг друга. По истечении времени оценивают ответы друг друга. (Можно использовать знаки +, -,⊥ , можно — отметки 3, 4, 5) .
Дети пишут на индивидуальных магнитных досточках ответы и показывают их учителю. Кто-нибудь вслух объясняет вычислительный прием.
|
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
Изучение нового. 1) Постановка проблемного вопроса
2) Выведение нового случая деления, когда в частном получается нуль в конце |
При проверке ваших тетрадей я увидела, что некоторые дети допускают ошибки при делении столбиком. Я выписала их на доску. Кто хочет объяснить вслух?
Молодцы! Я думаю, что вы не будете допускать таких ошибок. А теперь оцените себя, если вы правильно объяснили друг другу, то ставьте себе знак +.
Рассмотрите пример. Сколько раз образовывали неполные делимые? Назовите их. Почему в частном получились три цифры? Откуда взялся нуль? Кто может объяснить? При этом объяснении учитель обращает внимание детей на примеры из устного счета 280:4, 560:4. Вот, посмотрите, мы сегодня уже решали такого вида примеры, только используя устные приемы вычисления. Какой вывод можно сделать? |
При делении пятисот шестидесяти на четыре нуль закрываем, остается пятьдесят шесть.
Дети в парах друг другу проговаривают, в чем заключаются ошибки, показывают готовность отвечать, взявшись за руки и подняв их вверх.
Два. 6 и 8.
Дети обсуждают в парах. |
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
|
I способ Делим сотни 6с.  :2=3 с. :2=3 с.Делим десятки 8 д.:2=4 д. Делим единицы 0ед. :2=0 ед. Итого: 340 |
Кто может объяснить? При этом объяснении учитель обращает внимание детей на примеры из устного счета 280:4, 560:4. Вот, посмотрите, мы сегодня уже решали такого вида примеры, только используя устные приемы вычисления. Какой вывод можно сделать? На записи примеров 280:4 и 560:4 обращает внимание на стрелки, показывающие перенос нуля в частное. А можно было снести нуль и выполнить деление? Давайте попробуем это сделать. Пишет на доске и объясняет. (Выделено синим цветом) Сношу нуль, образую третье неполное делимое. Делю нуль на два, получится нуль. Пишу в частное нуль. Умножаю нуль на два, получается нуль. Вычитаю из нуля нуль. Можно так объяснить получение нуля в частном? В математике принято нуль не сносить, когда он стоит в конце делимого, и, если делимое до этого разделилось без остатка, нуль сразу переносят в частное, делая запись короче. Стирает записи, выделенные синим цветом.
Пишет на доске. Получился этот же ответ? Для чего нужно учиться решать примеры разными способами?
|
Когда восемь разделили на два без остатка, в делимом осталась еще одна цифра – нуль. Его мы переписываем в частное, так как мы это делали раньше при делении круглого числа. При делении круглого числа на однозначное число неразделившийся нуль переписываем в частное.
Да.
Дети объясняют. Да. Мы выполнили деление столбиком верно. Чтобы можно было проверять себя. Если число многозначное и очень большое, то разделить его устно будет трудно, тогда нужно будет делить столбиком, для этого мы и учимся делить столбиком. |
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
3) Первичное закрепление. |
Вы понимаете, что нужно владеть разными способами и приемами деления, поэтому мы уделяем объяснению разных способов столько времени, чтобы вы хорошо владели ими. Выполните № 1 на странице 19. В парах объясните решение примера всеми тремя способами. Были затруднения при проговаривании? Что было непонятным? Если у детей возникли затруднения, то учитель проводит коррекционную работу А теперь выполните деление семисот двадцати на шесть всеми тремя способами. (№ 2 на стр. 19) и поверьте друг друга. № 3 (а,в) выполним у доски с комментированием.
При проговаривании алгоритма письменного деления дети могут обращаться к записи алгоритма письменного деления (см. Приложение 3) |
Дети проговаривают все три способа, описанные в учебнике. Дети, которые хорошо поняли и могут решать самостоятельно, «зажигают» зеленый цвет на |
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
Самоконтроль.
Рефлексия |
А теперь проверьте себя, как вы научились выполнять деление столбиком, выполнив самостоятельно № 3(б) — I вариант, и №3 (г) — II вариант. Учитель оказывает индивидуальную помощь или просит быть консультантом тех, кто уже справился с заданием и готов оказать помощь другому. Самопроверка по решениям, приведенным на доске. Самооценка – «+», «», «-». Какую цель мы ставили перед собой в начале урока?
Удалось нам достичь этой цели? По плану, составленному в начале урока, проверяют, на все ли вопросы найдены ответы. В чем заключается суть данного случая деления? Чем отличается от других случаев деления? Например, от деления, когда в частном получается нуль в середине? |
Двое детей решают эти примеры с обратной стороны доски.
Рассмотреть новый случай деления, когда в частном получается нуль в конце.
Когда делим круглое число, неразделившийся нуль переписываем в конец частного. Алгоритм деления такой же, запись такая же, только при делении, когда в частном получается нуль в середине, он там получается, когда образуем неполное делимое и сносим две цифры подряд. А при делении, когда в частном получается нули в конце, мы их просто переписываем, если они в конце деления не разделились. |
Этапы урока и записи на доске |
Деятельность учителя |
Деятельность учеников, их примерные ответы |
Домашнее задание.
Задание на развитие логического мышления (если останется время) Другие задания (вместе с решениями) приведены в Приложении 3 |
Для закрепления дома решите № 4 на стр. 20. Каждый определит для себя, сколько ему нужно решить примеров, чтобы чувствовать себя уверенно на самостоятельной работе, которая будет на следующем уроке.
В этом уроке нам предлагают три номера с задачами на повторение. № 7 – с буквенными значениями; № 8 – задача на движение; в № 9 даны два выражения, по которым нужно придумать задачу и решить ее. Поставьте около каждой задачи знак вопроса, дома подумаете и решите ту из них, которая вам больше нравится. А сейчас я предлагаю вам выполнить задания на сообразительность.
Выполняют проверку. Учитель предлагает оценить себя, показав знаки «+», «⊥ », «-». |
Дети отмечают в учебнике-тетради задачи знаками «?» и
Находят лишние числа и объясняют друг другу по какому признаку они исключили то или иное число.
|
Опрос-итог
|
Что было главным на уроке? Что было интересного? Как вы оцениваете свою работу? Поставьте себе оценку на полях в учебнике, посмотрите на свои «+», «⊥», «-». Кто хочет вслух прокомментировать свою отметку? Учитель благодарит детей за работу и прощается с ними. |
Дети отвечают.
|
Как научиться решать деление столбиком 4 класс
Главная » Разное » Как научиться решать деление столбиком 4 класс
Как объяснить ребенку деление столбиком
В процессе обучения в школе очень часто возникает проблема, когда ребенок не смог понять на уроке операцию деления простых чисел. Взрослые думают, что это совсем не сложно. Но школьник сталкивается с этим впервые и не всегда самостоятельно может во всем разобраться.
В такой ситуации родители, набравшись терпения, должны предельно просто и ясно объяснить ему все непонятные моменты. Как правильно и доступно объяснить ребенку деление столбиком, читайте в материалах этой статьи.
Как правильно и доступно объяснить ребенку деление столбиком, читайте в материалах этой статьи.
Что нужно знать, что бы научиться делить
Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.
Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел.
Без этих основ вряд ли получится проводить арифметические операции с числами. Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен.
Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.
Принцип деления для детей
Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.
Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.
Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.
Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.
Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.
Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.
После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.
Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.
Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку». Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик.
Алгоритм деления в столбик
Для решения примеров делением в столбик рекомендуется пользоваться простым алгоритмом.
- Определить в примере, где находится делимое, а где делитель.
- Записать делимое и делитель под «уголок».

- Определить, какая часть делимого может использоваться для первичного деления.
- Определить сколько раз делитель умещается в выбранной части делимого.
- Произвести умножение делителя на полученное число под уголком, результат вписать под выбранную часть делимого.
- Найти разницу (остаток).
- Повторить действия, пока в остатке не окажется 0.
Более подробно этот алгоритм разберем на конкретном примере.
Методика обучения делению в столбик
Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.
Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.
Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.
Деление в столбик на конкретном примере
Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.
Ребенку предлагается разделить число 945 на 5 в столбик.
Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.
Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».
Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.
Вот и столбик скоро получится.
Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.
Спрашивают ребенка о результате и получают 4.
Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.
Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.
Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.
Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.
Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.
Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.
Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей. Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык.
Вместо заключения
Если у ребенка возникают проблемы с учебой, родители должны помочь ему преодолеть любые трудности.
Деление в столбик – программа 2-3 класса, конечно. Для родителей это давно забытые знания, но при необходимости и желании все можно восстановить в памяти и помочь своему школьнику.
Как научить делить в столбик: пошаговый метод
В этой статье я объясню, как обучить делению в столбик в несколько шагов. Вместо того, чтобы показывать студентам сразу весь алгоритм, мы искренне воспринимайте это «шаг за шагом».
До ребенок готов учить деление в столбик, он должен знать:
- таблицы умножения (по крайней мере неплохо)
- базовая концепция деления, основанная на таблицах умножения
(например, 28 ÷ 7 или 56 ÷ 8) - базовое деление с остатками (например 54 ÷ 7 или 23 ÷ 5)
Одна из причин, почему деление в столбик затруднено
Длинное деление — это алгоритм, который повторяет основные шаги
1) Делить; 2) Умножить; 3) Вычесть; 4) Отбросьте следующую цифру.
Из этих шагов №2 и №3 могут стать трудными и запутать учащихся, потому что они, по-видимому, не имеют отношения к разделению — они имеют отношение к нахождению остатка. На самом деле, чтобы указать на это, мне нравится объединять их в один «умножить и вычесть» шаг.
Чтобы избежать путаницы, я рекомендую обучать полному делению в таком мода на то, что дети сначала НЕ подвергаются всем этим шагам. Вместо этого вы можете научить этому в несколько «ступенек»:
- Шаг 1: Все цифры четные.
 Здесь студенты отрабатывают только разделительную часть.
Здесь студенты отрабатывают только разделительную часть. - Шаг 2: Остаток в единицах. Сейчас, студенты практикуют часть «умножить и вычесть» и связать это с поиском остаток.
- Шаг 3: Остаток в десятках. Ученики теперь используйте весь алгоритм, в том числе «отбрасывание следующей цифры», с использованием 2-значного дивиденды.
- Шаг 4: Остаток в любом месте ценности. Студенты практикуют весь алгоритм, используя более длинные дивиденды.
Шаг 1. Деление четное по всем цифрам
Мы делим числа, в которых каждая цифра сотен, десятков и единиц делится на делитель без остатка. ЦЕЛЬ на этом первом легком шаге — это приучить студентов к двум вещам:
- Чтобы привыкнуть к большому делению «угол», чтобы частное писалось сверху.
- Чтобы привыкнуть спрашивать, сколько раз делитель переходит в различные цифры делимого.
Ниже приводятся примеры проблем для этого шага. Студенты должны проверить каждый деление на умножение.
На этом шаге студенты также учатся смотреть на первые две цифры делимого, если делитель не «входит» в первую цифру:
.
Пошаговое руководство для длинного деления
Что такое длинное деление?
Деление в столбик — это способ решения задач деления с большими числами. По сути, это задачи разделения, которые вы не можете решить в уме.
Начало работы
Одна из проблем, с которой учащиеся сталкиваются с задачами с делением в столбик, — это запоминание всех шагов. Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, что означает:
.
D = разделить
M = умножить
S = вычесть
B = сбить
Эту последовательность букв сложно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:
Папа, мама, сестра, брат.
Напишите D M S B в углу рабочего листа, чтобы запомнить последовательность, которую вы собираетесь использовать.
Как записать
Во-первых, вы должны записать проблему в формате длинного деления. Типичная задача деления выглядит так:
Дивиденд ÷ Делитель = Частное
Чтобы записать это в формате длинного деления, это выглядит так:
Давайте попробуем довольно простой пример:
65 ÷ 5 =?
Теперь давайте запишем эту проблему в формате длинного деления:
Мы готовы использовать аббревиатуру: D M S B
Шаг 1: D для разделения
Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.
Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ: 1. Итак, вы помещаете 1 в линию частного.
Шаг 2: M для умножения
Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.
Шаг 3: S для вычитания
Затем вы вычитаете.В этом случае это будет 6 — 5 = 1.
Шаг 4: B для обрушения
Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5. Вы пишете 5 рядом с 1, в результате получается число 15.
Вы пишете 5 рядом с 1, в результате получается число 15.
Теперь вы начинаете все сначала:
Шаг 1: D для разделения
Сколько раз можно разделить 5 на 15.Ответ — 3. Итак, вы ставите 3 на частную.
Шаг 2: M для умножения
Вы умножаете свой ответ, полученный на шаге 1, на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.
Шаг 3: S для вычитания
Теперь вычтем 15 из 15.15 — 15 = 0.
В шаге 4 нет необходимости. Мы решили проблему.
Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.
K5 Learning предлагает несколько бесплатных заданий с полными делениями для 4-го, 5-го и 6-го класса. Ознакомьтесь с ними в нашем центре рабочих листов по математике.
,
Метод деления в столбик объяснил родителям | Как сделать длинное деление
Нужна помощь? Откройте
- Свяжитесь с нами
- Часто задаваемые вопросы
- Что говорят наши подписчики .
 ..
.. - Как посмотреть видео Зачем присоединяться?
The School Run
Электронная почта или имя пользователя *
Пароль *
- Зарегистрируйтесь бесплатно
- Забыли пароль?
Войти Подписка Зарегистрироваться
Форма поиска
Поиск
Форма поиска
Поиск
Главное меню
- Домой
- Learning Journey
- Английский
- Reception English Learning Journey
- Year 1 English Learning Journey
- Year 2 English Learning Путешествие
- Путешествие по изучению английского языка 3-го года
- Путешествие по изучению английского языка 4-го класса
- Путешествие по изучению английского языка 5-го года
- Путешествие по изучению английского языка 6-го года
- Математика
- Прием Математика Учебное путешествие
- Год 1-го года Обучение
2-е учебное путешествие по математике
- Английский
- 3-е учебное путешествие по математике
- 4-е учебное путешествие по математике
- 5-е учебное путешествие по математике
- 6-го класса учебное путешествие по математике
- 11+ Обучение
900 13.
Common Core Class 4 Math Curriculum
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21 века Автор: Бет Канзанский Название курса: Математика четвертого класса Название раздела: Операции и алгебраическое мышление Уровень 4
Государственные школы Audubon Достижение ~ Развитие глобальных навыков 21-го века Автор: Бет Кансанезе Название курса: Математика четвертого класса 9 9 Имя: и операции — Дроби Уровень класса: 4
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21 века Автор: Beth Canzanese Название курса Четвертый Класс Математика Название раздела: Числа и операции в десятичной системе счисления Класс: 4
Государственные школы Audubon Вовлечение учащихся ~ Воспитание Достижение ~ Развитие глобальных навыков 21 века Автор: Бет Канзанезе Название курса: Математика четвертого класса Название раздела: Измерения и данные Уровень оценки: 4
Учащиеся государственных школ Audubon Автор: Бет Канзанезе Название курса: Математика четвертого класса 9 0 0 Геометрия Уровень оценки: 4
|
Деление на 100 — Математика с мамой
Опубликовано Математика с мамой
Деление на 100- В этом примере мы делим 400 на 100.
- Чтобы разделить число на 100, переместите все цифры на два разряда вправо.

- Цифра «4» перемещает из столбца сотен в столбец единиц (единиц).
- «0» в столбце десятков перемещается в столбец десятков.
- «0» в столбце единиц перемещается в столбец сотых.
- 400 ÷ 100 = 4,00
- Если единственные цифры после запятой — нули, то их не следует записывать.
- Следовательно, мы можем написать: 400 ÷ 100 = 4.
- Деление на 100 имеет тот же эффект, что и удаление двух цифр «0» , только , если исходное число заканчивалось двумя цифрами «0» в столбцах десятков и единиц соответственно. .
Чтобы разделить на 100, переместите каждую цифру на два разряда вправо.
Если число заканчивается двумя цифрами «0» в столбцах десятков и единиц, деление на 100 имеет тот же эффект, что и удаление этих цифр.
- Чтобы разделить на 100, переместите все цифры на два разряда вправо.
- В этом примере цифра «5» перемещается из столбца сотен в столбец единиц.

- Цифра «2» перемещается из столбца десятков в столбец десятков.
- Цифра «7» перемещается из столбца единиц в столбец сотых.
- 527 ÷ 100 = 5,27
- Цифры «5», 2’ и 7’ в ответе остаются в том же порядке.
Чтобы разделить число на 100, переместите каждую цифру этого числа на два столбца разряда вправо .
Если число заканчивается двумя цифрами нуля в столбце десятков и единиц, то деление на 100 имеет тот же эффект, что и удаление этих двух цифр нуля.
Этот трюк работает только с целыми числами , которые находятся в таблице умножения на 100 (оканчивающиеся двумя нулями).
В приведенном выше примере у нас есть 400 ÷ 100 = 4.
Чтобы разделить число на 100, переместите все его цифры на две колонки разряда вправо.
Цифра «4» перемещается из столбца сотен в столбец единиц.
Цифра «0» в столбце десятков перемещается в столбец десятков сразу после запятой.
Цифра «0» в столбце единиц перемещается в столбец сотых.
400 ÷ 100 равно 4,00.
Если число имеет только нули после запятой, то это целое число и нет необходимости записывать эти нули.
Лучше писать: 400 ÷ 100 = 4.
Видно, что мы просто «убрали два нуля».
Этот трюк работает только для целых чисел , у которых на самом деле есть два нуля в столбцах десятков и единиц, которые нужно удалить.
Важно понимать, как работает деление любого числа на 100, потому что не все числа, которые мы делим на 100, оканчиваются двумя нулями.
Например:
Чтобы разделить 527 на 100, мы переместим каждую цифру в 527 на две позиции вправо .
Начнем с переноса «5» из столбца сотен на две позиции в столбец единиц .
Затем «2» и «7» будут следовать за «5».
2 перемещает из столбца десятков в столбец десятых , а 7 перемещает из столбца единиц в столбец сотых .
Каждая цифра сдвинулась на две позиции вправо, поэтому 527 ÷ 100 = 5,27.
Если самая большая цифра числа находится в столбце сотен, то эта цифра переместится в столбец единиц при делении на 100.
Остальные цифры справа будут отображаться в том же порядке справа от десятичной точки.
Таким образом, в этом примере «5» — это цифра слева от десятичной точки, а затем «2» и «7» будут в том же порядке, сразу после десятичной точки.
В следующем примере нам дано число меньше 100 и состоит только из двух цифр. Мы по-прежнему следуем тем же правилам деления на 100 и перемещаем каждую цифру на два разряда вправо .
Начнем с перемещения «1» на две позиции вправо из столбца десятков в столбец десятых . Затем следует цифра «9». Мы перемещаем его из столбца единиц в столбец сотых .
Всякий раз, когда слева от десятичной точки не остается цифр, в столбце единиц записывается одна цифра «0».
Следовательно, 19 ÷ 100 = 0,19.
Нас могут попросить разделить однозначное число на 100.
Например:
Хотя 6 имеет только одну цифру, мы по-прежнему следуем тому же правилу деления на 100. Мы перемещаем 6 на два разряда вправо . Он перемещается из столбца единиц в столбец 9.0007 десятый столбец .
Поскольку в столбце из единиц больше нет цифры, а в столбце из десятых есть пробел, мы записываем ноль в оба столбца, чтобы показать, что их значения равны нулю.
Следовательно, 6 ÷ 100 = 0,06.
Мы должны быть осторожны, имея дело с числами, где между двумя другими ненулевыми цифрами стоит ноль.
Например:
Чтобы разделить на 100, мы должны убедиться, что мы переместили каждая цифра в 30.2 два знака вправо, включая ноль . Мы перемещаем 3 из столбца десятков в столбец десятых , мы перемещаем ноль из столбца единиц в столбец сотых и мы перемещаем 2 из столбца десятых в столбец тысячных .
Цифры остаются в том же порядке . Итак, 30,2 ÷ 100 = 0,302.
Теперь попробуйте наш урок на Деление на 1000 , где мы узнаем, как делить число на 1000, с примерами и дальнейшей практикой.
Математические задания и игры для 4-го класса
Как математические игры и занятия повышают уровень знаний учащихся 4-го класса
Математические игры и занятия могут быть отличным инструментом, дополняющим и поддерживающим обучение математике. Использование математических игр в классе позволяет учащимся практиковать математику не только весело, но и эффективно. Ученики любят игры, потому что они увлекательны и увлекательны, а учителя любят игры, потому что они помогают учащимся практиковать то, чему они научились.
Учащиеся 4 класса расширяют свои знания о числах до 1000 и получают дополнительные знания о дробях, десятичных дробях, целых числах, разрядных значениях и свойствах операций. Благодаря использованию числовых линий, дробных линий, моделей площадей, счетчиков, весов, точечной бумаги, десятичных блоков, диаграмм разрядных значений и моделей разрядных значений, учащиеся будут не отклоняться от цели и получать удовольствие.
и поместить значение
Предложите учащимся использовать числовые квадраты для деления.
Чтобы разделить 73 на 2, учащиеся могут смоделировать 73 на диаграмме разрядных значений, а затем смоделировать распределение квадратов поровну между двумя наборами, что также показано на диаграмме разрядных значений. По мере того, как учащиеся начинают понимать процесс, они могут как объяснять свою работу, так и записывать ее.
Учащиеся, способные смоделировать алгоритм деления двух- или трехзначного числа на однозначное число и перевести свою работу в слова и символы, легко разовьют понимание процесса и уметь применять его к целым числам делимых и делителей любого размера. У них также будет необходимая основа для деления десятичных и целых чисел.
Ссылки
Лэмперт, М. (1992) Преподавание и изучение длинного деления для понимания в школе. Анализ арифметики для преподавания математики, 221-282, Hillsdale, NJ
Анализ арифметики для преподавания математики, 221-282, Hillsdale, NJ
Строка числа дробей показывает единичную дробь и ее кратные. Это помогает учащимся видеть дроби как числа и понимать их связь с 1. Кроме того, числовая линия дробей помогает учащимся видеть отношения между дробями, включая эквивалентность. Цель этой учебной модели — облегчить учащимся понимание сравнения дробей с одинаковыми или разными знаменателями.
Сначала учащиеся могут использовать числовую линейку для сравнения дробей с одинаковыми знаменателями точно так же, как они используют числовую линейку для сравнения целых чисел. В числовой строке число справа является большим числом. Студенты также могут видеть, что, когда знаменатели дробей одинаковы, они могут просто сравнить числители.
Подумайте: 7 ⁄ 8 больше, чем 3 ⁄ 8 7 ⁄ 4, потому что3 41151 8 находится справа от 3 ⁄ 8 на числовой прямой.
7 ⁄ 8 также больше, чем 3 ⁄ 8 , потому что 7 больше 3. нельзя просто сравнивать числители. Они должны сначала переименовать дроби в эквивалентные дроби с теми же знаменателями. Только после этого они могут сравнивать числители.
Подумайте: 2 ⁄ 3 больше, чем 3 ⁄ 6 , потому что 2 ⁄ 3 6 — 2 ⁄ 3 — 2 ⁄ 3 . числовой ряд. Числовая строка также показывает, что 2 ⁄ 3 эквивалентно 4 ⁄ 6 . Итак, чтобы сравнить 2 ⁄ 3 и 3 ⁄ 6 , вы можете сравнить 4 ⁄ 6 и 3 ⁄ 6 . 4 ⁄ 6 больше, чем 3 ⁄ 6 , потому что 4 больше, чем 3. Так, 2 ⁄ 3 больше, чем 3 ⁄ 6 .
Учащиеся, которые понимают, как использовать числовую прямую для сравнения дробей с разными знаменателями, поймут шаги, необходимые для сравнения и упорядочивания дробей без использования конкретных материалов или изображений, а также шаги, необходимые для сложения и вычитания дробей с разными знаменателями. .
Ссылки
Бернс, М. (2000), О преподавании математики: ресурс K-8, 223–237, Math Solutions Publications, Sausalito, CA.
Многие недавние исследования показывают, что практический опыт, который позволяет использовать технологии, может облегчить учащимся организацию данных и навыки построения графиков. Представленная здесь модель обучения является примером использования практического подхода, который может помочь учащимся выбрать подходящий график.
В следующем упражнении учащиеся должны определить, создание гистограммы или линейной диаграммы лучше отображает заданные данные.
Шаг 1: Разделите учащихся на группы по 3 или 4 человека. Попросите каждую группу выбрать тему для опроса (например, любимая еда или спортивная команда) и попросите их собрать свои данные в течение одного учебного дня.
Шаг 2: Затем попросите группы упорядочить данные своего опроса и создать гистограмму и линейную диаграмму. Попросите каждую группу поделиться с классом результатами своего опроса вместе с созданными ими графиками. Спросите: «Какой график лучше отображает собранную информацию?»
Шаг 3: С помощью технических средств попросите каждую группу построить гистограмму и линейную диаграмму, показывающую следующий конкретный пример: «Население школы меняется за 50 лет. В 1957 году было зачислено 110 учеников. В 2007 году было зачислено 820 учеников».
Дайте каждой группе время на создание этих графиков, но активно обсудите с ними, как будут выглядеть горизонтальная и вертикальная оси. Например, попросите студентов подумать, будет ли здесь полезна шкала в сотни.
Например, попросите студентов подумать, будет ли здесь полезна шкала в сотни.
После того, как графики будут готовы, спросите: «Какой график лучше показывает изменение численности учащихся с течением времени и почему?» Использование как практического, так и технологического опыта должно позволить учащимся увидеть и понять, что линейный график более эффективно отражает изменение во времени, а гистограмма лучше показывает сравниваемые данные. Предложите группам обсудить и записать все различия, которые они заметили в двух типах графиков.
Использование технологий в качестве средства обучения может предоставить учащимся несколько вариантов интерактивного создания графических дисплеев и управления ими. Например, они могут изменить масштаб осей быстрее, чем если бы они были созданы вручную. Тем не менее, лучше сосредоточить внимание на мероприятиях, которые активно вовлекают учащихся в сбор информации, проводят мозговой штурм, чтобы отобразить эти результаты, а затем активно создают график.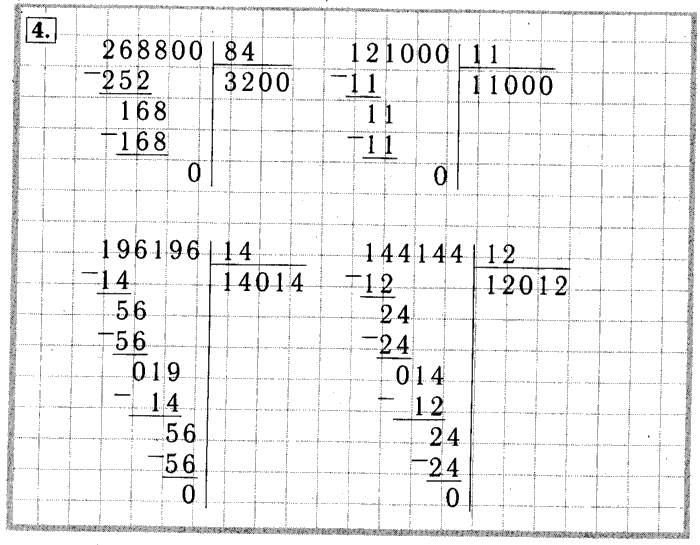 Это укрепит концептуальное понимание статистики и вероятностных тем.
Это укрепит концептуальное понимание статистики и вероятностных тем.
Ссылки
J.A. Ван Де Валле Математика в начальной и средней школе: обучение с точки зрения развития, Аддисон-Уэсли Лонгман, Бостон, Массачусетс (2001).
В исследовании Линдквист предложил учащимся понять, что каждую единицу измерения можно разделить на более мелкие части. Исследование Лерера показало, что многие студенты реагируют на линейные измерения с ненулевым началом, просто считывая любое число на линейке, совпадающее с объектом. Работа с числовой линией может помочь учащимся приобрести навыки, необходимые им для чтения различных шкал, имеющихся в реальных измерительных инструментах.
Студентов часто просят измерить с точностью до 1 ⁄ 2 дюймов или 1 ⁄ 4 дюймов. Учащиеся могут работать с дробной числовой прямой, округляя отмеченные точками дроби и смешанные числа до ближайших 1 ⁄ 2 и 1 ⁄ 4 .
Учащиеся могут работать с десятичной числовой строкой, готовясь к округлению до ближайшего сантиметра.
D равен 0,8 и округляется до 1.
E равен 1,3 и округляется до 1. для десятков могут подготовить учащихся к чтению шкал на термометрах.
G равно 26, а H равно 45.
Учащиеся, которые могут легко называть точки и округлять числа на числовой прямой, смогут применить эти навыки к использованию инструментов измерения.
Ссылки
Линдквист М. (1998) Стандарты измерений. Учитель арифметики, 37, 22–26
Лерер Р., Дженкинс М. и Осана Х. (1998) Лонгитюдное исследование рассуждений детей о пространстве и геометрии. Проектирование учебных сред для развития понимания геометрии и пространства, 137–167, Махва, Нью-Джерси: Erlbaum
Многие исследования показывают, что учащиеся лучше всего развивают свое раннее алгебраическое мышление с помощью конкретных действий и реальных проблемных ситуаций.
 Следующая учебная модель демонстрирует практическую деятельность, чтобы помочь учащимся осмыслить обратную зависимость между сложением и вычитанием и развить идеи переменных и выражений.
Следующая учебная модель демонстрирует практическую деятельность, чтобы помочь учащимся осмыслить обратную зависимость между сложением и вычитанием и развить идеи переменных и выражений.Прочтите или отобразите эту задачу: У Мэтта в рюкзаке 5 теннисных мячей. Остальные теннисные мячи он оставил дома. Всего у него 12 теннисных мячей. Сколько теннисных мячей Мэтт оставил дома?
Учащиеся могут смоделировать эту задачу, используя фишки на коврике «часть-часть-целое», или могут изобразить свою работу символически на коврике «часть-часть-целое».
Чтобы проверить эту задачу, учащиеся могут положить 7 фишек в пустую часть и посчитать, чтобы убедиться, что количество фишек в обеих частях равно количеству фишек в целом. Или учащиеся могут заменить на в мате на 7 и добавить, чтобы убедиться, что сумма чисел в частях равна числу в целом.
Ссылки
Van de Walle, J. A. (1998). Математика в начальной и средней школе: обучение в целях развития, 55, 401 New York, NY
A. (1998). Математика в начальной и средней школе: обучение в целях развития, 55, 401 New York, NY
Умножение
Модель площади, нарисованная на бумаге с сеткой, тесно связана с массивом, а также является мощным представлением алгоритма умножения.
1На приведенной ниже сетке показана площадь прямоугольника 12 на 13. Он также моделирует, как произведение 12 × 13 является суммой четырех частичных произведений, демонстрируя применение концепций позиционного значения и основных фактов умножения, что приводит к более глубокому пониманию распределительного свойства умножения над сложением.
Понимание этой модели и ее связи с распределительным свойством умножения над сложением приводит к использованию расширенного алгоритма умножения, как показано выше.
Учащиеся, которые понимают, что представляет собой каждое частичное произведение в этом расширенном алгоритме, смогут легко понять, что традиционный алгоритм умножения — это просто сокращение.
1 Национальный исследовательский совет. (2001). Сложение: помощь детям в изучении математики, 181–229.
Региональная модельПодразделение
Следующая учебная модель адаптирована из примера, представленного в
Добавление . Из-за размера чисел трудно использовать конкретные материалы для моделирования многозначного деления. Однако учащиеся могут построить эту модель области «сверху вниз», поскольку они вычитают из делимого равное делителю. Чтобы решить, сколько групп вычитать каждый раз, учащиеся должны оценить количество групп, которые они должны вычесть, в одном из вариантов стратегии «Угадай и проверь». Они проверяют это, умножая и вычитая. Если можно вычесть больше групп, они оценивают, сколько еще групп, и продолжают таким образом до тех пор, пока количество оставшихся групп не станет меньше делителя.
Разбивая делимое и делитель на числа, кратные 10, с остатком 5, учащиеся могут использовать следующую модель площади, чтобы продолжать вычитать числа, кратные 45 (40 и 5), до тех пор, пока остаток не станет меньше 45. Этот метод также развивает опыт оценки потому что учащиеся умножают на правильное число (50, затем 10, затем 2, затем 1), когда пишут каждое частичное частное.
Найдите 2846 ÷ 45.
Учащиеся, понимающие эту работу, могут записать ее по стандартному алгоритму деления. Поскольку они смогли вычесть 50 + 10 (60), группы по 45 из 2846, они могут начать писать частное над домом деления. То есть они могут написать 6 в разряде десятков и продолжить оттуда.
Ссылки
Van de Walle, J. A. (1998). Математика в начальной и средней школе: обучение с учетом развития, 55, 401 Нью-Йорк, штат Нью-Йорк.
Национальный исследовательский совет (2001 г.). Сложение: помощь детям в изучении математики, 181–229.
Ламперт, М. (1992) Преподавание и изучение длинного деления для понимания в школе. Анализ арифметики для преподавания математики, 221–282, Хиллсдейл, Нью-Джерси.
Блоки с основанием 10 могут помочь учащимся установить связь между целыми и десятичными числами. Начните с рассмотрения основы стоимостной оценки целого числа: между любыми двумя соседними разрядами существует отношение 10 к 1 и что при движении справа налево каждое место в 10 раз больше предыдущего места. Напротив, при движении слева направо каждое место на одну десятую меньше предыдущего места. (При использовании целых чисел единичный куб соответствует единице.)
Покажите, что между любыми двумя соседними знаками в десятичной дроби существует такое же соотношение. На этот раз квартира означает единицу.
Независимо от того, моделируете ли вы целочисленное разрядное значение или десятичное разрядное значение, помогите учащимся увидеть, что отношение 10 к 1 продолжается бесконечно влево или вправо. Студенты ограничены только в целях моделирования доступными блоками с основанием десять.
Студенты ограничены только в целях моделирования доступными блоками с основанием десять.
Учащиеся, которые понимают основы десятичных разрядов, смогут легче применять свои знания об упорядочивании и вычислении целых чисел в своей работе с десятичными дробями.
Учащиеся могут также использовать десятичные блоки вместе с десятичными квадратами, чтобы сделать работу по представлению десятичных дробей менее утомительной. Вместо того, чтобы раскрашивать десятичные квадраты, учащиеся могут размещать на квадратах плоскости, стержни и единицы.
Ссылки
Стикс, А. (1997) Обучение дробям и десятичным числам: забава с сетками изображений. ЭРИК ЭД408158
Многие исследования показывают, что ученики лучше всего развивают свое раннее алгебраическое мышление с помощью конкретных действий. Чашки и счетчики на весах являются полезными инструментами, помогающими учащимся решать уравнения, понимать и составлять таблицы функций.
Чтобы найти значение переменной в уравнении, таком как 3 a = 6 + 6, пусть учащиеся поместят три маленьких пластиковых стаканчика с этикетками и на левой стороне весов и две стопки по 6 жетонов на правой стороне.
Чтобы найти значение a , учащиеся должны определить, сколько жетонов положить в каждую чашку, чтобы обе стороны уравновесились. Учащиеся могут использовать стратегию «Угадай и проверить» или разделить. С правой стороны 12 фишек (6 + 6), поэтому с левой стороны должно быть 12 фишек, которые должны быть равномерно распределены по 3 чашкам. Учащиеся делят 12 на 3 и делают вывод, что в каждую чашку нужно положить по 4 фишки. Учащиеся помещают фишки в стаканчики, чтобы проверить этот ответ. Наконец, они могут символически показать свои открытия.
Чтобы смоделировать такую функцию, как y = x + 3, учащиеся могут поставить чашку с маркировкой y на левую сторону шкалы и чашку с маркировкой 5 х 9115s 9115s. на правой стороне шкалы.
на правой стороне шкалы.
Для представления различных значений x учащиеся могут положить разное количество фишек в чашку с надписью x . Затем они могут найти, сколько они должны положить в чашку с надписью 9.1155 и для балансировки весов. Наконец, они могут представить свою работу в таблице функций.
Учащиеся, умеющие пользоваться чашками, счетчиками и весами, должны хорошо понимать, что переменная может представлять одно или несколько значений, что обе части уравнения должны быть равны и что y -значения в функции зависят от соответствующих x -значений.
Ссылки
Ван де Валле, Дж. А. (1998). Математика в начальной и средней школе: обучение развитию, 55, 401 New York, NY
Carpenter, TP; Франке, М.Л.; Леви, Л. (2003) Математическое мышление: интеграция алгебры и арифметики в начальной школе. Портсмут, Нью-Хэмпшир. Хайнеманн.
Портсмут, Нью-Хэмпшир. Хайнеманн.
Понимание объемных фигур требует еще большей способности визуализировать пространственные отношения, чем понимание плоских фигур. Бумага с точками особенно полезна для изучения этих пространственных отношений, так как можно легко рисовать параллельные линии и разные углы.
Бумагу с квадратными точками можно использовать для создания сетей; плоские узоры, складывающиеся в сплошные фигуры. Вы можете предоставить учащимся сеть для определенной фигуры, например, сеть A ниже, которая образует прямоугольную призму. После того как учащиеся вырезают сетки, продемонстрируйте, как их складывать и склеивать.
Попросите учащихся назвать плоские фигуры, являющиеся гранями объемной фигуры. Затем попросите учащихся спроектировать другие сети, чтобы сделать такую же фигуру самолета, и протестировать их. Например, сетка B также может быть сложена в виде прямоугольной призмы, а сетка C — нет. Эта работа поможет учащимся понять, какой формы должны быть лица и где они соединяются.
Эта работа поможет учащимся понять, какой формы должны быть лица и где они соединяются.
Бумагу с треугольными точками можно использовать для рисования объемных фигур, что поможет учащимся понять, как трехмерные фигуры могут быть представлены в двух измерениях, как они появляются в их учебниках. Сначала попросите учащихся построить цельные фигуры из соединяющихся кубиков. Затем попросите их скопировать эти фигуры на бумагу с треугольными точками. Прежде чем учащиеся начнут, продемонстрируйте, как нарисовать один куб, а затем очень простую прямоугольную призму. Затем они могут перейти к более сложным фигурам.
Этот навык также поможет учащимся применять стратегию решения задач «Нарисуй картинку», описанную в этой главе.
Ссылки
Ран, Джеймс (2005) Проблемы с геометрией? Помогите учащимся подготовиться к стандарту геометрии и измерений в HSPSA. Университет Рутгерса, Пискатауэй, Нью-Джерси.
Университет Рутгерса, Пискатауэй, Нью-Джерси.
Цель этой учебной модели — помочь учащимся развить концептуальное понимание сложения и вычитания дробей. Учащиеся, которые могут визуализировать, что представляют числитель и знаменатель дроби, и могут писать дроби для моделей, могут легче понять, почему числители складываются и вычитаются и почему знаменатель остается неизменным. Такие учащиеся также могут понять, почему дроби с разными знаменателями можно и нужно переименовывать, чтобы их можно было складывать или вычитать.
Начните с раздачи фракционных полосок. Предложите учащимся наклеить две полоски с дробями, как показано ниже, на лист бумаги, чтобы смоделировать 3 ⁄ 8 + 1 ⁄ 8 .
Укажите связь между 3 ⁄ 8 + 1 ⁄ 8 , показанную нижней дробью. (Две полоски имеют одинаковый размер.) Попросите учащихся записать сумму «?» под своими моделями. Учащиеся могут спросить, почему 3 ⁄ 8 + 1 ⁄ 8 не равно 4 ⁄ 8 . Укажите, что 4 ⁄ 8 и «?» эквивалентны, и напомните учащимся, что «?» 4 ⁄ 8 в простейшей форме.
(Две полоски имеют одинаковый размер.) Попросите учащихся записать сумму «?» под своими моделями. Учащиеся могут спросить, почему 3 ⁄ 8 + 1 ⁄ 8 не равно 4 ⁄ 8 . Укажите, что 4 ⁄ 8 и «?» эквивалентны, и напомните учащимся, что «?» 4 ⁄ 8 в простейшей форме.
Продолжайте в том же духе со следующими моделями, чтобы продемонстрировать вычитание с одинаковыми знаменателями.
Ссылки
Van de Walle, J.A. (1999). Математика в начальной и средней школе: обучение с учетом развития, 55, 401 Нью-Йорк, Нью-Йорк
Результаты различных исследований показывают, что учащимся необходим постоянный опыт работы с конкретными моделями, чтобы связать дискретные величины с символическими представлениями.
 Используемые вместе с таблицами стоимостных значений, они помогают учащимся развивать аналогичные рассуждения о разрядном значении больших чисел. Прежде чем приступить к этому упражнению, поработайте со студентами, чтобы вырезать несколько маленьких квадратов из бирочной доски. Обозначьте квадраты: 100 000 000; 10 000 000; 1 000 000; 100 000; 10 000; 1000; 100; 10; и 1. Затем с помощью помеченных квадратов и диаграммы разрядных значений смоделируйте число, например 210 234 630. (На этой диаграмме ключ был использован для экономии места.)
Используемые вместе с таблицами стоимостных значений, они помогают учащимся развивать аналогичные рассуждения о разрядном значении больших чисел. Прежде чем приступить к этому упражнению, поработайте со студентами, чтобы вырезать несколько маленьких квадратов из бирочной доски. Обозначьте квадраты: 100 000 000; 10 000 000; 1 000 000; 100 000; 10 000; 1000; 100; 10; и 1. Затем с помощью помеченных квадратов и диаграммы разрядных значений смоделируйте число, например 210 234 630. (На этой диаграмме ключ был использован для экономии места.)
Работая слева направо и считая квадраты в каждом столбце таблицы, учащиеся также могут записать стандартную форму смоделированного числа. В столбце сотен миллионов есть 2 квадрата, в столбце с десятью миллионами — 1 квадрат, в столбце с миллионами — 0 квадратов и так далее. Итак, стандартная форма числа 210 234 630. Работая слева направо и записывая значения квадратов в каждом столбце, учащиеся могут написать расширенную форму смоделированного числа: 200 000 000 + 10 000 000 + 200 000 + 30 000 + 4 000 + 600 + 30.
Учащиеся также могут использовать свои числовые квадраты в диаграмме разрядов для моделирования счета и обратного счета на 10, 100 и 1000. Попросите их смоделировать число, например 45 832, на диаграмме. Чтобы считать на 10, они могут многократно добавлять один квадрат 10 в столбец десятков и произносить новые показанные числа: 45 842; 45 852; 45 862. Чтобы посчитать в обратном порядке на тысячи, они могут несколько раз удалить один квадрат 1000 из столбца тысяч и произнести новые показанные числа: 44 832; 43 832; 42 832.
На более поздних уровнях, по мере того как понятия разрядности распространяются на очень большие и очень малые числа, включая использование научных обозначений, абстракция чисел и их символических представлений возрастает. Моделирование понятий о месте на этом уровне и ранее укрепит понимание учащимися основных понятий о месте и подготовит их к более сложной работе.
Список литературы
Варелас, М. и Беккер, Дж. Развитие понимания у детей значения места: семиотические аспекты. Познание и обучение , v15 n2, 265–286, 1997 Бове, С. П., Значение места: вертикальная перспектива. Обучение детей математике, v1 n9, 542–46, май 1995 г.
и Беккер, Дж. Развитие понимания у детей значения места: семиотические аспекты. Познание и обучение , v15 n2, 265–286, 1997 Бове, С. П., Значение места: вертикальная перспектива. Обучение детей математике, v1 n9, 542–46, май 1995 г.
В следующей учебной модели используются числовые квадраты, созданные детьми для задания, разработанного для главы 1, и таблицы разрядных значений для изображения процесса перегруппировки алгоритмов сложения и вычитания. Прежде чем пытаться смоделировать сложение или вычитание со своими квадратами, учащиеся должны понять, что складывать или вычитать можно только квадраты с одинаковыми числами. Следовательно, им может понадобиться обменять десять клеток с единицами на одну клетку с 10 или наоборот.
Пример A: Модель 4 526 + 2 135.
По мере того, как учащиеся моделируют сложение справа налево, перегруппировываясь при необходимости, попросите их объяснить свою работу и записать ее. Запись показана ниже по шагам, но учащиеся могут показать все шаги по одному с одним набором дополнений.
Запись показана ниже по шагам, но учащиеся могут показать все шаги по одному с одним набором дополнений.
Пример B: Модель 4 178 − 2 543.
Учащиеся, способные моделировать сложение и вычитание с перегруппировкой и переводить свою работу в слова и символы, легко разовьют понимание понятий разрядного значения, лежащих в основе сложения и вычитания с целыми числами любого размера и любым количеством перегруппировок.
Ссылки
Национальный исследовательский совет, (2001). Сложение: помощь детям в изучении математики, 181–229
Фиори, К. и Цуккери, Л. (2005) Экспериментальное исследование шаблонов ошибок при письменном вычитании. Educational Studies in Mathematics, v60 n3 p323-331 ноябрь 2005 г.
Многие исследования показывают, что использование геоборда может улучшить пространственное чувство учащихся и навыки геометрии.
 Представленная здесь модель инструкций является примером того, как использовать манипулятивную геоборду для достижения этой цели.
Представленная здесь модель инструкций является примером того, как использовать манипулятивную геоборду для достижения этой цели.Чтобы изучить различные типы треугольников, учащиеся могут использовать резиновые ленты геоборда, чтобы построить различные трехсторонние варианты. Учащиеся могут оценить размеры сторон и углов при проектировании фигур, но окончательную проверку необходимо измерить с помощью линейки или транспортира и, наконец, записать в таблицу для дальнейшего исследования.
- Предложите учащимся нарисовать три разных треугольника, приведенных ниже.
(A) Треугольник без равных сторон.
(B) Треугольник с углом 90 градусов.
(С) Треугольник с противоположными равными углами. - После построения учащиеся должны использовать линейку и транспортир, чтобы убедиться, что треугольник, который они построили, соответствует описанию выше.
- Затем учащиеся должны записать все свои измерения и наблюдения в данную таблицу.

 Рисунок 1), магнитные досточки (по количеству учащихся), таблица «Стосчет» (по количеству учащихся) (см. Приложение 1), алгоритм письменного деления (по количеству учащихся) (см. Приложение 2), песочные часы.
Рисунок 1), магнитные досточки (по количеству учащихся), таблица «Стосчет» (по количеству учащихся) (см. Приложение 1), алгоритм письменного деления (по количеству учащихся) (см. Приложение 2), песочные часы.
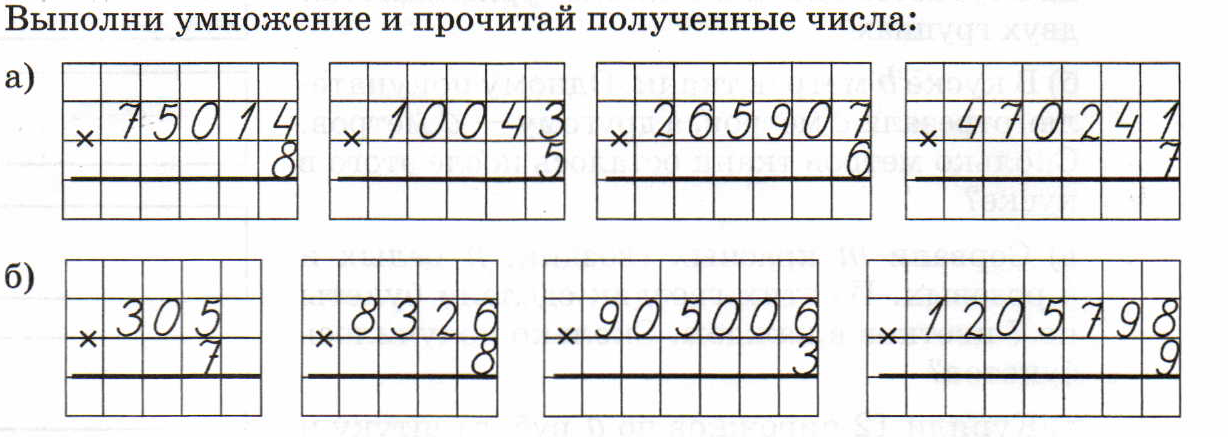



 28:4=7, потом нуль переносим в частное.
28:4=7, потом нуль переносим в частное. Проверьте, определите, что неправильно и объясните, на что нужно обратить внимание, чтобы не было таких ошибок.
Проверьте, определите, что неправильно и объясните, на что нужно обратить внимание, чтобы не было таких ошибок. 56 заменяем суммой удобных слагаемых 40 и 16. 40:4=10, 16:4=4, 10+4=14.Пишем в частное 14 и переносим туда же нуль.
56 заменяем суммой удобных слагаемых 40 и 16. 40:4=10, 16:4=4, 10+4=14.Пишем в частное 14 и переносим туда же нуль.

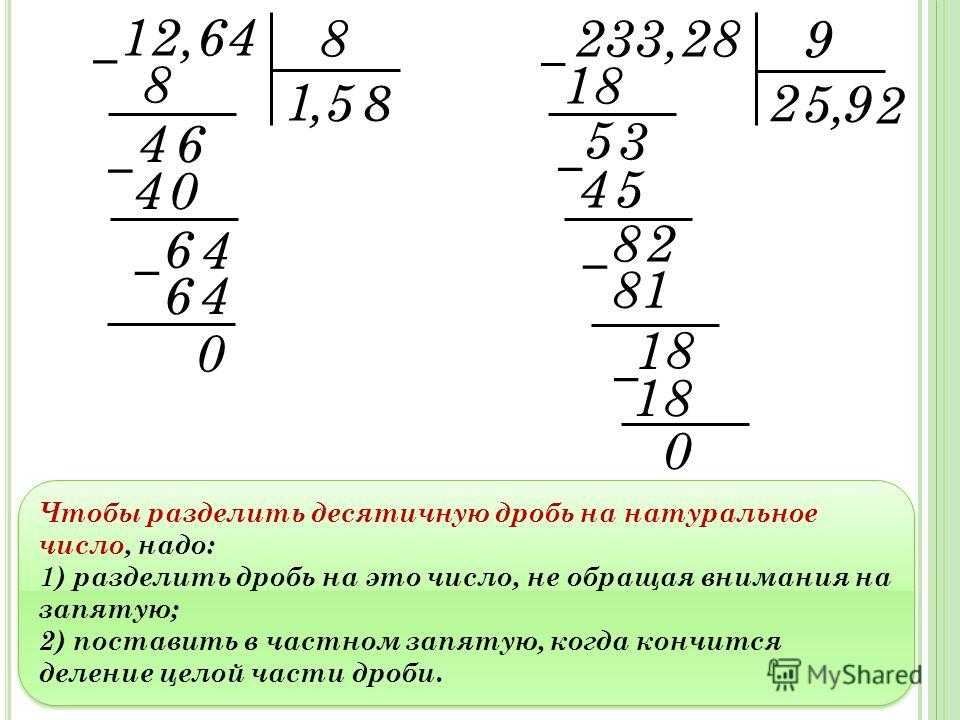


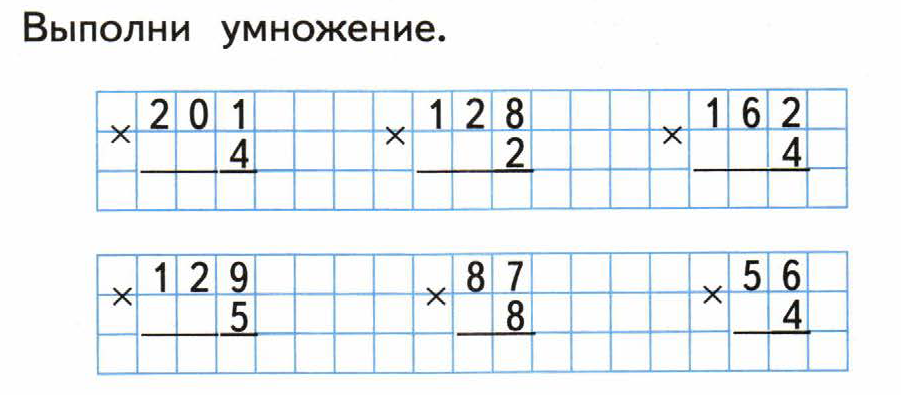 Остальные решают самостоятельно и в случае затруднения могут попросить помощь, просигналив красным цветом «светофора».
Остальные решают самостоятельно и в случае затруднения могут попросить помощь, просигналив красным цветом «светофора».
 № 10 на стр. 21 выполняем в парах.
№ 10 на стр. 21 выполняем в парах. Спросите себя, как я работал? Все ли понял? Чему научился? Оцените себя.
Спросите себя, как я работал? Все ли понял? Чему научился? Оцените себя.
 Здесь студенты отрабатывают только разделительную часть.
Здесь студенты отрабатывают только разделительную часть. ..
.. Повторение и применение умножения и
разделение фактов и стратегий для мысленно вычисляющих продуктов и
частные. Использование переменных для решения
задачи на умножение и деление.
Повторение и применение умножения и
разделение фактов и стратегий для мысленно вычисляющих продуктов и
частные. Использование переменных для решения
задачи на умножение и деление.



 Они рассмотрят и применят умножение
и деление фактов и стратегий для мысленно вычисляющих продуктов и
частные. Они также будут использовать
переменные для решения задач на умножение и деление.
Они рассмотрят и применят умножение
и деление фактов и стратегий для мысленно вычисляющих продуктов и
частные. Они также будут использовать
переменные для решения задач на умножение и деление. Понять
связь между десятичными знаками и дробями; сравнивать и упорядочивать десятичные дроби.
Понять
связь между десятичными знаками и дробями; сравнивать и упорядочивать десятичные дроби.


 Я могу использовать таблицы стоимостных значений для решения
проблемы.
Я могу использовать таблицы стоимостных значений для решения
проблемы. Они будут
попрактикуйтесь с манипулятивными и словесными задачами.
Они будут
попрактикуйтесь с манипулятивными и словесными задачами.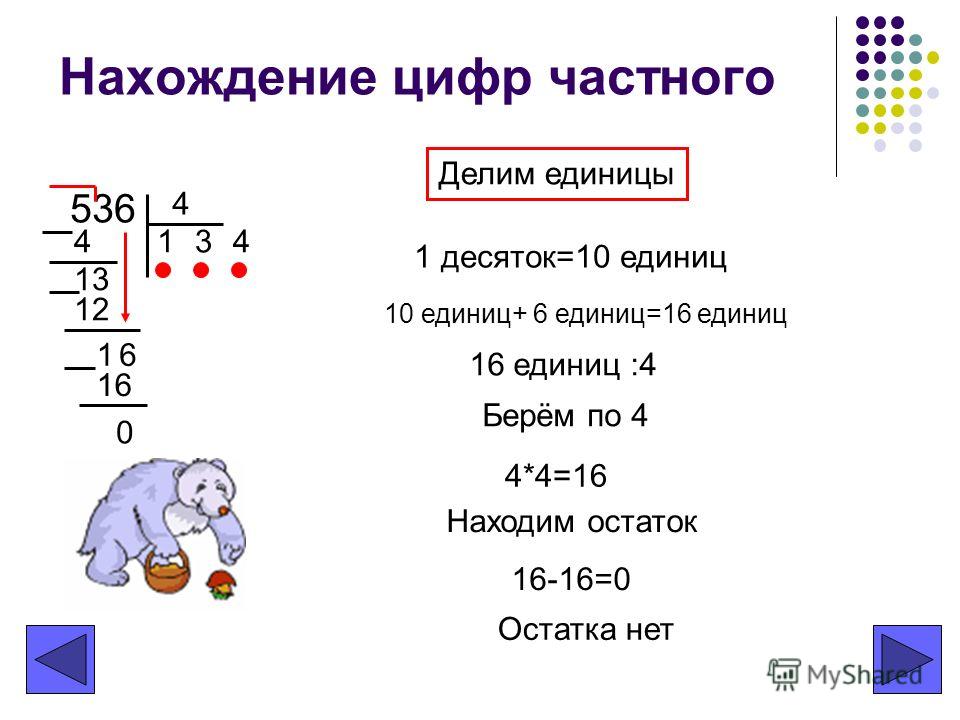 МД.1-4
МД.1-4
 Большая часть прикладной математики связана с измерениями.
Большая часть прикладной математики связана с измерениями.

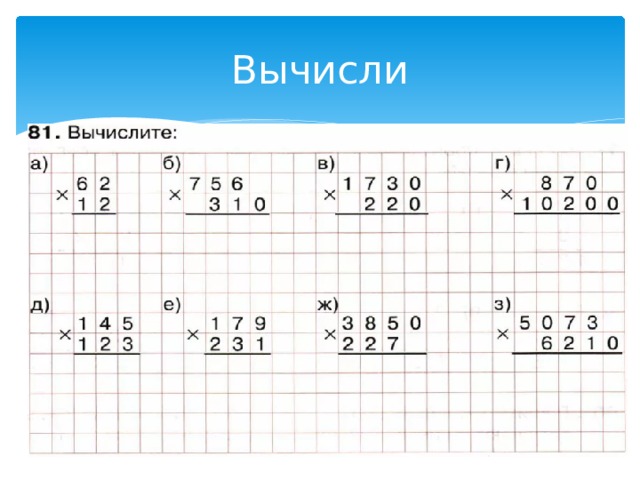 имеет.
имеет.
