Как научить деление столбиком. Как научить ребенка делению в математике
В классе много детей, и у учителя не всегда получается уделить внимание каждому. Однако если ребенок что-то пропустит или не поймет, то это затруднит изучение дальнейших тем. В этом случае на помощь ему должны прийти родители. К примеру, как научить ребенка делению? Сначала математический процесс лучше объяснять в игровой форме. Затем можно переходить к более сложным задачам.
Как научить ребенка делению в форме игры
Скучные учебники лучше отложить в сторону на время. Малыш быстро усвоит сложный материал, если мама или папа превратит обучение в интересную игру. Итак, как научить ребенка делению?
Для этого применяют упражнение:
- Для проведения домашних занятий следует запастись конфетами или яблоками. Также понадобятся игрушки, с которыми любит возиться ученик. Нужно попросить малыша, чтобы он разделил четыре яблока или конфеты между двумя-тремя мишками или куклами. Затем количество предметов, подлежащих делению, увеличивается до шести, восьми, десяти.

- Итак, игрушки «получили» конфеты или яблоки. Теперь ученик должен посчитать, сколько досталось каждому мишке или кукле. Обязательно следует подвести итог. Предположим, что игрушек было три и между ними были разделены шесть конфет. Следовательно, каждая «получила» по две. Нужно объяснить ребенку, что «разделить» означает всем раздать поровну.
- Как научить ребенка делению дома? Для лучшего усвоения материала стоит изменить условия задачи. К примеру, нужно дать малышу шесть яблок и попросить распределить их между бабушкой, дедушкой и кошкой поровну. Затем это же количество предметов следует предложить ему поделить между бабушкой и животным. Обязательно следует объяснить ученику, почему результат оказался разным.
Деление с остатком
Итак, малыш хорошо справляется с простыми задачами. Это означает, что пора использовать более сложные примеры. Как научить ребенка делению с остатком? Скажем, можно дать ученику пять конфет и предложить угостить ими дедушку и бабушку в одинаковом количестве. Остается одно лакомство, которое малыш забирает себе.
Остается одно лакомство, которое малыш забирает себе.
На этом примере можно объяснить ребенку, что одна конфета и является остатком. Затем можно предложить малышу, к примеру, разделить между бабушкой, дедом и кошкой восемь конфет поровну.
На примере таблицы умножения
Как научить ребенка делению, если он уже знает умножение? Малыш должен понять, что этот процесс подразумевает действия, противоположные умножению:
- Для начала пусть ученик умножит число 6 на 3. У него получится 18.
- Далее нужно обратить внимание ребенка на то, что число 18 является результатом умножения вышеуказанных чисел.
- Теперь следует разделить 18 на 6. Ребенок получит 3. Это станет для него наглядным примером того, что деление представляет собой действие, противоположное умножению.
Для закрепления материала непременно стоит рассмотреть примеры с другими цифрами. Деление освоится легко, если школьник хорошо знает умножение и сумеет понять связь между математическими действиями.
Определение понятий
Как научить ребенка делению чисел? Что ему необходимо знать? Малыш должен запомнить и названия чисел, которые участвуют в этом процессе.
- Делимое. Так называется число, которое необходимо разделить.
- Делитель. Это число, на которое разделяется делимое.
- Частное. Так называется результат деления.
Для наглядности стоит вновь вернуться к примерам с лакомствами и игрушками. Ребенок должен понять, что делимое — это количество конфет или яблок, которое следует раздать. Делитель же — число игрушек, на которое они делятся.
Усложняем задачу
От простого следует переходить к сложному. Как научить ребенка делению в столбик? К обучению следует переходить уже тогда, когда малыш хорошо усвоит таблицу умножения. Предположим, что нужно разделить 110 на 5.
Эти числа необходимо написать на чистом листке бумаги, а затем разделить их перпендикулярными линиями.
- Далее нужно объяснить ребенку, что число 110 является делимым, а число 5 — делителем.

- Первая цифра числа 110 — 1, ее нельзя разделить на 5. Следовательно, необходимо взять следующую цифру. Получится число 11, в которое 5 может поместиться два раза.
- В столбике под пятеркой нужно записать цифру 2. Далее необходимо попросить ученика умножить 5 на 2. У него получится 10. Эту цифру следует записать под числом 11.
- Затем вместе с ребенком нужно вычесть число 10 из 11. Получится 1, возле этой цифры нужно записать оставшийся нолик в столбике. Получится 10.
- Далее нужно разделить с малышом 10 на 5. Результат — 2, эту цифру нужно записать под пятеркой. Результатом деления является число 22.
Обучение лучше всего начинать с цифр, которые можно делить без остатка — однозначных, двузначных. Когда ребенок будет хорошо справляться с простыми операциями, задачу можно усложнить.
Алгоритм деления в столбик
Деление в столбик — задача, с которой поможет справиться знание простого алгоритма.
- Для начала следует понять, где в примере делимое, а где делитель.

- Далее делимое и делитель следует записать под «уголок». Чтобы ребенок не путался на начальном этапе обучения, можно сказать ему, что слева нужно записать большее число, а справа — меньшую цифру.
- Затем нужно определить часть делимого, которую можно использовать для первичного деления.
- Далее следует понять, сколько раз уменьшается в выбранной части делимого делитель. Можно обратить внимание ребенка на то, ответ не должен превышать 9.
- Затем делитель нужно умножить на полученное число под «уголком». Результат вписывается под выбранную часть делимого.
- Далее необходимо найти разницу (остаток).
- Действия повторяются до тех пор, пока не удастся получить в остатке цифру 0.
Как быстро научить ребенка делению? Начинать процесс обучения необходимо с простейших задач. К примеру, малышу нужно разделить апельсин на дольки между членами семьи. Он начнет с того, что будет перекладывать по одной штучке. Уже после этого можно предложить ему подсчитать изначальное количество долек, а затем количество, которое должно достаться каждому.
Результат обучения зависит не только от умения родителей выбирать простые примеры. Также важно запастись терпением, так как путь предстоит долгий. Если ребенок не понимает какой-то момент, обязательно следует возвращаться к нему и повторять еще раз. Ни в коем случае нельзя ругать малыша, если у него что-то не получается. Если он допускает ошибку, необходимо спокойно поправить его.
Нужна ли таблица
Как сделать, чтобы малыш быстро освоил деление? Как научить ребенка решать примеры? Чтобы успешно справиться с этой задачей, необходимо знать таблицу умножения. Однако сейчас появились и таблицы деления, которыми пользуются некоторые учителя в процессе обучения.
Нужна ли таблица деления? Или достаточно, чтобы ребенок понял, что деление — это умножение наоборот? Второй вариант предпочтительнее, так как побуждает малыша думать. Однако вовсе не обязательно отказываться и от таблицы деления, когда ребенок уже проникнет в тайны этого процесса.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел.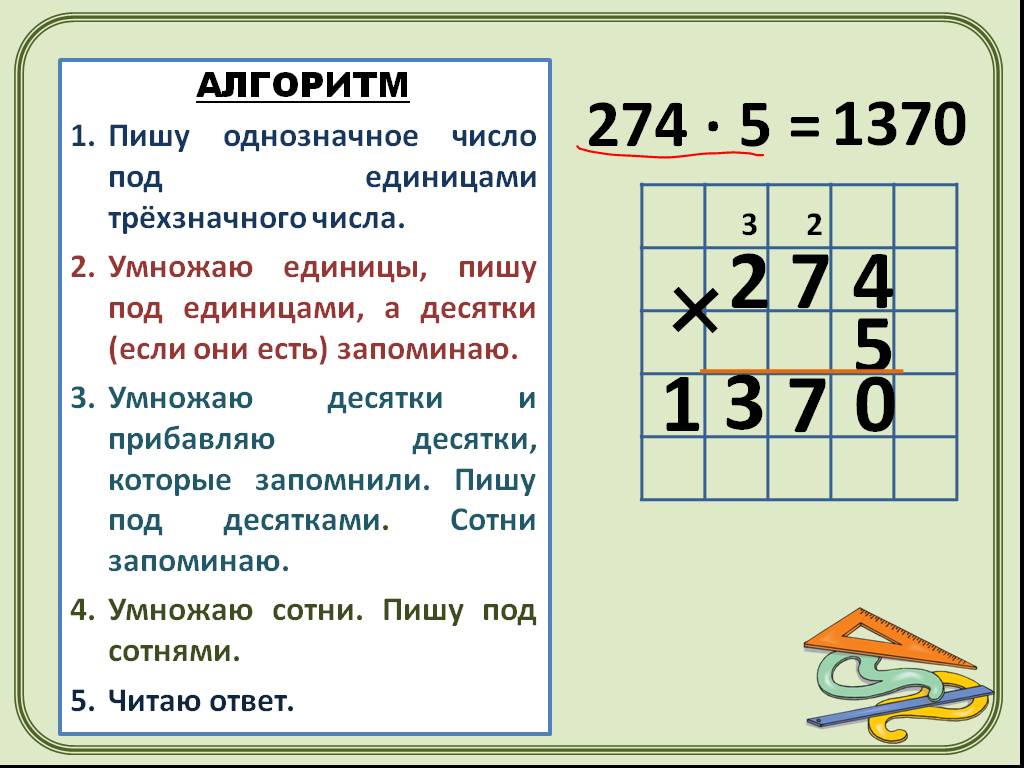 Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т. д.) во время конструирования, игр и наблюдений за природой.
д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.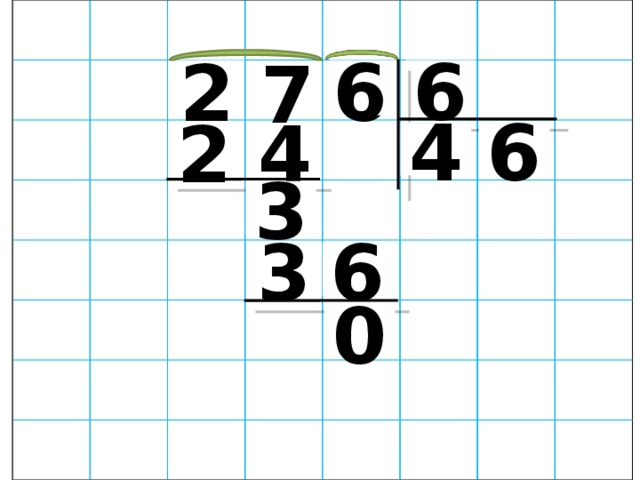
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Однако если ребенку тяжело все носить, то не стоит его перегружать.
Одним из наиболее важных этапов обучения вашего ребенка математическим операциям является обучение действиям деления простых чисел. Для обучения делению ребенка, нужно, чтобы к моменту обучения он уже освоил и хорошо понимал такие математические действия, как вычитание, сложение.
Кроме того, важно иметь четкое представление о самой сущности таких действий, как деление и умножение. Таким образом, он должен понимать, что в действии с делением заключается метод разделения чего-либо на равные доли. В заключение необходимо также обучиться операциям по умножению и хорошо знать таблицу умножения.
Обучаемся операции по делению на части
На данном этапе лучше сформировать понимание того, что главное в процессе деления, это разделение чего-то на равные части. Самым простым способом научиться этому для ребенка, это будет предложить ему поделить несколько предметов между ним и членами семьи или друзьями.
К примеру, возьмите 6 одинаковых предметов и предложите ребенку поделить их на две равные части. Можно немного усложнить задание, предложив поделить не на две, а на три равные части.
Можно немного усложнить задание, предложив поделить не на две, а на три равные части.
Важным моментом здесь считается проводить операции по делению четных количеств предметов. Такое действие окажется полезным на дальнейшем этапе, когда ребенку будет необходимо понимание того, что разделение, это действие, обратное умножению.
Делим и умножаем, при помощи таблицы умножения
Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.
Например : 2 умножить на 4 будет восемь. Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения.
Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.
Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное». Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!
Разделяем столбиком – легко и быстро
Перед тем, как начинать обучение следует вспомнить с ребенком, какое название имеет каждое число в процессе операции разделения. Главное, научиться быстро и безошибочно научиться определять данные категории.
Наглядный пример:
Попробуем разделить 938 на 7. В этом приведенном примере число 938 будет являться делимым, а число 7 будет делителем. В результате действия, ответ будет называться частное.
- Необходимо записать числа, разделив их «уголком».
- Предложите ученику из наименьшего числа делимого выбрать то, что больше делителя. Из цифр 9, 3, 8, наибольшим будет цифра 9. Предложите проанализировать, сколько семерок может содержать в цифре 9. Одним правильным ответом здесь будет только один. Первым результатом записываем 1.

- Оформляем деление в столбик.
Умножим делитель 7 на 1, ответ будет 7. Полученный результат вписываем под первое число нашего делимого, затем вычитаем в столбик. Таким образом, из 9 отнимаем 7 и в ответе получаем 2. Это тоже записываем.
- Видим число, получившееся меньше делителя, поэтому увеличиваем его. Чтобы это сделать, объединим его вместе с неиспользованным числом делимого, то есть с цифрой 3. Дописываем 3 к полученной 2.
- Затем анализируем сколько раз делитель 7 будет содержаться в числе 23. Ответ 3 раза и фиксируем его в частном. Результат произведения 7 на 3 (21) вписываем снизу в столбик под число 23.
- Остается только найти последнее число частного. Применяя тот же алгоритм, продолжает вычисления в столбике. Вычитает в столбике 23-21 получает разницу, равной числу 2. Из всего делимого, у нас остается только неиспользованное число 8. Его объединяем с полученным результатом 2, получаем в ответе 28.
- В заключение анализируем, какое количество, раз делитель 7 содержится в полученном нами числе.
 Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Самым наиболее главным при обучении ребенка методу деления, будет усвоение и четкое понимание алгоритма действий, ведь на самом деле он предельно прост.
Если ваш ребенок отлично умеет оперировать таблицей умножения, то с «обратным» делением у него не должны возникнуть трудности. Поэтому очень важно все время тренировать полученные навыки. Не стоит останавливаться на достигнутом.
Для легкого обучения юного ученика методу деления следует:
- в возрасте трех лет правильно усвоить термины «целое» и «часть». Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта.
- правильно понимать и разбираться в методах деления и умножения.
Чтобы занятия доставили ребенку удовольствие, следует возбуждать интерес к математике в ситуациях в быту, а не только в процессе учебы.
Поэтому тренируйте наблюдательность у ребенка, придумывайте аналогии математических действий во время игр, в процессе конструирования либо же в простых наблюдениях за природой.
Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению. Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс. Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее.
Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.
При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.
Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.
Вместе с этим ищут и читают:
Теперь вам необходимо решить, как научить ребенка делить. Если он уже перешел в третий класс, трудностей у вас возникнуть не должно. Для начала объясните малышу зависимость между делением и умножением. Продемонстрируйте ему, как правильно делить столбиком, используя таблицу умножения. Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.
Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.
Объясните ученику, который перешел в третий класс, что категории, описывающие деление, называются «делимое», «делитель», «частное». Продемонстрируйте это наглядно с помощью таблицы. Рассмотрите как можно больше примеров, чтобы малышу было понятнее. Это пригодится в дальнейшем, когда вы будете осваивать деление столбиком. По сути, вам необходимо научить кроху смотреть на таблицу умножения «наоборот».
Перед началом занятий еще раз вспомните категории деления. Теперь попробуем объяснить все наглядно. Например, разделим число девятьсот тридцать восемь на семь. Запишем числа, чтобы делить их столбиком. Если вы только начинаете обучение, то ребенку, который пошел в третий класс, будет проще для начала делить числа без остатка. Теперь показываем ученику числа делимого и предлагаем ему выбрать наименьшее число, которое будет больше, чем делитель. Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.
Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.
Умножаем семь на один, получаем семь. Этот результат мы записываем под девяткой из числа девятьсот тридцать восемь. Вычитаем от девятки семерку в столбик. В остатке получаем два. Аналогичным образом записываем результат. Полученное число меньше, чем делитель. Таким образом, нам необходимо его увеличить. Объединяем его со следующим неиспользованным числом – тройкой. «Плюсуем» тройку и двойку. Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.
Самое главное в процессе обучения малыша, который перешел в третий класс, чтобы он усвоил простой алгоритм. Развивайте наблюдательность у крохи, проводите аналогии с другими математическими действиями, больше играйте и наблюдайте за природой.
Карточки Деление столбиком — Стоматология в Химках
Математика 3 класс деление в столбик
С письменным приемом деления на однозначное число или, как его обычно называют, «в столбик», учащиеся начальной школы знакомятся в 3 классе и углубляют свои знания в 4 классе.
Прием письменного деления многозначного числа на однозначное получил еще одно название «деление уголком»
Деление в столбик нельзя начинать без подготовки. Для успешной работы необходимо знать:
- разряды натуральных чисел (десятки, сотни, тысячи) и легко ориентироваться в многозначном числе; таблицу умножения. Нужно блестящее знание таблицы умножения и деления; сложение и вычитание многозначных чисел; .
С помощью Карточек «Деление многозначного числа на однозначное» учитель осуществит проверку знаний, а учащимся тренировка поможет развить и систематизировать вычислительные навыки.
Готовые карточки «Деление на однозначное число в столбик» можно легко скачать и распечатать.
Готовые карточки деление столбиком
Карточка «Деление столбиком на однозначное число»
Скачать набор готовых карточек (10 шт) «Деление на однозначное число в столбик» вы можете по ссылке ниже
Карточка «Деление столбиком на однозначное число»
Готовые карточки деление столбиком
Карточка Деление столбиком на однозначное число.
Koncpekt. ru
13.11.2020 1:31:12
2020-11-13 01:31:12
Источники:
Https://koncpekt. ru/nachalnye-klassy/konspekty-urokov/matematika-3klass/4486-kartochka-delenie-stolbikom. html
Урок 66. приём письменного деления на однозначное число — Математика — 3 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Математика 3 класс деление в столбик
Как выполняется письменное деление на однозначное число?
Как применяется алгоритм деления трёхзначного числа на однозначное?
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют Разрядом.
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют Разрядными единицами:
— единицы называют единицами 1-го разряда;
— десятки называют единицами 2-го разряда;
— сотни называют единицами 3-го разряда и т. д.
Деление (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению.
Деление — это такая операция, в результате которой получается число (частное), которое приумножении на делитель даёт делимое.
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 92-94.
2. Волкова С. И. Математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018. С. 84-85.
3. Рудницкая В. Н. Математика. Дидактические материалы. Ч.1 3 кл. – М. «Вентана — Граф», 2016, с. 23-24.
Теоретический материал для самостоятельного изучения
Сегодня мы займёмся делением.
Вам предстоит научиться выполнять деление трёхзначных чисел в столбик.
Вы справитесь с этим без проблем, если хорошо знаете таблицу умножения.
Три математических действия — сложение, вычитание и умножение в столбик вы уже умеете выполнять. Осталось одно, но самое сложное. Помните, чем сложнее – тем интереснее!
Деленье нам служит на деле,
Оно нам поможет всегда.
Кто поровну трудности делит,
Разделит успехи труда.
Мы уже выяснили, что невозможно быстро и точно делить без знания таблицы умножения.
Надо ещё хорошо знать компоненты деления и взаимосвязь между ними, быстро и точно выполнять вычитание и конечно уметь работать с разрядами.
Вспомним компоненты деления: число, которое делим – делимое, число на которое делим – делитель, результат деления – значение частного.
В тех случаях, когда деление выполнить устно сложно, выручает умение делить в столбик, или уголком.
Это название придумали не случайно. Привычный знак деления заменён на уголок.
Записываем делимое, рядом чертим уголок. В верхнем углу записываем делитель, а в нижний угол вписываем цифры частного.
Обратите внимание, цифры делимого и частного имеют названия в зависимости от разряда, который обозначают.
Кроме этого, делимое придётся раскладывать на неполные делимые – первое, второе, третье. Это те числа, которые делим на делитель, пока не разделим всё число.
Рассмотрим пример 938 : 7
Записываем числа, разделив их «уголком».
Сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Умножаем делитель 7 ∙ 1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2. Записываем результат.
Число, которое мы видим, меньше делителя, поэтому его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7 ∙ 3) записываем внизу под числом 23 в столбик.
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23 — 21) получаем разницу. Она равняется 2.
Она равняется 2.
Из делимого у нас осталось неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное = 134.
Рассмотрим ещё деление в столбик на примере 512 : 8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит, в ответе будет ещё одно число, то есть, частное – двузначное число. Ставим вторую точку:
Ставим вторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
9 шаг. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Как и в остальных случаях выполнения письменных приёмов вычислений, при делении очень важно не отступать от алгоритма.
Когда число цифр разряда меньше делителя, надо добавить к нему число цифр следующего разряда.
Если при делении неполного делимого остался остаток, спускаем его под черту и к нему приписываем цифру следующего разряда.
Остаток не может быть больше делителя!
Если цифра неполного делимого меньше делителя, то в частном пишем 0.
Вы сегодня получили ключ к успеху в математике. Смело открывайте им замки любой сложности.
Помните, чем сложнее тем интереснее.
Resh. edu. ru
17.06.2018 23:25:37
2018-06-17 23:25:37
Источники:
Https://resh. edu. ru/subject/lesson/5714/conspect/
Деление в столбик ➗ примеры и правила, как научиться » /> » /> .keyword { color: red; }
Математика 3 класс деление в столбик
Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.
О чем эта статья:
3 класс, 4 класс
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить; 7 — делитель или то, на что нужно поделить: частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.
Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.
Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.
Это задание со звездочкой.
Теперь 29 будет делимым, а 6 делителем.
Skysmart. ru
20.11.2018 16:22:58
2018-11-20 16:22:58
Источники:
Https://skysmart. ru/articles/mathematic/delenie-v-stolbik
Как объяснить ребёнку деление в столбик
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
СодержаниеРаскрыть
- Осваиваем операцию разделения (деления) на части в игровой форме
- Умножаем и делим, используя таблицу умножения
- Делим столбиком – приведем пример
- Объясняем наглядно
- Как научить ребенка делению – закрепляем навык
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, как запомнить таблицу умножения легко и быстро. Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
Двигайтесь дальше, разбирая другие примеры из таблицы умножения.
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1. Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.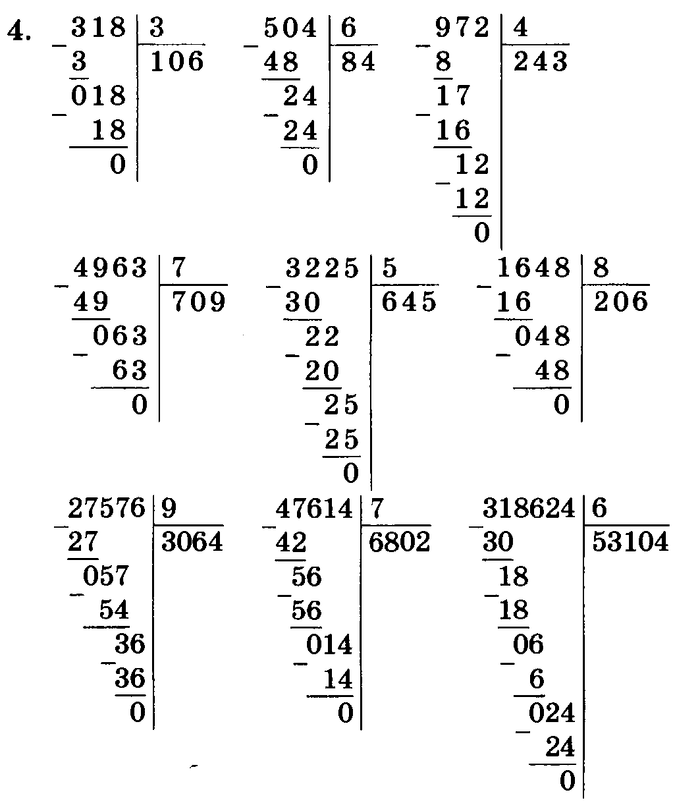
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть».
 У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта marypop.ru
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
youtube.com/embed/BP-YLWmDVpk» frameborder=»0″ allowfullscreen=»allowfullscreen»>8.1: Полное деление — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48996
- Томас Тредлер и Холли Карли
- CUNY New York City College of Technology через New York City Academic College of Technology at 9 CUNY2+4х+2}{х+3}\)
- Напомним процедуру деления натуральных чисел в длинное:
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Томас Тредлер и Холли Карли
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- остаток
- источник@https://academicworks.
 cuny.edu/ny_oers/1
cuny.edu/ny_oers/1
- Стратегии разрядности: использование чисел, кратных 10 (это должно было быть уже введено с умножением, поэтому это первое, с чего я начинаю работу с учениками)
- 6400 / 8 на самом деле 64 / 8 x 100
- Расширенная форма или свойство распределения (246 / 2) = (200 +400+6) / 2
- Модель площади
- Частичные частные
- Стандартный алгоритм — не бросать помидоры, но я всегда ввожу стандартный алгоритм, даже в 4-м классе, потому что я обнаружил, что, как только у них есть эти стратегии, они довольно быстро приходят к некоторым ученикам и становятся еще одной стратегией, которую они могут использовать.
 Наша конечная цель — полное и полное концептуальное понимание.
Наша конечная цель — полное и полное концептуальное понимание. - После того, как учащиеся продемонстрируют владение стандартным алгоритмом (или стратегиями), сделайте еще один шаг и попросите их погрузиться в анализ ошибок, где они могут продемонстрировать «обратное» понимание, оценивая сделанные ошибки. и исправить их. Способность выявить ошибку в чужой работе требует мышления более высокого порядка, которого нет в большинстве других проектов или видов деятельности и, конечно же, в базовом завершении математических фактов.
- Сначала научите студентов различать вычислительная ошибка и концептуальная ошибка.
- Вычисления — это когда они делают ошибку в основных математических фактах.
 Это может выглядеть так просто, как 64/8 не равно 7. Упс!
Это может выглядеть так просто, как 64/8 не равно 7. Упс! - Концептуальная или процедурная ошибка — это ошибка в процедуре или концепции. Обычно это происходит, когда учащиеся не понимают, почему стратегии или алгоритмы работают, и просто запоминают шаги.
- Я не могу сказать вам, сколько раз учащиеся показывают, что не владеют темой, когда ошибки, которые они делают, являются ВЫЧИСЛИТЕЛЬНЫМИ, а не концептуальными или процедурными. Им не нужно больше повторять, как использовать стратегию… им нужно замедлиться и уделить больше внимания своим математическим фактам.
- Вычисления — это когда они делают ошибку в основных математических фактах.
- После того, как мы представили типы ошибок (концептуальные и вычислительные), на которые должны обращать внимание учащиеся, мы переходим к фактическому анализу этих ошибок в чужой работе и , исправляя ошибку.
- Я создал задания по анализу ошибок для вас, чтобы вы могли использовать их со своими учениками, чтобы они могли определить ошибки, типы ошибок, переработать проблему, создать свою собственную версию проблемы и решить ее.
 Я добился больших успехов, включив эти задачи во ВСЕ мои математические разделы. У меня даже есть дети, которые умоляют взять свои задания по анализу ошибок на перерыв, чтобы закончить!
Я добился больших успехов, включив эти задачи во ВСЕ мои математические разделы. У меня даже есть дети, которые умоляют взять свои задания по анализу ошибок на перерыв, чтобы закончить!
- Сначала научите студентов различать вычислительная ошибка и концептуальная ошибка.
- Последним шагом в использовании анализа ошибок является фактическое исправление учащимися СОБСТВЕННЫХ ошибок. После того, как я проинструктировал о типах ошибок, я начну с того, что просто скажу им: «Ой! Вы сделали здесь вычислительную ошибку!» Таким образом, они не будут яростно искать ошибку в процедуре, вместо этого они будут искать, где они вычислили неправильно. И наоборот, я скажу им, если они допустили процедурную ошибку, и это может помочь им понять, что им нужно искать.
- Наблюдение за различными типами ошибок, которые допускают учащиеся, также важно для руководства моим обучением, поэтому, хотя оценка таких вещей занимает немного больше времени, это очень помогает мне, когда я вношу коррективы в свое обучение.
- Это не столько алгоритм, сколько критическое понимание цели разделения и возможность генерировать реальные сценарии, применимые к делению.

- Учащимся будет очень сложно, если мы попросим их просто решить задачу на деление, поэтому дайте им некоторые указания. Дайте им числа и темы, которыми они будут руководствоваться при создании проблем, чтобы они не застряли на двух довольно незначительных частях этого процесса. Например, я создал эти Напишите и решите карточки задач длинного деления . Он дает им числа и сценарий, и учащиеся должны сгенерировать и решить задачу на деление.
- Остатки — серьезная проблема для учащихся, особенно в 4-м классе. Помочь им интерпретировать свои остатки и оценить их на предмет разумности — это ключ к их успеху в делении. У меня есть несколько оставшихся напоминаний, которые я ВСЕГДА настаиваю на своих учениках. Этот плакат также включен в бесплатную загрузку выше!
- Подсказка Напоминания об остатках для студентов:
- Не бойтесь Словарь предметной области ! Обратите внимание, что слово «остаться» находится в слове «остаток».
 Это значение, которое остается и не может быть равномерно разделено на ваш делитель.
Это значение, которое остается и не может быть равномерно разделено на ваш делитель.
- Остаток не может быть больше делителя. Я сторонник математической лексики, поэтому для меня очень важно, чтобы учащиеся могли использовать этот конкретный язык (делитель, частное, делимое).
- Остаток МОЖЕТ иметь значение больше вашего частного. Такое бывает, и случается часто, поэтому обязательно приведите много примеров этому.
- Когда одно число делится на другое число без остатка, остаток технически равен НОЛЬ.
- Четное число, деленное на 2, никогда не должно иметь остатка.
- Ваш остаток всегда служит цели. Это не всегда просто «остатки». Мы поговорим об этом подробнее в ближайшее время.
- Не бойтесь Словарь предметной области ! Обратите внимание, что слово «остаться» находится в слове «остаток».
- Визуализация остатков:
- Используйте массивы, чтобы визуализировать остатки как остатки.
- Используйте манипуляторы для визуализации.
- Используйте самый простой способ манипуляции: человеческие тела! Разыграйте множество сценариев, используя учащихся вашего класса, в том числе задачи с остатками… сейчас самое время решить транспортную задачу.
 Например: Класс мисс Смит собирался на экскурсию. В классе было 24 ребенка, и в каждом микроавтобусе по 7 учеников. Сколько фургонов им понадобится?
Например: Класс мисс Смит собирался на экскурсию. В классе было 24 ребенка, и в каждом микроавтобусе по 7 учеников. Сколько фургонов им понадобится? - Используйте числовые линии для представления остатков
- Интерпретация остатков: Когда я начал добавлять урок или два по интерпретации остатков , понимание моими учениками не только остатка, но и понимания словесных задач резко возросло. Акту интерпретации остатков следует обучать после того, как учащиеся хорошо разберутся в выполнении деления с использованием стратегий или алгоритма. Мы сосредоточимся на трех различных способах использования остатков:
- Использование остатка — Это происходит, когда остаток на самом деле является ответом.
- Округление в большую сторону — Когда вы используете остаток для округления своего ответа. Частное — это не ваш ответ, но оно на единицу больше, потому что у вас есть остаток.
 (Например: когда вы распределяете детей по машинам, чтобы поехать в летний лагерь. Вы не можете просто оставить двух учеников, поэтому вам нужно добавить еще одну машину, чтобы перевезти всех)
(Например: когда вы распределяете детей по машинам, чтобы поехать в летний лагерь. Вы не можете просто оставить двух учеников, поэтому вам нужно добавить еще одну машину, чтобы перевезти всех) - Игнорировать — Иногда мы игнорируем остаток . Обычно это происходит, когда мы находим действительно равные группы.
- Разделить остаток в виде дроби или десятичных знаков — Я МОГУ немного рассказать своим ученикам об этой опции, особенно ученикам, готовым к этой информации, но в целом я делаю , а не , обучаю этому четырехклассников, когда он начинает замутить их понимание.
- При подъеме делим
- При опускании распределяем
- Вычитаем
- Перенести
- Повторять процесс до завершения
Решение
Описанные выше шаги выполняются следующим образом. Во-первых, мы находим наибольшее кратное \(11\), меньшее или равное \(35\). Ответ \(3\) записывается как первая цифра в верхней строке. Умножьте \(3\) на \(11\) и вычтите результат \(33\) из первых двух цифр \(35\) делимого. Остальные цифры \(71\) скопированы ниже, чтобы получить \(271\). Теперь повторяем процедуру, пока не получим остаток \(7\). Короче говоря, мы показали, что: 92+2x-2+\dfrac{8}{x+3} \номер\]
Умножьте \(3\) на \(11\) и вычтите результат \(33\) из первых двух цифр \(35\) делимого. Остальные цифры \(71\) скопированы ниже, чтобы получить \(271\). Теперь повторяем процедуру, пока не получим остаток \(7\). Короче говоря, мы показали, что: 92+2x-2+\dfrac{8}{x+3} \номер\]
Примечание
Так же, как и при делении чисел, при делении \(\dfrac{f(x)}{g(x)}\), \(f(x)\) называется делимым и \ (g(x)\) называется делителем . В результате деления \(f(x)\) на \(g(x)\) в длинное деление с частным \(q(x)\) и остатком \(r(x)\), мы можем написать
\[\dfrac{f(x)}{g(x)} = q(x)+\dfrac{r(x)}{g(x)} \nonumber \]
Если мы умножим это уравнение на \(g(x)\), мы получаем следующий альтернативный вариант: 92+3x+1} \номер\]
Примечание
Делитель \(g(x)\) является множителем \(f(x)\) ровно тогда, когда остаток \(r(x)\) равен нулю, то есть:
\[f( x)=q(x)\cdot g(x)\quad \iff\quad r(x)=0 \nonumber \]
Например, в приведенном выше примере \(\PageIndex{3}\) только часть (c) приводит к факторизации делимого, поскольку это единственная часть с нулевым остатком.
Эта страница под названием 8.1: Длинное подразделение распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Томасом Тредлером и Холли Карли (Нью-Йоркский городской технологический колледж в CUNY Academic Works) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Длинный отдел: стратегии и расширения для старших классов математики
Я так рад поговорить о делении в столбик! А, дивизия. У вас волосы на руках встают дыбом от одного упоминания об этом? И сроки! Почему нам всегда кажется, что мы учим делению на длинные числа во время курортного сезона, когда энергии много, а внимания мало? Вне зависимости от времени года наличие четкой, хорошо продуманной последовательности уроков деления может устранить большую часть обычного беспокойства, связанного с преподаванием длинного деления в 4-м классе… и за его пределами!
Этот стандарт 4-го класса призывает учащихся использовать стратегии разрядных значений для нахождения целых чисел и остатков с делимыми до четырех цифр и одноразрядными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. Это мелочь, но давайте разбираться!
Это мелочь, но давайте разбираться!
Когда мы думаем о дивизии и планируем нашу дивизию, первое, о чем я думаю, это конкретная стратегия развития, которую я собираюсь использовать для обучения этой концепции. Студенты просто должны иметь концептуальное представление о том, КАК работают процедуры деления. Несмотря на то, что это не является стандартом для 4-го класса, в конечном счете, наша цель — овладеть стандартным алгоритмом для деления в большую сторону , чтобы, когда они начнут выполнять множество шагов процедуры, они могли осмыслить каждый шаг и понять, что они делают, а не просто запоминают. ПРОДАЕТ ЛИ МАКДОНАЛДС ЧИЗБУРГЕРЫ. у меня точно ничего против акронима, и я определенно использовал его на якорной диаграмме, но понимание фактического процесса поможет им значительно больше, чем запоминание шагов, которые легко перепутать и перепутать. Вы можете увидеть мои якорные диаграммы делений и другие стратегии длинных делений в этом посте .
Повторение умножения и деления
Первое, что мне нужно сделать на этом этапе, это убедиться, что я уже подробно рассмотрел умножение и деление со своими учениками. Мы говорим о том, что это обратные операции, мы говорим о том, что такое деление, моделируем базовое деление и убеждаемся, что учащиеся знают, как использовать умножение для проверки своих ответов на деление (и наоборот). Почти ВСЕ стратегии деления, о которых мы собираемся поговорить, основаны на аналогичных стратегиях умножения, которые всегда кажутся менее сложными для учащихся, поэтому я призываю вас сначала заняться этими стратегиями умножения. Нужно освежить в памяти стратегию умножения? Прочтите в этом блоге все о стратегиях умножения .
Стратегии длинного деления
Давайте поговорим о стратегиях деления! Когда я говорю о стратегиях, я всегда представляю несколько, прежде чем перейти к стандартному алгоритму. Это очень важно для учащихся, чтобы понять, ПОЧЕМУ работает стандартный алгоритм. ПОЧЕМУ я представляю все эти стратегии студентам? Потому что у большинства детей ОДИН из них вызовет момент озарения, когда они скажут: «А! Я понимаю, ПОЧЕМУ я делаю то, что я делаю с этой конкретной процедурой прямо сейчас, и я знаю, ПОЧЕМУ я делаю этот шаг следующим». ЭТО моя конечная цель при обучении этим стратегиям.
ПОЧЕМУ я представляю все эти стратегии студентам? Потому что у большинства детей ОДИН из них вызовет момент озарения, когда они скажут: «А! Я понимаю, ПОЧЕМУ я делаю то, что я делаю с этой конкретной процедурой прямо сейчас, и я знаю, ПОЧЕМУ я делаю этот шаг следующим». ЭТО моя конечная цель при обучении этим стратегиям.
Вот краткий обзор стратегий, которым я обучаю своих четвероклассников:
Я создал эти бесплатных постеров с длинными делениями , чтобы помочь вам и вашим ученикам освоить эти стратегии!
Beyond Long Division Strategies
Вы еще не закончили, когда ваши ученики развили понимание стандартного алгоритма или другой стратегии! Есть так много других частей и частей деления, которым важно учить. Давайте углубимся в две области, которые имеют решающее значение для глубокого понимания деления и о которых часто забывают. Включение анализа ошибок и интерпретации остатков в вашу инструкцию деления имеет решающее значение. Независимо от того, обучали ли вы только стратегиям или стандартному алгоритму, я умоляю вас включить эти два компонента в ваше подразделение.
Анализ ошибок в длинном делении
Я большой поклонник анализа ошибок, который помогает развить критическое мышление и понимание. Вы можете прочитать все об анализе ошибок здесь . Марцано особо отмечает, что анализ ошибок имеет решающее значение для формирования у учащихся критического мышления и концептуального понимания. Способность судить, защищать, интерпретировать и исправлять ошибки требует гораздо больше размышлений и понимания, чем простое решение проблемы.
Марцано особо отмечает, что анализ ошибок имеет решающее значение для формирования у учащихся критического мышления и концептуального понимания. Способность судить, защищать, интерпретировать и исправлять ошибки требует гораздо больше размышлений и понимания, чем простое решение проблемы.
Использование анализа ошибок с делением в длину
Проблемы со словами на деление
Еще один небольшой совет, который поможет еще большему критическому пониманию деления… Пусть ваши ученики поработают над созданием своих собственных задач! Как только они смогут решить и проверить свою работу, им пора создавать свои собственные сценарии деления/словные задачи!
Устный перевод
Предоставление учащимся ШИРОКИХ возможностей интерпретировать функцию остатка (даже не требуя от учащихся решения задачи) имеет решающее значение для их понимания.
Я надеюсь, что эти советы помогли вам начать работу с подразделением!
Просмотры сообщений: 9,097
Длинное деление многочленов — ChiliMath
В этом уроке я рассмотрю пять (5) примеров с подробными пошаговыми решениями о том, как делить многочлены с помощью метода деления на длинное деление . Это очень похоже на то, что вы делали в Elementary, когда пытались разделить большие числа, например, у вас есть 1723 \div 5. Вы бы решили это так же, как показано ниже, верно?
Это очень похоже на то, что вы делали в Elementary, когда пытались разделить большие числа, например, у вас есть 1723 \div 5. Вы бы решили это так же, как показано ниже, верно?
Если вы можете выполнить простое числовое деление методом длинного деления, как показано выше, я убежден, что вы сможете решить приведенные ниже задачи. Единственная добавленная вещь — разделение переменных.
Примеры деления многочленов методом деления в длинную сторону
Пример 1 : Деление методом деления в длинную сторону стандартная форма. Многочлен в стандартной форме гарантирует, что его показатели находятся в порядке убывания слева направо. Быстрая проверка поможет нам предотвратить основные ошибки, которых можно было бы избежать.
При беглом рассмотрении я надеюсь, что вы согласитесь с тем, что и делимое, и делитель действительно имеют стандартную форму. Это означает, что теперь мы готовы выполнить процедуру.
ШАГ 1 : Рассмотрите как главные члены делимого, так и делителя.
ШАГ 2 : Разделите старший член делимого на старший член делителя.
ШАГ 3 : Поместите частичное частное сверху.
ШАГ 4 : Теперь возьмите частичное частное, которое вы поставили сверху, 3x, и распределите его на делитель \left( {2x + 4} \right).
ШАГ 5 : Поместите произведение \left( {3x} \right) и \left( {2x + 4} \right) под делимым. Обязательно выровняйте их по схожим терминам.
ШАГ 6 : Выполните вычитание, поменяв местами знаки нижнего многочлена.
ШАГ 7 : Продолжайте регулярно добавлять по вертикали. Обратите внимание, что первый столбец слева отменяет друг друга. Хороший!
ШАГ 8 : Перенесите следующий соседний «неиспользованный» член дивиденда.
ШАГ 9 : Затем посмотрите на нижний многочлен, — 14x — 28, возьмите его старший член, который равен -14x, и разделите его на старший член делителя, 2x.
ШАГ 10 : Снова поместите частичное частное сверху.
ШАГ 11 : Используйте полученное частичное частное, -7, и распределите его на делитель. Теперь видите образец?
ШАГ 12 : Поместите произведение -7 и делителя ниже в качестве последней строки ввода полинома.
ШАГ 13 : Вычитание означает, что вы поменяете знаки (выделено красным).
ШАГ 14 : Выполните регулярное сложение по столбцам похожих терминов
ШАГ 15 : Это замечательно, потому что остаток равен нулю. Это означает, что делитель является множителем делимого.
Окончательный ответ — это то, что находится над символом деления.
Пример 2 : Деление методом деления в большую сторону
Решение : Эта задача также считается «хорошей», как и первая, потому что и делимое, и делитель представлены в стандартных формах.
На этот раз вы делите многочлен с четырьмя членами на двучлен . Помните, что пример 1 представляет собой деление многочлена с тремя членами (трехчленного) на двучлен. Надеюсь, вы видите небольшую разницу.
Помните, что пример 1 представляет собой деление многочлена с тремя членами (трехчленного) на двучлен. Надеюсь, вы видите небольшую разницу.
Давайте разберемся с этим!
ШАГ 1 : Сосредоточьтесь на крайних левых членах делимого и делителя. 92}, чтобы умножить на делитель \влево( {3x — 2} \вправо).
ШАГ 5 : Поместите их продукт под дивиденд. Обязательно выровняйте их по схожим терминам.
ШАГ 6 : Выполните вычитание, чередуя знаки нижнего многочлена.
ШАГ 7 : Продолжайте регулярно добавлять по вертикали. Снова первый столбец компенсирует друг друга. Мне кажется шаблон!
ШАГ 8 : Перенести следующий соседний «неиспользованный» член дивиденда
ШАГ 9 : Возьмите крайний левый член нижнего многочлена и разделите его на крайний левый член делителя.
ШАГ 10 : Поместите ответ сверху, как обычно.
ШАГ 11 : Хорошо, выполните еще одно умножение на частичный ответ 2x и делитель \left( {3x — 2} \right). Принесите продукт ниже.
Принесите продукт ниже.
ШАГ 12 : Выполните вычитание, меняя знаки, и продолжайте обычное сложение.
ШАГ 13 : Перенесите последний неиспользованный член дивиденда. Мы почти там!
ШАГ 14 : Мы поднимаемся еще раз. Разделите старший член нижнего полинома на старший член делителя. Разместите ответ там!
ШАГ 15 : Это наша «последняя поездка» вниз, поэтому мы распределяем частичный ответ −1 на делитель \left( {3x — 2} \right) и помещаем произведение «вниз».
ШАГ 16 : Завершите это вычитанием, оставив как с остатком -7.
ШАГ 17 : Запишите окончательный ответ в следующей форме. 92}. Мне нужно вставить нулевые коэффициенты в качестве заполнителей для отсутствующих степеней переменной. Критической частью является правильное применение процедур в длинном делении.
Итак, я переписываю исходную задачу как
Теперь все х учтены!
ШАГ 1 : Сосредоточьтесь на начальных терминах внутри и снаружи символа деления.
ШАГ 2 : Разделите первый член делимого на первый член делителя.
ШАГ 3 : Поместите частичный ответ сверху. 93} и распределить на делитель \left( {x + 1} \right).
ШАГ 10 : Поместите ответ ниже, затем выполните вычитание.
ШАГ 11 : Уменьшить следующий соседний член делимого
ШАГ 12 : Снова подняться, разделив старший член ниже на старший член делителя.
ШАГ 13 : Спускайтесь вниз, распределяя ответ в неполном частном на делитель с последующим вычитанием.
Я считаю, что шаблон теперь имеет смысл. Да?
ШАГ 14 : Перенести последний член дивиденда.
ШАГ 15 : Поднимитесь снова, выполняя деление.
ШАГ 16 : Снова спускайтесь вниз при выполнении умножения.
ШАГ 17 : Сделайте последнее вычитание, и все готово! Остаток равен 20.
ШАГ 18 : Окончательный ответ:
Пример 4 : Разделить заданный многочлен методом деления в длину
Решение : В делимом явно не хватает многих переменных x. Это означает, что мне нужно вставить нулевые коэффициенты в каждую недостающую степень переменной.
Мне нужно переписать задачу таким образом, чтобы включить все показатели x в порядке убывания:
Помните основные шаги деления в длину:
Убедитесь, что шаги выполняются правильно в приведенном ниже примере.
Итак, окончательный ответ:
Пример 5 : Разделите заданный многочлен, используя метод деления в большую сторону
Решение : У нас есть многочлен, пять членов которого делятся на трехчлен. И делимое, и делитель имеют стандартную форму, и присутствуют все степени переменной x.


 Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134. У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.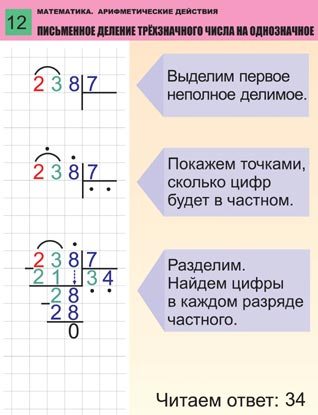 cuny.edu/ny_oers/1
cuny.edu/ny_oers/1 Наша конечная цель — полное и полное концептуальное понимание.
Наша конечная цель — полное и полное концептуальное понимание. Это может выглядеть так просто, как 64/8 не равно 7. Упс!
Это может выглядеть так просто, как 64/8 не равно 7. Упс!