правила и примеры (7 класс)

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число.

Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.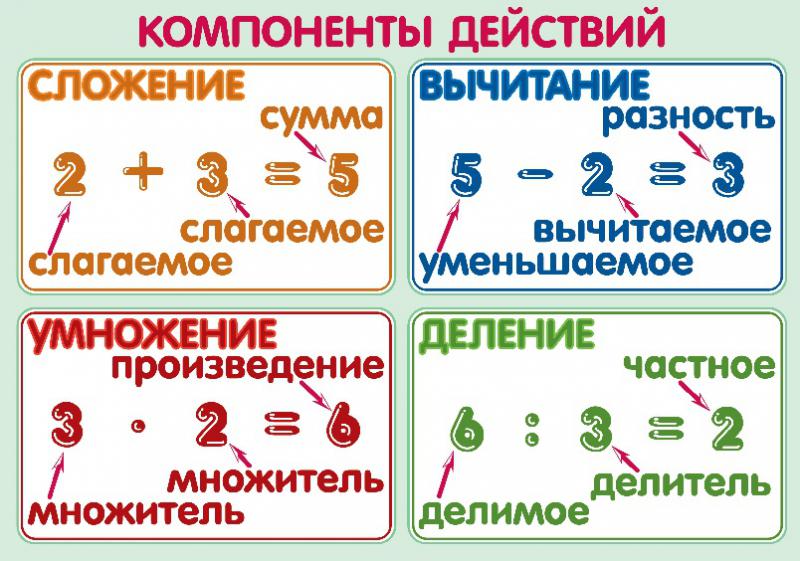

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример. (9 + 6) : 3=9: 3 + 6: 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть.

Пример. 12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\(5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\(xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)

Сумму одночленов называют многочленом. 3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

То части уравнения находится выражение в скобках. Чтобы раскрыть скобки, посмотрите на знак перед скобками. Если стоит знак плюс, при раскрывании скобок в записи выражения ничего не поменяется: просто уберите скобки. Если стоит знак минус, при раскрытии скобок необходимо поменять все знаки , стоящем изначально в скобках, на противоположные. Например, -(2х-3)=-2х+3.

Перемножение двух скобок.
Если в уравнении присутствует произведение двух скобок, раскрытие скобок по стандартному правилу. Каждый член первой скобки перемножается с каждым членом второй скобки. Полученные числа суммируются. При этом произведение двух «плюсов» или двух «минусов» дает слагаемому знак «плюс», а если множители имеют разные знаки, то получает знак «минус». 3
Формулы возведения выражения больше трех можно при помощи треугольника Паскаля.

Источники:

• формула раскрытия скобок

Заключенные в скобки математические действия могут содержать переменные и выражения разной степени сложности. Для перемножения таких выражений придется искать решение в общем виде, раскрывая скобки и упрощая полученный результат. Если же в скобках содержатся операции без переменных, только с численными значениями, то раскрывать скобки не обязательно, так как при наличии компьютера его пользователю доступны весьма значительные вычислительные ресурсы – проще воспользоваться ими, чем упрощать выражение.

Инструкция

Перемножайте последовательно каждое (или уменьшаемое с ), содержащееся в одной скобке, на содержимое всех остальных скобок, если требуется получить результат в общем виде. Например, пусть исходное выражение записано так: (5+x)∗(6-х)∗(x+2). Тогда последовательное перемножение (то есть раскрытие скобок) даст следующий результат: (5+x)∗(6-х)∗(x+2) = (5∗6-5∗х)∗(5∗x+5∗2) + (6∗x-х∗x)∗(x∗x+2∗x) = (5∗6∗5∗x+5∗6∗5∗2) — (5∗х∗5∗x+5∗х∗5∗2) + (6∗x∗x∗x+6∗x∗2∗x) — (х∗x∗x∗x+х∗x∗2∗x) = 5∗6∗5∗x + 5∗6∗5∗2 — 5∗х∗5∗x — 5∗х∗5∗2 + 6∗x∗x∗x + 6∗x∗2∗x — х∗x∗x∗x — х∗x∗2∗x = 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³.

Упрощайте после результат, сокращая выражения. Например, полученное на предыдущем шаге выражение можно упростить таким образом: 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³ = 100∗x + 300 — 13∗x² — 8∗x³ — x∗x³.

Воспользуйтесь калькулятором, если требуется перемножить икс равен 4.75, то есть (5+4.75)∗(6-4.75)∗(4.75+2). Для вычисления этого значения перейдите на сайт поисковика Google или Nigma и введите выражение в поле запроса в его исходном виде (5+4.75)*(6-4.75)*(4.75+2). Google покажет 82.265625 сразу, без нажатия кнопки, а Nigma нуждается в отправке данных на сервер нажатием кнопки.

На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.

Тема: Решение уравнений

Урок: Раскрытие скобок

Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.

Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.

Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим примеры.

Пример 1.

Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.

Пример 2.

Пример 3.

Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:

Замечание.

Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».

Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.

Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345.

Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.

Иллюстрирующий пример и правило.

Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.

С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.

Сформулируем правило:

Пример 1.

Пример 2.

Правило не изменяется, если в скобках не два, а три или более слагаемых.

Пример 3.

Замечание. Знаки меняются на противоположные только перед слагаемыми.

Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.

Сначала умножим первую скобку на 2, а вторую — на 3.

Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные

Список литературы

1. Виленкин Н. Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

1. Онлайн тесты по математике ().
2. Можно скачать указанные в п. 1.2. книги ().

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
2. Домашнее задание: № 1254, № 1255, № 1256 (б,г)
3. Другие задания: № 1258(в), № 1248

В данной статье мы подробно рассмотрим основные правила такой важной темы курса математики, как раскрытие скобок. Знать правила раскрытия скобок нужно для того, чтобы верно решать уравнения, в которых они используются.

Как правильно раскрывать скобки при сложении

Раскрываем скобки, перед которыми стоит знак « + »

Эта самый простой случай, ибо если перед скобками стоит знак сложения, при раскрытии скобок знаки внутри них не меняются. Пример:

(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.

Как раскрыть скобки, перед которыми стоит знак « — »

В данном случае нужно переписать все слагаемые без скобок, но при этом сменить все знаки внутри них на противоположные. Знаки меняются только у слагаемых из тех скобок, перед которыми стоял знак « — ». Пример:

(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.

Как раскрыть скобки при умножении

Перед скобками стоит число-множитель

В данном случае нужно умножить каждое слагаемое на множитель и раскрыть скобки, не меняя знаков. Если множитель имеет знак « — », то при перемножении знаки слагаемых меняются на противоположные. 2) * 12 = 1728.

Как раскрыть 3 скобки

Бывают уравнения, в которых перемножаются сразу 3 скобки. В таком случае нужно сначала перемножить между собой слагаемые первых двух скобок, и затем сумму этого перемножения умножить на слагаемые третьей скобки. Пример:

(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.

Данные правила раскрытия скобок одинаково распространяются для решения как линейных, так и тригонометрических уравнений.

Выражения со скобками

Главная / i / t

• Приоритет операций
• Раскрытие скобок
• Вынесение общего множителя за скобку

Приоритет операций

Какое значение имеет следующее выражение?

3+2∙4

Как считать? Сложить 3 и 2, получив 5, а потом умножить 5 на 4, тогда получится 20? Или сначала умножить, получив 8, затем прибавить 3 и получить 11?

Конечно же, больший приоритет имеет умножение и деление, и только потом сложение и вычитание. Поэтому вышеописанное выражение имеет значение 11:

3+2∙4=3+8=11

То же касается и деления – приоритет деления выше приоритетов сложения и вычитания:

3+4∶2=3+2=5

3−4∶2=3−2=1

В том случае, когда нам нужно все-таки сначала сложить два числа, а потом умножить полученный результат, то применяются скобки – они имеют наибольший приоритет:

(3+2)∙4=5∙4=20

Раскрытие скобок

Очень часто приходится выражение со скобками заменять равносильным ему без скобок. Попробуем избавиться от скобок в таком выражении, не складывая 3 и 5:

2∙(3+5)

Что значит умножить число 3+5 на 2? Это значит: увеличить его в два раза. Но обязательно ли для того, чтоб удвоить 3+5, предварительно складывать эти числа? Можно удвоить сначала 3, потом 5 и сложить результат:

2∙(3+5)=2∙3+2∙5

Следующий рисунок делает очевидным ответ на вопрос, почему два раза по восемь кругов равны двум разам по три и двум разам по пять кругов.

Проверим равносильность обоих выражений:

2∙(3+5)=2∙8=16

2∙3+2∙5=6+10=16

Как видно, оба выражения имеют значение 16 – значит, они равносильны и между ними можно поставить знак равно:

2∙(3+5)=2∙3+2∙5

Возьмем, к примеру, такое выражение:

2∙(x+5)

Здесь вместо удобного числа 3 оказалась переменная x, и сколько будет x+5 посчитать уже не удастся. Число x – это самое обычное число, просто оно не известно, и к нему можно применить тот же самый метод: домножить каждое слагаемое в скобке на 2:

2∙(x+5)=2∙x+2∙5

Знак равенства между этими выражениями означает, что первое выражение со скобками абсолютно равносильно второму, в котором нет скобок. Значит, можно вместо x подставить совершенно любое число в оба выражения и получить одно и то же значение. Например, подставим вместо x число 7 в выражение со скобками:

2∙(7+5)=2∙12=24

Получилось 24, а теперь подставим вместо x число 7 в выражение без скобок:

2∙7+2∙5=14+10=24

Попробуйте подставить любое другое число вместо x и оба выражения дадут совершенно одинаковый результат.

Умножая каждое число в скобках на число за скобками, следует учитывать какой знак стоит перед этими числами – «плюс» или «минус». Если перед числом нет ни плюса, ни минуса, значит, там стоит плюс, просто его не пишут. В следующем примере перед числом 8 и числом 11 нет знака (значит, считаем, что перед ними стоит плюс), а плюс на плюс – дает плюс, значит, и перед 8∙11 будет плюс, который там тоже не написан, но подразумевается. А вот перед числом 3 – знак «минус», а минус на плюс – дает минус, следовательно, перед 3∙11 будет стоять минус:

(8−3)∙11=8∙11−3∙11

(41−37)∙23=23∙41−23∙37

Слагаемых внутри скобок может быть сколько угодно, но суть метода от этого не меняется, чтобы раскрыть следующую скобку, нужно таким же образом умножить каждое число в скобках на 2:

2∙(1+2+3+4)= 2∙1+2∙2+2∙3+2∙4

И еще пример с минусами:

4∙(14−3+19—4+1−2)=

=4∙14−4∙3+4∙19−4∙4 +4∙1−4∙2

Вынесение общего множителя за скобку

Необходимо уметь еще и производить обратную операцию – заменять выражение без скобок равносильным со скобками. Например, возьмем число 14 в таком виде:

6+8

Если уменьшить это число в два раза, разделив каждое слагаемое на два, а затем умножить его на два, но уже не по отдельности, а все число сразу, то число 14 не изменится, а скобка появится:

Для упрощения каждую дробь можно заменить равным ему числом:

6+8=2∙(3+4)

Такое действие называется вынесением общего множителя за скобку.

Аналогичным образом выносят общий множитель за скобку при наличии минусов и большого количества слагаемых: делят все числа на число, которое будет общим множителем, и после умножают на него же:

Легко проверить, что по обе стороны от знака равно одно и то же число 3:

18−12−3=3∙(6−4−1)=3

Умножение скобки на скобку

Бывает и так, что скобка умножается на скобку:

(8+3)∙(5+2)

Чтобы раскрыть эти скобки, не складывая числа внутри, надо этот случай свести к предыдущему (как и везде в математике). Число в первой скобке – это просто число и ничего больше, значит, как и в предыдущем случае можно просто домножить на первую скобку каждое из чисел во второй скобке:

(8+3)∙(5+2)=(8+3)∙5+(8+3)∙2

И затем раскрыть каждую из скобок:

(8+3)∙5+(8+3)∙2= 8∙5+3∙5+8∙2+3∙2

Значит, оба выражения должны быть равными:

(8+3)∙(5+2)= 8∙5+3∙5+8∙2+3∙2

Значение выражения со скобками равно 77:

(8+3)∙(5+2)=11∙7=77

И значение выражения без скобок равно 77:

8∙5+3∙5+8∙2+3∙2= 40+15+16+6=77

Попробуем повторить то же самое с переменными:

(a+b)∙(x+y)=

=(a+b)∙x+(a+b)∙y=

=a∙x+b∙x+a∙y+b∙y

Но чисел может оказаться и гораздо больше:

(a+b+c)∙(x+y)=

=(a+b+c)∙x+(a+b+c)∙y

=a∙x+b∙x+c∙x+a∙y+b∙y+c∙y

Уже прослеживается некая закономерность: каждое число из первой скобки умножается на каждое из второй. И теперь нет нужды в промежуточном действии со скобками: нужно просто взять первое число в первой скобке и по порядку умножать его на каждое из второй, затем взять второе число из первой скобки и умножать его на каждое из второй: и так до тех пор, пока не дойдем до умножения последнего числа из первой скобки на последнее число из второй:

Попробуем новое правило в действии:

(3+7)∙(11+22)

И дальше

=3∙11+3∙22+7∙11+7∙22=

=33+66+77+154=330

И действительно, первая скобка, равная числу 10, при умножении на вторую скобку, равную числу 33 будет давать 10∙33=330.

Разумеется, следует понимать, что если в скобке перед b стоит минус, а перед y – плюс, то при умножении b на y перед b∙y будет минус, потому как плюс на минус дает минус. А если перед b и z — минусы, то когда b и z умножатся, перед b∙z будет плюс, так как минус на минус дает плюс:

(a−b)∙(x+y−z)=

=a∙x+a∙y−a∙z−b∙x−b∙y+b∙z

Подставим какие-нибудь числа и проверим:

(17−7)∙(18+3−1)=

=17∙18+17∙3−17∙1−7∙18−7∙3 +7∙1=

=306+51−17−126−21+7=200

Как видно, все сходится.

Дроби – такие же числа, и скобки с ними будут раскрываться, подчиняясь аналогичным правилам:

О том, как умножаются и складываются дроби, можно узнать тут, а пока продолжим:

Проверить эти вычисления можно, сложив дроби в скобках, после чего умножить:

Второй способ проще, но нам надо было научиться раскрывать скобки, потому как далеко не всегда будет возможность сложить числа внутри скобок.

Что такое умножение?

Что такое умножение? январь 2011 г. После трех моих статей о природе умножения в 2008 г. (Июнь, Июль Август, Сентябрь), Я пообещал себе оставить эту тему в покое на несколько лет. Фактически, Я вообще никогда не собирался писать эту серию. Первый был ответом на неожиданно широкую реакцию, которую я получил на то, что я считал довольно безобидным, одноразовым комментарием, который я сделал в конце предыдущей колонки. В той первоначальной публикации я отметил, что не стоит говорить студентам, что «умножение — это многократное сложение». Оказалось, что многие учителя думали, что это именно так, поэтому я был вынужден опубликовать то, что в итоге превратилось в три колонки, каждая из которых длиннее и глубже, чем предыдущая, объясняя, почему мем «умножение — это повторное сложение» ( MIRA) не только неправильна, но и опасна для распространения с точки зрения образования. Опасность была продемонстрирована в драматической форме большим объемом полученной мной корреспонденции и множеством последовавших за этим публичных тем в блогах, которые показали, что очень многие граждане горячо верят в MIRA.

Почему я говорю об опасности? «В конце концов, — говорили некоторые корреспонденты, — даже если MIRA ошибается, не все ли равно, верят ли люди в нее? Пока они умеют правильно пользоваться калькулятором и получать правильный ответ, ложная вера не причиняет вреда». Мой ответ на это двоякий. Во-первых, как у педагога у меня этическая позиция. Те из нас, кто преподает математику на любом уровне, просто не должны заниматься распространением лжи. Конечно, иногда мы говорим «не всю правду», чтобы предоставить нашим студентам управляемый путь к овладению тем, что может быть трудным понятием. Но когда мы делаем это, мы обязаны (1) не говорить вопиющей лжи и (2) оставлять открытой дверь для дальнейшего уточнения, расширения или других модификаций, когда ученик будет продвигаться дальше. Проблема с историей MIRA заключается в том, что, как показывают исследования, многие студенты остаются с твердым, но ложным убеждением, что умножение на самом деле является повторяющимся сложением. Зная это, мы должны перестать рассказывать эту конкретную историю.

Вторая часть моего ответа заключается в том, что в современном мире мы сталкиваемся с огромным количеством решений, которые зависят от понимания количества. Некоторые из них по своей природе аддитивны, некоторые мультипликативны, а некоторые экспоненциальны. Поведение этих трех разных видов арифметических операций резко различается, и, скажем, аддитивное мышление, когда задача является мультипликативной (или, что еще хуже, экспоненциальной), может привести к некоторым неверным решениям, которые во многих случаях действительно опасны. Приведу всего два примера: плохое численное представление о риске может привести к ненужным расходам на безопасность авиакомпаний, как я указал в колонке за последний месяц, а отсутствие понимания экспоненциального роста может ослепить умных людей от катастрофических опасностей глобального потепления. . (Здесь я подчеркиваю математическую мысль; здесь задействовано много других факторов.) Это факт жизни, что многие люди проживут жизнь, не умея заниматься математикой. Когда им понадобятся услуги математически способного человека, они наверняка найдут кого-нибудь. Но в мире, построенном не только на словах и языке, но и на числах и арифметике, наши ученики достигают совершеннолетия без понимания четырех основных арифметических операций , ради всего святого, мне кажется, что это ситуация, с которой тем из нас, кто занимается математическим образованием, не следует мириться.

Хотя первоначальный фурор, вызванный моими первоначальными публикациями, кажется, улегся, я все еще получаю электронные письма от учителей и родителей типа «Хорошо, я понимаю, что вы говорите, но не могли бы вы тогда точно сказать мне, что такое умножение?» и от учителей, которые просят меня подсказать, как им учить маленьких детей умножению. Эта колонка является ответом на эти запросы.

В общем и целом, мои ответы тем учителям, которые писали мне, исходили из той точки зрения, которую я избрал, когда писал первые три колонки. Я профессиональный математик, но не обученный учитель K-12. Мой опыт (и мои полномочия) связаны с математикой, а не с преподаванием. Как профессиональный математик, я могу (и считаю, что должен) давать советы по математике, которую преподают в школах, и конструктивно критиковать то, как ее преподают, но я не думаю, что мне уместно предлагать, как преподавать. Другие гораздо более опытны в этом, чем я. (Я думаю, что не случайно большинство профессоров математического образования — бывшие учителя. Трудно научить других делать то, чего не сделал сам.)

Обычно я отсылал своих корреспондентов к двум книгам, которые сам находил очень полезными для ознакомления с вопросами математического образования. Один Adding It Up: Helping Children Learn Mathematics, автором которой является Комитет по изучению обучения математике Национального исследовательского совета и опубликовано издательством National Academies Press в 2001 году. Другая книга — это превосходная книга Терезины Нуньес и Питера Брайанта, изданная в 1996 году. Дети занимаются математикой. Есть и другие книги, и множество опубликованных научных статей по этому вопросу. Например, в 1994, Гершон Харел и Джере Конфри отредактировали гигантский том (414 страниц) под названием «Развитие мультипликативного мышления в изучении математики», который содержит множество результатов исследований, идей и полезных советов. (Все три книги доступны на Google книги.)

Проблема с моим ответом в том, что у учителей редко есть время, чтобы продираться через том в несколько сотен страниц, написанный в первую очередь для профессоров. Я знал это, но это были лучшие источники, с которыми я был знаком.

Что я могу (и сделаю) здесь, так это попытаюсь объяснить свое собственное понимание умножения. В некоторых случаях я подозреваю, что именно об этом просили мои корреспонденты. Но в своих ответах я лишь сделал несколько расплывчатых замечаний о том, что «это гораздо больше основано на реальной концепции масштабирования, чем на сложении». Я не хотел идти дальше, потому что никто из нас на самом деле не знает, как мы сами изучаем или понимаем математику, не говоря уже о том, как это делают другие или могут найти в этом выгоду. Как профессиональный математик с многолетним стажем, мое понимание умножения может отличаться от понимания других, и, кроме того, некоторые его аспекты может быть трудно или невозможно передать ребенку, изучающему математику в первый раз. Никогда не преподавал на уровнях K-12, я бы не знал. Дело в том, что умножение и мультипликативные рассуждения сложны и многогранны. (Вот почему книга Харела-Конфри, которую я цитировал выше, занимает 414 страниц.)

Интересно, что сложности умножения почти никогда не возникают в повседневной деятельности профессионального математика. В самом деле, математик, который не задумывался о том, как этот предмет может — или должен — преподаваться на школьном уровне, может не знать об этих сложностях, хотя и сможет оценить их сразу же, как только на них укажут. (Это, безусловно, было моей ситуацией на протяжении большей части моей карьеры.) Для математика умножение — это абстрактная бинарная функция чисел (и других абстрактных объектов), поведение которой определяется аксиомами. Мы никогда не задаемся вопросом «Что это?» мы также не пытаемся определить его в терминах «более основных» функций. (Замечу попутно, что на уровне формальной, аксиоматической математики умножение просто нельзя определить как повторяющееся сложение, поскольку последнее не является четко определенной функцией, а представляет собой метасхему вне аксиоматических рамок.) Мы просто используем функцию так, как это определено аксиомами.

Моя концепция умножения

Концепция умножения, которую я использую, когда работаю в математике, является скорее операциональной, чем онтологической, и построена на аксиоматически определенной абстрактной бинарной функции, которая составляет одну из двух фундаментальных операций в поле (или, в более общем смысле, в кольце). Я знаю свойства умножения, как обязательные (например, ассоциативность), так и условные (например, коммутативность), как оно соотносится с другими функциями (например, дистрибутивность) и имеет ли конкретный пример обратную сторону. Мне удобно с этим справляться. Я не спрашиваю, что это такое; все, что имеет значение, это его свойства.

Я понимаю, что моя профессиональная концепция умножения абстрагирована от повседневного понятия умножения, которое я выучил в детстве и использую в своей повседневной жизни. Но мое абстрактное представление об умножении упускает из виду многие сложности, которые являются частью моей гораздо более сложной ментальной концепции умножения как познавательного процесса. В этом вся суть абстракции. Хотя многие нематематики отступают от математического уровня абстракции, на самом деле это очень упрощает дело. Математика — это максимальное упрощение.

Например, математическая концепция умножения целых или действительных чисел коммутативна: M x N = N x M. (Это одна из аксиом.) Порядок чисел не имеет значения. Здесь нет никаких единиц измерения: M и N — это чистые числа. Но неабстрактная, реальная операция умножения совершенно определенно не является коммутативной, и единицы измерения представляют собой серьезную проблему. Три мешка с четырьмя яблоками — это не то же самое, что четыре мешка с тремя яблоками. И взять эластичную ленту длиной 7,5 дюймов и растянуть ее в 3,8 раза — это не то же самое, что взять резинку длиной 3,8 дюйма и растянуть ее в 7,5 раза.

На самом деле природа единиц является основным различием между сложением и умножением, а также одной из нескольких причин, почему не стоит предполагать, что умножение является повторным сложением, даже в одном случае, когда повторное сложение имеет смысл, а именно, когда вы имеете дело с мощностями коллекций. Кроме того, две добавляемые коллекции должны иметь одинаковые единицы . Вы можете добавить 3 яблока к 5 яблокам, чтобы получить 8 яблок, но вы не можете добавить 3 яблока к 5 апельсинам. Чтобы сложить, вам нужно изменить единицы измерения, чтобы сделать их одинаковыми, скажем, классифицируя их как фрукты, чтобы 3 фрукта плюс 5 фруктов равнялись 8 фруктам. Но для умножения два набора имеют совершенно разную природу и обязательно имеют разные единицы измерения . С умножением у вас есть множимое (записывается вторым), умноженное на множитель (записывается первым). Единицей для множителя должны быть наборы единиц для множимого. Например, если у вас есть 3 мешка, в каждом из которых по 5 яблок, то вы можете умножить их, чтобы получить

[3 ПАКЕТА] x [5 ЯБЛОК В ПАКЕТЕ] = 15 ЯБЛОКОВ

Обратите внимание, как единицы измерения сокращаются: МЕШКИ X ЯБЛОКИ/МЕШОК = 9 ЯБЛОК.0010 В этом примере есть возможность выполнения повторного сложения: вы заглядываете в каждый мешочек по очереди и складываете. В качестве альтернативы вы опорожняете 3 мешка и подсчитываете количество яблок. В любом случае вы определите, что яблок 15. Конечно, вы получите тот же ответ, если умножите. Дело в том, что целочисленное умножение дает тот же ответ, что и многократное сложение. Но один и тот же ответ не делает операции одинаковыми.

Заблуждение MIRA становится очень очевидным, когда вы рассматриваете мой второй пример, где я беру эластичную ленту длиной 7,5 дюймов и растягиваю ее в 3,8 раза. Окончательная длина ремешка составляет 28,5 дюймов. Но что такое единицы? Что идет после числа 3,8 в расчете

[3,8 — — -] x [7,5 ДЮЙМА] = 28,5 ДЮЙМА ?

Ответ — ничего. У него нет единиц. В этом случае 3,8 является безразмерным масштабным коэффициентом .

Между прочим, даже когда начальная длина полосы и коэффициент масштабирования являются положительными целыми числами, нет смысла рассматривать этот пример как пример многократного сложения. Если я возьму резинку длиной 7 дюймов и растяну ее в 3 раза, ее окончательная длина составит

[3] x [7 ДЮЙМОВ] = 21 ДЮЙМ

Но я не брал 3 копии 7-дюймового ремешка и не соединял их вместе (дополнение), а масштабировал (растягивал) 7-дюймовый ремешок в 3 раза.

А как насчет использования умножения для вычисления площади прямоугольника? Если прямоугольник равен пи дюймов на е дюймов (где е — основание натуральных логарифмов), то его площадь равна

[ пи дюймов] x [ е дюймов] = пи.э кв. дюймов.

или, в приблизительном числовом выражении, 3,14 дюйма x 2,72 дюйма = 8,54 кв. дюйма. Опять же, обратите внимание на единицы. (Обратите внимание, что повторное сложение в этом примере далеко не уйдет.)

Существуют и другие приложения умножения, в которых множитель и множимое имеют разные интерпретации предметной области, но, поскольку я не хочу писать колонку на 414 страниц, я оставлю это в надежде, что вы поймете мою точку зрения.

Итак, какова моя ментальная концепция умножения? Это целостная смесь всего вышеперечисленного и нескольких вариантов, которые я не перечислил. Вот почему я говорю, что умножение сложно и многогранно. Доминирующий ментальный образ, который у меня есть, совершенно определенно является непрерывным масштабированием, и я вижу все остальные с точки зрения этого. Это означает, что моя концепция масштабирования в этом контексте является очень общей и охватывает такие примеры, как мои мешки с яблоками. Я могу рассматривать вычисление «3 мешка, в каждом из которых 5 яблок, всего 15 яблок» как «масштабирование» мешка с 5 яблоками в 3 раза. По моему опыту, овладение концепцией умножения равносильно созданию этой умственной амальгамы — амальгамы. это моя концепция умножения.

Я не знаю, как и когда я усвоил эту ориентированную на масштабирование концепцию умножения, и не могу передать ее словами (если только я просто не перечислил все ее многочисленные грани), но она была у меня, сколько я себя помню, и она определенно является единым, целостным понятием. Для меня эта концепция — то же самое, что умножение на . Таким образом, это числовая операция, которая соответствует очень общей форме масштабирования. Меня этому научили, или я просто развил его со временем? Я не знаю. Есть ли у других математиков такая же концепция? Вероятно, хотя, как я отмечал ранее, онтологическая природа умножения редко возникает в профессиональной математической деятельности, поэтому, вероятно, очень немногие удосужились поразмыслить над этим вопросом.

С другой стороны, масштабирование — это естественное физическое понятие, и абстрагирование от физического масштабирования к числовой операции умножения не сложнее, чем абстрагирование от физического действия по объединению двух длин вместе для получения числовой операции сложения. Преимущество подхода к умножению на основе масштабирования состоит в том, что результирующая числовая операция работает во всех случаях, тогда как подход MIRA работает только для положительных целых чисел. (Конечно, вы можете рассказывать истории, чтобы распространить полученное понятие RA на рациональные числа, но оно надумано, и окончательный переход к действительным числам проблематичен. Подход с масштабированием приводит вас к действительным числам за один раз, где действительные числа отождествляются с длинами. строк.)

Итак, для всех тех, кто спрашивал меня, это то, что I понимают под умножением: несколько обобщенное понятие масштабирования , построенное непосредственно на физической интуиции. И хотя, как я постоянно подчеркиваю, у меня нет опыта преподавания элементарной математики, я не могу понять, почему умножение не преподается таким образом.

Возможно, одна из причин того, что некоторые из нас более успешны в математике, чем другие, заключается в том, что нам удается формировать хорошие мыслительные концепции на ранних этапах процесса обучения. (Я не решаюсь использовать фразу «правильные понятия», так как я не знаю, что существует единственное правильное понятие умножения, и прекрасно осознаю свои собственные трудности с формулировкой своих слов.)

---

Угол Девлина обновлен в начале каждого месяца. Найти больше столбцов здесь. Подпишитесь на Кита Девлина в Твиттере в @nprmathguy.

---

Математик Кит Девлин (email: [электронная почта защищена]) Исполнительный директор Отдела гуманитарных наук Институт перспективных исследований и технологий (H-STAR) в Стэнфордском университете и Математик в выпуске выходного дня NPR. Его последний книга для широкого круга читателей Незаконченная игра: Паскаль, Ферма и Письмо семнадцатого века, сотворившее мир Современный, изданный Basic Books.

---

Математическая определение и как найти

, написанный

Малкольм МакКинси

12 января 2023

Проверка по фактам

Paul Mazzola

Продукт Математика. к задаче на умножение. Результатом умножения двух чисел является произведение.

Части задачи на умножение

При умножении каждая часть задачи имеет имя. В предложении умножения у вас есть множимое, множитель и произведение.

Вот пример предложения умножения:

Вы можете прочитать это предложение как произведение множимого, умноженное на множитель. Множимое — это первое число, × или * означает, что умножить на , множитель — это второе число, = означает, что равно , а ответ — произведение.

Части задачи на умножение

Все арифметические операции имеют названия частей уравнения. В делении у нас есть делимое, делитель и частное.

Найдите произведение в этих предложениях по умножению, чтобы убедиться, что у вас есть идея:

1. 12 × 12 = 144

2. 2 x * 9 = 18 x

3. 2(10+5) = 30

4. 17 = 2 * 8,5

Продукты в предложениях умножения были 144 , 18 x , 30 и 17 . Обратите внимание, что в последнем предложении произведение стоит перед множимым и множителем. Это совершенно нормально.

Обратите внимание, что в 2(10+5) мы вообще исключили символ умножить на , подразумевая умножение на круглые скобки.

Как найти произведение

Чтобы найти произведение, нужно решить задачу на умножение. Вы можете решать задачи на умножение с помощью повторного или быстрого сложения.

Возможно, старшеклассник подрабатывает, укладывая яблоки Gala в картонные лотки, чтобы наполнить коробки с фруктами. Лотки имеют четыре ряда по 9 штук.0013 шесть углублений для яблок.

Сколько яблок на подносе?

Вы можете сложить 6 + 6 + 6 + 6 и получить сумму 24 Гала яблок. Сумма – это ответ на задачу на сложение. Но с помощью умножения вы можете сказать, что у нас есть 6 гала-яблок в одном ряду, и мы возьмем один ряд четыре раза по :

Произведение 6 яблок, умноженное на 4 рядов, равно 24 гала-яблок.

Вы можете использовать калькулятор или таблицу умножения для умножения больших чисел или чисел, которые вы не можете быстро сделать в уме.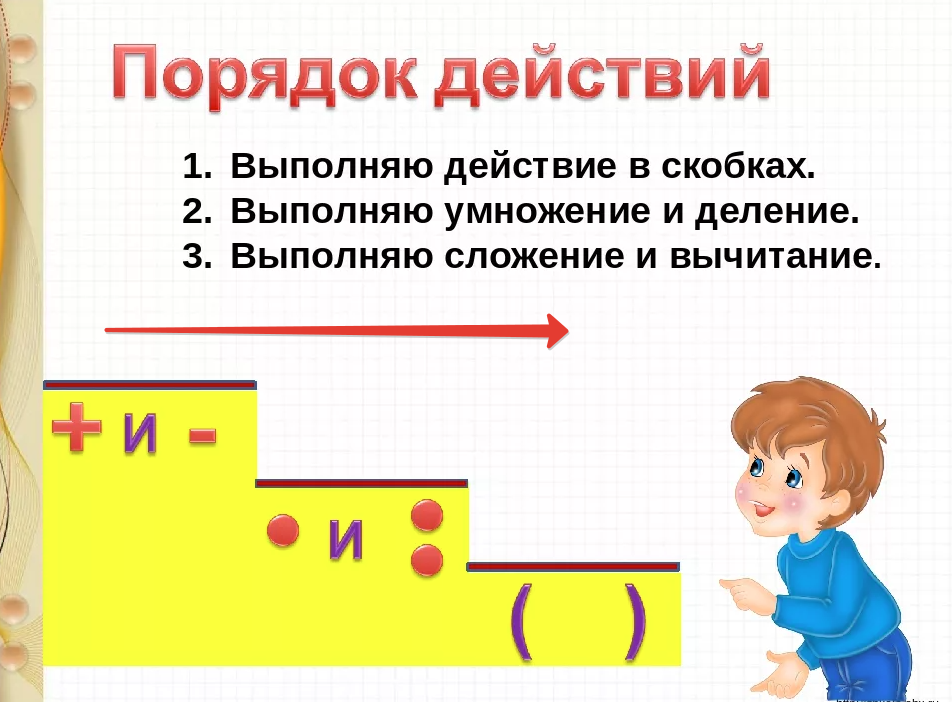

Аналогично работает и с отрицательными числами. Предположим, вы очищаете попытку и что бы узнать, сколько яблок вы убрали из четырех рядов.

Это будет означать 4 строк, умноженное на −6 , потому что вы видите, что в каждой строке есть шесть углублений для яблок. Знак минус означает, что вы вычли шесть для каждой строки.

Ваш ответ: −24 . Вы убрали 24 яблок с подноса.

Когда вы умножаете отрицательное число на положительное число, вы всегда будете писать свое произведение как отрицательное число.

Properties of multiplication

Multiplication has four properties, presented here in alphabetical order because none outranks another:

1. Associative property

2. Commutative property

3. Distributive property

4. Identity property of multiplication

Четыре свойства умножения

Особые случаи произведений в математике

При работе с умножением появляются два особых произведения.