| Табличка на двери |
6/2(1+2) | Блог инженера
Вот сижу что-то ночью опять… Решил написать своё мнение о популярном сейчас вопросе: один или девять?
Я думаю, по изображению сверху стало уже понятно, о чём идёт речь. Знак умножения – он опущен перед скобками, и… как считать?
Посмотрим с двух позиций.
1) Знак умножения просто опущен. Тогда изначальная запись выражения выглядит так: .
Шесть делим на два, умножаем на сумму единицы и двойки и (всё просто супер, детка) получаем девять. Ответ – 9. Вроде всё красиво, но…
2) Знак умножения не просто опущен. Как так – не просто? А просто так и нельзя опустить. Итак, вот есть инфа, которую, похоже, взяли из учебника за седьмой класс (изначальный источник не найден, но нагуглил в методичке какого-то математического лицея):
Случаи возможного пропуска знака умножения: 1) между буквенными множителями; 2) между числовым и буквенным множителем; 3) между множителем и скобкой; 4) между выражениями в скобках.
Что это для нас значит? А то, что если знак умножения опустили так, как описано в предыдущем пункте, то поступили неправильно, потому что двойка в примере – не множитель перед скобкой, а просто один из трёх множителей (если рассматривать деление как частный случай умножения). Поэтому, если он опущен правильно, то имеем.
И это в том случае, если правило выше абсолютно точное. Но без конкретного источника (утверждается, что это школьный учебник) можно не рассчитывать на то, что оно точное. В школьной математике много требований, которыми даже в разделах вышки порой пренебрегают.
Это правило, к тому же, может оказаться неполным: вдруг нельзя опускать знак между скобкой и множителем в такой ситуации? Составлял бы я правила, я бы так и поступил. Спорная ситуация? Ставь ещё одну пару скобок! Будет вполне однозначно и всем понятно.
От себя скажу, что я часть после деления воспринимаю как нечто целое, т.е. скобку с множителем, мне это кажется вполне естественным. Почему же возникает спор? Многие запоминают, что «всегда можно опустить знак умножения». Но это не так. 2 умножить на 3 не есть 23, а произведение переменных c, o и s не всегда будет правильно понято.
На первый взгляд становится понятно, что человек, сказавший, что ответ – 1, просто забыл о порядке действий, его смутило отсутствие знака умножения. Здесь это чем-то напоминает мне загадку о ножках в комнате (где вопрос о том, сколько ног у животных в комнате. Вскользь упоминается, что ещё стоит и кровать. Если человек забыл про ножки кровати, он лох, если посчитал их, то тоже лох, ибо это не ноги, а ножки. Если посчитал ноги животных, то тоже лох, ибо у них лапы. Короче, вне зависимости от ответа человек – лох и ставит жирафа на аватар). А так как его действия (которые сначала нам показались такими) неправильные, то наше образование – говно и всё такое. Но если копнуть глубже, то действительно встаёт вопрос – а сколько? Если в реальной жизни в важном месте встретить такое, то, независимо от правильного ответа, нужно серьёзно поговорить с человеком, который написал это выражение и не уточнил, что он имел в виду.
Да, помню в какой-то методичке по экономике (у нас слабо вёлся этот предмет, и методички слабые были) была буквенная формула с такой же проблемой. Знак деления, справа большое достаточно выражение. Я тогда засомневался, в итоге нашёл правильную формулу. Да, там после деления всё должно было быть знаменателем. Но там это было однозначно неверно. Люди, пишите не правильно, а понятно 🙂
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Правила при умножении (делении) чисел | |||||||||||||||
| |||||||||||||||
Почему нельзя делить на ноль?
«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.
Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.
Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.
Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число.
Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.
Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.
Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.
Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.
Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.
Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается.)
Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль.
Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.
Ответил: Александр Сергеев
Ученые назвали правильный ответ в спорном примере из школьного курса математики — Общество
МОСКВА, 1 августа. /Корр. ТАСС Олеся Кулинчик, Александра Рыжкова/. Правильный ответ в примере из школьной математики с делением и умножением, породившем споры в социальных сетях, — «16». Об этом ТАСС заявили известные российские математики.
Об этом ТАСС заявили известные российские математики.
28 июля один из пользователей опубликовал в Twitter пример из школьной программы по математике: «8:2(2+2)=?». Обсуждение примера вызвало широкий резонанс, и перешло на международный уровень, пользователи разных стран получали ответ «16» или «1».
Российский математик, доктор физико-математических наук, первый декан факультета математики Высшей школы экономики Сергей Ландо рассказал ТАСС, что правильный ответ в России будет 16. «На территории Российской Федерации деление и умножение имеют равные приоритеты. В США или Англии может быть другой порядок. В России сначала выполняется операция в скобках, потом деление на эту сумму, а потом результат умножается на следующий множитель. Правильный ответ — 16», — сказал он. Ландо добавил, что в подобных спорных случаях специалисты стараются обозначить порядок операций скобками.
Заведующий кафедры высшей математики Национального исследовательского университета «Московский институт электронной техники» (НИУ МИЭТ) Александр Прокофьев подтвердил ТАСС, что правильный ответ — 16, и объяснил, почему пример вызвал столько споров.
«Ошибаются, как я полагаю, преимущественно взрослые. У школьников вопросов быть не должно. Первой выполняется операция в скобках, затем, согласно приоритету арифметических действий, деление и умножение — они являются равноправными и выполняются слева направо. Студенты привыкают отделять косой чертой числитель от знаменателя, поэтому путаются в данном примере, полагая, что умножение двойки на скобку расположено в знаменателе», — сказал Прокофьев.
С ними согласилась и заведующая кафедры «Математика» Российского университета транспорта Людмила Кочнева. «Если бы стояла скобка после знака деление, то правильным ответом была бы единица. Если бы после восьмерки была горизонтальная черта — знак дробного деления — а внизу 2(2+2), это была бы единица. А раз все это в строчку, вы должны делать операции в том порядке, в котором они написаны. Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она.
Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она.
Математики решили пример, вызвавший споры в соцсетях – Москва 24, 02.08.2019
Фото: портал мэра и правительства Москвы
Известные математики раскрыли правильный ответ в примере с делением и умножением. Спорная задача вызвала дискуссии в соцсетях, передает ТАСС.
28 июля в Twitter опубликовали пример из школьной программы по математике: «8:2(2+2)=?». Поиски правильного ответа вышли на международный уровень: пользователи из разных стран называли два возможных варианта – «16» или «1».
Как пояснил доктор физико-математических наук, первый декан факультета математики ВШЭ Сергей Ландо, в России правильный ответ – «16», так как в нашей стране «деление и умножение имеют равные приоритеты». При этом, например, «в США или Англии может быть другой порядок», отметил математик.
По словам Ландо, «в России сначала выполняется операция в скобках, потом деление на эту сумму, а потом результат умножается на следующий множитель». В итоге получается «16», заключил ученый.
Почему школьный пример вызвал так много споров, рассказал завкафедрой высшей математики НИУ МИЭТ Александр Прокофьев. «Ошибаются, как я полагаю, преимущественно взрослые», – отметил он, добавив, что школьники, как правило, знают, что первой выполняется операция в скобках. Потом, уточнил математик, пример нужно решать «согласно приоритету арифметических действий», а так как деление и умножение равноправны, то и действия выполняют слева направо. «Студенты привыкают отделять косой чертой числитель от знаменателя, поэтому путаются в данном примере, полагая, что умножение двойки на скобку расположено в знаменателе», – пояснил Прокофьев.
Ранее сообщалось, что столичные школьники с успехом выступили на международных олимпиадах по биологии и математике. Математическая олимпиада проходила с 10 по 22 июля в Великобритании. В ней приняли участие команды школьников из 112 стран. Им предстояло показать свои знания по геометрии, алгебре и теории чисел. В итоге золотые медали получили Тимофей Ковалев и Олег Смирнов из школы-интерната имени Колмогорова. Обладателями серебряных наград стали Валерий Кулишов и Иван Гайдай-Турлов из школы № 57.
Математическая олимпиада проходила с 10 по 22 июля в Великобритании. В ней приняли участие команды школьников из 112 стран. Им предстояло показать свои знания по геометрии, алгебре и теории чисел. В итоге золотые медали получили Тимофей Ковалев и Олег Смирнов из школы-интерната имени Колмогорова. Обладателями серебряных наград стали Валерий Кулишов и Иван Гайдай-Турлов из школы № 57.
Читайте также
Математический пример разделил Твиттер на два лагеря из-за разных вариантов ответов. При этом оба правильные Статьи редакции
8÷2(2+2) — пример выглядит так, и он составлен неверно.
{«id»:109088,»url»:»https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»title»:»\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»services»:{«vkontakte»:{«url»:»https:\/\/vk.com\/share.php?url=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye&title=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»VK»,»title»:»\u0412\u041a\u043e\u043d\u0442\u0430\u043a\u0442\u0435″,»width»:600,»height»:450},»facebook»:{«url»:»https:\/\/www.facebook.com\/sharer\/sharer.php?u=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»FB»,»title»:»Facebook»,»width»:600,»height»:450},»twitter»:{«url»:»https:\/\/twitter.com\/intent\/tweet?url=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye&text=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»TW»,»title»:»Twitter»,»width»:600,»height»:450},»telegram»:{«url»:»tg:\/\/msg_url?url=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye&text=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432.
\u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»VK»,»title»:»\u0412\u041a\u043e\u043d\u0442\u0430\u043a\u0442\u0435″,»width»:600,»height»:450},»facebook»:{«url»:»https:\/\/www.facebook.com\/sharer\/sharer.php?u=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»FB»,»title»:»Facebook»,»width»:600,»height»:450},»twitter»:{«url»:»https:\/\/twitter.com\/intent\/tweet?url=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye&text=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»TW»,»title»:»Twitter»,»width»:600,»height»:450},»telegram»:{«url»:»tg:\/\/msg_url?url=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye&text=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»TG»,»title»:»Telegram»,»width»:600,»height»:450},»odnoklassniki»:{«url»:»http:\/\/connect.ok.ru\/dk?st.cmd=WidgetSharePreview&service=odnoklassniki&st.shareUrl=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»OK»,»title»:»\u041e\u0434\u043d\u043e\u043a\u043b\u0430\u0441\u0441\u043d\u0438\u043a\u0438″,»width»:600,»height»:450},»email»:{«url»:»mailto:?subject=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435&body=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»Email»,»title»:»\u041e\u0442\u043f\u0440\u0430\u0432\u0438\u0442\u044c \u043d\u0430 \u043f\u043e\u0447\u0442\u0443″,»width»:600,»height»:450}},»isFavorited»:false}
\u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435″,»short_name»:»TG»,»title»:»Telegram»,»width»:600,»height»:450},»odnoklassniki»:{«url»:»http:\/\/connect.ok.ru\/dk?st.cmd=WidgetSharePreview&service=odnoklassniki&st.shareUrl=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»OK»,»title»:»\u041e\u0434\u043d\u043e\u043a\u043b\u0430\u0441\u0441\u043d\u0438\u043a\u0438″,»width»:600,»height»:450},»email»:{«url»:»mailto:?subject=\u041c\u0430\u0442\u0435\u043c\u0430\u0442\u0438\u0447\u0435\u0441\u043a\u0438\u0439 \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0430\u0437\u0434\u0435\u043b\u0438\u043b \u0422\u0432\u0438\u0442\u0442\u0435\u0440 \u043d\u0430 \u0434\u0432\u0430 \u043b\u0430\u0433\u0435\u0440\u044f \u0438\u0437-\u0437\u0430 \u0440\u0430\u0437\u043d\u044b\u0445 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u043e\u0432 \u043e\u0442\u0432\u0435\u0442\u043e\u0432. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u0431\u0430 \u043f\u0440\u0430\u0432\u0438\u043b\u044c\u043d\u044b\u0435&body=https:\/\/tjournal.ru\/internet\/109088-matematicheskiy-primer-razdelil-tvitter-na-dva-lagerya-iz-za-raznyh-variantov-otvetov-pri-etom-oba-pravilnye»,»short_name»:»Email»,»title»:»\u041e\u0442\u043f\u0440\u0430\u0432\u0438\u0442\u044c \u043d\u0430 \u043f\u043e\u0447\u0442\u0443″,»width»:600,»height»:450}},»isFavorited»:false}
55 648 просмотров
В Твиттере набрал популярность математический пример, который рассорил пользователей соцсети, получавших разные ответы. Однако оказалось, что правы и первые, и вторые, а проблема заключается в неправильной нотации примера.
Подписчики, посчитайте
В реплаях подписчики разделились на два лагеря — у одних получилось 16, а у других — 1. Первые сразу же принялись издеваться над вторыми и посоветовали подтянуть математику, а другие отвечали тем же. Даже калькуляторы показывали разные ответы.
Всё, кроме 1, абсолютно неверно
ВЫ МЕНЯ ДОСТАЛИ
Подождите…
i do parenthesis, multiplication, then division so i believe it’s 1
103
5830
Сначала я подсчитала в скобках, потом умножила, потом разделила, так что у меня получился 1
Получится 16, боже, реплаи просто стыдно читать…
Ответ — 1. Всем, кто говорит 16, надо пересдать математику
Очевидно, что ответ — 1
@pjmdolI it’s 16 and if you say otherwise start packing your clown shoes 🤡3
233
Получится 16, если вы говорите что-то иное, то начинайте распаковывать свои клоунские ботинки
Ответ — 100
Некоторые из вас провалили математику, и это заметно
Никогда не видел кого-то, насколько уверенного в неправильном ответе
Никогда не видел кого-то, настолько уверенного в том, что он называет правильный ответ неправильным
Некоторые даже начали приводить свои научные степени и количество изученных курсов в качестве доказательства того, что их ответ — единственно верный.
У меня две степени по математике, ответ — 1
Я прошла 3 курса по вычислениям, дифференциальным уравнениям и линейной алгебре, получается 16, бро
Расхождение в ответах получилось из-за того, что одни пользователи сначала умножали, а другие, наоборот, делили.
В итоге пользователи Твиттера решили, что у всех получаются разные ответы в зависимости о того, какой порядок вычислений они выучили в школе. Те, кто сначала умножал, использовали метод PEMDAS со следующим порядком вычислений: сначала раскрыть скобки, а потом умножать, делить, складывать и вычитать. Те, кто сначала делил, а потом умножал, использовал BODMAS — в нём умножение и деление имеют одинаковый приоритет, а вычисления производится слева направо.
Если посчитать по PEMDAS, то ответ — 1. Если по BODMAS, то — 16
@pjmdolI In PEMDAS multiplication and division take equal priority so you do whichever is first from left to right. Same for addition and subtraction. https://t.co/1617gChUms2
142
При PEMDAS умножение и деление имеют одинаковый приоритет, нужно посчитать то, что идёт первым слева направо. То же касается сложения и вычитания
Поскольку одна часть мира использует PEMDAS, а другая BODMAS, алгебра может иногда стать запутанной
Однако на самом деле проблема заключается в нотации — авторы примера забыли расставить скобки, поэтому правильных ответов получилось два.
И 1, и 16 — правильные ответы, потому что нотация уравнения неверна. Можете теперь наконец нахрен заткнуться?
@korchasa Вот именно, что это не вопрос приоритетов. Это вопрос нотации. Типа я пишу a/b(x + y) — это дробь a/b умножается на (x + y). Если я хочу всю правую часть в знаменатель, то a/(b(x + y)8
Издатель «N+1» Андрей Коняев рассказал TJ, что скептически относится к подходам к порядку вычислений: «Люди — ленивые жопы. Их ломает расставлять скобки. Поэтому придумываются все эти подходы к порядку вычислений, которые, конечно, никому нах** не нужны и только всех запутывают. А потом эти порядки начинают принимать как математическую данность, хотя это просто интеллектуальный костыль».
Он также отметил, что в задачке не поставили знак умножения, что «тоже не добавило осмысленности». По словам Андрея, пример должен был выглядеть так — 8:(2*(2 + 2)). В этом случае правильный ответ равняется 1. А в этом — (8:2)*(2 + 2) — 16.
Арифметика— можете ли вы опровергнуть это правило PEDMSA? — (деление перед умножением, вычитание перед сложением)
Чтобы расширить ответ Losethegame
Losethegame ответил: «Я попал сюда, погуглил тот же вопрос, хотя я не уверен, что (м) кто-либо из комментаторов ответил на него конкретно. Я думаю, вы правы в том, что ваше правило не может быть нарушено. Это, вероятно, может быть доказано алгебраически, потому что a * (b / c) = (a / c) * b и a + (bc) = (ac) + b …? »
Я думаю, вы правы в том, что ваше правило не может быть нарушено. Это, вероятно, может быть доказано алгебраически, потому что a * (b / c) = (a / c) * b и a + (bc) = (ac) + b …? »
Я согласен с тем, что это, вероятно, может быть доказано алгебраически с помощью методов, подобных тому, о котором упоминает losethegame (хотя пример losethegame может быть ошибочным, поскольку, как указывает user21280, losethegame меняет местами операнды).Но, развивая идею алгебраического доказательства (и без перестановки операндов!), Я могу придумать некоторую алгебру, которая могла бы это доказать. (Aand предоставил user21280 считает, что мои примеры не учитывают все возможности. Его ответ с использованием логических формул мог бы).
Дано уравнение, в котором умножение идет текстуально перед делением, например 3 * 4/2 неважно, что вы сделаете в первую очередь. Так что буквальные PEMDAS или PEDMAS подойдут. Принимая во внимание уравнение, в котором деление происходит в текстовом виде до умножения e.грамм. 6/2 * 3 , тогда имеет значение, что вы сделаете в первую очередь. Традиционное прочтение PEMDAS или PEDMAS дает это правильно (потому что они говорят, что сначала делайте первый, и это разделение), буквальное PEDMSA дает это правильно. Буквальное прочтение PEMDAS ошибочно.
Вычитание и раздел этой собственности. Допустим, мы составили небольшое уравнение той части уравнения, в которой операторы конкурируют друг с другом. Если вычитание конкурирует с сложением и вычитание происходит первым (текстуально, в уравнении), оно должно быть выполнено первым.Если деление соперничает с умножением, и деление идет первым, деление должно быть выполнено первым. В то время как если бы сложение конкурировало с вычитанием, то независимо от того, происходит ли оно первым в тексте, не имеет значения, выполняется ли сначала сложение или вычитание. Точно так же, если умножение конкурирует с делением, если умножение происходит сначала в текстовом виде, тогда не имеет значения, выполняется ли сначала деление или сначала выполняется умножение. Таким образом, литерал PEDMSA всегда работает (т.е.е. строго деление перед умножением, вычитание перед сложением). Как и традиционное / правильное чтение PEMDAS / PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют равный приоритет и сначала выполняют первое, аналогично сложению и вычитанию.
Таким образом, литерал PEDMSA всегда работает (т.е.е. строго деление перед умножением, вычитание перед сложением). Как и традиционное / правильное чтение PEMDAS / PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют равный приоритет и сначала выполняют первое, аналогично сложению и вычитанию.
Так, например,
Принимая 1 * 2/3 , поэтому a * b / c
Следуя PEDMSA буквально дает 1 * (2/3) , поэтому a (b / c) После PEDMSA традиционно получается (1 * 2) / 3 , поэтому (ab) / c
И мы знаем алгебраически, что a (b / c) = (ab) / c
1 * 2/3 а * б / с
знак равно
1 * 2/3 ab / c
Принимая 1/2 * 3 , поэтому a / b * c Это оценивается одинаково независимо от того, следует ли строго упорядоченному PEDMSA или традиционному PEMDAS i.е. Независимо от того, делаете ли вы сначала деление, как правило, или первое из умножения и деления, это (a / b) * c в обоих случаях, так что очевидно одно и то же.
1/2 * 3 (а / б) * в
знак равно
1/2 * 3 (а / б) * в
С 1 + 2-3 , если мы сделаем a + b-c , который заказан PEDMSA, то есть a + (b-c) , это будет тот же результат, что и при использовании традиционного PEMDAS (a + b) -c. Мы знаем алгебраически a + (b-c) = a + b-c = (a + b) -c
Я вспоминаю, как мой учитель математики указывал на одну вещь, о которой вы хотите остерегаться / знать, — это - (a + b) , который мы просверлили в was -a-b, сильно отличается от -a + b .Вычитания всегда должны выполняться в первую очередь и по порядку … и если сначала выполняется вычитание или сначала первое из сложения и вычитания, то мы поддерживаем это правило.
1 + 2-3 а + (б-в)
знак равно
1 + 2-3 (а + б) -с
И для этого то же самое. алгебраически
алгебраически
1-2 + 3 (1-2) +3 (а-б) + в
знак равно
1-2 + 3 (1-2) +3 (а-б) + в
И я полагаю, наконец. 1-2-3 и 1/2/3 И независимо от того, выполняются ли строго заказанные PEDMSA или традиционные PEMDAS, это (1-2) -c и (1/2) / 3 так же там.
Я не уверен, все ли это возможности.
Это может оставить вопрос о том, что объясняет алгебру, например правило, что
a * (b / c) = (ab) / c
а также
а + (b-c) = (a + b) -c
Также это соглашение о синтаксическом анализе, которое, кажется, разработано в конце 20-го века, а не фундаментальное правило математики. https://www.quora.com/Is-the-order-of-operations-unclear-for-expressions-like-20-2-5+5
Неявное умножение? — Доктора математики
Я хочу завершить эту серию темой, которая постоянно возникает как в классах, так и в социальных сетях: как вы оцениваете такие выражения, как \ (a \ div bc \) или \ (8 \ div 4 (3-1) \ ), где умножение указано без конкретного символа? Есть несколько причин, по которым можно интерпретировать это иначе, чем рассмотренное нами правило, согласно которому умножение и деление выполняются слева направо.Сначала мы рассмотрим это с точки зрения учащихся и учителей, а затем (в следующий раз) исследуем некоторые исторические вопросы, чтобы завершить серию.
Два способа оценить ax ÷ по
Давайте сначала рассмотрим один из предыдущих вопросов, которые мы задавали по этой проблеме в 1999 году, чтобы подготовить почву:
Порядок действий Проблема была представлена так: а = 1,56 b = 1,2 х = 7,2 у = 0,2 ax / by =? Я решил эту проблему двумя способами: 1) Я сначала переписал задачу как [1.56 (7,2) / 1,2] (0,2). Во-вторых, a было умножено на x. Продукт был 11,232. Затем, поскольку скобок не было, я следил за порядком операций и разделил 11,232 на b, что составило 1,2. Частное было 9,36.Затем я умножил 9,36 на y, что составило 0,2. Окончательный ответ - 1,872. 2) По-другому, первое, что я сделал, это умножил a на x. Продукт, который был равен 11.232, был временно отложен. Затем b был умножен на y, что дало произведение 0,24. Теперь проблема была решена разделением 11.232 (или топор) на 0,24 (или на), чтобы получить окончательный ответ 46,8. Подскажите, пожалуйста, какой ответ правильный и почему?
(Обратите внимание, что в то время единственным способом ввести разделение в нашем электронном письме было использование косой черты \ (a / b \), которая, как я обычно предполагаю, представляет собой выражение, фактически записанное как \ (a \ div b \). Время от времени я буду вставлять обелус, ÷, где мы предприняли грубые попытки имитировать его.)
Первый способ следует за PEMDAS буквально, как обычно учат и как я представил его здесь, вычисляя слева направо как \ (a \ cdot x \ div b \ cdot y = ((a \ cdot x) \ div b ) \ cdot y \).
Второй видит это как \ (ax \ div by = (ax) \ div (by) \). Это не объясняется как следование какому-либо изучаемому правилу, а как выполнение того, что выглядит правильно, либо потому, что деление читается, как если бы это была дробная черта, либо просто потому, что « на » выглядит так, как будто оно принадлежит друг другу как единое целое. Мы увидим несколько причин, по которым студенты сделали это.
Хотя я проработал с Ask Dr. Math менее года, это был уже знакомый вопрос, на который я хотел подробно ответить ради архива:
Не только вы задаетесь этим вопросом.У нас было несколько других вопросов о выражениях, похожих на ваш, от сбитых с толку учителей и учеников, которые обнаружили, что разные книги или учителя дают разные ответы, и даже калькуляторы расходятся.
Обратите внимание, что не только студенты делают то, что считают правильным, но и некоторые учебники и калькуляторы используют второй метод.
Новое правило, или что выглядит правильным?
Я подробно остановился на двух методах, приняв версию PEMDAS за правильную (хотя у меня есть несколько дополнительных соображений по этому поводу):
Как написано, ваше выражение
топор / by
должно быть вычислено слева направо : умножить на x, разделить на b, умножить на y. Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение правильное.
Некоторые тексты содержат правило , как и во втором решении , что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме экспонент], включая «явное умножение» с использованием символа. . Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое.В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что намного хуже .
Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение правильное.
Некоторые тексты содержат правило , как и во втором решении , что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме экспонент], включая «явное умножение» с использованием символа. . Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое.В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что намного хуже . Мне кажется, что я придумал термин « подразумеваемое или неявное умножение », когда несколько месяцев назад отвечал на свой первый вопрос по этой теме, для обозначения умножения, обозначенного простым помещением двух чисел или переменных или выражений в скобках рядом с друг друга — « сопоставление », как другие называют это — например, \ (ab \), \ (2b \) или \ (a (b + c) \), в отличие от явного написания \ (a \ times b \ ) или \ (a \ cdot b \).
Мы видели несколько вопросов от студентов, чьи учебники преподавали только обычный PEMDAS, но оценивали второй способ на примерах или решениях без комментариев. Это могло произойти из-за того, что ответы на обратной стороне были написаны кем-то, кроме автора, но это непростительное несоответствие.
Зачем автору вводить это дополнительное правило? В разное время у меня были разные мнения о том, является ли правило хорошей идеей, но я всегда признавал, что это не то, чему обычно учат:
Я не знаю общего правила среди математиков, согласно которому подразумеваемое умножение должно выполняться перед явным умножением.Насколько мне известно, все умножения умещаются в одном и том же месте в порядке операций. Это не безосновательное правило , однако, поскольку кажется, что подразумеваемое умножение связывает операнды вместе более плотно, , по крайней мере, визуально ; но идея порядка операций (или приоритета, как его называют в компьютерном мире) должна гарантировать, что все будут интерпретировать неоднозначное выражение одинаково - так что , если некоторые тексты изменяют правила, или если люди делать то, что кажется естественным, цель потеряна .
Правило, которое не является правилом, бесполезно, каким бы разумным оно ни было. Да, «новое правило» — это естественный способ чтения \ (ax \ div by \), потому что \ (by \) выглядит как единое целое; но пока все этому не научат, мы не можем ожидать, что нас поймут все читатели.
В частности, многие студенты предполагают, что он представляет собой горизонтальную версию \ (\ displaystyle \ frac {ax} {by} \):
Проблема в том, что выражение выглядит так, как будто оно должно быть
топор
----
от
В Dr.Часто задаваемые вопросы по математике относительно написания математики в электронной почте, одна из наших рекомендаций - использовать круглые скобки везде, где это возможно, чтобы избежать двусмысленности , даже если правила должны прояснять это, потому что в некоторых ситуациях их можно легко забыть.
Итак, в электронном письме мы бы написали это так:
ax / (by) или (ax / b) * y
в зависимости от того, что задумано. Используя круглые скобки, мы можем избежать написания того, что люди, которых учили другим правилам или которые игнорируют правила, которым их учили, могли бы воспринять иначе, чем мы.
Выпуски калькулятора
При исследовании другого «пациента» доктора математики я обнаружил, что некоторые калькуляторы экспериментировали с этим правилом. У калькуляторов несколько иные потребности, чем у математиков, поскольку они должны принимать ввод линейно, один символ за другим, поэтому они вынуждены принимать решение по этому поводу. На веб-сайте TI я узнал, что они намеренно добавили эту «функцию» в TI 82, а затем убрали ее из TI 83, вероятно потому, что они решили, что это не стандартное правило и может сбить с толку людей.
Ссылка там давно испортилась; но когда в 2008 году возник конкретный вопрос о калькуляторе, я процитировал то, что TI сказала в своей базе знаний:
Калькуляторы предполагаемого умножения и TI ... Решение 11773: предполагаемое умножение против явного умножения на графических калькуляторах TI.Имеют ли подразумеваемое умножение и явное умножение одинаковый приоритет на графических калькуляторах TI? Подразумеваемое умножение имеет более высокий приоритет, чем явное умножение , что позволяет пользователям вводить выражения таким же образом, как они были бы написаны.Например, TI-80, TI-81, TI-82 и TI-85 оценивают 1 / 2X как 1 / (2 * X), в то время как другие продукты могут оценивать то же выражение как 1/2 * X слева направо. верно. Без этой функции было бы необходимо сгруппировать 2X в круглых скобках, что обычно не делается при написании выражения на бумаге. Этот порядок приоритета был изменен для семейства TI-83, семейства TI-84 Plus, семейства TI-89, TI-92 Plus, Voyage ™ 200 и карманного компьютера TI-Nspire ™ в режиме TI-84 Plus. Подразумеваемое и явное умножение имеют одинаковый приоритет.
Это проясняет, что разработчики калькуляторов должны выбирать свои собственные правила, которые не должны совпадать с правилами написания на бумаге; но педагоги, кажется, убедили их сохранить как можно больше ради учеников.
В заключение (вернемся к ответу 1999 года):
Итак, чтобы ответить на ваш вопрос, я думаю, что оба ответа можно считать правильными - что, конечно же, означает, что сам вопрос неверен . Я предпочитаю стандартный способ (ваш первый ответ) при разговоре со студентами, , если только их собственный текст не дает правило «сначала неявное умножение»; но на практике, если бы я натолкнулся на это выражение, я бы, вероятно, сначала проверил, откуда оно взялось, чтобы понять, что было задумано.Главный урок, который нужно усвоить, заключается не в том, какому правилу следовать, а в том, как избежать двусмысленности в том, что вы пишете сами. Не доставляйте другим людям такие неприятности.
Впоследствии у нас появилось еще много вопросов по этому поводу; Я просто процитирую несколько уникальных моментов из некоторых из этих ответов.
Старомодная математика?
Вот типичный пример школьного конфликта 2000 года:
Порядок ведения спора Задача гласит: N ÷ ml, где n = 12, m = 6 и l = 3. Я считаю, что правильный ответ должен быть.6666, так как 12, разделенное на 18, равняется этому. Мой муж со мной согласен. Мой сын пришел домой из школы очень расстроенным, с запиской своего учителя, что ответ был неправильным. Она указала, что мне следовало разделить 6 (m) на 12 (n), прежде чем я разделил 3 (l) на уравнение. Ее ответ был 6. Мой сын очень расстроен мной; его учитель сказал ему, что я занимаюсь «старомодной математикой». Мне нужно вернуться в школу?
Задача \ (N \ div ml \), и родители производят умножение первыми.Я ответил частично:
Я могу сообщить вам хорошие и плохие новости. Во-первых, плохие новости: в соответствии с обычным порядком действий, которым теперь обучают, ваш ответ неверен. ...
Я объяснил стандартные правила и добавил:
НО ... Вы не одиноки в своем мнении. Эта часть правила - одновременное умножение и деление - вероятно, последнее правило, которое стабилизировалось; Я знаю, что, по крайней мере, в 20-е годы соглашения не было. Кажется, что соглашение было достигнуто, но сейчас оно распадается, как я слышу от многих студентов, чьи тексты отвечают на подобные вопросы так же, как и вы.Похоже, что они добавляют неустановленное правило, которое кажется вполне разумным в данном контексте , что подразумеваемое умножение (обозначенное простым помещением двух переменных или выражений вместе, как в "ml") должно быть выполнено первым. Конечно, выглядит как , как будто это должно означать это. Проблема в том, что, хотя я слышал, что это правило следует за часто, я почти никогда не слышал о том, что преподает , поэтому эти тексты не следуют своим собственным установленным правилам.
В следующий раз я расскажу подробнее об истории.
Поскольку этот тип выражения настолько неоднозначен, что люди не соглашаются с правилами, а правила легко игнорировать, мое собственное мнение таково, что ни ваш ответ, ни ответ учителя не верны: вопрос неверен .Ни один ответственный математик не стал бы писать такое выражение; мы бы просто сказали п --- м л так что не было бы никаких сомнений в его значении. В конце концов, цель правил - позволить нам ясно общаться, а не помочь нам обмануть учеников и начать ссоры между семьями.Так что вы на самом деле можете быть «старомодным»; или вы можете быть на передовой. В любом случае, боюсь, вам просто нужно будет узнать, как они это делают в классе, и следить за ними. Больше не о чем беспокоиться.
В последнее время драки, как правило, происходят в социальных сетях!
Неправильное применение распределительного свойства
Я закончу самым последним заархивированным обсуждением. Это вопрос от 2017 года:
Еще больше о порядке операций Мне любопытно узнать, каков ответ на это: 8/4 (3–1) Если строго следовать PEMDAS, ответ - 4: 8/4 (2) 2 * 2 4 Однако, если вы следуете распределительному свойству, вы получите 1: 8 / ((4 * 3) - (4 * 1)) 8 / (12 - 4) 8/8 1 Какой из них будет правильным и почему? Оба действительны, поэтому я не согласен с тем, какой ответ был бы правильным.Он должен быть правильным или неправильным, а не двумя разными ответами.
Я ответил собранием моих стандартных ответов на такого рода вопросы; даже мой первый заархивированный ответ на эту тему в 1999 году был в основном стандартным ответом, который я давал другим раньше. Здесь я просто рассмотрю несколько замечаний, которые не были полностью рассмотрены выше.
Я сначала резюмировал, что происходило:
Проблема не в конфликте между PEMDAS и дистрибутивом; это то, что строгая интерпретация PEMDAS конфликтует с естественным впечатлением о значении выражения, так что вы неосознанно применяете альтернативную интерпретацию, когда думаете, что просто применяете свойство распределения.
Если вы помните более ранние утверждения о том, что PEMDAS (а) соответствует свойствам операций и (б) соответствует визуальному впечатлению от нашей нотации, то некоторые тревожные звонки уже должны звучать!
Когда вы распределяли, вы ПРЕДПОЛАГАЛИ, что именно 4, а не 8/4 умножали (3 - 1).2 \ div 4b + c \):
На самом деле, есть несколько разных причин, по которым люди приводят (это очень популярный вопрос), некоторые из которых лучше других.Как утверждает ваш друг, правила, которым обычно учат, говорят нам делать все умножения и деления слева направо (в пределах любого их кластера) и не делать исключений, которые заставили бы сначала вычислить 4b. Многие из нас здесь согласятся с этим, и покончить с этим. Некоторые люди сначала оценили бы 4b из-за неправильного понимания PEMDAS, , думая, что это означает, что умножение должно выполняться до деления . Я думаю, вы знаете, что они ошибаются. Еще одна неправильная причина, применяемая к несколько иному типу выражения, - это неправильное понимание скобок : правило, согласно которому скобки «предшествуют» всему остальному, заставляет их поверить, что в выражении вроде 12/4 (4-1) умножение 4 (4-1) должно быть выполнено в первую очередь.Но правило круглых скобок на самом деле говорит только о том, что сначала нужно оценить то, что ВНУТРИ круглых скобок; результат обрабатывается как любое другое число. (Иногда я называю это представлением « залипающих скобок ».) Другой причиной, приведенной в отношении этого второго типа выражения, является идея о том, что распределительное свойство вынуждает вас сначала выполнить умножение, потому что они сначала вычисляют 4 (4-1) = 4 * 4-4 * 1 = 12, а затем делить; но здесь возникает вопрос, потому что единственная причина, по которой они взяли 4, а не 12/4, в качестве множителя слева, заключается в том, что они так им казались.И, конечно же, свойство распределения - это всего лишь способ, которым вы можете, если хотите, переписать выражение, чтобы получить то же значение; это вне вопроса о том, что само по себе означает выражение. В конечном счете, большинство людей, вероятно, делают это просто , потому что это кажется правильным : 4b выглядит ближе друг к другу, поэтому мы, естественно, хотим сделать это в первую очередь.Но они не могут указать ни одного правила, которое бы это оправдало; а поскольку математика - это доказательство, и то, что вы ЗНАЕТЕ, правильно, а не только то, что кажется правильным, это плохо.
Пример «круглых скобок» см. В
.Связана ли двойка с числами в скобках?Пример того, как знак деления виден как дробная черта (и долгое обсуждение того, что внешний вид не влияет на него), см. В
Порядок операций и дробейНазад к ответу 2017 года…
Избегание - лучшая политика
В книгах и рукописной математике, выходящей за рамки элементарного уровня, мы почти никогда не используем символ горизонтального деления, а вместо этого используем дробные черты, что не оставляет двусмысленности.В результате у математического сообщества никогда не было необходимости делать выбор в этой ситуации! По сути, его оставили неопределенным , и именно авторы учебников придумали явные «правила» для описания того, что на самом деле является языком, который развился органически, , основанный не на тщательно сформулированных правилах, а на молчаливом соглашении . Итак, какой «правильный» способ читать такое выражение, зависит от того, какие правила действуют в конкретном сообществе (математический класс, журнал и т. Д.) - и что было задумано автором.Я закончил с призывом к миру:
В результате в таких проблемах, как эта, ошибка в первую очередь совершается не теми, кто дает «неправильные» ответы, а теми, кто изначально публикует проблему (или передает ее). Любой, кто действительно хочет правильно выполнять математические вычисления, захочет четко рассказать об этом и будет избегать всего двусмысленного или неопределенного. Они должны быть либо полностью заключены в круглые скобки, либо использовать горизонтальную дробную полосу, чтобы упорядочить порядок: 6 6 -------- или --- (2 + 1) 2 (2 + 1) 2Споры в социальных сетях по этому поводу - пустая трата времени.
Но размышления о наших условностях могут быть очень полезными. В следующий раз я закрою все, взглянув на историю и приведу несколько веских причин считать «новое правило» правильным.
Неоднозначно PEMDAS
14.04.2014: ссылок
- Пример форума hpmuseum
- Пример физического форума: 48/2 (9 + 3)
- защитников Делите и умножайте ранжируйте поровну и идите слева направо. и есть другие мемноники, такие как «Ешьте, пожалуйста, вкусные яблочные штрудели мамы».
- В этом научном блоге упоминается статья
Тара Хэлле
что довольно хорошо уже говорит о том, что происходит (если бы я видел эту статью, написанную 12 марта 2013 г.,
Я бы не стал записывать это, потому что в этой статье очень четко говорится, что первоначальная оценка того, что нет
договоренность о порядке умножения или деления верна). Тем не менее, эта тема побудила меня сказать что-то новое
о порядке операций одного и того же типа, например, D или E в PEMDAS, что выходит за рамки споров о BEDMAS.Вот интересная цитата из той статьи
"Интернет-слухи утверждают, что Американское математическое общество написало" умножение, указанное сопоставлением, осуществляется перед делением ", но в сети больше не существует оригинального источника AMS (если он вообще существовал). Тем не менее, некоторые ранние учебники по математике также учил студентов делать все умножения, а затем все деления, но большинство из них, например, эта алгебра средней школы 1907 года учебник, этот учебник 1910 года и этот учебник 1912 года рекомендовали выполнять все умножения и деления в порядок, в котором они появляются первыми, затем следуют сложения и вычитания.(Это соглашение имеет смысл также и с канадским и британские версии PEMDAS, такие как BEDMAS, BIDMAS и BODMAS, которые все перечисляют деление перед умножением на (аббревиатура). Самый разумный совет, содержащийся в «Mathematical Gazette» за 1917 год, рекомендовал использовать круглые скобки для избегать двусмысленности.В статье есть ссылки на источники учебников. Вот запись 242 в книге Флориана Каджориса «История математической записи» (стр. 274), которая упоминается в этой цитате. Я не вижу никаких указаний на рекомендации, данные в цитируемых учебниках для старших классов, например здесь, здесь, но упомянутая запись в книге Вебстера Уэллса об этом ясно сказано на странице 18: (Да!) Но даже известный историк математики Флориан Каджори написал в «Истории математических обозначений»
в 1928-1929 гг .: «Если арифметический или алгебраический член содержит / и х, в настоящее время нет согласия относительно того, какой
знак должен использоваться первым."
(Да!) Но даже известный историк математики Флориан Каджори написал в «Истории математических обозначений»
в 1928-1929 гг .: «Если арифметический или алгебраический член содержит / и х, в настоящее время нет согласия относительно того, какой
знак должен использоваться первым."
Обновление от 18 мая 2017 г .: В последнее время загадки вроде ниже появились, которые упускают из виду, что количество картофеля фри изменилось или что используется одна вишня) всплыли Эти головоломки успели стать вирусными не из-за PEMDAS, а потому что люди не смотрят на варианты (3 вместо 4 банана, 2 часа, а не 3 часа).Поначалу почти все ошибаются. Но есть еще и проблема PEMDAS. Некоторые получают 88. Но чтобы получить 88, нужно было написать скобка (2 + 3 + 3) * 11. (спасибо Абите Сукумаран за то, что поделился этим).
Обновление от 2 августа 2017 г .: Преш Талвалкар пишет
«Я делаю математические видео на YouTube на канале« MindYourDecisions ». Некоторые из самых популярных видео - это неоднозначные выражения, связанные с порядком действий. В ходе исследования я наткнулся на ваш веб-сайт и обнаружил проблему: Что такое 2x / 3y - 1, если x = 9 и y = 2? Я бы ответил 11, как сказал учитель 5-го класса.Я был ошеломлен тем, что ни один из 60 студентов вашего гарвардского курса математики ответил 11 (вы объяснили, что 58 получил ответ 2; а затем 2 получил ответ 18/5).Мой ответ:
«да, это интересная вещь. Конечно, ни один из ответов не« правильный » поскольку мы знаем, что интерпретации BEDMAS и PEMDAS могут использоваться без нарушения каких-либо полномочий.Как указано на странице, ответ 11 - это то, что есть у большинства компьютерных языков. Вас явно этому учили. Было бы интересно узнать, какой процент людей говорит 11.Мои эксперименты говорят, что это очень редкий. Большинство делают умножение перед делением, так как PEMDAS кажется более популярны и больше преподают в школах. БЕДМЫ PE (MD) AS, кажется, преподают значительно меньше. Единственное, что мы знаем, это то, что утверждение, что одним из ответов является единственный правильный ответ - это неправильно ".
Обновление от 5 августа 2017 г .: Джейкоб Пошоланн Кефоед Кристенсен присылает другой пример и замечание по поводу обелуса.
"Проблема в том, что изображение мобильного телефона получает 9 из уравнения: 6 ÷ 2 (2 + 1) что, по их мнению, будет 1.В своем споре вы определяете obelus и разделительную косую черту как имеющие разные значения. Ну да, на самом деле они имеют два разных значения, и поэтому обычно никогда не используйте обелус. Только американец может по-прежнему использовать его, но этот знак был удален в использовании уравнений научных работ из-за его исторической проблемности. Первое слово obelus в Северной Европе означает вычитание. Во-вторых, obelus рекомендуется удалить в научном использовании, потому что у нас уже есть знак для любого из них (разделительная косая черта («/») и вычитание («-»)).Хотя, по вашему мнению, обелус и косая черта деления должны означать два разные значения У вас часто есть только одна опция на калькуляторе, чтобы сделать знак деления ".
Мой ответ:
«Спасибо за пример 6 ÷ 2 (2 + 1). Он тоже показывает неоднозначность. Да, в зависимости от того, кто входит в команду PEMDAS или PEDMAS, получает 1 или 9. Это тоже прекрасный пример, когда можно увидеть жаркие дискуссии. Как указывалось и ранее другими в список литературы, там нет правильного ответа .3 / (3 + у). Я был удивлен и должен был написать на доске пояснение:Экзамен по-прежнему прошел хорошо. На этой фотографии, сделанной незадолго до экзамена, вы можете увидеть, что все были счастливы уйти: Урок очень ясен: как учитель, даже если вы знаете лучше, вы должны быть очень четкий, даже избыточный. Даже если нет двусмысленности, лучше быть на всякий случай.
Кстати, статья в Википедии упоминает пример1 + 2x3 = 9 Калькулятор Microsoft в стандартном виде 1 + 2x3 = 7 Калькулятор Microsoft в представлении программистовОн показывает, что один и тот же поставщик в рамках, где нет двусмысленности (никто никогда не сомневается, что умножение должно предшествовать сложению), двусмысленность в том же товар.В другом примере из этой статьи упоминаются калькуляторы Texas Instruments.1 / 2x = 1 / (2x) в калькуляторе TI-82 1 / 2x = (1/2) x в калькуляторе TI-83Самопровозглашенные правила вроде это вряд ли поможет.
Обновление от 19 января 2018 г .: Тимоти Масгроув любезно обратил мое внимание на глупую дискуссию о youtube в котором вопрос of 6 ÷ 2 (1 + 2) снова появляется (см. выше). Также эта история показывает, насколько богословские дебаты может стать уже тем фактом, что часть зрителей, которым нравится видео и неприязнь к видео примерно одинакова, показывает, что ответ на эту проблему должен быть неоднозначным.Выше я привел (частично вслед за Тарой Хэлле, которая написала этот Slate article), исторические указатели, показывающие, насколько неоднозначны вещи. Вот лагеря:Компьютеры в основном следуют за вторым или третьим.Большинство людей и особенно студенты (экспериментально) склонны следовать правилу PEMDAS. Литература указывает на неоднозначность.
- PEMDAS (умножение предшествует делению)
- PEDMAS (деление предшествует умножению)
- PE (MD) AS (Деление и умножение имеют одинаковый вес, зависит от того, что осталось)
- Неоднозначно (Нет установленного правила)
| PEMDAS | BEDMAS | PE (MD) AS | 6/2 * (1 + 2) | 1 | 9 | 9 | (1 + 2) * 6/2 | 9 | 9 | 9 |
 У нас в обоих случаях одинаковые
отвечать. Также компьютеры часто следуют «PE (MD) AS» и придерживаются точки зрения «слева» на «право».
У нас в обоих случаях одинаковые
отвечать. Также компьютеры часто следуют «PE (MD) AS» и придерживаются точки зрения «слева» на «право». Еще хуже, вероятно, спорят, когда спрашивают, что такое 8 ÷ 2/2 (некоторая средняя школа Учитель подтвердил мне, что деления (знаки обелуса и обратной косой черты) в некоторых учебниках трактуются по-разному, см. замечание "obelus" выше, сделанное Якобом Пошоланом Кефоедом Кристенсеном. Некоторые скажут, что ответ - 8, потому что / стоит перед ÷. Если двигаться слева направо, получаем 2.
Обновление от 4 сентября 2018 г. :
Я получил следующее приятное письмо:
| Как, черт возьми, можно сказать, что это двусмысленно, когда это АКСИОМАТИЧЕСКОЕ, что умножение и деление являются обратными операциями? Как можно сказать, что это неоднозначно, когда ЛЮБОЕ деление может быть выражено как умножение на обратное? Позор вам за увековечивание ерунды. |
Единственное, что немного беспокоит, так как писатель на самом деле кажется учителем. Независимо от аргумента, писатель, вероятно, должен перейти в профессию, где требуется как можно меньше человеческого взаимодействия. Я ответил
| Уважаемый ..., , вы, вероятно, ссылаетесь на http://www.math.harvard.edu/~knill/pedagogy/ambiguity/ Дело не в том, является ли деление обратным умножению. Это определение.2/3. Теперь, если вы посмотрите на литературу и историю, то оказывается, что нет однозначного ответа, что правильно. И если это так, мы назовем это неоднозначным. Есть лагерь, который защищает PE (MD) AS, где MD равны и где порядок имеет значение, если умножение используется вместе. Но это только усложняет ситуацию, поскольку у нас есть три разных интерпретации. Итак, если кто-то пишет такое выражение, как x / 3x, он должен быть осторожно и поставил кронштейны.Все остальное может вызвать недопонимание. Вы не единственный, кто чувствует себя очень сильным и эмоционально из-за этого. |
Обновление от 2 октября 2018 г. :
Мне прислали ссылку на следующий адрес
YouTube видео.
На данный момент это один из лучших материалов на YouTube.
Хорошо видно, что в реальном мире выражения
используется по-другому: например, в опубликованных статьях
mn / rs обычно в публикациях интерпретируется как (mn) / (rs) или
лекций Фейнмана, можно увидеть, что 1 / 2N 1/2 интерпретируется
как 1 / (2 N 1/2 ).В инженерии можно прочитать W = PVMg / RT.
Еще один замечательный момент, сделанный в этом видео, заключается в том, что можно написать x / 2
если 1 / 2x интерпретируется как (1/2) x. Никто бы не написал 1 / 2x, если бы они
означает x / 2. Итак, на практике интерпретируется
выражение как 1 / (2x), которое является PEMDAS, но отличается от BEDMAS или
интерпретация того, что умножение и деление лежат в одном и том же
опора. Также упоминается, что в руководстве AMS есть PEMDAS (умножение
предшествует делению). Также следует руководство Американского физического общества.
ПЕМДАС.Видео еще раз демонстрирует, что единственный способ избежать
двусмысленность заключается в использовании скобок.
24 октября 2018 г. : Изначально я планировал опубликовать на YouTube версию несколько слайдов от 28 апреля 2018 г. Harvard Extension STEM Club, но на это не было времени. Спасибо Ana Carolina Smith за возможность выступить. Вот часть слайдов:
СЛАЙДЫ PDF (76 стр.)
26 октября 2018 г. : Другой хороший пример от кого-то: Вот письмо:
Мне сказали, что когда вы умножаете и делите (так как порядок работы значения не имеет) вам никогда не нужно использовать круглые скобки, верно? Потому что 2 * 3/4 * 6 на моем калькуляторе дают мне 9, и я ожидал 0.25! Для меня это должно быть эквивалентно 2 * 3 / (4 * 6), потому что, поскольку мы не нужны круглые скобки, это единственный способ набрать его без них. Если я хочу вычислить 2 * 3/4 * 6, как мой калькулятор да, я должен набрать 2 * 3 * 6/4, это правильно?Мой ответ:
Порядок операций имеет значение.4 ноября 2018 г. : С.А. добавил в историю интересный ракурс: Рекомендуется сначала упростить, а затем удалить скобки.Вам нужно поставить скобка. Мне нравится ваш пример. Это уже хорошо это иллюстрирует. Большинство людей получат 6/24 = 1/4, как и вы. Большинство языков программирования (компьютеры) дают 9. Компьютер следует PEDMAS (деление перед умножением) 2 (3/4) 6 = 9 или используйте правило (MD), которое означает «все, что будет первым» ((2 * 3) / 4) * 6 = 9 Люди (и большинство рекомендаций, таких как профессиональные такие общества, как AMS, следуют PEMDAS, что означает вы сначала делаете умножение, а затем деление (2 * 3) / (4 * 6) = 1/4 Но следовать рекомендации не имеет смысла если существуют разные интерпретации и компьютеры это делают разные.3)) = 7625597484987 компьютер идет справа налево. Также здесь необходимы скобки.
Я читал ваш блог по вопросам программирования на MD или DM. Проблема в том, что все они противоречат первому закону алгебры. Упростите, а затем УДАЛИТЬ круглые скобки. Все эти соглашения нарушают это, говоря только упрощать скобки ВНУТРИ. Итак, сначала мне нравится, что вы сказали AMBIGUOUS на 6/2 (1 + 2) 1 или 9 Однако я вздремнул, астрально переместился к старому Евклиду, и он засмеялся.Доказательство 1 и 9. 6 / x = 1 или 6 / x = 9 Когда x = 2 (1 + 2) 2 (1 + 2) = 2 (3) = 6 6/6 = 1 Таким образом, не учить студентов убирать скобки в новой математике, это противоречит первому закону алгебры. Все эти условные обозначения аббревиатур необходимо исправить, чтобы они соответствовали 1-му закону алгебры. Итак, согласны ли вы, что новые математические соглашения должны согласовываться с первым правилом алгебры Евклида? Думаю, да.Вот мой ответ:
Это интересный ракурс. Но учтите, что рекомендация "упростить" Здесь находится проблема неоднозначности:3 декабря 2018 г. : Atmos добавил еще один интересный ракурс
Да, можно упростить 6/2 (1 + 2), введя x = 2 (1 + 2) = 6, а затем получить 6/6 = 1 Но можно также упростить, определив x = 6/2, а затем получить x (1 + 2) = 9.Собственно, это тоже исторически интересно. Вы упомянули Евклида. Евклид не использовал известную нам алгебру. Символическая алгебра появилась только с Вите в 16 веке. Насколько нам известно, только в ХХ веке реализовали что здесь действительно есть двусмысленность. Об этом ясно сказано в книге Каджори о математическая нотация, которая является авторитетом в этом вопросе.
Это тоже стало педагогическим вопросом: студентов сегодня в основном обучают правилу PEMDAS, которое формально ставит умножение перед делением и рекомендовал бы результат 6/2 (1 + 2) = 1.Если дать выражение системе компьютерной алгебры, они все дают 6/2 (1 + 2) = 9. Все эти обсуждения были вызваны такими примерами. Первое правило алгебры по-прежнему остается хорошим правилом. Это хороший совет. к несчастью это не устраняет двусмысленность. Но я согласен, что это помогает писателю избегать двусмысленность. Но знаете, в основном проблема возникла в образовательных учреждениях. Если учитель спрашивает ученика, что такое 6/2 (1 + 2), учитель не хочет упростите это, так как это уже решит проблему.Если сегодня учитель спросит студенты, что такое 6/2 (1 + 2), то это просто напрашивается на неприятности. Правильно do - это уточнить и написать либо (6/2) (1 + 2), либо 6 / (2 (1 + 2)). Каджори уже было ясно, что отказ от скобок не дает четко определенные математические выражения. Оливер
Потенциальным решением этого противоречия может быть то, что когда у вас есть коэффициенты и переменные, записанные вместе без операторов между тема.грамм. 5ab, мы можем рассматривать это как вложенную операцию. Другими словами, отсутствие символа оператора означает, что оператор отношения между ними имеют приоритет над любыми внешними операциями, т.е. 5ab представляет собой (5 * a * b). Итак, если у вас был / bc, записан только один оператор (разделение символ), а часть "bc" будет подразумеваться вложенной из-за упущение оператора внутри. Так что это все равно будет "a over bc", как именно это выглядит и сколько из нас учили.А потом, если нам нужно указать, что операция между a и b фактически занимает приоритет над отношениями между b и c, тогда мы просто вместо этого напишите a / b * c. Ни суеты, ни суеты. Разве это не более эффективный способ общения с математический язык здесь? И разве не в этом суть математического язык, чтобы эффективно передавать концепции? В противном случае этот вид путаница никогда не исчезнет, и нам придется написать намного больше круглые скобки в наших уравнениях (и никто не хочет этого делать).Немного людям нравится "новая математика" сверхстрогой интерпретации PEMDAS особенно потому, что это простой способ обмануть людей и сделать математику более запутанно, чем должно быть. Тем не менее, это, кажется, побеждает все Дело в том, почему мы вообще это делаем. У меня есть оба способа сделать это, но строгий метод PEMDAS кажется контрпродуктивен, потому что он вызывает так много проблем и делает вещи например, превратить якобы простую дробь вроде 2x / 3y в фактическ имея в виду 2xy / 3 вместо этого, что кажется совершенно безумным.Но если вместо этого мы просто используем PEMDAS, когда операторы на самом деле написаны, тогда все такого рода проблемы исчезнут буквально в одночасье. «Старая математика» и "новая математика", наконец, согласится, и мы сможем все это сделать с одним очень простым правилом. Что ты об этом думаешь?Я ответил
Привет, Атмос,
отказ от знаков умножения уже обычно делается.
На самом деле большую часть времени. Однако может возникнуть дополнительная проблема.
при использовании чисел, а не переменных вроде 3/45 не то же самое, что 3/4 5
Но вы вносите интересный момент, потому что теперь их стало еще больше.
двусмысленность:
3/45 = 3 больше 45 = 1/15
3 / (4 * 5) = 3 больше 20 = 3/20
(3/4) 5 = 3/4 умножить на 5 = 15/4
Проблема PEMDAS - это не «проблема, которую нужно решать».Это вопрос
Дело в том, что существуют разные интерпретации и что человек для
пример считывает x / yz с x = 3, y = 4 и z = 5 как 3/20, в то время как машина
(практически все языки программирования) дают другой результат.
Есть авторитеты, которые установили правила (большинство учеников учат
PEMDAS), что является одной из причин, по которой многие люди спрашивали о 3/4 * 5, давая 3/20
которые большинство машин просили дать 15/4:
Я набираю это в Mathematica
х = 3; у = 4; z = 5; x / y z и получаем 15/4
Это лингвистическая проблема, а не математическая.В случае
лингвистическая проблема, ее нельзя решить путем введения нового правила.
Единственный способ решить проблему - избежать ее. Можно избежать этого, чтобы
поставить скобки.
Оливер
Обновление от 14 декабря 2018 г. :В новейшем гайде по мультфильмам из серии Ларри Гонника (которые фантастические), есть еще кое-что о Порядок операций. Но далеко не идёт. "Если без скобок присутствуют, умножьте и разделите перед сложением и вычитанием ". Это очень грубое правило, но оно имеет то преимущество, что он не попадает в войны PEMDAS.
Обновление от 18 января 2019 г. :
Учитель математики прислал мне следующий пример. Здесь не только неоднозначность PEMDAS. Также вопрос "96 разделить на 6 из 4" появляется, что может означать "96/6 умножить на 4" или затем «96 / (6 * 4)». Это особенно интересный случай, потому что того, что:
Вопрос:Я учитель математики и недавно столкнулся с конкретным вопросом на PEMDAS (пожалуйста, проверьте приложение), где ученики получили два разных ответа (6 и 66).Причиной получения двух разных ответов было то, как студенты решили последнюю часть вопроса: 96 ÷ 6 из 4 |
| Мой ответ: в этой проблеме есть две двусмысленности, и да, все ответы даны.
студентами должны быть оценены как правильные. 1) Первое выражение: похоже, что ученики истолковали
57 ÷ 19 * 2 выражение равно 6, даже если это может быть 3/2, если используется PEMDAS (и официальные рекомендации
AMS или физического общества и используется в большинстве научных работ, особенно если выражения являются переменными).
Что происходит, так это то, что если бы вопрос был задан как 57/19 * 2, то многие интерпретировали бы его.
как 57/38. 57 / (19 * 2) -64 * 2/32 + 96 / (6 * 4) = 3/2 (57/19) * 2-64 * 2/32 + 96 / (6 * 4) = 6 (57/19) * 2-64 * 2/32 + (96/6) * 4 = 66 57 / (19 * 2) -64 * 2/32 + (96/6) * 4 = 123/2Пример снова показывает, что скобки нужно ставить всегда.Но это также показывает, что может произойти, если для описания арифметических операций используется "разговорный язык", так как это может может привести к другим двусмысленностям. «Что составляет две трети от 9» должно быть ясно как (2/3) * 9, а 2 ÷ 3 из 9 тоже можно интерпретировать как 2 / (3 * 9). Этот пример снова указывает на то, что люди могут интерпретировать знак обелуса ÷ иначе, чем знак деления /. |
| В швейцарской газете 20 Min задача 6/2 (1 + 2) = ???
тоже упоминается.К статье уже добавлено 1384 комментария. Как и в течение многих лет в социальных сетях, борьба
продолжается там. Самое интересное, насколько большинство уверены в своей правоте
со всех сторон. Что снова указывает на двусмысленность. Название статьи: «Миллионы не справляются с этим математическим уравнением!» В качестве «доказательства» есть видео на YouTube, которое дает ответ 9. Автор этого видео,
Преш Талуокер дает в своем
блог
ссылка
Леннес, Н. Дж. "Дискуссии: Относительно порядка операций в алгебре."The American Mathematical Monthly 24.2 (1917): 93-95 ..."
Лучше прочитать эту статью.
Итак, у нас есть это: это просто нонсенс, что 12 миллионов человек, которые делают это по-другому, не были «неспособны решить проблему».Мы определенно имеем дело с ситуацией, которую следует считать неоднозначной. Статья 1917 года - хорошая ссылка. Это уже подтверждает. Но с 1917 г. Правилу PEMDAS научили миллионы людей. Поразительно только то, как многие утверждают, что знают правильный ответ. Может быть, это просто человеческая природа. |
Прочтите в конце статью Леннеса, который писал уже в 1917 году:
| "Когда способ выражения получил широкое распространение, его нельзя изменить по желанию.Это дело лексикографа и грамматик записывать, а не то, что, по его мнению, должно означать выражение но что на самом деле понимают те, кто его использует. Язык алгебры содержит определенные идиомы, и при формулировании грамматики языка мы должны обратите внимание на них. Например, 9a 2 ÷ 3a означает 3a и not 3a 3 - такая идиома. Дело не логическое, а историческое. |
Лучше не скажешь! Значит, идиоты не 12 миллионов человек.Те, кто так утверждает, есть.
Это досадное математическое уравнение? Вот дополнение. Путаница (скорее всего намеренно) сводится к несоответствию используемых математических правил в начальной и средней школе.8 ÷ 2 (2 + 2) =? Проблема заключалась в том, что он дал два разных ответа, 16 или 1, в зависимости от порядка, в котором выполнялись математические операции. выполненный. В юном возрасте студенты-математики обучаются особым навыкам. соглашение о «порядке операций», которое диктует порядок следующим образом: круглые скобки, показатели, умножение и деление (подлежат рассмотрению на равных, с разрывом галстуков, работая слева направо), и сложение и вычитание (также равного приоритета, со связями аналогично сломанный).Я утверждал, что строгое соблюдение этой элементарной конвенции PEMDAS: приводит только к одному ответу: 16. Тем не менее, многие читатели (включая моего редактора), одинаково приверженные тому, что они рассматривали в качестве стандартного порядка операций, усиленно настаивал правильный ответ был 1. Что происходило? После прочтения много комментариев к статье, я понял, что большинство из этих респондентов были используя другое (и более сложное) соглашение, чем элементарное Конвенция PEMDAS, которую я описал в статье.В этом более сложном соглашении, которое часто используется в алгебры, неявному умножению дается более высокий приоритет, чем явному умножение или явное деление, в котором записываются эти операции явно с такими символами, как x * / или ÷. Под этим более изощренным соглашение, неявное умножение на 2 (2 + 2) дано выше приоритет, чем явное деление на 8 ÷ 2 (2 + 2). Другими словами, 2 (2 + 2) следует оценить в первую очередь. Это дает 8 ÷ 2 (2 + 2) = 8 ÷ 8 = 1. По тому же правилу многие комментаторы утверждали, что выражение 8 ÷ 2 (4) не было синонимом 8 ÷ 2x4, потому что круглые скобки требовали немедленного разрешение, что снова дает 8 ÷ 8 = 1.Это соглашение очень разумно, и я согласен, что ответ - 1. если мы будем его придерживаться. Но это не принято повсеместно. Калькуляторы встроенные в Google и WolframAlpha используют более элементарное соглашение; они не делают различия между явным и неявным умножением при указании вычислить простые арифметические выражения. Подпишитесь на Science Times Мы расскажем вам истории, отражающие чудеса человеческого тела, природы и космоса. Более того, после того, как Google и WolframAlpha оценивают все, что находится внутри набор круглых скобок, они эффективно удаляют круглые скобки и не больше расставляйте приоритеты по содержанию.В частности, интерпретируют 8 ÷ 2 (2 + 2) как 8 ÷ 2x (2 + 2) = 8 ÷ 2x (4), и обрабатываем это как синоним 8 ÷ 2x4. Затем, согласно элементарному PEMDAS, деление и умножение имеют равный приоритет, поэтому работаем слева направо и получаем 8 ÷ 2x4 = 4x4 и получили ответ 16. В своей статье я решил сосредоточиться на этом более простое соглашение. Другие комментаторы возражали против самого исходного вопроса. Посмотри как они отметили, что это было плохо поставлено. Это можно было бы сделать намного яснее если бы в нужном месте был вставлен только другой набор круглых скобок, записав его как (8 ÷ 2) (2 + 2) или 8 ÷ (2 (2 + 2)).Верно, но это упускает из виду: вопрос не был задан ничего ясно. Напротив, его безвестность кажется почти умышленно. Это, безусловно, искусно извращенное, будто построенное для причинить шалость. В выражении 8 ÷ 2 (2 + 2) используются круглые скобки - обычно это инструмент для сокращения путаница - в манере джиу-джитсу, чтобы усилить мутность. Оно делает это путем сопоставления цифры 2 и выражения (2 + 2), что означает неявно, что они предназначены для умножения, но не помещая явный знак умножения между ними.Зритель остается в недоумении следует ли использовать сложное соглашение для неявного умножения из класса алгебры или вернуться к элементарному соглашению PEMDAS из средней школы. Выбирает: "Итак, проблема в том, как она поставлена, смешивает обозначения начальной школы. с обозначениями средней школы, что не имеет смысла. Человек который хорошо помните математику в начальной школе, скажите, что ответ - 16. Люди кто помнит свою алгебру, с большей вероятностью ответит 1. " Как бы мы ни предпочли четкий ответ на этот вопрос, не один.Вы говорите помидор, я говорю томахто. Некоторые электронные таблицы и программное обеспечение системы категорически отказываются отвечать на этот вопрос - они упираются в его искаженную состав. Это тоже мой инстинкт, как и большинство математиков, которых я говорил с. Если вы хотите получить более четкий ответ, задайте более четкий вопрос.5 августа 2019 г. . Только что появилась еще одна сокровищница Дженни Горхэм на ютубе: 8 августа 2019 г. . Грег Макканн любезно указал эта ссылка на заархивированная копия руководящих принципов AMS.{-1} dt $. 17 августа 2019 г. Другой вопрос:
Мне любопытно, какие, по вашему мнению, ответы на это уравнение. 8 ÷ 2 (4). Для меня самый простой порядок действий - это умножение 2 * 4 во-первых, потому что мне еще нужно разобраться со скобками. Я просто считаю, что нам нужно провести какую-то математику, чтобы избавиться от скобок. Некоторые люди просто бросают их, не делая никаких вычислений. Я имею в виду, зачем они вообще, если их можно просто уронить в любой момент без каких-либо математических вычислений, чтобы их очистить.С. -------------------------------------------------- --------------------------------- Мой ответ: Да, это одна из последних загадок PEMDAS. Подобный Также Строгац обсуждал в New York Times. Вы упомянули, что 2 + 2 уже оценивается, но это не меняет ситуацию на 8 ÷ 2 (2 + 2), который теперь раздается. Но это та же история. Причина, по которой ставится скобка вокруг 4, заключается в том, что она не читается как 24. Но это не проясняет двусмысленность.Да, хочется сначала сделать 2 * 4 и получить результат 1. Большинство компьютерных программ оценивают его как 16. Пример: Ядро Mathematica 12.0.0 для Linux x86 (64-бит) Авторские права 1988-2019 Wolfram Research, Inc. В [1]: = 8/2 (4) Из [1] = 16 Почти все люди оценили бы его как 1. Мнения здесь не имеют значения, поскольку теперь хорошо задокументировано, что там просто нет консенсуса (ни авторитетом, ни историческим ростом, это лингвистический феномен, о котором так поздно осознали необходимость его точного определения).Вещи можно интерпретировать по-разному, и так останется. Чтобы прояснить ситуацию, необходимо разместить скобки.17 сентября 2019 г. . Ответ на некоторые вопросы проверки фактов из Нью-Йорк Таймс. Я ответил:
Резюме: -------------------------------------------------- ------------------------------------------ На вопрос 8/2 (2 + 2) есть разные ответы в зависимости от используемого правила. Его можно интерпретировать как (8 / (2 (2 + 2))) = 1 или (8/2) (2 + 2) = 16 в зависимости от правило.Общепринятого правила не существует, их несколько: PEMDAS, BEDMAS, PE (MD) AS. Невозможно сказать, что правильно, а что нет. Есть разные правила, приводящие к разным результатам. Выражение не очень хорошо определено. Похоже, что большинство людей естественно дают ответ 1 и большинство компьютеры и языки программирования возвращают ответ 16. Чтобы выражение было однозначным, нужно поставить скобки. Лишь сравнительно поздно (около 100 лет назад) стало ясно, что существует двусмысленность.Нет С тех пор был достигнут консенсус, так что нет альтернативы для уточнения выражения. Литература по этому поводу - Флориан Каджори, «История математической записи», Лондон, 1928 год. Н. Дж. Леннес, Относительно порядка операций в алгебре, Amer. Математика. Ежемесячно, 24 1917 -------------------------------------------------- ---------------------------------------------- Вот ответы на ваши вопросы: - Точно сказать, что согласно PEMDAS, «2 + 2» должны быть односторонне первая операция выполнена? Да! Но это не PEMDAS.Операция 2 + 2 выполняется первой, потому что вокруг него были установлены скобки. - Согласно математике нижнего уровня, решение этого уравнения должно быть 16? Нет. Существует правило PEMDAS, которое широко распространено. (дети выучивают «Пожалуйста, извините мою дорогую тетю Салли»), и при их следовании спрашивает делать умножение перед делением. Это дает 8 / (2 (2 + 2)) = 1. Как и сегодня, у большинства детей младшего уровня математики есть доступ к калькуляторам или онлайн-инструментов, они могут дать ответ 16. Причина утверждения, что это часть математики нижнего уровня, вероятно, то, что большинство учителей теперь используют калькулятор для проверки вещи, и компьютер сообщает им, что ответ - 16.Как студенты и их родители получают разные результаты (если они не используют компьютер) есть разногласия. - Справедливо сказать, что в алгебре или высшей математике операция 2 (4) имеет приоритет? Нет. Также здесь это зависит от используемого правила. Если использовать PEMDAS по назначению, то ответ - 1, что означает сначала вычислить 2 (2 + 2), поскольку M стоит перед D. Вопрос не в том, какой уровень или предмет использовать. Ответ зависит от того, какой правило используется. - Согласно высшим математическим стандартам, решение этого уравнения 1? Нет.Также это зависит от используемого правила. При выполнении теста со студентами большинство дает ответ 1. На самом деле, большинство людей дают ответ 1, если они не используют компьютер. Большинство людей читают такие выражения, как 1. Однако компьютеры, которые рассматривают умножение и деление часто находится на одном уровне и почти всегда дает ответ 16. В 2014 году я спросил у поступающих первокурсников (еще не старших математиков) во вступлении курс исчисления и все, кроме одного, использовали правило PEMDAS. Большинство людей отвечает 1. - В статье утверждается, что способ написания этого математического выражения вводит в заблуждение.Вы согласны с этим утверждением? Нет. Это не вводит в заблуждение, это неоднозначно. Было бы заблуждением, если бы правильный ответ, и выражение приведет к неправильному ответу. Это не тот случай. Нет правильного или неправильного ответа. Выражение неоднозначно и зависит от правило, которое используется. - Справедливо сказать, что по мере того, как человек переходит на более высокий уровень математики (уровень после начальной школы), деление вообще обозначается как дробь? Нет. В высшей математике используются все виды выражений.Разделение на математику более низкого уровня и математика более высокого уровня менее важна (по моему опыту) чем вычислить, как человек читает математику естественно (и большинство учебников это делают) или если вычислить выражение на компьютере. Это может быть психологическое, это может быть быть лингвистом, это может быть благодаря тому, что его так учат, это может быть чтение текстов, но большинство людей умножение перед делением в ситуациях, подобных рассмотренной. - Как бы записать это уравнение в дробной форме? В недвусмысленных выражениях используются скобки типа 8 / (2 (2 + 2)). Другая возможность - использовать выражение 8 ---------------- 2 (2 + 2) Это дает 1.При этом важно, чтобы была четкая длинная линия деления дроби, убедившись, что 2 (2 + 2) сделано до разделения. Другая версия была бы (8/2) (2 + 2), что дает ответ 16, как и большинство компьютеров.2 ноября 2019 г.: На этом сайте есть онлайн-калькулятор упоминание BODMAS BODMAS также является аббревиатурой от Bracket, Order / Of, Деление, умножение, сложение и вычитание. Веб-сайт и калькулятор полностью упускают из виду суть определения выражений. что можно понимать по-разному.Тем более, что сайт называется Калькулятор PEMDAS предполагает использование правила PEMDAS, в котором умножение перед сложением. Таким образом, калькулятор оценивает 2 * 9/3 * 2-1 как 11, как и большинство калькуляторов или программистов. языки делают, но это отличается от того, что на самом деле предлагает PEMDAS (2 * 9) / (3 * 2) - 1 = 2 и которые большинство людей оценивают, когда их спрашивают. Итак, калькулятор, а не помогает чтобы прояснить присутствующую двусмысленность, это просто калькулятор. Есть современные калькуляторы, которые предупреждают учащегося о том, что выражение неоднозначно и заключено в круглые скобки, поэтому что пользователь может, если эти круглые скобки не соответствуют тому, что имелось в виду, может их изменить.
6 апреля 2020 г. Другой вопрос:
Надеюсь, что все в порядке, я пишу тебе по электронной почте. Я наткнулся на вашу страницу во время дебаты по проблеме Facebook. Я в отпуске, так что у меня много времени в моих руках. Эта версия была 6/2 (1 + 2). Мне ответ на выше - 1 и только 1. Но я не хотел обсуждать это. Я хотел добавить что-то, чего я не видел на вашем сайте, что я думаю, больше промахов PEMDAS. Математику часто называют универсальным языком. Это позволяет общаться людям из разных культур.Когда вы читаете первый пример 2x / 3y - 1, когда x = 9 и y = 2, как вы это читаете? Ты прочитать два раза x разделить на три раза y минус один? Ты читаешь это два x больше трех y минус один? Подобно тому, как в английском языке есть правила, в математике тоже есть правила. Английский не идеален и не всегда следует правила. Математика такая же. Иногда умножение и группирование могут подразумевается.Мой ответ:
да, математика - универсальный язык, позволяющий общаться между разные культуры.Но языки также были созданы людьми и не всегда идеальны. Двусмысленность PEMDAS на самом деле просто упущение дизайна. Не было авторитета, который раз и навсегда сказал бы, что это это необходимо указать. Причина исторически ясна. Только один осознал проблему слишком поздно. Вы говорите, что для вас 6/2 (1 + 2) равно 1, да, почти все люди предполагают это. Если вы отдадите его компьютеру, это дает вам 9, почти все языки программирования. Да вроде английский, В математике есть правила. Но они далеки от совершенства.Языки меняются и со временем совершенствоваться. В ходе обсуждения PEMDAS выяснилось, что слишком поздно принимать правила. Некоторые пробовали, и многие из них фанатичны и думают, что их путь правильный. Например, в случае 6/2 (1 + 2) мы видим сторонников (например, на YouTube), которые спорят, только 9 - правильный ответ. Но, как вы говорите, читать это как 6/2 (1 + 2) - это укоренившиеся и изменяющиеся, что многих расстроило бы. Последние несколько слайдов в эта презентация [PDF] немного показывает, что говорят лингвисты. На самом деле это не математическая проблема, это лингвистическая проблема.То, что хорошо об обсуждении заключается в том, что теперь все учителя и ученики знают о двусмысленность и запишите уточненные выражения.
9 апреля 2020 г. Из другого электронного письма:
Я не математик. STEM всегда был моей сильной стороной, но Я предпочитаю применение теории, поэтому я техник по оборудованию в полупроводниковой промышленности (я чиню роботов, которые делают компьютер фишки). Я упоминаю об этом, чтобы сказать, что я, возможно, не эксперт, но и не мирянин.Мой первый опыт с этим вопросом возник, когда я пытался для программирования квадратной формулы в моем калькуляторе TI-83 + почти 20 много лет назад. Чтобы уравнение работало правильно, дополнительные скобки необходимы. Это потому, что стандартная алгебра обозначена неявным пути, а компьютеры никогда не улавливают подразумеваемых значений или только начинают совсем недавно. Об этом говорится в цитируемой вами статье NYT, но это высказанное в некотором смысле я считаю ошибочным. В нем говорится "просто или элементарно" математика 8/2 (4) такая же, как 8/2 * 4, и только в алгебре 8/2 (4) становится 8 / (2 * 4).Калькуляторы подвержены ошибкам, как вы указали MS Calculator. решает 1 + 2 * 3 как 9, а не 7, что никогда не бывает правильным. Распределительный закон умножения и деления »доказывает понятие двух правильных ответов недействительным. 8/2 (2 + 2) = 16 - полное нарушение закона распределения, таким образом недействителен. Если уравнение записано (8/2) * (2 + 2), то порядок операции будут диктовать, что деление происходит первым, а затем результат будет распределен во вторых скобках, как если бы он были написаны 8/2 * (2 + 2).Однако в любом уравнении, где написано 8/2 (2 + 2), то неявно (не явно) закон распределения должен применяться как часть круглой скобки до того, как произойдет разделение, в явном виде это будет 8 / (2 * (2 + 2)). Дело в том, что компьютеры (или калькуляторы) не понимают, что мы подразумеваем, не означает значение неверно, это означает, что компьютеры могут понимать только явные инструкции. Явное решение уравнения с подразумеваемыми факторами обычно приводит к неправильному ответу.2-4ac) / 2a, но оба дают совершенно неверные ответы с калькулятора. Очевидно, что квадратичная формула - это константа и не должны получать разные результаты, независимо от того, чему вас учили, это доказывает, что мы должны быть достаточно умными, чтобы правильно пользоваться нашим калькулятором, не то, чтобы калькуляторы безошибочны. Другой пример - уравнение «ab * cd». Решение этого выражения явно бы вы сделали «a * b * c * d = x», когда мы знаем, что это на самом деле (a * b) * (c * d), потому что () подразумеваются, как указано выше. Ваш алгебраический пример использования 2x / 3y-1 глуп.3 как указал Леннес в своей статье 1917 года. Причина 2x / 3y-1 = 11 на калькуляторе, потому что калькулятор не понимает, что неявная группировка. Каждый родитель понимал неявную группировку, что (2x) / (3y) -1 - подразумеваемое уравнение, хотя явно не записано как такой. Только когда вы введете в калькулятор 2 * 9/3 * 2-1, вы получите 11. Но 2 * 9/3 * 2-1 будет записано 2 * x / 3 * y-1, что сильно отличается от 2x / 3y-1, но калькулятор считает их одинаковыми. Это было доказано, когда у вас ваш класс по математике сделает это, двое из ваших учеников вбили это в свои калькуляторы, остальные 58 подсчитали правильно.Что это значит - это ты нужно научить этих двух учеников правильно пользоваться своими калькуляторами, не то чтобы есть некоторая универсальная двусмысленность. При программировании четырехугольной формы вы должны явно заключить в скобки всю неявную группировку, иначе это не сработает, это ограничение программного обеспечения, а не недостаток математики. Если здесь была ли какая-либо фактическая двусмысленность в результатах вашего класса исчисления были разделены ближе к 50 на 50, статистически очевидно, что устойчивый консенсус среди студентов, изучающих математику, относительно правильного метода.В Учитель математики, получивший 2x / 3y-1 = 11, должен работать в другой области.Мой ответ
спасибо за вашу заметку. Да, это очень интересная тема, особенно в связи с компьютерами. Вы правы, что с калькуляторами один нужно быть еще осторожнее и поставить больше скоб. Один из Причины, по которым калькуляторы HP имели большой успех, заключаются в том, что они использовали обозначение обратной полировки, позволяющее пропустить многие скобки. Я никогда не был в том лагере HP, но, как и вы, использовали калькуляторы TI.Пример 2x / 3y -1 не так уж и глупо. На самом деле это очень интересно. Да, вы правильно, что каждый человек читает это как (2x) / (3y) - 1, но компьютер дает что-то другое. Я рассчитываю это здесь с помощью Mathematica, одного из самые продвинутые системы компьютерной алгебры, и это дает -1+ 2xy / 3 не -1+ (2x) / (3y) (см. Прикрепленный снимок экрана). Я также согласен с тем, что PEMDAS двусмысленность не является недостатком математики, как ее часто представляют, это просто некоторые выражения нуждаются в большей ясности (значение скобки), чтобы иметь смысл.Немного компенсирует то, что там вокруг так много людей, которые верят, что есть определенный путь и только их путь правильный. В примере 2x / 3y -1 большинство людей просто естественно предположим, что это означает (2x) / (3y) - 1, но, по мнению некоторых фанатиков, есть только один способ увидеть это правильно, и это то, что дают компьютеры тебе нравится -1+ 2xy / 3. Также удивительно, как долго длится это обсуждение. продолжается. Но от этого становится еще интереснее. Нет только математическая или лингвистическая сторона, есть также социальный аспект к рассказу.И, как вы упомянули как инженер, это может иметь решающее значение. Если кто-то пишет программу, управляющую роботом, и упускает из виду что-то подобное, это просто не работает. Я рано понял, что программирование окончательный тест понимания. Это сложнее, чем читать или писать или учите предмет. Если процедура не работает, это доказательство того, что есть это то, чего еще не понимаешь.После другого вопроса о распределении, ведущем от главный пункт: Я пытался подчеркнуть, что в неоднозначной ситуации нет правильного или неправильного нравиться 8/2 (2 + 2) Есть ответы 1 или 16, в зависимости от того, какое правило вы использовать.Это причина, по которой люди продолжают спорить об этом. Ответ 1 - это ответ, который получает большинство людей. Ответ 16 - это то, что получают большинство компьютеров. Я пытался подчеркнуть это с самого начала в http://www.math.harvard.edu/~knill/pedagogy/ambiguity В своем последнем письме я указал, что это не проблема. с распределением. 2 (2 + 2) всегда равно 8, есть нет споров. Опять же: вопрос в том, является ли (8/2) сначала вычисляется, а затем умножается на (2 + 2), чтобы получить 16 или сначала вычисляется 2 (2 + 2) = 8 и 8/8 = 1 получается в результате.Это вопрос о том, деление или умножение выполняется в первую очередь. Это собственно говоря (наблюдение, глядя, какие люди напишите в сети), что есть те, кто верит одному из ответов правильный. Здесь нет правильного или неправильного. Вопрос тоже не в вводящие в заблуждение. Есть двусмысленность. Напрашивается вывод, что нужно более четко записывать, используя скобки.И еще одно электронное письмо: Думаю, я мог прорваться. Я принял это на данный момент умножение через сопоставление преподавалось как высший порядок умножения или равно всем порядкам умножения.Таким образом, 5 / 2x учили означать (5/2) * x или 5 / (2x) в зависимости от вашего учителя. Таким образом, единственное решение - четкое правило, определяющее умножение через сопоставление. Как определить, является ли умножение путем сопоставления это высший порядок или нет? Я думаю (хотя мне и больно) этот язык и грамматика может держать ключ. Но сначала я должен спросить о x * 2xy? Я никогда не видел, чтобы кто-нибудь писал что-то вроде этого, как x2xy или 2xyx или что-то еще, было бы это правильно сделать так? Если нет, то почему? Когда я вижу что-то подобное со мной показывает, что группировка подразумевает скобки, а не просто умножение, мысль на результат они бы не повлияли.на что я ответил
Некоторую двусмысленность можно избежать путем сопоставления, некоторые могут быть
делается по заказу, но остается неоднозначным, особенно если набирать.
Похоже, вы все еще думаете, что двусмысленность PEMDAS - открытая проблема.
который необходимо решить. Это не открытая проблема. Было решено
100 лет назад, когда осознал, что нужно просто написать больше скобок в
Общее. Это была лингвистическая оплошность. При написании грамматики
правил для арифметики, сначала не понимали, что были
детали, требующие большего количества скоб, чем предполагалось.При использовании только умножения проблемы нет. В
причина в том, что существует ассоциативность и коммутативность продукта
операция. Уже деление не ассоциативное и не коммутативное
(3/3) / 3 = 1/3 не равно 3 / (3/3) = 3
3/5 не 5/3
|
13 июля 2020 г. : Учитель средней школы указал мне на статью Переосмысление порядка операций в Журнал «Учитель математики» с октября 2017 года.2 или выражения типа 2x / 3y-1, если x = 9 и y = 2. Кроме того, приведенная выше статья «Переосмысление порядка операций» делает вещи более сбивает с толку. Это другое мнение. Нет необходимости в переосмыслении, если человек остается ясным. Указывая на то, что порядок умножения, деления или возведения в степень должен быть уточнял письменно умнейший больше. Каждый студент должен знать того факта, что такие выражения, как 18/3 * 2, часто оцениваются людьми как 3 (века математических писаний закрепили это), в то время как компьютеры оценивают это как 12.2 оценивается компьютерами справа налево. Также GEMA не дает любые направляющие линии здесь. Он просто остается неоднозначным без дополнительных разъяснение. Никакого "переосмысления" не исправить. Просто используйте скобки и все проблемы решены.
4 августа 2020 г. :
Только что дочитали на вашей веб-странице о неоднозначных уравнениях. Каково же мое удивление, узнав, что математическая конвенция не лечит умножение и деление одинаково. Я изучал математику уже 3+ лет (прежде чем прийти в себя) и преподавал на уровне колледжа.(1 / n), x ÷ n = x * (1 / n) и x - n = x + (-n). Однажды они поймали после этого они были поражены тем ловушкам, которых они избегали. Несмотря на это, раскрывая давние соглашения, интересно ... неоднозначность разрешается так, чтобы решение уравнения 8 ÷ 2 (2 + 2) можно найти? Я должен сказать, что я горячо утверждал, что ответ был 16, хотя я проигнорировал двусмысленность. Прочитав вашу веб-страницу, двусмысленность очевидна. Однако мой брат, инженер на пенсии, Ханиуэлл, чье понимание математики превосходит даже мое собственное, также пришло вверх с ответом 16.Интересно, что его первый инстинктивный ответ был 1. Однако ваша ссылка на ISO 31-0 и ссылка на видео YouTube («ПЕМДАС ошибается») отправил меня в кроличью нору. Между прочим, я обнаружил, что ISO 80000-1 теперь заменяет ISO 31-0, fyi. К несчастью, ISO 80000-1 недоступен бесплатно, поэтому мне пришлось прибегнуть к ISO 31-0. для уточнения. Возможное (?) Решение этого неоднозначного уравнения требует знания правила и условности Я подозреваю, что большинство людей не знают. В частности ... что обелус (÷) нарушает ISO 31-0.-1 " (альтернативно «a * 1 / b»). (товар записывается как "а б", «ab», «a * b» или «a x b». ), что при применении правил AMS и APS, умножение предшествует делению. (что "/ xy" условно математики понимают как "/ (xy)" _ Решение 1: 8 ÷ 2 (2 + 2) = 8/2 (2 + 2) (в соответствии с ISO 31-0) 8/2 (4) (на порядок операций) 8/8 (в соответствии с правилами AMS и APS, которые умножают предшествует делению) 1 Решение 2: 8/2 (2 + 2) можно переписать как 8 / [2 (2 + 2)] [на математическое соглашение о том, что "/ xy" = "/ (xy)", а также из-за сопоставления, посредством чего «2 (2 + 2)» можно было бы увидеть как «2y», используя замену, и «8 / 2y» = «8 / (2y)»] 8 / [2 (4)] 8/8 1 Многие люди заявляют, что проблема связана с лингвистикой и / или грамматикой.я рассматривают это как проблему перевода и что это входит в компетенцию математик, чтобы перевести задачу на общий язык. это аналогично тому, как иммигрант впервые слышит разговорный язык. Это напоминает мне русского комика Якова Смирнова, который немного где он говорил о странных идиомах. Он слышал, как кто-то сказал, что бросили курить холодная индейка. Он сказал: "Что ты куришь сейчас, ветчина?" Итак, я теперь верю, что математик, применяющий международную стандарты, а также соглашения AMS, могут переводить уравнение и разрешить двусмысленность.Что вы думаете? Моя логика верна? -------------------------------------------------- ----------------- Мой ответ: Ваш пример - типичный пример, когда люди и машины получают разные вещи. Если скармливать в компьютер, получается 16 [knill @ knill11:] математика Ядро Mathematica 12.1.1 для Linux x86 (64-бит) Авторские права 1988-2020 Wolfram Research, Inc. В [1]: = 8/2 (2 + 2) Из [1] = 16 Я думаю, что большинство людей получают 1 из-за обучения, PEMDAS и потому, что по математике и физическая литература, есть неявное предположение, что 2 (2 + 2) вместе сначала особенно с обелусом.Двусмысленность не может быть решена путем поиска правил, руководств AMS или стандартов ISO (особенно если они не доступны в открытом доступе) это факт (и вы подтверждаете что), что мы можем получить разные ответы. Многие люди в Интернете пытаются рассуждают так или иначе. Это бесполезно. Чем это поможет, если 99 из люди рассуждают так, а 99 компьютеров дают ответы наоборот? Да, и обелус даже немного запутывает, как вы указываете. Там нет логического способа решить двусмысленность.Это определение неоднозначно. Нет четкого стандарта, и если он будет, то он еще не принят. повсеместно. Единственный способ решить проблему - поставить скобки.
8 августа 2020 г. : Вот проницательный комментарий Элиаса Мартенсона из Швеция:
Я читал вашу статью о порядке операций, или как вы это называете «правило PEMDAS». Одна вещь, которая, если упомянуть, не сразу очевидна, - это то, что когда вы говорите, что «правилу пемдаса научили миллионы студентов», вы конкретно имеете в виду студентов в США.Меня учили математике в Швеции, и там нас учили, что есть три уровня приоритета: Возведение в степень Умножение и деление Сложение и вычитание Скобки на самом деле не упоминаются, потому что здесь нет двусмысленности. Кроме того, чтобы объяснить, что их можно использовать , чтобы переопределить правила по умолчанию. Сейчас я живу в Сингапуре, и мои дети ходят здесь в местную школу. я просто проверил с ними, и они действительно узнали так же, как я учили. На всех языках программирования, которые я знаю, а также на математических Программное обеспечение, которое я тестировал, отмечу, что они следуют именно этому правилу.Правило "PEMDAS" кажется способом превратить что-то довольно тривиальное в что-то сложное. В дополнение к этому, он также преподает это неправильно, так как если кто-то настаивает на его использовании, ему придется написать что-то вроде: PE [M / D] [A / S], чтобы уточнить эквивалентность в группы. Простое прочтение этого документа создает у студента впечатление, что умножение должно как-то выполняться перед делением во всех случаях, что редко бывает правдой. Я говорю «редко» здесь, потому что я согласен с вами в том, что, безусловно, есть случаях имеет смысл сначала выполнить умножение, например, ваш пример 1 / ху.Тем не менее, если вы напишете это как 1 / x y, это не так ясно anymore, что означает, что пробелы значительны. Как инженер-программист, который в свободное время изучает физику], я часто раздражают нечеткие обозначения в математике. Не только проблемы с горизонтальным написанием (как тема вашей статьи), но также правильным набирать уравнения с помощью LaTeX. Авторы склонны использовать сокращенные обозначения, повторно использовать символы и т. д., что означает, что вы должны иметь в виду контекст, когда выясняя, что происходит.Это тип проблемы, с которой я бы столкнулся надеялись, были ограничены областью лингвистики, а не математики, единственная научная область, где что-то можно доказать с уверенностью. Наконец, я хотел бы добавить, что причина, по которой я потратил слишком много времени думаю об этом, потому что я работал над новым интерфейсом для Maxima (символьная математическая система), которая представляет собой программную формы в математической нотации, а это значит, что я должен полностью однозначный. Если вам интересно, вот демонстрационное видео.Мой ответ:
спасибо за содержательные комментарии. Для меня это похоже, из Швейцарии,
где нас не учили явному правилу PEMDAS. Тем не менее, я бы все равно
утверждают, что миллионы людей были обучены PEMDAS. Я со всем согласен.
Особенно при работе с математическим программным обеспечением
потребность в точности и недвусмысленности становится все более важной.
Тема не только педагогическая, здесь можно допустить серьезные ошибки. Не только
делать неправильные вычисления, но также используя результаты, которые были
сказано неоднозначно.Было бы интересно узнать, сколько
студенты в Сингапуре или Швеции читают, скажем, 8/2 (2 + 2) как 16 и как
многие прочитали бы это как 1, особенно если разделение дано как обелус. я
предсказал бы, что большинство из них дадут ответ 1. Это потому, что я учу
часто студенты со всего мира (Этим летом также двое из Сингапура
кстати) и что вопросы о PEMDAS часто всплывают, если не
супер четкость при написании (даже при написании выражений типа 1 / x + 3 есть
все еще студенты, которые читают это как 1 / (x + 3) или сбиты с толку и спрашивают.я начал
чтобы даже прояснить такие вещи, написав (1 / x) + 3 или используя горизонтальный
обозначение дробей \ frac {1} {x}, чтобы убедиться, что оно правильно прочитано.
Добавлено 24 августа, 2020 :
Добрый день! Надеюсь, у тебя все хорошо. Совсем недавно у нас с коллегами было несколько жарких споров. о проблеме 8 ÷ 2 (2 + 2) или тому подобное. Как и следовало ожидать, есть люди, которые отвечают это как 16, а люди, которые отвечают на это как 1. Что касается нас, мы находимся в неоднозначный стан.Люди, у которых был уникальный ответ на проблему, продолжают цитировать PEMDAS, или BEDMAS, или PE (MD) (AS). И мы сказали им, что условность не универсальна. Итак, мы попытались найти документы чтобы поддержать нашу сторону. И вот мы нашли вашу статью. я прочел все. Я поражен тем, что вы так терпеливо отвечаете людям, которые отправляют вам электронные письма и дают им одинаковые ответы, повторяя ваши объяснения снова и снова. В любом случае, я только что написал вам по электронной почте, чтобы вы знали (на случай, если вы еще не видел) Раздел 7.1.3, стр.23 ISO 80000-1: 2009 "
| "Эти процедуры могут быть распространены на случаи, когда числитель или знаменатель, или оба они сами являются продуктами или частными. В таком сочетании солидус (/) не ставится. знаком умножения или деления на той же строке если не вставлены круглые скобки, чтобы избежать двусмысленности ". |
Кроме того, пример 1, следующий за абзацем, должен разрешить все эти споры. Спасибо, что нашли время прочитать мое письмо.Мой ответ
Большое спасибо за отзыв. Ссылка ISO очень ценна! На это уже указывалось ранее, но, к сожалению, эта часть ISO не является общедоступной. Нужно купить стандартный.У меня действительно был доступ к соответствующие страницы из Раздела 7.1.3 ISO 80000-1: 2009:
Добавлено 16 января 2021 г. : Электронная почта:
После бурного онлайн-обсуждения меня перенаправили на ваш сайт
http: // люди.math.harvard.edu/~knill/pedagogy/ambiguity/index.html.
Судя по тому, что я там читал, вы, кажется, вините путаницу в использованных
обозначение. Хотя я согласен с тем, что это может сбить с толку людей, я хотел бы
представить более универсальное объяснение этой проблемы, основанное на использовании
(или не используя) простые аксиомы алгебраических структур. Обозначения тогда
становится более или менее неуместным.
У данного уравнения 6: 2 (2 + 1) есть несколько ответов, которые
на первый взгляд кажется нелогичным. Но я думаю, что некоторые люди просто забывают
чтобы определиться с диапазоном определений, над которыми они работают.С простым
арифметика, умножение и деление одинаково упорядочены и имеют
просто для выполнения перед сложением / вычитанием, но после вычисления
скобки и показатели. Вот где появляются PEMDAS или другие мнемоники
из. Это работает слева направо и правильно само по себе
простой контекст. Калькуляторы последовательного ввода делают это таким образом.
Но если принять контекст формальных алгебраических структур, в
В этом случае поле рациональных чисел, применяются дополнительные аксиомы. Теперь,
«распределенность» и «ассоциативность сложения и умножения»
(среди прочего) определены как основные аксиомы в контексте этой области.При этом порядок операций теперь гораздо более ограничен теми, кто
характеристики.
В этом контексте уравнение 6: 2 (2 + 1) можно преобразовать следующим образом:
6: 2 (2 + 1) = 6: (2 + 1) 2 // Ассоциативное свойство умножения
(просто чтобы доказать свою точку зрения с помощью этой аксиомы поля): ab = ba; разделение
неассоциативен
= 6: (4 + 2) // Распределительное свойство: ab + ac = a (b + c)
= 6: 6 // Порядок операций (теперь тривиальный),
"скобки перед показателями перед умножением / делением перед
сложение / вычитание "
= 1
Соблюдая все аксиомы полевой структуры, разделение теперь должно быть
решается путем вычисления сначала делимого и стороны делителя отдельно, затем
частное.Любой другой способ нарушает одну из основных аксиом поля и
будет недействительным с точки зрения этого поля. Более сложные калькуляторы
запрограммированы уважать это.
Однако, если не ограничиваться контекстом этих аксиом, другие результаты
также может быть действительным (т.е. 6: 2 (2 + 1) = 9, с последовательным вычислением на
базовый арифметический уровень).
Так что, на мой взгляд, проблема не в нотации, а в предоставлении контекста.
и, таким образом, определяющие аксиомы. Знание используемых инструментов и их предположений
соответствующие способности / ограничения - как всегда - важны.Кстати, в Германии студенты изучают мнемонику «KLAPPS» (KLAmmer,
Potenz, Punkt, Strich) перед высшей алгеброй, которая, к счастью, игнорирует
любое предлагаемое предпочтение умножения / деления ("Punktrechnung"
= "точечные вычисления" на основе "точечных" символов, используемых в немецком языке
вычисление '.' = Unicode U + 22C5 для умножения и ':' для деления)
и сложение / вычитание ("Strichrechnung" = "вычисления строк", из
символы «линия / перечеркнутая линия» '+' и '-'). Это отсутствие последовательности
предложение, кажется, предотвращает путаницу в высших классах, по крайней мере,
немного.Большое спасибо за то, что уделили время, прочитав это. Я был бы признателен услышать
от вас, особенно если вы не согласны с моими выводами. Математика
конечно не моя сильная сторона, но я просто учусь этому снова
с домашним обучением моего сына (благодаря изоляции COVID19) и
до сих пор помню некоторые из моих прежних лекций по информатике и математике
давно.
С наилучшими пожеланиями из Баварии / Германии! Бернхард Новотны, M.Eng.
Мой ответ:Это интересный ракурс. Мне особенно приятно слышать о немецкое правило KLAPPS.Я ходил в школу в Швейцарии и еще не видел это. Правила также должны соблюдаться со студентами, и KLAPPS - это хорошее имя. Интересно, что он не решает двусмысленность PAMDAS. Ваше предложение устранить двусмысленность вполне может сработать, но проблема более социолингвистическая, чем математическая. Уже есть разные стандарты вокруг. Я не знаю, как вводить новый XKCD сказал это лучше всего.22 февраля 2021 г .: Вик:
Вы писали, что PEMDAS и BODMAS неоднозначны. Я не согласен.У меня есть степень магистра математики и преподаю математику 30 лет. Вы задали вопрос с помощью символа разделения /. Мне кажется, что этот символ разделения сбивает с толку, и я никогда его не использую. Мне интересно, что хотя все калькуляторы дали ответ 11 на ваш начальная проблема вы, кажется, думаете, что они должны что - выдать сообщение об ошибке? Ответ - 11. Здесь нет скобок, и я не понимаю, почему вы думаете вы можете вставлять скобки волей-неволей. Люди ошибаются, потому что они вычисляют по шаблонам, а не думают. «Какие здесь правила».Мой ответ:
Спасибо за ответ. Вы, конечно, можете не согласиться. Я дал много причины на моей странице, почему есть двусмысленность. Многие студенты дают ответ 2, а не 11 в исходном примере. Если вы прочитаете мой текст, вы увидите эта двусмысленность не означает наличие сообщения об ошибке. В большинстве случаев, несогласие происходит из-за отсутствия стандарта. Профессиональные ссылки приведенные на моей странице подтверждают, что нет стандарта. Ставить скобки нельзя помещенные «волей-неволей», они размещены, чтобы прояснить ситуацию и устранить двусмысленность.Во время обучения почему бы вам не провести эксперимент и не спросить студентов, что они подумайте, когда им нужно вычислить 2x / 3y -1 для x = 9 и y = 2. Большинство людей дает ответ 2, поскольку они заключают в скобки 3y как неразделимые (довольно много учителей подтвердили который). Это также стандарт, которому следуют многие книги (особенно если они придерживаются к более ранним профессиональным стандартам, таким как AMS, или правилам, таким как PEMDAS, которые часто учили и ставили умножение перед делением. Коджори, сегодня по-прежнему самый Авторский деятель по математике примечания написал еще в 1928 г. "Если арифметический или алгебраический член содержит / и х, в настоящее время нет соглашения о том, какой знак должен использоваться первым."Это актуально и сегодня Оливери продолжение Вика
PEMDAS не ставит умножение перед делением. Они идут по порядку слева направо. Просто потому, что ученики соединили 3й как неразлучные не означает, что ученики правы. Они делают предположение. . Какие книги нравятся студентам? Я никогда не видел ни одной из этих книг. / означает деление. Другого толкования нет. Так ты говоришь что PEMDAS не является общепринятым правилом? Так выражение вроде 2/3 + 5/8 x 7 может иметь много разных ответов в зависимости от того, где вы положили скобки?Мой ответ:
Вторую часть можно было бы прочитать как 5/56 и получить 127/168, в то время как компьютеры прочтите это как 2/3 + (5/8) 7 = 121/24 (на самом деле не все компьютеры, но большинство поколений калькуляторов давали другие результаты). 2.Ты скажем, вы делите торт на 2 человек, имея в виду торт / (2 человека), а не (торт / 2) чел. Часто, особенно для установленных формул, мы естественно берем их вместе. Популярный пример - 1 / 2pi, потому что 2pi часто сам по себе является стандартным устройством. Большинство людей читают это как 1 / (2pi) но компьютер читает это как пи / 2. Бывший 1 / (2pi) соглашается с написанием руководящие стандарты, выдвинутые AMS или APS.Снова Вик:
Если 2x / 3y означает 2x / (3y), как нам написать выражение 2 раза x затем разделить на 3, а затем умножить на y?Мой ответ:
Пример 2x / 3y - типичный пример, который большинство людей читают как (2x) / (3y).Компьютер читает это как 2xy / 3. Можно написать (2xy) / 3 или (2/3) xy или просто 2xy / 3 если бы кто-то хотел, чтобы это было написано так, как это читает компьютер. Это не двусмысленно и в целом, и никто не может его неправильно истолковать.23 февраля 2021 г., Джеймс:
Мне очень нравится ваша статья (я бы назвал ее так). Это привлекла мое внимание, потому что я начала видеть работы студентов которые вставляют в свои калькуляторы целые выражения, отражающие несоответствия, обсуждаемые в вашей статье.Одна вещь, которую я отмечу, касается примера 18/3 * 2, чтобы в котором вы утверждаете, что большинство людей придут к решению 3, а компьютеры - 12. Сразу после того, как увидели выражение, Я рассчитал, что решением будет 12. Я считаю, что прочитал это. как восемнадцать третей умножить на два. Я списываю это на то, что часто работаю с четвертями, третями и половинами вне работы и, когда я вижу "/" Я сразу думаю о дроби, а не об операции. Более доказательства в поддержку вашего аргумента о двусмысленности в математике и необходимость ясности в выражениях.Еще раз спасибо за приятное чтение. я в предвкушении исследуя остальную часть вашего сайта.Мой ответ:
Спасибо за ответ. Да, это очень интересная история. Это кажется, также во многом зависит от того, как это писать. Часто в научная литература (а также некоторые руководства от AMS или APS), указано, что такие вещи, как a / bc, следует читать как a / (bc) а не (a / b) * c. Причина также в том, что часто товары читают люди должны принадлежать друг другу. Если взять 18 / 2π, то большинство людей прочтите это как 9 / π, а не как 9π (как это делает компьютер).Только можно догадываюсь, но я подозреваю, что это было причиной создания PEMDAS (наиболее часто используемое сокращение), а не PEDMAS или PE (MD) AS (которые должны быть со сноской, что MD эквивалентны и читаются слева). Последнему вряд ли можно научить. PEMDAS уже трудно продать (многие студенты Гарварда неправильно понимают базовые PEMDAS и читают + перед *. В педагогических вопросах всегда переоценивают то, что сложности, которым люди могут научиться. Устанавливаем новый стандарт, такой как PE (MD) AS (они появляются уже в школах) также имеет проблему, которая многие тексты будут прочитаны неправильно.Если выражение принадлежит друг другу как RT в термодинамике или mc 2 в физике. Вернемся к вашему примеру: 18/3 * 2, да, думаю, многие прочитали бы это как 12, но если вы напишете 18 / ab с a = 3, b = 2, большинство прочитало бы это как 3. Забавно, как по-человечески Здесь сочетаются психология, лингвистика и история, а также математика. Это делает тему такой интересной.
28 февраля 2021 г. : хороший новый пример:
Я учитель математики в небольшой католической школе.Недавно я столкнулся с прикрепленной проблемой (# 12) в моей программе спирального обзора в шестом классе. Это похоже на вопрос, который вы задаете, но в нем используется знак деления вместо "/". Я разместил его в группе учителей математики, в которую я участвую, для средней и старшей школы по математике и СВЯТОЙ КОРОВЕ! Это привело к дебатам / спорам. Есть те, кто непреклонен, что ответ - 6, те, кто непреклонен. что ответ 24, и те, кто непреклонен, что ответ может быть любым. Конечно, каждая группа думает, что они правы! Ваша статья была размещена в ветке несколько раз.Я прочитал подавляющее большинство из них. Мне любопытно, если вы видите разницу в неоднозначности прилагаемой проблемы с разницей в использовании символов или если это останется такой же загадкой, как и проблема, которой вы поделились. Большое вам спасибо за ваше время! |
Мой ответ:
Спасибо. Это очень ценно, потому что это подтверждает, что единственный способ избежать таких обсуждений - это быть предельно ясным и добавить кронштейны. Добавил в коллекцию.Хорошо то, что все в вашей группе учителей правы. Есть веские аргументы в пользу группы 2c вместе, потому что это часто используется в литературе, там веские аргументы в пользу разделения в первую очередь, потому что это то, что делать. Кроме того, есть веские аргументы в пользу того, что оба правы. Но кто когда-нибудь выиграет аргумент все равно столкнется с дилеммой оценить это ... буря расстроенных учеников, родителей и других учителей. Я просто буду охватываю алгебру в моем учебном курсе по математике и могу упомянуть об этом
4 марта 2021 года : обсуждения в социальных сетях, похоже, все еще продолжаются: Я получил следующее электронное письмо:
Мне было интересно узнать об этом уравнении.2. Если это так, ПЕМДАС ГОВОРИТ «Экспоненты» - 2-й. Так что мой вопрос действительно в том, что экспоненты также являются формой умножения, так почему это теперь M такое же, как D в уравнении, где теперь он заменен на PE (M или D слева направо) (A или S слева направо)? В мои математические годы умножение в-третьих, потому что экспонента и умножение одинаковы. Также когда мы упрощать 6/9 упрощается как 2 (3) / 3 (3), мы не можем упростить это как ответ 6, когда должно быть 2/3. Вот новинка в социальных сетях: 24/4 (8/4) и мой ответ = 3.Некоторые говорят, что это 12. После того, что я объяснил над. Какой твой ответ? Заранее спасибо.Мой ответ:
Корпус 6/2 (1 + 2) теперь классический. Большинство людей получают 1. Это не потому, что это целое число, но потому что 2 (1 + 2) рассматривается как единица. Наиболее компьютеры получают 9, потому что (M и D) оцениваются на одном уровне. Новых 24/4 (8/4) не видел. У вас есть 3, что получает большинство людей. Миллионы из них, потому что это закреплено в правилах PEMDAS (M перед D) и потому, что это часто пишется в книгах как таковых.Большинство компьютеров получают 12. Здесь нет правильного или неправильного ответа. Вопрос только что поставлен неоднозначно. Это известно уже 100 лет. это Интересно, что соцсети до сих пор об этом гудят. Но это делает это интересно и осведомленно. Я написал краткое резюме с источниками в этот документ для курса, который я преподаю прямо сейчасОчевидно, что на гораздо более базовом уровне все неясно. Следующее электронное письмо иллюстрирует замешательство, которое может возникнуть даже у звездных студентов. Кажется, сложно даже достать через фундаментальные свойства PEMDAS, такие как возведение в степень перед умножением и разделение и скобка, перед которыми не оспариваются.2 = 1, то это однозначно, поскольку возведение в степень предшествует другим операциям. Если написать 9/3 (3), то это неоднозначно, потому что его можно прочитать как (9/3) (3) = 3 * 3 = 9 или 9 / (3 (3)) = 9/9 = 1. Случай 6/1 (1 + 2) - неоднозначный случай, потому что его можно читать как (6/1) (1 + 2) = 18 или 6 / (1 (1 + 2)) = 2. Это та ситуация, о которой мы говорили. Нет, 6 / (1 + 2) не является неоднозначным. Ясно, что 6/3 = 2. Нет обсуждения об этом случае, потому что скобки сделаны раньше.
13 марта 2021 г .:
По профессии я технический писатель, поэтому лаконичное, точное общение - это то,
моей страсти.Я также изучал математику в бакалавриате, так что это
обсуждение было прямо моим союзником. Спасибо за поддержку этой страницы. Это было приятное путешествие.
Как упомянул один из рассылающих по электронной почте, где это возможно, я предпочитаю наборные движки, например Латекс.
Почему бы никому не написать $ \ frac {2x} {3y} - 1 $ (или что-то подобное), если бы они
наличие выбора утомительно для меня, но это часть философии моей профессии.
Я беру время и когнитивные усилия, чтобы четко объяснить что-то, чтобы свести к минимуму
усилия, которые читатели должны приложить, чтобы понять это.В отдельном электронном письме упоминалось использование знака деления или обелуса: (LaTeX: $ \ div $),
что заставило меня понять, что я не оцениваю и / так же. Назначаю разные психические
вероятности к разным интерпретациям. Если бы мне вручили документ,
содержит ab (c), я бы сначала проклял автора и начал поиск контекстных подсказок. Если я
не нашли никаких подсказок, я бы отметил, что они нашли время, чтобы использовать персонажа вне основного
Набор ASCII. Это говорит мне, что они, возможно, а может быть, намеренно избегали
пресловутый, очевидно неоднозначный слэш.Поэтому я думаю: «Что бы наиболее распространенное,
Самая ленивая интерпретация этого уравнения была бы, если бы автор использовал косую черту? "
Вероятно, это то толкование, которого они пытались избежать.
Иногда мне доступен один кусочек контекста, когда я могу решить, сколько усилий они приложили
Чтобы избежать косой черты, они используют то устройство, которое они используют. Ввод текста в macOS
тривиально (Alt + /), но для набора текста на iPhone требуется либо копирование и вставка, либо
переход на отдельную клавиатуру стороннего производителя.
Так что это мой вклад! Это больше ориентированный на поведение подход: количество усилий, которые он
потребовалось, чтобы автор напечатал что-то, что может предложить их предполагаемое значение.С уважением,
Ник
Мой ответ:
Привет, Ник,
приятные моменты. Для меня также это то, что когда я пишу латексные формулы
в тексте и не отображается, я склонен использовать a / bc вместо \ frac {a} {bc}
потому что он лучше вписывается в страницу. Поскольку я знаю об этих войнах PEMDAS, я
Я больше не сомневаюсь и пожертвую красотой, если она может увеличить ясность. Этот
для меня как учителя особенно важно на экзаменах.
Повсюду используются знак деления, обелус и косая черта. Я также узнал,
особенно от учителей, что для них обелус используется иначе и
что это более сильное подразделение.Я сам стараюсь избегать обелуса.
Я знаю только, что видел это в начальной школе и не прикасался к нему
поскольку.
Да, ясность требует некоторых усилий, иногда также требуется жертва некоторых
элегантность. Но мы знаем это и по языку. Есть много выражений
которые становятся понятными только в контексте. Ответ однозначно - избыточность.
Даже язык нашего генома использует избыточность, чтобы избежать
ошибки связи.
Оливер
строк, целых чисел и чисел с плавающей запятой
В этом руководстве мы собираемся начать работать с основными типами Python: строки (для текста) и целые числа и числа с плавающей запятой (для числовых значений).
Обратите внимание, что в этом руководстве вы работаете в REPL (IDLE). Вы можете найти дополнительную информацию
о REPL и о том, как запустить Python в вашем cmd или терминале в руководстве по установке Python.
Привет, мир!
По традиции мы начнем с печати «Hello, World!» к
консоль. В Python функция для достижения этого метко названа print () .
Введите следующее рядом с >>> :
REPL просто напечатает текст прямо у вас.
Теперь напечатайте свое имя и немного поэкспериментируйте!
Несколько аргументов
Еще кое-что интересное в функции print () заключается в том, что вы можете передать ее
несколько аргументов для печати:
>>> print («Привет», «До свидания»)
Фактически, вы можете передать в печать столько информации, сколько захотите:
>>> print («один», «два», «три», «четыре», «пять», «шесть», «семь», «восемь», «девять»)
Конечно, вы также можете получить такой же результат с помощью этого:
>>> print («один, два, три, четыре, пять, шесть, семь, восемь, девять»)
Вам решать, что подходит и когда.
Математика
Любимое времяпрепровождение.
Простая арифметика
Python может выполнять простую арифметику. Для начала попробуем сложить:
Теперь вы должны увидеть результат этого вычисления в REPL.
Вычитание, умножение и деление работают одинаково.
>>> 6 - 2
>>> 8 * 4
>>> 9/3
А теперь попробуйте еще несколько, чтобы увидеть, какие результаты вы получите. Попробуйте свои силы во всех
основные математические операторы: + , - , * (умножение), / (деление), ** (экспоненты) и % (модуль).
Объединение операций
Возможность выполнять только одну операцию за раз довольно ограничивает, поэтому Python позволяет нам комбинировать математические операции. Попробуйте это:
А теперь попробуйте еще несколько. Вы можете комбинировать столько операций, сколько захотите.
Приоритет оператора
Заметили ли вы неожиданные результаты, когда начали комбинировать операции? Если вы этого не сделали, попробуйте это:
Python следует традиционным математическим правилам приоритета, которые гласят: это умножение и деление выполняются до сложения и вычитания.(Ты может вспомнить BODMAS .) Это означает, что в В нашем примере выше сначала умножаются 2 и 4, а затем результат вычтено из 10.
Мы можем изменить порядок операций, используя круглые скобки. Что-нибудь внутри круглые скобки выполняются первыми.
А теперь попробуйте вот так:
У вас должен быть другой ответ.
Из-за правил приоритета сложные операции, такие как наш первый пример, могут будет довольно сложно читать. Если вы обнаружите, что пишете более сложный выражений, нет ничего плохого в добавлении круглых скобок для ясности.
десятичных знаков
Одна из вещей, которая сбивает с толку новичков в программировании в целом, — это концепция чисел с плавающей запятой . В основном числа с десятичными точки имеют тенденцию вести себя немного странно, когда вы выполняете математические операции на них. Причины этого сложны и коренятся в природе. вычислений, поэтому пока давайте просто понимаем, что с десятичными числами происходят странные вещи.
Чтобы увидеть пример этого, попробуйте разделить 10 на 3 :
Ответ должен длиться вечно, но это не так.А теперь попробуйте что-нибудь немного более чувствительный к точности:
>>> 1.000000000000001 * 8
Наверное, не то, что вы ожидали, верно? А пока тебе просто нужно принять это в качестве ограничения, и позже вы узнаете, как другие программисты работают с Это.
Заключение
Теперь давайте объединим то, что мы узнали сегодня. Мы можем сказать print () для печати
сразу несколько вещей, разделенных запятой:
>>> print ('Результат 2 + 2 равен', 2 + 2)
Сохраните свою работу
В этом уроке вы кодировали REPL (IDLE), но много раз вы хотите чтобы вместо этого сохранить ваш код.В таких случаях вы можете сохранить свой код в файл с помощью текстового редактора. Мы даем некоторую информацию о текстовых редакторах в нашем Руководстве по началу работы.
Откройте текстовый редактор и напишите код из первого упражнения:
Сохраните файл как ex1.py . Вы можете называть файлы как хотите,
но они должны заканчиваться на .py , чтобы питон мог их легко прочитать.
Читая ваш файл в Python, вы снова будете использовать оболочку cmd или terminal .
Вы можете прочитать свой файл с помощью следующей команды (введите без знака $):
Если перед кодом указано >>> , значит, вы все еще находитесь в REPL (IDLE) и вам нужно выйти.
это с:
Тогда вы сможете загрузить файл.
На этом мы завершаем сегодняшнее руководство. В следующем уроке мы узнаем, как объединить результаты нескольких отдельных выражений с использованием переменных, получить ввод от пользователя и принимать решения на основе этой информации.
Дополнительная литература
В Руководстве разработчика Google есть очень хорошая вводная статья.
Вы также можете найти ресурсы для начинающих на веб-сайте Python. и обратитесь к документации Python, где объясняются основы языка.
Вернуться к обучающим материалам главная страница кодовой панелиРазъяснение правила PEMDAS! (Примеры включены) — Mashup Math
P: Круглые скобки
E: Экспоненты
M: Умножение
D: Деление
A: Сложение
S = Вычитание
Операции, указанные в правиле PEMDAS, выполняются слева направо.
Кроме того, правило PEMDAS для вызова математического порядка операций имеет несколько важных подправил, которые также необходимо соблюдать, если вы хотите правильно использовать PEMDAS (и получать правильные ответы на математические задачи).Эти важные подправила относятся к отношениям между умножением / делением и сложением / вычитанием.
Эти важные подправила правила PEMDAS подробно объясняются в следующем разделе:
Правило PEMDAS: ключевые моментыПравило PEMDAS существует уже несколько десятилетий как инструмент, помогающий учащимся запомнить математический порядок операций. . Многие предпочитают просто запоминать мнемоническое PEMDAS (произносится PEM-DAHS), в то время как другие предпочитают запоминать фразу Пожалуйста, извините мою дорогую тетю Салли.
Однако вы решили помнить, что правило PEMDAS не так важно, как запоминание ранее упомянутых подправил? Почему так важны подправила правила PEMDAS? Потому что вспомогательные правила часто определяют разницу между получением правильного или неправильного ответа на математическую задачу.
Правило PEMDAS может быть несовершенным, но если вы помните вспомогательные правила, оно может быть полезным инструментом, который поможет вам правильно применять математический порядок операций и получать правильные ответы как на простые, так и на сложные математические задачи при условии, что вы знаете важных подправила.
Важные подправила к правилу PEMDAS:1.) P: Выполняйте операции внутри скобок или групп, прежде чем делать что-либо еще (если нет групп или скобок, вы можете пропустить этот шаг) .
2.) E: Затем, после выполнения операций внутри скобок и группировок (если они есть), примените любые экспоненты (если нет показателей, вы можете пропустить этот шаг).
3.) M / D: Затем, после скобок, групп и экспонент, выполните умножение / деление слева направо в зависимости от того, какая операция будет первой).
★ Тот факт, что M стоит перед D в правиле PEMDAS, не означает, что вы всегда будете выполнять умножение перед делением.
4.) A / S: Наконец, после умножения и / или деления выполните сложение / вычитание слева направо в зависимости от того, какая операция будет первой).
★ Тот факт, что A стоит перед S в правиле PEMDAS, не означает, что вы всегда будете выполнять сложение перед вычитанием
★ = Чрезвычайно важно
Почему учителям математики пора отбросить BODMAS
Что означает BODMAS?
Акроним BODMAS означает скобки, порядки, деление, умножение, сложение, вычитание.
Иногда его называют BIDMAS (с «индексами» вместо «заказов») или правилом PEMDAS в Америке (с «круглыми скобками» и «экспонентами»).
Правило BODMAS
Это математическое правило диктует правильный порядок операций, которым нужно следовать, когда вы заполняете вопрос с математическим числовым предложением с различными операциями.
Первый шаг — сделать что-нибудь в скобках, затем заказать следующие (например, извлекать квадратный корень или индексы). Деление и умножение находятся на одном уровне, что означает, что им дается равный приоритет, и они должны выполняться слева направо, а не все деление, а затем все умножение.Точно так же сложение и вычитание находятся на одном уровне и должны выполняться слева направо.
Я начал свою педагогическую карьеру в средней школе. Молодой, нетренированный и еще не лысеющий, я оказался на самом крутом этапе обучения в моей жизни.
Еженедельные встречи с моим руководителем отдела были жизненно важны для обсуждения педагогики, и я строго придерживался его инструкций: «Никогда не сокращайте совокупную частоту», «Мы всегда подбрасываем монеты и получаем решку, мы никогда не подбрасываем монеты и не получаем орла», и что очень важно. , «Мы никогда, никогда не используем БОДМЫ».
Отказаться от использования BODMAS оказалось труднее, чем вы думаете. Приехали студенты, хорошо разбирающиеся в его применении.
Нам пришлось и научить этому. Нам приходилось убеждать комнаты, заполненные подростками, в том, что они должны изменить основные принципы своей арифметической системы убеждений. Это было сложно, потому что подростки ненавидят перемены и ненавидят прозелитизм взрослых.
Так зачем нам вообще беспокоиться? Что убедило весь отдел в том, что нужно приложить столько усилий для решения такого, казалось бы, тривиального вопроса?
BODMAS ошибается.Это то что.
Неправильный ответ
Буквы обозначают скобки, порядок (что означает степень), деление, умножение, сложение, вычитание. Таким образом, предполагается, что в этой последовательности происходит упрощение любого данного математического выражения.
Например, чтобы оценить 3 + (3 + 3) 3 ÷ 3 — 3 x 3 , мы действуем в указанном выше порядке:
Это был бы действительно полезный алгоритм, если бы он работал в любой ситуации, но рассмотрим гораздо более простое выражение 1 — 2 + 4 .Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и выполнять сложение с последующим вычитанием:
Это ошибочно. Правильное значение — 3. BODMAS нас подвел. Позор БОДМАМ!
Математические задачи
У нас не может быть волшебной мнемоники, которая не работает все время; Предположим, он решил не работать в важный момент. Представьте, что вы пытаетесь объяснить своему ученику, что причина, по которой он потерял оценку на экзамене, заключалась в том, что то, что вы сказали ему, всегда работает, на самом деле не сработало во всех случаях, и, фактически, один из таких случаев произошел тот документ GCSE.
Это не новая проблема. Я не первый, кто об этом пишет. Даже Википедия решает эту проблему и предлагает несколько альтернатив. Студенты любят Википедию! Так почему же BODMAS все еще актуален?
В Хайгейте вокруг него было такое клеймо, что некоторые партии высмеивали меня более десяти лет после того, как мой коллега пережил обмен в классе, который проходил примерно так:
Учитель: Как нам упростить это выражение?
Студент: БОДМАС, сэр.
Учитель: Мы здесь не используем БОДМЫ.
Студент: Но вот чему мистер Элтон научил нас в прошлом году, сэр.
После этого мне несправедливо присвоили прозвище «БОДМАС», которое преследовало меня повсюду. У меня не было защиты; Заявление подал платный студент, так что оно должно быть правдой. По крайней мере, один человек (он знает, кто он) все еще называет меня БОДМАСом чаще, чем он использует мое настоящее имя.
Несмотря на то, что я абсолютно не виновен в том, что запятнал умы невинных студентов, я чувствую себя обязанным исправить положение, поэтому я использую эту платформу именно так.Считайте это общественными работами.
Правильный ответ
Нет смысла бить BODMAS, не предлагая альтернативы. Проиллюстрированная выше ошибка вызвана тем фактом, что сложение и вычитание не обязательно должны происходить в таком порядке. Если у нас есть строка этих двух операций, она называется суммой, и мы должны работать слева направо:
Точно так же деление не более важно, чем умножение. Если у нас есть строка из этих двух операций, она называется продуктом, и мы снова будем работать слева направо:
Теперь у нас такой порядок: скобки, порядок, продукты, суммы.
Это дает нам BOPS, который на целый слог короче, чем BODMAS, и имеет значительное преимущество в том, что он надежен.
Я уверен, что если бы кто-то предложил BOPS до BODMAS, то последний был бы предан безвестности. Даже сейчас еще не поздно избавиться от двусложных арифметических сокращений.
Я призываю своих коллег по всему миру запретить BIDMAS и очистить PEMDAS. Не оставляйте от них никаких следов. Позвольте BOPS нанести победный удар молодым математикам во всем мире.
Оуэн Элтон — учитель математики, автор / исполнитель глупых песен и автор математических минут. Вы можете следить за ним в Твиттере по адресу @owenelton.
Как решить математическую задачу с помощью PEMDAS
Обновлено 15 декабря 2020 г.
Крис Дезил
Взгляните на следующее равенство:
x = 7 + 2 × (11-5) ÷ 3
Решите для x , выполняя математические операции в порядке слева направо, и вы получите 18, что является неправильным ответом.Чтобы получить правильный ответ — 11, вы должны соблюдать правильный порядок действий. Если вы не можете вспомнить правильный порядок, PEMDAS может вам помочь. Это аббревиатура, обозначающая круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
В общем, PEMDAS не так уж сложно запомнить, но если вы не можете это сделать, вам может помочь пара крылатых фраз. Один из них — «Прошу прощения, моя дорогая тетя Салли». Первая буква в каждом слове этой фразы является одной из букв в PEMDAS.Если вы предпочитаете называть круглые скобки скобками, вспомните аббревиатуру BEDMAS и крылатую фразу «Большие слоны уничтожают мышей и улиток». В этой фразе D и M меняются местами, но это нормально. Когда вы доходите до умножения и деления, вы обычно делаете то, что идет первым в выражении.
Некоторые люди, которым сложно запомнить PEMDAS, ищут порядок операций с помощью поиска PADMAS math. Это не поможет. Он игнорирует E для экспонент, а экспоненты — важная операция, которую необходимо выполнить, прежде чем вы перейдете к любой из других арифметических операций.
Как применять порядок операций
Всякий раз, когда вам нужно выполнить длинную цепочку операций, правила математики ясны. Вы всегда начинаете с выполнения операций в круглых скобках (скобках), а затем решаете экспоненты, которые представляют собой числа в форме x a . Следующие две операции — это умножение и деление. Если деление идет первым в выражении, вы делаете это в первую очередь. Точно так же, если сначала идет умножение, сделайте это в первую очередь.То же верно и для двух последних операций — сложения и вычитания. Выполняйте вычитание перед сложением, если они идут первыми в выражении, и наоборот.
Пример расчета
Еще раз взгляните на выражение в начале этой статьи. Применяя PEMDAS, вы решаете это следующим образом:
- E — Решите все экспоненты:
- M, D — Произведите умножение и деление:
- A, S — Выполните сложение и вычитание:
11-5 = 6
Таким образом, выражение теперь становится
x = 7 + 2 × 6 ÷ 3
Сначала идет умножение, поэтому начнем с этого.Теперь выражение выглядит следующим образом:
x = 7 + 12 ÷ 3
Теперь деление должно получиться:
x = 7 + 4
Необходимо выполнить только одно сложение, которое дает окончательный ответ:
x = 11
Иногда вы видите несколько скобок или скобок. Правило состоит в том, чтобы упростить все внутри скобок, начиная с внутренних, прежде чем переходить к остальным арифметическим операциям. Не забывайте следовать PEMDAS или BEDMAS даже при работе с числами в скобках.2 × 4
4 + 4 × 4
4 + 16





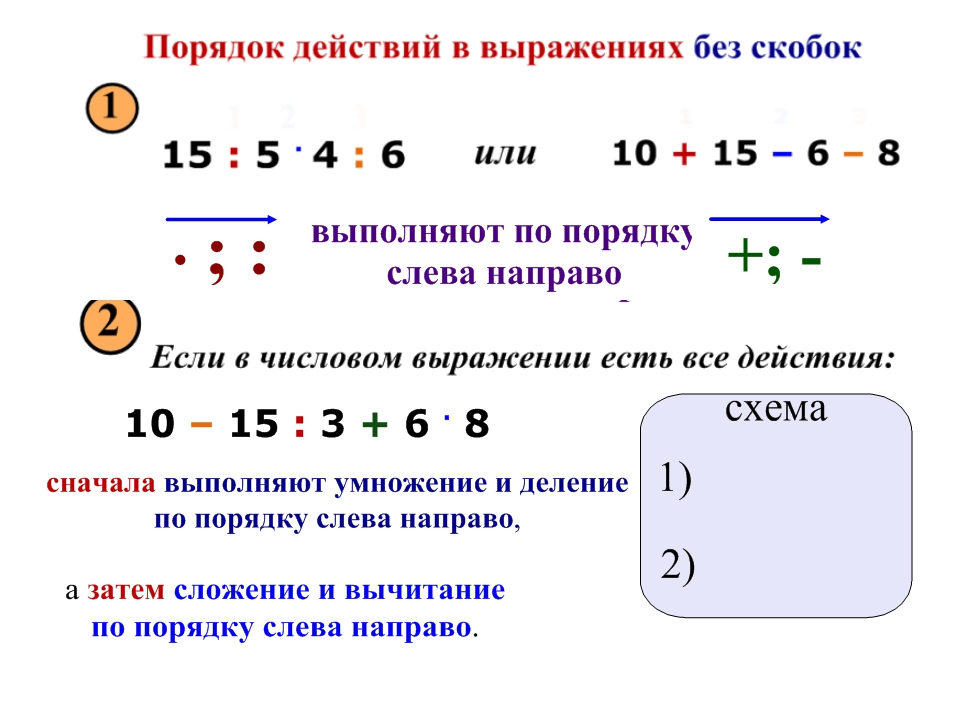 Вот как она звучит:
Вот как она звучит:

 ..
..

 В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение: При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 . Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками). Затем я умножил 9,36 на y, что составило 0,2. Окончательный ответ - 1,872.
2) По-другому, первое, что я сделал, это умножил a на x. Продукт, который был равен 11.232, был временно отложен. Затем b был умножен на y, что дало произведение 0,24. Теперь проблема была решена разделением 11.232 (или топор) на 0,24 (или на), чтобы получить окончательный ответ 46,8.
Подскажите, пожалуйста, какой ответ правильный и почему?
Затем я умножил 9,36 на y, что составило 0,2. Окончательный ответ - 1,872.
2) По-другому, первое, что я сделал, это умножил a на x. Продукт, который был равен 11.232, был временно отложен. Затем b был умножен на y, что дало произведение 0,24. Теперь проблема была решена разделением 11.232 (или топор) на 0,24 (или на), чтобы получить окончательный ответ 46,8.
Подскажите, пожалуйста, какой ответ правильный и почему?  Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение правильное.
Некоторые тексты содержат правило , как и во втором решении , что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме экспонент], включая «явное умножение» с использованием символа. . Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое.В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что намного хуже .
Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение правильное.
Некоторые тексты содержат правило , как и во втором решении , что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме экспонент], включая «явное умножение» с использованием символа. . Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое.В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что намного хуже . 
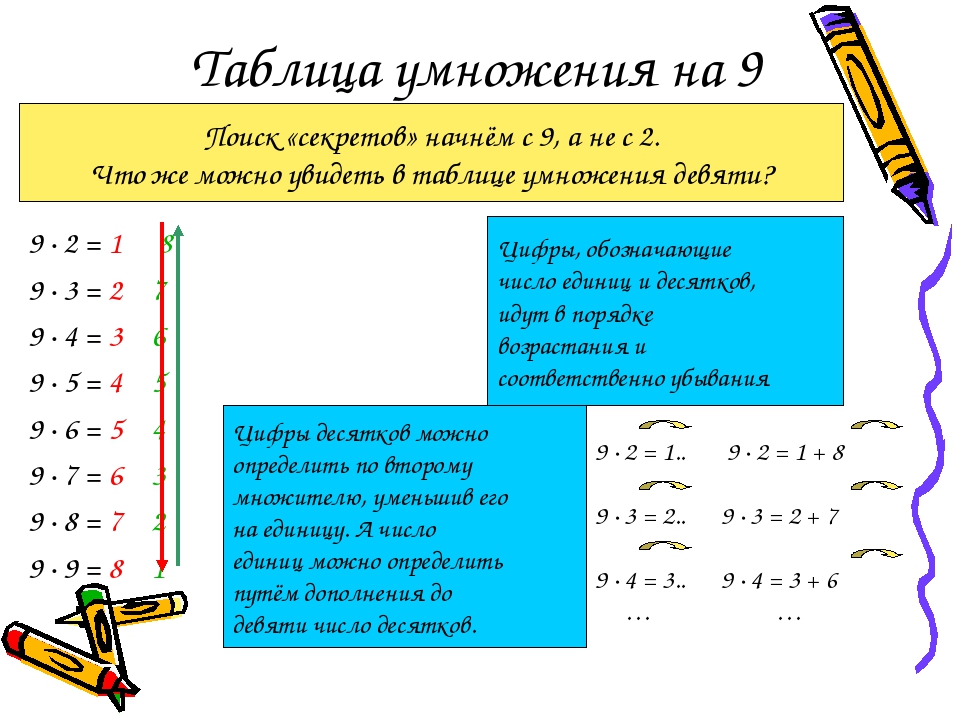 Имеют ли подразумеваемое умножение и явное умножение одинаковый приоритет на графических калькуляторах TI?
Подразумеваемое умножение имеет более высокий приоритет, чем явное умножение , что позволяет пользователям вводить выражения таким же образом, как они были бы написаны.Например, TI-80, TI-81, TI-82 и TI-85 оценивают 1 / 2X как 1 / (2 * X), в то время как другие продукты могут оценивать то же выражение как 1/2 * X слева направо. верно. Без этой функции было бы необходимо сгруппировать 2X в круглых скобках, что обычно не делается при написании выражения на бумаге.
Этот порядок приоритета был изменен для семейства TI-83, семейства TI-84 Plus, семейства TI-89, TI-92 Plus, Voyage ™ 200 и карманного компьютера TI-Nspire ™ в режиме TI-84 Plus. Подразумеваемое и явное умножение имеют одинаковый приоритет.
Имеют ли подразумеваемое умножение и явное умножение одинаковый приоритет на графических калькуляторах TI?
Подразумеваемое умножение имеет более высокий приоритет, чем явное умножение , что позволяет пользователям вводить выражения таким же образом, как они были бы написаны.Например, TI-80, TI-81, TI-82 и TI-85 оценивают 1 / 2X как 1 / (2 * X), в то время как другие продукты могут оценивать то же выражение как 1/2 * X слева направо. верно. Без этой функции было бы необходимо сгруппировать 2X в круглых скобках, что обычно не делается при написании выражения на бумаге.
Этот порядок приоритета был изменен для семейства TI-83, семейства TI-84 Plus, семейства TI-89, TI-92 Plus, Voyage ™ 200 и карманного компьютера TI-Nspire ™ в режиме TI-84 Plus. Подразумеваемое и явное умножение имеют одинаковый приоритет. Ни один ответственный математик не стал бы писать такое выражение; мы бы просто сказали
п
---
м л
так что не было бы никаких сомнений в его значении. В конце концов, цель правил - позволить нам ясно общаться, а не помочь нам обмануть учеников и начать ссоры между семьями.Так что вы на самом деле можете быть «старомодным»; или вы можете быть на передовой. В любом случае, боюсь, вам просто нужно будет узнать, как они это делают в классе, и следить за ними. Больше не о чем беспокоиться.
Ни один ответственный математик не стал бы писать такое выражение; мы бы просто сказали
п
---
м л
так что не было бы никаких сомнений в его значении. В конце концов, цель правил - позволить нам ясно общаться, а не помочь нам обмануть учеников и начать ссоры между семьями.Так что вы на самом деле можете быть «старомодным»; или вы можете быть на передовой. В любом случае, боюсь, вам просто нужно будет узнать, как они это делают в классе, и следить за ними. Больше не о чем беспокоиться.  2 \ div 4b + c \):
2 \ div 4b + c \):
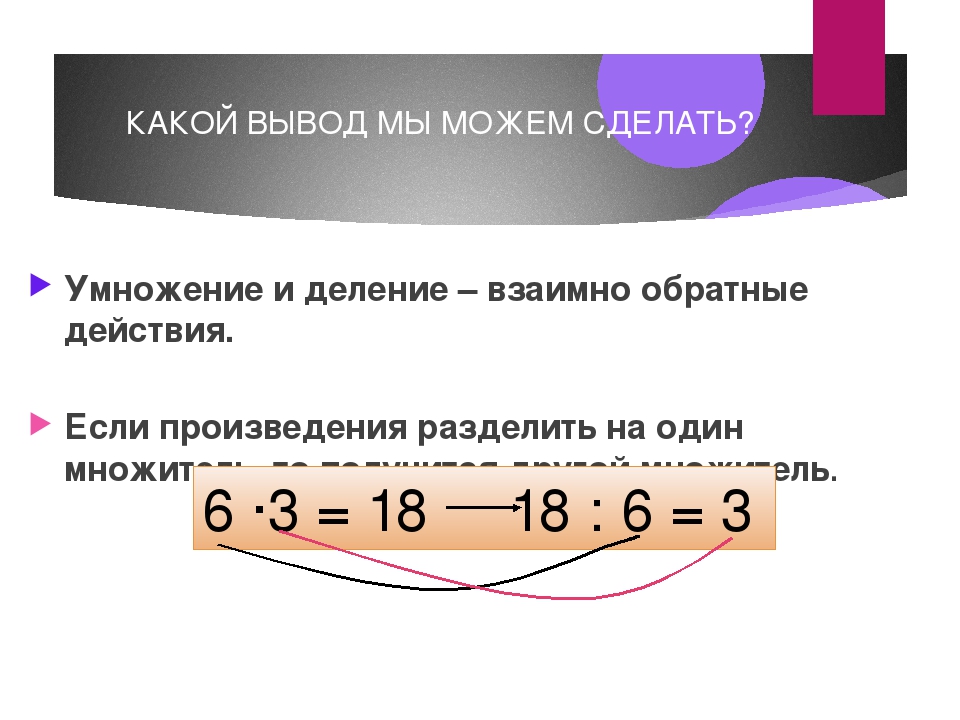 Но они не могут указать ни одного правила, которое бы это оправдало; а поскольку математика - это доказательство, и то, что вы ЗНАЕТЕ, правильно, а не только то, что кажется правильным, это плохо.
Но они не могут указать ни одного правила, которое бы это оправдало; а поскольку математика - это доказательство, и то, что вы ЗНАЕТЕ, правильно, а не только то, что кажется правильным, это плохо. Но размышления о наших условностях могут быть очень полезными. В следующий раз я закрою все, взглянув на историю и приведу несколько веских причин считать «новое правило» правильным.
Но размышления о наших условностях могут быть очень полезными. В следующий раз я закрою все, взглянув на историю и приведу несколько веских причин считать «новое правило» правильным. (Да!) Но даже известный историк математики Флориан Каджори написал в «Истории математических обозначений»
в 1928-1929 гг .: «Если арифметический или алгебраический член содержит / и х, в настоящее время нет согласия относительно того, какой
знак должен использоваться первым."
(Да!) Но даже известный историк математики Флориан Каджори написал в «Истории математических обозначений»
в 1928-1929 гг .: «Если арифметический или алгебраический член содержит / и х, в настоящее время нет согласия относительно того, какой
знак должен использоваться первым."
 Как указано на странице, ответ
11 - это то, что есть у большинства компьютерных языков. Вас явно этому учили.
Было бы интересно узнать, какой процент людей говорит 11.Мои эксперименты говорят, что это очень
редкий. Большинство делают умножение перед делением, так как PEMDAS кажется более
популярны и больше преподают в школах. БЕДМЫ PE (MD) AS, кажется, преподают
значительно меньше. Единственное, что мы знаем, это то, что утверждение, что одним из ответов является
единственный правильный ответ - это неправильно ".
Как указано на странице, ответ
11 - это то, что есть у большинства компьютерных языков. Вас явно этому учили.
Было бы интересно узнать, какой процент людей говорит 11.Мои эксперименты говорят, что это очень
редкий. Большинство делают умножение перед делением, так как PEMDAS кажется более
популярны и больше преподают в школах. БЕДМЫ PE (MD) AS, кажется, преподают
значительно меньше. Единственное, что мы знаем, это то, что утверждение, что одним из ответов является
единственный правильный ответ - это неправильно ".
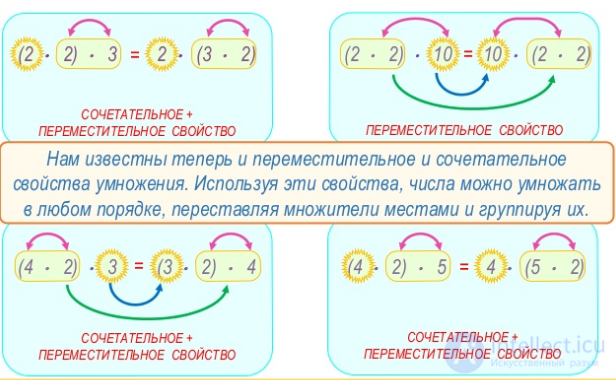 На этой фотографии, сделанной незадолго до экзамена, вы можете увидеть, что
все были счастливы уйти:
Урок очень ясен: как учитель, даже если вы знаете лучше, вы должны быть
очень четкий, даже избыточный. Даже если нет двусмысленности, лучше быть
на всякий случай.
На этой фотографии, сделанной незадолго до экзамена, вы можете увидеть, что
все были счастливы уйти:
Урок очень ясен: как учитель, даже если вы знаете лучше, вы должны быть
очень четкий, даже избыточный. Даже если нет двусмысленности, лучше быть
на всякий случай.
 Вам нужно поставить
скобка. Мне нравится ваш пример. Это
уже хорошо это иллюстрирует. Большинство людей получат
6/24 = 1/4, как и вы. Большинство языков программирования
(компьютеры) дают 9. Компьютер следует PEDMAS
(деление перед умножением)
2 (3/4) 6 = 9
или используйте правило (MD), которое означает «все, что будет первым»
((2 * 3) / 4) * 6 = 9
Люди (и большинство рекомендаций, таких как профессиональные
такие общества, как AMS, следуют PEMDAS, что означает
вы сначала делаете умножение, а затем деление
(2 * 3) / (4 * 6) = 1/4
Но следовать рекомендации не имеет смысла
если существуют разные интерпретации и компьютеры это делают
разные.3)) = 7625597484987
компьютер идет справа налево.
Также здесь необходимы скобки.
Вам нужно поставить
скобка. Мне нравится ваш пример. Это
уже хорошо это иллюстрирует. Большинство людей получат
6/24 = 1/4, как и вы. Большинство языков программирования
(компьютеры) дают 9. Компьютер следует PEDMAS
(деление перед умножением)
2 (3/4) 6 = 9
или используйте правило (MD), которое означает «все, что будет первым»
((2 * 3) / 4) * 6 = 9
Люди (и большинство рекомендаций, таких как профессиональные
такие общества, как AMS, следуют PEMDAS, что означает
вы сначала делаете умножение, а затем деление
(2 * 3) / (4 * 6) = 1/4
Но следовать рекомендации не имеет смысла
если существуют разные интерпретации и компьютеры это делают
разные.3)) = 7625597484987
компьютер идет справа налево.
Также здесь необходимы скобки.
 Собственно, это тоже исторически интересно. Вы упомянули Евклида.
Евклид не использовал известную нам алгебру. Символическая алгебра появилась только с
Вите в 16 веке. Насколько нам известно, только в ХХ веке реализовали
что здесь действительно есть двусмысленность. Об этом ясно сказано в книге Каджори о
математическая нотация, которая является авторитетом в этом вопросе.
Собственно, это тоже исторически интересно. Вы упомянули Евклида.
Евклид не использовал известную нам алгебру. Символическая алгебра появилась только с
Вите в 16 веке. Насколько нам известно, только в ХХ веке реализовали
что здесь действительно есть двусмысленность. Об этом ясно сказано в книге Каджори о
математическая нотация, которая является авторитетом в этом вопросе.