Что первым делается в примере умножение или сложение: Ошибка 403 — доступ запрещён

Содержание

Как делить со скобками, что вперед: деление или умножение, как решить 36:3(8–6) дробь 6, правильный ответ на пример — 17 января 2023

Сможете решить правильно?

Иллюстрация: Юрий Орлов / NGS.RU

Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.

Вот этот пример: 36 : 3 (8 − 6) дробь 6.

Некоторые люди готовы спорить часами, как решить этот пример

Фото: Александра Бруня / NGS.RU

— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов

Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.

— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.

Правильный ответ — 4.

— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.

В итоге это приводит к ошибке в вычислениях.

— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.

Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.

По теме

20 января 2023, 14:00
Один и тот же пример в разных странах решают по-разному. Как это получается?
18 декабря 2022, 11:30
«Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф
18 декабря 2022, 12:00
Русский не родной? 10 простейших слов, которые все пишут с ошибками
23 февраля 2023, 13:00
Зеркальная дата 23.02.2023: что не стоит делать в этот день, чтобы не накликать беду, — советы нумеролога
19 марта 2023, 17:00
Русский не забыли? 10 слов, в которых все неправильно ставят ударение, проверят это

Александра Бруня

Корреспондент

МатематикаРешениеПримерРазбор

ЛАЙК0
СМЕХ0
УДИВЛЕНИЕ0
ГНЕВ0
ПЕЧАЛЬ0

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ0

Гость

Войти

Новости СМИ2

Что в начале плюс или минус?

Ошибки › Какую клемму скинуть чтобы сбросить ошибки

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо сначала выполняется умножение и деление, а затем — сложение и вычитание.

Как правильно ставить знаки в алгебре?
Как решить пример по действиям?
Что значит сложить в математике?
Как называется деление в математике?
Как складывать положительные и отрицательные числа?
Что значит минус перед цифрой?
Какой ответ 10 10 * 10 10?
Как решить пример 3 а 8?
Как решать примеры выражения?
Как решать примеры с минусами и плюсами?
Как правильно складывать цифры?
Как складывать и вычитать числа с разными знаками?
Почему нельзя делить на ноль?

Как разделить 39 на 40?
Как называются числа при минусе?
Как запомнить знак больше или меньше?
Что дает минус на минус при умножении?
Как умножать положительные и отрицательные числа?
Какой ответ получится в выражении 9 3 1 3 1?
Как правильно решать примеры с остатком?
Как решить пример 16 4 3 1?
Как определить сложение?
Что такое порядок в математике?
Что такое вычитание 2 класс?
Как переносить знаки в математике?
Как пишется знак принадлежит в алгебре?
Как умножать знаки?
Что означают две вертикальные полоски в алгебре?

Как правильно ставить знаки в алгебре?

Рассмотрим подробней основные правила знаков:

Деление. Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус».

Умножение. Если мы умножаем «минус» на «плюс», то получаем всегда «минус».
Вычитание и сложение. Они базируются уже на других принципах.

Как решить пример по действиям?

Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо. Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Что значит сложить в математике?

Сложение — это арифметическое действие, в результате которого одно число увеличивается на количество единиц, содержащихся в другом числе. 5 — это первое слагаемое; 3 — второе слагаемое; 8 — сумма слагаемых чисел, или же просто сумма.

Как называется деление в математике?

Число, которое делят, называется делимое. Число, на которое делят делимое, называется делитель. Результат деления — частное. Числа, которые соединены знаком деления, тоже называются частное.

Как складывать положительные и отрицательные числа?

Чтобы сложить положительное и отрицательное число, нужно:

Найти модули слагаемых — то есть этих чисел.
Сравнить полученные числа.
Из большего модуля вычесть меньший.
Перед полученным числом поставить знак того слагаемого, модуль которого больше.

Что значит минус перед цифрой?

Знак минус

Оператор вычитания: бинарный оператор, указывающий на операцию вычитания, например 36 − 5 = 31; Как указатель отрицательных величин, например −5; Унарный оператор, который действует в качестве инструкции для замены операнда на противоположное число.

Какой ответ 10 10 * 10 10?

Ответ: 10 + 10 *10 = 110. Как добавить хороший ответ?

Как решить пример 3 а 8?

3 * (а + 8) = 3а+ 3 * 8 = 3а + 24. В ходе решения мы множитель 3 умножили на первое слагаемое в скобках — а, а затем умножили множитель 3 на второе слагаемое — 8. Ответ: 3а + 24.

Как решать примеры выражения?

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Сначала выполняется действие, записанное в скобках.
Затем выполняются действия деления и умножения слева направо.
В последнюю очередь выполняются действия сложения и вычитания слева направо.

Как решать примеры с минусами и плюсами?

Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

4+(−5)=4−5=−1.
−36+15=−21.
(−17)+(−45) =−17−45=−62.
−9+(−1)=−9−1=−10.

Как правильно складывать цифры?

Чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых. Чтобы сложить числа разных знаков, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.

Как складывать и вычитать числа с разными знаками?

Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше. Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.

Почему нельзя делить на ноль?

В арифметике

При а ≠ 0 не существует числа, которое при умножении на 0 даёт а, поэтому ни одно число не может быть принято за частное а ⁄0; при а = 0 деление на ноль также не определено, поскольку любое число при умножении на 0 даёт 0 и может быть принято за частное 0⁄0.

Как разделить 39 на 40?

Решение: Разделив 39 на 40, получаем 0 целых. Чтобы узнать, сколько будет в остатке к 39 добавляем 0, получаем 390, разделив которые на 40, получаем 9 (от 390 отнимаем 40 х 9 (360), получаем 30).

Как называются числа при минусе?

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым. Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают. Разность — это число, которое получается в результате вычитания.

Как запомнить знак больше или меньше?

Сложите большой и указательный пальцы правой руки в форме уголка, получится знак «больше». Точно также пальцы левой руки образуют знак «меньше». Осталось запомнить: правая рука– больше, левая рука — меньше.

Что дает минус на минус при умножении?

Как решаем: Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс.

Как умножать положительные и отрицательные числа?

Чтобы перемножить два числа с разными знаками, надо:

перемножить модули этих чисел;
перед полученным числом поставить знак «$-$».

Какой ответ получится в выражении 9 3 1 3 1?

9-3:1/3+1= 9 — 3 × 3 + 1 = 9 — 9 + 1 = 0 + 1 = 1. То есть при решении данного примера получается ответ равный 1. Как добавить хороший ответ?

Для того, чтобы решить пример с остатком нужно воспользоваться формулой: a / b = c + n, где а — это делимое, b — делитель, с — частное, n — остаток.

Как решить пример 16 4 3 1?

Правильный алгоритм таков: сначала вычисли результат в скобках, затем делим 8 на 4, а результат умножаем на то число, которое получилось в скобках. Таким образом мы получим: 8 / 4(3 — 1) = 8 / 4 х 2 = 2 х 2 = 4.

Как определить сложение?

Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно.

Что такое порядок в математике?

В математике

Порядок элемента группы — минимальная степень, в которую нужно возвести элемент группы для получения нейтрального элемента.

Что такое вычитание 2 класс?

Вычитание — это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым, результат вычитания — разностью.

Как переносить знаки в математике?

Лучше перенос делать на знаках равенства, больше, меньше, больше или равно, меньше или равно, а также параллельности и перпендикулярности. Можно также переносить на знаках действия «+» и «-», и только в крайнем случае на знаке умножения, при этом вместо знака умножения пишется не точка, а косой крест.

Как пишется знак принадлежит в алгебре?

Теория множеств и теория чисел

Символ TeX (Команда TeX)	Символ (Юникод)	Название
Произношение
(\varnothing)	∅ {}	«Пустое множество»
(\in) (\notin)	∈ ∉	Принадлежность/непринадлежность к множеству
«принадлежит», «из» «не принадлежит»

Как умножать знаки?

Ответы1.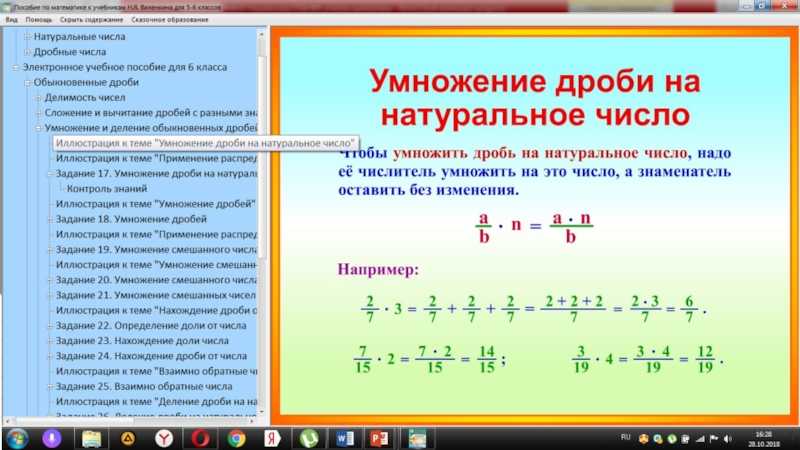 Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным числом поставить знак минус. Чтобы умножить два отрицательных числа, надо умножить модули этих чисел и перед полученным числом поставить знак плюс.

Что означают две вертикальные полоски в алгебре?

В C-подобных языках символ «|» служит для операции побитового «или» (дизъюнкция), а два таких символа, написанных слитно («||»), используются в операции логического «или».

алгебраических выражений. Порядок операций

Навыки
в н
A L G E B R A

Содержание | Дом

Четыре операции и их знаки

Функция скобок

«Условия» и «факторы»

Степени и показатели

Порядок операций

Раздел 2 :

Ценности и оценки

Переменные

Написание алгебраических выражений

АЛГЕБРА — ЭТО ПИСЬМЕННЫЙ НАВЫК. Это означает, что писатель решает проблему четко, эффективно и с наименьшим объемом текста. Как и любой навык — вождение автомобиля, выпечка печенья, игра на гитаре — он требует практики. Письменная практика. Тем не менее, давайте начнем.

Первое, что нужно отметить, это то, что в алгебре мы используем буквы так же, как и числа. Но буквы обозначают цифры. Мы имитируем правила арифметики буквами, потому что имеем в виду, что правило будет верным для

любые номеров.

Вот, например, алгебраическое правило сложения дробей:

б
в

а + б
в

Буквы a и b означают: цифры , находящиеся в числителях. Буква c означает: число в знаменателе. Правило означает:

«Что бы это ни было, сложите числители
и запишите их сумму над общим знаменателем.»

Алгебра говорит нам, как решить любую задачу, которая выглядит как .

В конце концов, символы для чисел — 1, 2, 3 — не что иное, как письменные знаки. А так письма. Как ученик увидит, алгебра зависит от

образует , которые принимают символы. То, что вы видите выше, называется формальным правилом для сложения дробей.

Цифры — это числовые символы, а буквы — буквенные символы.

Вопрос 1. Каковы четыре арифметических операции, и

какие признаки их работы?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай проблему сам!

1)	Дополнение: a + b . Знак операции + и называется знаком плюс . Читать a + b как « a плюс b ».

1)	Например, если a представляет 3, а b представляет 4, то a + b представляет 7.

2)	Вычитание: a − b . Знак операции — и называется знаком минус . Читать a − b как « a минус b ».

1)	Если a представляет, например, 8, а b представляет 2, то a − b представляет 6.

3) Умножение: a · b . Читать a · b как « a умножить на b ».

Знак умножения в алгебре — точка в центре. Мы не используем крест умножения ×, потому что не хотим перепутать его с буквой x .

Итак, если a представляет 2, а b представляет 5, то

a · b = 2 · 5 = 10.

«2 умножить на 5 равно 10».

Не путайте точку в центре — 2 · 5 , которая в США означает умножение — с десятичной точкой: 2 .

Однако мы часто опускаем точку умножения и пишем просто ab . Читать « a , b «. Другими словами, когда между двумя буквами или между буквой и числом нет знака операции, это всегда означает умножение. 2 x означает 2 раза x .

Подразделение:

а
б

. Читать

а
б

как « a разделить на b «.

В алгебре мы используем горизонтальную черту деления. Если 9Например, 0035 a представляет 10, а b представляет 2, тогда

а
б

10
2

= 5.

«10 разделить на 2 будет 5.»

Примечание: В алгебре мы называем a +

b «суммой», даже если мы не называем ответ.

Как увидит учащийся, мы называем что-то в алгебре просто по тому, как оно выглядит как . На самом деле вы увидите, что вы делаете алгебру глазами, а дальше следует то, что вы пишете на бумаге.

Точно так же мы называем a − b разностью, ab произведением и частным.

Этот знак = конечно же знак равенства, и мы читаем это —

— как « a равно (или равно) b «.

Это означает, что число слева, которое представляет a , равно числу справа, которое представляет b . Если мы напишем

а + б = в ,

и если a представляет 5, а b представляет 6, то c должно представлять 11.

Вопрос 2. Какова функция скобок () в алгебре?

3 + (4 + 5) 3(4 + 5)

Скобки означают, что мы должны рассматривать то, что они заключают в себе
, как одно число.

3 + (4 + 5) = 3 + 9 = 12. 3(4 + 5) = 3 · 9 = 27.

Примечание: Если между 3 и (4 + 5) нет знака операции, это означает умножение.

Задача 1. Как в алгебре написать

а) 5 умножить на 6? 5 · 6

б) x умножить на y ? ху

в) x разделить на y ?

г) х плюс 5 плюс х минус 2?

( х + 5) + ( х — 2)

д) х плюс 5 умножить на x минус 2?

( х + 5)( х — 2)

Задача 2. Различите следующее:

а) 8 – (3 + 2) б) 8 – 3 + 2

а) 8 — (3 + 2) = 8 — 5 = 3.

б) 8 — 3 + 2 = 5 + 2 = 7.

В а) мы рассматриваем 3 + 2 как одно число. В б) мы не делаем. Мы должны сначала вычесть 3, а затем добавить 2. (Но см. порядок операций ниже.)

Существует распространенное заблуждение, что скобки всегда означают умножение. Фактически, в Уроке 3 мы увидим, что мы используем круглые скобки, чтобы отделить знак операции от знака алгебры. 8 + (−2).

Вопрос 3. Условия и факторы.

Когда числа добавляются или вычитаются, они называются терминами.

Когда числа умножаются, они называются множителями.

Вот сумма четырех слагаемых: а − б + в − г .

В алгебре мы говорим о «сумме» терминов, даже если есть вычитания. Другими словами, все, что выглядит как то, что вы видите выше, мы называем суммой.

Вот произведение четырех множителей: abcd .

Слово делитель всегда означает умножение.

И снова мы говорим о «продукте» abcd , хотя мы не называем ответ.

Задача 3. Сколько терминов в следующем выражении? И сколько множителей у каждого члена?

2 a + 4 ab + 5 a ( b + c )

Есть три термина. 2 a — первый термин. Он имеет два множителя:
2 и a .
4 ab — второй член. Имеет три множителя: 4, a и b .
И 5 a ( b + c ) — все это один термин. Он также имеет три множителя: 5, a и
( b + c ). Круглые скобки означают, что мы должны рассматривать все, что заключено в них, как одно число.

Степени и показатели

Когда все факторы равны — 2 · 2 · 2 · 2 — мы называем произведение степенью этого множителя. Таким образом, · называется второй степенью числа или « в квадрате». a · a · a есть третья степень числа a , или « a в кубе». аааа равно а в четвертой степени и так далее. Мы говорим, что в само по себе является первой степенью в .

Теперь вместо того, чтобы писать aaaa , мы пишем a один раз и поместите маленькую 4:

⁴ (« до 4″)

Эта маленькая 4 называется показателем степени. Он указывает количество повторений и в качестве коэффициента.

8 ³ («8 в третьей степени» или просто «8 в третьей степени») означает 8 · 8 · 8.

Задача 4. Назовите первые пять степеней числа 2. 2, 4, 8, 16, 32.

Задача 5. Прочитайте, а затем рассчитайте каждое из следующих действий.

а) 5 ² «5 во второй степени» или «5 в квадрате» = 25,

б) 2 ³ «2 в третьей степени» или «2 в кубе» = 8,

в) 10 ⁴ «10 до четвертого» = 10 000.

г) 12 ¹ «12 к первому» = 12.

Однако в алгебре принято не писать показатель степени 1.

= ¹ = 1 .

Учащийся должен следить за тем, чтобы не спутать 3 и , что означает 3 , умноженное на , и , с и ³, что означает , умноженное на .

3 а	=	и + и + и , Урок 9арифметики
а ³	=	· · .

Вопрос 4. При наличии нескольких операций

8 + 4(2 + 3) ² — 7,

какой порядок операций?

Прежде чем ответить, отметим, что, поскольку знание естественных наук является причиной, по которой студенты должны изучать алгебру; а поскольку порядки операций появляются только в определенных формах, то на этих страницах мы представляем только те формы, с которыми учащийся может столкнуться в реальной алгебраической практике. Знак деления ÷ никогда не используется в научных формулах, только черта деления. Крест умножения × используется только в экспоненциальной записи, поэтому учащийся никогда не увидит следующее:

3 + 6 × (5 + 3) ÷ 3 − 8.

Такая задача была бы чисто академической, т. е. упражнением ради самого себя. Это не имеет практической ценности. Это никуда не ведет.

Порядок операций следующий:

(1)	Оцените скобки, если они есть, и если они требуют оценки.

(2)	Оцените степени, то есть показатели степени.

(3)	Умножать или делить — не важно.

(4)	Добавить или вычесть.

В примерах 1 и 2 ниже мы увидим, в каком смысле мы можем прибавить или вычесть . А в примере 3 мы встретим умножение на или разделить.

Примечание: «Оценить» означает назвать и написать число.

Пример 1. 8 + 4(2 + 3) ² − 7

Сначала оценим скобки, то есть заменим 2+3 на 5:

= 8 + 4 · 5 ² − 7

Так как теперь есть только одно число, 5, скобки писать не нужно.

Обратите внимание, что мы преобразовали один элемент, круглые скобки, и переписали все остальные.

Затем оцените показатели степени:

= 8 + 4 · 25 − 7

Теперь умножьте:

= 8 + 100 — 7

Наконец, прибавьте или вычтите , это не будет иметь значения. Если мы сначала добавим:

= 108 − 7 = 101,

Хотя если сначала вычесть:

8 + 100 — 7 = 8 + 93 = 101.

Пример 2. 100 − 60 + 3.

Первый:

100 − 60 + 3 означает ли , а не , 100 − 63.

Только при наличии скобок —

100 − (60 + 3)

— можем ли мы рассматривать 60 + 3 как одно число. При отсутствии скобок задача означает вычесть 60 из 100, затем прибавить 3:

100 − 60 + 3 = 40 + 3 = 43.

На самом деле не имеет значения, прибавляем мы сначала или вычитаем сначала,

100 — 60 + 3 = 103 — 60 = 43.

Когда мы подойдем к числам со знаком, мы увидим, что

100 − 60 + 3 = 100 + (−60) + 3.

Порядок, в котором мы их «добавляем», значения не имеет.

Пример 3.

11 · 35
5

Нет скобок для оценки и показателей степени. Далее по порядку умножаем или делим на . Мы можем сделать и то и другое — мы получим тот же ответ. Но обычно более искусно сначала делить, потому что тогда у нас будут меньшие числа для умножения. Поэтому сначала разделим 35 на 5:

11 · 35 5	=	11 · 7
	=	77.

См.: Навыки арифметики, свойство 3 раздела.

Пример 4. ½(3 + 4)12 = ½ · 7 · 12.

Порядок множителей не имеет значения: abc = bac = cab и так далее. Поэтому мы можем сначала сделать ½ · 12. То есть мы можем сначала разделить 12 на 2:

½ · 7 · 12 = 7 · 6 = 42.

(см. урок 27 арифметики, вопрос 1.)

Пример 5. Полоса разделения.

8 + 20
10 − 3

В любой задаче с делением, прежде чем мы сможем разделить, мы должны оценить верх и низ в соответствии с порядком операций. Другими словами, мы должны интерпретировать верх и низ как заключенные в круглые скобки.

8 + 20
10 − 3

означает

(8 + 20)
(10 − 3)

Теперь действуем как обычно и сначала оцениваем скобки. Ответ: 4.

Проблема 6. Оцените каждое из следующих действий в соответствии с порядком операций.

а)	3 + 4 · 5 =	б)	2 + 3 · 4 + 5 =

	3 + 20 = 23		2 + 12 + 5 = 19

в)	4 + 5 (2 + 6) =	г)	(4 + 5) (2 + 6) =

	4 + 5 · 8 = 4 + 40 = 44		9 · 8 = 72

e)	11 · 10 5	е)	½(3 + 4)8 =

	11 · 2 = 22 Сначала мы можем разделить.		½ · 7 · 8 = 7 · 4 = 28. (½ · 8 = 4) Навыки арифметики: Урок 27, вопрос 1

г)

2 + 2 · 3 ²
14 − 3 · 2 ²

2 + 2 · 9
14 − 3 · 4

2 + 18
14 − 12

20
2

10.

Раздел 2 :

Ценности и оценки

Переменные

Написание алгебраических выражений

Содержание | Дом

Вопросы или комментарии?

Электронная почта: [email protected]

Строки, целые числа и числа с плавающей запятой

Вы можете ознакомиться с нашими учебными пособиями, но имейте в виду, что, поскольку мы полагаемся на PR сообщества для обслуживания, они могут быть устаревшими.

В этом уроке мы начнем работать с основными типами Python: строки (для текста) и целые числа и числа с плавающей запятой (для числовых значений).

Обратите внимание, что в этом руководстве вы работаете в REPL (IDLE). Вы можете найти дополнительную информацию на REPL и как запустить Python в вашем cmd или терминале в руководстве по установке Python.

Привет, мир!

По традиции начнем с «Hello, World!» к консоль. В Python функция для достижения этого метко названа print() . Введите следующее рядом с >>> :

 print("Привет, мир!")

REPL просто напечатает текст прямо перед вами.

Теперь напечатайте свое имя и немного поэкспериментируйте!

Несколько аргументов

Что еще интересно в функции print() , так это то, что вы можете передать ее несколько аргументов для печати:

 >>> print("Привет", "До свидания")

На самом деле, вы можете передавать в печать сколько угодно вещей:

 >>> print("один", "два", "три", "четыре", "пять", "шесть", "семь", "восемь", "девять")

Конечно, вы также можете получить такой же результат:

 >>> print("один два три четыре пять шесть семь восемь девять")

Вам решать, что уместно и когда.

Математика

Всеобщее любимое занятие.

Простая арифметика

Python может выполнять простые арифметические действия. Для начала попробуем добавить:

 >>> 5 + 7

Теперь вы должны увидеть результат этого расчета в вашем REPL.

Вычитание, умножение и деление работают одинаково.

 >>> 6 - 2
>>> 8*4
>>> 9 / 3

Теперь попробуйте еще несколько, чтобы увидеть, какие результаты вы получите. Попробуйте свои силы во всех основные математические операторы: +, - , * (умножение), / (деление), ** (показатели степени) и % (модуль).

Объединение операций

Возможность выполнять только одну операцию за раз довольно ограничена, поэтому Python позволяет нам комбинировать математические операции. Попробуйте это:

 >>> 9 * 4 - 6

Теперь попробуйте еще несколько. Вы можете комбинировать столько операций, сколько хотите.

Приоритет оператора

Заметили ли вы неожиданные результаты, когда начали комбинировать операции? Если ты не пробовал, попробуй так:

 >>> 10 - 2 * 4

Python следует традиционным математическим правилам приоритета, которые гласят что умножение и деление выполняются раньше, чем сложение и вычитание. (Ты может помнить БОДМАС .) Это значит в В нашем примере выше сначала умножаются 2 и 4, а затем результат вычитается из 10.

Мы можем изменить порядок операций, используя круглые скобки. Что-нибудь внутри скобки выполняются первыми.

Теперь попробуйте так:

 >>> (10 - 2) * 4

У вас должен быть другой ответ.

Из-за правил приоритета сложные операции, такие как наш первый пример, могут быть довольно запутанным для чтения. Если вы обнаружите, что пишете более сложные выражения, нет ничего плохого в добавлении круглых скобок для ясности.

Десятичные точки

Одна из вещей, которая обычно сбивает с толку новичков в программировании, это концепция чисел с плавающей запятой . В основном, числа с десятичной точки имеют тенденцию вести себя немного странно, когда вы выполняете математические операции над ними. Причины этого сложны и коренятся в природе. вычислений, так что пока давайте просто понимаем, что странные вещи происходят с десятичными числами.

Чтобы увидеть пример, попробуйте разделить 10 по 3 :

 >>> 10 / 3

Ответ должен продолжаться вечно, но это не так. Теперь попробуйте что-нибудь немного более чувствительный к точности:

 >>> 1.000000000000001 * 8

Вероятно, это не то, что вы ожидали, верно? На данный момент вам просто нужно принять это в качестве ограничения, а позже вы узнаете, как другие программисты обходятся это.

Заключение

Теперь давайте объединим то, что мы узнали сегодня. Мы можем сказать print() для печати несколько вещей одновременно, разделенные запятой:

 >>> print('Результат 2 + 2 есть', 2 + 2)

Сохранение вашей работы

В этом уроке вы писали код в REPL (IDLE), но часто вам нужно чтобы вместо этого сохранить ваш код. В таких случаях вы можете сохранить свой код в файл с помощью текстового редактора. Мы даем некоторую информацию о текстовых редакторах в нашем Руководстве по началу работы.

Откройте текстовый редактор и напишите код из первого упражнения:

 print("Привет, мир!")

Сохраните файл как ex1.py . Вы можете называть свои файлы как хотите, но они должны заканчиваться на .py , чтобы python мог их легко прочитать. Читая ваш файл в Python, вы снова будете использовать оболочку cmd или terminal . Вы можете прочитать свой файл с помощью следующей команды (введите без знака $):

 $ питон ex1.py

Если перед вашим кодом стоит >>> , вы все еще находитесь в REPL(IDLE) и вам нужно выйти это с:

 >>> выйти()

После этого вы сможете загрузить файл.

На этом сегодняшний урок завершен. В следующем уроке мы узнаем, как объединить результаты нескольких отдельных выражений с использованием переменных, получить ввод от пользователя и принимать решения на основе этой информации.