Умножение чисел. Множимое, множитель и произведение

• Множимое, множитель и произведение
• Проверка умножения

Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.

Пример. Во дворе посадили  3  ряда ёлок, по  4  ёлки в каждом ряду. Сколько ёлок посадили во дворе?

Чтобы ответить на этот вопрос, надо найти сумму  3  слагаемых, каждое из которых равно  4.

4 + 4 + 4 = 12.

Складывая  3  раза по  4  ёлки, мы получим общее количество ёлок во всех трёх рядах.

Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.

Для записи умножения используется знак  х  (косой крест)  или  ·  (точка),  который ставится между числами. Например:

4 х 3   или   4 · 3

Эта запись означает, что  4  надо умножить на  3.  Справа от записи умножения ставится знак  =  (равно),  после которого записывается полученный результат:

4 · 3 = 12.

Умножение – это краткая запись сложения одинаковых слагаемых.

Пример. Умножить  6  на  5  — это значит найти сумму пяти слагаемых, каждое из которых равно шести:

6 + 6 + 6 + 6 + 6 = 30.

Сократим запись, заменив сложение на умножение:

6 · 5 = 30.

Оба выражения равны:

6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,

но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.

Множимое, множитель и произведение

Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:

4 · 3,

4  — это множимое,  3  — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.

Произведение — это число, которое получается в результате умножения. Например, в записи:

4 · 3 = 12,

12  — это произведение. При этом сама запись  4 · 3  тоже называется произведением.

Эту запись можно прочитать так:  произведение четырёх и трёх равно двенадцати,  четыре умножить на три равно двенадцати,  по четыре взять три раза, получится двенадцать.

Множимое и множитель иначе называются множителями или сомножителями.

Проверка умножения

Рассмотрим выражение:

4 · 3 = 12,

где  4  — это множимое,  3  — это множитель, а  12  — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:

1. Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:

   12 : 3 = 4.

2. Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно:
   12 : 4 = 3.

Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.

Деление дробей: простая инструкция — Лайфхакер

17 февраля 2021ЛикбезОбразование

Простая инструкция с примерами.

Поделиться

0

Как делить обыкновенные дроби

На другую дробь

Деление одной дроби на другую — это умножение её на вторую дробь в перевёрнутом виде. В отличие от сложения и вычитания, при делении неважно, какие у дробей знаменатели: одинаковые или разные. Просто умножьте числитель на числитель, а знаменатель на знаменатель и, если у вас получится неправильная дробь, выделите из неё целую часть.

Например, вам нужно разделить ³/₅ на ⁴/₉. Для этого поменяйте местами числитель и знаменатель второй дроби — она превратится в ⁹/₄ — и умножьте ³/₅ на неё.

Если в примере изначально есть смешанные числа, как 1⁷/₂₀, сначала нужно перевести их в неправильные дроби (в данном случае получится ²⁷/₂₀), а потом делить, как описано выше.

На целое число

Чтобы разделить обыкновенную дробь на целое число, нужно представить его также в виде обыкновенной дроби: в числителе будет оно само, а в знаменателе единица. А затем делить как дробь на дробь. Например:

Можно действовать и ещё проще: умножить знаменатель на данное в примере число, а числитель оставить как есть.

А чтобы, наоборот, разделить целое число на обыкновенную дробь, нужно перевернуть эту дробь и умножить число на неё. Например:

Вспомните, если нужно 👈

• Как умножать обыкновенные и десятичные дроби

Как делить десятичные дроби

На другую дробь

Это можно сделать двумя способами.

Первый — превратить десятичные дроби в обыкновенные. Например, 1,2 — это то же самое, что 1²/₁₀, или ¹²/₁₀ в виде неправильной дроби, или ⁶/₅ — если её сократить. Соответственно, процесс деления будет выглядеть так:

Теперь осталось перевести обыкновенную дробь обратно в десятичную. Для этого нужно умножить её на такое число, чтобы знаменатель получился кратным 10: 10, 100, 1 000 и так далее. В данном случае ⁴/₅ умножаем на 2. Мы получим ⁸/₁₀. Добавляем к этому нашу целую часть — 4 — и получаем итоговый результат 4,8.

Второй способ деления десятичных дробей — сначала превратить их в целые числа, а потом поставить запятую в получившемся результате.

• Найдите дробь, в которой больше всего знаков после запятой.
• Умножьте все дроби в примере на число, кратное 10, с таким же количеством нулей. Например, если у вас есть дробь 4,25 — это будет 100, а если 1,578 — 1 000.
• Разделите целые числа друг на друга столбиком.
• Отсчитайте слева направо столько знаков, сколько было добавлено нулей при умножении, и поставьте запятую.

Например: 7,44 ÷ 0,4 = (7,44 × 100) ÷ (0,4 × 100) = 744 ÷ 40 = 18,6.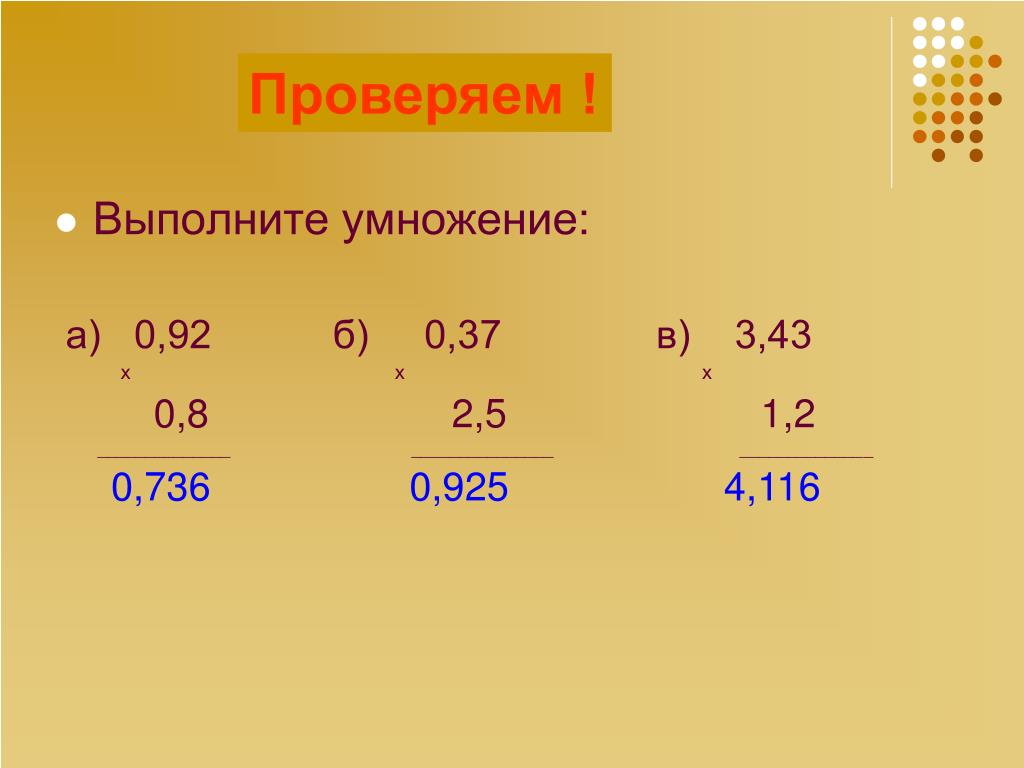

На целое число

Десятичные дроби на целое число делите так же, как и обычные числа, столбиком. Когда в делимом (слева) закончится целая часть, поставьте запятую в частном (справа под чертой). Если делимое не удаётся разделить без остатка, добавляйте к нему нули, пока не получите конечный результат.

Читайте также 🧐

• Как научить ребёнка считать играючи
• Как выучить таблицу умножения легко и быстро
• Гимнастика для ума: 10 увлекательных задач с числами

Порядок действий – Элементарная математика

Уменьшение двусмысленности по договоренности

В общем, никто не хочет быть неправильно понятым. В математике так важно, чтобы читатели понимали выражения именно так, как задумал автор, что математика устанавливает соглашения, согласованные правила для интерпретации математических выражений.

Означает ли 10 − 5 − 3, что мы начинаем с 10, вычитаем 5, а затем вычитаем еще 3, оставляя 2? Или это означает, что мы вычитаем 5 − 3 из 10?
Равно ли 2 + 3 × 10 50, потому что 2 + 3 равно 5, а затем мы умножаем на 10, или автор имеет в виду, что мы добавляем 2 к результату 3 × 10?

Чтобы избежать этих и других возможных неясностей, математика установила соглашения (соглашения) о том, как мы интерпретируем математические выражения. Одно из этих соглашений гласит, что когда все операции одинаковы, мы действуем слева направо, поэтому 10 — 5 — 3 = 2, поэтому автору, который хотел бы другую интерпретацию, пришлось бы писать выражение по-другому: 10 — (5). − 2). Когда операции не такие, как в 2 + 3 × 10, некоторым может быть отдано предпочтение перед другими. В частности, умножение выполняется перед сложением независимо от того, какое из чисел появляется первым при чтении слева направо. Например, в 2 + 3 × 10 умножение должно быть выполнено первым, даже несмотря на то, что оно стоит справа от сложения, а выражение означает 2 + 30.
Полные правила порядка операций см. ниже.

Условные обозначения для чтения и записи математических выражений

Основной принцип: «более мощные» операции имеют приоритет над «менее мощными».

Использование числа в качестве показателя степени (например, 58 = 390625) имеет, как правило, «самый сильный» эффект; использование того же числа в качестве множителя (например, 5 × 8 = 40) дает более слабый эффект; сложение имеет, как правило, самый «слабый» эффект (например, 5 + 8 = 13). Хотя эти термины (мощный, слабый) в математике не употребляются, смысл сохраняется в языке «возведение 5 в 8-ю степень». Возведение в степень «мощно», поэтому оно на первом месте! Сложение/вычитание «слабые», поэтому они идут последними. Умножение/деление находится между ними.

Когда важно указать другой порядок , как это иногда бывает, мы используем круглые скобки для упаковки чисел и более слабую операцию, как если бы они представляли одно число.

Например, хотя 2 + 3 × 8 означает то же, что и 2 + 24 (поскольку умножение имеет приоритет и выполняется первым), (2 + 3) × 8 означает 5 × 8, поскольку (2 + 3) пакетное предложение, количество, которое необходимо выяснить перед его использованием. На самом деле (2 + 3) × 8 часто произносится как «два плюс три, количество, умноженное на восемь» (или «количество два плюс три, умноженное на восемь»).

Краткое изложение правил:

• Сначала скобки. Обращение к ним как к «пакетам» часто помогает детям вспомнить их цель и роль.
• Экспоненты рядом.
• Далее умножение и деление. (Ни один из них не имеет приоритета, и когда они идут последовательно, они выполняются слева направо.)
• Сложение и вычитание в последнюю очередь. (Опять же, ни один из них не имеет приоритета, и последовательная строка из них выполняется слева направо.)

Распространенные заблуждения

Многие учащиеся изучают порядок операций, используя PEMDAS (скобки, возведения в степень, умножение, деление…) в качестве вспомогательного средства для запоминания. Это очень часто приводит к ошибочному представлению о том, что умножение предшествует делению, а сложение предшествует вычитанию. Понимание этого принципа, вероятно, является лучшим помощником в запоминании.

алгебраическое предварительное исчисление — Зачем сначала умножать?

Спросил 8 лет, 6 месяцев назад

Изменено 3 года, 7 месяцев назад

Просмотрено 15 тысяч раз

$\begingroup$

Почему мы сначала умножаем/делим, а потом складываем/вычитаем?

Я имею в виду, что меня интересует, это универсальное правило или правило, установленное человеком? Кроме того, как бы вы решили, что оперировать в первую очередь?

Например, если бы нас посетили инопланетяне, использовали бы они ту же математику? Будут ли они также сначала умножаться, а потом добавлять?

• алгебра-предварительное исчисление

$\endgroup$

6

$\begingroup$

Это всего лишь соглашение по нотации , позволяющее одному из выражений $$(a+b)\cdot c\qquad a+(b\cdot c) $$записываться без круглых скобок. Можно было бы выбрать другое (или для всегда требуются круглые скобки), но подумайте, насколько сложным было бы написание, например. полиномы (если они не записаны в виде произведения линейных множителей). То же самое относится и к тому, почему $a-b-c$ означает $(a-b)-c$, а не $a-(b-c)$. В качестве альтернативы можно ввести префиксную или постфиксную (вместо инфиксной) нотацию, также известную как. (обратная) польская запись, т. е. $ab+c\cdot$ или $\cdot +abc$ по сравнению с $abc\cdot+$ или $+a\cdot bc$.

$\endgroup$

4

$\begingroup$

В дополнение к тому, что сказали другие, порядок операций также является естественным следствием перезаписи выражений, чтобы избежать двусмысленности.

Например, $3\умножить на 4+1$. Если бы все это было сложением, не было бы проблем, потому что сложение коммутативно и ассоциативно.