Содержание урока |
|
| Организационный момент | — Прозвенел уже звонок? Да. — Уже кончился урок? Нет. — Только начался урок? Да. — Хотите учиться? Да. — Значит, можно всем садиться. |
| Звучит музыка. Создание атмосферы психологической комфортности. |
Дети, представьте себе, что вы маленькое
семечко (закрывают голову руками) Садовник очень
бережно относится к семечку, поливает его,
ухаживает за ним. С первыми лучами солнышка семечко начинает
медленно расти, появляются первые листочки (дети потягиваются, расправляют плечики) И вот наступает радостный момент, появляется
прекрасный цветок Цветок хорошеет И от этого цветка всем светло и тепло на душе. Я желаю вам успеха и удачи на этом уроке. Запись числа и классная работа в тетрадь. |
| Прогнозирование урока. | — Что вы ждёте от этого урока?
— Правильно, новые знания ждут нас сегодня. Ведь урок у нас будет необычный. У нас с вами урок – исследование. Что такое исследование? — Правильно, это что-то изучать, выводить новые знания. А чтобы исследование прошло результативно, вам
понадобится умение наблюдать, сравнивать,
обобщать и делать выводы. Ведь нам нужно зажечь
сегодня новую звезду знаний. |
| Актуализация изученных знаний. | Ну, а чтобы открыть что-то новое, нам
необходимо повторить, что мы уже с вами знаем. - Что мы изучали на прошлом уроке? Деление круглых чисел. Работа в парах. У вас на партах лежат математические цепочки. Поднимите руки, у кого бумага красного цвета. Поднимите руки, у кого бумага жёлтого цвета. Вам нужно в парах решить математические цепочки. Проверка на слайде. Взаимопроверка в парах. Отметьте на волшебной линейке степень трудности.
|
| Постановка проблемы. Постановка учебной задачи. |
А вот Маше и Мише была предложена такая
цепочка:
Маша её решила так:
— Как она рассуждала? Ответы детей. Правильно? — Да! А Миша решил вот так:
— Как он рассуждал? Ответы детей. Правильно? — Тоже верно! — Что вас удивило? Тогда почему ответы у них разные? Они считали в разном порядке, не договорились, в каком порядке будут считать. — От чего зависит результат вычисления? От порядка. — Что вы видите в этих выражениях? Числа, знаки. — Как в математике называют знаки? Действия. — О каком порядке не договорились ребята? О порядке действий. — Что мы будем исследовать? Мы будем исследовать порядок арифметических действий в выражениях. Запись темы урока в тетрадь. — Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях. |
| Решение учебной задачи. Знакомство с правилами порядка действий в выражениях.
Составление схемы на доске |
— Прочитайте выражения. Сравните их. — Чем похожи? 2 действия, числа — Чем отличаются? Скобки, разные действия Правило 1. Прочитайте правило на слайде. Дети читают вслух правило. В выражениях без скобок, содержащих только сложение и вычитание или умножение и деление, действия выполняются в том порядке, как они записаны: слева направо. О каких действиях здесь говорится? +, — или :, * Есть ли скобки? Нет. Как будем считать? Слева направо. — Как это можно записать? Это можно записать схемой.
Из данных выражений найдите только те, которые соответствуют правилу 1. Запишите их в тетрадь. Проверка.
|
|
Составление схемы на доске |
Правило 2. Прочитайте правило на слайде. Дети читают вслух правило. В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание. А здесь какие арифметические действия указаны?
Есть скобки? Нет. Какие действия будем выполнять сначала? *, : слева направо Какие действия будем выполнять потом? +, — слева, направо Это тоже можно записать схемой. Вызвать одного ученика к доске.
Выпишите выражения, которые относятся ко второму правилу. Найдите их значения. Проверка.
|
| Запись музыкальной физкультминутки | Чтоб успешно развиваться, Нужно спортом заниматься.  От занятий физкультурой Будет стройная фигура. |
| Правило 3. Прочитайте правило 3 на слайде. В выражениях со скобками сначала вычисляют действия в скобках, затем по порядку слева направо выполняется умножение или деление, а потом сложение или вычитание. |
|
|
Составляют схемы в парах |
Скобки есть? Есть. Какие арифметические действия? *, : и +, — Как сейчас будем вычислять? Работа в парах. Составьте схему у себя на парте. Проверка. Один ученик выходит к доске.
Выпишите выражения, которые относятся к данному правилу:
Проверка. |
| Объяснение домашнего задания. Домашнее задание по желанию. |
— Какие задания вы бы хотели выполнить
дома? Домашнее задание на выбор:
|
| Подведение итогов. | Мы сегодня много работали, открыли
много нового. Какую же тему урока мы сегодня изучили? Зачем нужен порядок действий в выражениях? — С какими правилами познакомились? Правила порядка действий. — Сколько таких правил? Три.
— Какие арифметические действия есть во 2 правиле?
— Какие арифметические действия есть в 3 правиле?
Какое правило вам показалось самым простым? Почему? |
| Рефлексия “Зажги звезду” | И последнее задание для вас. Звезда знаний у нас зажглась. А чтобы эти знания прочно осели в ваших головах, мы будем передавать звезду и говорить, что запомнили на сегодняшнем уроке. Спасибо за работу на уроке!!! |
Умножение
Дата: 02.05.2009
Автор: Коновалова Валентина Михайловна
Предмет: Математика.
Класс: 2.
Тема: Умножение.
Цели урока:
- Формирование знания конкретного смысла умножения.
- Формирование первого представления о переместительном свойстве умножения и случаях умножения 0 и 1, на 0 и 1.
- Формирование когнитивных (познавательных) компетенций: умения анализировать, обобщать, отыскивать причины, выявлять закономерности.
- Формирование отношения сотрудничества между учителем и учениками.

Технологии:
- проблемный диалог,
- интенсификация обучения на основе схемных и знаковых моделей (блочное изучение материала),
- развивающего обучения (ведущая роль теоретических знаний).
- словесные (беседа),
- наглядные (опорные схемы),
- практические (решение примеров и задач),
- репродуктивные (на этапе обобщения),
- индуктивные (от фактов к выводам на этапах составления опорных схем),
- проблемно-поисковые (обсуждение задания с элементами повышенной трудности).
Оборудование:
- Таблица с названиями компонентов умножения,
- листики для опорного сигнала,
- раздаточный материал: задача.
- Организационный момент.

- Актуализация знаний.
- Сколько прямых линий на чертеже? Сколько точек пересечения?
- Чем похожи примеры? Чем отличаются? Какое выражение лишнее?
6+6+6
3+3+3+3
1+2+3+4+5
— Одинаковые слагаемые в каждом выражении. Разное количество слагаемых. Лишнее – последнее выражение, т.к. в нём складываются разные числа.
- Решите задачу (письменно). В классе 3 ряда парт. В каждом ряду по 5 парт. Сколько всего парт в классе?
5+5+5=15(п.)
— Что показывает число 5?
— Сколько парт в одном ряду.
— Сколько раз по 5 взяли? Почему?
— 3 раза, т.к. рядов было 3.
— Что показывает число 15? — Сколько всего парт.
- Создание проблемной ситуации.

В ателье шили форму для первоклассников. На каждую рубашку пришивали по 4 пуговицы. Сколько надо пришить пуговиц на 20 рубашек?
— Что обозначает число 4? 20? Что надо узнать? Запишите решение.
— В чём затруднение?
— Получится очень длинная запись.
— Сколько раз надо взять слагаемым число 4? (20 раз) 4+4+…+4
- Поиск решения.
- Постановка задачи.
— Есть такое математическое действие, которое может заменить сложение. Как оно называется?
— Умножение.
- Замена сложения умножением.
— А как сосчитать, если мы не знаем таблицы умножения? (4+4=8)
Аналогично заменяем умножением 6+6+6 и 3+3+3+3 (два ученика у доски).
— Почему нельзя заменить умножением сложение чисел в последнем примере?
— Слагаемые – разные числа.

— Все ли примеры на сложение можно заменить умножением?
— Нет, только те, в которых слагаемые одинаковые числа.
- Постановка темы урока.
— Умножение.
— Запишите на листике. Умножение.
- Составление I блока опорной схемы.
— Как можно обозначить любое число? (латинской буквой). Обозначим первое число буквой а, второе число — буквой в.
а*в=а+а+…+а (слагаемое а беру в раз).
— Что же такое умножение?
— Сложение одинаковых слагаемых.
— Что показывает первое число а?
— Какое число берём слагаемым.
— Второе число в?
— Сколько раз берём слагаемое.
- Работа с учебником.
— Прочитайте объяснение (про себя, вслух читает один ученик).
— Что нового об умножении узнали?
— Знак умножения называется точкой.
— Как по-другому можно прочитать выражения.
— 4 умножить на 2 получится 8.
— Прочитайте таким же способом.
— 6 умножить на 3 получится 18.
— 3 умножить на 4 получится 12.
- Знакомство с названиями компонентов умножения.
— Прочитайте наши выражения третьим способом.
- Первичное закрепление.
5*3=15(п.)
— Мы сложение заменили умножением. А теперь наоборот замените умножение сложением и вычислите, чему равно произведение.
С обратной стороны доски:
2*5 Ученик у доски. Сигнальная карточка.
5*2 С места с комментированием. Сигнальная карточка.
Сигнальная карточка.
3*8 Решите самостоятельно и придумайте свои примеры на умножение.
8*3 Взаимопроверка.
— У кого получилось 24? Какие примеры вы придумали?
- Физминутка.
На «раз» молча хлопок, на «два» молча руками ударяем по ногам, на «три» касаемся пальцами плеч и произносим слово «Три». Игра идёт до 30.
- Составление II блока опорной схемы.
- Выдвижение гипотезы.
— Множители – числа одинаковые, только поменялись местами, и произведения тоже одинаковые.
— Какое же можно сделать предположение?
— От перестановки множителей произведение не меняется.
- Проверка гипотезы.
— Обозначу первое слагаемое 3 тремя горизонтальными прямыми, второе слагаемое 2- двумя вертикальными прямыми (чертёж делается на листке бумаги).
 Сколько точек пересечения получилось? (6). Поверну листик. Теперь какое первое слагаемое? (2) Второе? (3). Количество точек пересечения изменилось? (Нет). Значит, верно наше предположение? (Да).
Сколько точек пересечения получилось? (6). Поверну листик. Теперь какое первое слагаемое? (2) Второе? (3). Количество точек пересечения изменилось? (Нет). Значит, верно наше предположение? (Да).- Запись в схеме.
а*в=в*а
- Составление III блока опорной схемы.
— Какой пример на умножение показывает этот чертёж? 1*1=1 1*1=1 1*2=2 2*1=2 1*3=3 3*1=3
— Используйте переместительное свойство умножения. Полученные примеры запишите во второй столбик.
— Продолжите высказывание: « Если один множитель равен единице, то произведение равно … второму множителю».
— Запишем это в общей форме:
1*а=а
а*1=а
— Сколько горизонтальных линий на чертеже? (1). А вертикальных? (Нисколько, значит, 0). Сколько точек пересечения? (0).
— Какой пример на умножение показывает чертёж?
1*0=0
0*1=0
2*0=0
0*2=0
3*0=0
0*3=0
— Запишите примеры, используя переместительное свойство умножения?
— Какой же вывод можно сделать?
— Если один множитель равен нулю, то и произведение равно нулю.

— Запишем это в общем виде:
а*0 =
0*а=
- Первичное закрепление.
1. У жеребёнка 4 ноги. На каждой ноге по 1 копыту. Сколько всего копыт?
1*4=4(к.)
2. После обеда на столе осталось 3 тарелки. Ни на одной из них не было ни одной сосиски. Сколько всего сосисок на этих тарелках?
0*3=0(с.)
При проверке обратить внимание на первый множитель:
— Что показывает первый множитель?
- Обобщение.
— Что запомнили об умножении?
- Домашнее задание.
- Рефлексия.
Коллективное составление синквейна.
Умножение
Быстрое, сильное
Ускоряет, считает, решает
Заменяет сложение
Здорово (трудно, легко, интересно).

Самоанализ урока.
Первый этап.
- общее впечатление от урока: оценка, настроение, всё ли задуманное выполнено
- удовлетворён ли работой учеников, какова дисциплина на уроке
- тема урока
- обучающие задачи
- какие компетенции вырабатывались
- тип урока
- элементы каких образовательных технологий использовал
- какими методами обучения пользовался
- формы работы
- достигнуты ли на уроке поставленные задачи
- оптимально ли протекал учебный процесс
- целенаправленность обучения, воспитания, развития учеников
- формирование познавательного интереса школьников
- соблюдалось ли на уроке требование научной организации труда (экономия времени, чёткость организации рабочего места учителя и учащихся, рациональность затраченного времени и используемых приёмов)
- как работали учащиеся на уроке (активность, работоспособность, мера их занятости, внимание, отношение к делу, ответственность, самостоятельность)
- удалось ли установить контакт, благоприятен ли психологический микроклимат, не было ли безразличных учеников • что надо исправить, изменить, дополнить на следующем уроке.

Блочное изучение темы «Умножение»
(Математика. Моро М.И. Учебник для 2 класса, часть 2, с.40-49)
1 урок – изучение теории, создание опорного сигнала, первичное закрепление.
2 урок – воспроизведение конспекта в письменной и устной форме, закрепление.
3-10 уроки – устное проговаривание, тренировочные упражнения, контроль и взаимоконтроль.
11 урок – контрольная работа.
12 урок – работа над ошибками.
Литература:
- «Технология интенсификации обучения на основе схемных и знаковых моделей учебного материала в начальных классах». (http://festival.1september.ru/2005-2006/index.php?numb.artic=310668)
- Приём изучения умножения способом пересечения прямых линий. (Казакова М.А. «К вопросу об изучении умножения в начальном курсе математики». Жур. «Начальная школа» №8 2006г., с.68)
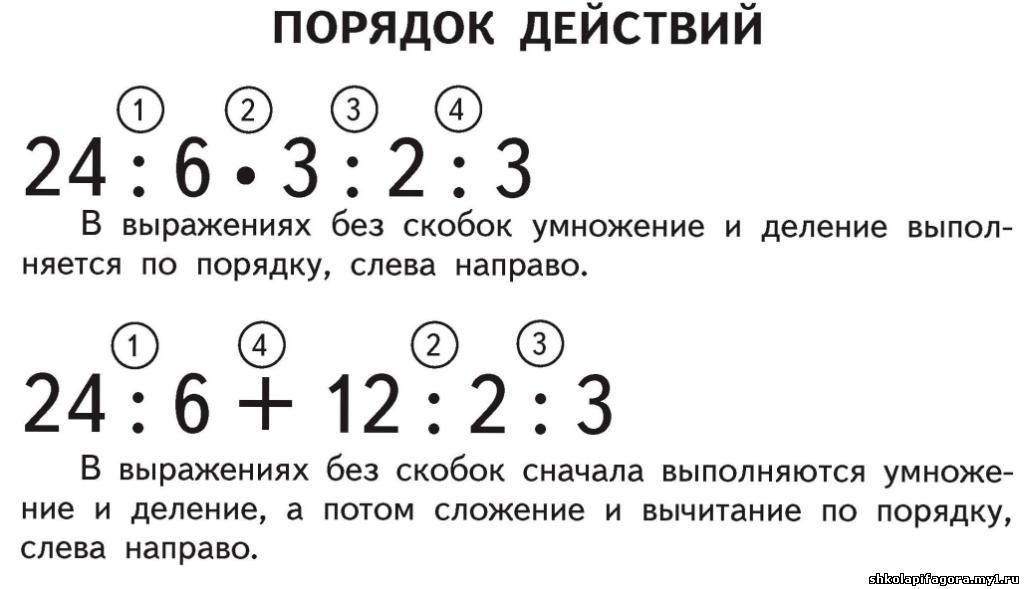
Как по порядку идут действия в примере. Порядок выполнения действий в выражениях без скобок и со скобками
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Yandex.RTB R-A-339285-1
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Определение 1В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Пример 4
Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13
Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции. С помощью видеоурока учитель имеет возможность быстрее достичь целей урока, повысить его эффективность. Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.
Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.
В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.
Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом. Затем представляются правила, составляющие порядок выполнения операций. Выводится первое правило порядка, которое указывает, что при отсутствии скобок в выражении, наличию действий одной ступени, данные действия необходимо производить по порядку. Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.
Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.
Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок. В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.
В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.
В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.
Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.
В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.
В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.
Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.
И деление чисел — действиями второй ступени.
Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом — действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).
Пример 1. Найдем значение выражения
а) х + 20 = 37;
б) у + 37 = 20;
в) а — 37 = 20;
г) 20 — m = 37;
д) 37 — с = 20;
е) 20 + k = 0.
636. При вычитании каких натуральных чисел может получиться 12? Сколько пар таких чисел? Ответьте на те же вопросы для умножения и для деления.
637. Даны три числа: первое — трехзначное, второе — значение частного от деления шестизначного числа на десять, а третье — 5921. Можно ли указать наибольшее и наименьшее из этих чисел?
638. Упростите выражение:
а) 2а + 612 + 1а + 324;
б) 12у + 29у + 781 + 219;
639. Решите уравнение:
а) 8х — 7х + 10 = 12;
б) 13у + 15у- 24 = 60;
в) Зz — 2z + 15 = 32;
г) 6t + 5t — 33 = 0;
д) (х + 59) : 42 = 86;
е) 528: k — 24 = 64;
ж) р: 38 — 76 = 38;
з) 43m- 215 = 473;
и) 89n + 68 = 9057;
к) 5905 — 21 v = 316;
л) 34s — 68 = 68;
м) 54b — 28 = 26.
640. Животноводческая ферма обеспечивает привес 750 г на одно животное в сутки. Какой привес получает комплекс за 30 дней на 800 животных?
641. В двух больших и пяти маленьких бидонах 130 л молока. Сколько молока входит в маленький бидон, если его вместимость в четыре раза меньше вместимости большего?
642. Собака увидела хозяина, когда была от него на расстоянии 450 м, и побежала к нему со скоростью 15 м/с. Какое расстояние между хозяином и собакой будет через 4 с; через 10 с; через t с?
643. Решите с помощью уравнения задачу:
1) У Михаила в 2 раза больше орехов, чем у Николая, а у Пети в 3 раза больше, чем у Николая. Сколько орехов у каждого, если у всех вместе 72 ореха?
2) Три девочки собрали на берегу моря 35 ракушек. Галя нашла в 4 раза больше, чем Маша, а Лена — в 2 раза больше, чем Маша. Сколько ракушек нашла каждая девочка?
644. Составьте программу вычисления выражения
8217 + 2138 (6906 — 6841) : 5 — 7064.
Запишите эту программу в виде схемы. Найдите значение выражения.
Найдите значение выражения.
645. Напишите выражение по следующей программе вычисления:
1. Умножить 271 на 49.
2. Разделить 1001 на 13.
3. Результат выполнения команды 2 умножить на 24.
4. Сложить результаты выполнения команд 1 и 3.
Найдите значение этого выражения.
646. Напишите выражение по схеме (рис. 60). Составьте программу его вычисления и найдите его значение.
647. Решите уравнение:
а) Зх + bх + 96 = 1568;
б) 357z — 1492 — 1843 — 11 469;
в) 2у + 7у + 78 = 1581;
г) 256m — 147m — 1871 — 63 747;
д) 88 880: 110 + х = 809;
е) 6871 + р: 121 = 7000;
ж) 3810 + 1206: у = 3877;
з) к + 12 705: 121 = 105.
648. Найдите частное:
а) 1 989 680: 187; в) 9 018 009: 1001;
б) 572 163: 709; г) 533 368 000: 83 600.
649. Теплоход 3 ч шел по озеру со скоростью 23 км/ч, а потом 4 ч по реке. Сколько километров прошел теплоход за эти 7 ч, если по реке он шел на 3 км/ч быстрее, чем по озеру?
650. Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
651. Найдите в таблице (рис. 61) все числа по порядку от 2 до 50. Это упражнение полезно выполнить несколько раз; можно соревноваться с товарищем: кто быстрее отыщет все числа?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Планы конспектов уроков по математике 5 класса скачать , учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиПри расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.
С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.
Если в выражении скобок нет, то:
Рассмотрим порядок действий в следующем примере.
Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).
При вычислении значения выражения можно вести запись двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
- Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

- Сначала выполняем все действия внутри скобок
- Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
- Выполняем оставшиеся действия в обычном порядке
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
- Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
- Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.
- Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
- Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
- При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
- Начать следует с умножения, далее – сложение.
- После того, как выражение в скобках решено, приступаем к действиям вне их.
- По правилам порядка действий, следующим шагом будет умножение.
- Завершающим этапом станет вычитание.
- Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
- Жалоба на педиатра
Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований.
 Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Согласно статье 4 Федерального закона «О порядке рассмотрения […] - Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
- Черный рынок доллара в Киеве Валютный аукцион по покупке доллара в Киеве Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе. Правила публикации объявлений на валютном […]
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Порядок действий и возведение в степень
Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:
Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2:3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
cleverstudents.ru
Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи
Post navigation
Примеры со скобками, урок с тренажерами.
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20.
 Онлайн тренажер.
Онлайн тренажер.2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1.
 Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»
3. Порядок действий (расставляем порядок и решаем примеры)
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie. info
info
Урок по математике 2 класс Порядок действий в выражениях со скобками.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»
Цель: 1.
2.
3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и
4. Учить работать в парах с целью развития коммуникативных качеств.
Оборудование * : + — (), геометрический материал.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – всем присесть.
Семь, восемь – лень отбросим.
Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:
6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см
Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?
1. Из числа 20 вычесть частное чисел 8 и 2.
2. Разность чисел 20 и 8 разделить на 2.
— Чем отличаются результаты?
— Кто сможет назвать тему нашего урока?
(на массажных ковриках)
По дорожке, по дорожке
Скачем мы на правой ножке,
Скачем мы на левой ножке.
По тропинке побежим,
Наше предположение было полностью правильно7
Где выполняются действия сначала, если в выражении есть скобки?
Смотрите перед нами «живые примеры». Давайте «оживим» их.
* : + — ().
m – c * (a + d) + x
k: b + (a – c) * t
6. Работа в парах.
Для их решения вам понадобиться геометрический материал.
Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.
Что нового вы узнали?
8. Домашнее задание.
Тема: Порядок действий в выражениях со скобками.
Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все
4 арифметических действия,
2. Формировать способность к практическому применению правила,
Формировать способность к практическому применению правила,
4.Учить работать в парах с целью развития коммуникативных качеств.
Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.
1 .Физминутка.
Девять, десять – тихо сесть.
2. Актуализация опорных знаний.
Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
1. Сравните выражения:
2. Расшифруй слово.
3. Постановка проблемы. Открытие нового.
Так как же называется дворец?
А когда в математике мы говорим о порядке?
Что вы уже знаете о порядке выполнения действий в выражениях?
— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).
20 – 8: 2
(20 – 8) : 2
Молодцы. А что интересного в этих выражениях?
Посмотрите на выражения и их результаты.
— Что общего в записи выражений?
— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?
Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?
Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.
4. Физминутка.
И по этой же дорожке
До горы мы добежим.
Стоп. Немножко отдохнем
И опять пешком пойдем.
5. Первичное закрепление изученного.
Вот мы и пришли.
Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.
6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2
Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.
Как нужно выполнять действия после решения в скобках?
На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
а + (а –в)
а * (в +с) : d – t
m – c * ( a + d ) + x
k : b + ( a – c ) * t
(a – b) : t + d
6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз Судебная экспертиза. Несудебная экспертиза Рецензия на экспертизу. Оценка Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]
Тема урока: « Порядок выполнения действий в выражениях без скобок и со скобками».
Цель урока : создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока.
Образовательные:
Закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
Развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,
коммуникативные навыки;
Воспитательные:
Воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке, аккуратность, самостоятельность, воспитывать интерес к занятиям математикой.
Формируемые УУД:
Регулятивные УУД:
работать по предложенному плану, инструкции;
выдвигать свои гипотезы на основе учебного материала;
осуществлять самоконтроль.
Познавательные УУД:
знать правила порядка выполнения действий:
уметь разъяснить их содержание;
понимать правило порядка выполнения действий;
находить значения выражений согласно правилам порядка выполнения;
действий, используя для этого текстовые задачи;
записывать решение задачи выражением;
применять правила порядка выполнения действий;
уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
слушать и понимать речь других;
выражать свои мысли с достаточной полнотой и точностью;
допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
устанавливать связь между целью деятельности и её результатом;
определять общие для всех правила поведения;
выражать способность к самооценке на основе критерия успешности учебной деятельности.
Планируемый результат:
Предметные:
Знать правила порядка выполнения действий.
Уметь разъяснить их содержание.
Уметь решать задачи с помощью выражений.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД ).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД ).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД ).
Ход урока
1. Организационный момент.
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
И друг другу улыбнитесь.
Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
Устный счёт.
Игра «Найди правильный ответ».
(У каждого ученика лист с числами)
Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.
Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
Соедините полученные результаты.
Какую геометрическую фигуру вы получили? (Треугольник)
Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
Продолжаем работать по карточке.
Найдите разность чисел 100 и 22. (78)
Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
Возьмите число 25 4 раза. (100)
Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
Сколько треугольников получилось? (5)
3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
4. Закрепление Выполнение тренировочных заданий на изученное правило
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
5. Подведение итогов.
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.
Какое действие делается первым умножение или в скобках?
Есть интересная методика умножения на пальцах.Правда,она для тех, кто знает таблицу умножения на цифру 5.Ее суть в том, что начиная с мизинца на обоих руках им приписываются свои числа.Мизинцы на правой и левой руке-это цифра 6.Безымянным пальцам приписывается цифра 7.Соответственно средним 8,а указательным-9.Большой же палец на той и другой руке это цифра 10.
А вот способ умножения больших чисел, если нет под рукой калькулятора и ручки.То есть в уме.Правда этот метод подходит цифрам от 90 до 100.
Еще метод умножения на цифру 9.
Еще другие методы вы можете посмотреть по этой ссылке
http://www.liveinternet.ru/users/3963863/post350076906/
Есть еще методика перемножения двухзначных чисел на пальцах.Но она требует определенного навыка.И, если честно, то посмотрев ее, мне легче сделать все это столбиком на бумажке.Но может кого-то заинтересует.Вот ссылка.
http://vk.cc/3ESm2o
То что я помню по геометрии — теорема Пифогора «сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы» — то есть как минимум 2*2+2*2=8. А 2*2=6 больше тянет на теорему Ферма, так она не доказана, насколько мне известно.
Вопрос конечно интересный, но из области казуистики, как сие ни печально…
А все дело в том, что червяк, как живое существо имеет только одну голову и один хвост. Да у него есть такая особенность, как способность к регенерации поврежденных частей тела. Правда надо заметить, что такой способностью обладает не все тело дождевого червя, а лишь его части с 9-ой по 15-ю, считая от головы. Так вот если в этой части червяка разрубить лопатой, то получится одна часть со старой головой и новым хвостом — этот червяк наверняка выживет. А вот у второй части будут два хвоста — старый и новый, но не будет ни одной головы… Потому такое существо точно погибнет, хотя наверное не сразу (просто от голода помрет).
Так что не рубите червяков, вы их так уж точно не умножите. Да и с делением ничего хорошего не выйдет — как был один червяк, так возможно один и останется.10 =1/6*6*6*6*6*6*6*6*6*6=1/60466176.
Что такое коммутативное, ассоциативное и распределительное свойство?
Коммутативное, ассоциативное и распределительное свойство
Как вы, возможно, уже поняли за годы уроков математики и домашних заданий, математика носит последовательный характер, а это означает, что каждая концепция основана на предшествующей работе. Арифметические навыки необходимы для овладения алгебраическими концепциями, которые затем развиваются для использования в математических расчетах и т. Д. По мере того, как вы строите эти концепции с течением времени, математический процесс может стать автоматическим, но причина или оправдание работы может быть давно забыто.В этом видео мы вернемся к основам и рассмотрим коммутативные, ассоциативные и распределительные свойства вещественных чисел , которые позволяют использовать математическую механику алгебры и не только.
Имена свойств, которые мы собираемся рассмотреть, помогают расшифровать их значения. Рассмотрим слово «коммутативный». Что вы думаете, когда видите это слово? Когда я смотрю на это слово, я вижу слово «добираться». Это слово напоминает мне ход, который в значительной степени позволяет вам делать коммутативное свойство при сложении или умножении алгебраических терминов.{2} \) и так далее. Чтобы доказать, что перемещение или перестановка терминов приемлемо, давайте рассмотрим несколько примеров коммутативного свойства, используемого в дополнительных задачах.
Если мы сложим \ (5 + 3 \), мы получим 8. Но если мы изменим наши условия и сделаем это \ (3 + 5 \), мы все равно получим 8. Итак, \ (5 + 3 = 3 + 5 \ ). Давайте немного изменим один из наших терминов для следующего примера.
\ (5 + (- 3) = 2 \) и \ ((- 3) + 5 = 2 \). Итак, \ (5 + (- 3) = (- 3) +5 \). Обратите внимание, что существует очень важное различие между сложением отрицательного целого числа и операцией вычитания.Важно отметить это различие, потому что свойство коммутативности не применяется к операции вычитания.
Например, \ (5-3 \) не дает того же, что и \ (3-5 \). Это свойство также не распространяется на разделение. \ (100 \ div 2 \ neq 2 \ div 100 \).
\ (100 \ div 2 = 50 \).
\ (2 \ div 100 = \ frac {1} {50} \).
Однако свойство коммутативности применимо к умножению. Например, \ (4 \ times 3 \ times 5 = 5 \ times 3 \ times 4 \). Давайте посчитаем, чтобы убедиться.{2} \)
.
\ (3 + 10 + 3 = 10 + 3 + 3 \).
\ (16 = 16 \).
После того, как мы сложим каждую сторону, у нас останется по 16 с обеих сторон, и это правда. \ (16 = 16 \).
Следующее свойство, которое мы рассмотрим, — это ассоциативное свойство . Опять же, имя дает полезный намек на его значение. Что приходит в голову, когда вы слышите слово «ассоциативный»? Для меня особое значение имеет слово «сотрудник», которое также может напоминать слово «группа». Соответственно, свойство ассоциативности позволяет нам группировать термины, которые соединяются путем сложения или умножения различными способами.Круглые скобки используются для группировки терминов и устанавливают порядок операций. Работа внутри скобок всегда выполняется в первую очередь. Математически свойство выглядит так:
Ассоциативное свойство сложения
\ ((a + b) + c = a + (b + c) \)
.
Ассоциативное свойство умножения
\ ((a \ cdot b) \ cdot c = a \ cdot (b \ cdot c) \)
.
Давайте посмотрим на пример использования этого свойства в задаче сложения. Этот пример покажет, что добавление двух последних терминов первыми или добавление первых двух терминов первыми просто не имеет значения.
Давайте посмотрим на \ (3+ (4 + 5) = (3 + 4) +5 \). Итак, сначала делаем то, что указано в скобках. \ (4 + 5 = 9 \) и \ (9 + 3 = 7 \).
\ (3 + 9 = 7 + 5 \).
\ (3 + 9 = 12 \) и \ (7 + 5 = 12 \).
\ (12 = 12 \).
Итак, \ (12 = 12 \), потому что это обе стороны уравнения.
Точно так же порядок, в котором мы выполняем умножение, тоже не имеет значения.
Допустим, у нас есть \ ((3 \ cdot 4) \ cdot 5 = 3 \ cdot (4 \ cdot 5) \).
\ (12 \ cdot 5 = 3 \ cdot 20 \).
\ (60 = 60 \).
Коммутативность умножения показывает, что при умножении можно переставлять члены. Напротив, ассоциативное свойство умножения перемещает скобки, чтобы упорядочить умножение.
И, наконец, последнее свойство, которое мы рассмотрим, — это дистрибутивное свойство , которое выглядит так:
\ (a \ cdot (b + c) = a \ cdot b + a \ cdot c \).
Обозначение еще раз указывает на то, что это свойство применяется только к операциям умножения и сложения.В частности, если член умножается на выражение в скобках, то умножение выполняется для каждого члена. Вот пример, чтобы доказать, что этот алгебраический ход оправдан.
\ (2 (3 + 7) = 2 \ cdot 3 + 2 \ cdot 7 \).
Скобки слева говорят нам сначала сложить 3 + 7.
\ (2 (10) = 6 + 14 \).
\ (20 = 20 \).
Сумма произведений в правой части уравнения дает тот же результат, что и умножение в левой части.
Хорошо, теперь, когда мы рассмотрели три свойства, давайте проверим вашу память.{2} \)
.
Думаете, вы поняли? Посмотрим!
Ответ для числа 1 — ассоциативное свойство, потому что скобки перемещены, чтобы упорядочить умножение. Ответ на номер два — свойство распределения, потому что 3 умножается на оба члена в круглых скобках. Это оставляет нам ответ на вопрос о том, что номер три является коммутативным свойством, потому что мы просто переставили термины.
Как вы можете видеть из нашей работы в этом видео, вы уже довольно давно используете коммутативные, ассоциативные и распределительные свойства, даже не задумываясь о том, почему.Вас попросят снова подумать об этих концепциях на курсах математики более высокого уровня, когда некоторые из этих свойств просто не работают! А до тех пор продолжайте с уверенностью использовать эти правила, чтобы направлять свою работу и мыслительный процесс.
Надеюсь, этот обзор был полезен! Спасибо за просмотр и удачной учебы!
4 распространенных заблуждения учащихся об умножении
Хотя это третья математическая операция, которой подвергаются учащиеся, умножение, как правило, является более сложной задачей для учащихся, чем их предыдущие встречи со сложением и вычитанием.Да, ученик может легко запомнить факты умножения. Но что происходит, когда их просят выйти за рамки таблицы умножения? Будь то поиск произведения двух или более значений или упрощение более сложных выражений, есть много места для ошибки. Вот четыре заблуждения учащихся при выполнении умножения:
1) Предполагая, что умножение всегда приводит к большему значению
Поскольку многие учащиеся изначально узнают, что умножение — это повторное сложение, имеет смысл сделать общий вывод о том, что произведение двух значений всегда будет больше, чем оба множителя.Это предположение справедливо только при работе с целыми числами. Введение десятичного или дробного множителя бросает вызов этому обобщению, поскольку умножение положительного числа на дробь меньше единицы фактически дает меньшее значение. Добавление отрицательных значений в смесь также противоречит этому предположению. Конечно, произведение двух чисел всегда будет меньше, если вы умножите положительное число на отрицательное.
2) Умножение чисел в порядке их перечисления
Коммутативные и ассоциативные свойства сложения представлены в некоторых учебных программах по математике уже во втором классе.После введения умножения учащиеся узнают, что эти свойства также распространяются на эту новую операцию. Во многих случаях эти свойства формулируются только как правила, а не преподаются в контексте, чтобы помочь в мысленных математических вычислениях. Рассмотрим произведение 5 x 13 x 2. Учащиеся, не знакомые с умножением на двузначные числа, могут столкнуться с трудностями при поиске умножения 5 на 13 в уме. Используя свойство коммутативности для перестановки чисел, гораздо проще вычислить это мысленно, сначала умножив 5 на 2, чтобы получить 10, а затем умножив это на 13, чтобы получить 130.Что приводит нас к следующему заблуждению…
3) Сложение нулей при умножении на степень 10
Студентам, впервые изучающим умножение, обычно говорят, что при умножении на степень 10 вам просто нужно добавить столько нулей к умножаемому числу. Те, кто соглашается с этим сокращением, не понимая основ математики, часто применяют это правило неправильно. Хотя простое добавление нулей работает при умножении целых чисел на степень 10 — например, 345 x 10 = 3450, этот метод не подходит при умножении десятичного значения на степень 10 (4.5 x 10 — это не 4,50). Добавление нуля здесь приводит к значению, которое точно такое же, как то, с чего вы начали. Учащиеся с этим заблуждением не понимают, что умножение на 10 фактически означает сдвиг десятичной точки.
4) Неправильное применение порядка операций
Спросите любого ученика, как оценить выражение, используя порядок операций, и вы, вероятно, получите ответ «Прошу прощения, дорогая тетя Салли» или PEMDAS, что означает сначала упрощение скобок, затем применение показателей степени, а затем умножение, деление, сложение. , и вычитание.Поскольку M стоит перед D, многие студенты ошибочно полагают, что вы должны выполнять умножение перед любым делением. Если выражение включает как умножение, так и деление, правильный метод фактически заставляет учащихся выполнять эти две операции слева направо в том порядке, в котором они появляются. Точно так же, упрощая выражение, такое как 3 (4-1) 2, некоторые студенты могут сначала распределить и умножить 3 на 4 и 1, потому что они узнают, что 3 соединены в круглые скобки, что, согласно мнемоническому приему , следует сначала упростить.На самом деле коэффициент 3 указывает на умножение, которое следует выполнять только после упрощения того, что указано в скобках, и возведения этого значения в квадрат.
Конечно, возникает еще одна масса заблуждений, когда ученики начинают вручную перемножать двузначные числа. Какие еще распространенные ошибки допускают учащиеся при умножении?
Меня не учили PEMDAS — Задайте вопрос профессору Puzzler
Эверетт из Иллинойса пишет: «Я родился в 1937 году в Южном Иллинойсе, округ Франклин.Нас не учили PEMDAS в школе. Когда начали обучать этому порядку действий? Сейчас этому учат во всем штате? »
Привет, Эверетт, с тех пор, как люди начали записывать математические идеи, математикам приходилось разрабатывать соглашения для обозначения значений выражений на бумаге. Эти правила не всегда были последовательными. Например, в качестве предшественника скобок некоторые математики использовали для написания выражений горизонтальную полосу сверху, чтобы указать, что элементы должны быть сгруппированы.
Рассмотрим выражения 7 x 2 + 3. Похоже, что должно быть 14 + 3 = 17. Но если автор текста хотел, чтобы сначала было выполнено добавление, он напишет:
_____
7 х 2 + 3 Как правило, это было громоздко и в конечном итоге привело к мысли, что можно использовать круглые скобки и что их будет проще писать. Впервые это было предложено в начале 1600-х годов, поэтому оно было в моде как математическое обозначение порядка и до вашего рождения.
Экспоненты были впервые использованы намного раньше 1600-х годов, но не было «официального» способа их записи. Некоторые использовали римские цифры для показателей степени, некоторые писали число после переменной, но не возводилось (таким образом, 3x означало 3 раза x, а x3 означало x в третьей степени). Вероятно, именно Рене Декарт сделал возвышенные обозначения популярными, и они стали стандартом. Декарт делал это в середине 1600-х годов (вскоре после того, как скобки стали популярными). И из-за того, как это было написано, за пределами обычной базовой линии уравнения, оно имело неявный порядок.Вы никогда не увидите следующее выражение:
2 3 + 1
и интерпретируйте это так, как будто сначала нужно объединить 3 и 1, а затем возвести 2 в 4-ю степень.
Итак, у вас есть первые два элемента PEMDAS — круглые скобки и экспоненты — которые неявно понимались с 1600-х годов.
Что касается умножения и деления, предшествующих сложению и вычитанию, я не могу точно сказать, когда они стали частью стандартной нотации упорядочивания. Однако , если вы посещали уроки алгебры в средней школе, вы использовали этот порядок операций, даже если никто не научил вас называть то, что вы делаете. Рассмотрим следующие примеры:
Пример первый: умножение перед сложением
5 + 3x
Если умножение не оценивалось перед сложением, оно было бы вычислено (как любят делать некоторые из моих учеников по алгебре) как:
5 + 3x = 5 + 3 · x = (5 + 3) x = 8x.
Порядок умножения и сложения косвенно указан в правилах того, как мы можем манипулировать терминами в выражении.
Пример второй: разделение перед добавлением
5 + 1 / х
Если деление не было оценено перед сложением, оно будет оцениваться как (5 + 1) / x или 6 / x. Опять же, этот порядок операций был неотъемлемой частью правил манипулирования терминами алгебраических выражений.
Что подводит меня к ответу на ваш вопрос. Во-первых, я действительно думаю, что возможно, что вас никогда не учили PEMDAS как конкретному условному обозначению, но все правила мнемоники PEMDAS существовали задолго до вашего рождения.Во-вторых, даже если вас этому специально не учили, вы все равно использовали его, когда занимались алгеброй, а если вы прошли уроки алгебры, значит, вы делали это правильно! Наконец, да, PEMDAS (или BODMAS *) постоянно преподается во всем мире. По-прежнему возникают споры о некоторых неоднозначных обозначениях (возможно, вы читали об этом один или несколько постов), но PEMDAS — это стандартное соглашение для интерпретации выражений во всем мире.
* BODMAS используется (я полагаю) в Великобритании, а также, возможно, в других местах.B = кронштейны, O = заказ. Скобки — это, конечно, круглые скобки, а слово «Порядок» используется для обозначения экспонентов, поэтому, хотя оно выглядит по-другому, это то же соглашение.
Основы алгебры — Свойства действительных чисел
В этом уроке мы рассмотрим некоторые свойства, применимые ко всем действительным числам. Если вы узнаете эти свойства, они помогут вам решать задачи по алгебре. Посмотрим на каждую подробно и примените его к алгебраическому выражению.
№1. Коммутативный
свойства
Коммутативный
Свойство сложения говорит о том, что мы можем складывать числа в любом порядке. Коммутативный
свойство умножения очень похоже. Он говорит, что мы можем умножать числа
в любом порядке, не меняя результата.
сложение
5а + 4 = 4 + 5а
умножение
3 х 8 х 5b = 5b x 3 х 8
№ 2.Ассоциативный
недвижимость
Оба
сложение и умножение можно выполнять одновременно с двумя числами.
Итак, если в выражении больше чисел, как нам решить, какие из двух
сначала на « associate «? Ассоциативное свойство сложения
сообщает нам, что мы можем группировать числа в сумму любым способом и при этом получать
Такой же ответ. Ассоциативное свойство умножения говорит нам, что
мы можем группировать числа в продукте любым способом и при этом получать то же самое
отвечать.
сложение
(4x + 2x) + 7x = 4x + (2x + 7x)
умножение
2x 2 (3y) = 3y (2x 2 )
№ 3.
Распределительная собственность
Распределительная собственность
свойство вступает в игру, когда выражение включает в себя как сложение, так и умножение.
Более длинное название для него — «распределительное свойство умножения».
сверх сложения.»Это говорит нам о том, что если член умножается на термины в
скобках, нам нужно « распределить » умножение на
все условия внутри.
2x (5 + y) = 10x + 2xy
Даже если в порядке операций указано, что вы сначала нужно добавить термины внутри скобок, свойство распределения позволяет упростить выражение, умножая каждый член внутри скобка рядом с множителем.Это упрощает выражение.
№ 4. Плотность
недвижимость
Плотность собственности
говорит нам, что мы всегда можем найти другое действительное число, которое находится между любыми
два действительных числа. Например, между 5,61 и 5,62 будет 5,611, 5,612,
5.613 и так далее.
Между 5.612 и 5.613, есть 5.6121, 5.6122 … и бесконечный список других чисел!
№ 5.Личность
недвижимость
Идентичность
свойство для сложения сообщает нам, что ноль, добавленный к любому числу, является числом
сам. Ноль называется «аддитивной идентичностью». Свойство идентичности
для умножения говорит нам, что число 1 умножается на любое число
дает сам номер. Число 1 называется «мультипликативным тождеством».
Дополнение
5лет + 0 = 5лет
Умножение
2c × 1 = 2c
назад наверх
10 советов по обучению детей начального уровня умножению
Сложение, вычитание, умножение и деление — это основные математические операции , которые учащиеся должны знать, поскольку они находятся на начальных уровнях.
К сожалению, очень часто дети испытывают затруднения, когда им приходится переходить от вычитания и сложения к умножению и делению.
Основная проблема заключается в том, что детям часто дается меньше времени, чтобы заняться умножением и делением, чем когда они узнают о сложении и вычитании.
Тем временем другие математические концепции, требующие умножения и деления, ждут своей работы. Это проблемы, которые часто возникают в школе.
Итак, без лишних слов, вот 10 советов по обучению умножению детей начального уровня:
Используйте практические материалы или изображения, чтобы представить
Не все дети способны переваривать абстрактные вещи, такие как числа. Не тратьте свою энергию на числа, если они не могут понять, что вы имеете в виду.
Прежде чем тратить свою энергию и время на слова, позвольте манипуляторам и инструментам работать на вас. Как только они овладеют концепцией, вы можете начать использовать число.
Начните работать с материалами, а затем переходите к числам.Убедитесь, что усвоили концепцию, прежде чем запоминать
Детям часто приходится овладевать числами умножения сразу после того, как есть много из понятий , которые им нужно знать в раннем возрасте.
Это определенно будет кошмар, когда детям, слабым в математике , очень скоро придется овладеть числами умножения . Они до сих пор не имеют представления об этой концепции, поэтому им будет сложно адаптироваться к этим различным представлениям.
Чтобы они не выгорели, постарайтесь, чтобы они действительно поняли эту концепцию и получили от нее удовольствие. Я имею в виду, им нужно знать, что это значимая концепция .
Запоминание каждой серии по порядку
Отбросив их факты умножения, дети очень скоро будут подавлены и сгорят. То же будет и со взрослыми. Поэтому никогда не пытается сразу отбросить факты.
- Начните с умножения 0 и 1. Они будут счастливы и уверены, что овладеют этими числами.
- Дайте им время попрактиковаться с первым.
- Постепенно получайте новое умножение один раз.
- Всегда дайте им время попрактиковаться, устно или письменно.
Ознакомьтесь с предыдущими сериями перед запуском новых
Постарайтесь дать детям несколько просмотреть для предыдущего умножения последовательно и случайным образом — прежде, чем вы познакомите их с новым умножением.Пример последовательности запоминания по материалам :
- Дайте понятие умножения 2 или двойных чисел.
- Выполните устную практику двойных чисел в последовательности (несколько дней или даже пару недель)
- Делайте устную практику двойных чисел случайным образом (несколько дней или даже пару недель)
- Дайте письменную практику
- Дайте концепцию умножения 3
- Выполните устную практику умножения 3 в последовательности (несколько дней или даже пару недель)
- Выполните устную практику умножения 3 случайным образом (несколько дней или даже пару недель)
- Смешайте обзор с умножением 0, 1 и 2
Рецензии предназначены не только для запоминания , но и для отработки рефлекса при ответах на вопросы.
Знакомство детей с семьей умножения и деления
Сложение всегда связано с вычитанием, а умножение должно сочетаться с делением на понятия. Вместо того, чтобы изучать пары по отдельности, практичнее изучать их одновременно. Вот пример:
Детям нужно читать семью по очереди:
2 х 3 = 6
3 х 2 = 6
6: 3 = 2
6: 2 = 3
Свяжите числа 2, 3 и 6 с термином:
- Продукты
- Факторы
- Частное
- Делитель
- Дивиденды
Звучит сложно, но мы не можем сразу понять термины. Рисование их на доске с изображениями или картинками, чтобы показать концепцию, будет полезно для наглядных учеников.
Используйте игры, чтобы помочь
Замечательно, если у вас есть подключение к Интернету для детских тренировок. Если у вас их нет, попробуйте найти или создать игры или настольные игры, которые помогут детям практиковать умножение.
Использование игр может повысить заинтересованность детей в учебе. Сухое обучение исчезнет.
- Наша любимая математическая программа — Reflex Maths.
- Я собрал несколько настольных игр на своей доске в Pinterest. Вы можете проверить их и найти интересующую вас тему.
Повесьте плакат на стены
Многие учащиеся наглядны. Им интересно видеть визуальное. Для наглядных учеников вы можете помочь , развесив плакаты или открытки на стенах.
Может быть в столовой, спальне, гостиной и везде, куда могут пойти дети.Если это в классе, вы можете повесить плакат, кроме времени тестирования.
Принесите шпаргалки
Листы Cheat очень полезны, чтобы помочь детям практиковать умножение где угодно. Возьмите бумагу и напечатайте на ней факты . Я сделал один для своего сына, и вы можете загрузить его в моем блоге. Вы можете скачать плакат умножения, таблицу умножения и карточки умножения.
Использование концепции умножения в повседневной жизни
Студент будет горд использовать умножение в своей повседневной жизни!Существует множество практических задач с использованием умножения, которые вы можете использовать, чтобы показать преимущества умножения с обучением .Вот несколько случаев, когда мы можем использовать умножение вместе с детьми:
- Купите товары в супермаркете или продуктовом магазине.
- Потребности в сбыте.
- Заказ еды.
- Расчет цены.
Изучите факты с помощью письменных или кинетических методов
Вы также можете использовать письмо, чтобы сделать вариант запоминания . Некоторые дети также обучаются кинетике. Постарайтесь найти некоторые методы запоминания, соответствующие их потребностям.
Умножение знаний — это долгосрочное вложение в обучение детей . и будут использоваться на протяжении всей их жизни.
Следовательно, учителям и родителям требуется много терпения, чтобы помочь детям освоить эту концепцию и сделать умножение рефлексом в любых математических случаях.
Наконец, попробуйте копнуть методы и настроить их в соответствии со стилем обучения детей, чтобы получить более быстрый результат. Оно работает!
6.2 — Операции с матрицами
6.2 — Операции с матрицамиРавенство
Две матрицы равны тогда и только тогда, когда
- Порядок матриц одинаковый
- Соответствующие элементы матриц одинаковые
Дополнение
- Порядок матриц должен быть таким же
- Сложите соответствующие элементы вместе
- Матричное сложение коммутативно
- Матрица сложения ассоциативна
Вычитание
- Порядок матриц должен быть таким же
- Вычесть соответствующие элементы
- Матричное вычитание не коммутативно (как и вычитание действительных чисел)
- Матричное вычитание не ассоциативно (как и вычитание действительных чисел)
Скалярное умножение
Скаляр — это число, а не матрица.
- Матрица может быть любого порядка
- Умножить все элементы в матрице на скаляр
- Скалярное умножение коммутативно
- Скалярное умножение ассоциативно
Нулевая матрица
- Матрица любого заказа
- Состоит из всех нулей
- Обозначается заглавной буквы O
- Аддитивный идентификатор для матриц
- Любая матрица плюс нулевая матрица является исходной матрицей
Умножение матриц
A m × n × B n × p = C m × p
- Количество столбцов в первой матрице должно быть равно количество строк во второй матрице.То есть внутренние размеры должны быть одинаковыми.
- Порядок произведения — это количество строк в первой матрице на количество столбцов в вторая матрица. То есть габариты изделия — это габариты внешние.
- Поскольку количество столбцов в первой матрице равно количеству строк во второй матрицу, вы можете объединить записи.
- Каждый элемент в строке i из первой матрицы объединяется в пару с элементом в столбце j из вторая матрица.
- Элемент в строке i , столбец j продукта формируется путем умножения этих парных элементов. и суммируя их.
- Каждый элемент в продукте представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
- Будет n продуктов, которые суммируются для каждого элемента в продукте.
См. Полный пример умножения матриц.
Умножение матриц некоммутативное
- Умножение действительных чисел.
- Внутренние размеры могут не совпадать при изменении порядка матриц.
Не просто перемножайте соответствующие элементы вместе
- Поскольку порядок (размеры) матриц не обязательно должны быть одинаковыми, может не быть соответствующие элементы умножаются вместе.
- Умножьте строки первого столбца на столбцы второго и сложите.
Нет матричного деления
- Не существует определенного процесса деления матрицы на другую матрицу.
- Матрица может быть разделена скаляром.
Идентификационная матрица
- Квадратная матрица
- На главной диагонали
- Нули везде
- Обозначается I. Если указан нижний индекс, это порядок единичной матрицы.
- I — мультипликативное тождество для матриц
- Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
- Умножение на единичную матрицу коммутативно, хотя порядок изменить
Идентификационная матрица размера 2
Идентификационная матрица размера 3
| I 3 = | 1 | 0 | 0 | ||
| 0 | 1 | 0 | |||
| 0 | 0 | 1 |
Свойства матриц
| Имущество | Пример |
|---|---|
| Коммутативность сложения | А + В = В + А |
| Ассоциативность сложения | А + (В + С) = (А + В) + С |
| Ассоциативность скалярного умножения | (кд) А = с (дА) |
| Скалярная идентичность | 1А = А (1) = А |
| Распределительный | c (A + B) = cA + cB |
| Распределительный | (с + г) А = сА + дА |
| Идентификатор добавки | А + О = О + А = А |
| Ассоциативность умножения | A (BC) = (AB) C |
| Распределительный левый | A (B + C) = AB + AC |
| Распределитель правый | (A + B) C = AC + BC |
| Скалярная ассоциативность / коммутативность | c (AB) = (cA) B = A (cB) = (AB) c |
| Мультипликативная идентичность | IA = AI = A |
Свойства действительных чисел, не являющиеся свойствами матриц
Коммутативность умножения
- Вы не можете изменить порядок задачи умножения и ожидать получить то же самое продукт.AB ≠ BA
- Вы должны быть осторожны при разложении общих множителей, чтобы убедиться, что они одно и тоже боковая сторона. AX + BX = (A + B) X и XA + XB = X (A + B), но AX + XB не учитывается.
Свойство нулевого продукта
- Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.
Мультипликативное свойство равенства
- Если A = B, то AC = BC. Это свойство все еще верно, но обратное не обязательно верно.То, что AC = BC, не означает, что A = B.
- Поскольку умножение матриц не коммутативно, вы должны умножение до или после умножения с обеих сторон уравнения. То есть, если A = B, тогда AC = BC или CA = CB, но AC ≠ CB.
Нет матричного деления
- Надо умножить на обратную матрицу
Оценка функции с помощью матрицы
Рассмотрим функцию f (x) = x 2 — 4x + 3 и матрицу A
Первоначальная попытка оценить f (A) будет заключаться в замене каждого x с помощью A, чтобы получить f (A) = A 2 — 4A + 3.Есть одно небольшое проблема, однако. Константа 3 равна не матрица, и вы не можете добавить матрицы и скаляры вместе. Итак, умножаем константа матрицей идентичности.
f (A) = A 2 — 4A + 3I.
Оцените каждый член функции, а затем сложите их.
| А 2 = | 1 | 2 | * | 1 | 2 | = | 7 | 10 | ||||||
| 3 | 4 | 3 | 4 | 15 | 22 |
| -4 А = -4 | 1 | 2 | = | -4 | -8 | ||||
| 3 | 4 | -12 | -16 |
| 3I = 3 | 1 | 0 | = | 3 | 0 | ||||
| 0 | 1 | 0 | 3 |
| f (А) = | 7 | 10 | + | -4 | -8 | + | 3 | 0 | = | 6 | 2 | ||||||||
| 15 | 22 | -12 | -16 | 0 | 3 | 3 | 9 |
Факторинговые выражения
Показаны некоторые примеры факторинга.Упрощайте и решайте как обычно, но помните эта матрица умножение не коммутативно и нет матричного деления.
2X + 3X = 5X
AX + BX = (A + B) X
ХА + ХВ = Х (А + В)
AX + 5X = (A + 5I) X
AX + XB не учитывает
Решение уравнений
Систему линейных уравнений можно записать как AX = B, где A — коэффициент матрица, X — вектор-столбец, содержащий переменные, а B — правая боковая сторона. В следующем разделе мы узнаем, как решить это уравнение.
Если существует более одной системы линейных уравнений с одним и тем же коэффициентом матрица, то вы можете расширить матрицу B, чтобы она содержала более одного столбца. Ставить каждую правую часть в свой столбец.
Умножение матриц
Умножение матриц включает суммирование произведения. Это уместно там, где вы нужно умножайте вещи вместе, а затем Добавлять. Например, умножение количества единиц на стоимость единицы будет дать общую Стоимость.
Единицы по продукту найдены путем выполнения модульного анализа на матрицы.Этикетки для продукта — это этикетки строк первого матрица и метки столбцов вторая матрица.
Комплексные числа: умножение
Комплексные числа: умножениеУмножение производится алгебраически.
Сложное умножение — это более сложная операция для понимания с алгебраической или геометрической точки зрения. Давайте сначала сделаем это алгебраически, а для умножения возьмем определенные комплексные числа, например 3 + 2 i и 1 + 4 i. В каждом есть два члена, поэтому, когда мы их умножим, мы получим четыре члена: (3 + 2 i ) (1 + 4 i ) = 3 + 12 i + 2 i + 8 i 2 .Теперь 12 i + 2 i упрощается до 14 i, конечно. А как насчет 8 i 2 ? Помните, что мы ввели i как сокращение для √ – 1, квадратного корня из –1. Другими словами, i — это то, что имеет квадрат –1.Таким образом, 8 i 2 равно –8. Следовательно, произведение (3 + 2 i ) (1 + 4 i ) равно –5 + 14 i.
Если вы обобщите этот пример, вы получите общее правило умножения
Помните, что ( xu — yv ), действительная часть продукта, является произведением действительных частей минус произведение мнимых частей, но ( xv + yu ) мнимая часть продукт, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте посмотрим на некоторые частные случаи умножения.
Умножение комплексного числа на действительное
В приведенной выше формуле умножения, если v равно нулю, вы получите формулу для умножения комплексного числа x + yi и действительного числа u вместе: ( x + yi ) u = xu + yu i .Другими словами, вы просто умножаете обе части комплексного числа на действительное число.Например, 2 умножить на 3 + i будет просто 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваиваете расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Вы можете думать об умножении на 2 как о преобразовании, которое растягивает комплексную плоскость C с коэффициентом 2 от 0; и умножение на 1/2 как преобразование, которое сжимает C в сторону 0.
Умножение и абсолютное значение.
Несмотря на то, что мы сделали только один случай для умножения, достаточно предположить, что абсолютное значение zw (то есть расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение ш. Это было тогда, когда w было действительным числом u чуть выше. На самом деле это так в целом:Проверка этого тождества — это упражнение по алгебре.Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не придется иметь дело с квадратными корнями. Мы покажем | zw | 2 = | z | 2 | w | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда согласно формуле умножения zw равно ( xu — yv ) + ( xv + yu ) i. Вспомните из раздела об абсолютных величинах, что
| z | 2 = x 2 + y 2Аналогично имеем
| w | 2 = и 2 + v 2и, поскольку zw = ( xu — yv ) + ( xv + yu ) i,
| wz | 2 = ( xu — yv ) 2 + ( xv + yu ) 2Итак, чтобы показать | zw | 2 = | z | 2 | w | 2 , все, что вам нужно сделать, это показать, что
( xu — yv ) 2 + ( xv + yu ) 2 = ( x 2 + y 2 ) ( u17 v 2 ) и это простое упражнение по алгебре. Более высокие степени i легко найти теперь, когда мы знаем i 4 = 1. Например, i 5 равно i умножить на i 4 , и это всего лишь i. . Вы можете уменьшить степень i на 4 и не изменять результат. Другой пример: i 11 = i 7 = i 3 = — i. Как насчет отрицательной степени i ? Что является обратным для i, то есть i –1 ? По той же причине, что вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i –1 = i 3 = — i. Таким образом, i является обратным — i. Представьте себе — число, обратное значение которого есть собственное отрицание! Конечно, легко проверить, что i раз — i равно 1, поэтому, конечно, i и — i являются обратными величинами. Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте их немного подождем. Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на x единиц справа от мнимой оси и на y единиц выше действительной оси. Точка z i расположена на y единиц слева и x единиц выше. Произошло то, что умножение на i повернулось в точку z на 90 ° против часовой стрелки вокруг начала координат до точки z i. Короче говоря, умножение на i дает поворот на 90 ° против часовой стрелки на 0. Вы можете проанализировать, что происходит при умножении на — i таким же образом. Вы обнаружите, что умножение на — i дает поворот на 90 ° по часовой стрелке вокруг 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, которое подразумевается против часовой стрелки. Тогда мы можем сказать, что умножение на — i дает поворот на –90 ° вокруг 0 или, если хотите, поворот на 270 ° вокруг 0. Пусть z и w — точки на комплексной плоскости C .Проведите линии от 0 до z и от 0 до w . Длины этих строк — абсолютные значения | z | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | zw | что равно | z | | Вт |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Чего мы не знаем, так это направления линии от 0 до zw. Ответ: «углы складываются». Мы определим направление линии от 0 до z под определенным углом, называемым аргументом из z , иногда обозначаемым arg ( z ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — прямая от 0 до z. Другая точка w имеет угол arg ( w ).Тогда произведение zw будет иметь угол, который является суммой углов arg ( z ) + arg ( w ). (На диаграмме arg ( z ) составляет около 20 °, а arg ( w ) составляет около 45 °, поэтому arg ( zw ) должно быть около 65 °. Полномочия
i. В следующем частном случае умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = –1. А как насчет i 3 ? Это всего лишь i 2 умноженное на i , то есть –1 умноженное на i. Следовательно, i 3 = — i. Это интересно: куб i — это собственное отрицание.Затем рассмотрим i 4 . Это квадрат i 2 , то есть квадрат –1. Таким образом, i 4 = 1. Другими словами, i — это корень четвертой степени из 1. Вы можете показать, что — i — это еще один корень четвертой степени из 1. И поскольку и –1, и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно,
1, i, –1 и — i. Это наблюдение связано с фундаментальной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня. Корни единства.
Различные корни из 1 называются корнями из единицы. В общем, по Фундаментальной теореме алгебры количество корней n -й степени из единицы равно n, , поскольку имеется n корней степени n -й степени z u — 1 = 0.Квадратные корни из единицы равны 1 и –1. Корни четвертой степени равны ± 1, ± i, , как отмечалось ранее в разделе, посвященном абсолютным значениям. Кроме того, в этом разделе упоминалось, что ± √2 / 2 ± i √2 / 2 были квадратными корнями из i и — i, и теперь с формулой умножения, которую легко проверить. Следовательно, восемь корней восьми из единицы равны ± 1, ± i, и ± √2 / 2 ± i √2 / 2. Обратите внимание на то, как эти восемь корней единицы равномерно распределены по единичной окружности. Умножение комплексного числа на
i. В нашей цели по поиску геометрической интерпретации комплексного умножения, давайте теперь рассмотрим умножение произвольного комплексного числа z = x + yi на i. z i = ( x + yi ) i =
— y + xi . Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока посмотрим на результаты без обоснования. Мы видели два особых случая умножения: один на вещественные числа, что приводит к масштабированию, другой на и , что приводит к вращению. Общий случай — это комбинация масштабирования и вращения.









 Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Согласно статье 4 Федерального закона «О порядке рассмотрения […]