Сложение и вычитание десятичных дробей
Вы уже умеете складывать обыкновенные дроби с равными знаменателями. Научимся складывать десятичные дроби. Найдем сумму 2,374 + 1,725. Обратив эти дроби в обыкновенные, получаем:
$2,374 + 1,725 = 2\frac{374}{1000} + 1\frac{725}{1000} = 3 + \frac{374 + 725}{1000} = 3 + \frac{1099}{1000} = 3 + 1\frac{99}{1000} = 4\frac{99}{1000} = 4,099$
Однако складывать десятичные дроби можно гораздо проще, не обращая их в обыкновенные.
Сходство способов записи десятичных дробей и натуральных чисел позволяет выполнять сложение десятичных дробей в столбик.
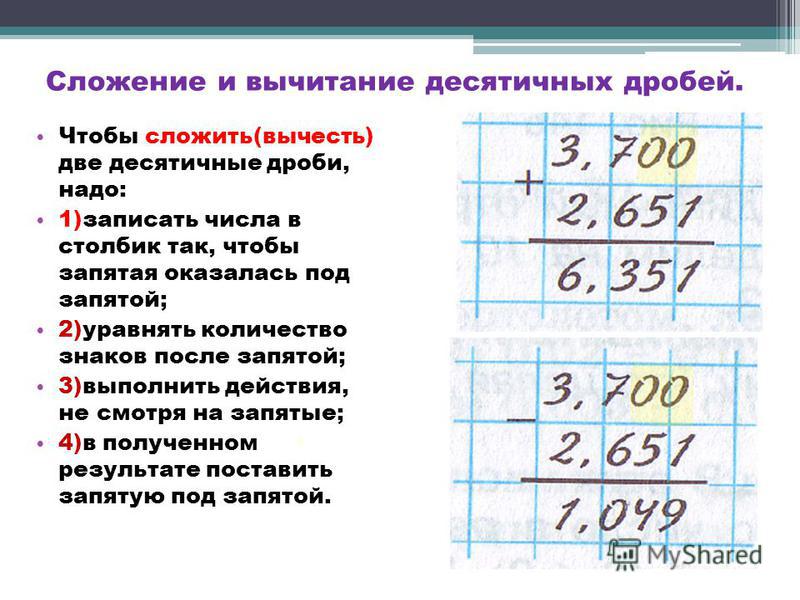
Чтобы сложить две десятичные дроби, надо:
1) уравнять в слагаемые количество цифр после запятой;
2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
3) сложить полученные числа так, как складывают натуральные числа;
4) поставить в полученной сумме запятую под запятыми в слагаемых.
На рисунках 207 + 208 показано, как найти суммы 2,374 + 1,725 и 7,6 + 11,35.
В столбик можно также вычитать десятичные дроби.
Чтобы из одной десятичной дроби вычесть другую, надо:
1) уравнять в уменьшаемом и вычитаемом количество цифр после запятой;
2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
3) произвести вычитание так, как вычитают натуральные числа;
4) поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.
На рисунке 209 показано, как найти разность 0,8 − 0,593.
Из приведенных примеров видно, что сложение и вычитание десятичных дробей выполнялось поразрядно, т.е. так, как мы производили соответствующие действия с натуральными числами. Это и есть главное преимущество десятичной формы записи дробей.
Свойства сложения натуральных чисел выполняются и для дробных чисел. Напомним эти свойства.
Напомним эти свойства.
a + b = b + a − переместительное свойство сложения,
(a + b) + c = a + (b + c) − сочетательное свойство сложения.
Пример 1. Вычислите разность 4 км 36 м − 768 м, записав данные величины в километрах.
Решение. Имеем:
$4 км 36 м — 768 м = 4\frac{36}{1000} км — \frac{768}{1000} км = 4,036 км — 0,768 км = 3,268 км.$
Ответ: 3,268 км.
Пример 2. Собственная скорость катера равна 30 км/ч, а скорость течения реки − 1,4 км/ч. Найдите скорость катера по течению и его скорость против течения реки.
Решение.
1) 30 + 1,4 = 31,4 (км/ч) − скорость катера по течению.
2) 30 − 1,4 = 28,6 (км/ч) − скорость катера против течения.
Ответ: 31,4 км/ч, 28,6 км/ч.
8-12. Сложение и вычитание десятичных дробей
Устный счет
Это надо знать
Сложение десятичных дробей выполняется поразрядно.Правило сложения десятичных дробей:
1) в дробях уравниваем количество знаков после запятой;
2) записываем дроби друг под другом так, чтобы цифры одинаковых разрядов были одна под другой, запятая под запятой;
3) выполняем сложение по разрядам, ставим запятую под запятыми.

Примеры:
Найти сумму чисел: а) 12,25 + 2,56; б) 69,78 + 4,568; в) 4,321 + 15.
Законы сложения:
1. Переместительный закон
От перемены мест слагаемых сумма не меняется.
a + b = b + a
2. Сочетательный закон
От перемены места расстановки скобок сумма не меняется.
(a + b) + c = a + (b + c)
Вычитание десятичных дробей выполняется поразрядно.
Правило вычитания десятичных дробей:
1) в дробях уравниваем количество знаков после запятой;
2) записываем дроби друг под другом так, чтобы цифры одинаковых разрядов были одна под другой, запятая под запятой;
3) выполняем вычитание по разрядам, ставим запятую под запятыми.
Примеры:
Найти разность чисел: а) 12,25 — 2,56; б) 69,78 — 4,568; в) 24,321 — 15.
Видеоурок
Домашнее задание
К уроку 8 (на 13.09)П. 2.1
1 уровень (учебник)
№ 2.2
№ 2.7
2 уровень (сборник задач)
№ 1.25 стр. 9
Найдите число, которое больше десятичной дроби 11,063 на:
Найдите сумму:
К уроку 9 (на 14.09)
П. 2.1
1 уровень (учебник)
№ 2.11
№ 2.18
2 уровень (сборник задач)
№ 1.22 (1-4) стр. 8
Выполните сложение:
№ 1.
 23 стр. 9
23 стр. 9 № 5.12 стр. 120
Сумма двух последовательных четных чисел равна 978. Найдите эти числа.
К уроку 10 (на 15.09)
П. 2.2
1 уровень (учебник)
№ 2.29
№ 2.30
2 уровень (сборник задач)
№ 1.26 стр. 9
Используя законы сложения, найдите сумму:
1) 4,83 + 6,669 + 3,331 + 5,17;
2) 9,6099 + 15,03 + 4,07 + 0,9001;
3) 351,75 + 30,048 + 0,25 + 0,952;
4) 6,094 + 6,099 + 3,006 + 2,001.
№ 1.39 стр. 11
Расположите числовые выражения A, B, C, D в порядке убывания их значений, если:
A = 12,9086 + 5093,1;
B = 129,086 + 5093,1;
C = 12,9086 + 5,0931;
D = 12,9086 + 509,31.
№ 5.13 стр. 120
Сумма двух последовательных нечетных чисел равна 2044.
К уроку 11 (на 16.09)
П. 2.3
1 уровень (учебник)
№ 2.41
№ 2.42
2 уровень (сборник задач)
№ 1.27 стр. 9
Найдите разность: 1) 197,364 — 0,364; 2) 51,0098 — 51; 3) 2673,48 — 73,48; 4) 6,4957 — 0,0957.
№ 1.40 стр. 11
Расположите числовые выражения P, T, K, M в порядке возрастания их значений, если:
P = 0,0298 — 0,00043;
T = 0,0298 — 0,0043;
K = 0,00298 — 0,000043
M = 0,298 — 0,0043.
№ 5.46 стр. 125
Доберман съедает порцию корма за 7 мин, а чау-чау ту же порцию — за 5 мин. За какое время, не конфликтуя, собаки съедят одну порцию корма вдвоем?
К уроку 12 (на 19.09)
П. 2.3
1 уровень (учебник)
№ 2.60
№ 2. 57 (1-4)
57 (1-4)
2 уровень (сборник задач)
№ 1.29 стр. 9
Найдите значения выражения:
1) 25 — 24,39; 2) 95 — 0,62; 3) 100 — 99,99; 4) 3,489 — 2; 5) 791,54 — 91; 6) 304,89 — 4,89.
№ 1.37 стр. 11
Найдите значение выражения:
1) 9,604 — 5,21 — 0,809;
2) 99,009 — 9,09 — 9,9;
3) 72,6012 — 0,0012 — 32,6;
4) 315,06403 — 5,064 — 100,003.
№ 3.1 (1, 2) стр. 76
Решите уравнение:
1) х + 7,293 = 18,293;
2) 50,101 + у = 49.
Сложение и вычитание десятичных дробей
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Десятичные дроби
Здесь мы рассмотрим, как складывать и вычитать десятичные дроби.
Чтобы сложить или вычесть десятичные дроби, нужно записать числа столбиком так, чтобы запятая стояла под запятой. Затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой.
Затем выполнить действие не обращая внимание на запятую, а в ответе поставить запятую под запятой.
Пример: 1) Сложение и вычитание дробей, если одинаковое количество цифр после запятой
| + | 1 | 7 | , | 6 |
| 9 | , | 7 | ||
| 2 | 7 | , | 3 |
| — | 1 | 7 | , | 6 |
| 9 | , | 7 | ||
| 7 | , | 9 |
2) Вычитание дробей, если разное количество цифр после запятой. Дроби 147,33 — 89,7. Сначала нужно уровнять количество цифр после запятой, для этого мы добавим справа в конце один ноль, затем выполним действие столбиком.
| + | 1 | 4 | 7 | , | 3 | 3 |
| 8 | 9 | , | 7 | 0 | ||
| 2 | 3 | 7 | , | 0 | 3 |
| — | 1 | 4 | 7 | , | 3 | 3 |
| 8 | 9 | , | 7 | 0 | ||
| 5 | 7 | , | 6 | 3 |
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Десятичная запись дробных чисел
Сравнение десятичных дробей
Приближенные значения чисел. Округление чисел
Округление чисел
Умножение десятичных дробей
Деление десятичных дробей
Среднее арифметическое
Десятичные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1215, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1257, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1259, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1376, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1387, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1439, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 984, Мерзляк, Полонский, Якир, Учебник
Номер 1026, Мерзляк, Полонский, Якир, Учебник
Номер 1040, Мерзляк, Полонский, Якир, Учебник
Номер 1125, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 92, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 125, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 521, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 948, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1031, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1057, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1146, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1247, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1255, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1414, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
урок с примерами, карточками и видео
В пятом классе на занятиях по математике ученики знакомятся с десятичными дробями. В дальнейшем этот вид дробей становится основным для школьников. Однако те ребята, которые не освоили сложение десятичных дробей в столбик, потом испытывают значительные сложности в решении задач.
Основные правила сложения десятичных дробей
Не забывайте, что в ответе запятую ставим под запятыми в исходных дробяхВсе десятичные дроби имеют одинаковый знаменатель, что позволяет записывать дробную часть в сокращённом виде: после целой части ставится запятая, далее записывается числитель дробной части. Например, в числе 56,8 целой частью является 56, а 8 — числитель десятичной дроби. При сложении в столбик необходимо располагать целые части складываемых чисел строго друг над другом, таким же образом разместить и дробные. На практике это легко сделать, ориентируясь на запятые — они должны располагаться друг над другом.
На практике это легко сделать, ориентируясь на запятые — они должны располагаться друг над другом.
Сложение производится по общим правилам: по разрядам, начиная с меньшего. После получения значения суммы в этом числе также ставится запятая, строго под запятыми слагаемых.
Если количество знаков после запятой у слагаемых неравное, можно поставить 0 на месте недостающего знака. Это действие необязательно, не будет ошибкой оставить пустое пространство при записи.
Карточки для работы
На начальном этапе освоения сложения десятичных дробей в предлагаемых примерах запись уже произведена с учётом сопоставления целых и дробных частей.
Для закрепления материала в заданиях учащимся самим требуется произвести запись в столбик.
Фотогалерея: варианты карточки для уроков
Видео: как сложить десятичные дроби в столбик
youtube.com/embed/E65Cn50c-6E?feature=oembed» frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»»/>
Операции с десятичными дробями — базовые для программы средней школы по математике. Их успешное освоение позволит школьнику и в дальнейшем получать отличные результаты.
Оцените статью: Поделитесь с друзьями!Онлайн Тренажер ДРОБИ. Сложение, Вычитание, Умножение и Деление ⏳
Менталар представляет вам бесплатно онлайн тренажер Дроби.
Тренажер дроби для любого класса
Данный тренажер подходит для изучения и закрепления дробей в игре – начиная с 2 класса по изучению этой темы
3 класса , 4 класса, 5 класса, 6 класса дроби, 7 класса , 8 класса, 9 класса, 10 класса, 11 класса
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь будет состоять из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, является числителем . Второе число под линией – знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-то делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби – это обозначить линию, разделяющую каждое число, «вне». Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Упрощение дробей Тренажер
Первый метод – разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить. В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54.
- Снова разделите на 2, чтобы получить 6/27.
- Разделите на 3, чтобы получить 2/9
Добавление дробей Тренажер
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Дополнение: Пример 2
Допустим, вы хотите сложить дроби и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ – 3/6. Упростите это до ½.
Вычитание дробей по тренажеру
Вычитание дробей работает аналогичным образом:
- Шаг 1. Убедитесь, что знаменатели совпадают
- Шаг 2 – вычтите числители
- Шаг 3 – При необходимости упростите дробь
Вычитание: пример 1
Допустим, вас попросили потренироваться ¾ – ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ – be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.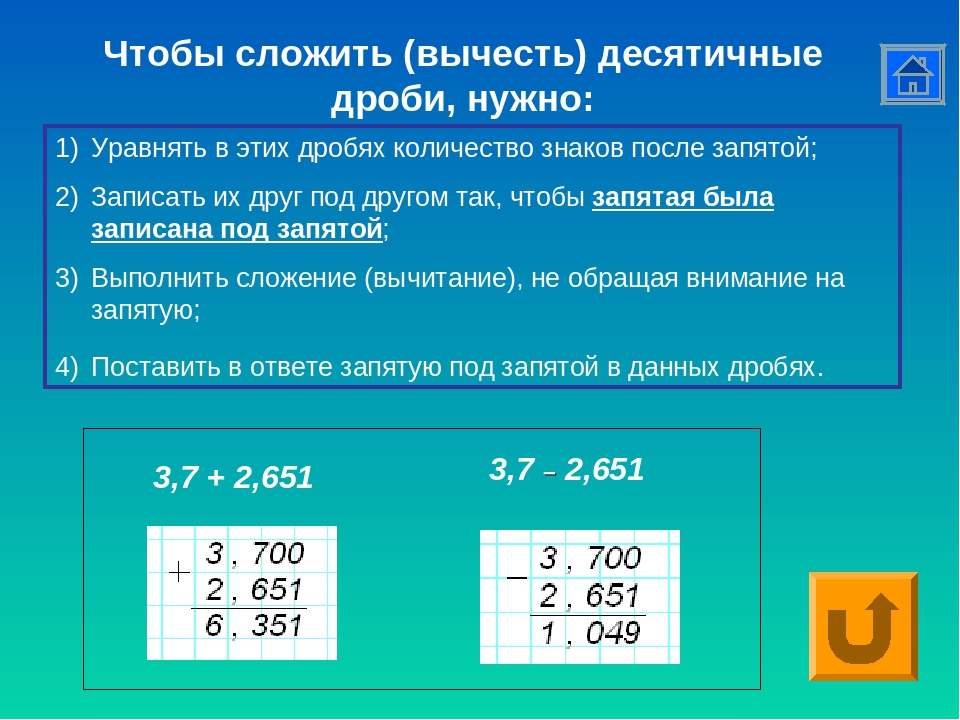
Умножение дробей Тренажер
Умножение дробей относительно легко; вы просто перемножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
Деление дробей Тренажер
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и вы получите 3/2.
Может потребоваться дальнейшее уменьшение фракции для достижения сложной фракции.
Исследуй дальше Обратные Числа
Распространенные ошибки и на что следует обратить внимание. Тренажер
Давайте возьмем пример, сложив вместе ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Другие распространенные ошибки включают:
Оставляйте знаменатель неизменным во время вопросов, касающихся умножения или сложения.
Как неправильную дробь перевести в смешанное число. Тренажёр
Любую неправильную дробь можно превратить в смешанную. Для этого нужно выделить из нее целую часть.
Чтобы из неправильной дроби выделить целую часть, нужно:
разделить с остатком числитель на знаменатель;
частное без остатка будет целой частью;
остаток (если он есть) дает числитель дробной части, а знаменатель дробной части остается тем же, что и у неправильной дроби.
Тренажёр по этой теме поможет вам закрепить эту тему.
Как смешанное число перевести в неправильную дробь Тренажёр
Рассмотрим как любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Тренажёр и тест помогут вам закрепить эту тему.
Умножение и деление десятичных дробей Онлайн тренажер
Давайте проверим себя, как вы умеете умножать и делить десятичные дроби. Вспомните, как нужно умножать и делить дроби, а затем поработайте на нашем тренажёре. В нём всего 21 пример, но будьте внимательны!
Задания в тренажёре включают умножение и деление на 0,1; 0,01; 0,001; 0,0001 и т.д, а также умножение и деление десятичных дробей на 10, 100, 1000 и т.д. То есть мы учимся правильно переносить запятую.
Как умножать десятичные дроби на 10, 100, 1000, 10 000 и т. д?
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Например:
8,963 · 10 = 89,63
0,062 · 1000 = 0062 = 62 (нули перед числом не пишутся)
2,9 · 10000 = 2,9000 · 10000 = 29000
Как умножать десятичные дроби на 0,1; 0,01; 0,001 и т.
 д?
д?Умножить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).
Например:
54,3 · 0,1 = 54,3 : 10 = 5,43
0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001
Как делить десятичные дроби на 0,1; 0,01; 0,001 и т.д?
Разделить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что умножить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в делимом на столько знаков вправо, сколько нулей стоит в делителе перед единицей (ноль перед запятой тоже считаем).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
Например:
54,87 : 0,1 = 548,7
34,56 : 0,0001 = 34,5600 : 0,0001 = 345600
24 : 0,001 = 24,000 : 0,001 = 24000
Как делить десятичные дроби на 10, 100, 1000 и т.д?
Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.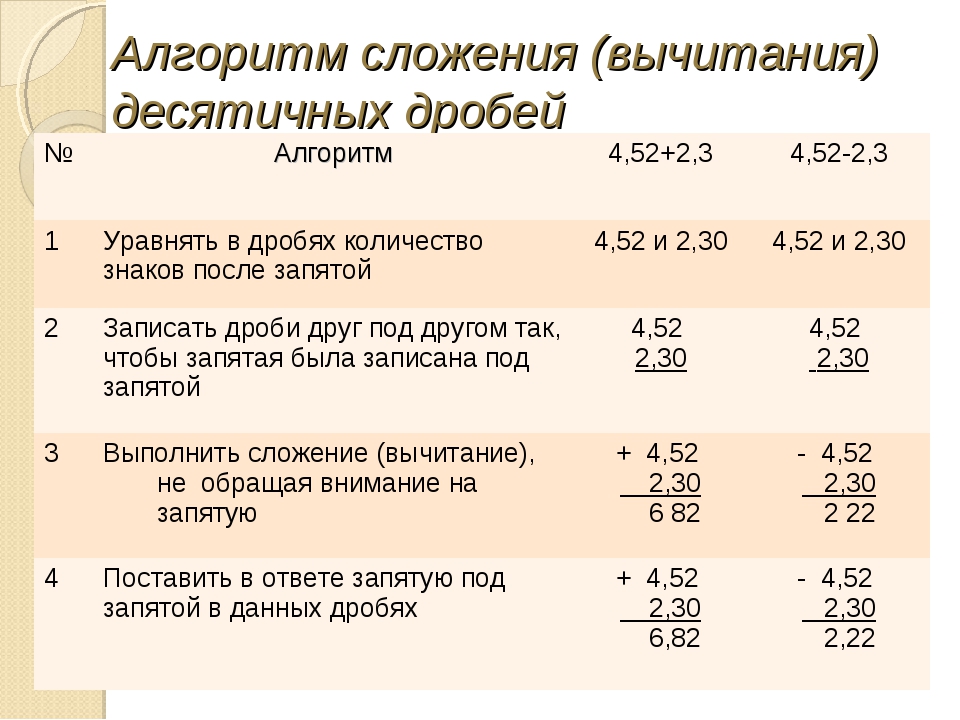
При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.
Например:
374,5 : 100 = 3,745
5,021 : 1000 = 0005,021 : 1000 = 0,005021
0,1 : 100 = 000,1 : 100 = 0,001
В этом онлайн тренажере необходимо выбрать правильный ответ и нажать на него. В случае правильного ответа он загорится зеленым цветом, если ответ неверный — красным. В этом случае попробуйте найти правильный ответ, а затем нажмите кнопку «Дальше».
Онлайн тренажер по математике из раздела «Умножение и деление десятичных дробей»
Закрепляющие файлы для работы.
Менталар желает Вам легкой плодотворной усвояемой работы над собой.
Верьте в себя и у вас все получится!!!
Ваш сайт Менталар.
5.5.2. Сложение десятичных дробей.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 32 Опубликовано
Чтобы сложить десятичные дроби, нужно: 1) уравнять в этих дробях количество десятичных знаков; 2) записать их друг под другом так, чтобы запятая была записана под запятой; 3) выполнить сложение, не обращая внимания на запятую, и поставить в сумме запятую под запятыми в слагаемых дробях.
Примеры. Сложить десятичные дроби.
1) 0,07+13,23.
Решение. Применим переместительный закон сложения: 0,07+13,23=13,23+0,07 и запишем дроби друг под другом так, чтобы запятая оказалась под запятой. Складываем, не обращая внимания на запятую. В полученной сумме поставим запятую под запятыми в слагаемых. Нуль на конце полученного результата 13,30 можно отбросить.
13,23+0,07=13,3.
2) 11,21+9,3.
Решение. Записываем данные дроби друг под другом так, чтобы запятая оказалась под запятой. Уравниваем количество знаков после запятых в слагаемых. Для этого припишем справа нуль к дроби 9,3. Складываем, не обращая внимания на запятые и ставим в сумме запятую под запятыми в слагаемых.
11,23+9,3=20,51.
3) Вычислить рациональным способом. 1,245+(0,755+3,02).
Решение. Используем переместительный и сочетательный законы сложения.
1,245+(0,755+3,02)=(1,245+0,755)+3,02=2+3,02=5,02.
Пояснение: у слагаемых 1,245 и 0,755 одинаковое количество знаков после запятых (по три цифры), поэтому, удобно сложить их устно, как складывают целые числа, а затем отделить справа запятой три цифры, как было в слагаемых. Получилось 2,000. Три нуля после запятой отбрасываем, получается число 2. Прибавили 3,02 и получили 5,02.
1,245+(0,755+3,02)=5,02.
Сложение и вычитание десятичных дробей
Тема урока: « Сложение и вычитание десятичных дробей»
Класс:6
Тип урока: «открытие нового знания»
Планируемые образовательные результаты:
личностные:
—овладеть умением правильно и корректно выражать собственное мнение;
-овладеть умением учиться самостоятельно;
-овладеть умением выражать свои мысли в письменной форме;
-научиться применять полученные знания и умения к решению новых проблем
овладеть умениями совместной деятельности: согласование и координация деятельности с другими ее участниками; объективное оценивание своего вклада в решение общих задач коллектива;
метапредметные:
-умение понимать и использовать математические средства наглядности (таблицы, схемы и др.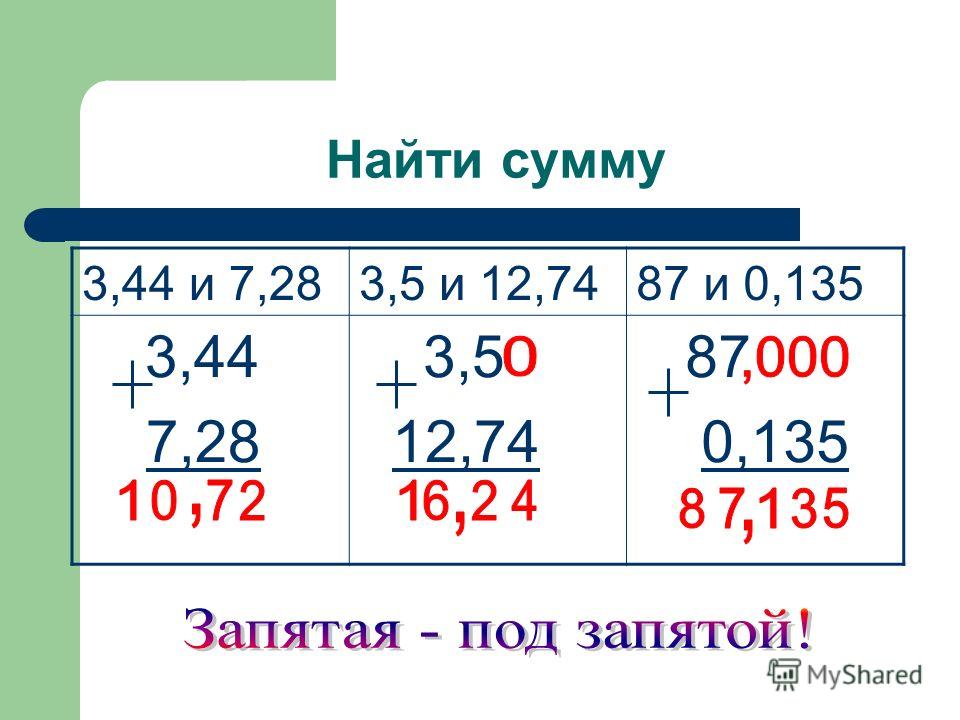 ) для иллюстрации, интерпретации, аргументации;
) для иллюстрации, интерпретации, аргументации;
-умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
-понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
-умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
-умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
— овладение смыслом понятий «десятичные дроби», «равные десятичные дроби», «сложение и вычитание десятичных дробей»;
—формирование умений строить алгоритмы сложения и вычитания десятичных дробей;
— формирование умений складывать и вычитать десятичные дроби;
— понимать и правильно употреблять в устной и письменной речи математические термины «десятичные дроби», «целая и дробная части десятичных дробей», «равные десятичные дроби», «сложение и вычитание десятичных дробей», понимать их в речи учителя;
— применять в различных ситуациях (от простой к более сложной) умение складывать и вычитать десятичные дроби
Ход урока:
Раздаточный материал:
карточки с алгоритмом сложения и вычитания десятичных дробей;
эталон для самопроверки.
1. Мотивация к учебной деятельности.
Здравствуйте ребята, начинаем урок.
Откройте тетради, запишем сегодняшнее число.
Ребята, с каким настроением вы пришли на урок?
Нарисуйте в тетрадях смайлик, который будет отражать ваше настроение на уроке.
Сегодня на уроке мы должны выяснить чего мы не знаем и найти самостоятельно выход из затруднения.
− Чтобы узнать что-то новое, что надо сделать сначала? (Повторить те знания, которые нам понадобятся на уроке.)
Посмотрите на доску и вспомните, что мы знаем об этих числах:
2,13; 0,50; 13,63; 15,800; 0,500, 223,0; 2,130
Прочитайте десятичные дроби.
Назовите целые и дробные части.
Какие дроби можно записать короче?
Назовите десятичную дробь в которой в разряде десятых стоит число 6.
Назовите равные дроби.
Что мы еще умеем делать с десятичными дробями?
Сравните дроби: 3,6 и 3,15; 5,31 и 5,127; 0,713 и 0,8
https://uchi. ru/teachers/groups/1012309/subjects/1/course_programs/6/cards/19392
ru/teachers/groups/1012309/subjects/1/course_programs/6/cards/19392
— Каким алгоритмом мы пользуемся при сравнении двух десятичных дробей?
Уравнять число знаков после запятой, приписав к одной из них справа нули.
Отбросив запятую, сравнить получившиеся натуральные числа.
Переходим по ссылке на отработку перевод десятичной дроби в обыкновенную:
https://uchi.ru/teachers/groups/1012309/subjects/1/course_programs/6/cards/12312
2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии.
-Как можно сложить две десятичные дроби?
3,6 +4,271=?
(Заслушиваются ответы учащихся)
— Что нового вы увидели в этом задании? (примеры на сложение десятичных дробей)
-Сможете ли вы выполнить это задание?
3. Выявление места и причины затруднения.
− Какое задание нужно выполнить? (Сложить десятичные дроби.)
− Подойдут ли к нашему заданию известные алгоритмы? (Нет. )
)
− Где же возникло затруднение?
− Почему же вы не смогли справиться с этим заданием? (Мы не знаем алгоритм сложения десятичных дробей.)
4. Построение проекта выхода из затруднения.
− Чем мы сегодня будем заниматься на уроке? (Учиться складывать и вычитать десятичные дроби)
− Сформулируйте тему урока. (Сложение и вычитания десятичных дробей.)
-Запишите тему урока.
-Мы знаем алгоритмы сложения смешанных чисел. Можно ли им воспользоваться для сложения десятичных дробей? (Можно.)
-Найдите сумму десятичных дробей, представив каждую десятичную дробь в виде смешанного числа.
3,6 + 4,271 = 3,600+4,271=3 + 4= 7 = 7,871
-Проанализируем результат выполнения действия.
— Запись десятичной дроби больше похожа на запись смешанного числа или на запись натурального числа? (На запись натурального числа.)
-Как складываются натуральные числа? (По разрядам.)
-Найдите сумму десятичных дробей, используя запись сложение в столбик. (Возможны различные варианты.)
(Возможны различные варианты.)
3,6
+4,271
3,6
+4,271
3,6
+4,271
-Сравниваем результаты сложения смешанных чисел и десятичных дробей.
5. Реализация построенного проекта.
После обсуждения решения учащиеся выбирают правильный ответ.
На доске
3,600
+
4,271
7,871
— Сформулируйте алгоритм сложения десятичных дробей.
Уравнять в этих дробях количество знаков после запятой;
Записать их друг под другом так, чтобы запятая была под запятой;
Выполнить сложение, не обращая внимания на запятую;
Поставить в ответе запятую под запятой в данных дробях.
Ребята в парах проговаривают алгоритм.
— Как вы думаете, поможет ли данный алгоритм достижению цели нашего урока?
Физкультминутка.
− Если я называю натуральное число, вы поднимаете руки вверх, а если десятичную дробь – хлопаем в ладоши.
25; 732; 18,5; 22; 99; 147,15; 87,2; 92; 610; 15,33; 750; 2,11.
6. Первичное закрепление с проговариванием во внешней речи.
А сейчас я предлагаю вам выполнить №246 (стр.73)
Выполните сложение (выполнение действия у доски с проговариванием вслух).
Переходим по ссылке на отработку
https://uchi.ru/teachers/groups/1012309/subjects/1/course_programs/6/cards/19393
7. Включение в систему знаний и повторение.
— Какое действие непосредственно связано со сложением? (вычитание)
— Как вы думаете, будет ли отличаться алгоритм вычитания десятичных дробей от алгоритма сложения. (нет)
— Сформулируйте алгоритм вычитания десятичных дробей.
Уравнять в этих дробях количество знаков после запятой;
Записать их друг под другом так, чтобы запятая была под запятой;
Выполнить вычитание, не обращая внимание на запятую;
Поставить в ответе запятую под запятой в данных дробях.
Выполните вычитание десятичных дробей по алгоритму:
23,4-5,37= 23,40-5,37=18,03 7,4-3,256=7,400-3,256=4,144
-23,40
5,37
18,03
-7,400
3,256
4,144
— Сформулировать алгоритм для сложения и вычитания десятичных дробей.
Уравнять в этих дробях количество знаков после запятой;
Записать их друг под другом так, чтобы запятая была под запятой;
Выполнить сложение (вычитание), не обращая внимание на запятую;
Поставить в ответе запятую под запятой в данных дробях.
-Откройте учебник на стр.148 и прочитайте алгоритм
8. Самостоятельная работа
https://uchi.ru/b2t/teacher/check/2588326
А сейчас я вам предлагаю решить задачу:
Винни Пух за завтраком съел 0,15 бочонка меда, а на обед — 0,2 бочонка. Какая часть бочонка меда у него осталась?
Рассмотрите разные способы решения этой задачи.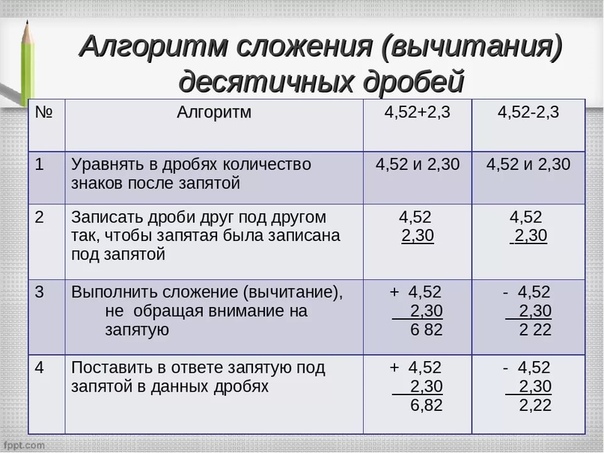
9. Рефлексия учебной деятельности на уроке.
Было ли вам сегодня интересно на уроке?
Что нового вы узнали на уроке?
Какие числа мы научились складывать и вычитать? (Десятичные дроби).
Как складывают и вычитают десятичные дроби? (Формулировка алгоритма).
Какие цели вы сегодня ставили?
Достигли вы этих целей?
Уверены ли вы, что поняли новый материал? Поднимите сигналы.
Кто сможет выполнить домашнее задание самостоятельно? Поднимите сигналы.
Рефлексивная деятельность учащихся (ответы на вопросы) следующего характера:
Каким опытом вы владеете в данный период времени? (Подчеркните)
— умею слушать и слышать
— умею выслушать товарища
— активно участвовал в ходе урока
— могу объяснить учителю новую тему
— могу объяснить товарищу эту тему
— могу придумывать сам дроби для сложения и вычитания.
— подумайте, над какой проблемой можно завтра работать на уроке при сложении и вычитании дробей?
— ребята, с каким настроением вы заканчиваете урок?
Нарисуйте в тетрадях смайлик, который отражает ваше настроение сейчас.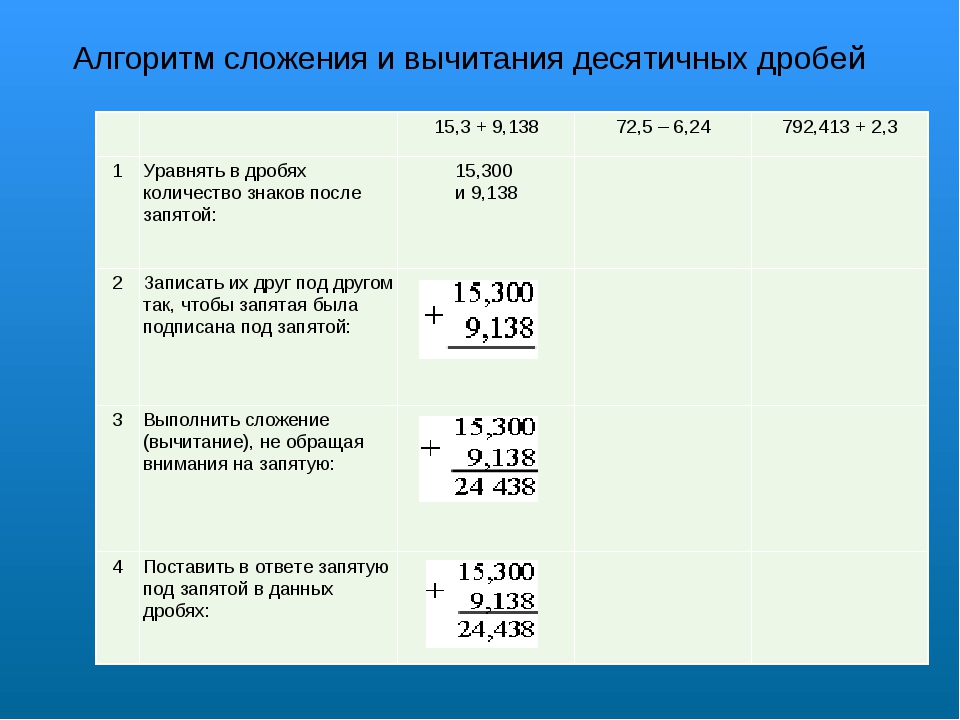
Домашнее задание:
Откроем дневники и запишем домашнее задание: п.4.1, стр.148-149 (выучить алгоритм сложения и вычитания десятичных дробей), №250
https://uchi.ru/teachers/groups/1012309/subjects/1/course_programs/6/cards/19396
Что такое сложение и вычитание десятичных знаков?
Сложение и вычитание десятичных знаков
Десятичное число
Десятичное число — это дробь, знаменатель которой является степенью 10. Например, дробь 4 ⁄ 10 может быть записана в десятичной форме как 0,4, где:
Точка называется десятичной точкой.
Число справа от десятичной точки обозначает числитель дроби, то есть дробную часть.
Число слева от десятичной точки обозначает целую часть дроби.
Например, 4 3 ⁄ 10 выражается как 4,3, где 4 — это целая часть числа, а 0,3 — дробная часть.
Десятичная точка отделяет целую часть числа от дробной части.

Десятичные знаки в реальной жизни
Мы занимаемся сложением и вычитанием десятичных дробей в повседневной жизни, имея дело с:
десятичных знаков можно складывать или вычитать так же, как мы складываем или вычитаем целые числа.
шагов для сложения или вычитания десятичных знаков:
Преобразует десятичные дроби в десятичные. (Десятичные числа с одинаковым количеством цифр после десятичной точки похожи на десятичные числа).
Запишите десятичные дроби друг под другом в соответствии с местами цифр.
Добавляйте или вычитайте, начиная с крайней правой цифры и двигаясь к крайней левой цифре.
Поместите десятичную точку под десятичной точкой в ответе.
Пример : прибавить 23,45; 13,101 и 345,5
1. Преобразовать в одинаковые десятичные числа : Наивысший десятичный разряд равен 3, поэтому мы добавляем нули в другие числа и получаем в них 3 десятичных разряда.
13.101
23,45 = 23,450
345,5 = 345,500
2. Выровнять десятичные знаки :
3. Добавить :
4. Место десятичной дроби в ответе :
Пример : У Кайли было 25 м ленты. Для украшения юбки она использует 8 м и 13 см. Сколько ленты осталось у Кайли?
Решение :
Длина ленты у Кайли = 25 м = 25,00
Длина ленты Кайли = 8 м 13 см = 8,13
Оставшаяся длина ленты = 25,00 — 8,13
= 16.87
Интересные факты
|
Добавление десятичных знаков | Math Goodies
Пример 1: Добавить: 52,3 + 973,41
Анализ: Давайте используем наши знания о смешанных числах, чтобы помочь нам проанализировать эту проблему.
52,3 = и 973,41 =
Напомним, что десятичное число может иметь целочисленную и дробную части. При добавлении десятичных знаков вы должны сначала выровнять все десятичные точки в столбце . Выравнивание десятичных знаков гарантирует, что каждая цифра находится в правильной позиции разряда. Как только каждая цифра находится в правильном положении разряда, части целого числа выстраиваются друг с другом, а дробные части выстраиваются друг с другом. Это показано в таблице ниже.
Теперь, когда мы выровняли десятичные точки, вы заметите, что добавляемые числа не имеют одинакового количества десятичных цифр. Давайте посмотрим на эту проблему на бумаге без диаграммы.
52,3
+ 973,41
Вы можете записать дополнительный ноль справа от последней цифры первого десятичного знака, чтобы оба десятичных знака имели одинаковое количество десятичных цифр.
52,30
+ 973,41
Как и в случае с целыми числами, начните справа и добавляйте каждый столбец по очереди. Обратите внимание, что вы добавляете цифры в одну и ту же позицию разряда.
Обратите внимание, что вы добавляете цифры в одну и ту же позицию разряда.
52,30
+ 973,41
1025,71
Поставьте десятичную точку в сумме.
52,30
+ 973,41
1025,71
Ответ: Сумма 52,3 и 973,41 составляет 1025,71.
Пример 2: Добавить: 0,078 + 3,09 + 0,6
0,078
3,090
+ 0,600
Анализ: Если вам нужно носить с собой (т.е. если сумма столбцов превышает 9), не забудьте добавить цифру десятков этого столбца к следующему столбцу.
1
0,078
3,090
+ 0,600
3,768
Ответ: Сумма 0,078 и 3,09 и 0,6 составляет 3,768.
Пример 3: сложить: 77,23 доллара и 88 долларов
Анализ: Каждое из этих чисел представляет деньги; однако второе записывается как целое число. Измените второе число так, чтобы оно состояло из двух десятичных цифр, а затем выполните сложение.
77,23 $
+ 88,00 $
165,23 $
Ответ: Сумма 77,23 и 88 долларов составляет 165,23 доллара.
Процедура: Чтобы добавить десятичные дроби, выполните следующие действия:
- Выровняйте все десятичные точки в столбце.
- При необходимости напишите один или несколько дополнительных нулей справа, чтобы в обоих десятичных разрядах было одинаковое количество десятичных цифр.
- Начните справа и добавляйте каждый столбец по очереди. (Добавьте цифры в той же позиции разряда.)
- Если вам нужно перенести, не забудьте добавить цифру десятков из этого столбца в следующий столбец.
- Поставьте десятичную точку в сумме.
Пример 4: Добавить: 28,5 + 34,5
Анализ: Вам нужно будет нести более одного раза. Соответственно, дополнение будет разделено на три этапа, чтобы показать процесс ношения.
| 1 1 1 1 1 28,5 28,5 28,5 + 34.5 + 34,5 + 34,5 0,0 3,0 63,0 |
Ответ: Сумма 28,5 и 34,5 составляет 63.
Пример 5: Добавить: 3.986 + 37 + 25.902
| 1 1 1 1 1 3.986 3.986 3.986 37.000 37.000 37.000 + 25.902 + 25.902 +25.902 .888 6.888 66.888 |
Ответ: Сумма 28,5 и 34,5 составляет 66,888.
Пример 6: Добавить: 12,95 долларов + 67,89 долларов + 54,55 долларов
1 2 1 1 2 1 |
Ответ: Сумма 12,95 доллара и 67,89 доллара и 54,55 доллара составляет 135,39 доллара.
Пример 7: Дайм свернул 5,8794 см, а затем свернул 7,48 см. Как далеко это вообще зашло?
| 1 1 1 1 1 1 5,8794 5,8794 5,8794 + 7,4800 + 7,4800 + 7,4800 . 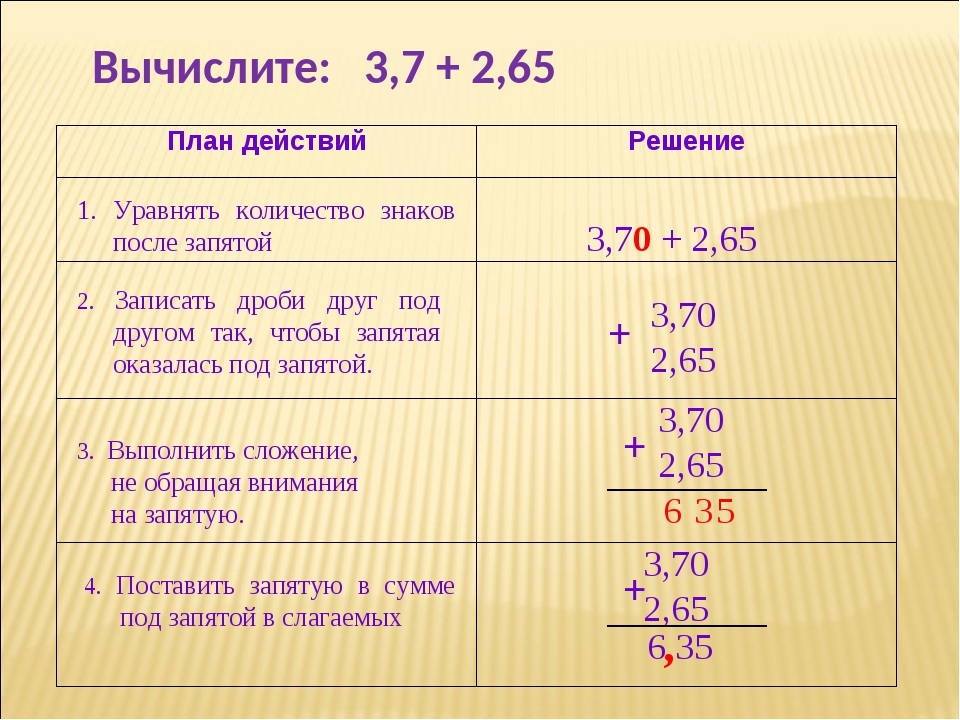 3594 3.3594 13,3594 3594 3.3594 13,3594 |
Ответ: Сумма 5,8794 см и 7,48 см составляет 13,3594 см.
Сводка: при добавлении десятичных знаков вы должны сначала выровнять все десятичные точки в столбце. Выравнивание десятичных знаков гарантирует, что каждая цифра находится в правильной позиции разряда. Затем вы можете складывать цифры в той же позиции разряда, чтобы найти сумму.
Упражнения
Указания: прочтите каждый вопрос ниже. Вы можете использовать бумагу и карандаш, чтобы помочь вам добавить.Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
| 1. | Добавить: 46.907 + 2.0184 |
2. | Добавить: 504,6 + 13,7 + 0,029 |
| 3. | Добавить: 234,50 $ + 187,95 $ |
| 4. | Добавить: 15.419 + 0.3 + 297.0651 |
| 5. | Джилл купила два свитера по 19,99 доллара каждый и пару джинсов за 27 долларов. Сколько она вообще заплатила (при условии отсутствия налога с продаж)? |
Рабочие листы для сложения десятичных дробей 5-й класс
Добро пожаловать в наши рабочие листы сложения десятичных чисел для 5-го класса.
Здесь вы найдете широкий спектр бесплатных распечатываемых десятичных рабочих листов для 5-го класса, который поможет вашему ребенку научиться и практиковать сложение десятичных чисел в уме.
Здесь вы найдете подборку дополнительных листов к пятому классу, предназначенных для помогите своему ребенку улучшить свои умственные способности.
Листы отсортированы таким образом, чтобы более легкие были вверху.
Использование этих листов поможет вашему ребенку:
- сложите числа, состоящие из десятых и сотых долей вместе;
- решить сумму сложения, где ответ дан, но одно из слагаемых отсутствует.
- Сложение с числами до 5 с одним десятичным знаком;
- Сложение с числами до 10 с 1dp;
- Сложение с числами до 1 с 2 dp;
- Сложение с числами до 5 с 2dp.
Листы разделены на 3 разных раздела:
- Добавление десятых
- Добавление сотых
- Задачи по добавлению десятичных знаков (для детей, которые уже уверенно добавляют десятичные дроби)
В нашем разделе задач мы представили несколько интересных задач, связанных с десятичным сложением.
Цифры должны быть помещены в отведенные места, чтобы давать как можно больший или как минимум возможные ответы.
Иногда задача состоит в том, чтобы подсчитать конкретную сумму, правильно расставив цифры.
Эти листы — хороший ресурс, чтобы научить детей применять свои навыки сложения для решения математических задач.
Ответ на каждую задачу обычно имеет несколько разных ответов — дети, сумевшие найти одно решение. можно было бы побудить найти другого.
Листы сортируются в первую очередь по самому легкому.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Здесь вы найдете ряд бесплатных рабочих листов для зачисления в пятый класс.
В следующих таблицах используется сложение на уровне 5-го класса.
Использование этих листов поможет вашему ребенку:
- мысленно складывать десятичные дроби, включая десятые и сотые;
- добавить столбцы с многозначными числами, включая десятичные.

Все бесплатные задания по математике для 5-х классов в этом разделе получены в соответствии с контрольными показателями по элементарной математике для 5-го класса.
Использование этих листов поможет вашему ребенку:
- вычесть десятичные дроби, включая десятые и сотые, мысленно;
- вычитайте многозначные числа, включая десятичные, используя вычитание столбцов.
На листах этого раздела пропущенные числа заполняются последовательно.
Они помогут вашему ребенку рассчитывать и рассчитывать с точностью до 0,1.
Использование этих листов поможет вашему ребенку:
- отсчет и обратный отсчет с кратностью 0,1;
- заполнить пропущенные числа по порядку;
- считать и вернуться в отрицательные числа.
Эти листы придадут вашему ребенку большую уверенность в мысленном добавлении и вычитании десятичных знаков.
Здесь вы найдете ряд бесплатных печатных игр по математике для 5-х классов.
Все дети любят играть в математические игры, и вы найдете хороший здесь вы найдете ряд математических игр для 5-го класса, в которые ваш ребенок сможет поиграть и развлечься.
Следующие игры включают в себя различные математические упражнения для 5-х классов. занятия, которыми вы и ваш ребенок можете наслаждаться вместе.
Все бесплатные задания по математике для 5-х классов в этом разделе следуйте контрольным показателям по элементарной математике для 5-го класса.
Здесь вы найдете ряд распечатанных математических головоломок для 5-х классов, которые понравятся вашему ребенку.
Головоломки помогут вашему ребенку практиковаться и применять свои факты сложения, вычитания, умножения и деления, а также развивать свои навыки мышления и рассуждения в увлекательной и увлекательной форме.
Эти пазлы помогут вашему ребенку:
- учиться и практиковать их сложение фактов, включая десятичные дроби;
- практикуют свои факты вычитания, включая десятичные дроби;
- практиковать и применять факты умножения и деления;
- развивать навыки решения проблем и рассуждений.

Все головоломки поддерживают тесты по элементарной математике для 5-го класса.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Сложение и вычитание десятичных знаков — объяснение и примеры
Сложение и вычитание десятичных знаков кажется немного сложным по сравнению с выполнением операций с целыми числами.В этой статье мы узнаем, как с легкостью выполнять сложение и вычитание десятичных знаков.
И в этом случае, прочитав эту статью, вы не будете проводить бессонные ночи, беспокоясь о том, как складывать и вычитать десятичные дроби, потому что объяснения были пошагово упрощены для вашего понимания.
Как складывать десятичные дроби?
Сложение десятичных чисел выполняется с использованием следующих шагов:
- Сначала десятичные числа записываются одно под другим числом, так что десятичные точки выстраиваются в линию.

- Числа преобразуются в аналогичные десятичные дроби путем добавления нулей. Количество добавляемых нулей зависит от числа с максимальным количеством цифр после десятичной точки.
- Цифры каждого номера выстроены так, чтобы каждый столбец содержал цифры в одном и том же месте.
- Добавление осуществляется обычным способом, начиная справа налево.
- Десятичная точка затем помещается на место в виде цифр над ней.
Пример 1
Добавьте следующие десятичные знаки: 0.9, 236,8, 1,83 и 21,105.
Решение
Мы можем легко решить эту проблему, выполнив шаги, описанные выше:
- Преобразуйте числа в десятичные дроби и расположите их одно над другим.
- Выполните обычное сложение, начиная справа.
0. 900 900 | ||||
| 236.800 | ||||
| + | ||||
| 260,635 |
Итого 260.635
Пример 2
Сложите следующие числа: 7.39, 65.007, 213.8 и 91.2.
Решение
- Преобразуйте числа в аналогичные десятичные дроби и расположите их одно над другим.
- Выполните обычное сложение, начиная справа.
| 7.390 | |||||||||
| 65.007 | |||||||||
| + | 377,397 |
Ответ — 377. 397.
397.
Как вычесть десятичные числа?
Чтобы выполнить операцию вычитания десятичных чисел, выполните следующие шаги:
- Запишите десятичные числа в столбец так, чтобы десятичные точки были выровнены.
- Преобразует указанные десятичные дроби в аналогичные десятичные, добавляя нули.
- Напишите большее число над меньшим в столбце.
- Расположите числа для вычитания в столбце так, чтобы все цифры находились в одном месте.
- Выполните обычное вычитание, начиная справа.
- Разместите десятичную точку в ответе в том же месте, что и числа над ним.
Пример 3
Вычесть: 27.59 с 31.4.
Решение
- Преобразуйте два десятичных числа в одинаковые десятичные числа, добавив несколько нулей.
- Расположите числа в столбце так, чтобы меньшее число было внизу
| 48 | |||
| 4848 | |||
| — | 27. 59 59 | ||
| 3,81 |
Ответ: 3,81.
Пример 4
Вычесть: 402,1 — 243,86.
Решение
- Преобразуйте числа в десятичные числа.
- Расположите числа в столбце.
| 402.100 | ||||||||||||||||||||||||||||||||||||
| — | 243,86 | |||||||||||||||||||||||||||||||||||
| 158,24 | Практические вопросы |
| а. 0,9 + 0,2 =
_____ 1,9 + 0,2 = _____ | г. 0,5 + 0,7 =
_____ 3,5 + 0,7 = _____ | г. 0,8 + 0,7 =
_____ 0,8 + 2,7 = _____ | г. 1,8 — 0,9 =
_____ 5,8 — 0,9 = _____ |
3. Добавьте десятичную дробь, чтобы получилась сумма
следующее целое число.
а. 2,1 + ______ = 3 | б. 4.5 + ______ = ____ | г. 8.9 + ______ = ____ | г. 5,3 + ______ = ____ |
4. Найдите недостающее дополнение.
а. _____ + 0,5 = 3 | б. 0,2 + _____ = 8 | г. 0,4 + _____ = 1,2 | г. 0,7 + _____ = 1,4 |
5. Сложить и вычесть.
а. 2,3 + 0,9 = 2.3 + 0,8 = | г. 1,5 + 0,7 = 1,8 + 0,4 = | г. 2,2 + 3,4 = 2,2 + 5,6 = | г. 4,7 — 0,7 = 6,6 — 0,5 = |
6. Напишите числа.
а. 3 десятых, 5 единиц г. c. 4 десятых, 3 единицы, 6 десятков | г. Впишите числа в заказывать. 9 8,9 9,1 9,0 9,9 1,9 |
7. Продолжить выкройки, многократно добавляя или вычитая одно и то же число.
а. 0.1 + 0,2 = _____ + 0,2 = _____ + 0,2 = _____ + 0,2 = _____ + 0,2 = _____ + 0,2 = _____ | г. 1,1 + 0,5 = _____ + 0,5 = _____ + 0,5 = _____ + 0,5 = _____ + 0,5 = _____ + 0,5 = _____ | г. 2,5 + 0,3 = _____ + 0,3 = _____ + 0.3 = _____ + 0,3 = _____ + 0,3 = _____ + 0,3 = _____ | г. — 0,4 = _____ — 0,4 = _____ — 0,4 = _____ — 0,4 = _____ — 0,4 = _____ — 0,4 = _____ |
8. Помните? 1 миллиметр — одна десятая сантиметра. Или 1 мм = 0,1 см.
| а. Нарисуйте линию длиной 4,7 см. | г. Измерьте линию в
сантиметры. |
9. Перерабатывать. В (c) сложите и дайте ответ в сантиметрах.
а. 0,5 см = ______ мм 1,2 см = ______ мм | г. 7 мм = ______ см 35 мм = ______ см | г. 4 см + 3,4 см = ______ см |
10. Две стороны прямоугольника
измерения 6,5 см и 3,6 см.
Нарисуйте прямоугольник.
Каков его периметр?
Этот урок взят из книги Марии Миллер Math Mammoth Decimals 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Рабочие листы с десятичными знаками
Спасибо, что посетили американскую версию формата десятичных дробей и процентов рабочих листов на Math-Drills.Com, где мы делаем ЗАДАЧУ, помогая студентам учиться. На этой странице вы найдете рабочие листы десятичных знаков по различным темам, включая сравнение и сортировку десятичных знаков, сложение, вычитание, умножение и деление десятичных знаков, а также преобразование десятичных знаков в другие числовые форматы.Для начала вы обнаружите, что печатные формы общего назначения могут быть полезны в обучении понятиям десятичных дробей и разряда. Более подробная информация о них содержится под заголовком. Если вы предпочитаете десятичные дроби в формате, отличном от английского (например, в качестве десятичных знаков используются запятые), посетите страницу Десятичные знаки европейского формата.
Далее по странице рабочие листы округления, сравнения и упорядочения десятичных знаков позволяют учащимся лучше освоить десятичные дроби, прежде чем они перейдут к выполнению операций с десятичными знаками.На странице есть много операций с рабочими листами с десятичными знаками. Для студентов было бы действительно хорошей идеей иметь хорошие знания о сложении, вычитании, умножении и делении, прежде чем пытаться ответить на эти вопросы. В конце страницы вы найдете десятичные числа, используемые в вопросах порядка операций.
Самые популярные рабочие листы с десятичными знаками на этой неделе
Распечатки общего пользования
Десятичные распечатки общего назначения используются в различных контекстах и помогают студентам в ответах на математические вопросы, связанные с десятичными знаками.
Сетки и диаграммы , полезные для обучения десятичным дробямСетка тысячных долей — полезный инструмент для представления десятичных знаков. Каждый маленький прямоугольник представляет одну тысячную. Каждый квадрат представляет собой сотую. Каждая строка или столбец представляет собой десятую часть. Вся сетка представляет собой одно целое. Сетка сотых долей может использоваться для моделирования процентов или десятичных дробей. Диаграмма значений десятичных разрядов — это инструмент, используемый студентами, которые первыми изучают разряды, связанные с десятичными знаками, или для тех студентов, у которых возникают трудности с разрядами при работе с десятичными знаками.
Расширенная форма с десятичными знаками
Расширенная форма с рабочими листами с десятичными знаками, включая преобразование стандартной формы в развернутую и из развернутой формы в стандартную.
Запись десятичных чисел в стандартной форме в развернутой форме Студентам, испытывающим трудности с расширенной формой, попробуйте ознакомить их с таблицей значений десятичных разрядов и позвольте им использовать ее при преобразовании чисел стандартной формы в развернутую.На самом деле существует пять способов (на два больше, чем с целыми числами) для записи развернутой формы для десятичных чисел, и какой из них вы используете, зависит от вашего приложения или предпочтений. Вот краткое описание различных способов использования десятичного числа 1,23.
1. Расширенная форма с использованием десятичных знаков: 1 + 0,2 + 0,03
2. Расширенная форма с использованием дробей: 1 + 2 ⁄ 10 + 3 ⁄ 100
3. Расширенная форма с использованием десятичных знаков: (1 × 1) + (2 × 0,1) + (3 × 0,01 )
4.Сформировать расширенные коэффициенты с использованием дробей: (1 × 1) + (2 × 1 ⁄ 10 ) + (3 × 1 ⁄ 100 )
5. Расширенная экспоненциальная форма: (1 × 10 0 ) + (2 × 10 -1 ) + (3 × 10 -2 )
Конечно, также важна возможность преобразовывать числа из развернутой формы в стандартную.Все пять версий десятичной развернутой формы включены в эти рабочие листы.
Рабочие листы с округлением десятичных знаков
Рабочие листы с округлением десятичных чисел с опциями округления различных десятичных чисел до различных знаков.
Округление десятичных знаковОкругление десятичных знаков аналогично округлению целых чисел; вы должны знать свою ценность! Изучая округление, также полезно узнать об усечении, поскольку оно может помочь учащимся правильно округлить.Простая стратегия округления включает в себя усечение, использование цифр после усечения, чтобы определить, остается ли новая завершающая цифра прежней или увеличивается, с последующим увеличением, если необходимо, и отбрасыванием остальных. Вот простой пример: округлите 4,567 до ближайшей десятой. Сначала обрежьте число после разряда десятых 4.5 | 67. Затем посмотрите на усеченную часть (67). Это больше, чем на полпути к 99 (т.е. 50 или больше)? Это так, поэтому будет принято решение об увеличении.Наконец, увеличьте значение десятых на 1, чтобы получить 4,6. Конечно, ситуация немного усложняется, если конечной цифрой является 9. В этом случае может потребоваться некоторая перегруппировка. Например: округлите 6,959 до ближайшей десятой. Усечь: 6,9 | 59. Примите решение об увеличении, поскольку 59 — это больше, чем половина пути до 99. Увеличение приводит к необходимости перегруппировать десятые доли в одно целое, поэтому результат равен 7,0. Следите за тем, чтобы ученики не писали 6.10. В этом случае вы захотите исправить их сразу же.И последнее замечание: если есть три усеченных цифры, тогда вопрос будет в том, чтобы число больше, чем на полпути к 999. Точно так же для одной цифры; это число больше чем на полпути к 9. И так далее …
Следует также упомянуть, что в некоторых научных и математических «кругах» округление немного отличается «на 5». Например, большинство людей округлило бы до 5, например: 6.5 -> 7; 3,555 -> 3,56; 0,60500 -> 0,61; и т. д. Другой способ округления до 5 — это округление до ближайшего четного числа, то есть до 5.5 будет округлено до 6, а 8,5 будет округлено до 8. Основная причина этого не в том, чтобы исказить результаты большого количества событий округления. Если вы всегда округляете до 5, в среднем результаты будут немного выше, чем следовало бы. Поскольку большинство дошкольников округляют до 5, это то, что мы сделали в следующих таблицах.
Таблицы сравнения и заказа десятичных знаков
Сравнение и упорядочение десятичных знаков в рабочих листах, чтобы помочь учащимся распознавать порядковые номера в десятичных числах.
Рабочие листы сравнения десятичных знаков позволяют учащимся сравнивать пары чисел, а рабочие листы упорядочивания десятичных знаков позволяют учащимся сравнивать список чисел, сортируя их.
Сравнение рабочих листов с десятичными знаками.Студенты, которые научились сравнивать целые числа, должны обнаружить, что сравнивать десятичные дроби довольно легко. Самая простая стратегия — сначала сравнить числа до десятичной дроби (целая часть числа) и сравнивать десятичные части только в том случае, если части целого числа равны.Подобные вопросы позволяют учителям / родителям понять, поняли ли ученики концепцию десятичных дробей или нет. Например, если ученик думает, что 4,93 больше 8,7, ему может потребоваться немного больше инструкций по разряду. Близкие числа означают, что были приняты меры, чтобы числа выглядели одинаково. Например, они могут быть близкими по стоимости, например 3.3. и 3.4 или одна из цифр может быть изменена, как в 5.86 и 6.86.
Порядок или сортировка десятичных чиселПорядок десятичных знаков очень похож на сравнение десятичных знаков, за исключением того, что здесь больше двух чисел.Как правило, учащиеся определяют наименьшее (или наибольшее) десятичное число для начала, вычеркивают его из списка, затем повторяют процесс, чтобы найти следующее наименьшее / наибольшее число, пока не дойдут до последнего числа. Всегда полезно проверять список в конце.
Преобразование десятичных дробей в дроби и другие числовые форматы
Преобразование десятичных знаков в рабочие листы в основном для преобразования десятичных знаков и дробей, а также процентов и соотношений.
Преобразование десятичных знаков в дроби и другие числовые форматыЕсть много веских причин для преобразования десятичных дробей в другие числовые форматы.Работать с дробью в операциях часто проще, чем с эквивалентной десятичной дробью. Рассмотрим 0,333 … что эквивалентно 1/3. Умножить 300 на 0,333 … сложно, но умножить 300 на 1/3 очень просто! Студенты должны быть знакомы с некоторыми из наиболее распространенных преобразований дробной / десятичной дроби, чтобы при необходимости они могли переключаться вперед и назад.
Преобразование дробей в завершающие десятичные дроби Преобразование дробей в завершающие и повторяющиеся десятичные дроби Преобразование завершающих десятичных знаков в дроби Преобразование завершающих и повторяющихся десятичных знаков в дроби Преобразование дробей в сотые Преобразование дробей в десятичные числа, проценты и частичные отношения Преобразование дробей в десятичные числа, проценты и отношения части к целому Преобразование десятичных дробей в дроби, проценты и частичные отношения Преобразование десятичных дробей в дроби, проценты и отношение частей к целому Преобразование процентов в дроби, десятичные дроби и частичные отношения Преобразование процентов в дроби, десятичные дроби и отношения части к целому Преобразование соотношений частей к частям в дроби, десятичные дроби и проценты Преобразование целого числа в дроби, десятичные дроби и проценты Преобразование различных дробей, десятичных знаков, процентов и соотношений частей к частям Преобразование различных дробей, десятичных знаков, процентов и целых соотношений Преобразование различных дробей, десятичных знаков, процентов и соотношений частей к частям с точностью до 7 и 11 Преобразование различных дробей, десятичных знаков, процентов и целых чисел с 7-ми и 11-ми. СТАРЫЙ Преобразование между дробями, десятичными знаками, процентами и соотношениямиРабочие листы сложения и вычитания десятичных знаков
Рабочие листы для сложения и вычитания десятичных знаков с различными трудностями, включая добавление и вычитание сами по себе, а также смешанные на странице.
Добавление десятичных знаковПопробуйте следующую стратегию сложения десятичных знаков в уме. Начните с игнорирования десятичных знаков в вопросе о сложении. Сложите числа, как если бы они были целыми числами. Например, 3,25 + 4,98 можно рассматривать как 325 + 498 = 823. Используйте оценку, чтобы решить, где разместить десятичную дробь. В примере 3,25 + 4,98 примерно равно 3 + 5 = 8, поэтому десятичная дробь в сумме должна находиться между 8 и 2 (т.е. 8,23)
. Рабочие листы с вычитанием десятичных знаковБазовые десять блоков могут использоваться для десятичного вычитания.Просто переопределите блоки, так что большой блок равен единице, плоский — десятой, стержень — сотой, а маленький куб — тысячной. Моделируйте и вычитайте десятичные дроби, используя базовые десять блоков, чтобы учащиеся могли «увидеть», как на самом деле работают десятичные дроби.
По горизонтали с сложение и вычитание десятичных рабочих листовДобавление и вычитание десятичных знаков довольно просто, когда все десятичные дроби выровнены. С вопросами, расположенными по горизонтали, учащимся предлагается понять значение разряда применительно к десятичным дробям.Замечательная стратегия размещения десятичной дроби — использовать оценку. Например, если вопрос — 49,2 + 20,1, ответ без десятичной дроби — 693. Оцените округлением 49,2 до 50 и от 20,1 до 20. 50 + 20 = 70. Десятичное число в 693 должно быть помещено между 9 и 3, как в 69,3, чтобы приблизить число к оценке 70.
Приведенная выше стратегия поможет учащимся понять операции с десятичными числами, но также важно, чтобы у них был прочный фундамент в виде числовой ценности и навыки эффективных стратегий, чтобы полностью успешно ответить на эти вопросы.Как и любой другой математический навык, неразумно преподносить его учащимся, пока они не получат необходимые предварительные навыки и знания.
Рабочие листы по умножению и делению десятичных знаков
Рабочие листы умножения и деления десятичных знаков с различными уровнями сложности.
Умножение десятичных знаков на целые числаУмножение десятичных дробей на целые числа очень похоже на умножение целых чисел, за исключением того, что нужно иметь дело с десятичной дробью.Хотя у учащихся изначально могут возникнуть проблемы с округлением и оценкой, они, как правило, могут получить его довольно быстро. Многие учителя советуют ученикам игнорировать десятичную дробь и умножать числа, как если бы они делали целые числа. Это хорошая стратегия для использования. Выяснить, где находится десятичная дробь в конце, можно, посчитав, сколько десятичных знаков было в исходном вопросе, и дав ответ на это количество десятичных знаков. Чтобы лучше понять этот метод, учащиеся могут округлить два множителя и умножить в уме, чтобы получить оценку, а затем поместить десятичную дробь на основе своей оценки.Например, умножая 9,84 × 91, ученики могут сначала округлить числа до 10 и 91 (оставить 91, так как умножить на 10 легко), а затем получить оценку 910. Фактически умножение (без учета десятичной дроби) дает вам 89544. Чтобы получить это число. рядом с 910 десятичная дробь должна находиться между 5 и 4, таким образом, 895,44. Обратите внимание, что в ответах есть два десятичных знака в множителях и два десятичных знака, но оценка сделала его более понятным, а не просто методом.
Умножение
на десятичные числа Умножение десятичных знаков в различных диапазонах Разделение десятичных знаков на целые числа Деление на частных, которые хорошо работаютЕсли вы не знакомы с делением с десятичным делителем, общий метод ответа на вопросы заключается в том, чтобы избавиться от десятичной дроби в делителе.Это делается путем умножения делителя и делимого на одну и ту же величину, обычно на степень десяти, такую как 10, 100 или 1000. Например, если вопрос деления составляет 5,32 / 5,6, вы должны умножить делитель и делимое на 10, чтобы получить эквивалентную задачу деления, 53,2 / 56. Завершение этого деления приведет к тому же частному, что и исходное (попробуйте его на своем калькуляторе, если вы нам не верите). Основная причина завершения десятичного деления таким образом — получение десятичной дроби в правильном месте при использовании U.S. алгоритм деления в длину.
Намного более простая стратегия, на наш взгляд, состоит в том, чтобы изначально игнорировать десятичные дроби вместе и использовать оценку для помещения десятичной дроби в частное. В том же примере, что и выше, вы должны заполнить 532/56 = 95. Если вы «гибко» округлите оригинал, вы получите около 5/5, что примерно равно 1, поэтому десятичная дробь в 95 должна быть размещена так, чтобы 95 было близко к 1. В этом случае вы поместите его непосредственно перед 9, чтобы получить 0,95. Сочетание этой стратегии с приведенной выше также может помочь в решении более сложных вопросов.Например, 4,584184 ÷ 0,461 можно сначала преобразовать в эквивалент: 4584,184 ÷ 461 (вы можете оценить частное около 10). Ответьте на вопрос о делении без десятичных знаков: 4584184 ÷ 461 = 9944, затем поместите десятичную дробь, чтобы 9944 было около 10. Это дает 9,944.
Деление десятичных чисел не должно быть слишком сложным, особенно с рабочими листами ниже, где десятичные числа хорошо работают. Чтобы создать эти рабочие листы, мы сначала случайным образом сгенерировали делитель и частное, а затем умножили их вместе, чтобы получить дивиденд.Конечно, вы увидите частные только на странице ответов, но создание вопросов таким образом позволяет решить любую задачу десятичного деления.
Горизонтально десятичное делениеЭти рабочие листы, вероятно, будут использоваться для расчетов и расчетов.
Порядок операций с десятичными знаками Рабочие листы
Порядок операций с десятичными знаками на листах с положительными и отрицательными десятичными знаками и различной степенью сложности.
Порядок операций с
десятичными знаками Порядок операций с десятичными запятымиПорядок операций с
десятичными и смешанными дробями Сложениедесятичных знаков
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Добавление десятичных знаков аналогично сложению целых чисел. Шаги, связанные с добавлением десятичных знаков:Шаг 1: Поместите цифры в соответствии со значением разряда, то есть одна под другой, убедившись, что десятичные дроби также находятся точно один под другим.
Единицы, меньшие единицы, десятые и т. Д. Шаг 2: Измените десятичные дроби на десятичные. Шаг 3: Добавьте как обычно.Начнем с сотых. При необходимости перенесите. Шаг 4: Поместите десятичную запятую в ответ в том же месте, что и числа над ним.
Пример: 2,37 + 3,8 =?
| 2 . 37 + 3 . 8 ——— 2 . 37 |
Примеры добавления десятичных знаков
1) Добавить: 23,11 + 3.8
| 23 . 11 + 3 . 80 ——— 26 . 91 |
________________________________________________________________
2) 23 + 18.94
Решение:
| 23 . 00 + 18 . 94 ——— 41 . 94 |
________________________________________________________________
3) 162.1 + 16.21
Решение:
| 162 . 10 + 16 . 21 ——— 178 . 31 |
________________________________________________________________
4) 13,8 + 124,56
Решение: Сначала напишите большее число, а под ним в соответствии с десятичными знаками напишите 2-е число.
| 124 . 56 + 13 . 80 ——— 138 . 36 |
Практика
Q.1 Добавить:
1) 562,9 + 49,3
2) 0,1 + 1 + 11,60
3) 9 + 1,8
4) 9,85 + 0,61
5) 17,5 + 16,87
Q.2 Сравните, используя>, <или =
1) 5,72 + 3,80 () 8,52
2) 2,5 + 3,09 () 5,95
3) 61,2 + 5,31 () 48,72 + 12,9
4) 10 + 0,01 () 10,01
5) 3 + 0,05 () 0,35
Введение десятичных знаков
•
Расширение десятичных знаков• Сравнение десятичных знаков
• Добавление десятичных знаков
• Вычитание десятичных знаков
• Умножение десятичных знаков
• Деление десятичных знаков
• Преобразование десятичных знаков в дробные От добавления десятичных знаков к введению десятичных знаков
Система счисления
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.




 99 кг, 107,81 кг и 19,207 кг. Рассчитайте их общий вес.
99 кг, 107,81 кг и 19,207 кг. Рассчитайте их общий вес. 72.
72. Вы на 0,7, а вы
прыгните на пять десятых вправо.
_____________________________________
Вы на 0,7, а вы
прыгните на пять десятых вправо.
_____________________________________
 7 десятков, 8 единиц, 4 десятых
7 десятков, 8 единиц, 4 десятых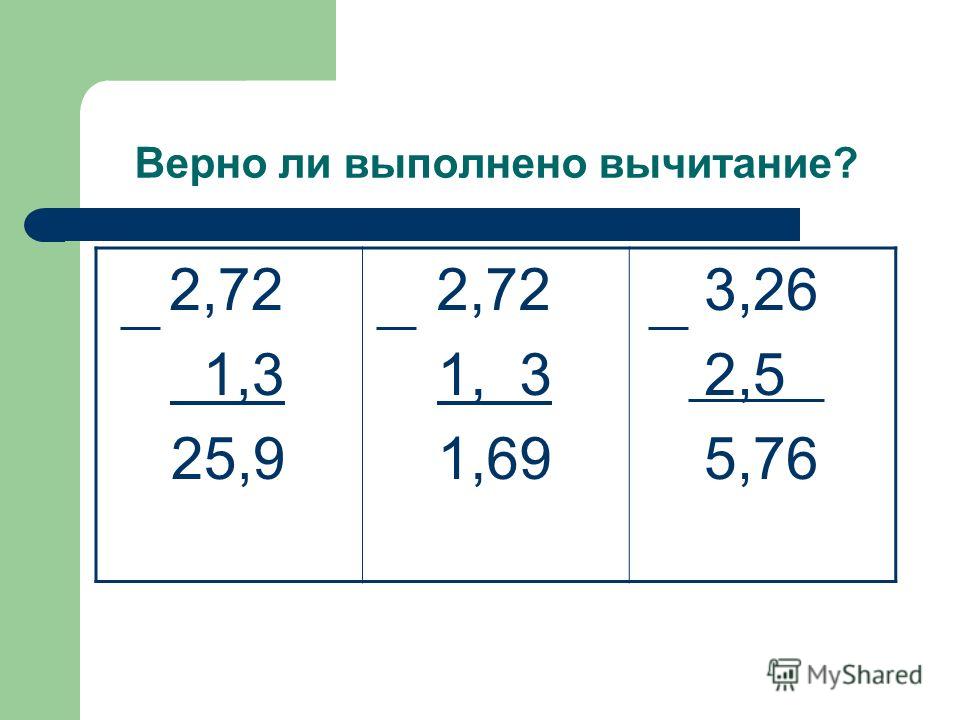 3,6
3,6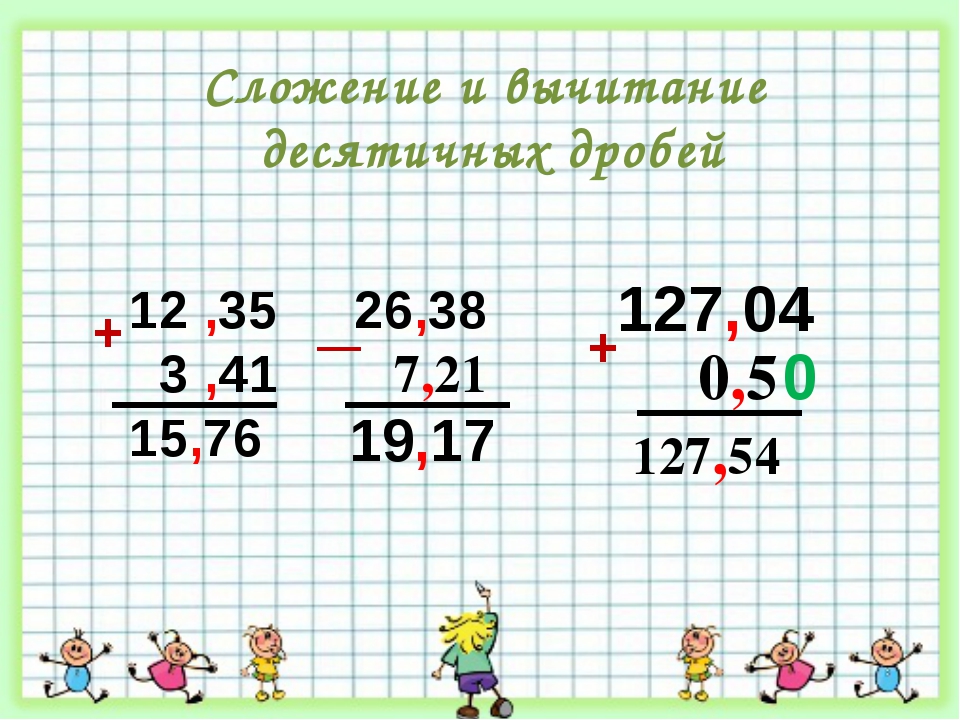 5 мм + 0,9 см = ______ см
5 мм + 0,9 см = ______ см