Умножение дробей | План-конспект урока (6 класс) по теме:
Автор Шарафутдинова Р.Л. – учитель математики МКОУ СОШ с. Карамалы-Губеево 1.Введение.
Ребята, здравствуйте, добрый день! Сели на свои места, посмотрели друг на друга- улыбнулись, посмотрели на меня- улыбнулись
Слайд1
Ну-ка, проверь, дружок
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке-
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ли внимательно глядят?
Удача ожидает вас,
За работу, в добрый час!
Сегодня. Ребята у нас необычный урок, К нам в гости пришёл, (учитель показывает рисунок доктора Айболита) кто, ребята?
-Ребята хором «доктор Айболит!»
— Правильно! Он за вами будет наблюдать весь наш урок и, конечно же, даст советы. Вот что он говорит:
Слайд 2
Я тот самый Айболит
Что всех излечит, исцелит!
Но к вам пришёл я не затем,
Чтоб ставить градусники всем,
В волшебную страну
Хочу всех пригласить
Рецепты здоровья
Там с вами добыть.
Здоровье – это бесценный дар, который преподносит человеку природа. Без него очень трудно сделать жизнь человека интересной и счастливой. Но как часто мы, растрачиваем этот дар попусту, забывая, что потерять здоровье легко, а вот вернуть его очень и очень трудно.
Ребята, как вы думаете, зачем человеку важно быть здоровым? ( Ребята отвечают) Правильно, и для того, чтобы хорошо учиться! Поэтому девиз сегодняшнего урока:
«В здоровом теле- здоровый ум»
Слайд3. Тема урока « Умножение дробей»
Слайд 4. Цели урока
-научиться умножать дроби на натуральное число;
-развитие навыков устной работы;
-воспитание сознательной дисциплины
2.Устная работа по слайдам 5, 6, 7. Ребята, перед вами лежат листы оценок. После каждого вида деятельности не забывайте себя оценить.
3. Изучение нового материала. Дети изучают самостоятельно по странице 71 учебника, делаем выводы.
Учитель с помощью учащихся решает на доске примеры. 3\4х2\3, 3\10х5\7, 4\7х14\5, 1\2х3\4х4\9
3\4х2\3, 3\10х5\7, 4\7х14\5, 1\2х3\4х4\9
Ещё раз повторяем правило умножения дроби на дробь.
Есть древняя, но актуальная по сей день мудрость: если ты заболел- измени питание, если не помогло- образ жизни, и только потом обратись к врачу. Почему же так? Оказывается
Слайд8. «Здоровье человека лишь
на 2/25 зависит от медицинской помощи,
на 3/20-от генетических факторов,
на 1/5 — от экологии, и более чем
на 1/2 -от образа жизни»
А теперь, ребята, умножьте дроби, которые встречаются в этом предложении. Один ученик работает на закрытой доске, затем ответы проверяются. Получилось 3\2500. Теперь умножим полученную дробь на дробь 200000\3. Что получилось? Правильно 80! О чём говорит это число? Каждому о своём конечно, да? Кто то из вас получил 80 пятёрок может быть, чьей то бабушке исполнилось 80 лет, а для нашего района какое значение имеет это число? Правильно в этом году исполнилось 80 лет нашему району. Молодцы!
Чтобы быть здоровым, нужно заниматься спортом. Подошло время физкультминутки.
Подошло время физкультминутки.
4. Физкультминутка.Слайд9.
Капля первая упала-кап!
И вторая пробежала-кап!
Мы на небо посмотрели,
Капельки кап-кап запели,
Намочились лица,
Мы их вытирали.
Туфли- посмотрите-
Мокрыми стали.
Плечами дружно поведём
И все капельки стряхнём.
От дождя убежим,
Под кусточком посидим.
Отдохнули. Теперь пора продолжать работу.
5. Закрепление материала.
Решаем №419 пункты е, ж, и, м, р у доски по очереди.
Ребята посмотрите, какие пункты мы решили? Вы не нашли пункта р? Если внимательно посмотреть какое слово получится, если добавить букву р? Правильно, режим!
Слайд10 Режим дня- это система распределения нагрузки и отдыха, которая обеспечивает сохранение сил и энергии для нормальной жизнедеятельности организма. Режим дня является основой оздоровительного и профилактического воздействия на организм всех факторов учебно-воспитательной работы.
Значит, делаем вывод, что нужно соблюдать режим дня. Но и этого недостаточно для сохранения здоровья. Что ещё важно для здоровья, узнаем решив следующие примеры.
Но и этого недостаточно для сохранения здоровья. Что ещё важно для здоровья, узнаем решив следующие примеры.
6. Самостоятельная работа по листочкам, задания для каждого.
Теперь посмотрим ключ. Там написаны ответы к примерам.Слайд11
3/4 п
8/35 и
1/5 н
1/2 а
10 т
1 е
Какое слова получится? Правильно, питание!
Слайд12. Пища-это источник энергии для человека, и избыток или недостаток её- проблема. Если человек много ест, у него развивается ожирение, сахарный диабет, заболевания желудочно-кишечного тракта, если ест мало, обрушивается дистрофия, сахарный диабет и много других заболеваний. Где же выход? Смолоду научиться соблюдать золотую середину, не допуская переедание, так и недоедание. Надо жить в гармонии с собой и окружающими вас продуктами.
Теперь для вас предлагается тест. Подобрав к ответу букву, вы узнаете верного спутника здоровья.
Слайд13.
- 1/2
к) неправильная дробь
с) правильная дробь
в) целое число
- 8 %
п) 0,08
г) 0,8
в) 0,008
- 1/2 х 2
р) 2
н) 4
о) 1
- 3/4 х 16/3
и) 16
р) 4
е) 3
- 7/3
т) неправильная дробь
п) правильная дробь
к) десятичная дробь
Получилось слово «Спорт».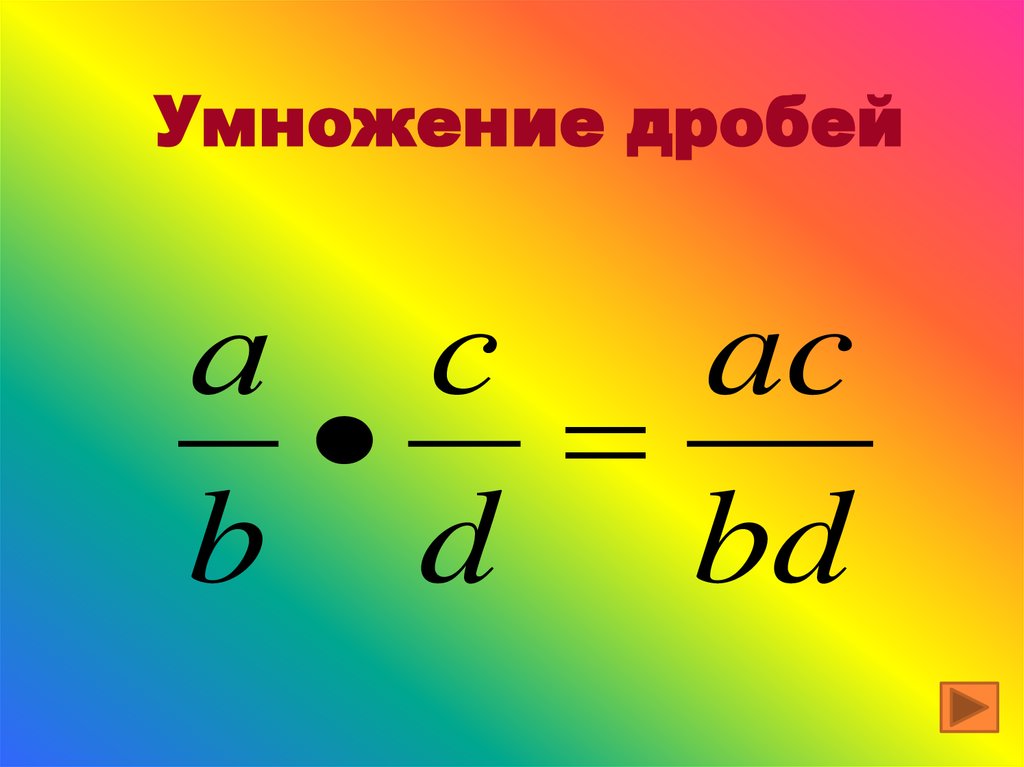
Слайд14.
По утрам ты закаляйся,
Водой холодной обливайся
Будешь ты всегда здоров
Тут не нужно лишних слов
7.Домашняя работа
№ 457 (а – з),
№ 464,
придумать задачу на умножение дробей
8. Итоги урока. Чем занимались на уроке? Понравился ли вам урок? Какие оценки получились? Ребята, не забывайте, что здоровье бесценный дар и мы должны сделать всё, чтобы его сберечь. И не забывайте слова Айболита.
Слайд14.
Мы рождены, чтоб жить на свете долго:
Грустить и петь, смеяться и любить.
Но, чтобы стали все мечты возможны,
Должны мы все здоровье сохранить
Желаю всем крепкого здоровья!
Как умножать дроби | Математика
В мире, в котором мы живем, мы оказываемся в окружении множества математических операций, которые могут возникнуть в нашей повседневной жизни. Особенно во всем, что относится к академической сфере, поскольку мы должны уделять внимание предмету математики. Среди различных существующих операций важно знать как умножать дроби.
Это то, чему нас учат в начальной школе, хотя многие люди часто забывают, как это делать. Помни это все, что связано с математическими формулами Если вы хотите запоминать, его нужно практиковать постоянно. Поэтому, если вы разучились это делать и хотите учиться снова, эта статья для вас.
Вы также можете быть заинтересованы в: Как умножить на десятичные дроби
Оглавление:
Что такое дробь?Чтобы правильно начать этот текст, мы начнем с нуля. То есть, прежде чем углубиться в тему и объяснить, как умножать дроби, мы вам расскажем что такое дробь. Таким образом, у вас будут свежие знания, чтобы понять все, что мы вам будем объяснять.
В математике число, полученное делением целого числа на равные части, называется дробью. Следуя этому определению, мы должны понимать под дробью a определенная часть от общего числа.
Эти виды операций представлены в письменной форме с числа, которые написаны друг над другом с дробной чертой между другими. Следовательно, в дроби всего два числа: одно с функцией числителя, а другое с функцией знаменателя.
Следовательно, в дроби всего два числа: одно с функцией числителя, а другое с функцией знаменателя.
К счастью, определить их очень просто. Числитель это тот, который находится в верхней части строки и знаменатель снизу. Точно так же важно понимать функцию обоих чисел.
Во-первых, числитель представляет количество частей, которые были учтены в общей единице. С другой стороны, знаменатель представляет собой количество равных частей, на которые он был разделен.
Следовательно, если мы находим что-то вроде этого: значит, он берет четверть от общей суммы. Хотя, когда дело доходит до чтения дробей, следует читать как «Одна четверть». Точно так же не забывайте, что дроби обычно представлены разными типами графиков, чтобы облегчить их понимание.
Как шаг за шагом умножать дроби?Теперь, используя сами по себе дроби, вы можете выполнять всевозможные математические операции. Дроби можно складывать, вычитать, умножать и делить. Это основные операции, которые мы выполняем с обычными числами.
Это основные операции, которые мы выполняем с обычными числами.
В этом тексте мы сосредоточимся только на объяснении вам как умножать дроби. Итак, после того, как вы кратко объяснили, что такое дробь, пора продолжить. Для этого в этом разделе статьи мы шаг за шагом объясним, как выполнить эту математическую операцию.
Как умножить дроби друг на друга?Когда они дают вам математическое упражнение с две дроби, которые необходимо умножить друг на друга Первое, что вам следует сделать, это упростить операцию. Для этого все, что вам нужно сделать, это разложить числа дроби на простые множители.
То есть, если да, вы должны найти их основные множители. Для 4 это будет 2 x 2. В то время как для 8 будет 2 x 2 x 2. Итак, следующий шаг — замените числа в дроби на их уже упрощенные числа. Это то, что вы должны сделать с обеими дробями, которые вам были даны в упражнении.
После этого все те же самые упрощенные числа необходимо вычеркнуть. Оставшиеся разные числа умножаются друг на друга, если они находятся в одной строке. То есть, если сверху осталось два разных числа, они умножаются друг на друга.
Оставшиеся разные числа умножаются друг на друга, если они находятся в одной строке. То есть, если сверху осталось два разных числа, они умножаются друг на друга.
С другой стороны, если останется только два уникальных числа, останется только перевести конечный результат умножения дроби. Без сомнения, это самый простой и реальный способ провести операцию такого типа между дробями.
Как умножить дробь на целое число?С другой стороны, есть вероятность, что назначенное вам математическое упражнение будет немного сложнее. Это происходит, когда вас помещают дробь рядом с целым числом, и они посылают вас умножать их друг на друга. Без сомнения, это упражнение вызвало не одну головную боль. Но не волнуйтесь, сегодня мы дадим вам самый простой способ решить эту проблему.
Все, что вам нужно сделать, чтобы уметь организовать упражнение так, чтобы оно было похоже на обычное умножение дробей. ставить 1 под целым числом. То есть, если вам сказали умножить x 5, вы должны поместить это как x. Таким образом, преобразовав целое число, которое вам дано, в дробь, операция становится обычным умножением дробей.
То есть, если вам сказали умножить x 5, вы должны поместить это как x. Таким образом, преобразовав целое число, которое вам дано, в дробь, операция становится обычным умножением дробей.
Вам не нужно выполнять какие-либо другие операции или увлекаться этим упражнением. Всякий раз, когда возникает такая ситуация, все, что вам нужно сделать, это преобразовать целое число в дробь. И правильный способ сделать это — поставить число один в качестве знаменателя.
Как только вы превратите операцию в умножение дробей, все становится проще простого. Речь идет об упрощении, удалении повторяющихся чисел, умножении различных и готовых. Следовательно, вам нужно только повторить шаги предыдущего объяснения после преобразования целого числа в дробь.
Нет ли автоматизированного способа умножения дробей?Теперь, когда вы узнали как умножать дроби, вы знаете, как это просто. Однако, если вы ищете более автоматизированный способ, все зависит от поиска в Интернете. Вы обязательно найдете калькулятор, позволяющий умножать дроби.
Вы обязательно найдете калькулятор, позволяющий умножать дроби.
Конечно, мы не рекомендуем использовать его, если упражнения выполняются из академических соображений, поскольку это было бы обманом. Однако, если вы работаете с дробями в повседневной жизни, вы можете легко использовать эти типы онлайн-инструментов.
Этапы | Ход урока | Время | ||||||||||||||||||||||||||||||||||||
I Орг. Цель: психологическая установка на урок. | — Здравствуйте, ребята. Сегодня нам предстоит серьезно потрудиться, мне хочется, чтобы от работы на уроке вы получили удовлетворение. Ведь успех – это состояние души. Девизом сегодняшнего урока я предлагаю слова: (слайд 2) «Человеческий ум, «растянутый» новой идеей, никогда не сможет вернуться к своим прежним размерам». — А сейчас не будем больше терять времени, оглядываться назад и будем вместе, двигаться только вперед! | 1 мин | ||||||||||||||||||||||||||||||||||||
II Сообщение темы, целей | — Откройте тетради, запишите число и тему нашего урока… (слайд 3) — Ой, что случилось с презентацией? Все буквы рассыпались. Помогите определить тему нашего урока. ( Ребята называют тему из рассыпанных букв «Умножение дробей») — Спасибо. Запишем ее в тетрадь.(слайд 4) Для вас эта тема новая? — Нет. — А как по вашему, зачем мы ее опять записали? — Что бы ни забыть и закрепить. — Тогда скажите, какую цель мы перед собой поставим? — Отработать (закрепить) правила умножения дробей. Отработать знания и умения, связанные с правилами умножения дробей: — А также – Внимание! — Ребята, у вас на столах лежат оценочные листы (слайд 6), где записаны все этапы нашего урока. Ваша задача оценить свою работу на каждом этапе урока и поставить себе баллы, по одному за каждый правильный ответ. Оценка за урок будет зависеть от набранных баллов.
| 2 мин | ||||||||||||||||||||||||||||||||||||
III Проверка домашнего задания. 1.Проверка домашнего задания и задание на дом | — Начнем с актуализации знаний. (слайд 7) Если вы правильно решите примеры, то сможете назвать фамилию ученого-математика. А, внимательно послушав сообщение Олега, сказать, что нового он ввел в математику. — Перед вами карточки с числами, среди которых есть ответы примеров, если ответы ваши совпали с данными числами и правильные, то с обратной стороны карточки будет буква, а в углу стоять цифра на какое место ее нужно вам поставить в зашифрованное слово.
— И так, какая фамилия у нас получилась? (Пеануд) — Поставьте себе в оценочный лист баллы. — Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Пеануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение. — Кто может сказать, что же нового ввел в математику Максим Пеануд? — Название “числитель” и “знаменатель”. | 5мин | ||||||||||||||||||||||||||||||||||||
IV Работа по теме урока. Цель: отработка и систематизация знаний по теме. 2. Индивидуальная работа | — У меня на столе лежат карточки с заданиями разных цветов (слайд 9). — 2 балла (зеленая карточка)
— 3балла (синяя карточка)
— 4балла ( красная карточка)
— Кто справился с заданиями, проверяет себя по карточке-информатору. у кого красная карточка — ставят себе столько баллов, сколько правильных заданий было решено; у кого синяя – на 1 балл меньше от правильно решенных заданий; у кого зеленая – в 2 раза меньше правильно решенных заданий. | 6мин | ||||||||||||||||||||||||||||||||||||
V Физкультминутка | — Ребята, улыбнитесь. Передайте своему товарищу мысленно положительные эмоции, поделитесь капелькой теплоты, добра. Быстро встали, улыбнулись. | 1мин | ||||||||||||||||||||||||||||||||||||
VI Работа по теме урока (продолжение) 3. Найти ошибку. | — И так, приступим к следующему этапу, на котором нам предстоит вспомнить правила, с помощью которых выполнялись предложенные задания (слайд 11). — На экране вы видите записанные правила, которые содержат ошибки. Ваша задача найти их и исправить. 1). Чтобы умножить дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменений. 2). Произведением двух дробей является дробь, числитель которой равен произведению знаменателей, а знаменатель – произведению числителей. (слайд 12) 3).Чтобы умножить смешанные числа, надо сначала записать их в виде правильных дробей, а затем воспользоваться правилом умножения дробей. (слайд 13) 4). Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют умножением дробей. (слайд 14) — Молодцы, нашли все ошибки. — Выставляем себе по одному баллу за каждую найденную ошибку. | 3мин | ||||||||||||||||||||||||||||||||||||
4.Изучение нового Цель: изучить правило умножения N числа на смешанное. | — ( слайд 15 а). А сейчас, ребята, я хочу предложить вам немного подумать как же проще (рациональней) можно умножить натуральное число на смешанное число, попытаться смоделировать это правило, найдя закономерность при умножении этих чисел. — Например, нам нужно умножить следующие числа: 2* 4 — Как бы вы стали их умножать? — Перевести смешанное число в неправильную дробь, а затем умножить. — Верно, по изученным правилам это возможно. Давайте найдем это значение: = 2 * = = = 8 — Может еще, кто предложит свой способ умножения? — … — Посмотрите внимательно на пример и ответ. (слайд 15б) — Что было, а что стало с целой частью, с числителем и знаменателем? — Целую часть и числитель умножили на N число, а знаменатель не изменился. Правильно заметили, но перед тем, как сформулировать правило, давайте еще раз проверим, выполняется ли эта закономерность при других числах. Умножив двумя способами числа… которые предложите вы сами. Одно – N число, др. – смешанное число. Будут ли у нас одинаковые результаты? — Учащиеся придумывают числа и двое выполняют решение у доски каждый своим способом. Приходят к выводу, что ответы получились одинаковые, но вторым способом намного быстрее и проще, т.е.- рациональней. Формулируют правило, (слайд 16 ) и один записывает его модель на доске. (слайд17 ) — Чтобы умножить смешанное число на N число, надо его целую часть и числитель умножить на это число, а знаменатель оставить без изменения. — Оказывается, есть и научное обоснование этому правилу. С помощью распределительного закона умножения, который мы повторяли на прошлом уроке. Давайте это разберем устно. Может, у кого-то из вас получиться обосновать это правило с помощью распределительного закона умножения? ( слайд 18) (Ребята с учителем доказывают правило с помощью распределительного закона умножения) — Молодцы! Поставьте себе по баллу за каждое верное задание выполненное у доски или верный устный ответ. | 7мин | ||||||||||||||||||||||||||||||||||||
5.Угадай слово | — Приступим к закреплению полученных знаний. А помогут нам в этом, уникальные животные. — На островах Тихого океана живут черепахи – гиганты. Они такой величины, что дети могут кататься, сидя у них на панцире. Узнать название самой крупной в мире черепахи поможет нам следующие задание. (слайд 19) -Выполните умножение дробей. — Из волшебной коробочки вы должны достать букву и перемножив соответствующие числа из таблицы, определить на какое место ее вписать. (По одному примеру обучающиеся решают у доски с комментариями, а оставшиеся примеры делят между собой, выбирая из коробочки буквы).
— Итак, как называется самая крупная в мире черепаха? — Дермохелис. — Вы ребята хорошо справились со всеми примерами. Поставьте баллы в свой оценочный лист. | |||||||||||||||||||||||||||||||||||||
6. Проверка знаний | — В завершении нашего урока проведем небольшой контроль знаний, что позволит понять достигли мы поставленной в начале урока цели. — Каждому из вас будет предложена карточка, где выполнив задания по цепочке нужно ответить на вопрос. А после поделиться с классом тем, что нового вы узнали, выполняя это задание. — Решаем прямо в карточке и вставляем пропущенные числа. Карточка 1.
Карточка 2
Карточка 3
— Поменяйтесь карточками и проверьте решение друг у друга. Ответы записаны на доске. За каждый верный ответ – 1 балл. (слайд 22) — Выставляем баллы в оценочные листы. Карточки с решением сдаем. — Послушаем, что вы узнали о животных выполняя задание. (слайд 23,24, 25) (Ребята делятся своими ответами) | 2мин | ||||||||||||||||||||||||||||||||||||
VII № Н Д А а, б, д, е) + Составить решение для задачи. | — Запишем домашнее задание (слайд 8), вы уже заметили, что оно зашифровано. А узнать его можно заменив буквы из угаданной фамилии на соответствующие числа. — Запишем задание на дом. № 463 а, б, д, е) — Задание с + для желающих получить дополнительную оценку. Составить решение для задачи, по которому, на следующем уроке, мы будем составлять условие задачи. — Рассмотрим № 463. Всем ли знают, как решать эти примеры? | |||||||||||||||||||||||||||||||||||||
VIII Итог урока. | — (слайд 26). Подсчитаем баллы, которые вы заработали за урок и ставим себе оценку по следующим критериям: (слайд ) От 10 до 14 – оценка «3» От 15 до 19 – оценка «4» От 20 и выше – оценка «5». — Выберите смайлики, которые дадут понять как вам было на уроке. Вам было на уроке: Легко Обычно Трудно — Молодцы! Наш урок я хочу закончить словами…(слайд 28) Поверь, лишь тот знаком С душевным наслаждением, Кто приобрёл его Трудами и терпеньем. (В. Гете) — Спасибо за урок. До свидания. | |||||||||||||||||||||||||||||||||||||
Полное руководство — Mashup Math
Умение умножать дроби, будь то дробь на дробь или умножение дробей на целые числа, является важным навыком, который рано или поздно должен освоить каждый, кто изучает математику.
Это полное руководство по умножению дробей представляет собой пошаговое руководство по умножению дробей и включает в себя несколько примеров, анимированный видео-мини-урок, а также бесплатный рабочий лист и ключ к ответу.
Начнем!
Прежде чем мы изучим, как умножать дроби, давайте быстро повторим базовое умножение:
Рисунок А
Рисунок С
Рисунок В
Рисунок D
Что вы заметили в отношениях между фигурами A, B и C?
Почему на рисунке D 2 x (1/2) равно 1 ?
Чтобы помочь вам понять рисунок D выше, давайте начнем с изучения правил умножения дробей:
Правило: При перемножении дробей умножайте числители вместе, а затем умножайте знаменатели вместе.
Правила умножения дробей так же просты, как и применение правила к множеству различных задач. Давайте продолжим и применим это правило на нескольких примерах.
Пример 1 (умножение дробей на дроби):
Сколько будет (3/4) x (1/2) ?
Начните с применения правила и умножения числителей вместе, а затем знаменателей вместе следующим образом:
Обратите внимание, что дробь (3/8) не может быть упрощена (поскольку 8 и 3 не имеют общего делителя)
Ответ: (3/4) x (1/2) = 1/8
Пример 2 (умножение дробей на целые числа): Сколько будет 2 x (1/2) ?Эта проблема должна показаться вам знакомой, потому что она изображена на рисунке D выше.
Теперь, когда вы понимаете, как использовать правило умножения дробей, вы можете решить эту задачу, где вам нужно умножать дроби и целые числа.
Вы по-прежнему будете использовать правило для поиска ответа, но потребуется один дополнительный шаг.
Поскольку вы умножаете дроби на целые числа, вам нужно преобразовать целое число в дробь.
В этом случае вы можете переписать целое число 2 как (2/1) следующим образом:
Затем примените правило и решите следующим образом:
Ответ: 2 x (1/2) = 1
) х (3/4) ?Это будет наш последний пример.
На этот раз вам придется умножать дроби, а затем упростить ответ.
Начните с применения следующего правила:
Подождите! Есть еще один шаг.
15/24 можно упростить, потому что и 15, и 24 делятся на 3 (это НОД 15 и 24). Таким образом, вы можете упростить дробь, разделив ОБА числитель и знаменатель на 3 следующим образом:
Вот и все!
Ответ: (5/6) x (3/4) = (5/8)
Все еще запутались? Посмотрите анимационный видеоурок ниже:
Посмотрите видеоурок ниже , чтобы узнать больше об умножении дробей и других бесплатных практических задачах:
Бесплатный рабочий лист!
Вы ищете дополнительную практику умножения дробей? Нажмите на ссылки ниже, чтобы загрузить бесплатные рабочие листы и ключ ответа:
Нажмите здесь, чтобы загрузить свой бесплатный рабочий лист
Теги: Умножающие фракции, умножительные фракции и целые числа, практика умножений фракций, умножение фракций, упрощенные фракции
Сохраняйте обучение:есть мысли? Мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — щелкните здесь, чтобы получать наш еженедельный информационный бюллетень!) Автор: Энтони Персико. Вы часто можете увидеть, как я с удовольствием разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Вы часто можете увидеть, как я с удовольствием разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Комментарий
4 простых шага с визуальными моделями
Введение: умножение и деление дробейКрутые существа — дроби!
Дроби считаются одним из самых сложных математических понятий для маленьких детей, потому что они имеют иные обозначения, чем целые числа. Это абстрактное понятие, которое побуждает маленьких рок-звезд работать лучше.
Операции с дробями усложняют задачу, так как детям становится трудно понять, что означают эти операции, и поэтому их визуализация может привести к лучшему пониманию концепции. Умножение и деление дробей может противоречить уже существующему пониманию умножения и деления целых чисел.
Умножение и деление дробей может противоречить уже существующему пониманию умножения и деления целых чисел.
Например, умножение двух целых чисел всегда приводит к большему произведению, но это не относится к умножению дробей.
Точно так же при делении двух целых чисел частное обычно меньше делимого, но это не относится к делению дробей.
Деление дробей отличается от деления двух целых чиселИз-за отсутствия должного понимания этих понятий, даже среди учителей, учащиеся с трудом понимают дроби. Это также вызывает путаницу и неправильные представления среди них.
Цель этой статьи — предложить увлекательные методы, которые помогут детям визуализировать понятия умножения и деления. Кроме того, мы также попытаемся облегчить понимание процедур, связанных с умножением и делением дробей, с помощью простой методики, включающей всего 4 шага.
Читайте дальше и сделайте изучение дробей легким и приятным!
Содержание- Глоссарий
- Необходимые знания
- Введение в умножение дробей
- Первый шаг в умножение дробей: визуальное моделирование
- Умножение дробей: 4 простых шага
- Анализ: умножение дробей в сравнении с умножением целых чисел
- Деление дробей: 4 простых шага
- Резюме
- Часто задаваемые вопросы (FAQ)
- Дробь – Часть целого числа, записанная в виде a/b
- Знаменатель – Нижнее число дроби
- Числитель – Верхнее число дроби 1 9018 Единица Дробь —
- Понимание умножения и деления целых чисел
- Понимание дробей и их визуальных моделей
- Представление целых чисел в виде дробей
- эквивалентные фракции
- Упрощающие фракции в их самую низкую форму
- Преобразование ненадлежащей фракции в смешанное число и наоборот
- Связанный срок .
 БЕСПЛАТНЫЙ СТАРИТЕЛЬСКИЙ СТАРИТЕЛЬСКИЙ. Введение: умножение дробей
БЕСПЛАТНЫЙ СТАРИТЕЛЬСКИЙ СТАРИТЕЛЬСКИЙ. Введение: умножение дробей Перед тем, как приступить к умножению дробей, необходимо выработать концептуальное понимание умножения дробей. Дети должны уметь визуализировать умножение и должны знать, что означает умножение дроби на целое число или дробь.
Совет: Начните с моделирования умножения или деления, используя только целые числа. Затем вы можете перейти к дробным числам. Таким образом, существующие знания детей об умножении или делении целых чисел будут обновлены, и они смогут связать их с построением моделей умножения или деления дробей.
Начнем с умножения дробей.
Первый шаг к умножению дробей: моделирование Использование визуальных моделей в качестве учебного пособия делает процесс преподавания и обучения более эффективным, увлекательным и интерактивным. Это ориентированный на учащихся подход, который помогает детям визуализировать ключевые математические концепции, что в дальнейшем помогает им глубже понять концепцию на корневом уровне.
Для учителей визуальные модели могут вызвать обсуждение математических идей и отношений с ранее известными концепциями. Это помогает им лучше понять, как учащиеся понимают концепцию.
По этой причине обучение умножению дробей сначала с помощью моделей, а затем переход к стандартным процедурам было бы идеальным подходом.
Начнем с того, что умножение дробей может принимать 3 разные формы.
Уровень 1a : целая фракция
Уровень 1B: Фракция × ВСЕ
Уровень 2 : Фракция × Фракция
Примечание: Мы не будем делать смеси. отдельный случай, потому что это тоже дроби, записанные в другой форме. Чтобы помочь своим детям узнать о смешанных числах и неправильных дробях с помощью веселых игр, вы можете зарегистрироваться здесь!
Уровень 1A: Целое × Дробь
Пример 1: Тим использовал ¼ тыквы, чтобы испечь один тыквенный пирог.
Он испек 3 пирога. Давайте узнаем, сколько всего тыкв он использовал.
Поскольку он использовал одну четверть тыквы 3 раза , его выражение умножения будет 3 × ¼
3 раза 1/4 равно 3/4Итак,
3/4
Итак, Тим использовал три четверти тыквы, чтобы испечь 3 пирога.
Пример 2: Если бы Тиму нужно было испечь 5 пирогов, сколько тыкв ему понадобилось бы?
5 раз 1/4 равно 5/45 × ¼ = 5/4
Итак, Тиму понадобится 1 целая тыква и четверть куска, чтобы испечь 5 пирогов.
Уровень 1B: Дробь × Целое
Визуализация модели Дробь × Целое может быть очень сложной для детей.
Начнем с того, что первое число в предложении умножения обозначает количество групп или количество повторений чего-либо. Но, в
Но, в
Пример: ¼ × 8
Мы можем описать это выражение простыми словами как одна четвертая от восьми . Математически слово «из» означает умножение.
Давайте нарисуем модель для этого выражения.
Шаг 1 :
Шаг 2:
Шаг 2 – Умножение дроби с целым числомSO, ¼ × 8 = 2
Пример 1: ¾ × 8
Это означает: Три четверти из восьми
Пример 1-Умножение добычи с целым номеромSO, . × 8 = 6
Давайте попробуем еще несколько примеров.
Пример 2: Джейми приготовил 4 стакана сока из 3 лаймов. Найдите количество плодов лайма, которые он использовал для каждого стакана сока.
Это означает, что он использовал четверть 3 лайма для приготовления одного стакана сока.
Математическое выражение, которое необходимо решить для этого примера: ¼ × 3
Возьмем три лайма как A, B и C.
Пример 2 – Умножение дробей с целыми числами Одна четвертая часть всех времен на каждой тарелкеКаждая тарелка представляет собой одну четвертую или четверть всей партии, то есть 3 лайма.
Сколько четвертей в одной тарелке? Три четверти
Итак, ¼ × 3 = ¾
Джейми использовал ¾ лайма на один стакан сока.
Пример 3: Узнайте, сколько лаймов Джейми использовал для 3 стаканов сока.
Это значит, что нам нужно узнать, сколько составляет три четверти от 3 лаймов .
Математическое выражение, которое нужно решить для этой ситуации: ¾ × 3
Выяснение, сколько лаймов используется для 3 стаканов сока
Сколько четвертей в 3 тарелках? Девять четвертых
Итак, ¾ × 3 = 9/4
Джейми использовал три стакана сока лайма 9/4 в 903.
Что означает дробь x целое?Похожие чтения: Лучшие платформы онлайн-обучения набирают популярность в наши дни
Уровень 2: Дробь × Дробь
Умножение дроби на дробь также является сложной формой, и учащимся довольно сложно понять применение умножения двух дробей.
Теперь мы можем помочь им визуализировать эту концепцию с помощью этого увлекательного и простого занятия по складыванию бумаги.
Пример 1: Визуализируйте и решите: ⅓ × ½
В общем случае это выражение будет означать одну треть половины . Вы можете помочь своему ребенку смоделировать этот сценарий, используя лист бумаги.
Попросите вашего маленького ученика выполнить следующие простые шаги:
- Возьмите прямоугольный лист бумаги и сложите его пополам.

- Затем сложите половинку на 3 равные части.
- Раскрасьте одну из сложенных сторон, чтобы показать треть половины.
- Откройте лист обратно.
- Определите, какую часть целого представляет заштрихованная часть.
⅓ × ½ = ⅙
ДОЛЖЕН ПОПРОБОВАТЬ БОЛЬШЕ!
Предложите детям попробовать умножить разные дроби, используя один и тот же метод.
Давайте рассмотрим еще несколько примеров:
Следующие модели следуют тому же принципу, что и в приведенном выше упражнении по складыванию бумаги. Упомянутый принцип заключается в моделировании двух фракций в одной модели.
Пример 2: Сколько будет ¼ × ½?
Представляет четверть половины.
Пример 2 – Умножение дроби на дробьСовет по умножению дроби на дробьПример 3: 5/7 × ¾
Пример 3. Умножение дроби на дробь
Умножение дроби на дробьПример 4: 1/3 × 1⅗
Пример 4. Умножение дроби на дробьПосле нескольких примеров вы можете предложить своему ребенку непосредственно нарисовать комбинированную модель.
Нарисуйте модель умножения двух дробей, выполнив следующие шаги:
- Нарисуйте большой прямоугольник.
- Разделите ее на столько равных горизонтальных полос, сколько знаменатель первой дроби. Заштрихуйте части, чтобы представить первую фракцию.
- Далее эту же модель разделите на столько равных вертикальных полос, сколько знаменатель второй дроби. Заштрихуйте части, чтобы представить вторую фракцию.
- Определите перекрывающуюся часть модели. Представленная дробь является произведением двух дробей.
Попросите детей наблюдать за произведениями, полученными из моделей, а также скажите им, какое правило соблюдается при умножении дробей.
Мы можем помочь им понять процесс с помощью этих 4 простых шагов умножения дробей.
- Запишите оба числа в виде дроби.
- Умножьте числители. Произведение является новым числителем.
- Умножьте знаменатели. Продукт является новым знаменателем.
- Перепишите ответ в форме наименьшего или смешанного числа.
Посмотрите несколько примеров.
Пример 1:
Пример 1 – Этапы умножения дробейПример 2:
Пример 2 — Шаги масштабирования фракцийПример 3:
Пример 3 — Шаги масштабных фракций Анализ : Умножение фракций
Вопрос :
. мы всегда получаем большее произведение при умножении двух чисел?
Обратите внимание на следующие задачи на умножение.
6 × 4 = 24
2 × 9 = 18
3 × 1 = 3
5 × 7 = 35
10 × 8 = 80
19 × 1 = 19
8 × 0 = 0
7 × 11 = 77
16 × 2 = 32
Вы думаете, что и то же вопрос актуален и для умножения с дробями?
Ответ на это: « иногда ».
Давайте рассмотрим несколько случаев, чтобы лучше их понять.
Случай 1: Когда одно из множимых равно 0
Произведение также будет равно нулю независимо от другой дроби.
¼ × 0 = 0/4 = 0
⅗ × 0 = 0/5 = 0
7/2 × 0/0/2 = 0
Кейс 2: когда 2: 0/2 = 0
. одно из множимых меньше 1
Произведение будет меньше, чем другая дробь.
3/4 × 7/3 = 21/12 = 7/4 (< 7/3)
1/4 × 7/8 = 7/32 (< 7/8)
3/4 × 1/9 = 1/12 (< 1/9)
Случай 3: Когда одно из множимых является дробью, эквивалентной 1
, произведение будет таким же, как и другое число.
1 × 7/8 = 7/8
6/6 × 9/5= 54/30= 9/5 5
Случай 4: Когда одно из множимых является дробью больше 1
Произведение будет больше, чем другая дробь .
8/3 × 2/5= 16/15 (> 2/5)
6/10 × 9/5= 54/50= 27/25 (> 6/10)
9/6 × 1/7= 9/42= 3/14 (> 1/7)
Случай 5: Когда оба множимых являются дробями больше 1
Произведение будет больше обеих дробей.
8/3 × 3/2 = 4 (> 8/3, 3/2)
6/4 × 5/2 = 30/8 (> 6/4, 5/2)
Похожие материалы: Различные типы графических органайзеров для учителей и учащихсяДеление дробей в реальной жизни: Введение
В повседневной жизни мы сталкиваемся с ситуациями, когда мы применяем концепцию дробного деления. Разделение на дроби можно сделать интересным, а концепцию можно полностью внедрить в сознание детей, если им будет предложено решать сценарии из реальной жизни.
Это поможет детям визуализировать и понять деление на дроби.
Пример: Предположим, у вас есть 3 яблока, каждое из которых разрезано пополам. На сколько человек вы сможете раздать эти 3 яблока, если каждому достанется по половинке?
На сколько человек вы сможете раздать эти 3 яблока, если каждому достанется по половинке?
Давайте представим эту ситуацию и решим ее. В конце концов, одно яблоко в день избавит вас от математической хандры!
Разделение трех яблок между 6 людьмиЗадачу можно расширить, изменив дробь.
Например, что, если вы решите раздать каждому человеку по четверти? Сколько человек можно обслужить сейчас?
Понимание дробного деленияПонимание дробного деленияИли что, если вы решите дать каждому человеку три четверти? Сколько человек можно обслужить сейчас?
Концептуальное понимание деления на дроби Концептуальное понимание деления на дроби
Понимание проблемы и последующее ее моделирование — важный шаг в любом сценарии решения проблем с делением на дроби. Предложите учащимся попытаться визуализировать сценарий, а затем найти его решение.
Рисуй и решай!
Группа друзей купила пиццу. Они поровну поделили пиццу и съели ее.
Попробуйте определить, сколько было друзей, если у каждого из них было:
| one-eighth of the pizza | two-eighth of the pizza | |
| 8 friends | 4 friends | |
| SO, 1 ÷ ⅛ = 8 | SO, 1 ÷ 2/8 = 4 |
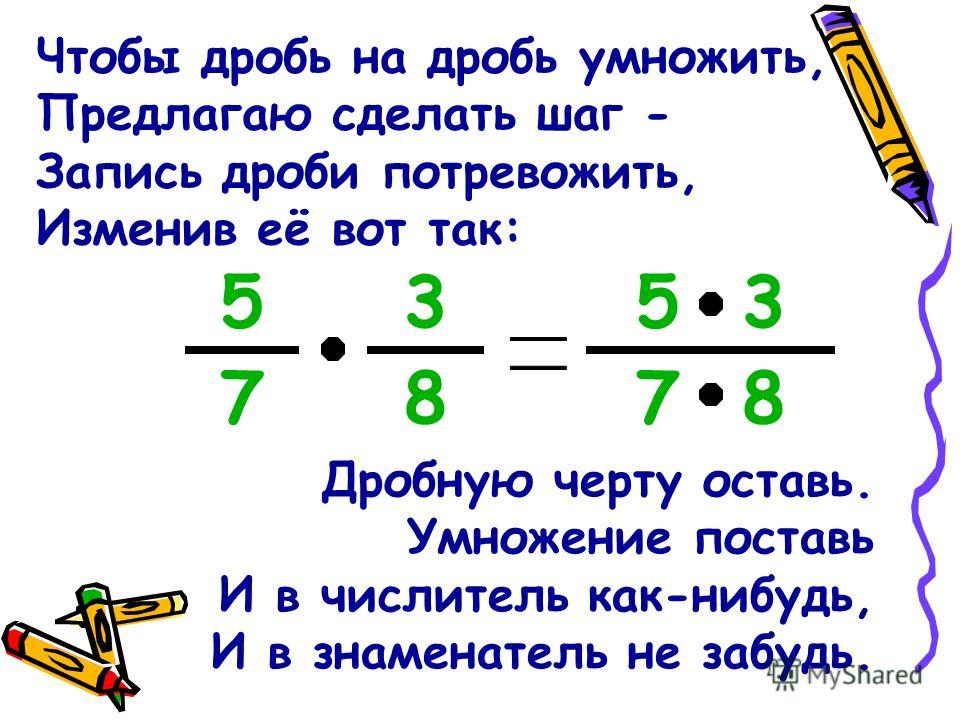 при моделировании задач на деление дробей метод поиска ответа прост.
при моделировании задач на деление дробей метод поиска ответа прост.Поэтому и для деления дробей предлагается подход от визуального к незрительному методу. Для студентов такой подход более правдоподобен, так как закладывает прочную концептуальную основу.
Давайте рассмотрим несколько примеров.
Целое число ÷ дробьПример 1:
Пример 1 – Деление целых чисел на дробиПример 2:
Пример 2 – Деление целых чисел на дроби0285 Связанное чтение: Самые важные математические символы, которые учащиеся должны решать задачиСовет: ) может быть образован из (делимого)?» или «Сколько групп (делителя) содержится в (делимом)». Эти описания помогают детям легче визуализировать ситуацию.
Дробь ÷ Целое Деление дроби на целые числа Дробь ÷ Дробь Деление дроби на дробь Смешанное число ÷ Дробь Деление смешанных чисел на дроби Деление дробей на 9079 Остаток 9080 Пример 1 Пример 1 – Деление дроби с остаткомПример 2:
Пример 2 – Деление дроби с остатком Некоторые распространенные трудности при делении дробей- Учащиеся часто пытаются понять разницу между делением на 2 и делением на ½.

Следующие модели помогут им легко увидеть разницу.
Проблемы с делением дробей Проблемы с делением дробей- Учащимся часто трудно понять, что деление дробей не всегда приводит к уменьшению частного.
Крайне важно, чтобы мы поощряли детей наблюдать за частными, полученными из моделей, и рассказывать им, какое правило следует при умножении дробей. Выполнение таких действий с ними может помочь в развитии навыков логического вывода и рассуждения.
Помогите им освоить процедуру деления дробей за 4 простых шага.
- Переверните дробь делителя.
- Изменить знак с ÷ на ×
- Умножьте дроби.
- Упрощение.
Понимание дробей и операций с ними станет намного проще, когда дети приобретут навыки визуализации задачи и знания того, что нужно вычислить. Но чтобы обрести такую уверенность, им нужно попрактиковаться в большом количестве математических задач. Необходимо, чтобы они смоделировали проблему, а затем решили ее.
Но чтобы обрести такую уверенность, им нужно попрактиковаться в большом количестве математических задач. Необходимо, чтобы они смоделировали проблему, а затем решили ее.
Вы можете обратиться к этим рабочим листам на SplashLearn, которые легко загрузить и распечатать, чтобы помочь вашему ребенку лучше понять умножение дробей.
Подводя итог- Для более глубокого понимания концепции обязательно создайте для детей среду, способствующую обучению на основе опыта.
- Вы можете использовать предыдущие и существующие знания ваших детей об умножении и делении целых чисел, чтобы получить новые знания об умножении и делении дробей.
- Поощряйте детей визуализировать проблемы и моделировать их. Сделайте так, чтобы они чувствовали себя комфортно, задавая вопросы.
- Крайне важно меньше сосредотачиваться на правильном ответе и больше на рассуждениях и мыслительном процессе ребенка.
- Как родитель, свяжите математические задачи с ситуациями из реальной жизни и приведите примеры из повседневной деятельности.

Упростите дроби с SplashLearn
Благодаря интерактивным играм и наградам, повышающим уверенность и баллы вашего ребенка, вы теперь можете сделать обучение легким и беспроблемным. Присоединяйтесь к нашему сообществу из 40+ миллионов бесстрашных учеников уже сегодня!
Зарегистрируйтесь бесплатно!
Часто задаваемые вопросы (FAQ)
Q1 – Как шаг за шагом умножать дроби?
- Запишите оба числа в виде дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Упростите или перепишите ответ в форме смешанного числа.
Q2 – Как делить дроби шаг за шагом?
- Переверните дробь делителя.
- Изменить знак с ÷ на ×.
- Умножьте дроби.
- Упрощение.
Q3 – Как определить, приведет ли умножение на дробь к большему или меньшему произведению?
Сравните числитель и знаменатель дроби, чтобы проверить, будет ли произведение больше или меньше числа, на которое они умножаются.
Большее произведение → Числитель > Знаменатель. Примеры: 3/2, 4/3, 8/5 и так далее.
Меньший продукт → Числитель < знаменатель. Примеры: 3/4, 4/7, 5/9 и так далее.
Как научить умножать дроби с помощью шаблонов — смешивание и математика
ДробиМатематические манипуляцииУмножение
Автор Бриттани Хеге
В первый год преподавания я унаследовал примерно 1 000 000 математических манипуляторов — пластиковые
«Что в мире могут делать ученики с блоками шаблонов в четвертом и пятом классе?» Интересно.
Если бы я только знал, какой невероятный инструмент для обучения дробям, эти блоки шаблонов нашли бы гораздо больше применения (и мои ученики поняли бы дроби намного лучше!).
Кубики теперь мой самый любимый способ обучения всем понятиям дроби. Что делает их такими мощными, так это то, что учащиеся должны полагаться на свое понимание дробей как отношения часть часть весь . Кроме того, наличие разных форм помогает учащимся действительно увидеть, как одни части вписываются в другие. Поскольку на деталях нет меток дробей, возможности использования блоков шаблонов безграничны!
Хотя сейчас я использую блоки шаблонов для обучения всем понятиям дробей, моя любимая концепция дробей для обучения с блоками шаблонов — это умножение дробей. Поскольку алгоритм умножения дробей выглядит таким простым, возникает соблазн дать учащимся «ярлык» и пропустить построение концептуального понимания.
Но формирование концептуального понимания НАСТОЛЬКО важно, особенно с дробями!
Умножение дробей может быть трудной задачей для практического применения, но блоки шаблонов делают это простым (и очень увлекательным!). Давайте рассмотрим несколько примеров задач, чтобы вы могли применить это мощное упражнение в своем классе!
Давайте рассмотрим несколько примеров задач, чтобы вы могли применить это мощное упражнение в своем классе!
посмотреть видео…
Прежде чем мы перейдем к обучению умножению дробей с помощью блоков шаблонов, убедитесь, что вы (и ваши ученики!) понимаете, какую дробь представляет каждый блок шаблонов. Хотя вы можете сделать так, чтобы любая часть представляла собой единое целое, чаще всего я использую шестиугольник как единое целое.
На приведенном ниже рисунке показано значение каждой части блока рисунка, когда шестиугольник представляет собой одно целое.
В отношении блоков шаблонов важно отметить, что вы будете ограничены знаменателями половин, третей и шестых для задач, которые вы создаете! Они делают набор дополнительных блоков шаблона для четвертых и двенадцатых , если вы хотите дополнить блоки, которые у вас уже есть!
Теперь, когда вы знаете значение каждого блока шаблона, давайте углубимся в то, как учащиеся могут использовать блоки шаблона для моделирования различных типов задач на умножение дробей и смешанных чисел.
Существует четкая последовательность построения задач на умножение дробей. Первым шагом в прогрессии является умножение на несколько групп или равных групп .
Просмотр умножения в виде нескольких групп относительно прост для понимания учащимися, поскольку он следует тому же принципу мышления, что и умножение целых чисел. Для учащихся не составит большого труда перейти от понимания 2 групп по 3 (2 x 3) к пониманию 2 групп по ⅔ (2 x ⅔).
Однако потребуется много практических занятий, прежде чем учащиеся откроют для себя алгоритм умножения целого числа на дробь. (И они увидят это ! Доверьтесь процессу и не навязывайте алгоритм, пока ученики не будут готовы!)
Вот пример задачи с несколькими группами:
Собака Стеллы съела 3 пакета собачьего корма последним неделя. Если в каждом пакете было ⅔ фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
На математическом коврике ученики моделировали три группы по ⅔. Они могут назвать это 6/3 или переставить части в целые, чтобы увидеть, что ответ — два целых. На прошлой неделе собака Стеллы съела 2 фунта собачьего корма.
Они могут назвать это 6/3 или переставить части в целые, чтобы увидеть, что ответ — два целых. На прошлой неделе собака Стеллы съела 2 фунта собачьего корма.
Задачи на несколько групп также могут включать смешанные числа в качестве множимого, например, 3 группы по 1 ½. Пока множитель (количество групп) является целым числом, он будет моделироваться аналогично тому, как моделировалась последняя задача. Взгляните на рисунок ниже, чтобы увидеть, как вы будете моделировать 3 x 1 ½ с помощью блоков шаблона.
Для четвертого класса большинство государственных стандартов останавливаются здесь (конечно, проверьте свои собственные стандарты, чтобы быть уверенным!). Однако для пятого класса им нужно понять другой тип задачи на умножение дробей.
Задачи на частичные группы Цель этого шага в последовательности умножения состоит в том, чтобы учащиеся начали рассматривать умножение как масштабирование , в частности изменение размера, чтобы найти часть группы . Это может показаться большим отклонением от того, что студенты думают они знают об умножении, а именно: «умножение делает числа больше!»
Это может показаться большим отклонением от того, что студенты думают они знают об умножении, а именно: «умножение делает числа больше!»
Именно в этот момент они узнают, что умножение может привести к меньшему произведению, а это означает, что мы обязательно должны дать учащимся возможность смоделировать эту концепцию, , иначе это может показаться невероятно запутанным!
Часть целогоЗадача первого типа о частичных группах — найти часть целого .
Давайте вернемся к нашей реальной ситуации с кормом для собак, чтобы посмотреть, как это выглядит.
На прошлой неделе собака Стеллы съела ⅔ пакета собачьего корма. Если в каждом пакете было 3 фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
Хотя уравнение для этой задачи такое же, как и для предыдущей задачи (⅔ x 3 против 3 x ⅔), процесс моделирования выглядит совсем иначе. В этом случае учащиеся должны понимать, что они находят ⅔ группы из 3. Другими словами, это ⅔ из 3.
В этом случае учащиеся должны понимать, что они находят ⅔ группы из 3. Другими словами, это ⅔ из 3.
Ученикам нужно много возможностей с обоими типами задач, чтобы распознать их как умножение!
Чтобы смоделировать ⅔ из 3, учащиеся должны начать с 3 целых, а затем им нужно будет выяснить, как разделить их на трети (или три равные группы). Они увидят, что им нужно вложить одно целое в каждую из третей. Поскольку мы хотим знать, что такое ⅔ от 3, мы знаем, что ответ будет включать в себя две трети, что составляет два целых, потому что в каждой трети есть одно целое. На рисунке ниже показано, как это смоделировать.
Давайте разовьем этот тип мышления в частичных группах немного дальше, рассмотрев, как моделировать дробь за дробью.
Часть части Следующий тип частичной групповой задачи — часть части . Опять же, давайте воспользуемся нашим реальным контекстом, чтобы помочь нам понять, что это на самом деле означает.
Собака Стеллы съела ⅔ пакета собачьего корма. Если в каждом пакете ½ фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
Вместо того, чтобы найти часть группы, эта ситуация требует поиска части другой части… Что такое ⅔ ½ фунта еды? Чтобы смоделировать это, им нужно будет немного обменяться, чтобы помочь им разыграть это. Мы знаем, что трапеция (1 половина) эквивалентна 3 треугольникам (или 3 шестым), а это значит, что учащиеся могут обменять трапецию на 3 треугольника. Это поможет нам, когда мы попытаемся выяснить, что такое ⅔ половины.
Посмотрите на рисунок ниже, чтобы увидеть, как учащийся поместит одну шестую в каждую из третьих частей, чтобы понять, что 2 трети половины равны двум шестым.
Самое интересное — самый последний шаг в этой последовательности умножения дробей. Теперь учащимся действительно сложно применить то, что они узнали!
Объединение кратных и неполных групп Последний шаг на пути к истинному пониманию умножения дробей — это сочетание кратных групп и неполных групп. Это означает, что множитель (количество групп) является смешанным числом, заставляющим учащихся думать о равном количестве групп и часть группы или часть.
Это означает, что множитель (количество групп) является смешанным числом, заставляющим учащихся думать о равном количестве групп и часть группы или часть.
Давайте посмотрим на пару примеров ниже, как это выглядит на самом деле!
В прошлом месяце собака Стеллы съела 2 ⅓ пакета собачьего корма. Если в каждом мешке 4 фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
В этой ситуации собака Стеллы съела 2 пакета корма (2 x 4 фунта — несколько групп) и ⅓ пакета корма (⅓ x 4 фунта — неполные группы). Студенты должны объединить свое понимание обоих типов умножения дробей, чтобы успешно решить эту задачу.
Эта проблема смоделирована на рисунке ниже.
Объединив 2 группы по 4 и ⅓ по 4, вы увидите, что собака Стеллы съела в общей сложности 9 ⅓ фунтов собачьего корма.
Давайте рассмотрим еще одну задачу, где множимое (то, что умножается) является дробью!
Собака Стеллы съела 2 ⅓ пакета собачьего корма. Если в каждом пакете было ½ фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
Если в каждом пакете было ½ фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
В этой ситуации собака Стеллы съела 2 группы по ½ фунта (несколько групп) и ⅓ по ½ (часть части). На графике ниже вы можете видеть, что если все это объединить, то собака Стеллы съела 1 ⅙ фунта собачьего корма.
В последней задаче, которую мы рассмотрим в этом посте, учащиеся решают задачу на умножение дроби, которая включает смешанное число на смешанное число.
На прошлой неделе собака Стеллы съела 2 ½ пакета собачьего корма. Если в каждом пакете было 2 ⅓ фунта собачьего корма, сколько фунтов корма съела собака Стеллы?
В этой задаче есть 2 ½ группы по 2 ⅓, то есть 2 полные группы по 2 ⅓ (несколько групп) и ½ группы по 2 ⅓ (неполные группы). Поскольку у студентов, как мы надеемся, был большой опыт работы с несколькими группами и частичными группами до этой задачи, этот процесс абсолютно выполним для студентов (хотя это может напрячь их мышление!).
 момент
момент Мы ее уже изучали на прошлых уроках.
Мы ее уже изучали на прошлых уроках. Актуализация знаний
Актуализация знаний
 И послушаем сообщение из истории дробей. Из которого вы должны будете сказать, что же нового Пеануд ввел в математику.
И послушаем сообщение из истории дробей. Из которого вы должны будете сказать, что же нового Пеануд ввел в математику. Решив правильно красную карточку, сможете набрать 4 балла, синюю –3балла, а зеленую — 2 балла. Эти баллы вы занесете в оценочный лист. Ваша задача выбрать себе карточку по своим возможностям и решить предложенные в ней задания. После, вы получите карточку – информатор, в которой будет записан верный ответ и приведено решение. Т.о. вы сможете проверить себя, а так же проверить правильность записи решения.
Решив правильно красную карточку, сможете набрать 4 балла, синюю –3балла, а зеленую — 2 балла. Эти баллы вы занесете в оценочный лист. Ваша задача выбрать себе карточку по своим возможностям и решить предложенные в ней задания. После, вы получите карточку – информатор, в которой будет записан верный ответ и приведено решение. Т.о. вы сможете проверить себя, а так же проверить правильность записи решения. И выставляет себе баллы в оценочный лист следующим образом (слайд 10):
И выставляет себе баллы в оценочный лист следующим образом (слайд 10):

 (слайд 15 в)
(слайд 15 в)
 (слайд 20)
(слайд 20) Самая большая ядовитая змея – это …
Самая большая ядовитая змея – это …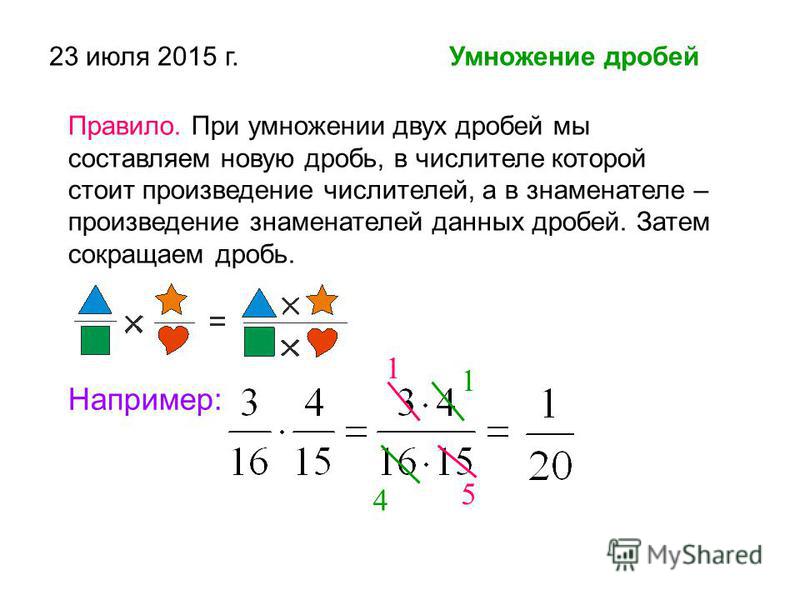
 (слайд 27)
(слайд 27)

