Открытый урок по математике по теме «Порядок действий в выражениях со скобками».
Открытый урок по математике во 2 классе
по теме «Порядок действий в выражениях со скобками».
Основные цели:
1) формировать умение строить правила на примере вывода правила порядка действий в выражениях со скобками, содержащих все арифметические действия, умение использовать это правило при нахождении значений выражений;
2) тренировать вычислительный навык, умение решать текстовые задачи.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение.
Ход урока:
1. Мотивация к учебной деятельности.
Цель:
1) включение учащихся в учебную деятельность на личностно значимом уровне;
2) определение содержательных рамок урока: порядок действий в выражениях;
3) актуализация требований к учащимся со стороны учебной деятельности.
Организация учебного процесса на этапе 1:
На одном из предыдущих уроков мы говорили о порядке. О каком именно порядке шла речь? (О порядке дома, в детской комнате, о порядке в математике.)
С какой темой был связан порядок в математике? (С порядком действий в выражениях без скобок.)
В окружающем нас мире, в природе тоже есть свой порядок. Какой порядок в природе вам приходилось наблюдать? (Смена времён года, смена времени суток…)
Сегодня вы продолжите разговор о порядке в математике, и узнаете что-то о порядке в природе.
Как вы будете работать? (Мы сначала сами поймем, что мы еще не знаем, а потом постараемся сами «открыть» новое правило.)
Учитель открывает на доске картинку № 8 с изображением бабочки Д-1.
Посмотрите, кто вам в этом поможет… (Бабочка. )
)
Интересно узнать, как это произойдёт? Тогда, за работу.
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
Цель:
1) актуализировать знание порядка действий в выражениях со скобками, не содержащих умножение и деление, порядок действий в выражениях без скобок, содержащих все 4 действия, тренинг вычислительного навыка;
2) актуализировать мыслительные операции анализ, синтез, сравнение, аналогия;
3) мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;
4) организовать фиксацию образовательной цели и темы урока;
5) организовать выполнение пробного действия и фиксацию затруднения;
6) организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.
Организация учебного процесса на этапе 2:
1) Актуализация известных порядков действий.
Учитель открывает на доске задание 1 для этапа 2 (Д-2), раздает аналогичные задания на карточках Р-1:
85 – 5 · 4 + 7 · 5 = (30 – 18) + (14 + 8) =
Что поможет вам найти значение этих выражений? (Правила нахождения значения выражений без скобок и со скобками, где только сложение и вычитание.)
Расставьте порядок действий в первом выражении.
Один из учащихся находит значение выражения.
Один из учащихся расставляет порядок действий у доски с комментированием.
Учитель открывает на доске эталон Д-4.
Отлично! Договоримся, что после удачно выполненных заданий я буду вешать на доску ещё одну картинку, но изображением к доске. В конце урока по картинкам, вы узнаете, о каком порядке, существующем в природе, хочет поведать вам бабочка.
Учитель вывешивает картинку № 7 из набора Д-1 изображением к доске.
2) Пробное действие.
Что вы повторили? (Мы повторили порядок действий в выражениях без скобок, и в выражениях со скобками, где только действия сложение и вычитание, потренировались в вычислениях.)
Почему я выбрала именно это? (Это нам пригодится для открытия нового знания.)
Какое следующее задание я вам предложу? (Задание, в котором будет что-то новое.)
Зачем вы его получите? (Чтобы мы сами узнали, что мы еще не знаем.)
Учитель открывает на доске задание для пробного действия (Д-5), аналогичное задание раздает учащимся на карточках Р-2:
40 – 32 : (48 : 6) ∙ 4 + 3 ∙ (54 – 45)
Чем это выражение отличается от предыдущих выражений? (В выражении есть скобки, и есть действия умножения и деления.)
Что нужно будет сделать? (Расставить порядок действий и найти значение этого выражения. )
)
Я вам предлагаю только расставить порядок действий.
Учащиеся выполняют пробное действие на карточках Р-2.
Учащиеся поднимают руки.
Что вы не смогли сделать? (Мы не смогли расставить порядок действий в выражении со скобками со всеми арифметическими действиями.)
Кто выполнил задание, как вы расставили порядок действий?
Учитель записывает на доску варианты расстановки порядка действий. Вероятнее всего, учащиеся смогут правильно расставить порядок действий. Затруднения в этом случае фиксируется так:
Назовите правило и покажите эталон, по которому вы действовали.
Учащиеся в замешательстве, так как эталона у них нет.
Что вы не можете сделать? (Мы не можем назвать правило, по которому действовали.)
Что вы теперь должны сделать? (Разобраться, в чем и почему возникло затруднение. )
)
3. Выявление места и причины затруднения.
Цель:
выявить место и причину затруднения.
Организация учебного процесса на этапе 3:
Какое задание вы должны были выполнить? (Мы должны были расставить порядок действий в выражении, в котором есть, скоби и все арифметические действия.)
Какими правилами вы пользовались? (Правилом расстановки действий в выражениях со скобками со сложением и вычитанием, и правилом расстановки действий в выражениях без скобок со всеми действиями.)
В чем затруднение? (В выражении со скобками есть действия умножения и деления.)
Почему же возникло затруднение? (У нас нет правила порядка действий в выражениях со скобками, в которых есть все четыре арифметических действия.)
Учитель вывешивает на доску картинку № 2 из набора Д-1 изображением к доске.
4. Построение проекта выхода из затруднения.
Цель:
1) согласовать и зафиксировать цель и тему урока;
2) построить план и определить средства достижения цели.
Организация учебного процесса на этапе 4:
Какую цель вы поставите перед собой на уроке? (Построить правило расстановки порядка действий в выражениях со скобками, в которых есть все четыре арифметических действия.)
Сформулируйте тему урока? (Порядок действий в выражениях со скобками со всеми действиями.)
Учитель записывает или открывает тему на доске.
Какие правила вы можете использовать для построения нового эталона? (Правила расстановки порядка действий в выражениях со скобками и в выражениях без скобок, содержащих все четыре арифметических действия.)
По какому плану вы будете действовать? (Сначала мы применим правило расстановки действий со скобками, а затем правило расстановки порядка действий без скобок, сформулируем новое правило. )
)
Молодцы! Ваша награда – ещё одна картинка.
Учитель вывешивает на доску картинку № 6 из набора Д-1, изображением к доске.
5. Реализация построенного проекта.
Цель:
1) реализовать построенный проект в соответствии с планом;
2) зафиксировать способы записи выражений на эталоне;
3) организовать фиксацию преодоления затруднения;
4) организовать уточнение общего характера нового знания.
Организация учебного процесса на этапе 5:
В случае необходимости актуализируются правила работы в группах.
Группы работают на индивидуальных планшетках Р-3. В случае возникновения затруднений у учащихся работы в группах, учитель организует подводящий диалог:
Какой первый шаг в плане? (Применить правило порядка действий в выражениях со скобками. )
)
Что это зачать? (Сначала выполняем действие в скобках.)
Обозначьте действия в скобках.
Один из учащихся обозначает порядок действий в скобках на доске, остальные работают на карточках Р-2:
В каком порядке вы начали расставлять порядок действовать? (Слева направо.)
Какой следующий шаг? (Расставить порядок действий по правилу порядка действий в выражениях без скобок, содержащих все виды арифметических действий.)
Выполните этот шаг.
Один из учащихся обозначает порядок действий на доске, остальные работают на карточках Р-2:
Если учащиеся работали в группах, то учитель организует защиту проектов. Учитель вывешивает на доску планшетки с результатом от каждой группы. Одна из групп озвучивает свою работу. Например:
Сначала мы расставили порядок действий в скобках, в порядке слева направо. Потом обозначили слева на право действия умножения или деления, а потом сложение или вычитание.
Потом обозначили слева на право действия умножения или деления, а потом сложение или вычитание.
Далее работа организуется фронтально:
Итак, какие действия надо выполнять сначала? (Действия в скобках.)
К акие действия потом? (Действия умножение или деление.)
А потом? (Сложение или вычитание.)
Что важного вы еще не сказали? (Работаем слева направо.)
Какой следующий шаг? (Составить эталон.)
Посмотрите на доску. Какой эталон из уже имеющихся эталонов вам поможет? (Эталон порядка действий в выражениях без скобок.)
Что мы должны сделать? (Дополнить первый шаг.)
Какой? (Сначала делаем действие в скобках.)
Учитель дополняет эталон Д-3 шагом Д-6.
Что теперь нужно сделать? (Проверить наше «открытие». )
)
Откройте учебники на странице 33. Прочитайте правило.
Один из учащихся читает правило вслух.
Вы справиться с затруднением? (Да.)
Что теперь вы можете? (Находить значения выражений со скобками, содержащих все четыре арифметических действия.)
Учитель раздает учащимся эталоны Р-4.
Учитель вывешивает на доску картинку № 3 из набора Д-1.
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
зафиксировать во внешней речи правило порядка действий в выражениях со скобками.
Организация учебного процесса на этапе 6:
1) Фронтальная работа.
№ 5, стр. 34
Учитель заранее выносит задание на доску.
Учащиеся по цепочке выходят к доске и выполняют задание с комментированием.
2) Работа в парах.
№ 4 (1 ст.), стр. 34
Найдите № 4 на странице 34.
Выполните 1 столбик в этом задании в парах.
Учащиеся выполняют задание в парах с комментированием. Проверка организуется по образцу Д-7.
Проверьте свои результаты.
Кто из вас ошибся?
В чем ошибка?
Исправьте ошибки.
Ну что ж, вот и ещё одна картинка.
Учитель вывешивает на доску картинку № 5 из набора Д-1.
Какой следующий шаг на уроке? (Проверить себя, справимся ли мы самостоятельно.)
7. Самоконтроль с самопроверкой по эталону.
Цель:
1) тренировать способность к самоконтролю и самооценке;
2) проверить умение применять правило порядка действий в выражениях со скобками.
Организация учебного процесса на этапе 7:
№ 4 (2 ст.), стр. 34
Учащиеся выполняют самостоятельную работу в учебниках. Проверка организуется по образцу Д-8. Учитель вывешивает образец рядом с эталоном Д-6.
У кого задание вызвало затруднение?
В каком случае? (…)
Исправьте ошибку.
Сделайте вывод. (Нужно еще потренироваться.)
Кто не ошибся?
Сделайте вывод. (У нас нет затруднений.)
Вы заработали следующую картинку.
Учитель вывешивает на доску картинку № 1 из набора Д-1.
8. Включение в систему знаний и повторение.
Цель:
1) включить новое знание в систему знаний;
2) тренировать умение решать текстовые задачи.
Организация учебного процесса на этапе 8:
№ 3, стр. 33
Найдите № 3 на странице 33.
Прочитайте первую задачу.
Один из учащихся читает задачу вслух.
Что требуется узнать? (Все количество яблок на двух тарелках.)
Каким действием можно будет ответить на вопрос? (Действием умножения.)
Можно сразу записать выражение? (Нет, мы не знаем количество яблок на одно тарелке.)
Как это узнать? (2 + 4.)
Составьте выражение и найдите его значение.
Один из учащихся составляет выражение на доске:
5 · (2 + 4) = 30 (ябл.)
Далее работа организуется аналогично.
Учитель вывешивает на доску картинку № 4 из набора Д-1.
9. Рефлексия учебной деятельности на уроке.
Цель:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить свою работу и работу класса на уроке;
4) наметить направления будущей учебной деятельности;
3) обсудить домашнее задание.
Организация учебного процесса на этапе 9:
Что нового вы сегодня узнали? (Правило расстановки порядка действий в выражениях со скобками.)
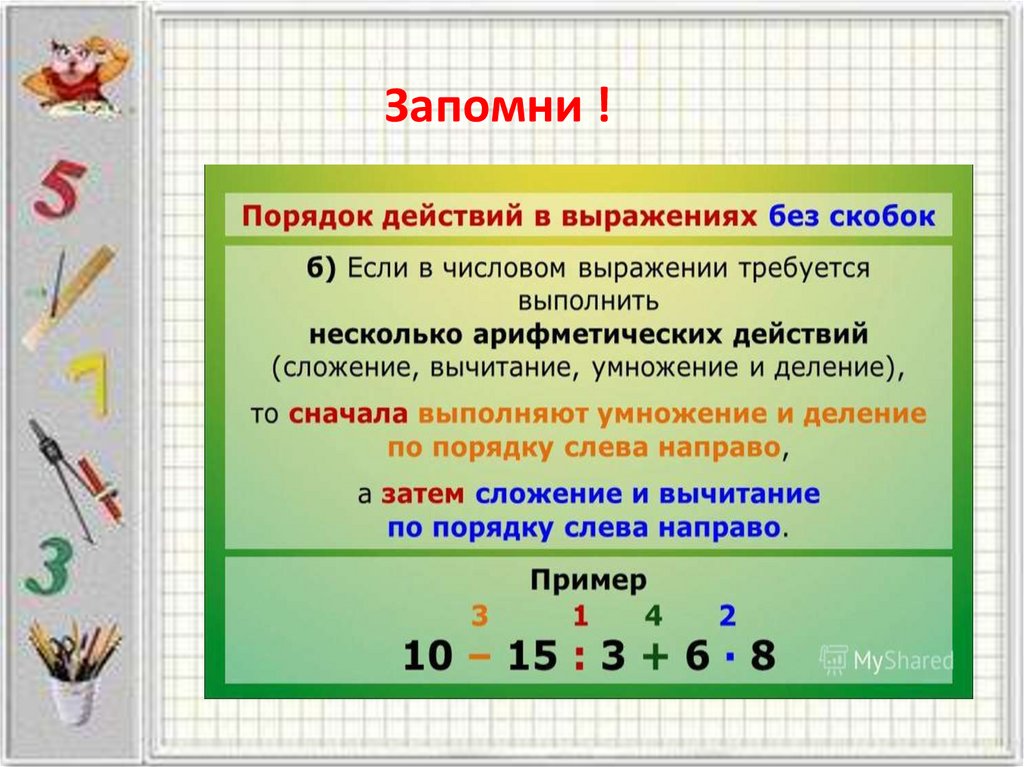
Каков порядок действий в выражениях со скобками? (В выражениях со скобками сначала выполняют действия в скобках, затем, в полученном выражении сначала выполняют умножение, деление слева направо, а затем сложение, вычитание слева направо. )
)
Где пригодятся вам полученные знания? (При нахождении значений числовых выражений при решении задач,…)
Кто столкнулся с затруднениями? В чем? Почему?
О каком ещё порядке шла речь в начале урока? (О порядке в природе.)
И сейчас вы узнаете, какая загадка таиться на картинках на доске.
Учитель переворачивает картинки на доске.
Да, но порядка в них, по-моему, не наблюдается. Давайте-ка, наведём его и выясним, о каком порядке идёт речь. (Это последовательность или порядок превращения гусеницы в бабочку.)
Один из учащихся расставляет картинки на доске в нужном порядке, остальные с места ему помогают.
Верно, это превращение считается одним из самых удивительных и красивых превращений существующих в природе.
Теперь я предлагаю вам оценить свою работу на уроке. Положите перед собой «лестницу успеха». Покажите, на какой ступеньке вы находитесь в конце урока. Если вы выполнили самостоятельную работу без ошибок, и у вас нет вопросов, то поставьте себя на верхнюю ступеньку. Если вы выполнили самостоятельную работу, но у вас остались вопросы, поставьте себя на среднюю ступеньку. Если вы ошиблись в самостоятельной работе, у вас остались вопросы, поставьте себя на нижнюю ступеньку.
Положите перед собой «лестницу успеха». Покажите, на какой ступеньке вы находитесь в конце урока. Если вы выполнили самостоятельную работу без ошибок, и у вас нет вопросов, то поставьте себя на верхнюю ступеньку. Если вы выполнили самостоятельную работу, но у вас остались вопросы, поставьте себя на среднюю ступеньку. Если вы ошиблись в самостоятельной работе, у вас остались вопросы, поставьте себя на нижнюю ступеньку.
Учащиеся оценивают себя с помощью лестницы успеха Р-5. Учитель проводит рефлексию оценивания учащихся.
Далее идет обсуждение домашнего задания.
Домашнее задание:
№ 2, № 5 (доделать), стр. 34;
☺ № 10, стр. 35
7
Урок математики 1 клас «Действия со скобками.»
Орг. момент: – Я приветствую тех,
Кто с удовольствием шёл в школу;
У кого сегодня хорошее настроение;
Кто хочет учиться; (Дети встают)
– Что люди желают перед тем, как начать любое дело? (Они желают друг другу успеха) давайте друг другу улыбнемся
И наша формула успеха =
ЗНАНИЯ+ВНИМАНИЕ+СОТРУДНИЧЕСТВО+ТЕРПЕНИЕ
Мотивация
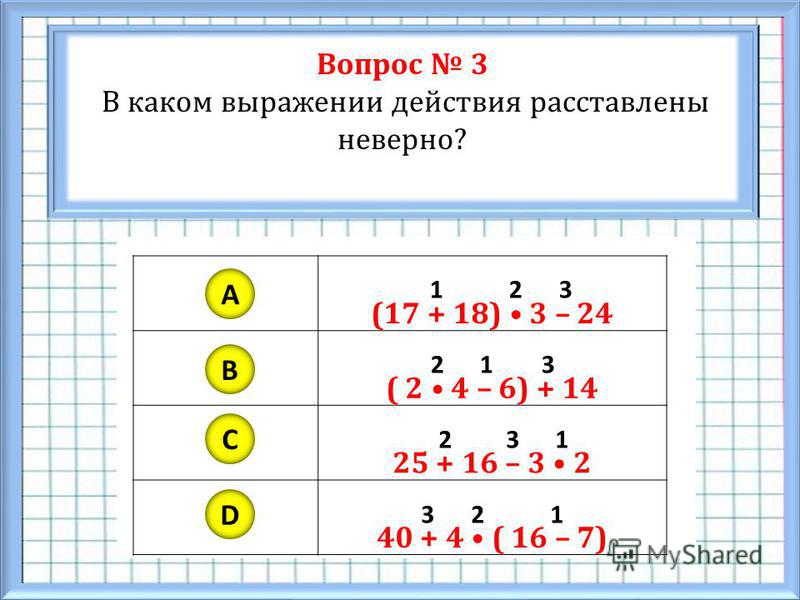
8 – 3 + 4 (8 – 3) + 4 8 – (3 + 4)
— Сравните два выражения. В чем сходство, в чем отличие? Значение, какого выражения можете найти?
В чем сходство, в чем отличие? Значение, какого выражения можете найти?
Актуализация опорных знаний.
Начнем урок с того, что уже знаем. Посмотрите на записи. Какое задание можно к ним придумать?
8 – 2 10
— Назовите высказывания. Как называются остальные записи? (выражения)
— Назовите «лишнее» выражение. Обоснуйте свой ответ.
8 – 2 — на вычитание. Прочитайте его, используя термин «разность».
а + с — буквенное выражение
9 + 5 — прием счёта с переходом через десяток. Прочитайте его разными способами.
10 – 4 + 3 — содержит два действия. Прочитайте его. (10 вычесть 4, прибавить 3).
— Расставьте порядок действий в этом выражении. Как выполняются действия? (по порядку слева направо). Прочитайте другим способом (Помощь – поставить карточку «разность. К разности чисел 10 и 4 прибавили 3).
— Чему равно значение выражения? ( 9)
Постановка цели урока.
(Г) – Запишите выражения:
Из числа 8 вычесть 3
8 – 3 = 5
К полученной разности прибавить 4
5 + 4 = 9
Итак, 8 – 3 + 4 =9 (запись на доске)
Выполните программу № 2
К числу 3 прибавить 4
3 + 4 = 7
Из числа 8 вычесть полученную сумму
8 – 7 = 1
Итак, 8 – 3 + 4 = 1 (запись на доске)
— Сравните выражения и результаты в программах №1 и №2. Что заметили?
Что заметили?
(Выражения одинаковые, а результаты разные)
-Почему? (Разный порядок действий)
-Как вы выполняли действия?
-Итак, тема нашего урока: порядок действий в выражениях.
-Как нам изменить выражения?
(Необходимо как-то обозначить в записи порядок действий)
-Какая возникла проблема? (Не умеем обозначать порядок действий)
-Попробуйте сформулировать цель урока, т.е. чему мы будем учиться.
-Итак, цель нашего урока — научиться обозначать в записи порядок действий.
Каковы будут критерии успеха на уроке? Научиться устанавливать порядок действий в выражениях, правильно читать числовые выражение, находить значение числовых выражений.
Открытие нового. Поиск решения проблемы.
-Предположите свои способы обозначения порядка действий.
1 2
(Указать сверху: 8 — 3 + 4 = 1)
-Может быть надо ограничить, отделить действия одно от другого? Попробуйте. .
.
8 –/ 3 + 4/= 1
— В математике принято обозначать очерёдность действий с помощью скобок. — Кто поставит в данном примере скобки там, где нужно?
8 — (3 + 4) = 1
-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками.
(Сначала выполняются действия в скобках, а потом остальные по порядку.)
-Сравним наше новое знание с научным в учебнике.
В выражениях со скобками первым выполняется действие над числами, записанными в скобках. Затем – действия – вне скобок.
-Как по-другому назовем это правило? (алгоритм)
(К) Правильно прочитайте числовые выражения со скобками:
Физкультминутка.
Мы сейчас все дружно встанем,
Отдохнём мы на привале…
Вправо, влево повернитесь!
Наклонитесь, поклонитесь!
Руки вверх и руки в бок
И на месте прыг да скок!
А теперь бежим вприпрыжку,
Молодцы, вы, ребятишки!
Работа в парах: Пройдите лабиринт через числовые выражения со значением 10, и вы узнаете, кто из хоккеистов забил гол.
Ответ: гол забил хоккеист в синей форме.
Физкультминутка для глаз: Закрыть глаза, сильно напрягая глазные мышцы, на счёт 1-4, затем раскрыть глаза, посмотреть вдаль на счёт 1-6. Повторить 3 раза.
Самостоятельная работа : Прочитайте выражения, найдите их значения красный лыжник – 1 вариант, жёлтый лыжник – 2 вариант
Критерии успеха:
1.Правильно прочитать выражение, записать в тетрадь
2.Расставить порядок действий.
3. Найти значение выражения.
Как и когда использовать кронштейны в грамматике []
Описание
Дизайн кругов с символом кронштейна в Orange Circle
ИСТОЧНИК
Созданный YourDictionary
Lights
.
Скобки — это больше, чем просто квадратные скобки. На самом деле, не все скобки имеют квадратную форму — некоторые фигурные, другие угловатые, и все они полезны по-своему. Даже если вы не используете эти знаки препинания каждый день, вы все равно должны знать, что они означают, когда вы их видите.
Даже если вы не используете эти знаки препинания каждый день, вы все равно должны знать, что они означают, когда вы их видите.
Что такое скобки?
Скобки — это знаков препинания , которые окружают текст. Как и скобки, скобки работают парами — одна скобка открывает текст, а вторая закрывает его [ вот так ] .
Существует три основных типа скобок, которые вы встретите в письме. Вы даже можете увидеть ссылку на круглые скобки — это ваши стандартные скобки . Но когда вы слышите только слово скобка , люди обычно имеют в виду квадратные скобки.
Описание
Четыре различных символа скобок в оранжевых кругах с их именами
Источник
, созданные Yourdictionary
LEARD
.
Хотя квадратные скобки используются не так часто, как круглые скобки, они все же весьма полезны и необходимы во многих ситуациях.
- Мужчина заявил, что «никогда не хочет их видеть» [ его соседи ] еще раз».

- «Я никогда раньше не летал на простом [ sic ] », — сказал солдат.
- Перед посещением занятий вам понадобится экземпляр книги профессора ( История философии [ 2016 ] ).
- Как сказал Уинстон Черчилль: «Мы никогда не сдадим [ курсив добавлен ] ».
- Помните испанскую пословицу «Zapatero, a tus zapatos [ Сапожники, к вашей обуви ] ».
Как печатать скобки
Скобки появились на пишущей машинке после круглых скобок, но на самом деле их легче печатать на современном компьютере, чем круглые скобки (вы создаете круглые скобки с помощью Shift + 9 и 0).
В большинстве случаев нажатие клавиши скобки (сразу после «P» на клавиатуре) дает открывающую скобку, а клавиша рядом с ней дает закрывающую скобку.
Когда использовать скобки
Скорее всего, вы увидите и будете использовать скобки при работе с
 Независимо от того, добавляете ли вы контекст к цитате, смещаете текст в скобках или переводите цитату на другой язык, скобки добавляют ясности вашему письму.
Независимо от того, добавляете ли вы контекст к цитате, смещаете текст в скобках или переводите цитату на другой язык, скобки добавляют ясности вашему письму.Примеры использования скобок
Нажмите, чтобы посмотреть и скачатьИспользуйте скобки, чтобы добавить важные слова в цитаты
Писатели используют скобки в академическом письме, чтобы добавить информацию к цитате, не меняя смысла предложения. Это означает, что автор может добавлять слова, если это необходимо, чтобы сделать предложение более ясным, или добавлять исправления или комментарии к цитируемому материалу.
Если вы добавляете слова для уточнения слова, которое уже находится в кавычках, не заменяйте это слово скобками — помните, кавычки менять нельзя. Вы можете только добавить к ним.
- «Книги, используемые [ в классах ] показывают методы поиска информации, но мало информации при подготовке обзора.» (Либутти и Копала, 1995, стр.
 15).
15). - «Пожар начался здесь [ на кухне ] и перешел в гостиную», — сообщил пожарный.
Используйте скобки для внесения редакционных изменений
Квадратные скобки позволяют писателю или редактору исправлять ошибки в цитате, добавлять пояснительную информацию, изменять цитату, чтобы она соответствовала предложению, или выделять слово жирным шрифтом или курсивом.
- «Мы принимаем средства ненасилия , потому что наша цель — сообщество в мире с самим собой [ курсив добавлен ] ». —Мартин Лютер Кинг-младший
- «Это один маленький шаг для человека, но гигантский скачок для человечество [ ударение наше ]
Используйте скобки внутри круглых скобок
Когда вы ссылаетесь на книгу или другое письменное произведение, добавляйте дату публикации в скобках, особенно если у книги более одного издания.

- Она сослалась на свою старую книгу ( Большая книга [ 1976 ] ) в своей новой книге.
- В новой книге Гэри об образовании ( Running Your Classroom [ 2019 ] ), он обсуждает лучший подход к управлению классом в мире, богатом технологиями.
Используйте скобки для отображения ошибок в кавычках
Иногда кавычки содержат орфографические и грамматические ошибки. Они могут свести с ума редакторов, но поскольку вы не можете изменить цитируемый текст, эти ошибки должны остаться.
Редакторы и писатели часто используют латинское слово sic (означающее «так» или «таким образом»), чтобы указать, что ошибка была частью исходной цитаты, и они не допустили ошибки, переформулировав ее. Sic обычно выделяется курсивом и появляется в квадратных скобках сразу после ошибки.
- «Китай украл исследовательский беспилотник ВМС США в международных водах в результате беспрецедентного акта [ sic ] ».

- «Я всегда знал, что тоже попаду [ sic ] в высшую лигу», — написал новый питчер в социальных сетях.
Используйте скобки в переводах
Когда вы цитируете другой язык, добавьте английский перевод в скобках.
- Джен наняла Мела для съемок фильма, заявив: «У этой женщины только что было определенное je ne sais quoi
- Мой отец всегда говорил: «Finché c’è vita c’è speranza [ Пока есть жизнь, есть надежда ] ».
Другие типы скобок
Существует несколько различных типов символов, которые технически можно считать скобками. Каждая пара оценок имеет свои правила академического использования .
Скобки или круглые скобки ( )
Чаще всего в английском языке используются круглые скобки. Эти круглые скобки добавляют к предложению дополнительную (обычно несущественную ) информацию или ссылаются на источники.

- Джордж Вашингтон (первый президент США) произнес прощальную речь в 1796 году.
- Национальное управление по аэронавтике и исследованию космического пространства (НАСА) запустило свой первый марсианский зонд (Viking I) еще в 1976 году.
- Представления задач могут иногда различаться между учеником и инструктором (Цветок, 19 лет).94) и даже от новичка к более опытному ученику.
Угловые скобки
Угловые скобки, также известные как шевроны , в современном письме встречаются редко. Наиболее распространенное использование угловых скобок за пределами компьютерного программирования для выделения URL-адресов в тексте или работах, цитируемых страницах .
Фишман, Стивен М. и Люсиль Паркинсон Маккарти. Джон Дьюи и задача школьной практики . Серия исследований практиков. Нью-Йорк Урбана, Иллинойс: Издательство педагогического колледжа, Национальный совет учителей английского языка, 19.
 98. < https://searchworks.stanford.edu/view/3885600 >
98. < https://searchworks.stanford.edu/view/3885600 >Скобки или фигурные скобки { }
Скобки или фигурные скобки в основном используются в математике, компьютерном программировании или музыке. Исключением было бы, если бы писатель хотел создать список элементов, все из которых являются равными. В противном случае этот знак препинания не использовался бы в академическом письме.
Как насчет скобок в математике?
Скобки также появляются в математических уравнениях , где они работают так же, как и при письме — скобки группируют части уравнения и отделяют их от других частей. Но в отличие от использования грамматики, где скобки помещаются внутри круглых скобок, использование математики помещает скобки снаружи, а круглые скобки внутри.
- [(9 + 7) — (3 х 2) х 3] х 5
- 103 — [(8 х 9) — (4 х 2)] х 2
Фигурные скобки также чаще встречаются в математике, чем в грамматике, поскольку они указывают на то, что числа находятся в наборе.
(Например: {1,3,5,7,11} — простые числа)
Советы по использованию скобок вместо скобок
Все еще нужна помощь при выборе скобок и скобок? Задайте себе эти вопросы, прежде чем выбирать округлые или квадратные знаки препинания.
- Добавляет ли рассказчик или говорящий дополнительную информацию? Используйте скобки.
- Добавляет ли редактор или репортер дополнительную информацию? Используйте скобки.
- Не могли бы вы удалить информацию, и предложение по-прежнему имеет смысл? Используйте скобки.
- Есть ли в тексте цитата? Используйте скобки (если вы не цитируете цитату).
- У вас уже есть скобки? Используйте скобки внутри.
Решение сбалансированных скобок в Javascript со стеками | by noam sauer-utley
Какова цель алгоритма Balanced Brackets?
«По заданной строке, содержащей скобки, определите, все ли скобки имеют соответствующий аналог. Если все скобки в строке образуют сбалансированные пары, вернуть true.

Примечание : я использую слово « скобки ”в данном случае для обозначения круглых скобок, фигурных скобок, квадратных скобок и угловых скобок (‘), {, [ <, >, ], }, )’). Не каждое испытание может потребовать от вас включения всех четырех типов!
Когда я впервые столкнулся с этой проблемой, моим первым побуждением было попытаться просто отсортировать строку на подстроки в зависимости от того, является ли каждый символ открывающей или закрывающей скобкой, и сравнить длины подстрок.
Такой подход может сработать для случайной простой строки, но он довольно быстро выйдет из строя. Нам нужно знать не только то, что для каждой открывающей скобки есть закрывающая скобка, но и то, что определенный тип открывающей и закрывающей скобки соответствует друг другу. Мало того, если бы мы хотели, чтобы эта функция была полезна для любого вида подсветки синтаксиса IDE или другого практического применения, она должна была бы идентифицировать не только то, что открывающие и закрывающие скобки существуют в правильном количестве и типе, но также и то, что они расположены в правильном порядке — что каждая открывающая скобка имеет соответствующую закрывающую скобку в правильном месте в строке, чтобы фактически закрыть ее.

Вот что имеется в виду, когда говорят, что скобки «сбалансированы» — они не только существуют в правильном количестве совпадающих пар, но и что эти пары расположены правильно, так что закрывающие скобки могут уравновешивать открывающие скобки.
Моя первоначальная идея сортировки строки на подстроки и сравнения длин подстрок явно не срабатывала на нескольких интервалах задачи.
Мне нужен был другой подход.
Инструментом, который я в итоге использовал для решения этого алгоритма, была структура данных, которую я раньше не использовал.
Ранее я уже писал о преимуществах использования хеш-таблиц и рекурсивных деревьев для разделения сложных задач. Я знаю, что структуры данных могут стать замечательными инструментами для деконструкции проблем, требующих алгоритмических решений.
Но прежде чем заняться этой конкретной проблемой, я нечасто сталкивался со стеками¹.
В Javascript мне нравится думать о них как о массиве с некоторыми ограничительными правилами.

Обычно с массивами в Javascript можно манипулировать самыми разными способами. Вот что делает их такими удобными. Вот почему я начинаю большинство алгоритмических решений с создания пустого массива. Нам почти всегда он нужен в качестве среды для управления или организации наших данных.
Стеки в Javascript используются только при работе с массивом с использованием методов push и pop . Эти методы будут помещать новый элемент на вершину стека или извлекать его из вершины соответственно.
В то время как к элементам обычного массива можно обращаться с любого направления (не сдвигая его с переднего края, смещая на задний план, нарезая прямо в середину или из середины или просто редактируя на месте), я думаю о стеке как о массив, который был полностью запечатан, так что он недоступен, кроме одной двери. Новые вещи могут быть протолкнуты через дверь, но тогда только самая последняя добавленная вещь, та, что находится прямо перед дверью, может быть доступна или каким-либо образом манипулирована.
 Если этот элемент удалить с помощью array.pop() , тогда элемент позади него теперь доступен для изменения или удаления. Однако, если его не удалить, а вместо этого вставить через дверь новый элемент, ранее доступный элемент снова становится недоступным.
Если этот элемент удалить с помощью array.pop() , тогда элемент позади него теперь доступен для изменения или удаления. Однако, если его не удалить, а вместо этого вставить через дверь новый элемент, ранее доступный элемент снова становится недоступным.Этот подход называется FILO, или First In Last Out .
(Эта аббревиатура может быть знакома всем, кто работал на кухнях или рядом с ними, которые неизбежно подчиняются родственному, но противоположному закону 9.0038 FIFO или First In First Out в попытке избежать пищевых отходов и порчи.)
Почему мы намеренно ограничиваем наши прекрасные универсальные массивы?
Ну, этот процесс сохраняет определенный порядок — элементы могут быть удалены только в том порядке, в котором они были первоначально добавлены, сохраняя первоначальный порядок или шаблон.
Именно это нам и нужно сделать с нашими скобками — определить не только количество и тип скобок, включенных в нашу строку, но и их определенный порядок.

Итак, мы знаем, что стеки позволяют вам манипулировать данными внутри массива, сохраняя при этом исходные упорядоченные шаблоны данных, что похоже на то, что нам нужно сделать. Давайте приступим к использованию этого инструмента в алгоритмическом решении нашей задачи.
Итак, немного псевдокода для начала:
Я знаю, что используя стек , я могу сохранить запись порядка моих скобок, что позволит мне проверить, правильно ли они сбалансированы (все открывающая и закрывающая скобки совпадают, и они расположены в правильном порядке, чтобы уравновесить друг друга) или нет.
Сначала я создам для себя несколько рабочих переменных.
Я сохраняю строку со списком всех моих потенциальных открывающих и закрывающих скобок в переменную с именем скобки .
Примечание : в этой строке открывающая и закрывающая скобки объединены вместе.
Это важно.

Мое конкретное решение не сработало бы , если бы строка скобок была записана как «9».0038 [{(<]})> », например.
Скобки могут быть в любом порядке по типу (например, « ()[]{}<> » и « <>(){}[] 90 оба являются отлично), но открывающая и закрывающая скобки должны быть записаны вместе .
Следующая переменная, которую я создаю, это просто пустой массив, который мы можем назвать stack , так как это будет наш стек.
Я набросал начальный цикл через нашу входную строку, заполненную на данный момент только псевдокодом.
Примечание : этот цикл перебирает элементы ввода, а не индексы. Лично мне нравится использовать for…in / for…of циклов , но вы всегда можете использовать более традиционный цикл for (например, « for (пусть i = 0; i < input.
 length, i++) ») и по-прежнему используйте это решение с небольшими изменениями, если хотите.
length, i++) ») и по-прежнему используйте это решение с небольшими изменениями, если хотите. Единственная оставшаяся работа нашей функции будет заключаться в том, чтобы возвращать true или false после разрешения цикла.
Пришло время разработать наш стек и применить его!
Во-первых, еще одна рабочая переменная в самом цикле:
скобкиIndex : я хочу убедиться, что роль этой переменной совершенно ясна, прежде чем двигаться дальше!
Мы перебираем input , строку скобок, которая передается в функцию для тестирования.
скобкиИндекс НЕ является индексом во вводе текущей скобки .
скобкиIndex ищет индекс текущей скобки в ранее сохраненных скобках 0030 переменная. So if the first bracket in input were a “ ( “, its bracketsIndex would be 4 .
 Its index in input is, of Курс, 0 , но Индекс из « (» в Кроншеты IS 4 , так что его BracketsIndex — 4 .0005
Its index in input is, of Курс, 0 , но Индекс из « (» в Кроншеты IS 4 , так что его BracketsIndex — 4 .0005Помните немного о том, как важен порядок скобок в строке скобок? Мы приближаемся.
Итак, теперь у нас есть переменная скобкиIndex , которая может искать нашу текущую скобку в переменной скобки .
Теперь мы наконец можем приступить к работе с нашим стеком.
Из-за того, как мы организовали нашу ссылочную строку скобок , мы знаем, что открывающие скобки имеют четные индексы (0, 2, 4 и 6), а закрывающие скобки имеют нечетные индексы (1, 3, 5, 7) .
Итак, если наша текущая скобка Индекс четна, мы знаем, что текущая скобка является открывающей скобкой.

Мы можем проверить это с помощью оператора по модулю. Операции по модулю, вызываемые в Javascript оператором по модулю , то есть « % » (обычно называемым знаком процента), делят первое число на второе число, а затем возвращают остаток. Таким образом, один из способов проверить четные или нечетные числа — запустить число % 2 === 0, Два будет делиться без остатка на четное число, давая в остатке ноль (возвращая истину), но не на нечетное число (возвращая ложь).
Затем мы можем поместить в стек позицию в скобках нужной закрывающей скобки, найдя скобку с индексом скобокIndex + 1. Опять же, из-за того, как мы написали наши скобки , за открывающей скобкой всегда будет следовать соответствующая закрывающая скобка. Благодаря этому мы можем увеличить скобкиIndex любой открывающей скобки, чтобы найти адрес закрывающей скобки.

Теперь, когда мы повторяем входные данные, наш стек будет хранить записи о закрывающих скобках, необходимых для балансировки входной строки.
Примечание : скобкиIndex , целое число, это то, что помещается в стек, а не сама закрывающая скобка.
Пример: If our loop had iterated through the elements “ (, <, [“ , the stack would hold the indexes in brackets of “ ) , >, ] ” и таким образом будет [5, 7, 1] .
Наш цикл будет продолжать выполнять эту задачу до тех пор, пока мы будем сталкиваться с открывающими скобками.
Круто. Что происходит, когда мы сталкиваемся с закрывающей скобкой?
Если текущая скобка входной скобки является закрывающей скобкой и, следовательно, имеет нечетный индекс, то (из-за нашего условного выражения, которое выполняется на основе проверки четности/нечетности скобок , индекс ), будет запущена новая задача.

Array.pop() удаляет самое последнее добавление из нашего стека, изменяя длину массива, и возвращает этот удаленный элемент, позволяя нам ссылаться на этот элемент, если это необходимо.
Итак, если текущая скобка закрывается, мы извлечем из стека последний элемент и сравним их. Если наши кронштейны сбалансированы, они должны совпадать.
В этом вся цель использования стека — когда мы перебираем нашу входную строку, необходимая закрывающая скобка помещается в стек для каждой открывающей скобки, а затем выталкивается, когда достигается соответствующая закрывающая скобка. Если что-то в стеке нарушает этот шаблон, мы знаем, что наша входная строка не сбалансирована.
Example: If our loop had iterated through the elements “ (, <, [“ , the stack would hold the indexes in brackets of “ ) , >, ] ” и таким образом будет [5, 7, 1] .

Если следующая итерация натолкнется на элемент « ] », то наше выражение будет проверять stack.pop() (i.e. 1 ) against the bracketIndex of the current bracket (the current bracket being ] would have a скобкаIndex из 1 ) и, поскольку они действительно равны, вернет true, что позволит перейти к следующему элементу в input . stack going forward would be [5, 7] , as the execution of stack.pop() permanently removed 1 from the stack множество.
Нам нужно проверить еще одну вещь — когда этот цикл разрешится, стек должен быть пуст.
 Если это не так, это означает, что осталась лишняя несбалансированная скоба или больше.
Если это не так, это означает, что осталась лишняя несбалансированная скоба или больше.Итак, я проверяю, что стек имеет нулевую длину в конечном логическом возврате. Выражение stack.length === 0 вернет нужное нам логическое значение.
Если весь цикл выполняется без возврата false и при его разрешении стек пуст, мы знаем, что наша входная строка сбалансирована, и функция должна возвращать true. В противном случае наша функция должна вернуть false.
Запустим эту функцию в консоль и посмотрим, что у нас получится!
Отлично! 🌟 Я протестировал isBalanced() работает с различными сбалансированными и несбалансированными строками² и возвращает правильное логическое значение для каждой из них! В отличие от моей первой идеи, эта функция может успешно проверять не только правильное количество и типы скобок, но и проверять их определенный порядок, чтобы убедиться, что они совпадают.
Я все еще хочу добавить в нашу функцию еще один элемент функциональности.
 На данный момент, если ввод содержит что-то кроме чистых скобок, наша функция сломается. Это не сильно нам поможет, если мы действительно хотим создать собственную подсветку синтаксических скобок или другое практическое применение нашей функции. Итак, мы можем добавить еще одно условие в наш цикл.
На данный момент, если ввод содержит что-то кроме чистых скобок, наша функция сломается. Это не сильно нам поможет, если мы действительно хотим создать собственную подсветку синтаксических скобок или другое практическое применение нашей функции. Итак, мы можем добавить еще одно условие в наш цикл.Если текущий элемент не находится в квадратных скобках (что дает индекс -1), мы просто направляем наш цикл на переход к следующему символу в нашей входной строке. Одно это изменение делает нашу функцию намного более адаптивной!
Этот вызов алгоритма заставил меня по-настоящему оценить использование стека, хотя в моем предыдущем опыте этой конкретной структурой данных пренебрегали. Есть и другие способы решить эту проблему, но многие из них включают в себя написание большого количества повторяющегося кода для проверки каждого отдельного типа скобок, что дало мне много возможностей сделать опечатки и заскучать.
Если вам трудно визуализировать работу стека, я рекомендую добавить в этот код несколько отладчиков или console.

- Мужчина заявил, что «никогда не хочет их видеть» [ его соседи ] еще раз».

 Независимо от того, добавляете ли вы контекст к цитате, смещаете текст в скобках или переводите цитату на другой язык, скобки добавляют ясности вашему письму.
Независимо от того, добавляете ли вы контекст к цитате, смещаете текст в скобках или переводите цитату на другой язык, скобки добавляют ясности вашему письму.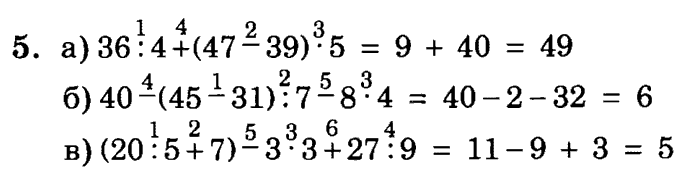 15).
15).







 Если этот элемент удалить с помощью array.pop() , тогда элемент позади него теперь доступен для изменения или удаления. Однако, если его не удалить, а вместо этого вставить через дверь новый элемент, ранее доступный элемент снова становится недоступным.
Если этот элемент удалить с помощью array.pop() , тогда элемент позади него теперь доступен для изменения или удаления. Однако, если его не удалить, а вместо этого вставить через дверь новый элемент, ранее доступный элемент снова становится недоступным.

 length, i++) ») и по-прежнему используйте это решение с небольшими изменениями, если хотите.
length, i++) ») и по-прежнему используйте это решение с небольшими изменениями, если хотите.  Its index in input is, of Курс, 0 , но Индекс из « (» в Кроншеты IS 4 , так что его BracketsIndex — 4 .0005
Its index in input is, of Курс, 0 , но Индекс из « (» в Кроншеты IS 4 , так что его BracketsIndex — 4 .0005


 Если это не так, это означает, что осталась лишняя несбалансированная скоба или больше.
Если это не так, это означает, что осталась лишняя несбалансированная скоба или больше. На данный момент, если ввод содержит что-то кроме чистых скобок, наша функция сломается. Это не сильно нам поможет, если мы действительно хотим создать собственную подсветку синтаксических скобок или другое практическое применение нашей функции. Итак, мы можем добавить еще одно условие в наш цикл.
На данный момент, если ввод содержит что-то кроме чистых скобок, наша функция сломается. Это не сильно нам поможет, если мы действительно хотим создать собственную подсветку синтаксических скобок или другое практическое применение нашей функции. Итак, мы можем добавить еще одно условие в наш цикл.