функторов — от теории категорий к кошкам | by Krzysztof Grajek
Franck Mahon (модифицированный) @ Flickr.com CC 2.0 Сегодня мы собираемся разобрать Functor как еще одну концепцию теории категорий, широко используемую в функциональном программировании. Идея Functor кажется тривиальной, и многие люди, когда их спрашивают, что это такое, быстро отвечают, что это «что-то, на что можно нанести карту» — это правда, но стоит знать полную картину, что на самом деле отображается и как. Здесь на помощь приходит теория категорий (и, конечно, Бартош Милевски).
Я еще раз очень рекомендую серию видеороликов Бартоша Милевски о теории категорий для программистов на YouTube, а также серию его постов в блоге об этих концепциях.
Что такое функтор
С математической точки зрения, функтор представляет собой очень простую идею — это отображение объектов из одной категории в другую категорию. Это предложение очень напоминает идею «нечто, на что можно нанести карту», повторяющуюся снова и снова в мире программирования. Но на этом история не заканчивается.
Но на этом история не заканчивается.
Мы знаем, что Категория — это объекты и морфизмы (стрелки), мы также знаем, что Категория связана с композицией и идентичностью, а структура Категории определяется через композицию. Functor позволяет нам отображать категории и сохранять структуру. Чтобы сохранить структуру, нам нужно отображать не только объекты, но и морфизмы. Другими словами, мы можем думать о функторе как о наборе функций, отображающих набор стрелок из одной категории в набор стрелок из другой.
Функтор — это тип отображения объектов и морфизмов, который сохраняет композицию и идентичность.
У нас есть две категории: A и B . В категории A у нас есть два объекта a и b с морфизмом f . Наш функтор представляет собой отображение объектов a и b в Fa и Fb и отображение морфизмов, в данном случае одиночного морфизма: f в Ff .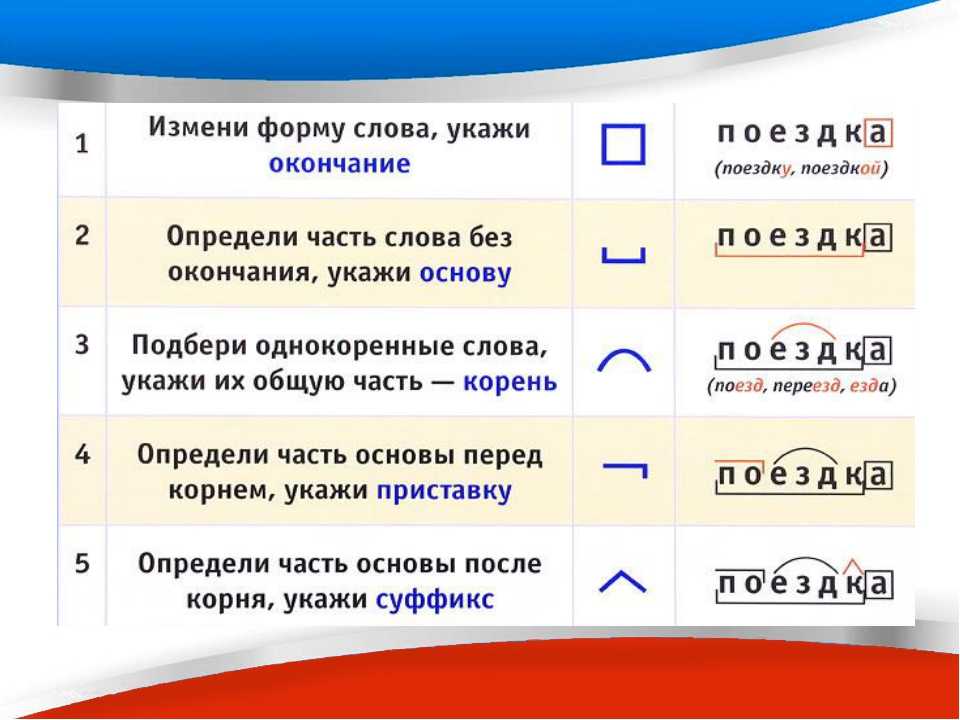
Продолжая структуру категории, если вы можете скомпоновать два морфизма в одной категории, вы можете скомпоновать их в другой при использовании функтора:
У нас есть морфизм в Категории A между a и c ( f · g ), который является композицией морфизмов f и g , и в нашей Категории B мы отобразили B объекты и морфизмы соответственно с Функтором, так что
F(g · f) = Fg · Ff
Еще одно требование к нашему Функтору — сохранять идентичность. В категории A мы знаем, что id a = a , поэтому наша сопоставленная версия должна выглядеть следующим образом:
Fid a = Fa или на самом деле F(id(a)) , но мы можем сократить его до Fa
Хорошо, это теория, а теперь давайте рассмотрим несколько примеров.
Пример
Одним из простейших случаев объяснения Functor является что-то вроде Scala Option .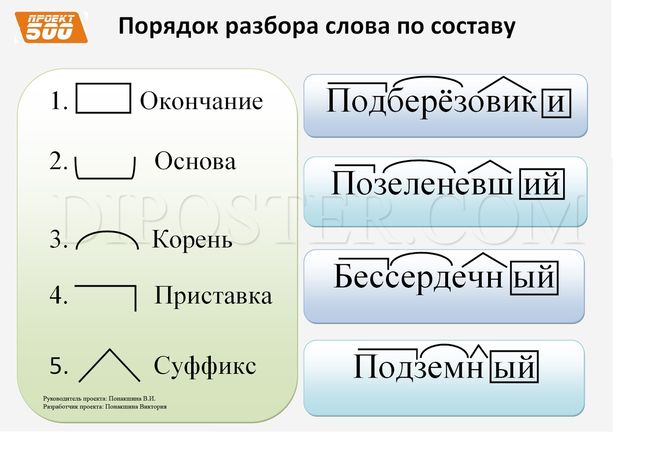 Допустим, мы хотим сопоставить объект типа
Допустим, мы хотим сопоставить объект типа A с объектом типа Option[A]
Оставаясь немного дольше в режиме теории категорий, но с примером Option, допустим, что у нас есть некоторые объекты и морфизм объектов в одной категории, и мы хотим сопоставить их с другой категорией с помощью функтора.
В приведенном выше примере мы сопоставляем объект a с Option[a] и объект b с Option[b] , мы также сопоставляем морфизм f с функцией fmap . Имя fmap используется здесь намеренно, так как мы все знаем, что реальный Scala's Option не имеет доступной функции fmap (если только не используется с классом типов cat неявного Functor, но мы скоро вернемся к этому)
Когда отображение конкретного объекта с помощью Опция у нас может быть два возможных значения: Some или None . Таким образом, нашему Functor должен выполнить следующее:
Картирование Нет :
Картирование Некоторые (.: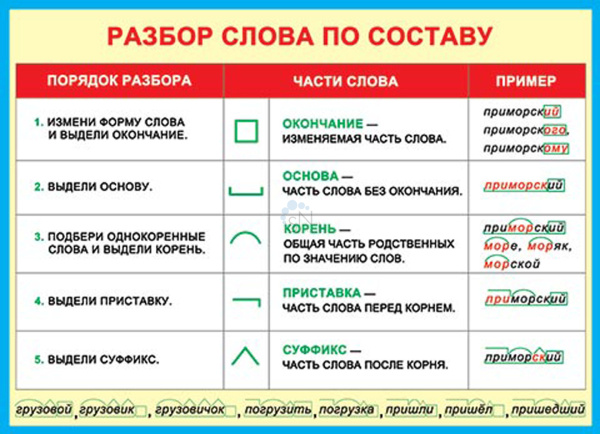 .)
.)
Картирование Морфизм F :
Состав презентации:
ПРЕДОСТАВЛЕНИЯ:
. Как видите, наш функтор представляет собой набор функций, отображающих объекты и морфизмы из одной категории в другую. Случай, когда мы отображаем весь морфизм f между объектами a и b называется подъемом , как вы вскоре увидите в разделе Cats Functor ниже.
В Scala наш fmap из приведенных выше определений хотел бы функцию двух аргументов, первый из которых является функцией, которую мы хотим применить, а второй — экземпляром Functor (Option, List и т. д.). Это, конечно, не работает так в Scala. В Scala по соглашению map() вызывается для экземпляра класса и принимает только один аргумент — функцию, которую мы хотим применить, принципы остаются прежними.
Если мы подумаем о примерах Functor , мы знаем, что Functor — это то, что может воздействовать на типы, как наш ранее упомянутый Option[A] или List[A] , поэтому за исключением того, что Functor является ` набор функций», мы также можем думать о Functor как о конструкторе типов, который поддерживает fmap операций, или, кроме того, мы также можем думать о Functor как о контейнере.
Важное примечание: не путайте слова fmap используется здесь с Scala flatMap . Имя fmap здесь заимствовано из Haskell и речь идет о отображении, как map в Scala, а не о отображении и сглаживании результата, как
3 flat Map.
Cats Functor
Среди множества классов типов, доступных в Cats для различных понятий, заимствованных из теории категорий, у нас также есть Functor.
Functor— это класс типов, который абстрагируется от конструкторов типов, которые могут быть преобразованы. Примерами таких конструкторов типов являютсяList,OptionиFuture.
Как вы можете видеть ниже, Functor map выглядит как классическая функция map , а lift поднимет вызов функции до эквивалента Functor (сопоставление морфизмов упоминалось ранее):
Для всех любителей теории категорий есть также реализация fmap:
, как вы можете видеть, имеет ту же сигнатуру, что и наша старая добрая функция map .
Примеры использования
Возможно, большинство из нас привыкло к функции Functor map для работы с эффектами. Например, мы можем сопоставить Future , чтобы применить некоторую чистую функцию к значению, обернутому в наш эффект (Future), без необходимости разворачивать и оборачивать значение обратно в эффективную оболочку. Другими словами, мы работаем со значением, не выходя из контекста эффекта. Это очень полезно, но мы можем получить еще больше от простого 9.0003 Концепция Functor .
Составление с вложенными типами данных
Самый распространенный пример для Functor , который вы, возможно, увидите, касается сопоставления вложенных типов данных. При обычном подходе Scala вам нужно будет использовать map внутри других вызовов map для выполнения некоторой чистой функции над значением, вложенным глубоко внутри такой структуры, например:
Принимая во внимание, что с Functor
Option и Список с cats. implicits._
implicits._ вы можете сделать следующее: или с Nested Functor обертка:
Это становится еще более полезным, когда структура, которую мы хотим использовать, более сложная:
С цепочка из состоит из вызовов и Functor неявных , предусмотренных для List и Option , мы можем выполнять функции на глубоко вложенных структурах.
Если Функтор неявный недоступен для нашей структуры, мы можем создать свой собственный:
Нет Functor доступного для Карта , поэтому с помощью простого трюка типа мы можем создать его для себя и составить его, чтобы иметь Functor , который мы можем использовать для нашего сложного контейнера .
Как видите, мы можем использовать функторов , доступных для вас через экземпляров cat.* , создать функторов для существующих типов контейнеров в Scala, а также объединить их для работы с более сложными структурами.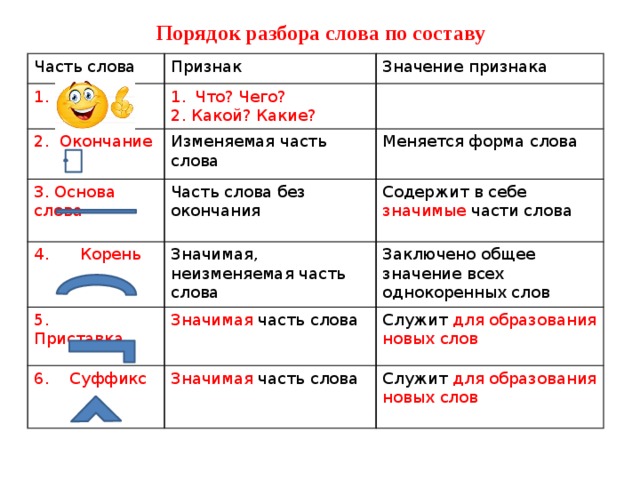
 implicits._
implicits._