Состав числа 6, 7, 8, 9: урок математики в 1 классе
Цели и задачи урока:
Совершенствовать навыки табличного сложения.
Закрепить умения решать задачи.
Развивать речь, память, внимание, логическое мышление, математические способности.
Воспитывать гуманное отношение друг к другу, умению выслушивать мнения каждого.
УУД
Регулятивные: определяют план выполнения задания, применяют изученные способы действия для решения задач в различных ситуациях.
Познавательные: перерабатывают полученную информацию: сравнивают и группируют математические объекты: числа, числовые выражения, равенства и неравенства.
Коммуникативные: решают совместно с соседом по парте поставленную задачу, обдумывают, обмениваются своими мнениями.
Личностные: осваивают роль «хорошего» ученика, регулируют своё поведение на основе усвоенных норм и правил.
Формы работы: индивидуальная, самостоятельная, фронтальная.
ХОД УРОКА
Организационный момент
Цель ‒ настроить учащихся для плодотворной работы на уроке, организовать внимание учащихся.
Вход под весёлую музыку…
А ну-ка, дети, встаньте в ряд!
Готов к работе мой отряд?
Занимай свои места.
Математика сложна.
Но скажу с почтеньем
Математика нужна
Всем без исключения!
— Прежде чем начать, урок создадим себе и друг другу хорошее настроение. А хорошее настроение начинается с улыбки. Улыбнёмся друг другу. Думаю, что сегодняшний день принесёт нам радость и удачу.
— Назовите тему сегодняшнего урока.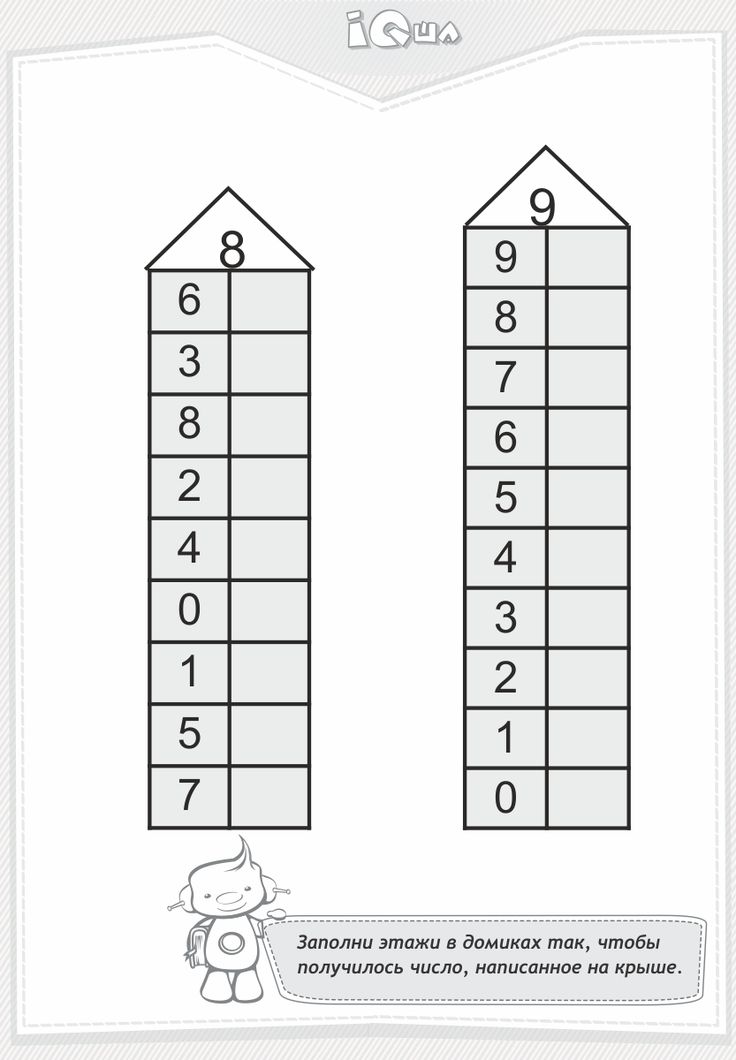 (Состав числа 6, 7, 8, 9)
(Состав числа 6, 7, 8, 9)
— Скажите, чему мы будем сегодня учиться? (Решать учебные задачи. Повторять составы изученных чисел.)
— Вам предстоит проявить свою находчивость, показать свои успехи в нашей теме, для того, чтобы в будущем уметь решать более сложные задачи и математические выражения.
— Ребята, отгадайте загадку.
Ветви белой краской разукрашу,
Брошу серебро на крышу вашу.
Тёплые весной придут ветра
И меня прогонят со двора.
Что это? (Зима)
— Сегодня 12-й день зимы. Назовите месяц. Сегодня 12 декабря. А какое число было вчера? Какое число будет завтра? В декабре мы встречаем самый радостный праздник, назовите его.
— Вы любите новый год?
— Ребята, у меня для вас сюрприз.
— Нам пришло звуковое письмо из города Великий Устюг (на слайде Родина Деда Мороза).
Послушайте его.
(Голос на магнитофоне)
«Дорогие ребята! Это пишу вам я, Дед Мороз. Прежде чем отправиться к вам в путь, я решил узнать, какие у вас успехи в учебе? Шлю вам мой морозный привет. До скорой встречи на новогоднем представлении! Ваш Дед Мороз.»
— Ребята, давайте покажем, что у нас отличные успехи…
— А поможет нам в работе …. Угадайте, кто это? (Загадка о снеговике)
Мы слепили снежный ком,Шляпу сделали на нем,
Нос приделали и в миг Получился... Въезжает снеговик.
Актуализация знаний
Работа с натуральным рядом чисел.
Сегодня посланец Деда Мороза Снеговик предлагает математические задания.
Первое ‒ Поработать с числами.
— Ой, а где же наши числа, наверное их раздул по классу зимний ветер. Давайте соберём их. (По классу развешаны карточки с цифрами 5, 2, 8, 3, и др.) Дети собирают цифры и крепят на доску.
Давайте соберём их. (По классу развешаны карточки с цифрами 5, 2, 8, 3, и др.) Дети собирают цифры и крепят на доску.
— Запишите числа в порядке возрастания.
Работа в тетради (Я тетрадочку открою…) Правила посадки!
Там, где точка через клетку.
Постановка проблемы.
— Давайте придумаем ещё задания с этими числами.
— Предлагаю сравнить числа.
— Клетку от написанного вниз запись сравнения, запись двух неравенств.
— Как вы думаете, используя только эти числа, можно ли составить числовые выражения?
— Запись в тетрадях. (2 выражения) Состав каких чисел повторили?
Снеговик доволен вашей работой. Предлагает отдохнуть.
Физминутка для глаз
Внимание! Послушайте загадку:
Колкую, зелёную
Срубили топором.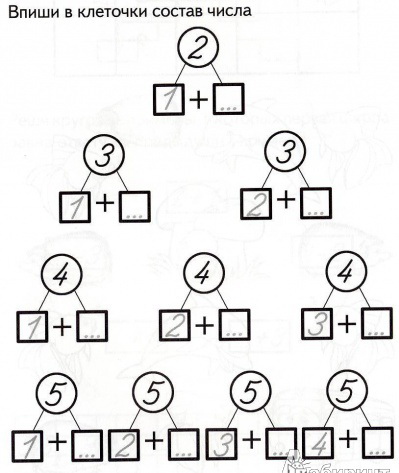
Красивую, зелёную
Принесли к нам в дом.
— Что же принесли в дом? (ёлку)
На слайдах природа зимнего леса.
Каждая ёлочка мечтает оказаться в праздничном зале.
Постановка учебной задачи на слайде «Наряди ёлочку».
А вот и наша гостья. Снеговик предлагает выполнить следующую учебную задачу. Нарядить ёлочку шарами. Но не всё так просто.
— Давайте исследуем, какие шары можно повесить на нашу зелёную красавицу. А для этого нам понадобятся наши знания. Ведь шары можно вешать только … зная состав чисел.
Игра «Наряди ёлочку»
Вывод…
(Молодцы, мы со Снеговиком довольны, как вы справились с заданием. Ребята, мы со Снеговиком увидели, что ещё не все ребята дают правильные ответы, некоторые путаются, но это не беда, потому что на следующих уроках мы продолжим совершенствовать свои знания.
— Пока мы наряжали ёлочку, нам пришло по электронной почте письмо из Великого Устюга от Деда Мороза. (на слайде электронное письмо)
— Давайте прочитаем его содержание.
— Что нам предстоит выполнить? (решить логическую задачу)
Решение логической задачи.
На уроке технологии Миша вырезал несколько снежинок, а Маша столько же. Теперь у ребят 8 снежинок. Сколько вырезал каждый? (на слайде)
— Молодцы. Состав какого числа мы повторили?
Физпауза
Работа по учебнику.
— Напомните, мне чему мы учимся? (Повторяем составы изученных чисел)
— Новый год ‒ это праздник волшебства. Я предлагаю вам оказаться в роли волшебников. Откройте учебники на стр. 107, № 256 (1 столбик).
— Математические выражения заколдованы.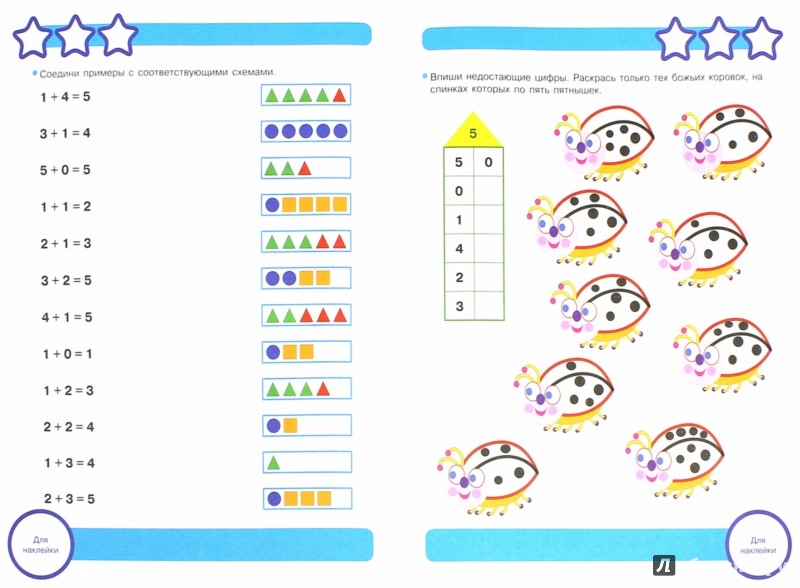 Подумайте, какую работу предстоит выполнить? (вычислить) Для работы понадобится веер.
Подумайте, какую работу предстоит выполнить? (вычислить) Для работы понадобится веер.
Молодцы!
Работа с геометрическим материалом.
— У вас в пакетиках геометрические фигуры. Достаньте их.
— Назовите фигуры. (Треугольник, круги, четырёхугольники.) Снеговик предлагает провести эксперимент.
— «Кто самый внимательный?» Он просит из данных фигур выполнить портрет его друга. (на слайде снеговик из фигур) Даётся 15 сек.
Проверка.
— Какая фигура оказалась лишней?
— Молодцы! (убрали фигуры)
— Вы были внимательными. Такое задание тренирует вашу память, развивает мыслительную деятельность. Я довольна, что все справились с заданием.
Самостоятельная работа
— Наш Снеговик взял с собой волшебный сундучок. Что же в нём? Снежки. Не простые, а с заданиями. Подумайте, какую работу предстоит выполнить? (Вставить числа, что бы равенства были верные)
Не простые, а с заданиями. Подумайте, какую работу предстоит выполнить? (Вставить числа, что бы равенства были верные)
Проверка на слайде с правильными ответами.
— Давайте оценим свой успех по шкале правильности. У кого всё правильно?
— Ставим х возле верхней планки.
— Если 1-2 ошибки ‒ х посередине.
— Если больше 2 ошибок ‒ х внизу.
(Молодцы, я довольна вашими результатами.)
(Ничего страшного, на следующих урокам мы продолжим работу и у вас всё получится)
— Все задания на сегодняшнем уроке направлены на поверку знаний состава чисел. Без них мы бы не смогли выполнить одно из сложных заданий урока. Вы готовы с ним справиться?
Мультимедийная игра «Кроссворд»
Итог Молодцы! Приятно работать с такими замечательными детьми!
Рефлексия
Предлагаю оценить свою работу смайликами.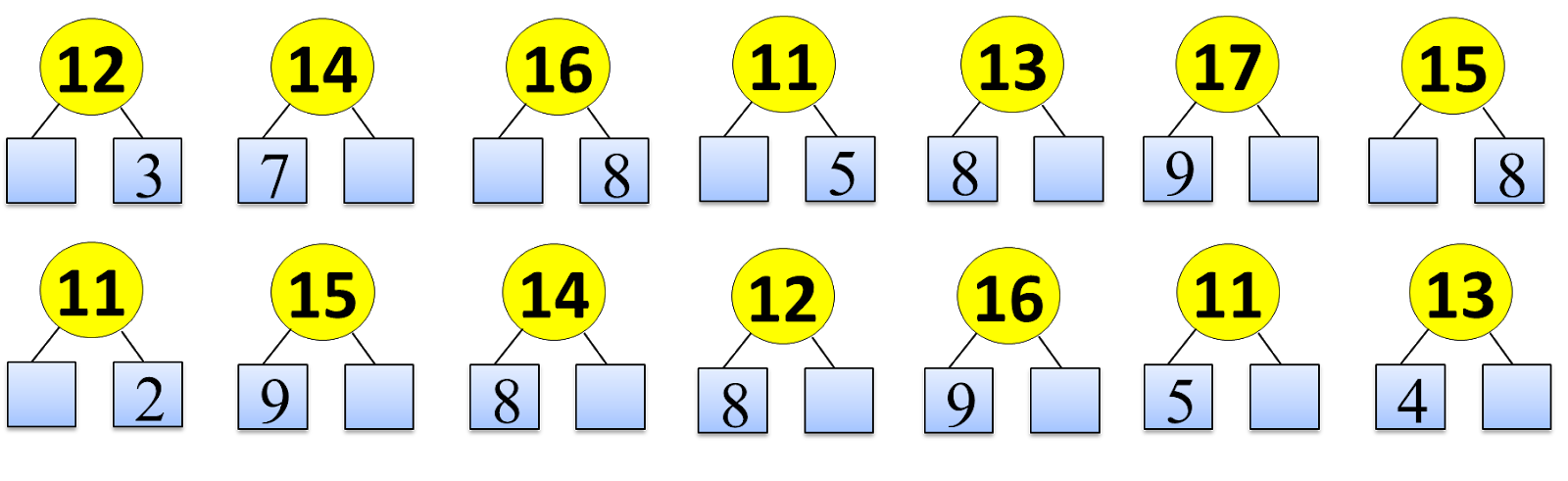
— Очень понравилось, всё понял.
— Буду внимательным, есть трудности.
— Что-то огорчило, не понял.
– Снеговик благодарит всех за работу! И Деду Морозу обязательно доложит о наших успехах!
– Спасибо за урок!
Деятельность учителя | Деятельность обучающихся | |
I. Огранизацион- ный момент. | -Здравствуйте, ребята! Сейчас у нас урок математики. Проверьте своё рабочее место, всё ли у вас готово к уроку. | |
II. Постановка учебной задачи. | -На уроке мы повторим состав чисел 11, 12, 13, а также соответствующие случаи вычитания. -Кто готов внимательно слушать-улыбнитесь. Кто готов активно работать-хлопните один раз в ладоши (слайд 2). | |
III. Минутка красивого письма. | -Итак, открываем тетради, записываем дату и классная работа. Мы начинаем урок с минутки красивого письма. Посмотрите на доску, назовите числа (слайд 3). -Какое число «лишнее»? Почему? Зачеркните его. -Запишите остальные числа в порядке возрастания. Что это значит? -Проверьте запись у соседа по парте. У кого встретились ошибки? -Состав каких чисел мы ещё с вами не изучали? -Представьте эти числа в виде суммы разрядных слагаемых. -Состав каких чисел мы уже знаем? -Давайте вспомним, почему числа называются так. -Как они образовались? (слайд 4). | 11, 16, 3, 12, 13, 18 -«Лишнее» число 3, так как оно однозначное, а все остальные двузначные. -Записать числа в порядке возрастания-это значит от маленького числа до большого. 11, 12, 13, 16, 18 16, 18 16=10+6, 18=10+8 11, 12, 13 -Слог «дцать» обозначает десяток. Если мы на десяток поставим 1 единицу, то получим один-на-дцать, 2 единицы: две-на-дцать, 3 единицы: три-на-дцать. |
IV. Устный счёт. | -Для закрепления состава этих чисел поиграем в игру «Математическая рыбалка». Кто из рыбаков поймал больше всего рыбок? -Почему одна рыбка не попалась на крючок? (слайды 5,6). | Рыбак под номером 11. Значение выражения на этой рыбке равно 9. |
V. Повторение и обобщение. 1. Выполнение неравенств. | -Наши рыбаки хорошо усвоили состав чисел 11, 12, 13. Посмотрим, насколько хорошо его знаете вы. Для этого решим первый столбик неравенств из № 174 стр. 52. | 6+5=7+4 3+8 6+6 5+7 9+4 4+7 8+2 |
Физминутка | ||
2. Работа с моделями десятков и единиц. | -Молодцы! С этим заданием вы справились, посмотрим, как справитесь со следующим. Но сначала проведём подготовительную работу. -Посмотрите на доску, что вы видите? (слайд 7). -Объясните, что обозначает каждое число в записи под рисунком? -Какой способ решения записан под рисунками? -Почему в первом выражении убрали сначала 1 единицу, а во втором сначала 3 единицы? -Сколько всего единиц вычли в первом выражении? -А во втором? | -Модели десятков и единиц. 11-целое число, 1 и 3-единицы, которые вычитают. 13-целое число, 3 и 1-единицы, которые вычитают. -Способ вычитания по частям. -Убираем количество единиц до десятка, а затем оставшуюся часть. 4 4 |
3. Решение выражений способом вычитания по частям. | -Решим следующие выражения тем же способом (стр. 51 № 170 2 столбик, 1, 2, 4, 5 строка) -У кого это задание вызвало затруднение? | 11-1-2=8 12-2-1=9 13-3-1=9 13-3-4=6 |
4. Работа с моделями десятков и единиц. | -Для выполнения следующего задания нам снова понадобятся модели десятков и единиц (слайд 8). -Объясните, что обозначает каждое число в записи под рисунком? -Какой способ решения записан под рисунками? -Почему в первом выражении сначала прибавили1, а во втором сначала прибавили 4? -Сколько всего единиц прибавили в 1 выражении? -А во втором? | -К 9 единицам сначала прибавляют 1, затем 3. -К 6 единицам сначала прибавляют 4, затем ещё 4. -Сложение по частям. -Добавили до 1 десятка, а затем оставшуюся часть. 4 8 |
5. Решение задачи. | -Этот способ поможет нам решить задачу (стр. 52 № 172). Прочитайте её. -Из каких частей состоит задача? — Что известно по условию задачи? -Сформулируйте вопрос задачи. -Что осталось сделать? | -Условие, вопрос, решение, ответ. -В саду 9 яблонь, а груш на 4 меньше. -Сколько груш в саду? -Изобразить с помощью схемы условие задачи, затем её решить и записать ответ. |
На доске появляется схема условия и выражение для решения задачи. -Вернёмся к моделям десятков и единиц. Какой рисунок поможет нам решить задачу? Почему? -Решим задачу и запишем ответ. | -Первый. Число 4 разложим на 1 и 3 и выполним сложение по частям. 9+4=13 (г.) Ответ: 13 груш в саду. | |
Физминутка для глаз | Слайд 9. | |
VI. Подведение итога урока | -Подведём итог урока. Что повторяли? -Какие виды работ выполняли? -Какой вид работы ещё не выполняли? | -Состав чисел 11, 12, 13. -Складывали и вычитали по частям, работали с моделями десятков и единиц, сравнивали, решали задачу. -Самостоятельную работу. |
VII. | -Выполните работу в ТПО (стр. 27 № 63) самостоятельно, проверьте как вы усвоили состав числа 11. | Работа в ТПО, самопроверка. |
VIII. Релаксация. Оценивание работы обучающихся. | -Вам понравился урок? Оцените свою работу на уроке. -Возьмите ручку другого цвета и нарисуйте улыбку напротив того задания, которое вам больше всего понравилось. | Ответы детей. |
IX. Домашнее задание. | Слайд 10. |
Урок математики по теме «Состав числа 4». 1-й класс
Цель: создать условия для усвоения состава числа 4.
УУД
Познавательные:
- общеучебные соотношение числа 4 с количеством предметов, письмо цифры 4;
- соотнесение цифры 4 и числа 4;
- образование числа 4, определение места числа 4 в последовательности чисел от 1 до 4, сравнение, сложение и вычитание чисел в пределах 4;
Логические:
- осуществление синтеза как составление целого (число 4) из частей.

Регулятивные:
- в сотрудничестве с учителем ставить новые учебные задачи;
- принимать и сохранять учебную задачу;
- составлять план и последовательность действий, отличают верно выполненное задание от неверного
Коммуникативные:
- учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; формулировать собственное мнение и позицию;
- договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов;
- строить монологическое высказывание, владеть диалогической формой речи, умеют обмениваться мнениями в паре, слушать друг друга
Личностные:
- имеют желание учиться; осознают необходимость самосовершенствования;
- участвуют в творческом, созидательном процессе;
- осознают себя как индивидуальность, способную к самооценке своих действий.

Сценарий урока
I. Мотивация к учебной деятельностиЦель: организовать включение учащихся в образовательный процесс на основе механизма «надо» – «хочу» – «могу».
Учитель:
Встало солнышко давно,
Заглянуло к нам в окно,
На урок торопит нас –
Математика сейчас.
Ученики.
Мы рады приветствовать вас в нашем классе.
Возможно, есть классы и лучше, и краше.
Но пусть в нашем классе вам будет светло,
Пусть будет уютно и очень легко.
Учитель. (правила поведения из презентации «Мир деятельности»)
Понапрасну не болтай,
Рассуждай и убеждай.
Здесь не нужен шум и гам,
Ты решай задачи сам.
Если же не сможешь вдруг,
Пусть придёт на помощь друг.
– К нам в класс пришёл ваш друг .
Открыть на обычной доске изображение Смайлика или презентацию.
– Это Смайлик — житель Маленькой страны (начальной школы).
Он, как и каждый из вас, учится в 1 классе. Смайлик никогда не грустил и всем дарил свою улыбку. Посмотрите друг на друга и подарите свои улыбки
II. Актуализация знаний и фиксирование индивидуального затруднения в пробном учебном действииЦель: подготовить учащихся к проблемному изложению нового знания (понятия, свойства, способа действия и пр.).
Но вот однажды улыбка исчезла с лица Смайлика. (учитель убирает лучики солнышка со стенда). В дальнейшем ученики будут открывать для себя каждое качество личности, и солнышко постепенно заполнится лучиками.)
Учитель обращает внимание детей на солнышко без лучиков. С лучиков нашего солнышка куда-то исчезли надписи качеств, помогающие ученику учиться. Раз мы друзья значит мы поможем Смайлику, чтобы он снова от радости стал светиться, как солнышко. Каждое выполненное нами задание будет возвращаться солнечными лучиками с качествами которые помогают нам учиться.
Каждое выполненное нами задание будет возвращаться солнечными лучиками с качествами которые помогают нам учиться.
– Какие шаги каждому из вас надо сделать, чтобы узнать что-то новое? (Надо понять, что я не знаю, и самому найти способ.)
Как всегда, начнём урок с повторения
— Сосчитайте по порядку от 2 до 7; от 9 до 5.
Найдите ошибку в записи ряда и восстановите порядок
1 2 7 4 3 5 6 8 9 10
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
— Обведите красным цветом число последующее число 2; 7(ответы 3; 8)
— Обведите синим цветом числа предыдущие числам 10; 3 (9; 2)
— Обведите зеленым цветом числа стоящие между 6 и 8; (7)
— Обведите желтым цветом соседей числа 5 (4,6)
— Что вы можете рассказать о числе 3
ВЗАИМОПРОВЕРКА ПО ЭТАЛОНУ.
Какие качества нам здесь понадобились, чтобы выполнить это задание.
III. Проблемное объяснение нового знанияЦель: ввести новое знание с помощью подводящего или побуждающего диалога.
Графический диктант
— Поставьте точку в уголке клетки. Проведите линию
- на две клетки вправо,
- на две клетки вниз,
- на две клетки влево,
- на две клетки вверх.
— Что у вас получилось? (Квадрат)
— Разделите квадрат на четыре маленьких одинаковых квадрата. Как это сделать? (Провести две линии)
— Как вы провели линии? (От стороны к стороне)
— Сколько всего квадратов? (Один большой и четыре маленьких)
— Сколько у квадрата сторон? (4)
— Сколько у квадрата углов? (4)
— Поэтому квадрат как еще можно называть четырёхугольником.
— Можно получить треугольники из квадрата? Как это сделать?
(Нужно провести две линии от угла к углу) Сколько всего треугольников получилось? (8)
Сколько из них маленьких?(4) А больших?(4)
– Может кто-нибудь догадался о каком числе мы будем сегодня говорить? (Появляется цифра 4)
— Ребята, где вам приходилось встречать число 4? (На часах, на домах, на автобусах, 4 колеса у машины, 4 ножки у стула и стола, 4 угла в комнате).
– Какую цель поставим для себя.
— Посмотрите на числовой ряд. На каком месте в натуральном ряду стоит число 4, на сколько число 4 больше предыдущего?
— На сколько число 4 меньше последующего?
— Назовите соседей числа 4.
— Как мы можем получить число 4?
А поможет нам в этом ребята (выходят 3 девочки и 1 мальчик) Первым к нам вышел Ваня? А потом сколько девочек вышли? Сколько получилось ребят?
Как получили?
А теперь девочки встанут к доске? Сколько девочек у доски? Ваня подойди к девочкам? Сколько всего стало? Как получили?
Составьте равенства .1+3…3+1 Какой знак можно поставить между ними. Почему?
Как выдумаете как еще можно получить 4?
1 девочка садится.
Сколько мальчиков у нас? А девочек? Как сделать так чтобы мальчиков стало столько же?
Теперь сколько мальчиков? А девочек? А всего сколько?
Как можно получить число 4?
(Молодцы, справились с заданием и вернули еще лучик. )
)
Цель: организовать усвоение учащимися нового знания.
Работа в парах ( повторение правил работы в парах.
А ВЫ ЛЮБИТЕ СКАЗКИ?
Задание № 1с (на слайде) соотнесите картинки со схемами(работа в тетради с.45 №1.
Побывал Иван-царевич в медном царстве, серебряном и золотом. Добыл трёх царевен.
Три царевны да Иван — всего их …
Сели они в лодку. Двое с одной стороны, двое напротив. Всего…
Доплыли до острова. Первым на берег вышел Иван. В лодке остаюсь — …
Вышли царевны. В лодке никого не осталось.
- Какая схема к какому рисунку подходит?
- Запиши равенства к каждой схеме.
Проверка на доске(дети выходят к доске, соотносят картинку со схемой и записывают выражения)
(Молодцы, справились и с этим заданием и вернули еще лучик.)
V. Самостоятельная работа с самопроверкой
Самостоятельная работа с самопроверкой Цель: организовать самопроверку учащимися умения применять новое знание в типовых ситуациях и коррекцию допущенных ошибок.
(Учащиеся самостоятельно выбирают способ составления модель числа 4)
А теперь попробуйте самостоятельно составить модель числа 4 (используют геометр. фигуры, карточки с точками, заселить домик).
Проверка по эталону.
Справились. Еще 1 лучик.
VI. Включение нового знания в систему знаний и повторениеЦель:
- выявить границы применимости нового знания и научить использовать его в системе изученных ранее знаний;
- повторить учебное содержание, необходимое для обеспечения содержательной непрерывности.
Разноуровневое задание (по выбору)
1 уровень
Задание №1 в тетради с.45.
№1 Раскрасить столько фруктов, сколько получилось в ответе. Запиши ответ.
Запиши ответ.
- 3-1=
- 4-2=
- 4-1=
2 уровень из учебника с.77 №5.
На острове стояли 2 дуба и несколько берез. Всего на острове было 4 дерева. Нарисуй столько треугольников сколько всего деревьев. Закрась столько треугольников сколько берез.
Проверка по эталону
VII. Рефлексия учебной деятельностиЦель: подвести итог урока и определить направления дальнейшей учебной деятельности.
Если б мы не потрудились,
То ничему б не научились,
Сегодня очень вы старались,
И вот – заданий не осталось.
ПРИЕМ «Микрофон» (учитель дает микрофон учащимся и задает вопросы. Дети отвечают)
— Какое число изучали?
— Как можно получить число 4?
— Сколько лапок у котенка?
— Сколько лапок у тигренка?
— Сколько ножек у стола?
— Столько ног и у слона.
Смотрите солнышко наше заулыбалось. Давайте откроем лучики и еще раз повторим какие качества нужны, чтобы хорошо учиться.
Давайте откроем лучики и еще раз повторим какие качества нужны, чтобы хорошо учиться.
Я предлагаю вам оценить свою работу со смайликом.
Состав | NCETM
Знание того, что числа состоят из двух или более других меньших чисел, предполагает понимание «часть-целое». Научиться «видеть» целое число и его части одновременно — ключевой момент в понимании детьми чисел. Разделение чисел на другие числа и их повторное сложение лежит в основе понимания сложения и вычитания как обратных операций.
Типичное развитие ключевых идей в этой концепции
Детям нужна возможность увидеть маленькие числа в большой коллекции. «Числовые беседы» позволяют детям обсуждать то, что они видят. Например, с гигантскими божьими коровками: «Всего пятен 5. Я вижу 4 и 1, я вижу 3 и 2, и я вижу 1 и 1, 1, 1 и 1». Детям предлагается внимательно смотреть на числа, чтобы увидеть, что еще они могут увидеть. Это усиливает концепцию сохранения.
Это усиливает концепцию сохранения.
Деятельность и возможности:
- поощрение заключения договоренностей с (например) десятью. Убедитесь, что дети рассказывают о различных механизмах, которые они могут видеть в целом .
Детям нужна возможность разделить ряд вещей на две группы и понять, что эти группы можно рекомбинировать, чтобы получить одинаковую сумму. Предложите детям назвать целое число, которое составляют «части» вместе.
Деятельность и возможности:
- изучение песен; например, «Пять булочек со смородиной» — покажите, что всего осталось пять, но часть есть в магазине, а часть увезли; проверьте, что осталось еще пять булочек со смородиной
- играет в кегли и смотрит сколько стоит. Сколько упало? Сколько их всего?
Детям нужна возможность изучить различные способы разделения целого числа. Акцент здесь делается на выявлении пар чисел, составляющих сумму. Дети могут сделать это двумя способами — физически разделив группу или сконструировав группу из двух видов вещей.
Действия и возможности:
- Башни Нумикон: наслоение частей Нумикона из одной и той же суммы
- положить вещи в два контейнера разными способами
- делает номер из двух разных вещей. Например, сделать фруктовую шпажку из пяти кусочков фруктов, используя на выбор тарелки с бананами/клубникой; затем попросите детей описать, как они сделали свои. Они должны сравнить его с партнером: «Что такого же в ваших шашлыках? Чем отличается?»
- Кроличьи ушки: используйте пальцы как кроличьи ушки. «Двумя руками покажи мне пять пальцев. Вы можете сделать это по-другому? Или «Покажи вместе с другом пять пальцев»
- Рассыпать бобы: используя двухсторонние жетоны или бобы, одна сторона которых окрашена, бросьте коллекцию и отметьте, сколько каждого типа можно увидеть и сколько всего
- , используя шесть кресел-мешков с разной тканью с каждой стороны, бросьте коллекцию и отметьте, сколько можно увидеть каждого типа.
Детям нужна возможность изучить различные способы разделения чисел, т. е. более чем на две группы. Ситуации, способствующие этому, включают увеличение количества горшков, в которые можно положить определенную сумму, например. посадка десяти семян в три или более горшков.
е. более чем на две группы. Ситуации, способствующие этому, включают увеличение количества горшков, в которые можно положить определенную сумму, например. посадка десяти семян в три или более горшков.
Деятельность и возможности:
- ролевая игра, напр. в магазине игрушек нужно расставить десять игрушек на трех полках. Как вы их организуете?
- иметь более двух мест для сортировки в любом данном контексте, например. расстановка персонажей игры в маленьком мире по разным локациям
- игр, таких как «Шикарные утки» (Гриффитс, Р., Бэк, Дж. и Гиффорд, С. (2016) три разных места (гнездо, вода, настил), бросьте кубики и сделайте так, чтобы одна группа соответствовала указанной сумме, не добавляя и не убавляя.
Детям нужна возможность сказать, сколько скрыто в известном количестве вещей. Например: «Пять игрушек входят в палатку, потом выходят две. Сколько осталось в палатке?» Ребенок должен ответить, что в палатке еще три игрушки.
Занятия и возможности:
- игры в прятки с несколькими предметами в ящике, под тканью, в палатке, в пещере и т.
 д.
д. - , используя классные процедуры, такие как время уборки, чтобы определить, сколько еще не хватает в горшке с этикеткой с номером.
- детей, предполагающих, что спрятано большее число, чем общее количество.
Может ли ребенок:
- разделить малые группы на большее число?
- угадать скрытое число?
- в контексте укажите две группы, которые составляют большую сумму? Например, как могут приземлиться (шесть) мешков с фасолью? У вас может быть три с полосками вверх и три с пятнами вверх.
Загрузки
Загрузите диаграмму прогрессии для этой концепции
Как научить математику в раннем возрасте — без проблем! Ultimate Guide
Введение
Первые несколько лет жизни ребенка особенно важны для развития математики. Для многих экспертов в области образования ни одна другая группа не представляет больше возможностей для улучшения математических стандартов, чем дети в раннем возрасте.
Для многих экспертов в области образования ни одна другая группа не представляет больше возможностей для улучшения математических стандартов, чем дети в раннем возрасте.
Чем больше у маленьких детей знаний о математических понятиях, тем лучше их будущие результаты. И наоборот, исследования показывают, что дети, которые начинают отставать в математике, как правило, остаются позади на протяжении всего своего образовательного пути.
На этой странице мы рассмотрим:
- Что мы подразумеваем под ранними годами?
- Как выглядит обучение в раннем возрасте
- Почему так важна теория когнитивной нагрузки?
- Какие стратегии мастерства доступны для детей младшего возраста?
Что мы имеем в виду, когда говорим о ранних годах?
В марте 2017 года правительство Великобритании опубликовало Положение об основах дошкольного образования. В нем устанавливаются стандарты обучения, развития и ухода за детьми от рождения до пяти лет.
Области обучения
Структура EYFS выделяет семь областей обучения:
- Общение и язык
- Физическое развитие
- Личное, социальное и эмоциональное развитие
- Грамотность
- Математика
- Познание мира
- Выразительное искусство и дизайн
Математика в EYFS
В контексте математики в структуре говорится, что детям должна быть предоставлена возможность развивать свои навыки в следующих областях:
- Счет
- Понимание и использование чисел
- Вычисление простых задач на сложение и вычитание
- Описание форм, пространств и размеров
Пересмотренное руководство
DfE опубликовало пересмотренное руководство в марте 2021 г., которое вступит в силу в сентябре 2021 г.
Математический компонент теперь включает многие элементы углубленного подхода.
В частности, пересмотренная структура гласит:
Дети должны уметь уверенно считать, развивать глубокое понимание чисел до 10, отношения между ними и закономерности внутри этих чисел. Предоставляя частые и разнообразные возможности для построения и применения этого понимания — например, используя манипулятивные средства, в том числе маленькие камешки и рамки десятков для организации счета — дети разовьют надежную базу знаний и словарный запас, на которых строится мастерство математики. Кроме того, важно, чтобы учебная программа включала в себя широкие возможности для развития у детей навыков пространственного мышления во всех областях математики, включая форму, пространство и меры. Важно, чтобы дети развивали позитивное отношение и интерес к математике, искали закономерности и взаимосвязи, находили связи, «пробовали», говорили со взрослыми и сверстниками о том, что они замечают, и не боялись делать ошибки.
Цели раннего обучения
Последняя структура имеет следующие цели раннего обучения математике:
Количество
Дети на ожидаемом уровне развития:
- Имеют глубокое понимание числа до 10, включая состав каждого числа
- Субитис (распознавание количества без подсчета) до пяти
- Автоматически вспоминать (без привязки к рифмам, счету или другим вспомогательным средствам) числовые связи до пяти (включая факты вычитания) и некоторые числовые связи до 10, включая двойные факты
Числовые модели
Дети ожидаемого уровня развития:
- Устно считают до 20, распознавая схему системы счета
- Сравнивать количества до 10 в различных контекстах, распознавая, когда одно количество больше, меньше или равно другому количеству
- Исследуйте и представляйте закономерности в числах до 10, включая четные и нечетные числа, двойные факты и то, как количества могут быть распределены поровну
Reception
Приемный класс — это первый год обучения в начальной школе в Англии, как правило, для детей в возрасте от четырех до пяти лет. В отличие от любого другого учебного года, дети не обязаны посещать приемную, хотя это хороший способ познакомить их со школьной жизнью.
В отличие от любого другого учебного года, дети не обязаны посещать приемную, хотя это хороший способ познакомить их со школьной жизнью.
Обучение в раннем возрасте
Первые несколько лет жизни ребенка особенно важны для развития математики, сообщает Национальный центр передового опыта в области преподавания математики.
Исследования показывают, что раннее знание математики предопределяет более позднюю способность к чтению, общее образование и социальный прогресс.
Уже в возрасте восьми месяцев дети начинают понимать названия чисел и включают их в свою речь, как только начинают говорить. Когда дети слушают разговоры вокруг них, они знакомятся с числами благодаря возможностям, которые возникают в повседневной жизни, и испытывают различные рифмы с числами. Это поддерживает их растущее знание имен чисел.
Согласно NCETM, существует:
Шесть ключевых областей математического обучения
- Количество элементов и счет
- Сравнение
- Состав
- Узор
- Форма и пространство
- Меры
Кратко рассмотрим каждый по очереди:
Количество и подсчет
Когда дети понимают количество чисел, они знают, что означают числа с точки зрения знания того, к скольким предметам они относятся.
Сравнение
Сравнение чисел предполагает знание того, какие числа стоят больше или меньше друг друга.
Композиция
Умение «видеть» целое число и его части одновременно является ключевым моментом в понимании детьми чисел.
Образец
Развитие понимания узора помогает маленьким детям замечать и понимать математические отношения.
Форма и пространство
С математической точки зрения области формы и пространства связаны с развитием навыков визуализации и понимания взаимосвязей, таких как эффекты движения и комбинирования форм
Меры
Измерение в математике основано на идее использования количества единиц для сравнения атрибутов, таких как длина или емкость.
Счет
Умение считать в раннем возрасте — это фундаментальный навык и ключ к освоению математических понятий в будущем, но это гораздо больше, чем вы можете себе представить, — говорит Сабрина Пиннок, учительница начальных классов из Йоркшира.
По словам исследователей Рочел Гельман и Ч. Р. Галлистела, для успешного подсчета необходимо выполнить следующие шаги:
- Принцип «один к одному»: дети должны называть каждый предмет, который они считают, и понимать, что есть две группы: тот, который был посчитан, и тот, который еще не посчитан
- Принцип стабильного порядка: дети должны уметь считать в правильном порядке
- Главный принцип: дети должны понимать, что последнее число в наборе — это общая сумма
- Считать что угодно: дети должны понимать, что сосчитать можно все, не только предметы, к которым можно прикоснуться, но и такие вещи, как хлопки и прыжки
- Порядок подсчета не имеет значения: дети должны понимать, что порядок подсчета в наборе не имеет значения и все равно приведет к той же сумме
Оценка детей, чтобы выяснить, с каким шагом они борются, является ключом к тому, чтобы помочь им преодолеть трудности и стать уверенными счетчиками.
Как дети развивают навыки счета?
Очень маленькие дети начинают считать спонтанно, а позже начинают совершенствовать свои навыки, указывая пальцем на предметы, которые они считают.
Они часто пытаются ввести в свой счет названия всех известных им чисел, водя пальцем по предметам. Они также повторно используют числа. Если они не закончили и использовали все свои известные номера, они снова начнут использовать те же номера. Например, ребенок может решить сосчитать восемь ракушек, которые он собирает на пляже. Она может аккуратно выстроить их в ряд, присвоить им номера, указывая пальцем на ракушки и быстро считая вслух: «один, два, три, четыре, пять, один, два, три, четыре, пять, один, два три.»
В своем стремлении придать смысл детям не терпится поэкспериментировать, приобретая новые небольшие математические знания. Чрезвычайно важно уважать их развивающееся понимание и не ожидать «идеальной» последовательности счета.
Ценя частичное понимание детей, дети разовьют интерес к числам и станут уверенными математиками.
Занятия по развитию чувства числа в приемном классе
Детям нужно много возможностей для развития чувства числа и углубления их концептуального понимания. Вот несколько простых действий, которые помогут подсчитать учащихся вашего года приема:
Вот несколько простых действий, которые помогут подсчитать учащихся вашего года приема:
Контроль толпы
Отобразите количество детей, разрешенных в каждой области, используя графические изображения кубов на 10-й рамке. Как только дети начинают понимать, сколько их разрешено находиться в этом районе, они начинают обсуждать, что значит больше и меньше. Например, «детям больше нельзя входить» или «вы можете входить, потому что на одного больше трех — четыре».
Кроличьи ушки
Побуждайте детей показывать числа пальцами над головой. «Уши кролика шесть» означает, что они кладут пальцы над головой, чтобы показать шесть. Они могут решить использовать по три пальца на каждой руке. По мере того, как они станут более уверенными, вы можете ввести обмен, когда они показывают одно и то же число, но с другим расположением пальцев, в данном случае два и четыре или пять и один.
Группировка соломинок
Каждое утро бросайте разное количество соломинок для творчества на ковер. Скажите что-нибудь вроде: «О, нет, класс, я не могу в это поверить. Я снова уронил все свои соломинки. Все они были в десятках. Вы можете помочь мне?» Это упражнение помогает детям закрепить счет предметов и побуждает их задуматься о том, чтобы остановиться после того, как они сделают 10. Предоставление резинок поможет им отслеживать свои группы по 10.
Скажите что-нибудь вроде: «О, нет, класс, я не могу в это поверить. Я снова уронил все свои соломинки. Все они были в десятках. Вы можете помочь мне?» Это упражнение помогает детям закрепить счет предметов и побуждает их задуматься о том, чтобы остановиться после того, как они сделают 10. Предоставление резинок поможет им отслеживать свои группы по 10.
10 самых быстрых кадров
развили хорошее понимание смысла чисел и тех, кто нуждается в дальнейшей поддержке. Дайте каждому ребенку свою рамку и кубики. Назовите им число и посмотрите, как они размещают кубики на рамке. Если дети работают с числом восемь, произносят ли они названия каждого числа, помещая кубик на рамку, или понимают, что восемь на два меньше десяти? Если да, то они должны ставить кубики быстрее, чем другие дети.
Что они делают, когда вы говорите следующее число? Например, для числа пять они автоматически убирают три кубика или убирают все кубики и начинают заново считать от одного до пяти?
Ежедневные вопросы для развития чувства числа
Эти вопросы для детей в возрасте от пяти до шести лет помогают развить чувство числа и позволяют им практиковаться в использовании математических терминов.
При приготовлении обеда или перекуса считайте вместе с ребенком различные продукты, а когда будете накрывать на стол, считайте разные продукты. Задайте ребенку такие вопросы, как:
- Сколько здесь виноградин?
- Сколько помидоров?
- Сколько тарелок?
Попрактикуйтесь в использовании терминов больше чем, меньше чем и столько же, спросив:
- Винограда больше, чем помидоров?
- Помидоров меньше, чем винограда?
- Столько ли тарелок, сколько человек ест?
Не забывайте повторять каждое предложение:
- Винограда больше, чем помидоров
- Помидоров меньше, чем винограда
- Тарелок столько, сколько членов семьи едят
При счете убедитесь, что вы считаете одно число для одного элемента, чтобы укрепить чувство взаимного соответствия вашего ребенка.
Числовые рифмы
Тщательно отберите числовые рифмы, включив в них те, с которыми дети знакомы дома. Убедитесь, что рифмы включают:
Убедитесь, что рифмы включают:
- Счет назад и счет вперед
- «Нет» или «нет» (Пять утят однажды пошли купаться)
- Счет парами (два, четыре, шесть, восемь, Маша у ворот дачи)
- Счет до пяти, 10 и далее
Решение задач, рассуждение и счет
EYFS требует поддержки детей в развитии их понимания решения задач, рассуждения и счета в широком диапазоне контекстов, в которых они могут исследовать, получать удовольствие, учиться, практиковать и говорить о своем развитии понимание. Им должны быть предоставлены возможности практиковать эти навыки и обрести уверенность.
Маленькие дети лучше всего учатся в игре. Чтобы их обучение было эффективным, им нужна чуткая и информированная поддержка со стороны взрослых.
Все дети могут быть успешными в математике, если у них есть возможность исследовать идеи способами, которые имеют для них личное значение, и возможности развивать концепции и понимание. Дети должны знать, что практикующие заинтересованы в их мышлении и уважают их идеи.
Основы
Математика — без проблем! Foundations разработан с учетом всей теории и строгости, которые лежат в основе настоящего мастерства. Он отвечает всем требованиям начальной стадии национальной учебной программы. Но Математика — не проблема! Foundations не уклоняется от внедрения обучения через игру в Reception.
Подлинное обучение через игру в раннем возрасте — это то, чем занимается команда . Математика — без проблем! очень волнуется. То, что может показаться простыми играми, на самом деле является тщательно разработанными занятиями, в которых основное внимание уделяется математическому мастерству.
Математика — нет проблем! Foundations — это комплексная приемная программа, которая включает в себя журналы с рабочими тетрадями, иллюстрированные книги и онлайн-руководства для учителей с печатными листами ресурсов — все в одном пакете.
Математика — нет проблем! Набор продуктов , в том числе учебники, рабочие тетради, революционный онлайн-инструмент оценки, подготовка учителей мирового класса и многое другое, основан на сингапурском методе, который сочетает в себе 30-летний опыт международных исследований с кропотливым мастерством и постоянным усовершенствованием.
Изготовление знаков
Исследования Carruthers and Worthington в области детской математической графики показывают, что маленькие дети используют свои собственные знаки и представления для изучения и передачи своего математического мышления. Эти графические изображения включают:
- каракули
- Чертежи
- Письмо
- Счетные метки
- Придуманные и стандартные символы, включая цифры
Графические исследования маленьких детей «основаны на том, что они уже знают о знаках и символах, и закладывают основы для понимания математических символов и последующего использования стандартных форм письменной математики», — говорят исследователи.
В публикации 2009 года Департамента по делам детей, школ и семьи Великобритании говорится, что практикующие врачи должны: «Ценить собственные графические и практические исследования детей в решении проблем» и наблюдать «контекст, в котором маленькие дети используют свои собственные графические изображения».
Развитие понимания с помощью тщательных вопросов
Когда дети играют и взаимодействуют с другими детьми, всегда есть возможность поговорить о математике, чтобы помочь им развить глубокое понимание, — говорит Сабинра Пиннок.
Например:
- Я сделал выкройку. Какой у вас узор?
- На сколько блоков выше моя модель по сравнению с вашей?
- Откуда мы знаем, что эта область заполнена?
- У меня три машины, сколько у тебя?
- У вас есть еще?
- Откуда ты знаешь?
Дайте учащимся достаточно времени, чтобы они обдумали свой ответ и дали ответ, но не настолько долго, чтобы это мешало ходу игры.
Добавление разговоров о математике в распорядок дня
Развитие математической речи в повседневной жизни дает учащимся возможность понять концепции, используя концепции из реальной жизни. Это также означает, что дети могут закрепить то, что они узнали.
Следующие занятия помогут вам начать работу:
Сколько детей ходит в школу?
Попросите свой класс определить, сколько детей ходит в школу, поместив свое изображение или встречное изображение на 10 больших рамок. Задайте им такие вопросы, как:
Задайте им такие вопросы, как:
- Откуда мы знаем, что эти 10 кадров заполнены?
- Сколько детей отсутствует?
- Откуда ты знаешь?
- Что ты можешь рассказать мне о номере семь?
Сортировка и группировка объектов в классе
Сортировка и группировка объектов в классе помогает детям научиться рассуждать и искать закономерности. Каждый день давайте им разные кнопки и задавайте открытые вопросы, например: «Как мы можем отсортировать кнопки?» Они могут использовать навыки критического мышления, чтобы придумать ряд идей, таких как сортировка по размеру, цвету, рисунку и форме.
Проголосуйте за рассказ
Сначала попросите ребенка выбрать две книги. Каждый в классе может проголосовать (например, с помощью кусочка лего), какую из книг следует прочитать. В конце дня подсчитайте голоса, чтобы определить победителя. Это может привести к таким вопросам, как:
- Почему?
- Откуда ты знаешь?
- На сколько больше голосов проголосовала одна книга, чем другая?
Ключ к овладению мастерством в первые годы жизни заключается в том, чтобы занятие было увлекательным и частью вашей повседневной жизни. Чем больше учащиеся изучают математику в игре, тем больше они вовлекаются.
Чем больше учащиеся изучают математику в игре, тем больше они вовлекаются.
Понимание закономерностей
Доктор Сью Гиффорд, почетный научный сотрудник Университета Рохэмптона, говорит, что недавние исследования показали, что способность ребенка определять математические закономерности может предсказать будущие математические успехи в большей степени, чем другие способности, такие как счет. Это также показывает, что осознание закономерностей может сильно различаться у разных людей.
Австралийские исследователи Папик, Маллиган и Митчелмор обнаружили, что дошкольников можно эффективно обучать осознанию закономерностей, что оказывает положительное влияние на их более позднее понимание чисел.
Явное обучение познанию паттернов связано с поощрением «обнюхивания паттернов» у детей старшего возраста с целью развития математического понимания и мышления.
Что такое понимание математических моделей?
Паттерны — это в основном отношения с некоторой регулярностью между элементами. В первые годы Папик и др. предполагали, что существует три основных типа:
В первые годы Папик и др. предполагали, что существует три основных типа:
- Фигуры с правильными чертами, такие как квадрат или треугольник с равными сторонами и углами, а также фигуры, состоящие из нескольких точек, расположенных на одинаковом расстоянии друг от друга
- Повторяющаяся последовательность: наиболее распространенными примерами являются последовательности AB, такие как красный, синий, красно-синий узор с кубиками. Более сложными являются шаблоны ABC или ABB с повторяющимися единицами, такими как красный, зеленый, синий или красный, синий, синий .
- растущий узор, например лестница с одинаковыми ступенями
Дети, хорошо осведомленные о закономерностях, могут замечать закономерности такого рода: они могут воспроизводить закономерности и предсказывать, как они будут продолжаться.
Почему так важно распознавать закономерности?
Выявление лежащих в основе закономерностей важно для определения множества различных видов математических взаимосвязей. Это лежит в основе запоминания последовательности счета и понимания операций с числами, например, признания того, что если вы складываете числа в другом порядке, их сумма остается неизменной.
Это лежит в основе запоминания последовательности счета и понимания операций с числами, например, признания того, что если вы складываете числа в другом порядке, их сумма остается неизменной.
Осознание закономерностей было описано как раннее алгебраическое мышление, которое включает:
- Замечание математических особенностей
- Выявление связи между элементами
- Наблюдение за закономерностями
Упражнение «Создание паттернов» фокусируется на повторяющихся паттернах и предлагает некоторые увлекательные способы развития понимания паттернов с подсказками для обдумывания ответов детей. Дети могут собирать паровозики из разных игрушек, делать узоры из веточек и листьев снаружи или распечатывать и приклеивать узоры в дизайнерских занятиях.
Повторяющиеся узоры
Важно познакомить детей с разнообразными повторяющимися узорами, переходящими от ABC и ABB к ABBC.
Сосредоточение внимания на чередующихся узорах AB может привести к тому, что некоторые маленькие дети будут думать, что «синий, красный, красный» не может составить узор. Они говорят что-то вроде: «Это не шаблон, потому что у вас не может быть двух одинаковых цветов рядом друг с другом».
Они говорят что-то вроде: «Это не шаблон, потому что у вас не может быть двух одинаковых цветов рядом друг с другом».
Foundations — Your Reception Solution
Эта программа развития навыков для детей младшего возраста поощряет обучение через игру и направляет детей на путь к глубокому пониманию математики.
Узнать больше
Теория когнитивной нагрузки
Теория когнитивной нагрузки приобрела большую популярность в последние годы, поскольку преподаватели используют научно обоснованные исследования для информирования своей развивающейся практики, говорит Росс Динс, учитель KS2 и руководитель отдела математики в Борнмуте, Англия.
Что такое теория когнитивной нагрузки и почему она важна?
Почему новые учителя настолько перегружены работой, что более опытные учителя могут совмещать множество других обязанностей?
Ответ прост — новые навыки требуют большего внимания.
Эту логику можно применить к любой ситуации. Например, когда вы учитесь водить машину, вы тщательно сосредотачиваетесь на каждой мелочи. Это умственное напряжение может быть очень требовательным. Сравните это с ощущением от вождения после того, как вы занимаетесь этим годами; вы можете едва помнить диск, процесс настолько знаком.
Например, когда вы учитесь водить машину, вы тщательно сосредотачиваетесь на каждой мелочи. Это умственное напряжение может быть очень требовательным. Сравните это с ощущением от вождения после того, как вы занимаетесь этим годами; вы можете едва помнить диск, процесс настолько знаком.
Теперь поставьте себя на место своих учеников. Каждый урок предлагает новое обучение и новые навыки для освоения. Подумайте, что происходит в головах ваших учеников, когда они сталкиваются с новой информацией, новыми навыками и новым словарным запасом.
Рабочая память
Теория когнитивной нагрузки, разработанная Джоном Свеллером, признает, что рабочая память очень ограничена.
Рабочая память — это информация, которую мы храним в уме во время обучения. Количество вещей, которые мы можем удерживать в рабочей памяти одновременно, равно приблизительно четырем, плюс-минус один, а у детей, возможно, даже меньше.
Важно помнить об этом при планировании и проведении уроков. Если наши учащиеся не могут сбалансировать более четырех вещей в своей рабочей памяти, то нам нужно быть очень осторожными с информацией, которую мы хотим им представить.
Если наши учащиеся не могут сбалансировать более четырех вещей в своей рабочей памяти, то нам нужно быть очень осторожными с информацией, которую мы хотим им представить.
Внутренняя и внешняя нагрузка
Внутренняя нагрузка включает все, что необходимо для обучения желаемому навыку. Другими словами, самое необходимое.
Чрезмерная нагрузка — это все, что отвлекает от желаемого обучения. Другими словами, то, что должно быть максимально сокращено.
Во время обучения может возникнуть соблазн украсить уроки детскими изображениями и трюками. Хотя важно доставлять удовольствие, мы не должны отвлекать учащихся от основных компонентов урока.
Поддержка перехода к долговременной памяти
Признавая влияние теории когнитивной нагрузки, мы можем принять во внимание следующее, чтобы поддержать наших учащихся: чего мы хотим, чтобы наши ученики достигли. Помните об ограничениях рабочей памяти и дайте им руководство при выборе контента, который вы решите включить в урок.
Активировать предварительное обучение
В начале урока вы можете разработать задание, которое побудит учащихся восстановить основные навыки. Это означает, что их рабочая память может удерживать новые знания во время урока.
Четкое представление информации
При планировании уроков уделите время тому, чтобы информация была представлена ясно. Избегайте ненужных дополнений, которые могут отвлечь от цели обучения. Держите слайды чистыми и похожими по стилю.
Избегайте когнитивной перегрузки
В математике задачи часто бывают подробными и сложными. Попробуйте разбить вопросы на части, чтобы учащиеся могли усваивать каждую часть отдельно. Убрав последний вопрос, вы можете сделать математическую задачу бесцельной.
Овладение математикой для детей младшего возраста
Учитывая важность развития прочного понимания математики в раннем возрасте, подход к овладению математикой может быть особенно полезен, учитывая его акцент на решении задач и обучении всего класса.
Ранние годы и CPA
Если вы преподаете подход «Конкретно, изобразительно, абстрактно» (CPA) в первые годы, лучше всего сосредоточиться на C и P. Вот как эффективно использовать конкретное и графическое представление.
Модель CPA блестяще работает в начальных классах, но для самых младших учащихся слишком ранний переход к абстрактным понятиям вызывает трудности. Проводя как можно больше времени с конкретными предметами и графическими изображениями, дети овладевают числовыми навыками.
К тому времени, когда они достигнут ключевого этапа 2, дети должны развить свое понимание чисел, умея визуализировать, как выглядит бетон в их голове. Таким образом, хорошо, что пересмотренная структура EYFS фокусируется на числах до 10 вместо 20 ранее.
Если учащиеся разовьют глубокое понимание чисел до 10, их шансы на понимание больших чисел значительно возрастут.
C для бетона
Бетон – этап «исполнения». На этом этапе учащиеся используют конкретные объекты для моделирования проблем. В отличие от традиционных методов обучения математике, когда учителя демонстрируют, как решить задачу, подход CPA воплощает концепции в жизнь, позволяя детям испытывать и обращаться с физическими (конкретными) объектами.
В отличие от традиционных методов обучения математике, когда учителя демонстрируют, как решить задачу, подход CPA воплощает концепции в жизнь, позволяя детям испытывать и обращаться с физическими (конкретными) объектами.
Проведение времени с реальными объектами
Теоретик Джером Брунер подчеркивает важность того, чтобы дети проводили время, изучая математику с помощью материальных предметов. Тратить много времени на использование реальных объектов, решение реальных проблем и манипулирование абстрактными конкретными объектами (когда они готовы), такими как кубики и счетчики, очень важно в первые годы.
Идеи включают подсчет фруктов во время перекуса, сравнение, сортировку и подсчет различных кнопок, макарон и даже «волшебных бобов», связанных с конкретными темами.
Ранние годы и числовые связи
Овладевая числовыми связями на раннем этапе, ученики создают основу, необходимую для последующего обучения, и лучше подготовлены для развития мыслительных стратегий и беглости математических вычислений. Развивая сильное чувство числа, ученики могут решить, какие действия предпринять, пытаясь решить проблемы в уме.
Развивая сильное чувство числа, ученики могут решить, какие действия предпринять, пытаясь решить проблемы в уме.
Как преподавать числовые связи
Дети обычно знакомятся с числовыми связями с помощью Конкретного, Графического, Абстрактного подхода. Вот только один из способов представить числовые связи и научить их этому.
Бетонная ступенька
Дети начинают с подсчета знакомых объектов реального мира, с которыми они могут взаимодействовать. Затем они используют счетчики для представления объектов реального мира. Отсюда они переходят к группировке счетчиков в две группы.
Разделив пять фишек на две группы, дети узнают, как можно сделать пять фишек. Например, 3 и 2, как показано ниже. При дальнейшем изучении дети отрабатывают другие способы разбить числа на две группы.
Иллюстрированный шаг
Теперь, когда они понимают концепцию с практическими предметами и опытом, дети переходят к написанию числовых связей в рабочих тетрадях или на доске. Ранние исследования числовых связей могут просто отражать две группы счетчиков, которые они создали на конкретном этапе, наряду с другими комбинациями.
Ранние исследования числовых связей могут просто отражать две группы счетчиков, которые они создали на конкретном этапе, наряду с другими комбинациями.
Абстрактный шаг
После выполнения конкретных и иллюстрированных шагов дети переходят к представлению абстрактных задач с использованием математических обозначений (например, 3 + 2 = 5).
Ранние годы и разрядное значение
Числовое и разрядное значение являются основополагающими понятиями для любого изучения математики. Это означает, что нам нужно как можно раньше решить, как преподавать значение места, чтобы ученики могли закрепить свое знание концепции.
Как вы развиваете раннее понимание ценности места в классе начальной школы? Начнем с определения стоимости места. Это система записи цифр, в которой положение каждой цифры определяет ее значение. Каждое значение кратно общему основанию 10 в нашей десятичной системе.
Вот несколько стратегий обучения, которые я считаю полезными, помогая учащимся развить раннее понимание ценности места.
Систематический прогресс в изучении понятий
Развитие понимания значения места требует систематического прогресса. Каждая новая концепция должна основываться на предыдущем учебном опыте, чтобы учащиеся могли получить более глубокое, относительное понимание по ходу дела.
Этот подход гарантирует, что знания развиваются, совершенствуются и правильно применяются, поскольку числа становятся значимыми инструментами для решения проблем, а не просто набором символов на странице. Самое главное, это открывает нашим учащимся путь к тому, чтобы стать уверенными в решении проблем и выявлении закономерностей.
Использование подхода КПВ для установления значения
Подход КПВ (конкретный, иллюстрированный, абстрактный) помогает учащимся связать физическое представление числа (конкретные манипуляции) с тем же количеством, которое показано на рисунках или графиках (иллюстрациях), и, наконец, к фактическому написанному имени и символу для этого числа (аннотация).
Конкретные ресурсы создают смысл. Они добавляют смысл абстрактным представлениям чисел, чтобы, когда учащиеся переходят к абстрактной фазе, они знали, что означают эти числа, что они означают и как они связаны друг с другом.
Если учащийся может определить значение каждого компонента задачи, он гораздо более уверен в том, как он работает над ее решением.
Обучайте «десятичности 10»
На начальном уровне уделяйте как можно больше времени изучению чисел от 0 до 10, так как понимание 10-сти 10 имеет решающее значение для достижения математики, и это не может быть помчался.
Как только это понимание зафиксируется, последуйте за ним введением в числовые связи. Начните с аддитивных отношений между числами меньше 10, затем переходите к сложению и вычитанию до 10. Это гарантирует, что учащиеся будут рассматривать 10 как важное «базовое» число во всех своих будущих математических приложениях.
Прогрессируйте до 20, затем до 40
Я уделяю время обучению десятичным и подростковым числам, чтобы у меня сложилось правильное понимание разрядности чисел до 20.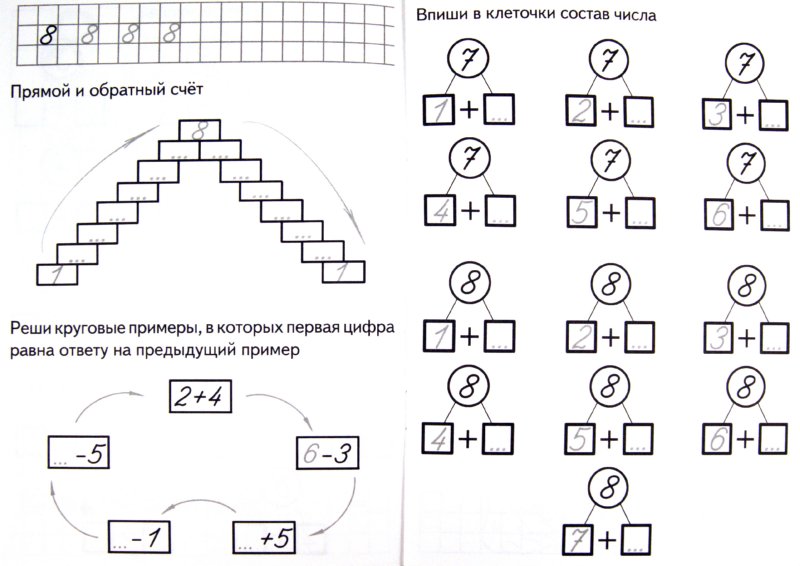
Затем я расширяю концепцию разряда, работая с числами до 40, а затем сложением и вычитанием до 40.
Поскольку ученики научились составлять 10 и использовать числовые связи, они готовы начать работать с многозначными числами. и перегруппировка. Сосредоточение внимания на числах до 40 при разработке концепции разряда также позволяет учащимся связывать числа с легко управляемыми физическими величинами (создателями значения).
Используйте блоки с основанием 10 для 100 и 1000
Работа, которую мы проделали для постепенного понимания разрядного значения, подготовит учащихся к переходу к трехзначным числам. Итак, теперь мы можем перейти к изучению числа до 100.
Здесь мы начнем с понимания чисел в многозначных представлениях. Например, одна тысяча пятьсот — это 15 сотен или 150 десятков.
Как только они освоятся, учащиеся оттачивают свои навыки счета, чтения и письма для чисел до 1000. Переход к сложению и вычитанию чисел до 1000 — с перегруппировкой и без — это следующий шаг.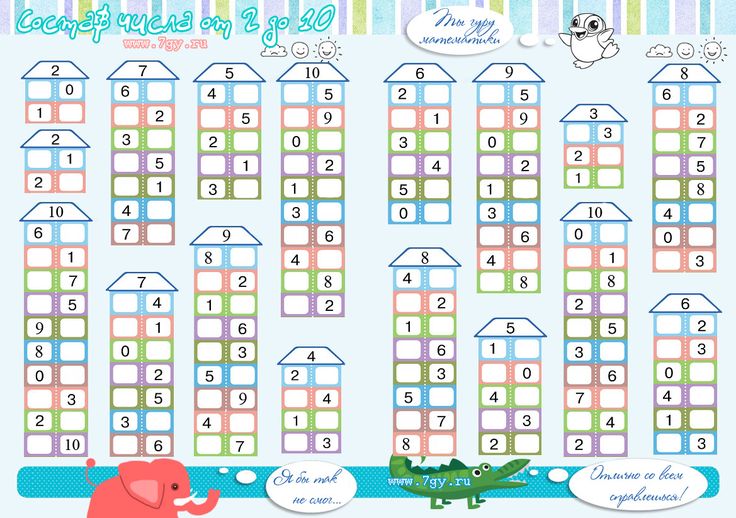
Здесь наша работа по установлению раннего понимания разрядного значения является ключевой, потому что ученики будут знать, почему эти алгоритмы работают для трех- и четырехзначных чисел. Блоки с основанием 10 — отличный инструмент, помогающий укрепить прежние идеи разрядности при работе с числами до тысяч.
Подход к большим числам таким же образом
Подход CPA снова является нашим ответом на изучение значения места в больших числах. Применяйте эти навыки и всегда ищите возможности для расширения концепций чисел и разрядов.
Например, вы можете определить и дополнить числовые шаблоны или найти пропущенные цифры в числовой строке.
Здесь вы можете изучить стратегии ментальной математики, а также сложения и вычитания чисел до 10 000. Познакомьте учащихся еще глубже, попросив их изучить разрядность с акцентом на умножение, деление и десятичные дроби.
Усвоение математических понятий, таких как разрядное значение, в первые годы жизни является не только ключом к успеху в классе. Он готовит учащихся к глубокому пониманию математики на протяжении всей жизни, предоставляя им бесценные практические инструменты, такие как устойчивость и способность решать проблемы.
Он готовит учащихся к глубокому пониманию математики на протяжении всей жизни, предоставляя им бесценные практические инструменты, такие как устойчивость и способность решать проблемы.
А тот, кто уверенно решает задачи по математике, уверенно решает задачи и в жизни.
Заключение
Вы молодцы, что дошли до конца нашего Полного руководства по раннему развитию.
Мы рассмотрели определение дошкольного возраста и то, что рекомендует правительство в своем пересмотренном руководстве, а также подробно рассмотрели некоторые из наиболее эффективных стратегий обучения математике в дошкольном возрасте.
Мы также обсудили теорию когнитивной нагрузки и ее значение для учителей начальной школы.
Если вы хотите узнать больше о программе Early Years, мы рекомендуем перейти по следующим ссылкам:
- NCETM: Как дети раннего возраста развивают математическое мышление (подкаст)
- NRICH: Домашняя страница начальной стадии
- Школа школы: Эпизод 17 Игра и ранние годы (Подкаст)
- Математика — не проблема! Подход CPA
Также не пропустите другие наши полные руководства:
- Математика — без проблем! Полное руководство по овладению математикой
- Математика — не проблема! Полное руководство по оценке
Как создавать группы? — Eberly Center
Состав группы влияет на многие аспекты группового проекта, например, на эффективность совместной работы членов группы и объем соответствующих знаний, которыми они могут поделиться. При принятии решения о том, как создавать группы для проекта, вы должны:
При принятии решения о том, как создавать группы для проекта, вы должны:
- Решить, как настроить группы.
- Определите характеристики членов группы, имеющие отношение к целям обучения проекта.
- Решите, кто отвечает за выбор членов группы.
- Разработайте план действий на случай, если членство в группе изменится во время проекта.
Решите, как настроить группы
При настройке групп следует учитывать два основных фактора:
Размер. Небольшие группы, как правило, работают эффективно, потому что легче координировать усилия и графики между меньшим количеством людей. Однако, несмотря на то, что большие группы несут более высокие затраты на координацию, теоретически они могут выполнять более крупные и сложные проекты. Некоторые эксперты утверждают, что группы из более чем пяти-шести студентов, как правило, неуправляемы, но жестких правил нет. Как и другие аспекты групповой работы, размер группы должен определяться целями обучения проекта.
Роли. В некоторых проектах требуется, чтобы каждый член группы играл специальную роль, имитирующую рабочую среду (например, менеджер проекта, аналитик данных, писатель). Некоторые преподаватели определяют роли, которые должны быть представлены в каждой группе, а затем позволяют учащимся присоединяться к группам в зависимости от их сильных сторон. Следует отметить, что если цель курса состоит в том, чтобы научить учащихся играть разные роли, может оказаться эффективной противоположная стратегия: вы можете назначить учащимся роли, которые выводят их из зоны комфорта и развивают новые навыки.
Определите соответствующие характеристики членов группы
Характеристики членов группы могут повлиять на то, насколько эффективно учащиеся достигают учебных целей проекта. Не существует единого набора соответствующих характеристик для членов группы, потому что это зависит от вашего курса, ваших целей, ваших студентов и характера проекта. Приходите поговорить с нами, чтобы мы могли обсудить лучший подход для вас.
Ниже приведены общие характеристики, которые следует учитывать при составлении групп:
Предыдущие знания, предыдущий опыт и навыки. Если вы хотите структурировать группы для распределения определенных типов знаний (например, навыков программирования, опыта проектирования, опыта исторических исследований) между группами, вы можете оценить предшествующие знания учащихся или попросить их заполнить список навыков. На некоторых междисциплинарных курсах преподаватели используют специальность студента в качестве показателя предшествующих знаний. Имейте также в виду, что навыки, относящиеся к групповым проектам, могут быть как межличностными, так и дисциплинарными.
Мотивация. Студенты имеют разные уровни мотивации в рамках курса: некоторые отдают приоритет работе над проектом, чтобы преуспеть, некоторые довольствуются получением минимального проходного балла, некоторые проходят курс из-за искреннего интереса, а некоторые проходят курс, чтобы удовлетворить требование. Смешивание студентов с разными мотивами в группе может вызвать напряженность и проблемы. Чтобы противостоять этому, некоторые преподаватели группируют студентов по мотивации. Распространение анкеты, в которой учащиеся размышляют о своей мотивации, рабочих привычках и желаемой оценке, а затем делятся анкетами друг с другом, но не с преподавателем, может помочь учащимся определить одноклассников, с которыми им будет хорошо работать.
Смешивание студентов с разными мотивами в группе может вызвать напряженность и проблемы. Чтобы противостоять этому, некоторые преподаватели группируют студентов по мотивации. Распространение анкеты, в которой учащиеся размышляют о своей мотивации, рабочих привычках и желаемой оценке, а затем делятся анкетами друг с другом, но не с преподавателем, может помочь учащимся определить одноклассников, с которыми им будет хорошо работать.
Разнообразие взглядов. Если одной из целей обучения проекта является ознакомление с несколькими точками зрения, вы можете составить разные группы. Мы часто думаем о разнообразии с точки зрения пола, культуры, расы/этнической принадлежности и родного языка, но вы также можете учитывать значимость социально-экономических, политических, географических и других различий для учебных целей проекта. Однако важно убедиться, что в каждой группе есть критическая масса, чтобы отдельные представители определенной социальной категории (например, расы, пола) не оказались изолированными в группе. Например, в классе, в котором четыре женщины и четыре группы, вместо того, чтобы помещать одну женщину в каждую группу, рассмотрите возможность разделения двух женщин на две группы.
Например, в классе, в котором четыре женщины и четыре группы, вместо того, чтобы помещать одну женщину в каждую группу, рассмотрите возможность разделения двух женщин на две группы.
Знакомство учащихся друг с другом. Учащиеся, которые раньше эффективно работали вместе в группах, с большей вероятностью будут снова эффективно работать вместе. Прежде чем учащихся распределит по группам, вы можете спросить их, насколько эффективно они работали с одноклассниками над предыдущими групповыми проектами. Если вы хотите, чтобы учащиеся сосредоточились больше на продукте, чем на процессе групповой работы, это может быть важной характеристикой. Точно так же, если вы назначаете другой групповой проект позже в этом курсе или ожидаете его в будущем курсе, на который студенты могут записаться, может быть полезно сгруппировать студентов таким образом, чтобы они соответствовали учебным целям текущего проекта и готовили студентов к работе. снова вместе в будущем.
Личность. Склонность учащихся действовать как экстраверты или интроверты имеют отношение к ролям, которые могут быть определены формально или развиваться неформально. Например, ученик-экстраверт может показаться естественным выбором в качестве лидера группы для проведения групповых собраний. Однако ученик-интроверт, ориентированный на детали, также может быть эффективным лидером группы, следя за тем, чтобы другие члены группы соблюдали график. Если одной из целей вашего курса является помощь учащимся в развитии навыков, необходимых для разных ролей, рассмотрите возможность назначения или поощрения учащихся к выбору ролей, в которых у них меньше опыта или навыков.
Склонность учащихся действовать как экстраверты или интроверты имеют отношение к ролям, которые могут быть определены формально или развиваться неформально. Например, ученик-экстраверт может показаться естественным выбором в качестве лидера группы для проведения групповых собраний. Однако ученик-интроверт, ориентированный на детали, также может быть эффективным лидером группы, следя за тем, чтобы другие члены группы соблюдали график. Если одной из целей вашего курса является помощь учащимся в развитии навыков, необходимых для разных ролей, рассмотрите возможность назначения или поощрения учащихся к выбору ролей, в которых у них меньше опыта или навыков.
Вы можете учитывать любую из этих характеристик, а также другие, при составлении групп. Существует также несколько программ (например, CATME), которые помогают преподавателям создавать команды в соответствии с заданными ими критериями.
Определите, кто отвечает за выбор членов группы
Вам также необходимо решить, кто отвечает за выбор членов группы. Эту ответственность можно рассматривать как континуум между группами, выбранными инструктором, и группами, выбранными студентами. Студенты, как правило, любят выбирать членов своей группы, но они часто образуют группы, которые являются однородными, например, с точки зрения пола, специальности, родного языка, культуры и расы/этнической принадлежности. Однако эта однородность может не поддерживать учебные цели проекта.
Эту ответственность можно рассматривать как континуум между группами, выбранными инструктором, и группами, выбранными студентами. Студенты, как правило, любят выбирать членов своей группы, но они часто образуют группы, которые являются однородными, например, с точки зрения пола, специальности, родного языка, культуры и расы/этнической принадлежности. Однако эта однородность может не поддерживать учебные цели проекта.
Если инструктор выбирает членов группы без участия учащегося, инструктор может выбрать группы, которые служат целям обучения проекта, но не предвидят межличностных проблем между членами группы.
В качестве гибридного подхода вы можете позволить учащимся выбирать членов своей группы с определенными ограничениями (например, ни в одной группе не может быть более трех участников или более одного инженера). Вы также можете запросить мнение учащихся, прежде чем создавать группы самостоятельно, например, попросив учащихся заполнить короткую анкету об их компетентности в соответствующих навыках или о наличии межличностных проблем с одноклассниками, которые могут помешать эффективному групповому взаимодействию.
 10. 2013 г.
10. 2013 г. На уроке у нас присутствуют гости — поздоровайтесь с ними (слайд 1).
На уроке у нас присутствуют гости — поздоровайтесь с ними (слайд 1).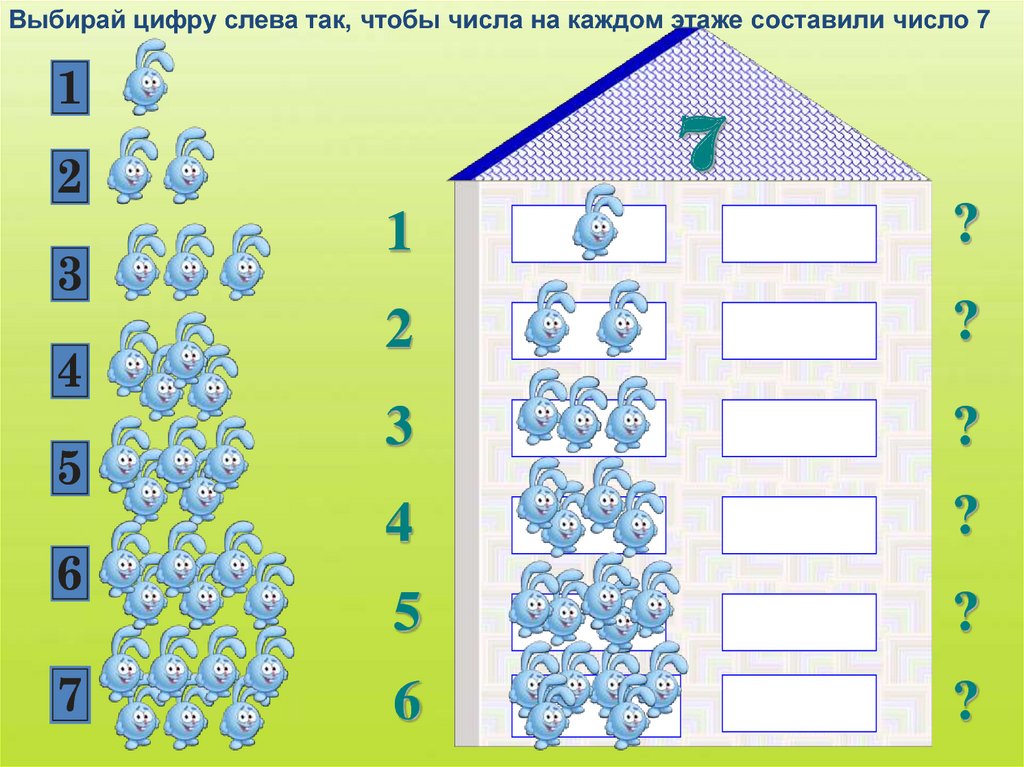 Запишите.
Запишите.

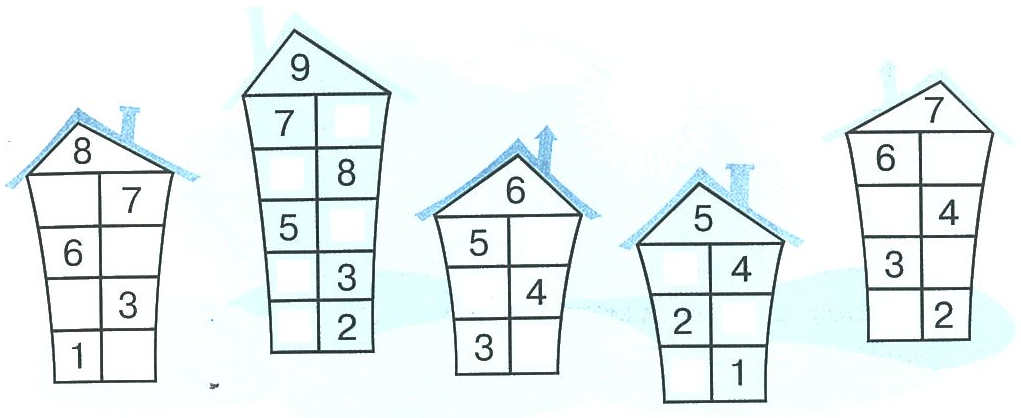
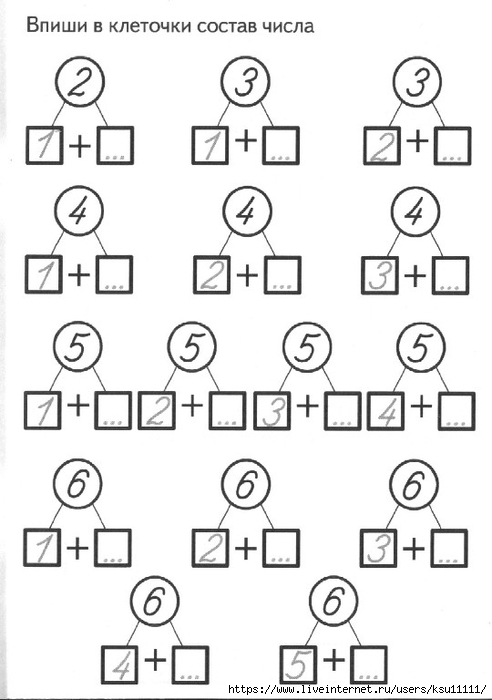
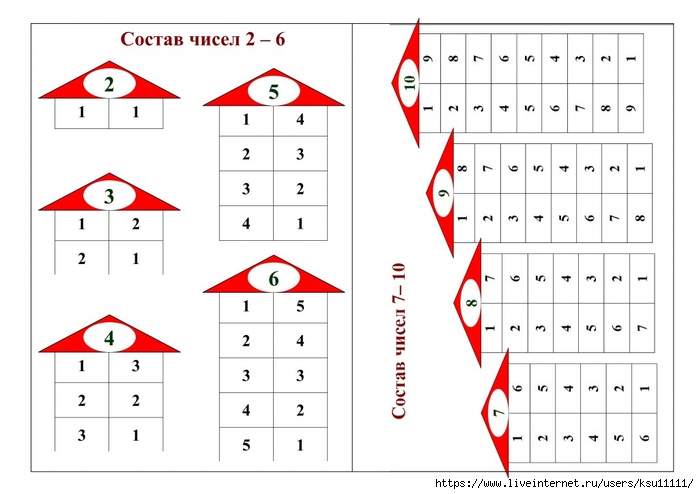 Самостоятельная работа.
Самостоятельная работа.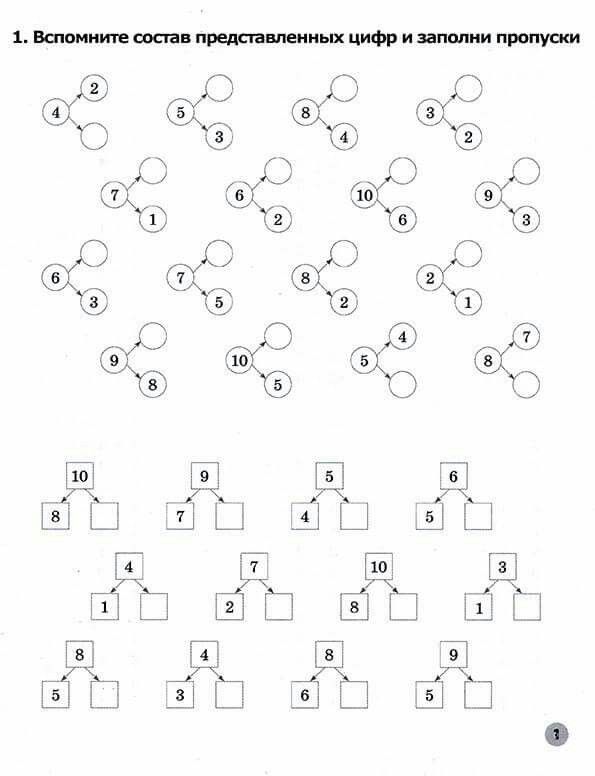


 д.
д.